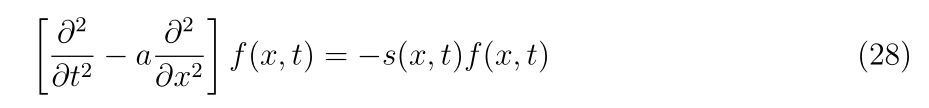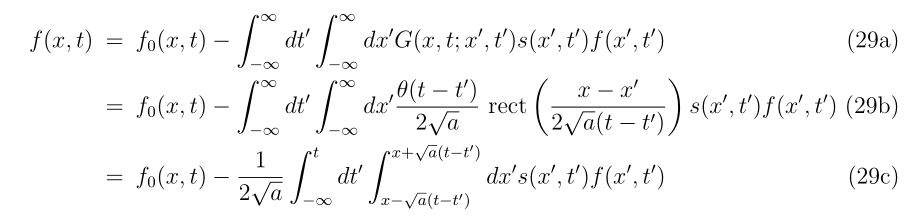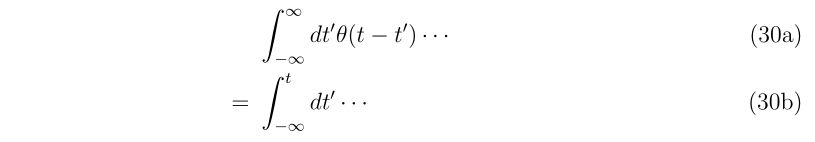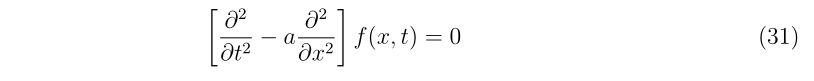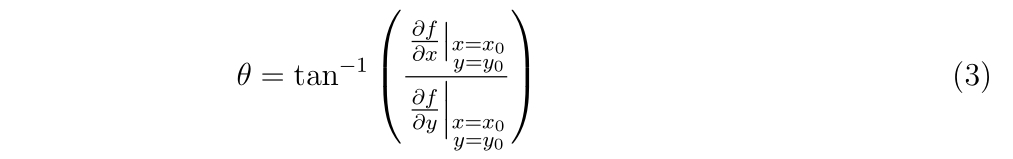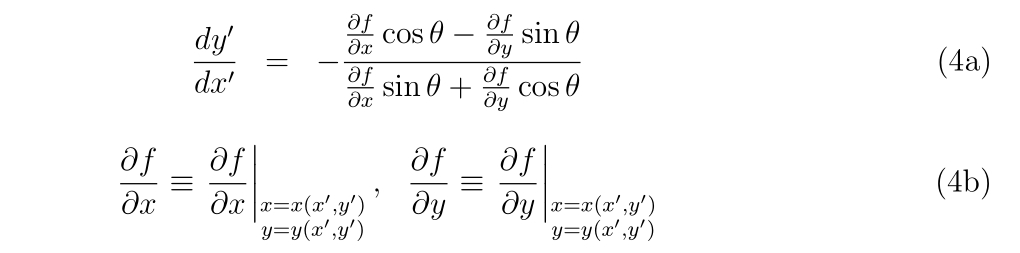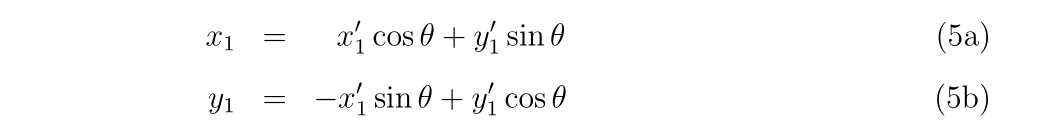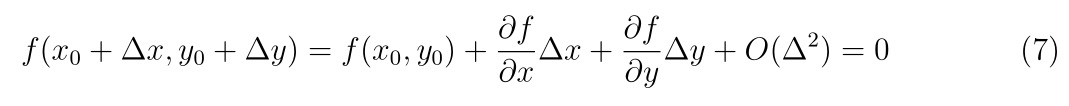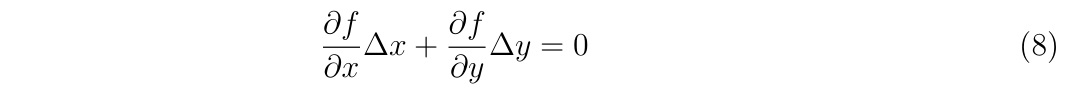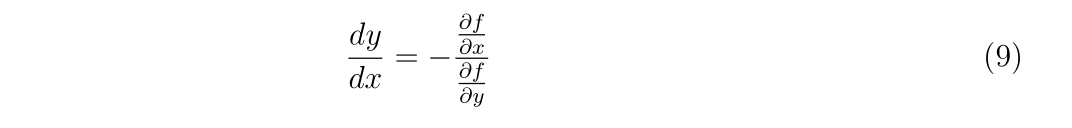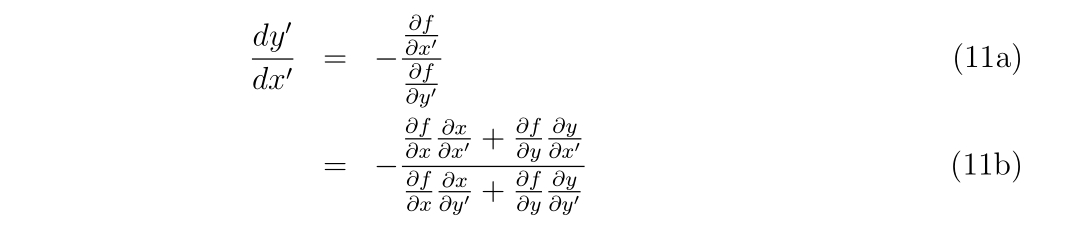sikino のすべての投稿

未分類

Internet Explorerがwindowsアクセサリに見つからない場合

2021年10月3日 sikino コメントする

まとめ

Internet Explorer 11(IE11)はここにありました。

C:\Program Files (x86)\Internet Explorer\iexplore.exe

そもそもIEが自分のパソコンにインストールされているかどうかの確認は、

コントロールパネル → プログラム → windowsの機能の有効化または無効化

より、

☑ Internet Explorer 11

にチェックが入っているかを確認してください。

チェックが入っていれば、PCにそのプログラムはインストールされています。
入っていなければ、チェックを入れ指示に従ってインストールしましょう。

IEが消えた？

推奨ブラウザがIE11であることが現在でもたまにあります。
自分のPCにも入っていると思っていましたが、なぜか検索ボックスに入れても出てこなく、
あるとされているwindowsアクセサリにもありませんでした。
例えば、以下のリンク先のように検索しても出てこなかったんです。

Windows 10 で Internet Explorer を使用する　-Microsoft

　　・WindowsアクセサリにIE11実行ファイルが入っているか？
　　・そもそもPCにInternet Explorerがインストールされているか？
　　・インストールされているなら、実行ファイルはどこにあるか？

の順で調べていきましょう。

まずは、WindowsアクセサリにInternet Explorerの実行ファイルが入るようですので、入っているか調べましょう。

スタートボタン → Windowsアクセサリ

で調べられます。

もしなかったら、そもそもIEが自分のパソコンにインストールされているかどうかの確認します。
これは、

コントロールパネル → プログラム → windowsの機能の有効化または無効化

より、

☑ Internet Explorer 11

にチェックが入っているかで確認することができます。
チェックが入っていれば、PCにそのプログラムはインストールされています。
入っていなければ、チェックを入れ指示に従ってインストールしましょう。

WindowsアクセサリにIE11が無い場合は次の手順でみつけることができます。

WindowsアクセサリにIE11が無い場合

見つからない場合は既定のブラウザを選択して、本当に入っているかを特定、その後ファイルの場所を探しましょう。
IEを見つけるための手順は、
　　

既定のwebブラウザをIEに設定
htmlファイルを開く
タスクマネージャーで起動中のファイルの場所を開く
IEの場所が判明。ショートカットを作るなりする
（既定のwebブラウザを元に戻す）

の通りです。

具体的に説明していきましょう。

既定のwebブラウザをIEに設定

スタートボタン → 設定 → アプリ → 既定のアプリ → Webブラウザー

で既定のアプリを変えてしまいます。なぜかこの画面ではIEが出てきます。

htmlファイルを開く

IEを開くために、メモ帳で「a.html」という名前のファイルを作ります（中身は空白で構いません）。
a.htmlをダブルクリックすると、既定のブラウザ(IE)で開かれます。

タスクマネージャーで起動中のファイルの場所を開く

タスクマネージャーを開き、「詳細」タブから、IEのロゴが表示された項目を右クリックし、「ファイルの場所を開く」を選択します。
すると、エクスプローラーが開きます。

IEの場所が判明。ショートカットを作るなりする

IEの実行ファイルが分かりましたので、ショートカットを作るなりしてください。

最後に、元のブラウザに既定のアプリを戻すことを忘れないようにしましょう。

プログラミングと数値計算

Fortran90で構造体を使う

2021年9月2日 sikino コメントする

Fortran90で自分で型を定義し、それを使用します。
本稿でいう”型”は、一般には構造体と呼ばれます。
Fortran使用者にとっては”型”という名称が分かりやすいでしょう。

整数型、倍精度型などと同列にあるもの、と考えて差し支えないです。

本稿では基本的なことしか書いていません。

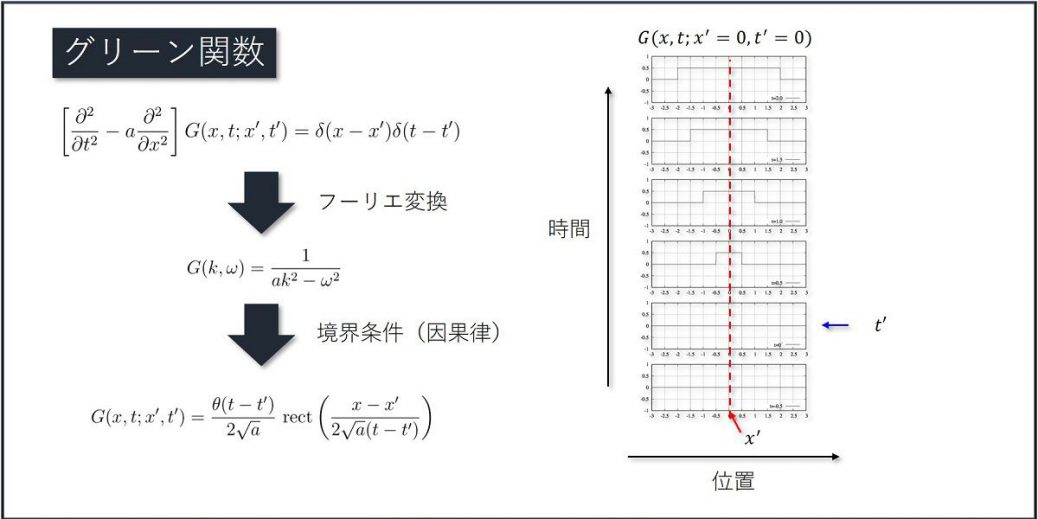
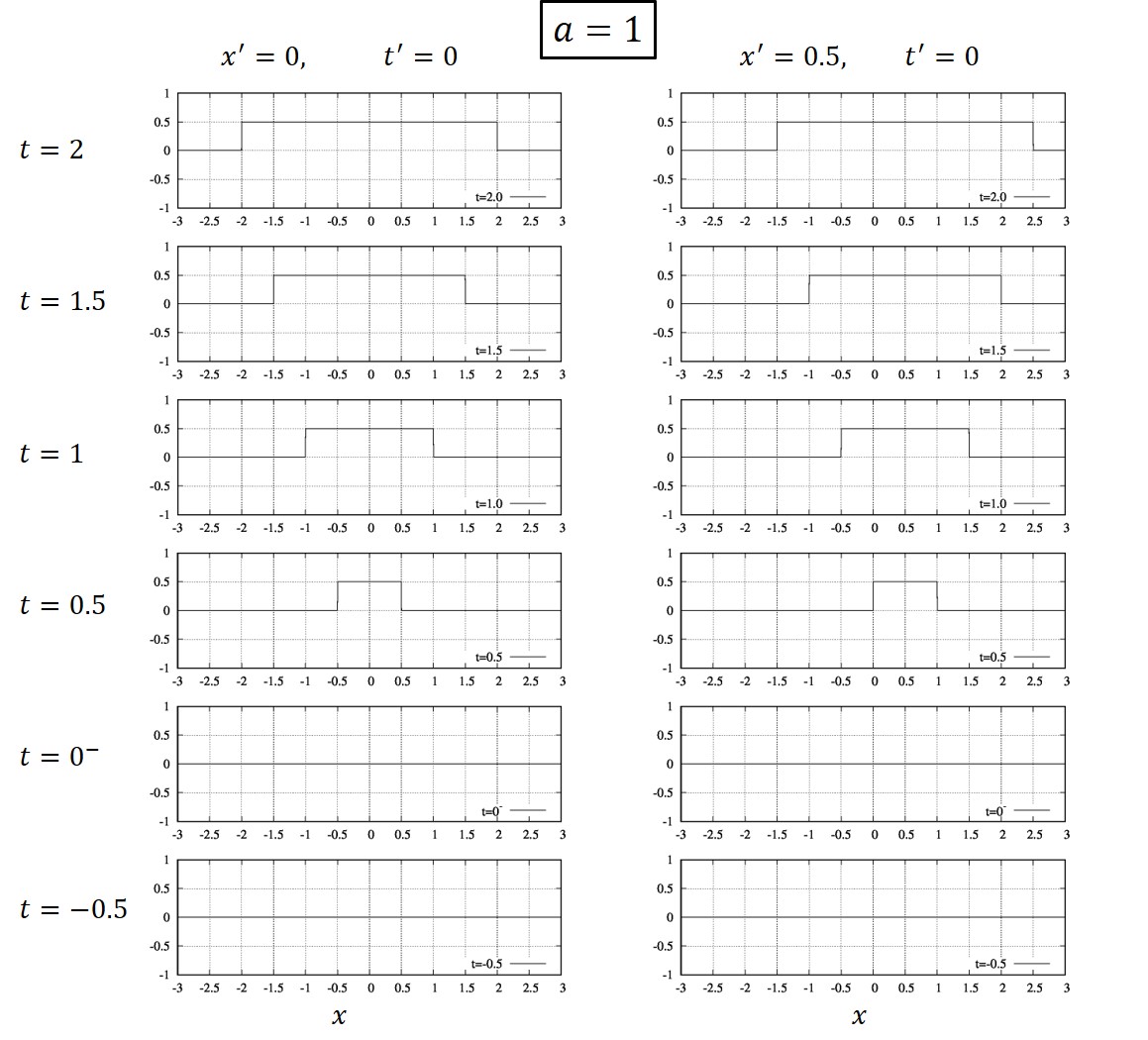
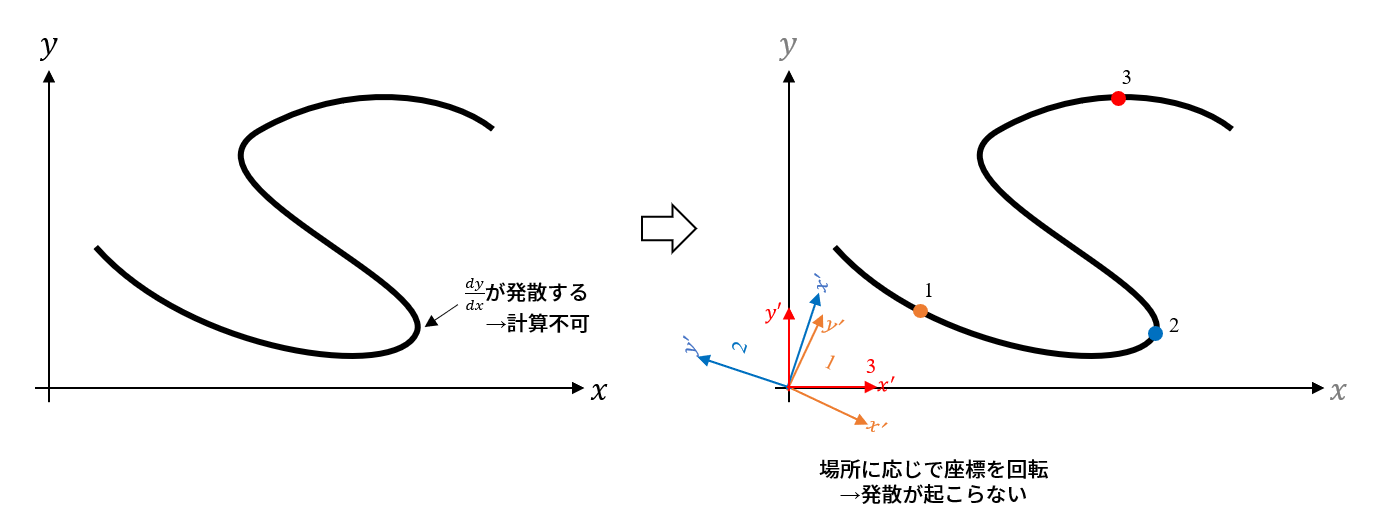
二階偏微分の計算の時でも構造体の考えを使用していますので、もう少し例が欲しい方はこちらもどうぞ。
Hyper-dual numbersによる二階偏微分の計算 -シキノート

概要

簡単な実例


module CEOM_mod

  implicit none

  type Particle

     double precision::m,x,v

  end type Particle

end module CEOM_mod



program main

  use CEOM_mod

  implicit none

  type(Particle)::p1



  p1%m  = 1d0

  p1%x  = 2d0

  p1%v  = 3d0



  write(6,*)p1%m,p1%x,p1%v



  stop

end program main

実行結果

$ ./a.out
1.0000000000000000 2.0000000000000000 3.0000000000000000
$

説明

上は、粒子p1が質量m, 位置x, 速度vを持つ、ということを想定しています。

そこで、Particleという新しい”型”（複素数型みたいに、実部と虚部という２つの独立な変数を１つの複素数型変数が持つ、みたいな変数の型）を定義しました。
Particle型を持つ変数は、すべてm, x, vを内包するというイメージです。

mainプログラムではparticle型が定義されているモジュールを呼び出すために

use CEOM_mod

という文を入れ、実際にparticle型の変数p1を定義するために

type(Particle)::p1

と書いています。変数p1が定義されると自動的にp1が持つm,x,vの固有な値も定義されます。固有の値をいじる場合は

p1%m = 1d0

と書いて、変数に%をつけてm,x,vのいずれかを書いて代入します。

例

配列


module CEOM_mod

  implicit none

  type Particle

     double precision::m,x,v

  end type Particle

end module CEOM_mod



program main

  use CEOM_mod

  implicit none

  integer::i,N

  type(Particle),allocatable::p(:)



  N=5

  allocate(p(1:N))

  do i=1,N

     p(i)%m  = 1d0

     p(i)%x  = dble(i)

     p(i)%v  = 0.1d0*i

  enddo



  do i=1,N

     write(6,*)i,p(i)%m,p(i)%x,p(i)%v

  enddo



  stop

end program main

実行結果

$ ./a.out
1 1.0000000000000000 1.0000000000000000 0.10000000000000001 
2 1.0000000000000000 2.0000000000000000 0.20000000000000001 
3 1.0000000000000000 3.0000000000000000 0.30000000000000004 
4 1.0000000000000000 4.0000000000000000 0.40000000000000002 
5 1.0000000000000000 5.0000000000000000 0.50000000000000000
$

サブルーチンの利用


module CEOM_mod

  implicit none

  type Particle

     double precision::m,x,v

  end type Particle

end module CEOM_mod



subroutine twicemass(N,p)

  use CEOM_mod

  implicit none

  integer,intent(in)::N

  type(Particle),intent(inout)::p(1:N)



  integer::i

  

  do i=1,N

     p(i)%m  = 2 * p(i)%m

  enddo

  

  return

end subroutine twicemass



program main

  use CEOM_mod

  implicit none

  integer::i,N

  type(Particle),allocatable::p(:)



  N=3

  allocate(p(1:N))

  do i=1,N

     p(i)%m  = 1d0

     p(i)%x  = dble(i)

     p(i)%v  = 0.1d0*i

  enddo



  call twicemass(N,p)

  

  do i=1,N

     write(6,*)i,p(i)%m,p(i)%x,p(i)%v

  enddo



  stop

end program main

実行結果

$ ./a.out
1 2.0000000000000000 1.0000000000000000 0.10000000000000001 
2 2.0000000000000000 2.0000000000000000 0.20000000000000001 
3 2.0000000000000000 3.0000000000000000 0.30000000000000004 
$

補足

オブジェクト指向になれている方は、構造体の中身を外部から直接アクセスできる点で褒められた書き方ではないでしょう。
Fortran90にオブジェクト指向の考え方を持ってくるのは、計算速度というFortran90の長所を潰してしまうので、このくらいで良いでしょう。

物理学

クーロンポテンシャルによる散乱（量子力学）

2021年8月18日 sikino コメントする

詳細

本稿では概要だけを説明し、導出過程や詳細は以下のpdfで説明します。
https://slpr.sakura.ne.jp/qp/wp-content/uploads/2021/08/scattering_coulomb.pdf

概要

電荷$q_A$を持つ原子核に、遠方から$q_B$を持つ電子が衝突する過程を考えます。
例えば、水素原子の原子核である陽子1個($q_B=+e$, eは電気素量)に対し、遠方から電子($q_A=-e$)が衝突する過程です。
図で表せばこのような感じです。

相対座標に対する時間依存しないシュレーディンガー方程式は、

と書くことができます。ここで、$\hbar$はプランク定数、$\varepsilon_0$は真空の誘電率、$\mu$はAとBの換算質量を表し, $E$は衝突のエネルギーを表します。
簡単にするために係数をまとめて

と書きます。ここで、

という量を定義しました。
これから、波数$k$で定義される平面波が入射したらどのように応答するか？を知りたいので、式(1)を境界条件

の下で解いていきます。

導出した結果は、

となります。この展開は$|r-z|\to 0$となる$z$軸上もしくはz軸近傍では使えないことを注記しておきます。元々の境界条件(4)は、$z\to -\infty$だけで決まっており$x,y$には条件はありませんが、結論として得られるものは$z$軸からは離れた領域でなければならない、とより制限された範囲でのみ導ける、となっています。

ここで

であり、$\gamma$はSommerfeld parameterと呼ばれる量であり、$\nu=\frac{\hbar k}{\mu}$は２粒子間の相対速度を表しています。また、

はクーロン散乱振幅と呼ばれる量であり、波数$k$を持って入射した平面波が、入射方向に対して角度$\theta$方向にどれだけ球面波が歪むか？を表す量です。

導出過程や詳細は以下のpdfで説明しています。
https://slpr.sakura.ne.jp/qp/wp-content/uploads/2021/08/scattering_coulomb.pdf

本稿では、散乱状態の導出にとどめております。
解釈、流束などについては、次回説明します。

数学, 物理学

古典的な一次元波動方程式のグリーン関数

2021年8月8日 sikino コメントする

本稿のpdfはこちらをどうぞ
https://slpr.sakura.ne.jp/qp/wp-content/uploads/2021/08/Green_1dclassical5.pdf

問題

古典的な一次元波動方程式で、非斉次項を持つ問題

を解くことを考えます。この形は、有限範囲内しか相互作用を引き起こさない物に十分遠方から波が入射してきた場合を考える際に現れたりします。

この形の方程式が出てくる状況を考えてみましょう。

の問題を考えます。移項して

ですので、グリーン関数を用いると

となります。ここで、

を満たす関数（一般解）であり、グリーン関数を
で与えられます。ここを満たす関数（特殊解）としました。
式(4)の右辺に解$f(x,t)$が含まれていますが、このままの形でとどめておきます。この形にしておくと、ほかの式に$f(x,t)$をダイレクトに代入できたり、近似を使うときに便利な形です。

（式（7）はありません）

本稿の目的は、$\hat{D}$が$\hat{D}=\frac{\partial^2}{\partial t^2}-a\frac{\partial^2}{\partial x^2}$で与えられている場合に、$G(x,t; x’,t’)$の具体的な形を導出することです。

導出

今、解きたい問題は、

です。デルタ関数をそのまま扱う場合、積分が絡んでこないと扱うのが難しいです。そうでなければ、フーリエ変換を用いて波数・周波数空間で解いていくのが良いでしょう。グリーン関数や、デルタ関数のフーリエ変換を考えると

となります。ここで、基底関数が$e^{ikx}, e^{-i\omega t}$と符号が異なることに注意しましょう。
また、積分区間はいつも負の無限大から正の無限大であり、いちいち書くのは面倒なので省略しています。
フーリエ変換として考えるのではなく、基底関数へ射影した時の係数と考えましょう。

実際に式(8)に代入すると

となります。

ここで$e^{i[k(x-x’)-\omega(t-t’)]}$はゼロにならないので、その前の項[ ]内がゼロにならなければなりません。よって

が導けます。よって式(9)に代入して

が計算できれば位置と時間のグリーン関数が得られます。

さて、この積分を計算してみましょう。
右辺の$e^{i\omega t}/\omega$の形を持つ積分は複素関数論において頻出する積分です。この積分の特徴として、$\omega$に渡る積分を実軸上で実行する際に、たまたま$\omega=\pm \sqrt{a}k$に等しい点を通ってしまうため、実軸上では被積分関数が発散する、という特徴があります。この発散する点は極と呼ばれており、積分を行う際に積分経路をうまく選んで極を迂回しなければなりません。しかし、厄介なことに極を上に回るか下に回るかで積分結果が変わってしまいます。

もし、天才でしたら当たり前のように適切な積分経路をすぐに思いつくでしょうが、我々凡人には具体的に試してみるくらいしか思いつきません。ですのでちょっとズルしながら因果律を満たす解を探しましょう。

今、我々はグリーン関数について考えています。ということは、計算した結果の境界条件は、因果律を満たすような結果が欲しいわけです。
つまり、グリーン関数が得られた場合、$\theta(t-t’)$の形が出てくるであろうことは予想できます。そのため、これを考慮して極を回る方向を考えてグリーン関数を求めていきましょう。

式(14b)の第一項

について考えます。ヘヴィサイド関数を積分表記で表すと、

と書けることを使います。ここで$i$は虚数単位です。もう嬉しいですね。かなり似通った形であることが分かるでしょう。
式(16)の形に持っていくためには変数変換を行えば良さそうです。つまり、極は上に回れば因果律を満たすグリーン関数が得られそうです。

では具体的に計算していきましょう。変数変換$y=\omega+\sqrt{a}k$を使って、

となります。分母に$+i\varepsilon$を加えるようにして

と求めることができます。

続いて式(14b)の第二項

についても同様に計算していきましょう。変数変換$y=-\omega+\sqrt{a}k$を使って、

ヘヴィサイド関数を考えると、

の形が使えそうです(式(16)の$\omega\to-\omega$の変数変換ですね)。ですので、

と求められます。

式(18c)と式(22c)より、式(14b)に代入すると

となります。

さて、$\frac{\sin x}{x}$の形はsinc関数と呼ばれているほど面白い性質を持つ関数です。そのフーリエ変換は矩形になることが知られています。その計算は実際に
\begin{align}
\int_{-\infty}^{\infty}\frac{\sin(k)}{k}e^{ikx}\frac{dk}{2\pi}=\frac{1}{2}\Bigl[\theta(x+1)-\theta(x-1)\Bigr]
\end{align}
となります。

立ち戻り、変数変換$\kappa=\sqrt{a}k(t-t’)$を考えれば、

と、グリーン関数が求められました。グリーン関数は$x-x’, t-t’$の形をしていることが分かります。そのため、

と書いても良いことが分かるでしょう。ここで、

です。

まとめと補足

まとめ

まとめますと、偏微分方程式

の因果律を満たす解は、

となります。以上から、波動方程式

の因果律を満たす一般解は

となります。

補足

補足します。因果律を満たすグリーン関数である、ということが暗に意味される場合、積分(29a)の時間に渡る積分はグリーン関数に含まれるヘヴィサイド関数を先に利用して、

と積分範囲を組み込んで表記する場合があります。実際の例が式(29c)であり、その時間積分の積分範囲のようになることを見越している、ということです。

少しグリーン関数の物理的な意味を考えてみましょう。
グリーン関数は、ある特定の時刻、ある特定の位置でデルタ関数という非常に特殊な衝撃が生じた結果を記述します。
言い換えれば、偏微分方程式で表されている系が、デルタ関数によってどのような応答を起こすか？という関数です。

式(27b)を見てみると、１つのヘヴィサイド関数$\theta(t-t’)$と１つの矩形関数$\text{rect}\left(\frac{x-x’}{2\sqrt{a}(t-t’)}\right)$が使われています。
$\theta(t-t’)$の部分は、まさに因果律を示しており、衝撃が加わる前の時刻$(t-t’ \lt 0)$においては系の応答は無いよ、ということを表しています。至極全うでしょう。

矩形関数の部分は、衝撃が生じた後にその衝撃は波及する範囲を表しています。具体的に、時刻$t=t’$, 位置$x=x’$において衝撃が生じた場合、矩形関数の中身が値を持つ範囲は$[x’-\sqrt{a}(t-t’), x’+\sqrt{a}(t-t’)]$の範囲です。つまり、衝撃が時々刻々と広がっていることを示しています。グリーン関数を図示すると、このような感じです。

衝撃が加わる$t=0$を境にグリーン関数が値を持ち始め、それが時間とともに広がっていくのが分かると思います。

ついでにグリーン関数の広がる速度を計算してみましょう。

矩形関数の中身が値を持つ範囲$x$は、時間$\Delta t=t-t’$の間に、距離$x-x’=\pm \sqrt{a}(t-t’)$だけ波及しますから、衝撃の結果が速度$\pm\sqrt{a}$で広がっていることが分かります。
これは、古典的な波動方程式でよく知られているように、系の速度が

の系の速度は$\pm\sqrt{a}$である、という事実と一致します。
つまり、衝撃が加わった時刻以外では、系そのものの性質しか存在しませんので、衝撃が波及していく速度が一致することは何ら不思議ではありません。むしろ、一致しなければなりません。

数学, 物理学

デルタ関数、ヘヴィサイド関数に関係する数式

2021年8月8日 sikino コメントする

本稿のpdfはこちら
https://slpr.sakura.ne.jp/qp/wp-content/uploads/2021/08/Green_related_functions1.pdf

定義

ヘヴィサイド関数

符号関数

矩形関数

デルタ関数

デルタ関数$\delta(x)$は、

を満たす関数です。この定義式を満たす場合、デルタ関数は以下の性質を持つことが分かります。

フーリエ関数

性質、関係式

積分表示

定積分が関係する場合

デルタ関数

ヘヴィサイド関数

sinc関数に関係する式

畳み込み積分

数学, 物理学

位相速度、群速度とは！？調べてみました！！(パロディ)

2021年6月13日 sikino コメントする

近頃SNSやインターネットでよく見る言葉、「位相速度」「群速度」。

元ネタや原理を分かった気になって使っている方、多いのではないでしょうか。
せっかくなので調べてみました！！！

（数式で殴りに殴ったものを以下のページに書きました。真面目に詳細を知りたい方はこちらをどうぞ。）
https://slpr.sakura.ne.jp/qp/group-phase-velocity-delay/

そもそも「位相速度」「群速度」って何？
学会騒然。ある波数近傍だけ値を持つ場合にテーラー展開!?
位相速度はどうやって!?驚きの仮定
簡単だと思いました？注意です！
いろいろなところに群速度に関する議論が！
最後に
Note

そもそも「位相速度」「群速度」って何？

なにはともあれwikipedia!!
関連するキーワードをササッと知るには強い味方です。
「位相速度」「群速度」を調べるとこのように説明されていました。

群速度（ぐんそくど、英: group velocity）とは、複数の波を重ね合わせた時にその全体（波束）が移動する速度のことである。

群速度　-wikipedia

位相速度（いそうそくど、英語: phase velocity）は、位相、すなわち波の山や谷の特定の位置が移動する速度のことである。

位相速度　-wikipedia

どうやら、波束や波の速度を表現する際に都合が良い言葉なようです。

波束とは何なのでしょう…？また変な言葉が出てきました。wikipediaの出番です！！

波束（はそく、英: wave packet, wave train）は、局所的に存在する波うち/波動であり、移動する1個の波動の塊のようにふるまう。

波束 -wikipedia

うーん、つまり一回だけ波打って、ある程度まとまった波みたいなものですかね。
水面に水が一滴だけ落ちたときに発生する波みたいなものでしょう。

具体的にどういう意味なのでしょうか。気になりますよね！

皆さんも群速度、位相速度の導出が気になったら「tweet」、お願いします！

学会騒然。ある波数近傍だけ値を持つ場合にテーラー展開!?

角周波数が波数の関数として書けている場合、分散関係があるといいます。
つまり、角周波数$\omega$が波数$k$に依存して$\omega=\omega(k)$と書けている場合、波形のほとんどは

とように書けます！！
本来、位置$x$と時間$t$で書ける関数は、$k$と$w$の二重積分で表現されなければなりませんが、分散関係のおかげで$\omega$が強制的に決まってしまうので、一重積分で良くなるのですね！
うーん、とても嬉しい！！！！

…でも、あまりに一般的過ぎて分かりませんね。
しかし！！
応用で重要なのは、ゆっくり振動する包絡線と早く振動する波の掛け算で表されていることが多いのです。

つまり、これから考える波が持つ波数は、$k= k_0$の周りしか値を持たないのです。ここで、早く振動する波の波数を$k_0$と置きました。

$k_0=5$の場合、これから考えていく$f(k)$はこんな感じの特徴を持っています！ババン！

こんな特徴を持つのならば、$k=k_0$以外ではどうせ$f(k)\to 0$となるので、考えてもしょうがないっていう近似が使えそうですよね。

そ　こ　で　！

波数$k=k_0$周りでいろいろテーラー展開して使用していきます。つまり、$k=k_0$の近傍さえ合っていれば、$k_0$以外でどんな振る舞いになろうとも$f(k)$がゼロになるので大丈夫でしょう！ということです。

早速、分散関係についてテーラー展開を行うと

となります。式を簡単に書くために$\omega'(k_0)\equiv \frac{d\omega}{dk}\bigr|_{k=k_0}$と置きました。

計算を進めると、

より、

のように書けます。つまり、式(4)が言っていることは、
時刻$t$の波形とは、初期状態$t = 0$の波形 $f(x,0)$を$\omega'(k_0)t$だけ平行移動させた波に、時間だけに依存する位相に関する変化分 $e^{−i[\omega(k_0)−k_0 \omega'(k_0)]t}$が掛け合わされたもの、と表すことができる。と言っています。

以上から、初期状態の波が時刻$t$に至るまでの速度は$\omega'(k_0)$で決まることが分かり、これは
群速度
と呼ばれます！！

位相速度はどうやって!?驚きの仮定

さて、ここまでで群速度が求まりましたが、位相速度が求められていません。
そこで、もう少し具体的な波の形を定義しましょう。
波が、

と書けている場合を想定します。ここで、振幅$A(x,t)$は実数値関数で波の包絡線を表しています。また$A(x,t)$の変化は $k_0$ に比べて非常にゆっくり変化しているものとします。
つまり、

今まで考えてきた仮定が全部使える

んですね！

式(5)に代入しますと

となります。つまり、振幅の変化はいつも初期状態の単なる平行移動として表現することができ、位相の変化も簡単に表せられます。

そこで、振幅が平行移動する速度を群速度$v_g$、位相が平行移動していく速度を位相速度 $v_p$ として定義すると、式(6c) よりそれぞれ

と定義してしまうのが良さそうです！

簡単だと思いました？注意です！

注意しなければならないのは、群速度と位相速度の概念は、

振幅と位相を記述する部分がはっきりと区別できるような状況でなければ、定義できない

ということです！振幅部が早く振動していたら、これまでの議論が使えなくなることに注意しましょう。
その場合、群速度と位相速度の概念が変わってしまうので、意味をなさなくなってしまいます。

いろいろなところに群速度に関する議論が！

様々なところにリンクがあります。やはり皆、群速度の概念を理解するのに苦労しているようですね。

「yam＠広島大」物理化学Monographシリーズ　”3. 物体の速度と物質波の速度　－E=hνの本質の理解－”

最後に

いかがでしたか？気に入ったなら是非、記事の下にある「like!」ボタンや「tweet」して皆さんに共有して下さいね!
それでは皆さん、良い物理ライフを!

Note

本記事の大枠の構成はいかがでしたか?　-ニコニコ大百科を参照しています。

Q氏とR博士

負の周波数とは何か

2021年5月30日 sikino コメントする

三角関数で負の周波数はいらない。
負の周波数という言葉が出てくるならば、それは指数関数で表現されていることを暗に意味する。

Q氏とR博士の会話１

Q「負の周波数というものがあると聞きました」
Q「周波数は正ではないのでしょうか」

R「それは”周波数”の意味が違うのだな」
R「詳しくは基底関数だ。正の時と負の時とで、基底関数が違う」

Q「意味が分かりません。もう少し詳しくお願いします」

R「そうだな」
R「別の言い方をすれば、”周波数”と言ったときに、大きく２つの周波数があるのだ」
R「１つはsin, cosの三角関数の周波数、もう１つはexpの指数関数の周波数だ」
R「この説明でどうかな」

Q「周波数は周波数でしょう。関数で意味が変わるのでしょうか。意図がつかめません。もう少しお願いします」

R「素直でよろしい。その通り、周波数の意味は関数によって変わるのだ」
R「具体的に考えよう。周波数を引数に持つ関数を考えてみようか」
R「わたしが、『時間tに依存する周波数f=1を持つ関数yを考える』と言ったら、君はどういう関数yを想像するかな」

Q「三角関数ですね。$y=\sin(2\pi t)$を想像します」

R「そうだ。そこが負の周波数が受け入れられない原因なのだ」
R「私は$y=\exp(i2\pi t)$という指数関数を想定して周波数f=1と伝えた」
R「しかし君は勝手に三角関数の周波数として理解してしまった、理解できてしまった」
R「三角関数の周波数ならば、その周波数は正の周波数しかありえない」（数式による補足）
R「なぜなら、三角関数の周波数が負になったところで、それは正の周波数を持つ波の定数倍で表現できてしまうからだ」
R「つまり、$\sin(-t)=-\sin(t)$だからな。負の周波数は不要だ。」

Q「なるほど」

R「負の周波数という言葉は指数関数を考えていることを暗に示している」
R「指数関数の場合、$\exp(-it)$を$\exp(it)$を使って表現することができないのだ」
R「だから負の周波数が絶対に必要になる」

Q「問題文の説明不足が原因でしたか。理解できました」

Q氏とR博士の会話２

Q「周波数の成分が少なく済む三角関数の方が便利ではないですか」
Q「負を考える必要がないのでしょう」

R「１つ、伝えていなかったな。どちらも同じ程度の便利さだ。」
R「先ほどsinの正の周波数だけで表現できるとしたが、実はこれでは不十分なのだ」
R「ある関数を三角関数で表すならば、必ずsin, cosの両方を用いなければならない」
R「つまりsin関数の周波数ゼロから正の無限大、cos関数の周波数ゼロから正の無限大の二つを用いる関数だ」
R「反対にexp関数を使う表現方法ならば、周波数は負の無限大から正の無限大の一つを用いる関数だ」
R「”周波数”にも”sin関数の周波数”、”cos関数の周波数”、”exp関数の周波数”の３つがあるわけだ」
R「指数関数ならば１つの関数系(exp)で済むから、その意味で簡単だ。しかし、負の周波数が出てきたり、複素関数として扱わなければならなくなる。」
R「三角関数ならば２つの関数系(sin, cos)を用いなければならない。どちらの周波数を考えているかいちいち説明しなければならないが、実部だけで話ができる利点がある。」

Q「なるほど。理解しました」
Q「どちらも場合によるのですね」
Q「フーリエ変換を考えたい場合は指数関数の方がよさそうですね」

R「その通り。まぁ、指数関数による表現がまさにフーリエ変換だがな」
R「ちなみに、基底関数という言葉は、ここでいう三角関数や指数関数のことだ」
R「どういう関数で展開したか？の”どういう関数”が基底関数と呼ばれる」

数式による補足

任意の関数$y(x)$を表現する場合、振動関数であるsin, cosまたはexpを考えます。
任意の関数を適当な関数系で表現するためには、その関数系が完全系であることが求められます。
つまり、三角関数を用いる場合、
$\displaystyle
y(x)=\int_0^{\infty} A(f) \sin(2\pi f x) df+\int_0^{\infty} B(f) \cos(2\pi f x) df
$
として表現できます。反対に、指数関数を用いるならば、
$\displaystyle
y(x)=\int_{-\infty}^{\infty} C(f) e^{i2\pi f x} df
$
と書かなければなりません。
つまり、負の周波数という言葉は指数関数が現れる場合にしかあり得ないのです。

もちろん、積分の変数変換によってsin, もしくはcos関数の周波数を負の無限大からゼロなどに変更することが可能ですが、こんなことをわざわざやる必要性、あり得ますかね。

私が昔見たことがある説明で
$\displaystyle
\begin{align}
y(x)&=\cos(\omega x) \\
&=\frac{1}{2}\cos(\omega x)+\frac{1}{2}\cos(-\omega x)
\end{align}
$
と変形できるから正の周波数と負の周波数になる、というものを見たことがありますが、これは完全に間違いを誘発させるための説明です。

なぜなら、$\cos$の係数に任意性があるためで
$\displaystyle
\begin{align}
y(x)&=\cos(\omega x) \\
&=100\cos(\omega x)-99\cos(-\omega x)
\end{align}
$
としても全く問題ないからです。三角関数の引数が負であるものと正であるものは独立ではないのです。

未分類

割り勘のお金のやりとりを表示する計算ツール

2021年5月22日 sikino コメントする

数人で旅行を行う際に、代表者がまとまって支払うことが多々あると思います。
旅行終了後に割り勘をする場合に計算が大変になりがちです。
その場合にスマホでも使える計算ツールを実装しました。

旅費計算ツール
https://slpr.sakura.ne.jp/qp/calc/splitcheck/split.html

発展版
https://slpr.sakura.ne.jp/qp/calc/splitcheck/split_v1.1.html
https://slpr.sakura.ne.jp/qp/calc/splitcheck/split_v1.2.html

例えば4人(A,B,C,Dさん)の旅行を考えます。グループとして支払った額を以下のように仮定します。
・旅館代としてAさんが4人分を3万円まとめて払ったとします。
・ご飯台としてBさんが4人分を1万円まとめて払ったとします。
・車台としてCさんが4人分を7000円まとめて払ったとします。
・Dさんは支払いをしていません。

旅行が終わった際に旅行全体で割り勘したいと考えたとき、計算とお金のやり取りをどうすればいいか悩みます。
少ないお金のやり取りで済ませたいですよね。そのためのツールがこれです。

人数を入れ、支払い額を入力し実行しますと結果が出ます。