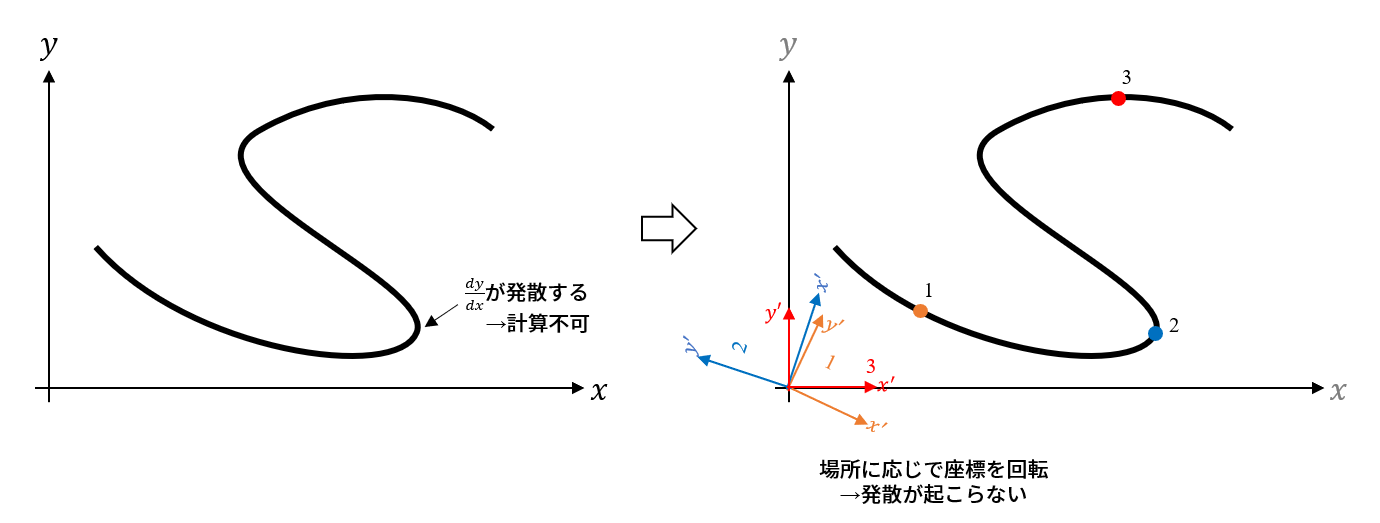
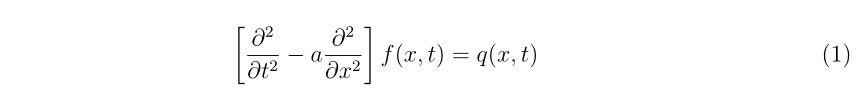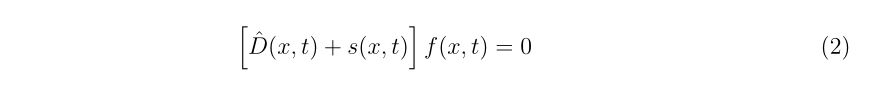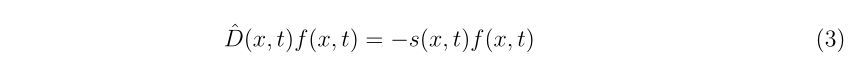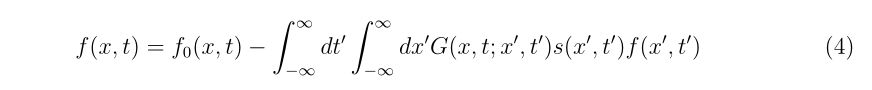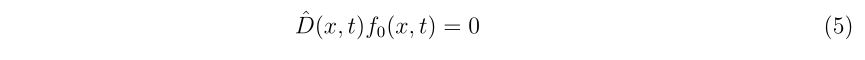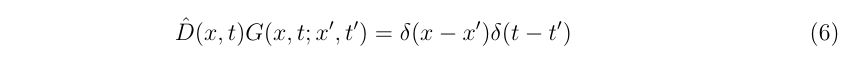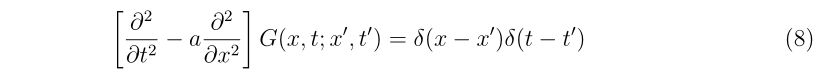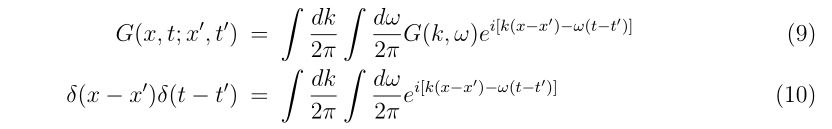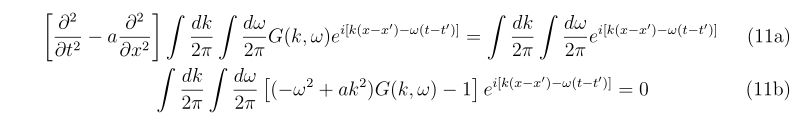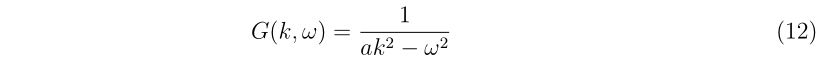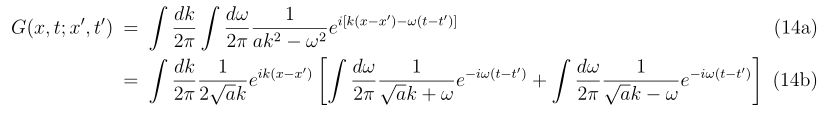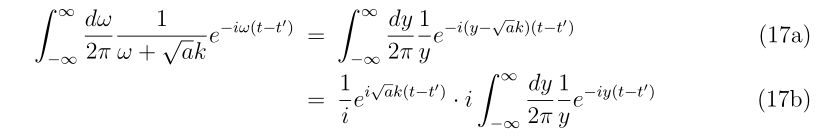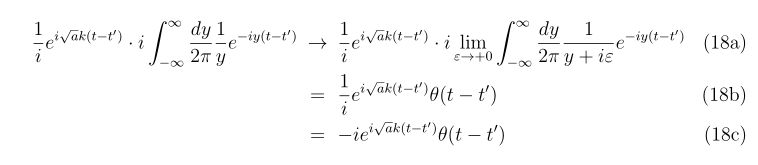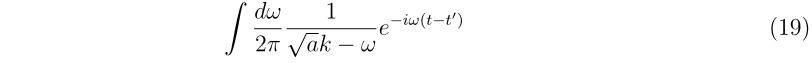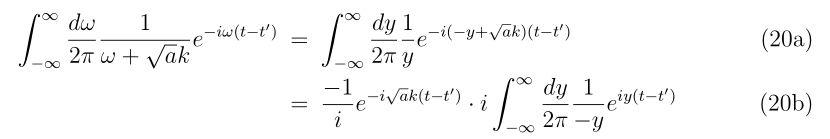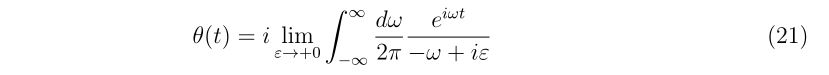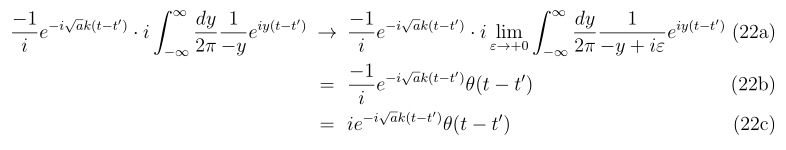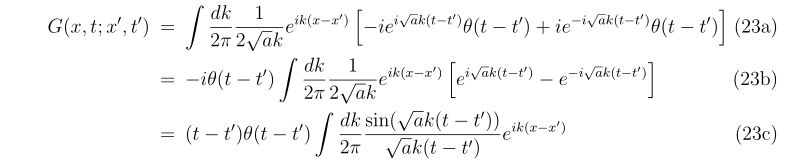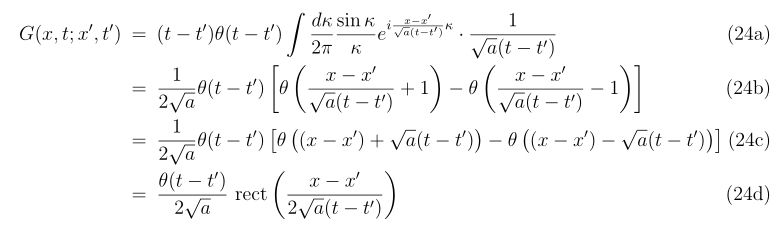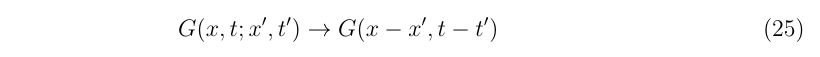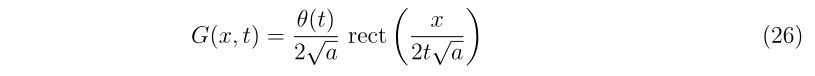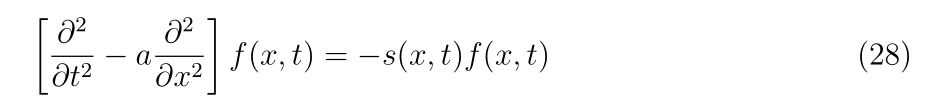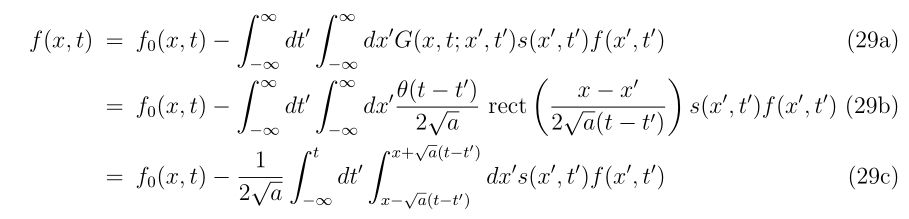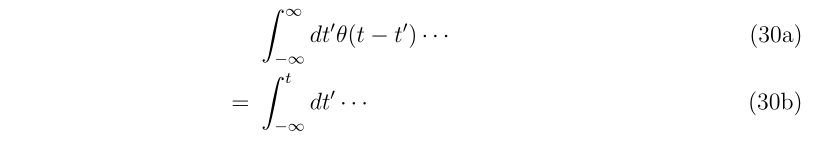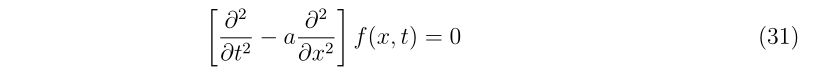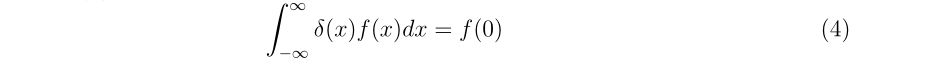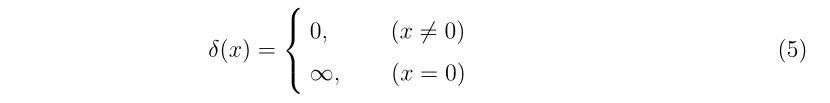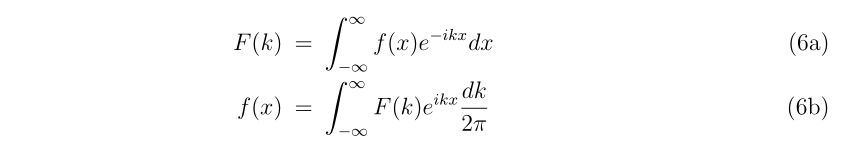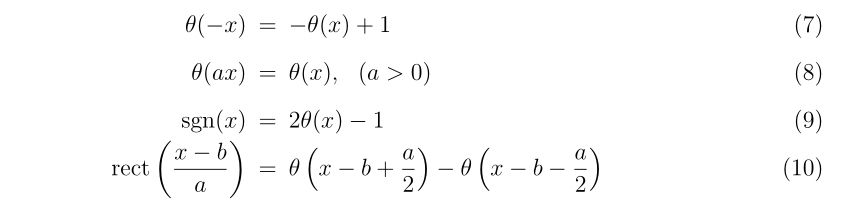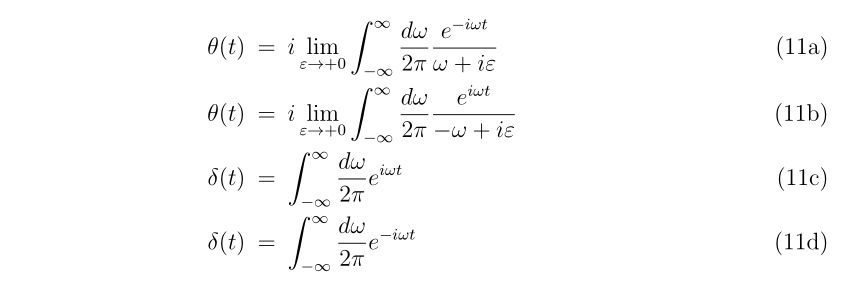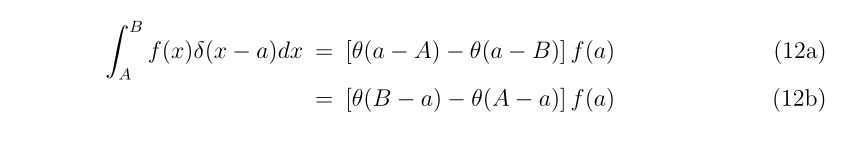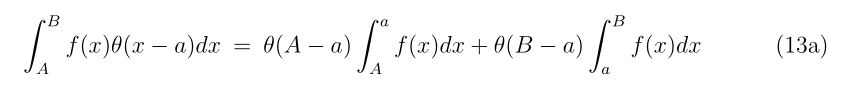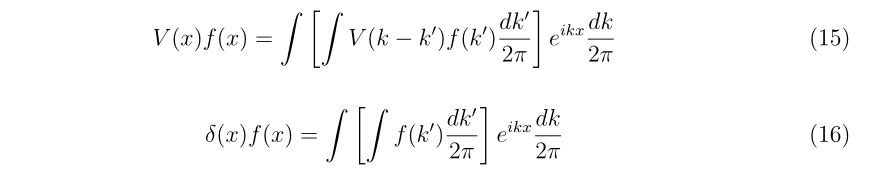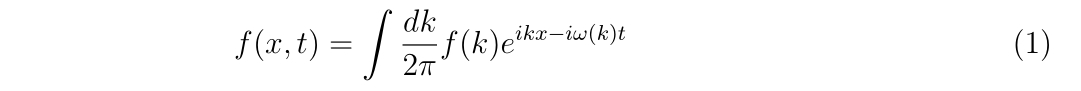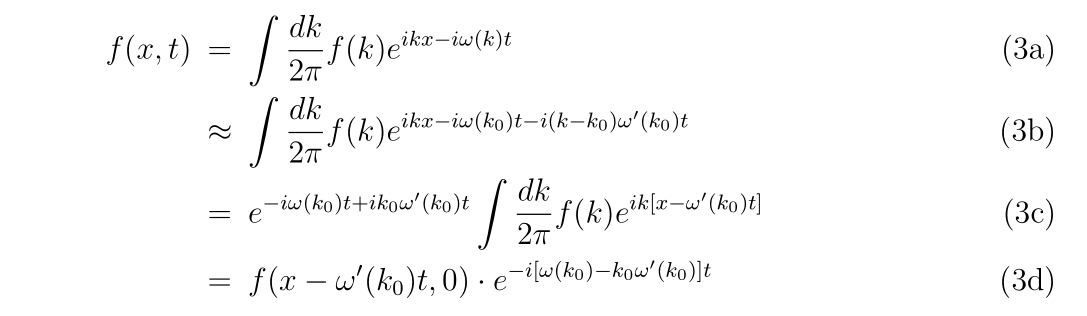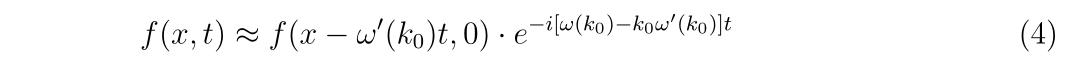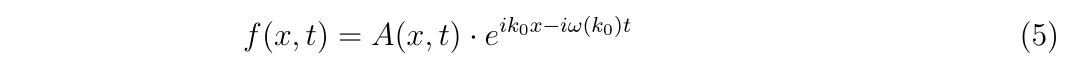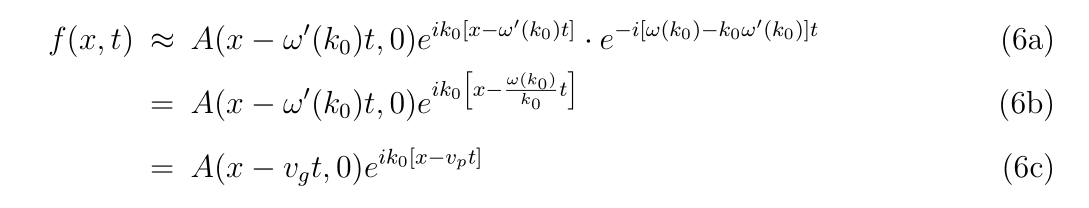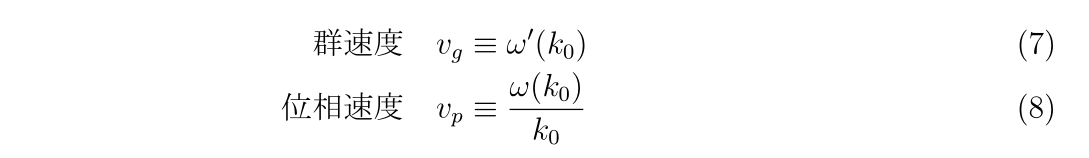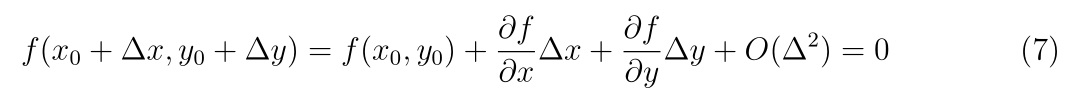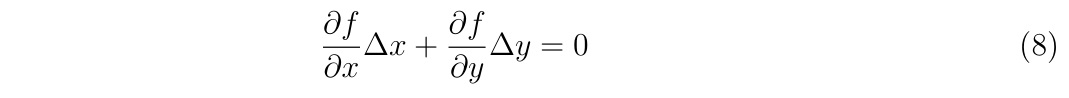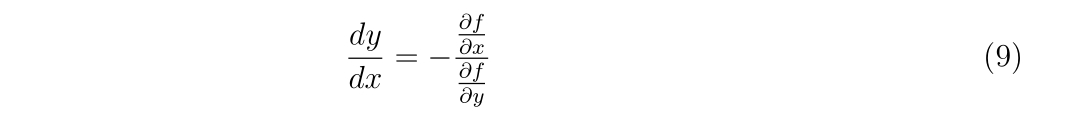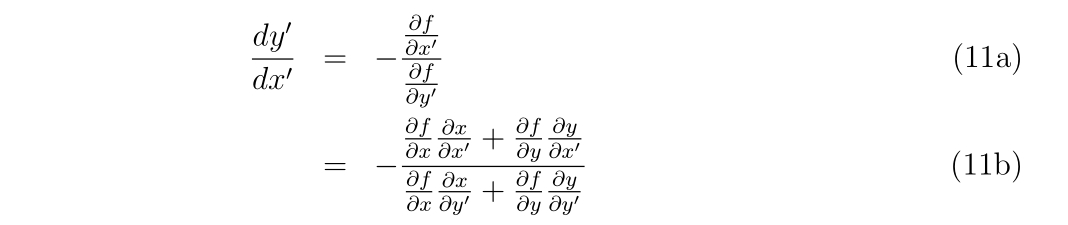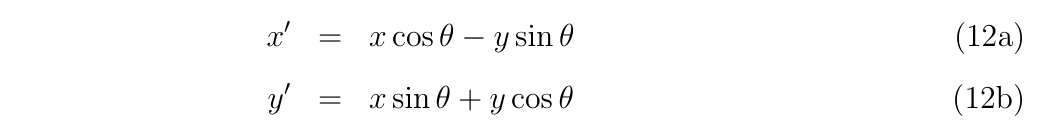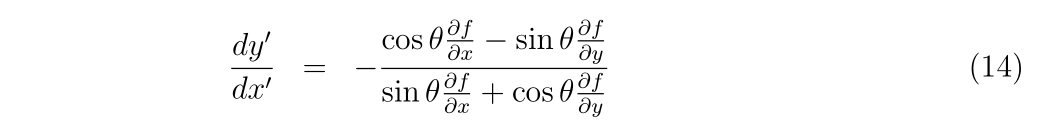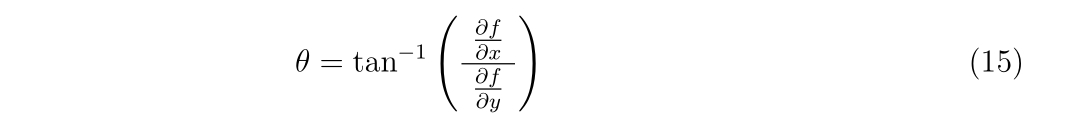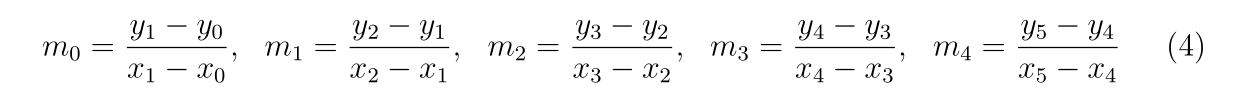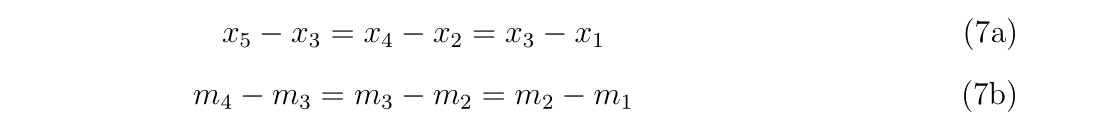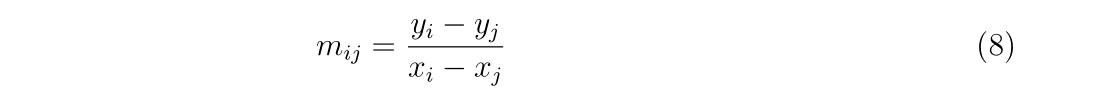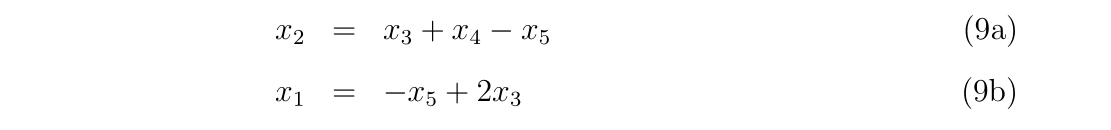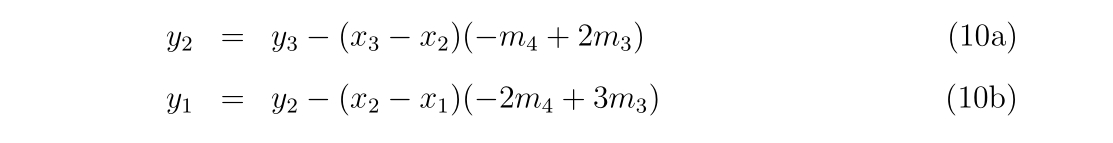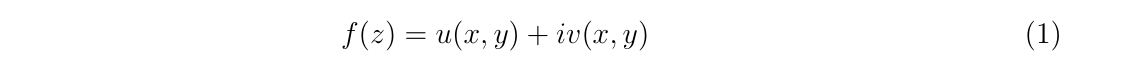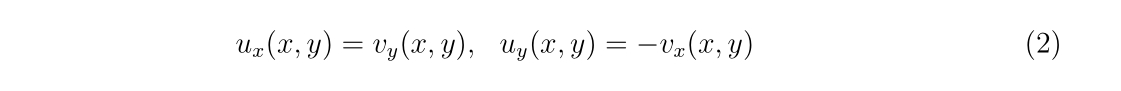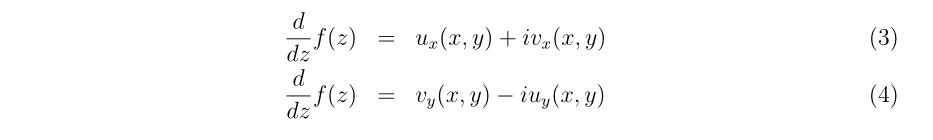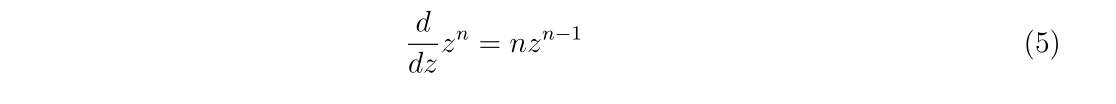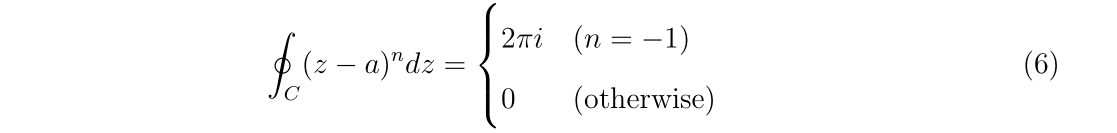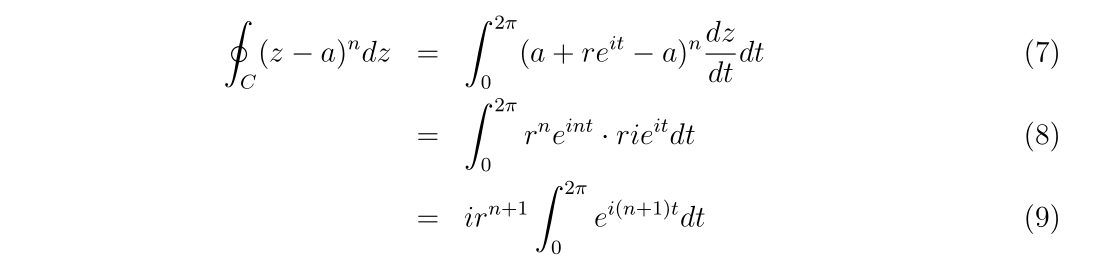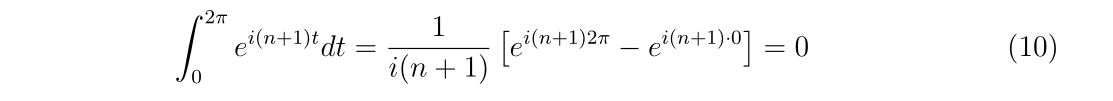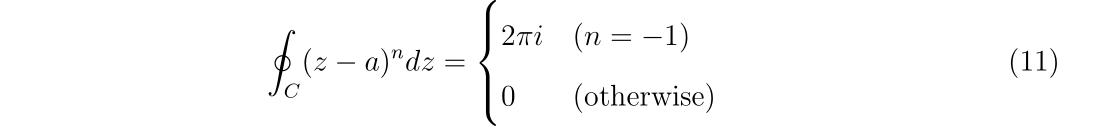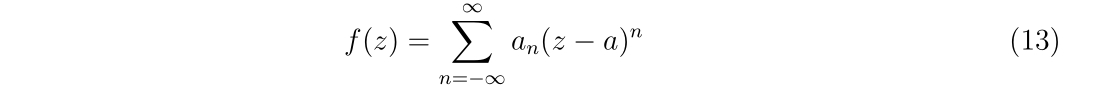ニュートン法に関するお話です。
”ニュートン法”と呼ばれる方法は
2種類(1.初期値近傍の極小値を求めるニュートン法、2. ゼロ点を求めるためのニュートン法)
があるようですが、ここでは2. 関数のゼロ点を求める方のニュートン法についてのお話です。
- まとめ
- 1次元のニュートン法
- 初期値の推定
- 導関数の近似
- 1次元ニュートン法のプログラム
- 2次元ニュートン法
- 2次元ニュートン法のプログラム
- 多次元ニュートン法
- 多次元ニュートン法のプログラム
- 高次のニュートン法?
- 補)ニュートン法が使われる問題
- 参考文献
まとめ
1次元の場合
\(\displaystyle
x_{n+1}=x_{n}-\frac{f(x_{n})}{f'(x_{n})},~~n=0,1,2\cdots,
\)
ここで、\(x_0\)は解の近傍であること。
2次元の場合
\(
\begin{align}
\left(
\begin{array}{c}
x_{n+1} \\
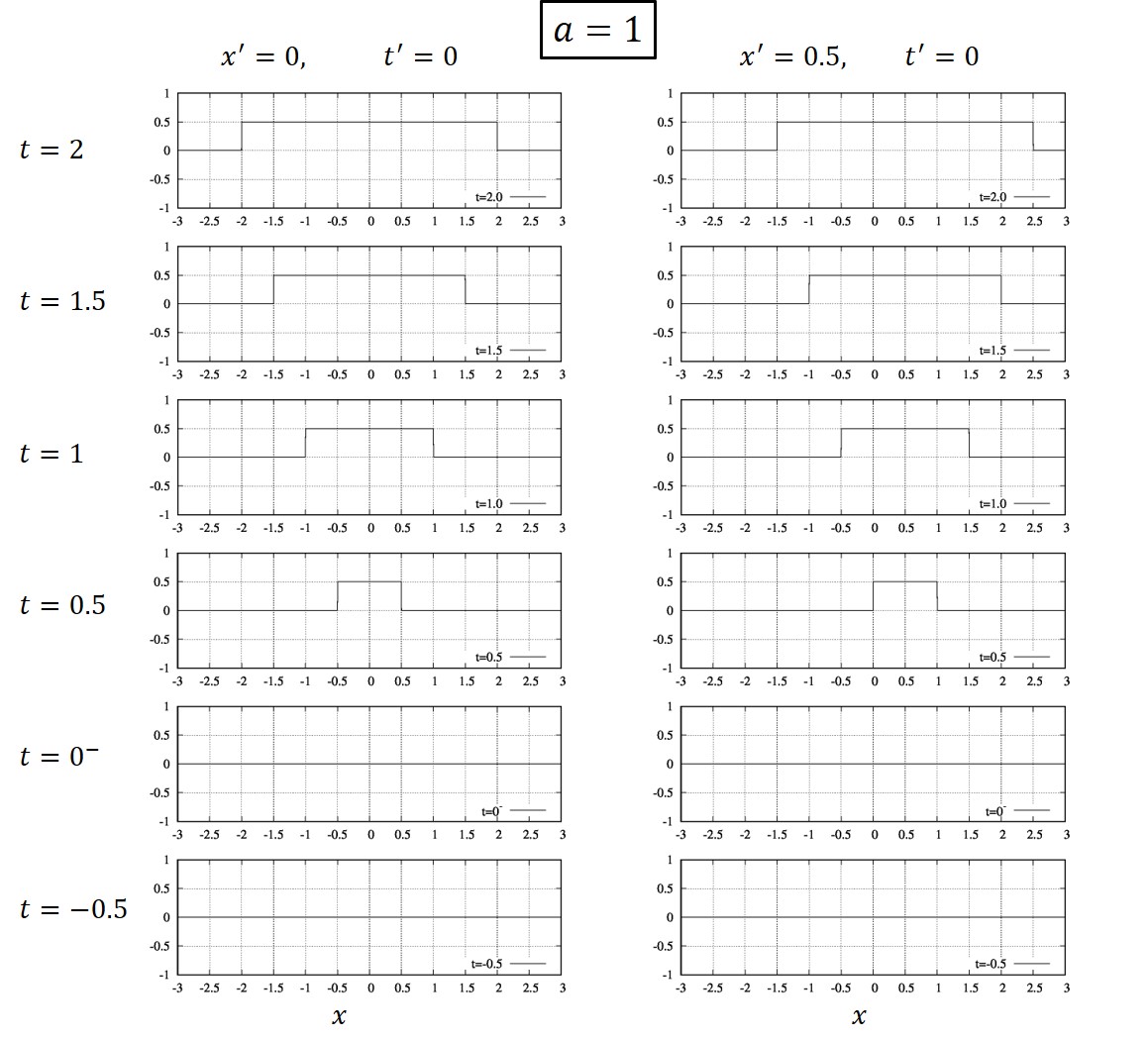
y_{n+1}
\end{array}
\right)
=
\left(
\begin{array}{c}
x_n \\
y_n
\end{array}
\right)
-\left(
\begin{array}{cc}
f_x(x_n,y_n) & f_y(x_n,y_n) \\
g_x(x_n,y_n) & g_y(x_n,y_n)
\end{array}
\right)^{-1}
\left(
\begin{array}{c}
f(x_n,y_n) \\
g(x_n,y_n)
\end{array}
\right)
\end{align}
\)
\(
\begin{align}
&\left(
\begin{array}{cc}
f_x(x_n,y_n) & f_y(x_n,y_n) \\
g_x(x_n,y_n) & g_y(x_n,y_n)
\end{array}
\right)^{-1} \\
&~~~~=
\frac{1}{f_x(x_n,y_n) g_y(x_n,y_n)-f_y(x_n,y_n)g_x(x_n,y_n)}
\left(
\begin{array}{cc}
g_y(x_n,y_n) & -f_y(x_n,y_n) \\
-g_x(x_n,y_n) & f_x(x_n,y_n)
\end{array}
\right)
\end{align}
\)
ここで、
\(
\begin{align}
f_x(x_n,y_n) &= \left.\frac{\partial f(x,y)}{\partial x}\right|_{x=x_n,~y=y_n} ,~~& f_y(x_n,y_n) = \left.\frac{\partial f(x,y)}{\partial y}\right|_{x=x_n,~y=y_n} \\
g_x(x_n,y_n) &= \left.\frac{\partial g(x,y)}{\partial x}\right|_{x=x_n,~y=y_n} ,~~& g_y(x_n,y_n) = \left.\frac{\partial g(x,y)}{\partial y}\right|_{x=x_n,~y=y_n}
\end{align}
\)
多次元の場合
\(
\mathbf{x}_{n+1}=\mathbf{x}_{n} – \mathbf{J}_n^{-1}\mathbf{f}_n
\)
ここで、
\(
\begin{align}
\mathbf{x}_n=
\left(
\begin{array}{c}
x_1\\
x_2\\
\vdots \\
x_N
\end{array}
\right)_n
,~~
\mathbf{f}_n=
\left(
\begin{array}{c}
f_1(\mathbf{x}_n)\\
f_2(\mathbf{x}_n)\\
\vdots \\
f_N(\mathbf{x}_n)
\end{array}
\right)
,~~
\mathbf{J}_n=
\left.\left(
\begin{array}{cccc}
\frac{\partial f_1}{\partial x_1} & \frac{\partial f_1}{\partial x_2} & \cdots & \frac{\partial f_1}{\partial x_N} \\
\frac{\partial f_2}{\partial x_1} & \frac{\partial f_2}{\partial x_2} & \cdots & \frac{\partial f_2}{\partial x_N} \\
\vdots&\vdots&\ddots&\vdots \\
\frac{\partial f_N}{\partial x_1} & \frac{\partial f_N}{\partial x_2} & \cdots &\frac{\partial f_N}{\partial x_N}
\end{array}
\right)\right|_{\mathbf{x}=\mathbf{x}_n}
\end{align}
\)
※\((~~)_n\)の添え字nはn回目の繰り返しにおけるベクトル\(\mathbf{x}\)を表しています。
[adsense1]
ここから本文
1次元のニュートン法
方程式
\(
f(x)=0
\)
を満たす\(x=a\)を求めることを考えます。
まず、この問題をグラフ
\(
y=f(x)
\)
のゼロ点(\(y=0\)となるような\(x=a\))を探す問題だ、という問いに置き換えます。
これを、解近傍で関数をテーラー展開で表し、その展開式のゼロ点を探すことで解を近似することで方程式を解きます。
関数\(f(x)\)が与えられたとき、任意の点\(x’\)周りにおけるテーラー展開は、
\(
f(x) = f(x’)+f'(x’)(x-x’) + O(\Delta^2),~~\Delta=|x-x’|
\)
と書くことが出来ます。もしも\(x\)と\(x’\)が近接していれば、\(\delta=|x-x’| \ll 1\)となるので、\(\Delta^2\)の項は無視できるほど小さくなると期待します。
さて、この式を導く際に用いた条件は、\(x\)と\(x’\)が近くにある、という条件のみです。なので、求めたい解\(a\)と\(a\)の近くの適当な点\(x_0\)を用いれば、
\(
\begin{align}
f(a) &= f(x_0)+f'(x_0)(a-x_0) +O(\Delta^2)~~~…(1)\\
f(x_0) &= f(a)+f'(a)(x_0-a) +O(\Delta^2) ~~~…(2)
\end{align}
\)
の2通りの式を考えることが出来ます。(2)に含まれる\(f'(a)\)は本当の\(a\)が分からないと評価するのが難しいので、(1)を選びます。
(1)の左辺は条件よりゼロです。残りの右辺の\(a\)について解けば、
\(
\begin{align}
0 = f(x_0)+f'(x_0)(a-x_0)+O(\Delta^2) \\
\to a = x_0-\frac{f(x_0)}{f'(x_0)}+O(\Delta^2)
\end{align}
\)
ここで、\(f(x_0)=f'(x_0)=O(\Delta^0)\)を想定しているため、\(f'(x_0)\)の割り算を行っても誤差のオーダーは変化せず、\(\Delta\)に対して2乗のままとなります。
\(O(\Delta^2)\)を無視すると、得られる解は近似値となります。この近似値を\(x_1\)と置くと
\(\displaystyle
x_1 = x_0-\frac{f(x_0)}{f'(x_0)}
\)
得られる解\(x_1\)は\(x_0\)よりも解\(a\)に近いため、\(O(\Delta^2)\)はさらに小さくなります。なので、もう一度計算します。この時の近似値を\(x_2\)と置くと
\(\displaystyle
x_2 = x_1-\frac{f(x_1)}{f'(x_1)}
\)
ここで得られた\(x_2\)は更に\(a\)に近いため、・・・と繰り返していきます。
すなわち、解\(a\)に近い初期値\(x_0\)を与えた時、漸化式
\(\displaystyle
x_{n+1}=x_{n}-\frac{f(x_{n})}{f'(x_{n})},~~n=0,1,2\cdots,
\)
を繰り返すことで解\(a\)に近づいていく、ということです。
この式から分かる通り、解近傍で導関数がゼロになる場合はゼロ割発生するかもしれないので危険です。
もしもこのステップが無限回繰り返されれば、無限回目のステップの近似値\(x_\infty\)は
\(
x_\infty=a
\)
に収束します。
以上のように導関数を用いて方程式の解を求める方法は、ニュートン法(またはニュートン=ラフソン法)と呼ばれます。
この方法は、解に近いに所の値とその導関数が分かりさえすればいいので、この方法は1次元、多次元でも使用する事ができ、また複素関数でさえ使用することが出来ます。
さらに、誤差が\(O(\Delta^2)\)で減衰していくため、一度繰り返すごとに厳密解に一致する桁数が2倍になっていきます。
しかし問題があり、
1. 初期値を解の近傍に取らないと失敗する
2. 導関数が分からないと使えない
という大きな問題を抱えています。
また、解近傍でテーラー展開可能でなければならず、解近傍で導関数がゼロになる点があってはいけません。
-
初期値の推定
ニュートン法は解の近傍で、テーラー展開可能な領域から始めなければ用いることは出来ません。
これは工夫をするしかありません。
解近傍の初期値を推定する方法として、以下の2つの方法が良く取られます。
1. 解の範囲を限定し、その近傍からニュートン法を行う(1次元のみ)。
2. 適当な項を落とせば方程式が解けてしまう場合、その解を出発点とし、残りの項を摂動的に加えながら逐次解く。
-
解の範囲を限定する
これは1次元の場合に使える方法です。
単純な考え方で、例えば広い区間\([x_a,x_b]\)にゼロ点があることだけが分かっているとします。
この区間を\(N+1\)分割し、
\(
x^{(0)}=x_a,x^{(1)},\cdots,x^{(k)},x^{(k+1)},\cdots, x^{(N-1)},x^{(N)}=x_b
\)
とします。もしも\(x^{(k)}\)と\(x^{(k+1)}\)の符号が違う場合、この区間でゼロを横切っているということになりますので、この点からニュートン法を始めれば良いのです。
問題は、解の範囲を狭めるために関数を\(N+1\)回評価しなければならない、という点で計算コストがかかってしまう、という点です。
-
既知の解から摂動的に逐次解く
これは若干特殊な方法で、あてずっぽうな上の考えとは違います。
本来解きたい式を
\(
f(x)=f_0(x)+g(x)
\)
と分けます。ここで、
\(
f_0(x)=0
\)
の解は簡単に解けて、\(x=a_0\)が関数\(f_0(x)\)のゼロ点であるとします。この\(a_0\)を初期値とし、\(\lambda\)を十分小さい値にとり
\(
f_0(x)+\lambda_1 g(x)=0
\)
を解きます。ここで、\(\lambda_m\)は\(0\lt\lambda_1\lt\lambda_2\cdots \lt\lambda_{M-1} \lt \lambda_M=1\)を満たすとします。
この方程式の解\(a_1\)が得られたら、この解を初期値とし、
\(
f_0(x)+\lambda_2 g(x)=0
\)
を解きに行き、これを\(\lambda_M=1\)まで続けます。
こうすることにより、最後の答え\(a_M\)がもともと解きたかった式の答えとなっているのです。
関数の一回の評価に時間がかかってしまう場合、この解き方の方が早く解けます。
しかし、関数\(g(x)\)によってゼロ点の位置が増えたり、消えたりしてしまう時にこの方法は使うことが出来ず、連続的に解が動いてくれないと使うことが出来ない点に注意してください。
-
導関数の近似
導関数を求める簡単な方法は、差分を使うことです。すなわち、導関数\(f'(x)\)を差分に置き換えます。
\(\displaystyle
f'(x)\approx \frac{f(x+h)-f(x)}{h} + O(h)
\)
すると、漸化式は
\(\displaystyle
x_{n+1}=x_{n}-h\frac{f(x_{n})}{f(x_n+h)-f(x_n)},~~n=0,1,2\cdots,
\)
と得られます。
この方法は導関数を必要とせず、実装が簡単であるという意味で有用な式です。
導関数を求める際の前進差分の刻み幅\(h\)は、計算機の扱える丸め誤差\(\epsilon\)(単精度ならば約\(\epsilon=10^{-8}\)、倍精度ならば約\(\epsilon=10^{-16}\))の\(1/2\)乗の2倍、つまり
\(
\displaystyle h\sim 2\sqrt{\epsilon}
\)
とすると良いです。
この刻み幅の導出は折りたたんでおきますが、以下のように導出することが出来ます。
参考文献[3,4]
前進差分は
\(\displaystyle
\frac{df(x)}{dx}\approx\frac{f(x+h)-f(x)}{h}
\)
とする近似です。
コンピュータを用いる以上、関数\(f(x+h),f(x)\)は丸め誤差\(\pm \epsilon\)の範囲で決まるので、右辺は最悪の場合、\(|\frac{2\epsilon}{h}|\)の誤差を持ちます。
また、微分の近似を用いたことから、その近似に由来する打切り誤差があります。それは
\(\displaystyle
\frac{df(x)}{dx}=\frac{f(x+h)-f(x)}{h}-\frac{h}{2}f^{\prime\prime}(x)+O(h^2)
\)
として表されるので、おおよそ\(|\frac{h}{2}f^{\prime\prime}(x)|\)の誤差があります。
よって、数値的な誤差\(E\)は丸め誤差と打切り誤差の絶対値を足せばいいので、
\(\displaystyle
E=|\frac{2\epsilon}{h}|+|\frac{h}{2}f^{\prime\prime}(x)|
\)
と求められます。この誤差を最も小さくする刻み幅\(h\)は、極値をとるときなので、
\(\displaystyle
\frac{\partial E}{\partial h}=-\frac{2\epsilon}{h^2}+\frac{|f^{\prime\prime}(x)|}{2}=0
\)
を満たす\(h\)です。よって、
\(\displaystyle
h=2\sqrt{\frac{\epsilon}{|f^{\prime\prime}(x)|}}
\)
と決まります。
この式から分かることは、\(|f^{\prime\prime}(x)|\)が大きい、すなわち\(x\)における関数の曲率が大きい場合は刻み幅は小さく、曲率が小さければ刻み幅は大きい方が良い、ということです。
物凄く大雑把には、倍精度計算であれば\(10^{-16}\)まで扱えるので\(\epsilon \approx 10^{-16}, |f^{\prime\prime}(x)|\approx 1\)と考えてしまえば
\(
\displaystyle h\sim 2\times 10^{-8}
\)
程度が良い、という事です。
参考文献[1][3][5]
1次元ニュートン法のプログラム
以下のプログラムは、1次元のニュートン法のプログラムで、
方程式
\(
x^2-4 = 0
\)
を初期値\(x_0=3\)から始めて解くプログラムです。
このコードを動かすと、ステップを繰り返すごとに急激に解に近づいていっていることが分かります。
(デフォルトではコメントアウトしてあります。)
$ gfortran main.f90
$ ./a.out
1 2.1666666616021075
2 2.0064102565311974
3 2.0000102400381690
4 2.0000000000262466
5 2.0000000000000000
2.0000000000000000 ---result
$
上には出力していませんが、初期値の評価もしています。
なので、ニュートン法は6回呼び出されたことになります。
ニュートン法1回当たり関数は2回呼び出されますので、12回関数が呼び出されたことになります。
例えば比較対象として、二分法を考えますと、1回目に関数は3回,そのほかで1回ずつ呼び出されます。
二分法の解は1ステップ当たり区間の半分になりますので、16桁一致するまでには50回ほど繰り返す必要があります。そのため、52回位関数が呼び出されます。
ニュートン法の方が圧倒的に早いことが分かります。
program main
implicit none
double precision::a,tol,x0
double precision,external::f
x0=3d0
tol=1d-10
call newton1d(x0,f,tol,a)
write(6,*)a," --- result"
stop
end program main
function f(x)
implicit none
double precision,intent(in)::x
double precision::f
f=x**2-4d0
return
end function f
subroutine newton1d(x0,f,tol,sol)
implicit none
double precision,intent(in)::x0,tol
double precision,intent(out)::sol
double precision,external::f
! sikinote, http://slpr.sakura.ne.jp/qp
! author: sikino
! date: 2018/07/18 (yyyy/mm/dd)
integer::i
integer,parameter::itrmax=100 ! maximum iteration
double precision,parameter::h=2d-8 ! stepsize for forward difference
double precision,parameter::tny=tiny(1d0) ! machine epsilon
double precision::a,c,f1,f2,g,d
a=x0
do i=1,itrmax
c = a
f2 = f(a+h)
f1 = f(a)
g = f2-f1
if(abs(g).le.tny)then
write(6,*)"zero dividing, Newton method"
exit
endif
d = h*f1/g
a = a - d
!write(6,'(i5,f25.16)')i,a
if(abs(a).gt.1d0)then
if(abs(d/a).le.tol)exit
else
if(abs(d).le.tol)exit
endif
enddo
sol=a
return
end subroutine newton1d
複素関数の1次元ニュートン法のプログラム
$ gfortran main.f90
$ ./a.out
1 ( -1.2933333304320405 , 0.72000000272341036 )
2 (-0.78207788228079722 , 0.60930726266833468 )
3 (-0.43844290526861285 , 0.73503785880633421 )
4 (-0.50851135934742864 , 0.89043164725052448 )
5 (-0.50009896196621662 , 0.86666395460253720 )
6 (-0.49999991066297655 , 0.86602581130981315 )
7 (-0.49999999999985084 , 0.86602540378453374 )
8 (-0.50000000000000000 , 0.86602540378443860 )
(-0.50000000000000000 , 0.86602540378443860 ) ----result
$
ソースコードはこちら。
program main
implicit none
double precision::tol
complex(kind(0d0))::a,z0
complex(kind(0d0)),external::h
z0=dcmplx(-2d0,1d0)
tol=1d-10
call cnewton1d(z0,h,tol,a)
write(6,*)a," ----result"
stop
end program main
function h(z)
implicit none
complex(kind(0d0)),intent(in)::z
complex(kind(0d0))::h
h=z*z*z-1e0
return
end function h
subroutine cnewton1d(x0,f,tol,sol)
implicit none
complex(kind(0d0)),intent(in)::x0
double precision,intent(in)::tol
complex(kind(0d0)),intent(out)::sol
complex(kind(0d0)),external::f
! sikinote, http://slpr.sakura.ne.jp/qp
! author: sikino
! date: 2018/07/18 (yyyy/mm/dd)
integer::i
integer,parameter::itrmax=100 ! maximum iteration
double precision,parameter::tny=tiny(1d0) ! machine epsilon
double precision,parameter::h=2d-8 ! stepsize for forward difference
complex(kind(0d0))::a,c,f1,f2,g,d
a=x0
do i=1,itrmax
c = a
f2 = f(a+h)
f1 = f(a)
g = f2-f1
if(abs(g).le.tny)then
write(6,*)"zero dividing, Newton method"
exit
endif
d = h*f1/g
a = a - d
!write(6,*)i,a
if(abs(d).le.tol)exit
enddo
sol=a
return
end subroutine cnewton1d
2次元のニュートン法
続いて方程式
\(
\begin{eqnarray}
\left\{~~
\begin{aligned}
f(x,y)&=0,\\
g(x,y)&=0
\end{aligned}
\right.
\end{eqnarray}
\)
を満たす\(x=a,y=b\)を見つけることを考えます。
1次元の時と同様に、任意の点\(x’,y’\)周りにおけるテーラー展開は、
\(
\begin{eqnarray}
\left\{~~
\begin{aligned}
f(x,y) &= f(x’,y’)+f_x(x’,y’)\cdot(x-x’)+f_y(x’,y’)\cdot(y-y’)+ O(\varepsilon^2)\\
g(x,y) &= g(x’,y’)+g_y(x’,y’)\cdot(x-x’)+g_y(x’,y’)\cdot(y-y’)+ O(\varepsilon^2)
\end{aligned}
\right.
\end{eqnarray}
\)
ここで、
\(\displaystyle \left. f_x(x’,y’)=\frac{\partial f(x,y)}{\partial x}\right|_{x=x’,y=y’}\)
\(\displaystyle \left. f_y(x’,y’)=\frac{\partial f(x,y)}{\partial y}\right|_{x=x’,y=y’}\)
\(\displaystyle \Delta x=|x-x’|=O(\varepsilon^1),~~\Delta y=|y-y’|=O(\varepsilon^1)\)
と書きました。
1次元の時と同様に初期値\((x_0,y_0)\)が解\((a,b)\)に近ければ、
\(
\begin{eqnarray}
\left\{
\begin{aligned}
0 &= f(x_0,y_0)+f_x(x_0,y_0)\cdot(a-x_0)+f_y(x_0,y_0)\cdot(b-y_0) +O(\varepsilon^2)\\
0 &= g(x_0,y_0)+g_x(x_0,y_0)\cdot(a-x_0)+g_y(x_0,y_0)\cdot(b-y_0) +O(\varepsilon^2)
\end{aligned}
\right.
\end{eqnarray}
\)
を同時に満たす\((a,b)\)を探せばよい、ということになります。
行列形式で書けば
\(
\begin{align}
\left(
\begin{array}{cc}
f_x(x_0,y_0) & f_y(x_0,y_0) \\
g_x(x_0,y_0) & g_y(x_0,y_0)
\end{array}
\right)
\left(
\begin{array}{c}
a-x_0 \\
b-y_0
\end{array}
\right)
=
-\left(
\begin{array}{c}
f(x_0,y_0) \\
g(x_0,y_0)
\end{array}
\right)+O(\varepsilon^2)
\end{align}
\)
と書けます。\(a,b\)について解けば
\(
\begin{align}
\left(
\begin{array}{c}
a \\
b
\end{array}
\right)
=
\left(
\begin{array}{c}
x_0 \\
y_0
\end{array}
\right)
-\left(
\begin{array}{cc}
f_x(x_0,y_0) & f_y(x_0,y_0) \\
g_x(x_0,y_0) & g_y(x_0,y_0)
\end{array}
\right)^{-1}
\left(
\begin{array}{c}
f(x_0,y_0) \\
g(x_0,y_0)
\end{array}
\right)+O(\varepsilon^2)
\end{align}
\)
となります。丁度一次元のニュートン法と似た形になりました。
右辺の
\(
\begin{align}
\mathbf{J}_0=\left(
\begin{array}{cc}
f_x(x_0,y_0) & f_y(x_0,y_0) \\
g_x(x_0,y_0) & g_y(x_0,y_0)
\end{array}
\right)
\end{align}
\)
は\(x=x_0,y=y_0\)のヤコビアンです。また、
\(
\mathbf{a}=\left(
\begin{array}{c}
a \\
b
\end{array}
\right),~~
\begin{align}
\mathbf{x}_0=\left(
\begin{array}{c}
x_0 \\
y_0
\end{array}
\right),~~
\mathbf{f}_0=\left(
\begin{array}{c}
f(x_0,y_0) \\
g(x_0,y_0)
\end{array}
\right)
\end{align}
\)
と表記すれば、2次元のニュートン法は
\(
\mathbf{a}=\mathbf{x}_0 – \mathbf{J}_0^{-1}\mathbf{f}_0+O(\varepsilon^2)
\)
と書くことが出来ます。
近似として、\(O(\varepsilon^2)\)の項を無視すれば
\(
\mathbf{x_1}=\mathbf{x}_0 – \mathbf{J}_0^{-1}\mathbf{f}_0
\)
と書けます。繰り返せば、漸化式
\(
\mathbf{x}_{n+1}=\mathbf{x}_{n} – \mathbf{J}_n^{-1}\mathbf{f}_n
\)
を解いていけば良い、ということになります。
ニュートン法を実行するにあたり、ヤコビアンの逆行列を解くことが一番の問題となります。
良く知られているように、2次元の逆行列は、計算コストもさほどかからずに解けてしまい、
\(
\begin{align}
\mathbf{J}_n^{-1}=
\frac{1}{f_x(x_n,y_n) g_y(x_n,y_n)-f_y(x_n,y_n)g_x(x_n,y_n)}
\left(
\begin{array}{cc}
g_y(x_n,y_n) & -f_y(x_n,y_n) \\
-g_x(x_n,y_n) & f_x(x_n,y_n)
\end{array}
\right)
\end{align}
\)
として求める事が出来ます。
参考文献[2],[6]
[adsense2]
2次元ニュートン法のプログラム
以下のプログラムは、2次元のニュートン法のプログラムで、
方程式
\(
\begin{eqnarray}
\left\{~~
\begin{aligned}
f_1(x,y)&=x^2+y^2-1 = 0 \\
f_2(x,y)&=y-x^3 = 0
\end{aligned}
\right.
\end{eqnarray}
\)
を初期値\(x_0=2,~y_0=1\)から始めて解くプログラムです。
program main
implicit none
double precision::a,b,tol,x0,y0
double precision,external::f1,f2
x0=2d0
y0=1d0
tol=1d-10
call newton2d(x0,y0,f1,f2,tol,a,b)
write(6,*)a,b," ---result"
stop
end program main
function f1(x,y)
implicit none
double precision,intent(in)::x,y
double precision::f1
f1=x*x+y*y-1d0
return
end function f1
function f2(x,y)
implicit none
double precision,intent(in)::x,y
double precision::f2
f2=y-x*x*x
return
end function f2
subroutine newton2d(x01,x02,f1,f2,tol,x1,x2)
implicit none
double precision,intent(in)::x01,x02,tol
double precision,intent(out)::x1,x2
double precision,external::f1,f2
! sikinote, http://slpr.sakura.ne.jp/qp
! author: sikino
! date: 2018/07/18 (yyyy/mm/dd)
integer::i,key
integer,parameter::itrmax=100 ! maximum iteration
double precision,parameter::tny=tiny(1d0) ! machine epsilon
double precision,parameter::h=2d-8 ! stepsize for forward difference
double precision::c1,c2,d1,d2
double precision::J11,J12,J21,J22,J
double precision::A11,A12,A21,A22
double precision::f11,f12,f21,f22,f10,f20
x1=x01
x2=x02
do i=1,itrmax
key=0
c1 = x1
c2 = x2
! For forward difference
f10 = f1(x1 ,x2 )
f11 = f1(x1+h,x2 )
f12 = f1(x1 ,x2+h)
f20 = f2(x1 ,x2 )
f21 = f2(x1+h,x2 )
f22 = f2(x1 ,x2+h)
! Jacobian
J11 = (f11-f10)/h ! df1/dx1
J12 = (f12-f10)/h ! df1/dx2
J21 = (f21-f20)/h ! df2/dx1
J22 = (f22-f20)/h ! df2/dx2
J=J11*J22-J12*J21
if(abs(J).le.tny)exit
! Inverse matrix
A11 = J22 / J
A12 = - J12 / J
A21 = - J21 / J
A22 = J11 / J
d1 = A11*f10 + A12*f20
d2 = A21*f10 + A22*f20
x1 = x1 - d1
x2 = x2 - d2
!write(6,'(i5,4f25.16)')i,x1,x2
! Convergence check
if(abs(x1).ge.1d0.and.abs(d1/x1).le.tol)key=key+1
if(abs(x1).lt.1d0.and.abs(d1 ).le.tol)key=key+1
if(abs(x2).ge.1d0.and.abs(d2/x2).le.tol)key=key+1
if(abs(x2).lt.1d0.and.abs(d2 ).le.tol)key=key+1
if(key.eq.2)exit
enddo
return
end subroutine newton2d
このコードを動かすと、ステップを繰り返すごとに解に近づいていっていることが分かります。
$ gfortran main.f90
$ ./a.out
1 1.3571428532359113 0.2857142813732352
2 0.9844126813492445 0.4401111876910193
3 0.8485699953676349 0.5590406123395349
4 0.8265084709901402 0.5633730814110012
5 0.8260315915076198 0.5636240770681390
6 0.8260313576542442 0.5636241621612319
7 0.8260313576541870 0.5636241621612585
0.82603135765418700 0.56362416216125855 ---result
$
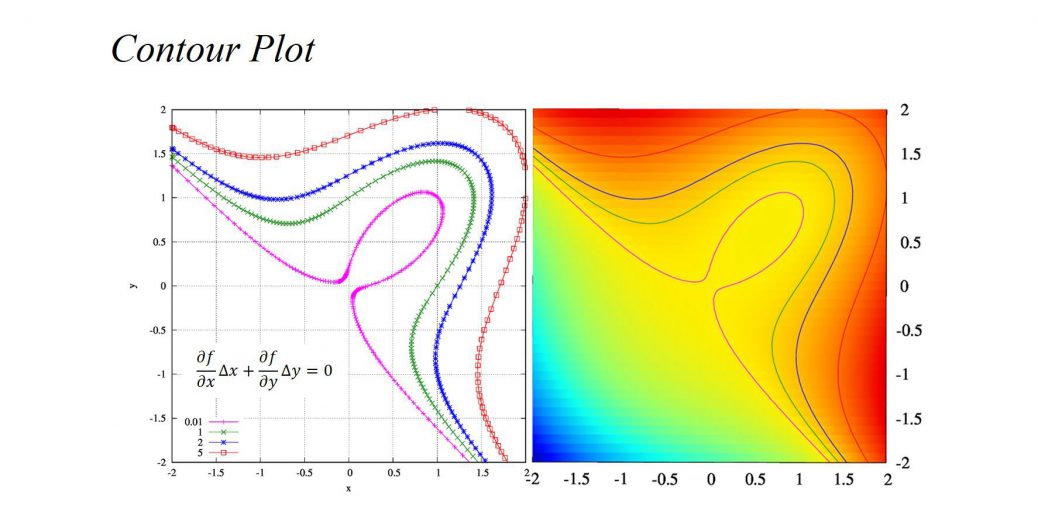
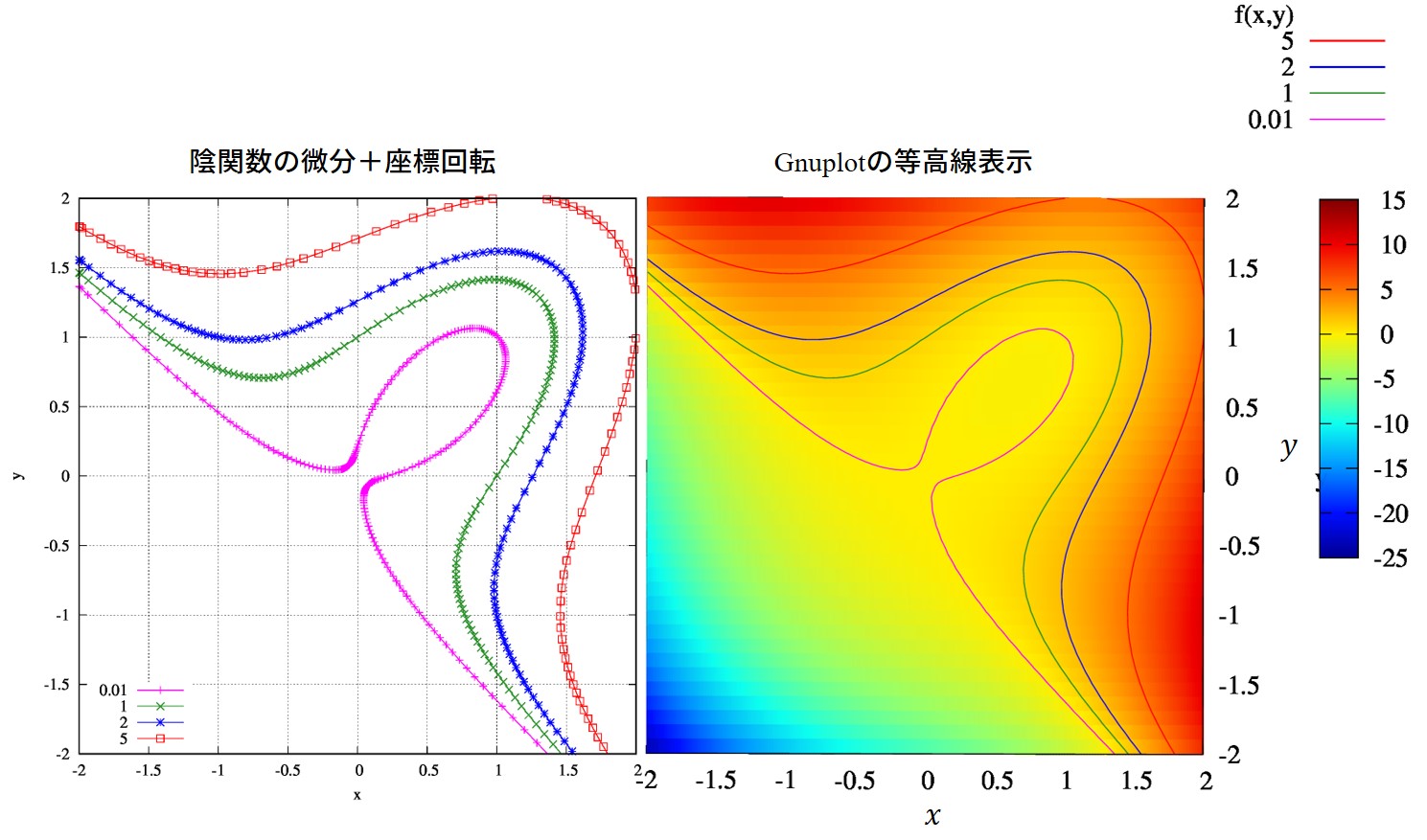
この問題の答えは\(f_1=0,~f_2=0\)の陰関数の交点です。
図示すれば、下図の紫色の経路を辿って解に収束していくことが分かります。
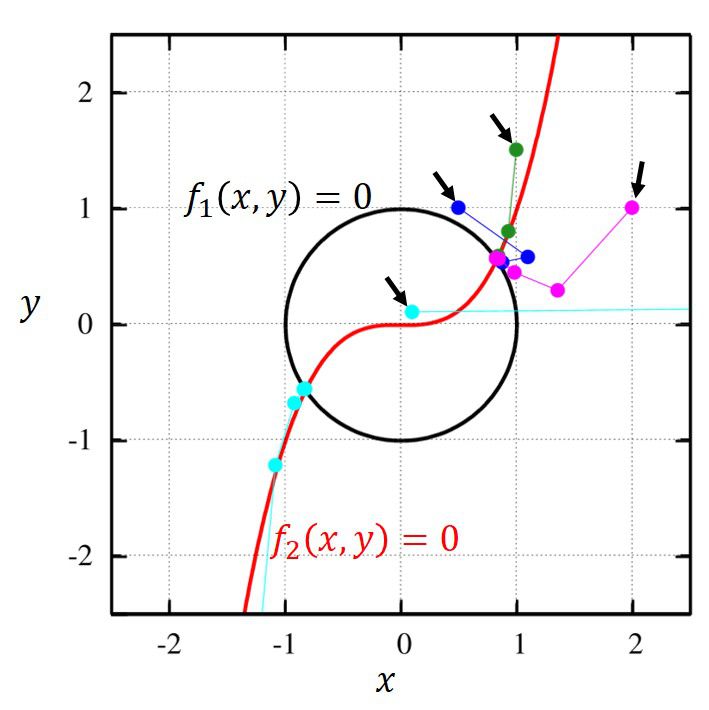
ひとつ、注目しておかなければならない点として、解に近いからと言って、その解に収束するとは限らないということに注意してください。
図中の水色の線は初期値こそ右上の解に近いですが、実際に計算してみるともう一つの解に収束していることが分かります。
適当な初期値を用意し、ニュートン法が収束する点を調べるという問題はニュートン写像と呼ばれる分野です。
力学系とかそういう言葉が出てきます。
私も過去に複素関数でやったことがありますので、リンクだけ載せておきます。
ニュートン写像に現れる綺麗な画像 -シキノート
2次元の複素関数のニュートン法
置いておきます。
program main
implicit none
double precision::tol
complex(kind(0d0)),external::f1,f2
complex(kind(0d0))::a,b,x0,y0
x0=dcmplx(2d0,1d0)
y0=dcmplx(1d0,0d0)
tol=1d-8
call cnewton2d(x0,y0,f1,f2,tol,a,b)
write(6,*)a,b," ---result"
stop
end program main
function f1(x,y)
implicit none
complex(kind(0d0)),intent(in)::x,y
complex(kind(0d0))::f1
f1=x*x+y*y-1d0
return
end function f1
function f2(x,y)
implicit none
complex(kind(0d0)),intent(in)::x,y
complex(kind(0d0))::f2
f2=y-x*x*x
return
end function f2
subroutine cnewton2d(x01,x02,f1,f2,tol,x1,x2)
implicit none
complex(kind(0d0)),intent(in)::x01,x02
double precision,intent(in)::tol
complex(kind(0d0)),intent(out)::x1,x2
complex(kind(0d0)),external::f1,f2
! sikinote, http://slpr.sakura.ne.jp/qp
! author: sikino
! date: 2018/08/07 (yyyy/mm/dd)
integer::i,key
integer,parameter::itrmax=100 ! maximum iteration
double precision,parameter::tny=tiny(1d0) ! machine epsilon
double precision,parameter::h=2d-8 ! stepsize for forward difference
complex(kind(0d0))::c1,c2,d1,d2
complex(kind(0d0))::J11,J12,J21,J22,J
complex(kind(0d0))::A11,A12,A21,A22
complex(kind(0d0))::f11,f12,f21,f22,f10,f20
x1=x01
x2=x02
do i=1,itrmax
key=0
c1 = x1
c2 = x2
! For forward difference
f10 = f1(x1 ,x2 )
f11 = f1(x1+h,x2 )
f12 = f1(x1 ,x2+h)
f20 = f2(x1 ,x2 )
f21 = f2(x1+h,x2 )
f22 = f2(x1 ,x2+h)
! Jacobian
J11 = (f11-f10)/h ! df1/dx1
J12 = (f12-f10)/h ! df1/dx2
J21 = (f21-f20)/h ! df2/dx1
J22 = (f22-f20)/h ! df2/dx2
J=J11*J22-J12*J21
if(abs(J).le.tny)exit
! Inverse matrix
A11 = J22 / J
A12 = - J12 / J
A21 = - J21 / J
A22 = J11 / J
d1 = A11*f10 + A12*f20
d2 = A21*f10 + A22*f20
x1 = x1 - d1
x2 = x2 - d2
write(6,'(i5,4f25.16)')i,x1,x2
! Convergence check
if(abs(x1).ge.1d0.and.abs(d1/x1).le.tol)key=key+1
if(abs(x1).lt.1d0.and.abs(d1 ).le.tol)key=key+1
if(abs(x2).ge.1d0.and.abs(d2/x2).le.tol)key=key+1
if(abs(x2).lt.1d0.and.abs(d2 ).le.tol)key=key+1
if(key.eq.2)exit
enddo
return
end subroutine cnewton2d
多次元のニュートン法
さて、この形まで持ってくると多次元への拡張が簡単にできます。
多次元のニュートン法は
\(
\mathbf{x}_{n+1}=\mathbf{x}_n – \mathbf{J}_n^{-1}\mathbf{f}_n
\)
の形がそのまま使えます。
ここで、
\(
\begin{align}
\mathbf{x}_n=
\left(
\begin{array}{c}
x_1\\
x_2\\
\vdots \\
x_N
\end{array}
\right)_n
,~~
\mathbf{f}_n=
\left(
\begin{array}{c}
f_1(\mathbf{x}_n)\\
f_2(\mathbf{x}_n)\\
\vdots \\
f_N(\mathbf{x}_n)
\end{array}
\right)
,~~
\mathbf{J}_n=
\left.\left(
\begin{array}{cccc}
\frac{\partial f_1}{\partial x_1} & \frac{\partial f_1}{\partial x_2} & \cdots & \frac{\partial f_1}{\partial x_N} \\
\frac{\partial f_2}{\partial x_1} & \frac{\partial f_2}{\partial x_2} & \cdots & \frac{\partial f_2}{\partial x_N} \\
\vdots&\vdots&\ddots&\vdots \\
\frac{\partial f_N}{\partial x_1} & \frac{\partial f_N}{\partial x_2} & \cdots &\frac{\partial f_N}{\partial x_N}
\end{array}
\right)\right|_{\mathbf{x}=\mathbf{x}_n}
\end{align}
\)
です。
問題となるのは(ヤコビアンの逆行列)×(f)の計算です。
この計算を数値計算的に何とかするべく改良が重ねられてきたのが準ニュートン法(本稿では書きません)と呼ばれるアルゴリズムです。
逆行列を数値的に計算することは宜しくないですので、
\(
\begin{align}
\mathbf{r}&=\mathbf{J}_n^{-1}\mathbf{f}_n \\
\to \mathbf{J}_n \mathbf{r} = \mathbf{f}_n
\end{align}
\)
という方程式を解く問題に帰着させます。これはLU分解を用いて効率的に解くことができ、解ければ、ニュートン法の次のステップを
\(
\mathbf{x}_{n+1}=\mathbf{x}_n – \mathbf{r}
\)
として求める事が出来るのです。
多次元のニュートン法のプログラム
実際に、LAPACKのLU分解を使用したプログラムの例を載せておきます。
program main
implicit none
integer::Ns
double precision,allocatable::x(:)
double precision,allocatable::z(:)
double precision::tol
external::gnr
Ns=2
allocate(x(1:Ns),z(1:Ns))
x(1)=2d0
x(2)=1d0
tol=1d-10
call Newton(Ns,x,gnr,tol)
write(6,*)x(1),x(2)," ---result"
stop
end program main
subroutine gnr(N,x,f)
implicit none
integer,intent(in)::N
double precision,intent(in)::x(1:N)
double precision,intent(out)::f(1:N)
! Equation, f(i)=0, (i=1,...,N)
f(1) = x(1)**2+x(2)**2-1d0
f(2) = x(2)-x(1)**3
return
end subroutine gnr
subroutine Newton(Ns,x,gnr,tol)
implicit none
integer,intent(in)::Ns
double precision,intent(inout)::x(1:Ns)
double precision,intent(in)::tol
external::gnr
integer::i,k,info,key
integer,parameter::itrmax=100 ! maximum iteration
double precision,allocatable::Jac(:,:)
double precision,allocatable::w(:,:),f(:)
integer,allocatable::ipiv(:)
allocate(Jac(1:Ns,1:Ns),w(1:Ns,1:1),f(1:Ns),ipiv(1:Ns))
ipiv=0
Jac=0d0
f=0d0
w=0d0
info=0
do k=1,10 !itrmax
write(6,'(2f12.5)')x(1),x(2)
! Function values and Jacobian
call Jacobian(Ns,x,gnr,f,Jac)
! LU factorization
call dgetrf(Ns,Ns,Jac,Ns,ipiv,info)
w(1:Ns,1) = -f(1:Ns)
call dgetrs('N',Ns,1,Jac,Ns,ipiv,w,Ns,info)
! --> Now, w is \Delta x
! x^{(k+1)} = x^{(k)} + Delta x
do i=1,Ns
x(i) = x(i) + w(i,1)
enddo
! Convergence check
key=0
do i=1,Ns
if(abs(x(i)).ge.1d0)then
if(abs(w(i,1)/x(i)).le.tol)then
key=key+1
else
exit
endif
else
if(abs(w(i,1)).le.tol)then
key=key+1
else
exit
endif
endif
enddo
if(key.eq.Ns)exit
enddo
return
end subroutine Newton
subroutine Jacobian(N,x,gnr,f,Jac)
implicit none
integer,intent(in)::N
double precision,intent(in)::x(1:N)
double precision,intent(out)::f(1:N),Jac(1:N,1:N)
external::gnr
integer::i,j
double precision::dx
double precision,parameter::delta=2d-8
double precision,allocatable::g(:),tx(:)
Jac=0d0
allocate(g(1:N),tx(1:N))
g=0d0; tx=0d0
call gnr(N,x,f)
do j=1,N
tx(1:N) = x(1:N)
dx=sqrt(abs(x(j)))
if(dx.lt.1d0)dx=1d0
dx=delta*dx
tx(j) = tx(j)+dx
call gnr(N,tx,g)
do i=1,N
Jac(i,j) = (g(i)-f(i)) / dx
enddo
enddo
return
end subroutine Jacobian
高次のニュートン法?
1次元のニュートン法は
\(\displaystyle
a = x_0-\frac{f(x_0)}{f'(x_0)}+O(\Delta^2)
\)
の形で求めていきますが、二階微分が分かっていればもっと収束が早くなりそうです。
実際、
\(\displaystyle
a = x_0-\frac{f^{\prime}(x_0)}{f^{\prime\prime}(x_0)}\pm\sqrt{{f’}^2(x_0)-2f(x_0)f^{\prime\prime}(x_0)}+O(\Delta^3)
\)
と解けます。しかし、2次関数ですので
解が見付からないかもしれない
という可能性があります。1次のニュートン法であれば、導関数がゼロでない限り、必ず\(y=0\)と交わる点が見付かります。しかし、2次で解に近づけると交点が見つからないことがあるかもしれません。
なので、1次のニュートン法を繰り返して使う方が(2次と比べたら)安定な解法なのです。
参考ページ
[1]1 Newton 法:壱変数の場合
https://www.astr.tohoku.ac.jp/~chinone/Planck/Planck-node6.html
[2]2 Newton 法:弐変数の場合
https://www.astr.tohoku.ac.jp/~chinone/Planck/Planck-node7.html
[3]Newton法
http://www.misojiro.t.u-tokyo.ac.jp/~murota/lect-suchi/newton130805.pdf
[4]アルゴリズムによる誤差
http://www.aoni.waseda.jp/ykagawa/chap2html/node9.html
[5]Newton 法による方程式の近似解法
http://www.math.u-ryukyu.ac.jp/~suga/C/2004/7/node9.html
[6]多次元のニュートン・ラフソン法
http://www.slis.tsukuba.ac.jp/~fujisawa.makoto.fu/cgi-bin/wiki/index.php?%C2%BF%BC%A1%B8%B5%A4%CE%A5%CB%A5%E5%A1%BC%A5%C8%A5%F3%A1%A6%A5%E9%A5%D5%A5%BD%A5%F3%CB%A1
[7]山本 有作, 行列計算における高速アルゴリズム
http://www.cms-initiative.jp/ja/events/0620yamamoto.pdf
[8]中田 和秀, 大規模線形方程式を解くためのクリロフ部分空間法の前処理
http://www.kurims.kyoto-u.ac.jp/~kyodo/kokyuroku/contents/pdf/1288-6.pdf