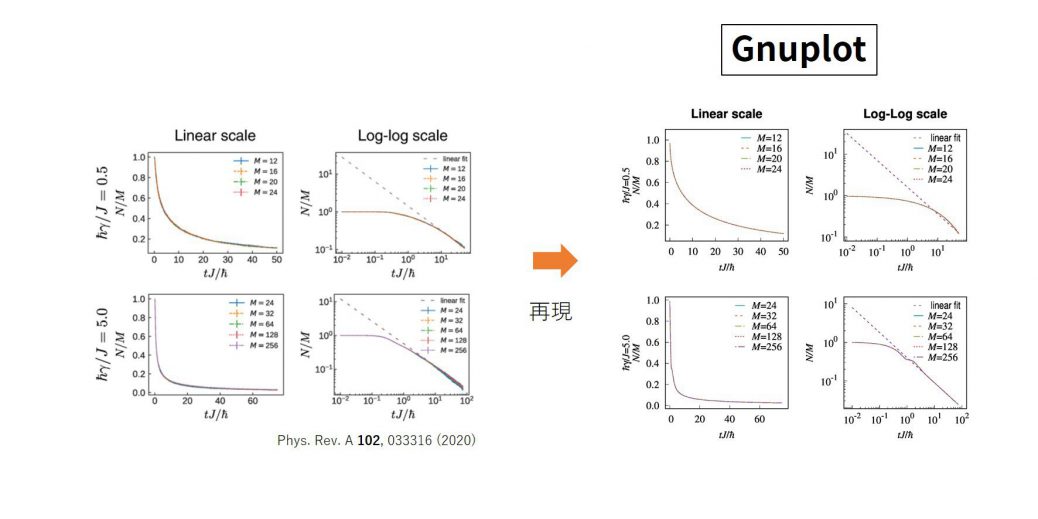
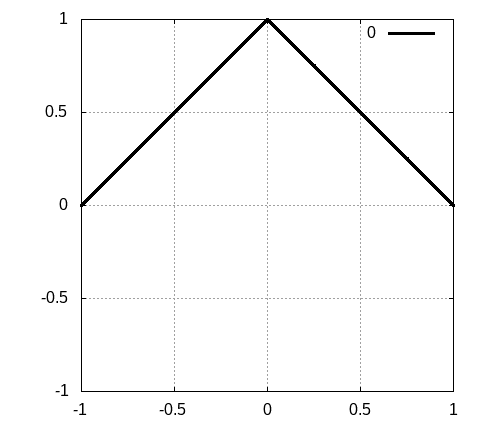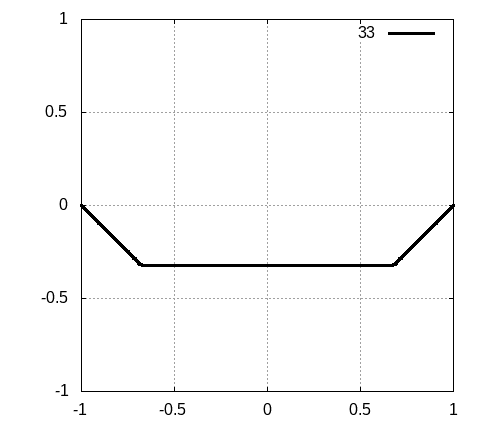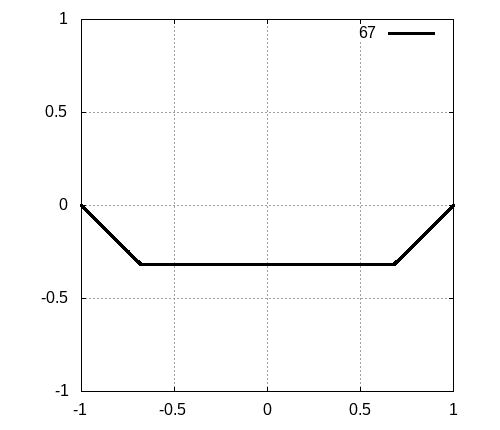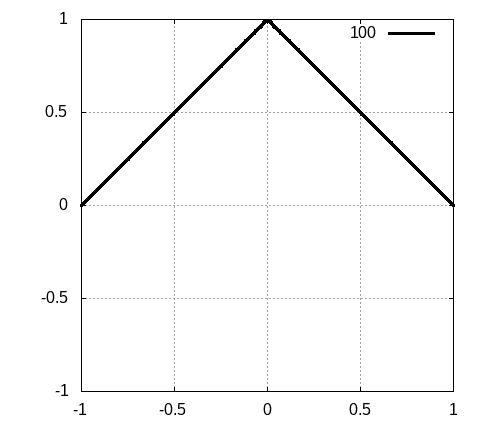月別アーカイブ: 2020年9月

gnuplot

論文に使える図をgnuplotで作る

コメントする

本稿の目的は、論文に用いることができるレベルの図をgnuplotで制作することです。
gnuplotはVersion 5.2 patchlevel 8を利用しています。

方針

本稿の方針としては、実際の論文からとってきた図を再現することです。
元データはないので、あくまで枠線や、フォントなどを合わせることを目的とします。

対象とする図は以下の[1]の図3と[2]の図3にします。
これらを選んだ理由は特にないですが、これらを再現することを目標にします。

[1]の図3を再現

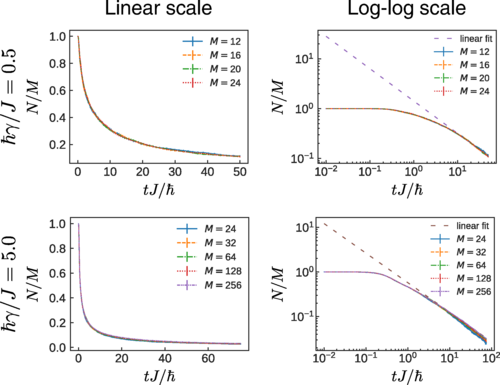
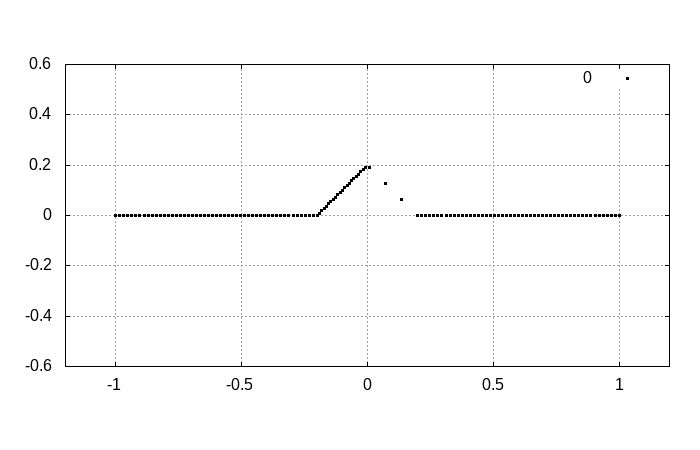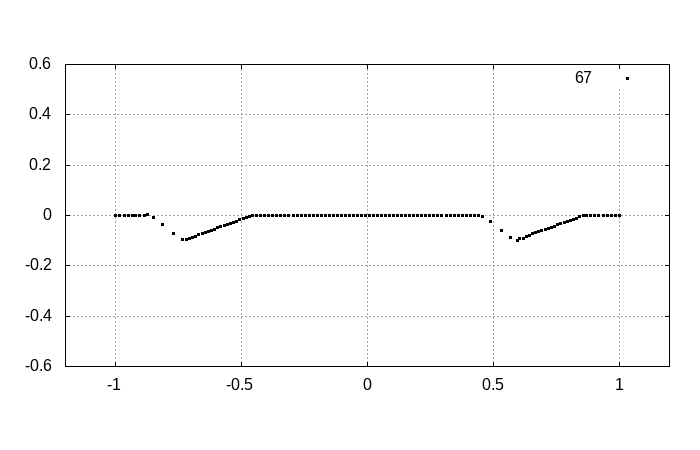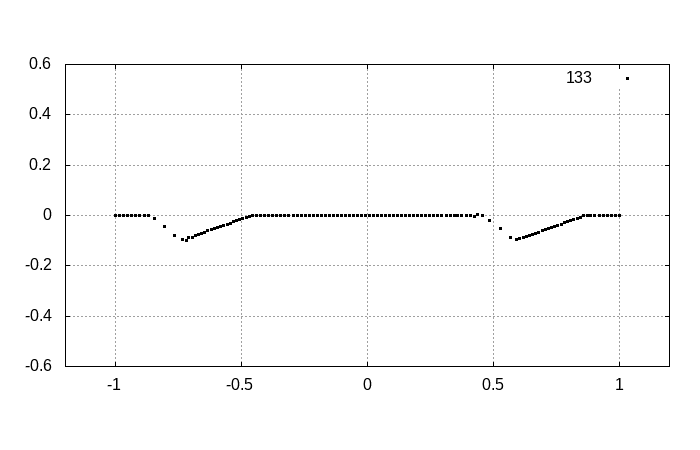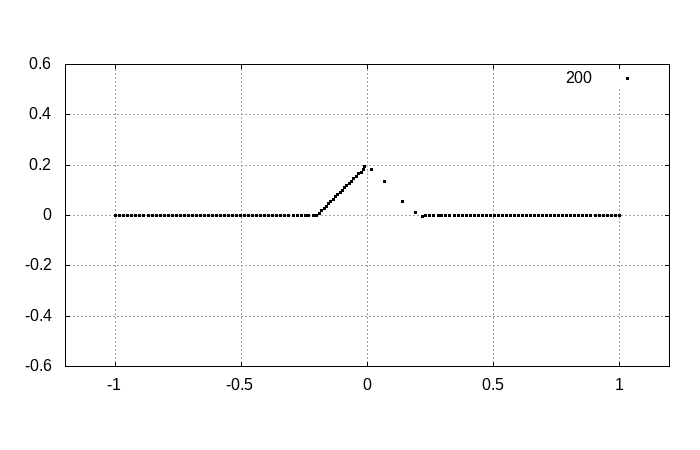
ではまず、Phys. Rev. A 102, 033316 (2020)の図3を再現しましょう。

[1]の図3

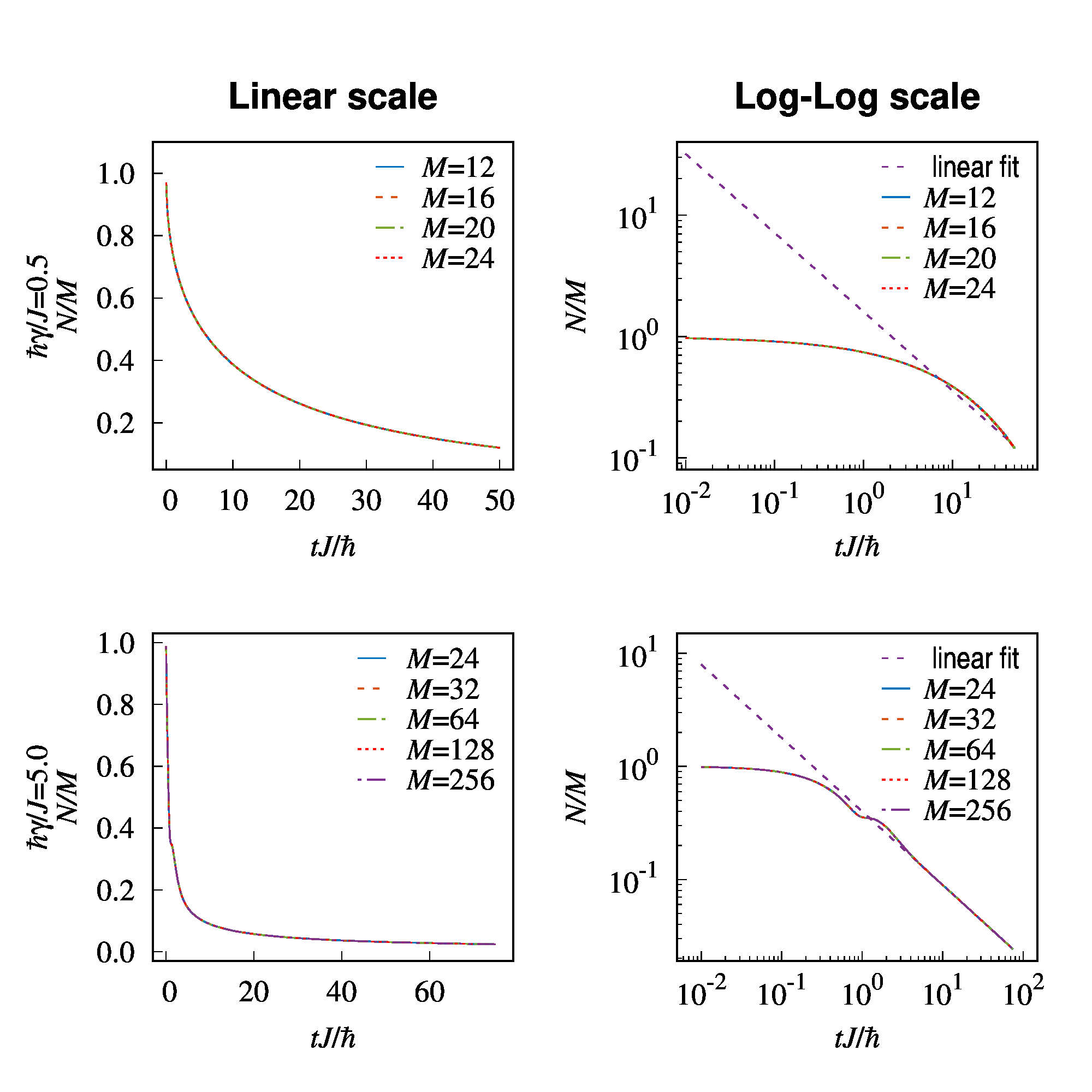
[1]の図3をgnuplotで再現した図

gnuplotで用いた全コードは以下に折りたたんでおきます。

データは適当に作成しました。データのダウンロードは以下からどうぞ。
https://slpr.sakura.ne.jp/qp/supplement_data/PRA102_033107_Fig3likedata.tar.gz

細かな説明をしていきます。

  • 線の色の指定
    線の色はlinetypeで決定していきます。

    set linetype  1 lc rgb '#0072bd' lw 1 # blue

    の意味は、gnuplotでプロットした時の1番目の線を、カラーコード’#0072bd’, 線の太さ”1″とすることを指定しています。プロット時に”lc 1″としてもこの1番目の色に変更できるようになります。linetype 6まで同じです。

  • 複数画面の表示位置指定
    続いて、

    # left top figure(1) position
    lx1=0.14; ly1=0.87
    rx1=0.47; ry1=0.57

    ~~~

    set lmargin screen lx1
    set tmargin screen ly1
    set rmargin screen rx1
    set bmargin screen ry1

    の部分について説明します。個別画面の左上の座標\((lx1, ly1)\)と右下の座標\((rx1, ry1)\)を決定します。座標の原点は全体の左下\((0,0)\), 全体の右上\((1,1)\)としたときに決められます。実際にその値を適用しているのがlmargin, tmarginなどです。詳しい説明は、gnuplotで複数の図を載せるを参照してください。

  • eps出力のためのターミナル指定
    • if(@ARG1 == 1){
      set terminal postscript eps size 5,5 dashed enhanced color font 'Roman,20'
      set output "PRA102_033107_Fig3.eps"
    }

    の部分は、出力ターミナルの設定を行っています。条件分岐は引数によってターミナルに出力するのか、epsとして画像出力するのかを指定するためです。使いやすさのためです。重要なのは、 size 5,5 の箇所です。ここを正方形にしておかないとxyの比が変わってしまうので扱いづらくなります。
    eps画像の切り抜き(Boundary boxの変更)はgsviewなどでできるので、画面四方の空白はいくらあってもよいです。そのサイズをgnuplot上で合わせるよりも、gnuplotで思った通りの出力をすること優先しましょう。
    フォントも重要ですね。経験上、2×2の画像であればsize5,5の時フォントサイズ20よいと思います。論文の本文はRomanフォントが使われるため、図もRomanにしておいたほうがよいでしょう。

  • 個別画面の細かい指定
    1. タイトルの指定
      set title "{/Gothic-bold=24 Linear scale}" offset 0,0

      タイトルを指定します。図のLinear scaleと書かれた太字です。[1]の図を見ると、どうもゴシック体の太字で書いているようです。なので、フォントをGothic-boldとして、文字の大きさを24に変更します。

    2. 凡例の指定
      3. set key reverse samplen 1 width 0

      凡例はkeyで指定します。reverseは凡例の中の”文字-線の種類”の表示順を”線の種類-文字”に変更します。samplenは、凡例内の線の長さを変更する（デフォルトで4）、wigthは線の種類と文字の間隔を指定するパラメータとして考えればよいでしょう。具体的な値は実際に出力させて何度も気に入るまでトライアンドエラーしています。

    3. x,y軸の設定
      4. unset log x
      set xr[-2:52]
      set xtics 10 nomirror
      set mxtics 1
      set format x "%2.0f"
      set xl "{/Roman-Italic {/=20 tJ}}/{/=14 @^{/Symbol=14 -}{/Roman-Italic {/=20 h}}}"

      軸設定をまとめて説明しますが、特に特殊文字の出力が難しいと思うのでここに注目します。プランク定数は特殊文字であり、postscriptターミナルでは出力することができないと思います。なので、文字hとハイフンを組み合わせて出力しています。私が思いついたわけではなくググりました。[4]に詳細が書いてありまして、それから持ってきました。文字サイズが違うので適当に合わせました。
      y軸も同じですので、省略します

    4. グラフのプロット
      5. plot "hJ5_fit.d" u 1:2 w l lw 2 lc 5 dashtype 2 ti "{/Gothic-Condensed linear fit}",\
           "hJ5.d" u 1:2 w l lw 2 lc 1 dashtype 1 ti "{/Roman-Italic M}=24   ",\
           "hJ5.d" u 1:2 w l lw 2 lc 2 dashtype 2 ti "{/Roman-Italic M}=32   ",\
           "hJ5.d" u 1:2 w l lw 2 lc 3 dashtype 4 ti "{/Roman-Italic M}=64   ",\
           "hJ5.d" u 1:2 w l lw 2 lc 4 dashtype 3 ti "{/Roman-Italic M}=128 ",\
           "hJ5.d" u 1:2 w l lw 2 lc 5 dashtype 5 ti "{/Roman-Italic M}=256 "

      最後にグラフをプロットします。dashtypeは実線、破線を決定するパラメータです。私の環境では実線が1, 破線は2以降になっていますが、環境によって違うかもしれません。各自合わせましょう。
      また、linear fitという文字は、なんというかｷﾞｭｯとまとまっています。しかもRoman体ではなくゴシック体です。これを指定するには、

      ti "{/Gothic-Condensed linear fit}"

      と入力することで実現可能です。

以上でおおよその説明が終わりです。

重要なのはトライアンドエラーです。ターミナルによって表示が異なるので、postscriptで出力すると決めたら確認はpostscriptで行いましょう。実際に最終出力図をqtターミナルの表示上では、このようになります。

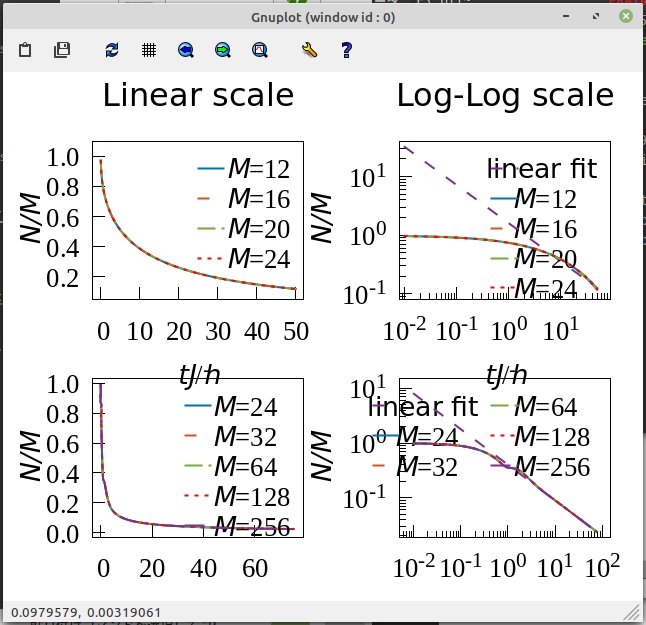
ベクタ形式であるEPS画像のサイズは102.5kBです。論文に投稿する場合でも許容できるサイズではないでしょうか。

ラスタライズ形式であるPNGをimagemagickを用いて

convert -density 400x400 -background white -flatten -alpha off PRA102_033316_Fig3.eps PRA102_033316_Fig3.png

で変換すると、91.8kBです。この程度の差であれば、ベクタ形式のほうが良いでしょう。

[2]の図3を再現

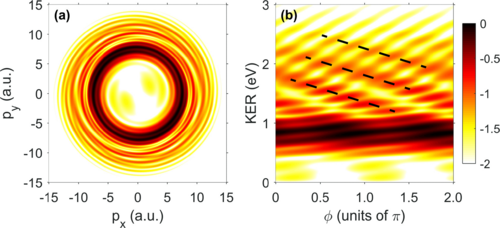
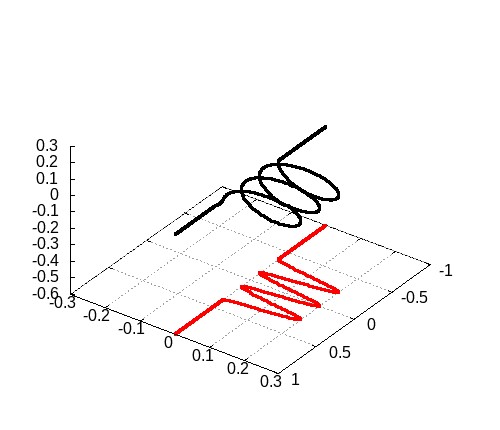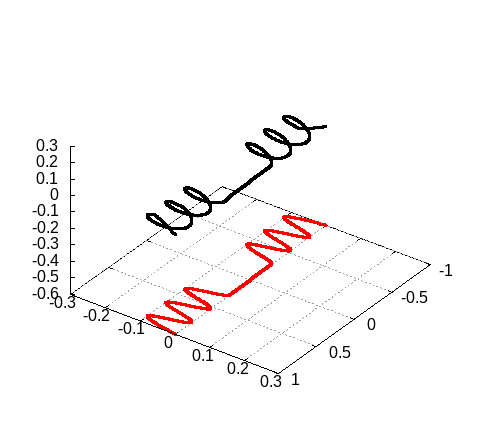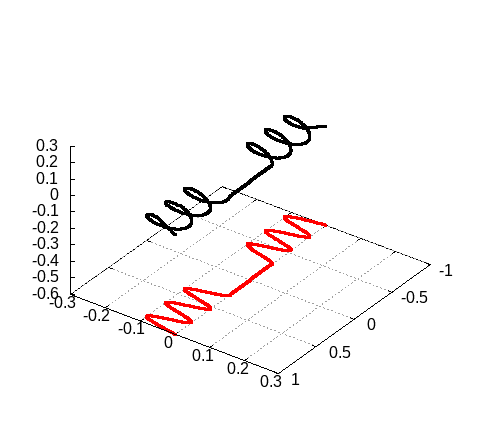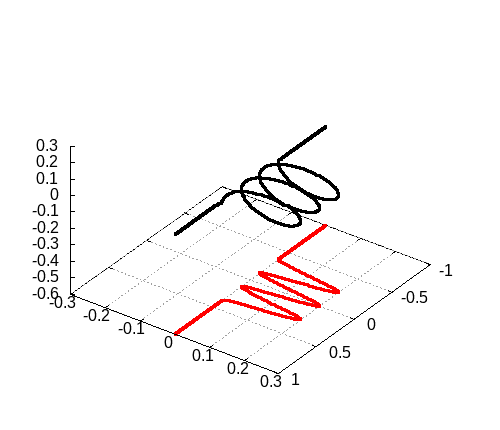
続いてPhys. Rev. A 102, 033107 (2020)の図3を再現しましょう。
大きな違いはカラーマップを利用した図であることです。

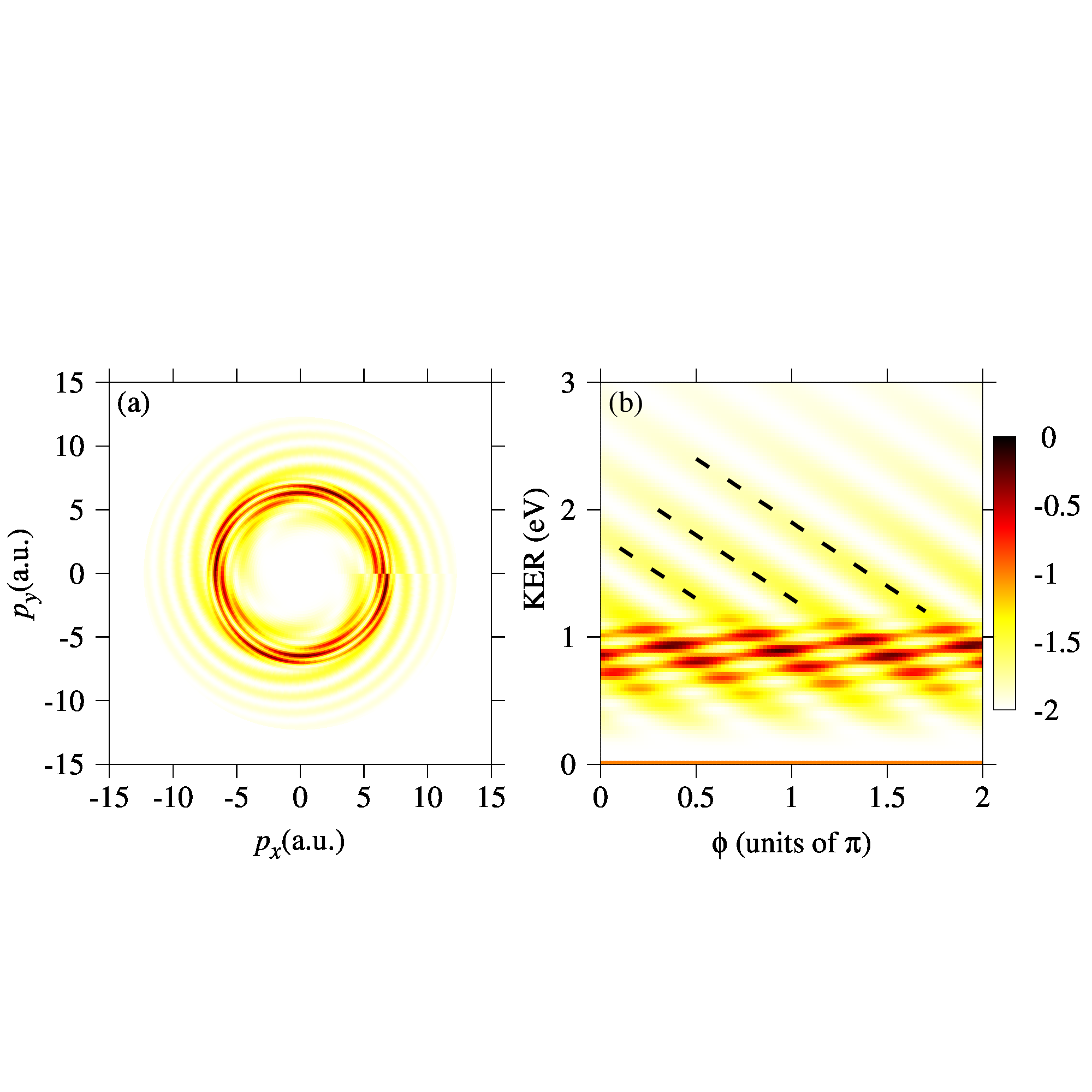
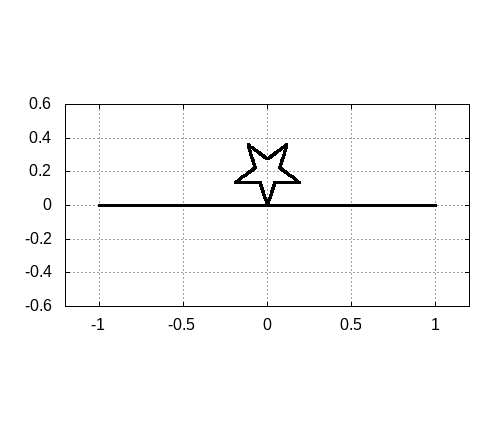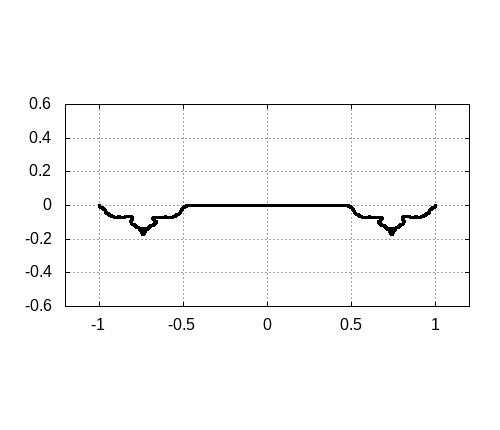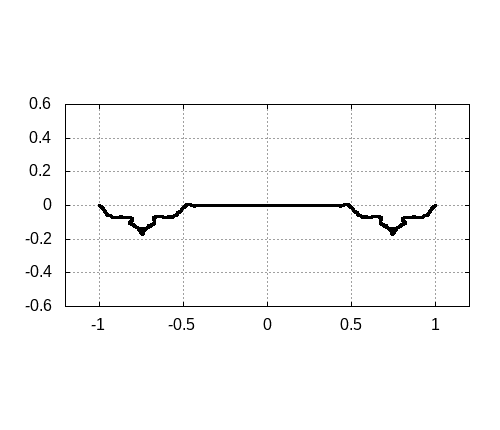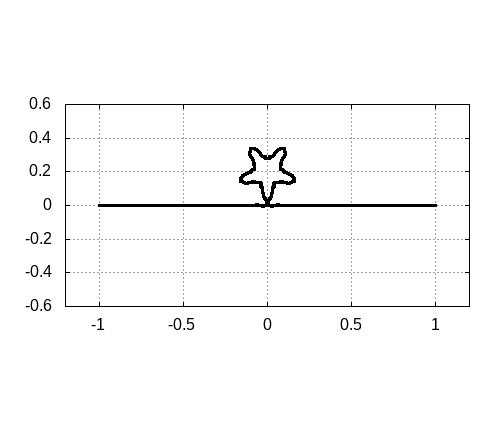
[2]の図3

[2]の図3をgnuplotで再現した図

データは適当に作成しました。データのダウンロードは以下からどうぞ。
https://slpr.sakura.ne.jp/qp/supplement_data/PRA102_033107_Fig3likedata.tar.gz

※ギリシャ文字Φは、

{/Symbol-Oblique f}

とすることでギリシャ文字のイタリックを用いることができます。

[1]と同じ部分がかなりあるので、違う部分だけを説明していきます。

  • カラーマップの設定
    見た目で[3]の’hot’と呼ばれるカラーセットだとわかったので、それを用います。

    set palette rgb 21,22,23 negative # colormap setting

    ただし、カラーマップの色が反対になっているので、それを指定するnegativeを追加しています。

  • カラーボックスの設定
    unset colorbox

    ~~~~

    set cbtics 0.5 scale 0 # scale 0, to delete tics line in colorbox
    set cbr[-2:0]
    set colorbox user origin 0.91,0.35 size 0.02,0.25 border # change size of colorbox

    カラーボックスに注目すると、左図(a)はカラーボックスがないですが、右図(b)にはあります。なので、カラーボックスを出力しないunset colorboxを指定しています。
    また、(b)のカラーボックスはカラーの値を示すところにticsが入ってないため、cbticsのscale（ticsの線の大きさ）を0にしています。
    さらに見ると、カラーボックスの大きさが少し小さいです。なので、カラーボックスの大きさ位置を指定するために、set colorbox user origin …を指定しています。

  • テキストボックスの表示
    set label tc rgb "black" at graph 0.02, graph 0.95 front "(a)"

    グラフ上のテキスト(a), (b)は、テキストボックスを追加して画面上に表示します。上のような指定で表示できます。

ベクタ形式であるEPS画像のサイズは752kBです。論文に投稿する画像としては、許容できるといえばできるサイズですが、若干大きいです。

ラスタライズ形式であるPNGをimagemagickを用いて

convert -density 400x400 -background white -flatten -alpha off PRA102_033107_Fig3.eps PRA102_033107_Fig3.png

で変換すると296kBです。2倍少し容量が小さくなるので論文全体の画像数が多いのならば、ラスタライズ形式の方が良いかもしれません。共著者と相談するとよいでしょう。

以上で説明を終わります。

参考文献

[1]S. Goto and I. Danshita, “Measurement-induced transitions of the entanglement scaling law in ultracold gases with controllable dissipation”, Phys. Rev. A 102, 033316 (2020)

[2]Z. Chen and F. He, “Interference of nuclear wave packets carrying different angular momenta in the dissociation of H2+ in strong circularly polarized laser pulses”, Phys. Rev. A 102, 033107 (2020)

[3]color mapについて
http://www.gnuplotting.org/?s=color

[4]6.4 What if I need h-bar (Planck’s constant)?　-gnuplot FAQ
http://www.gnuplot.info/faq/#x1-610006.4

そのほか有用なページ

gnuplotでoption詰め込んで論文用figureを作ってみた[1]　-qiita, @ucc_white
https://qiita.com/ucc_white/items/544b85e009a58d046d3c

Gnuplotのいろは -東京工業大学　科学技術創成研究院　佐藤千明研究室
http://www.csato.pi.titech.ac.jp/From2014/software/how-to-gnuplot.html

プログラミングと数値計算, 物理学

連成振動

コメントする

弦を考えます。弦は重さ\(M\), 長さ\(L\), ばね定数\(K\)を持ちます。

この弦を波動方程式に頼らないで定式化しましょう。
波動方程式は、2次元の波動のうち、1次元分の方向を\(y=y(x, t)\)として表現するため、x軸にとって多価関数となる弦を表現することが出来ません。物性物理学等で格子の振動を考える場合は、結晶を構成する原子が平衡位置から殆ど動かないのでこういった問題は起こりません（起こったとしても無視される位少ないので、大多数の振る舞いを考える場合には問題になりません）。
よって多次元の問題を考えるには波動方程式を元にして考えるのは不適切です。そのため、弦を単なる連成振動として考えて、完全に2次元の問題として扱いたいと思います。

図のような連成振動のモデルを考えます。

質量\(m\)を持つ\(i\)番目の質点が、位置ベクトル\(\mathbf{x}_i\)で指定され、隣り合う質点との間が、ばね定数\(k\)、自然長\(l\)を持つ理想的なばねで繋がれているとします\((i=1,2,\cdots, N)\)。この時、運動方程式を立てると
\begin{eqnarray}
m\frac{d^2 \mathbf{x}_i}{dt^2}&=&
+k(|\mathbf{x}_{i+1}-\mathbf{x}_{i}|-l) \frac{\mathbf{x}_{i+1}-\mathbf{x}_{i}}{|\mathbf{x}_{i+1}-\mathbf{x}_{i}|}
-k(|\mathbf{x}_{i}-\mathbf{x}_{i-1}|-l)\frac{\mathbf{x}_i-\mathbf{x}_{i-1}}{|\mathbf{x}_i-\mathbf{x}_{i-1}|}
\end{eqnarray}
となります。全く同じですが、見通しをよくするため式変形すれば、
\begin{eqnarray}
m\frac{d^2 \mathbf{x}_i}{dt^2}&=& k\Bigl[A_i \mathbf{x}_{i+1}-\bigl(A_i+A_{i-1}\bigr)\mathbf{x}_{i}+A_{i-1} \mathbf{x}_{i-1}\Bigr]
\end{eqnarray}
と表せます。ここで、
\begin{equation}
A_i = \frac{|\mathbf{x}_{i+1}-\mathbf{x}_{i}|-l}{|\mathbf{x}_{i+1}-\mathbf{x}_{i}|},~~(i=1,\cdots, N, A_N = 0)
\end{equation}
と置きました。

さて、こうしたモデルを考えた時に、連成振動として考えた\(N\)分割した1つ1つの小さいばね（”ミクロなばね”と名づけます）とその弦を1つにみなした時の大きなばね（”マクロなばね”と名づけます）の間の関係式を考えましょう。
仮定として、等間隔に分割し、弦の密度は一様であるとします。

この条件の下で、
マクロなばねの重さ\(M\), 自然長\(L\), ばね定数\(K\)
と
ミクロなばねの重さ\(m\), 自然長\(l\), ばね定数\(k\)
の間の関係式を導出します。

結論として、マクロとミクロなばねの間に成り立つ関係は
\begin{eqnarray}
L&=&N l \\
M&=&N m \\
K &=& k/N
\end{eqnarray}
となります。

自然長

自然長\(L\)の弦を\(N\)分割するので、
\begin{equation}
L=N l
\end{equation}
の関係があります。

重さ

重さ\(M\)の弦を\(N\)分割するので、
\begin{equation}
M=N m
\end{equation}
と書けます。

ばね定数

最後にばね定数の関係を考えましょう。この関係は、弾性エネルギーを考えることで導くことができます。
マクロなばねとして全体を見た場合に長さ\(D\)だけ縮んだ時に蓄えられる弾性エネルギーと
同じだけ縮んだ時にミクロな\(N\)個のばねに蓄えられる弾性エネルギーが同じであってほしいと要請します。すなわち、ミクロなばねの縮みの合計がマクロなばねの縮み\(D\)に等しいとすると、
\begin{equation}
D=N d
\end{equation}
と書けます。
実は、大胆な過程をしないとマクロなばねとミクロなばねの関係を求めることが出来ません。
なぜなら、マクロなばねはいつでも線形応答をするかのように現在考えていますが、ミクロなばねでは場所ごとに違っても良いという様に定式化しています。なのでもともと無理な話なのです。
ではどうやって妥当な関係式を導出すればよいかといえば、ばねが非常にゆっくり運動が行われるときを仮定するのです。ゆっくり動くときの振る舞いは全てのばねが同じ動きをするとして差し支えないでしょう。そうして定式化します。
よって、
\begin{eqnarray}
\frac{1}{2}K D^2 &=& N\cdot \frac{1}{2} k d^2 \nonumber \\
\to ~~ K &=& k/N
\end{eqnarray}
という関係式が導けます。

あとは数値計算を行うだけです。陽的ルンゲクッタ法で解いたプログラムを以下に示します。

https://slpr.sakura.ne.jp/qp/supplement_data/wave_particles.tar.gz

実行は、

$ gfortran rkf45.f90 main.f90
$ ./a.out

でokだと思います。初期状態や、重さや自然長はinputファイルを見てください。

実行後、動画をgnuplot上で出力したければ、

$ gnuplot
$ call "movie.plt" 100

としてください。100は表示する時間ステップを表します。この引数の値の最大はinputファイルの中のNtまでです。

数値計算結果

実際に数値計算を行う条件として、自然長や重力があると波動方程式と若干異なる振る舞いになってしまうので、対応を見る上ではなくしています。すなわち、自然長\(L=0\)、重力\(g=0\)として計算します。

三角パルス

三角形の波がパルス状に存在するとします。
そして初期状態として、初速度がゼロであることを仮定しましょう。

この場合、波動方程式の考察から、
同じ関数であらわされる右向きの波\(f(x-vt)\)と左向きの波\(f(x+vt)\)の重ね合わせとして書かれることが分かっています。すなわち、解\(y=y(x,t)\)は
\begin{equation}
y(x,t)=f(x-vt)+f(x+vt)
\end{equation}
と書かれます。図で表せば以下のように時間発展していくことが期待されます。

これが本稿の連成振動モデルで実際にそうなっているのかを確かめるのは良い問いかけでしょう。
実際に連成振動を数値的に解くと以下の通りになります。

ゆっくりと時間発展を見ていくと

となります。明らかに右向きに進む波と左向きに進む波として分離します。分離した結果から、初期状態がそれらの波の重ね合わせで表現されていたことが分かるでしょう。

矩形パルス

矩形パルスを考えてみます。実際に数値計算をするとこんな感じです。

結局右向きと左向きの重ね合わせとしてあらわされることも確認できますが、決して単純なそれらの足し合わせで書かれているわけではないことがわかります。この振る舞いは、波動方程式に対応するように連成振動モデルを作っていないことから由来します。波動方程式としてあらわした二階微分の偏微分方程式の場合は多価関数をとることができません。なので縦に弦が伸びる場合、間に質点を置くことができないので質点の位置がいきなり飛ぶことになります。しかし、連成振動モデルではその制約をして初期状態を準備しているわけではありませんのでその違いが出て来ます。図で表せば、以下のようになります。

両者の違いがあるので、波動方程式の結論である
\begin{equation}
y(x,t)=f(x-vt)+f(x+vt)
\end{equation}
が成り立っていない、と解釈することができます。

少しずつ時間発展をみるとこの通りになります。

三角形の波

端まで三角形のパルスであった場合にどのように振る舞うかを見てみましょう。特に面白い振る舞いがあるわけではなく、上のパルスの、右向きと左向きの波の重ね合わせで説明ができるので、単にシミュレーション結果を載せるだけにとどめます。実際に計算してみると以下のようになります。

星形

初期状態が星型である場合も見てみましょう。振る舞いも同じです。

注意点としては、実際にこの振る舞いは起こりえないことに注意しておきましょう。なぜなら、本当の弦で行った場合、重なる場所があると弦の衝突が起こります。しかし、この連成振動モデルでは計算上、衝突は起こりません。

偏りがある三角形のパルス

偏りがある場合も波動方程式では記述することができません。こんな感じの初期状態です。

これを実際にシミュレートすると以下の通りになります。

3次元の場合

3次元の場合も載せておきます。ふるまい自体はそんなに変わるわけではないので、シミュレーション結果を載せるだけにとどめておきます。