gnuplot上で行う任意関数のフィッティング

gnuplotには、”fit”というコマンドがあります。
これを利用すると、データ列に対して、任意の自由度を含んだ関数\(f(x)\)でフィッティングを行うことが出来ます。
手法はMarquardt-Levenberg法に基づいた非線形最小二乗法によるフィッティングです。

gnuplot ver4.6の場合

データ列”data.d”を\(f(x)=ax^2+bx+c\)でフィッティングする\(a,b,c\)を求めたい場合、gnuplot上で

f(x)=ax**2+bx+c
fit f(x) "data.d" u 1:2 via a,b,c

※gnuplot ver5.0以降の場合、エラーバーで重みづけしたフィッティングが出来るようです。
http://gnuplot.sourceforge.net/demo_5.0/fit.html

説明

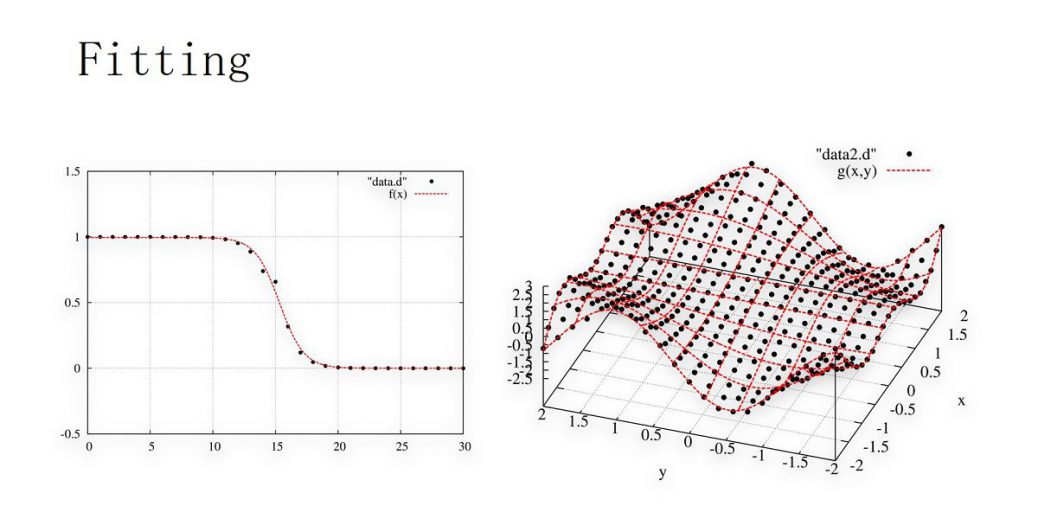
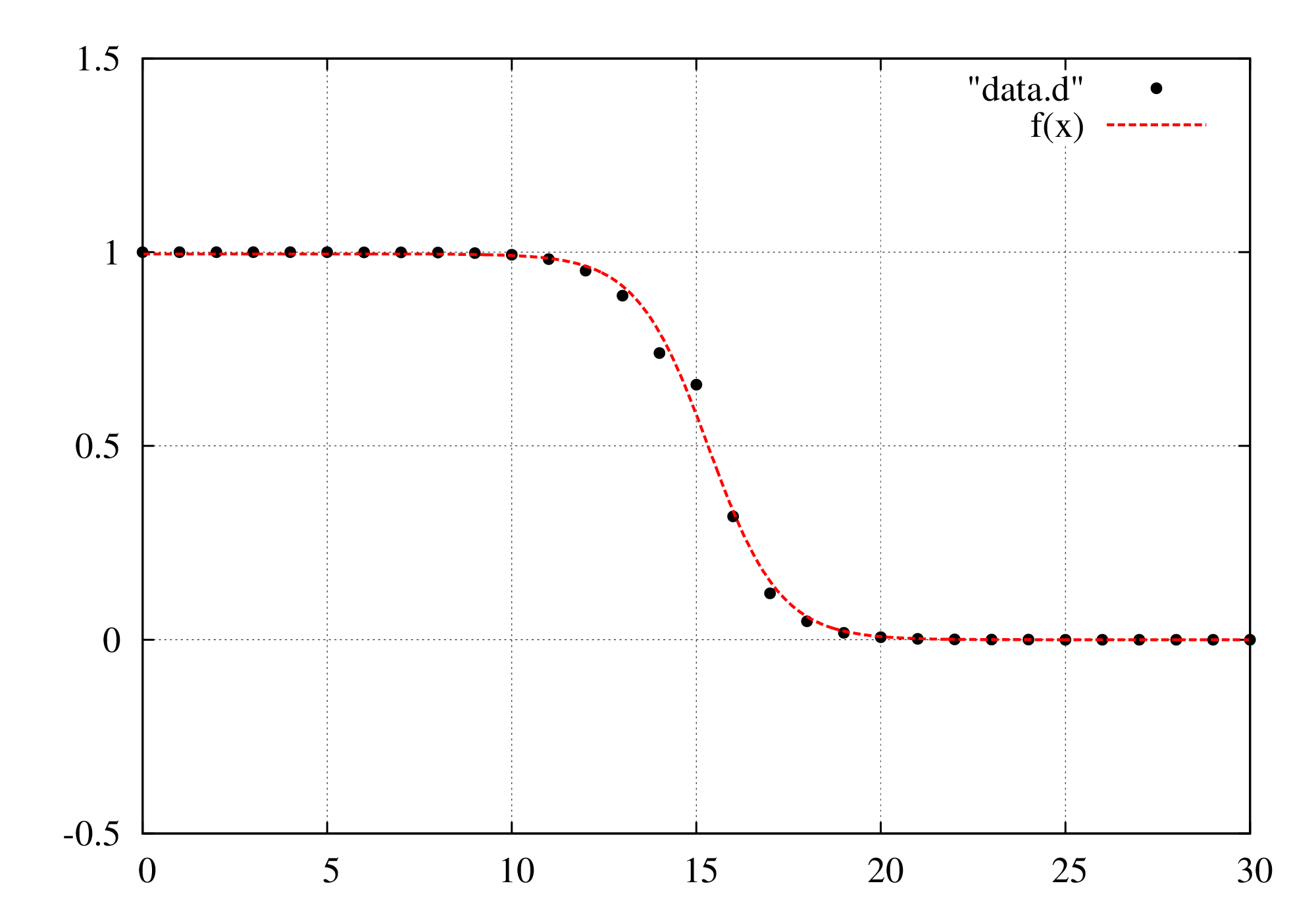
以下のデータ列（ファイル名”data.d”）に対してgnuplot上でフィッティングを行います。

▼ここクリックでこの場にデータを展開

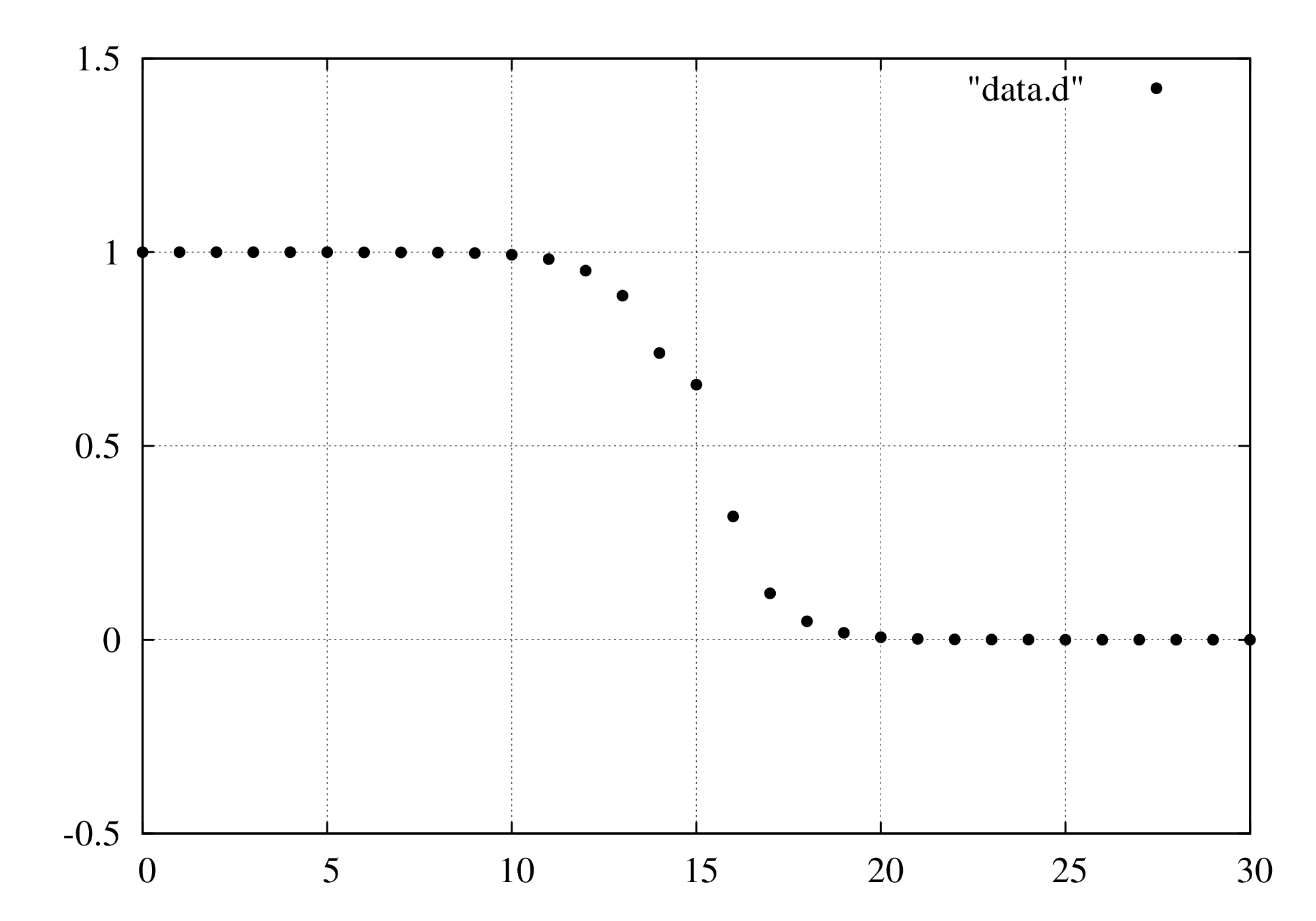
データは、関数
\(
\displaystyle f(x)=\frac{1}{1+e^{x-15}}
\)
に乱数を与えて生成したデータです。

このデータ列に対して、
\(
\displaystyle f(x)=\frac{a}{1+e^{(x-b)/c}}
\)
でフィッティングを行い、未知の定数\(a,b,c\)を決めたいと思います。

gnuplot上で

f(x)=a/(1+exp((x-b)/c))
a=1e0
b=10e0
c=0.5e0
fit f(x) "data.d" u 1:2 via a,b,c

と打つと、\(a,b,c\)にフィッティングした後の定数が入ります。
ここで、フィッティング前に\(a,b,c\)の値を入れているのは初期値です。
初期値があまりにも違うとうまくフィッティングが失敗するので、出来るだけ近い値を入れましょう。

実際に動かすと

> fit f(x) "data.d" u 1:2 via a,b,c
...

Final set of parameters Asymptotic Standard Error
======================= ==========================

a = 0.995618 +/- 0.005679 (0.5704%)
b = 15.3268 +/- 0.051 (0.3327%)
c = 0.970465 +/- 0.04439 (4.574%)

...
>

という文章が出力されます。

フィッティングの結果、
\(a=0.995618,b=15.3268,c=0.970465\)と求められました。
乱数を与える前のデータは\(a=1,b=15,c=1\)ですので、元の関数に近いことが分かります。
fitコマンドを動かした後は既に\(a,b,c\)に値が代入されているので、そのまま

plot f(x)

とすれば、フィッティング結果をプロットすることが出来ます。

データと共に載せれば以下のようになります。

フィッティングする範囲を制限したければ、

fit [10:20] f(x) "data.d" u 1:2 via a,b,c

とすると、\(x\)の範囲を\([10,20]\)に制限することが出来ます。

2変数関数のフィッティング

2変数関数であろうとフィッティングは可能です。
元のデータ
(https://slpr.sakura.ne.jp/qp/supplement_data/data2.d)
は、関数
\(
g(x,y)=x\sin(xy+0.5)
\)
に適当な乱数を足して作られたデータです。グラフにすれば

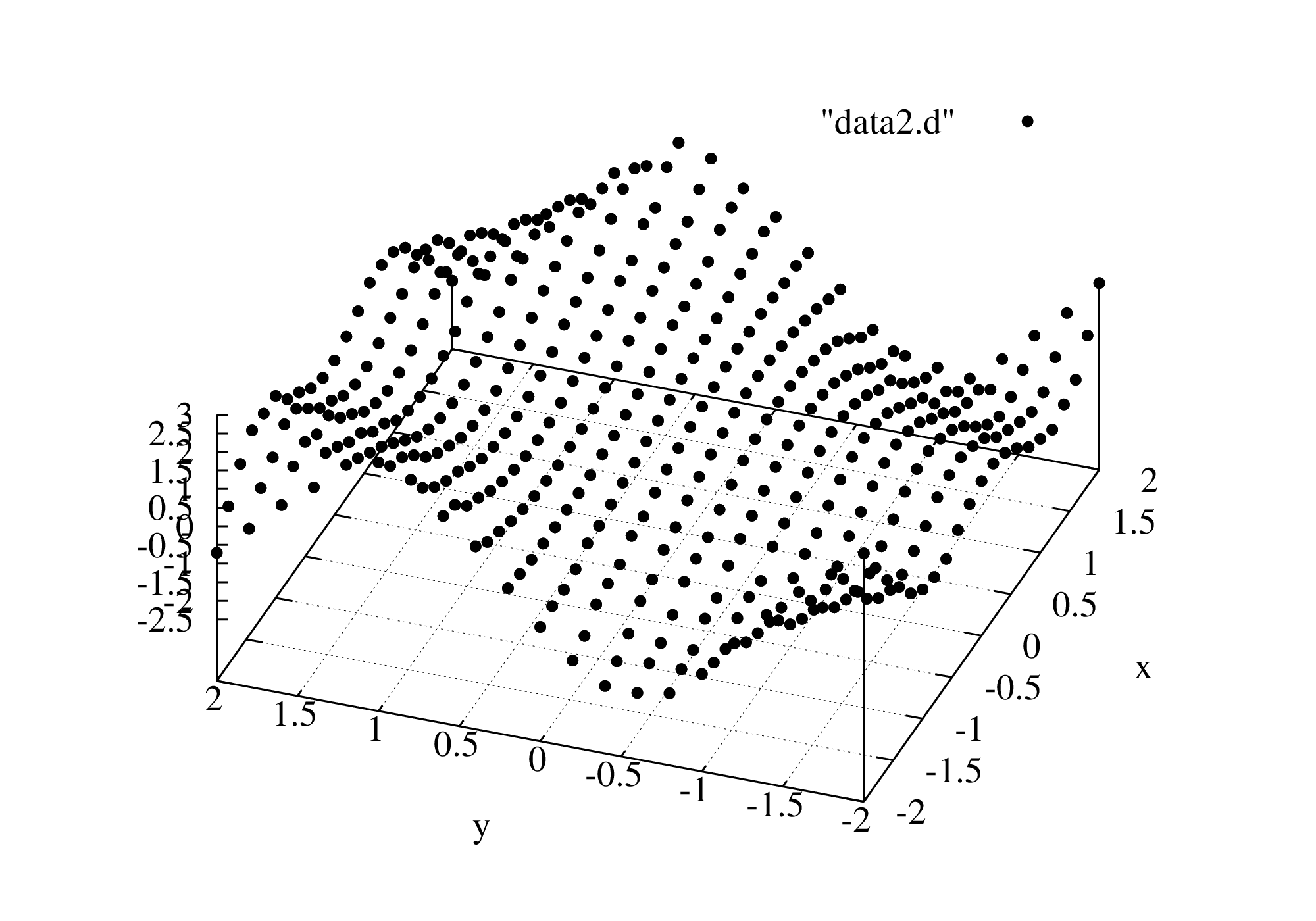
となります。

このデータに対して、gnuplot上で関数
\(
g(x,y)=ax\sin(bxy+c)
\)
によるフィッティングを行います。コマンドは

g(x,y)=a*x*sin(b*x*y+c)
a=1.3e0
b=0.7e0
c=0.3e0
fit g(x,y) "data2.d" u 1:2:3 via a,b,c

です。
実行すると

>fit g(x,y) "data2.d" u 1:2:3 via a,b,c

...
Final set of parameters Asymptotic Standard Error
======================= ==========================

a = 1.16313 +/- 0.004072 (0.3501%)
b = 1.00073 +/- 0.001672 (0.1671%)
c = 0.495134 +/- 0.003432 (0.6932%)
...

>

と得られますので、フィッティング結果と共にプロットすれば

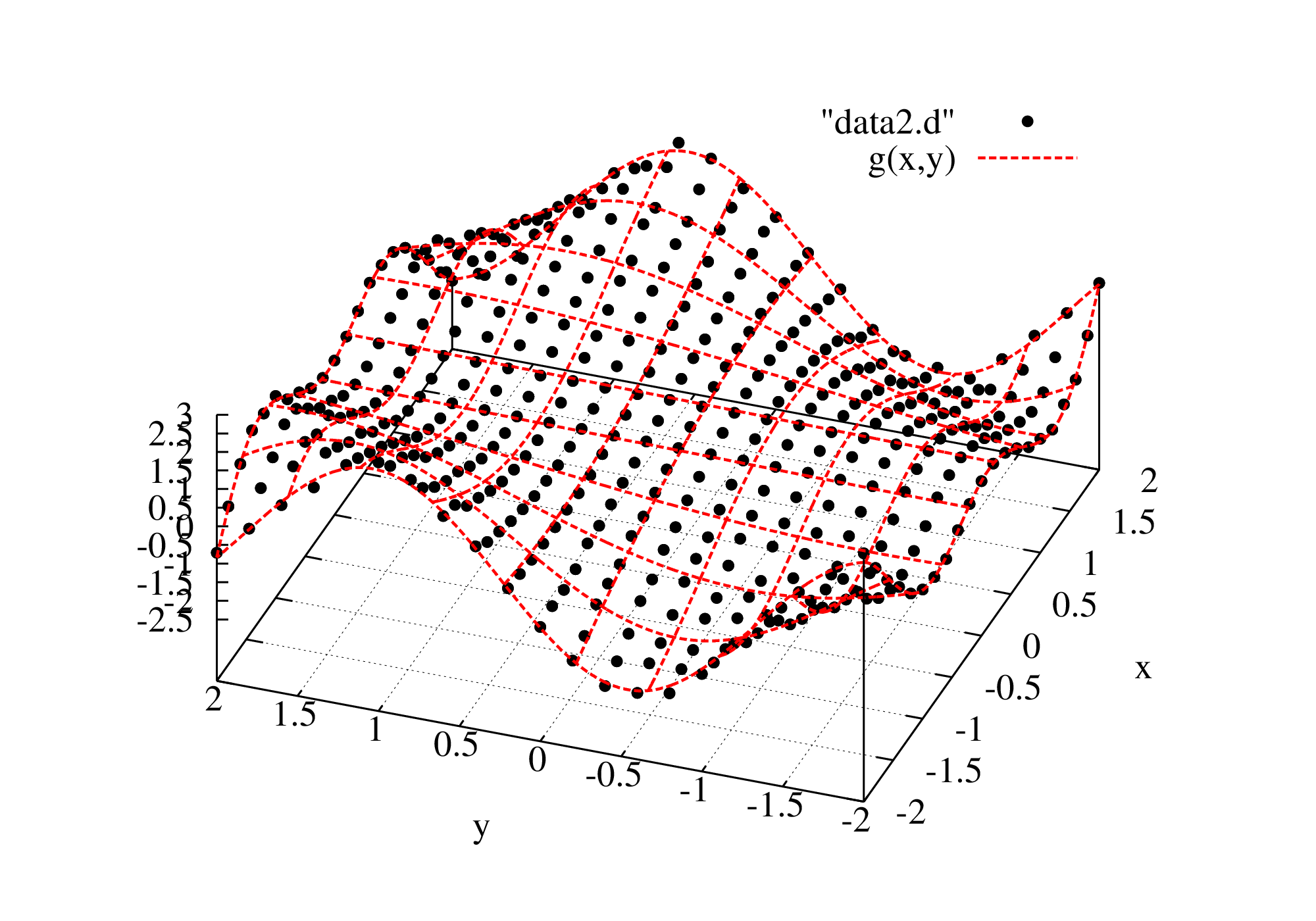
となります。