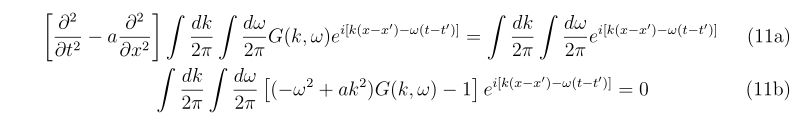古典的な一次元波動方程式のグリーン関数

本稿のpdfはこちらをどうぞ
https://slpr.sakura.ne.jp/qp/wp-content/uploads/2021/08/Green_1dclassical5.pdf

問題

古典的な一次元波動方程式で、非斉次項を持つ問題

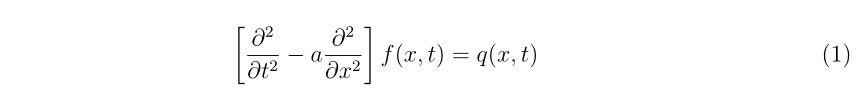
を解くことを考えます。この形は、有限範囲内しか相互作用を引き起こさない物に十分遠方から波が入射してきた場合を考える際に現れたりします。

この形の方程式が出てくる状況を考えてみましょう。

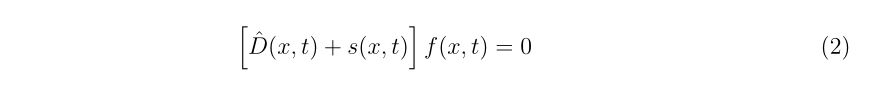
の問題を考えます。移項して

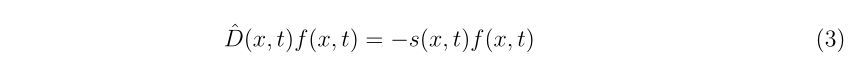
ですので、グリーン関数を用いると

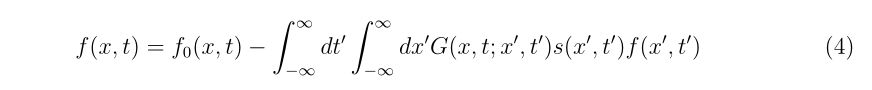
となります。ここで、

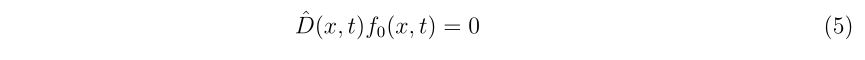
を満たす関数（一般解）であり、グリーン関数を
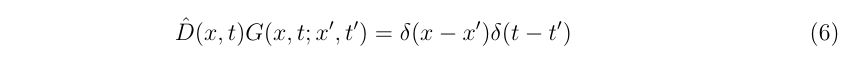で与えられます。ここを満たす関数（特殊解）としました。
式(4)の右辺に解$f(x,t)$が含まれていますが、このままの形でとどめておきます。この形にしておくと、ほかの式に$f(x,t)$をダイレクトに代入できたり、近似を使うときに便利な形です。

（式（7）はありません）

本稿の目的は、$\hat{D}$が$\hat{D}=\frac{\partial^2}{\partial t^2}-a\frac{\partial^2}{\partial x^2}$で与えられている場合に、$G(x,t; x’,t’)$の具体的な形を導出することです。

導出

今、解きたい問題は、

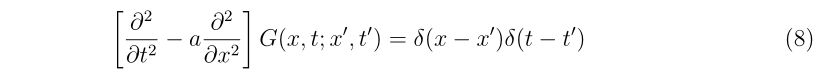
です。デルタ関数をそのまま扱う場合、積分が絡んでこないと扱うのが難しいです。そうでなければ、フーリエ変換を用いて波数・周波数空間で解いていくのが良いでしょう。グリーン関数や、デルタ関数のフーリエ変換を考えると

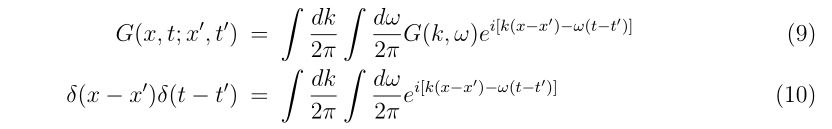
となります。ここで、基底関数が$e^{ikx}, e^{-i\omega t}$と符号が異なることに注意しましょう。
また、積分区間はいつも負の無限大から正の無限大であり、いちいち書くのは面倒なので省略しています。
フーリエ変換として考えるのではなく、基底関数へ射影した時の係数と考えましょう。

実際に式(8)に代入すると

となります。

ここで$e^{i[k(x-x’)-\omega(t-t’)]}$はゼロにならないので、その前の項[ ]内がゼロにならなければなりません。よって

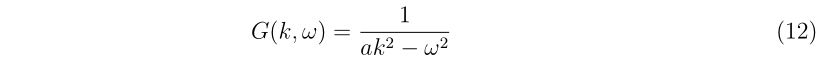
が導けます。よって式(9)に代入して

が計算できれば位置と時間のグリーン関数が得られます。

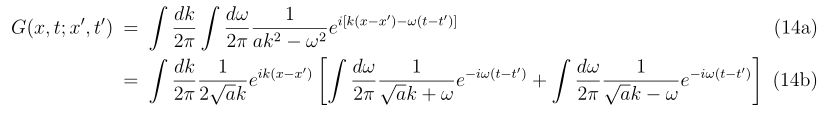
さて、この積分を計算してみましょう。
右辺の$e^{i\omega t}/\omega$の形を持つ積分は複素関数論において頻出する積分です。この積分の特徴として、$\omega$に渡る積分を実軸上で実行する際に、たまたま$\omega=\pm \sqrt{a}k$に等しい点を通ってしまうため、実軸上では被積分関数が発散する、という特徴があります。この発散する点は極と呼ばれており、積分を行う際に積分経路をうまく選んで極を迂回しなければなりません。しかし、厄介なことに極を上に回るか下に回るかで積分結果が変わってしまいます。

もし、天才でしたら当たり前のように適切な積分経路をすぐに思いつくでしょうが、我々凡人には具体的に試してみるくらいしか思いつきません。ですのでちょっとズルしながら因果律を満たす解を探しましょう。

今、我々はグリーン関数について考えています。ということは、計算した結果の境界条件は、因果律を満たすような結果が欲しいわけです。
つまり、グリーン関数が得られた場合、$\theta(t-t’)$の形が出てくるであろうことは予想できます。そのため、これを考慮して極を回る方向を考えてグリーン関数を求めていきましょう。

式(14b)の第一項

について考えます。ヘヴィサイド関数を積分表記で表すと、

と書けることを使います。ここで$i$は虚数単位です。もう嬉しいですね。かなり似通った形であることが分かるでしょう。
式(16)の形に持っていくためには変数変換を行えば良さそうです。つまり、極は上に回れば因果律を満たすグリーン関数が得られそうです。

では具体的に計算していきましょう。変数変換$y=\omega+\sqrt{a}k$を使って、

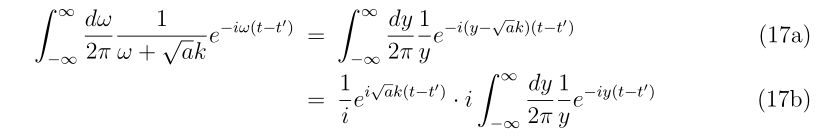
となります。分母に$+i\varepsilon$を加えるようにして

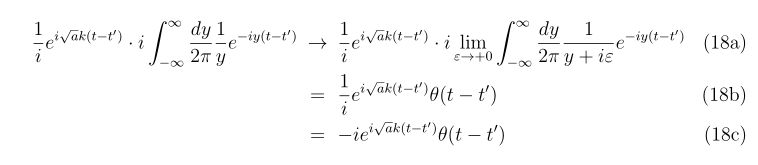
と求めることができます。

続いて式(14b)の第二項

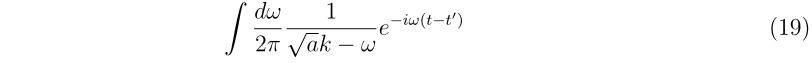
についても同様に計算していきましょう。変数変換$y=-\omega+\sqrt{a}k$を使って、

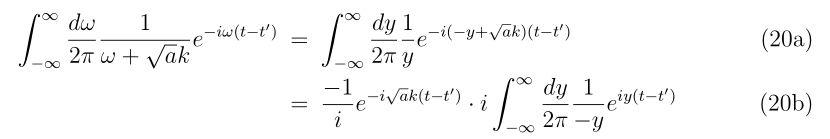
ヘヴィサイド関数を考えると、

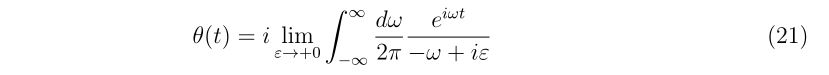
の形が使えそうです(式(16)の$\omega\to-\omega$の変数変換ですね)。ですので、

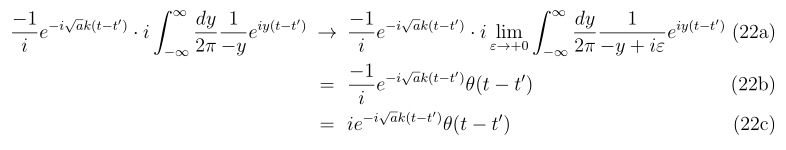
と求められます。

式(18c)と式(22c)より、式(14b)に代入すると

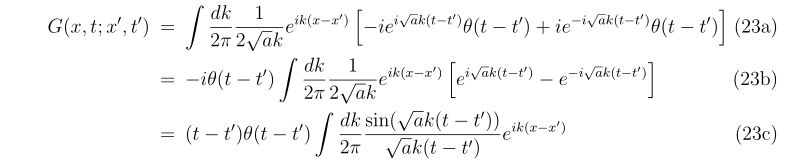
となります。

さて、$\frac{\sin x}{x}$の形はsinc関数と呼ばれているほど面白い性質を持つ関数です。そのフーリエ変換は矩形になることが知られています。その計算は実際に
\begin{align}
\int_{-\infty}^{\infty}\frac{\sin(k)}{k}e^{ikx}\frac{dk}{2\pi}=\frac{1}{2}\Bigl[\theta(x+1)-\theta(x-1)\Bigr]
\end{align}
となります。

立ち戻り、変数変換$\kappa=\sqrt{a}k(t-t’)$を考えれば、

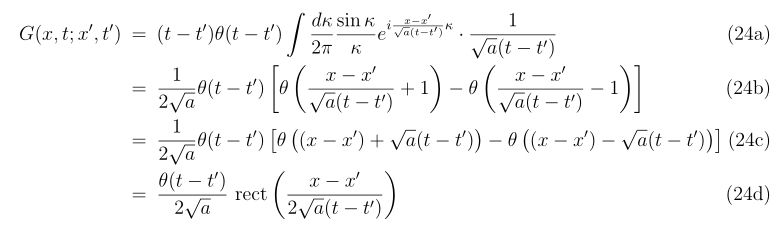
と、グリーン関数が求められました。グリーン関数は$x-x’, t-t’$の形をしていることが分かります。そのため、

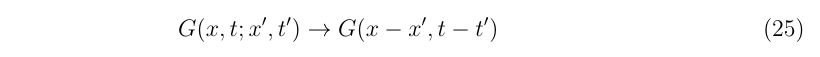
と書いても良いことが分かるでしょう。ここで、

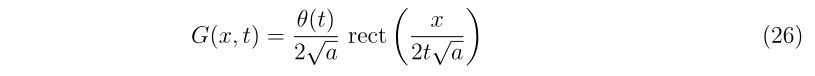
です。

まとめと補足

まとめ

まとめますと、偏微分方程式

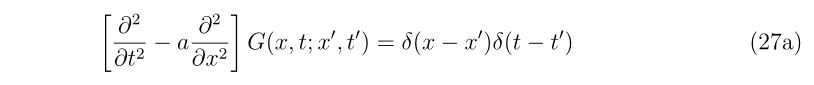
の因果律を満たす解は、

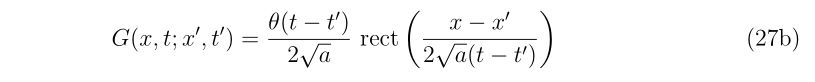
となります。以上から、波動方程式

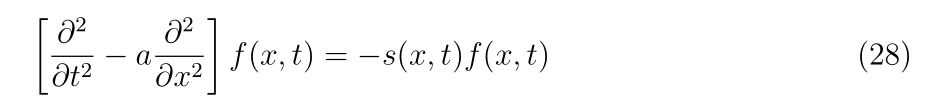
の因果律を満たす一般解は

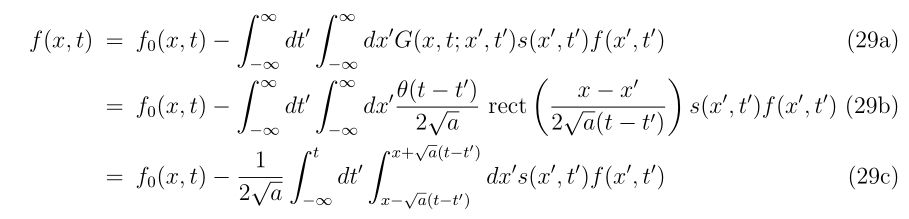
となります。

補足

補足します。因果律を満たすグリーン関数である、ということが暗に意味される場合、積分(29a)の時間に渡る積分はグリーン関数に含まれるヘヴィサイド関数を先に利用して、

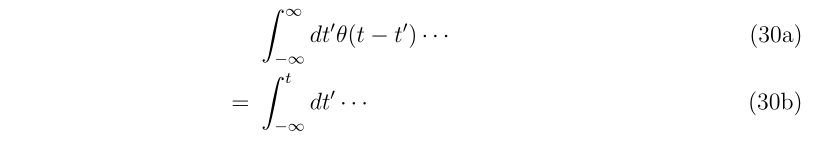
と積分範囲を組み込んで表記する場合があります。実際の例が式(29c)であり、その時間積分の積分範囲のようになることを見越している、ということです。

少しグリーン関数の物理的な意味を考えてみましょう。
グリーン関数は、ある特定の時刻、ある特定の位置でデルタ関数という非常に特殊な衝撃が生じた結果を記述します。
言い換えれば、偏微分方程式で表されている系が、デルタ関数によってどのような応答を起こすか？という関数です。

式(27b)を見てみると、１つのヘヴィサイド関数$\theta(t-t’)$と１つの矩形関数$\text{rect}\left(\frac{x-x’}{2\sqrt{a}(t-t’)}\right)$が使われています。
$\theta(t-t’)$の部分は、まさに因果律を示しており、衝撃が加わる前の時刻$(t-t’ \lt 0)$においては系の応答は無いよ、ということを表しています。至極全うでしょう。

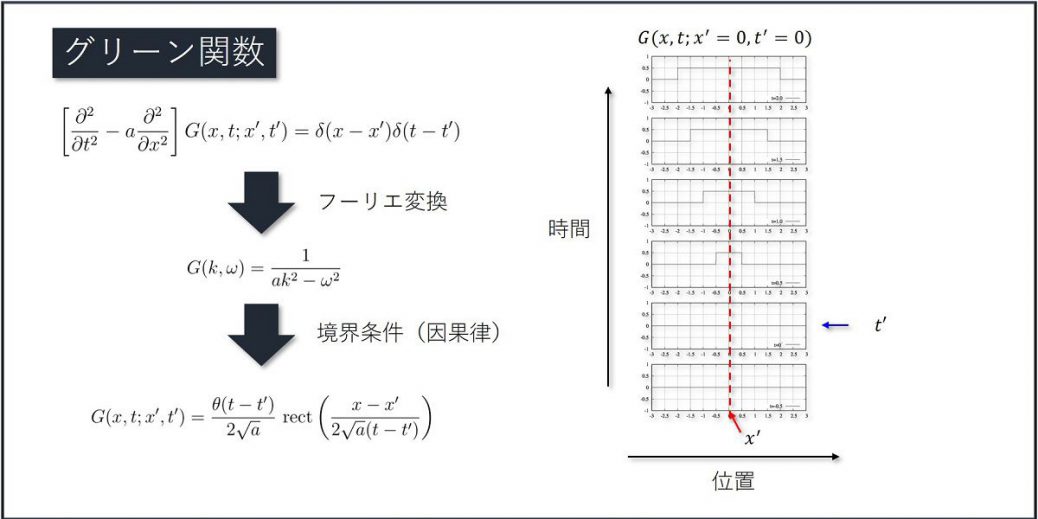
矩形関数の部分は、衝撃が生じた後にその衝撃は波及する範囲を表しています。具体的に、時刻$t=t’$, 位置$x=x’$において衝撃が生じた場合、矩形関数の中身が値を持つ範囲は$[x’-\sqrt{a}(t-t’), x’+\sqrt{a}(t-t’)]$の範囲です。つまり、衝撃が時々刻々と広がっていることを示しています。グリーン関数を図示すると、このような感じです。

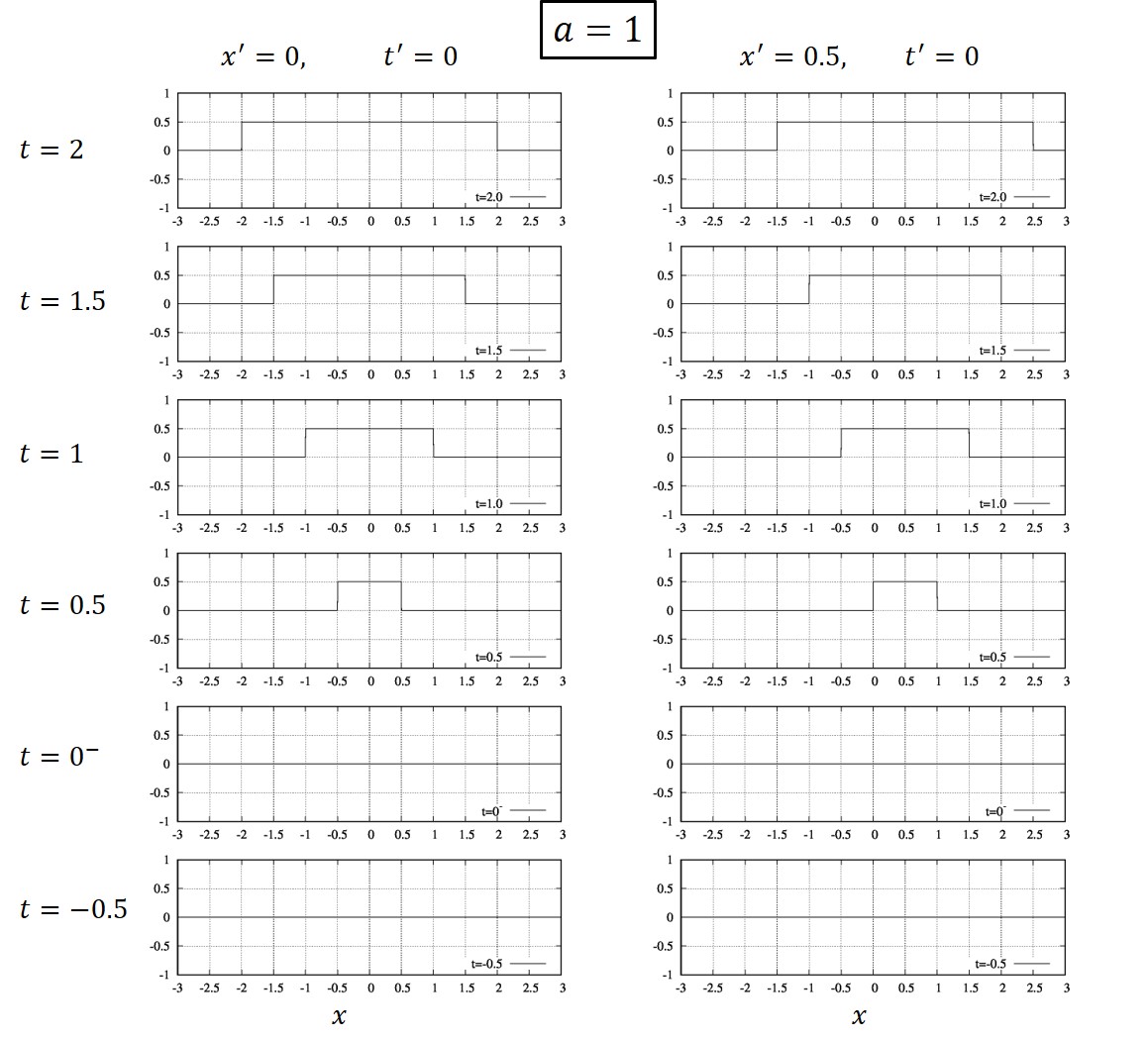
衝撃が加わる$t=0$を境にグリーン関数が値を持ち始め、それが時間とともに広がっていくのが分かると思います。

ついでにグリーン関数の広がる速度を計算してみましょう。

矩形関数の中身が値を持つ範囲$x$は、時間$\Delta t=t-t’$の間に、距離$x-x’=\pm \sqrt{a}(t-t’)$だけ波及しますから、衝撃の結果が速度$\pm\sqrt{a}$で広がっていることが分かります。
これは、古典的な波動方程式でよく知られているように、系の速度が

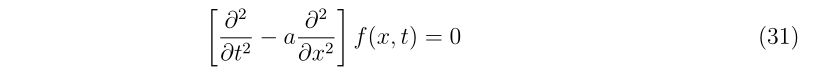
の系の速度は$\pm\sqrt{a}$である、という事実と一致します。
つまり、衝撃が加わった時刻以外では、系そのものの性質しか存在しませんので、衝撃が波及していく速度が一致することは何ら不思議ではありません。むしろ、一致しなければなりません。