本稿では簡単にまとめのみを載せます。
詳細は以下のPDFにまとめていますので、ご参照ください。
https://slpr.sakura.ne.jp/qp/supplement_data/groupphase_velocitydelay/group_phase_velocity_delay.pdf

本編では、なぜインパルス応答と初期状態の畳み込みが応答になるのか、なぜ畳み込みが出てくるのかを数式でおおよそ説明しています。

まとめ

---

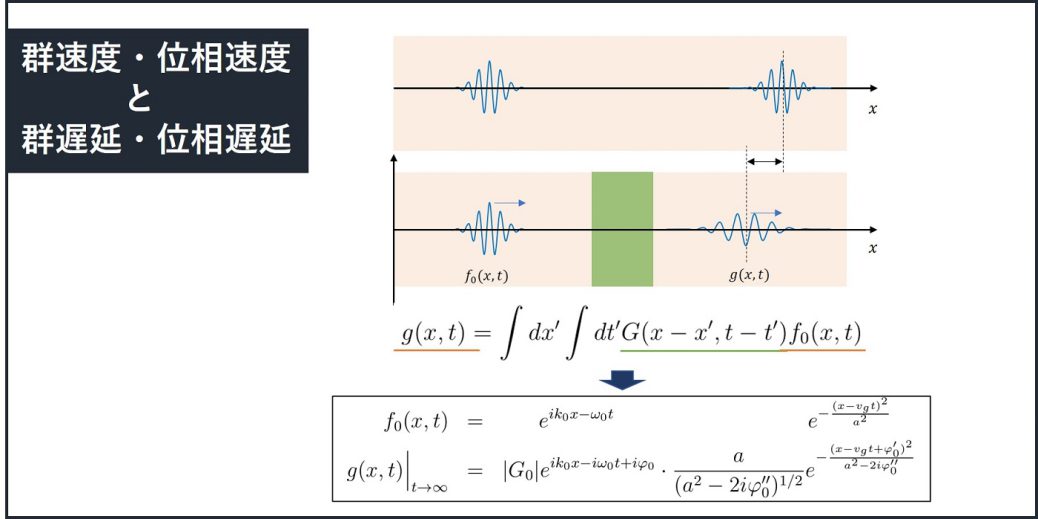
分散関係\(\omega = \omega(k)\)を満たす媒質中で、波\(f\)が位置\(x\)と時間\(t\)の変数として書けている場合、
波\(f(x,t)\)は
\(\displaystyle
f(x,t)=\int \frac{dk}{2\pi} f(k) e^{ikx} e^{-i\omega(k) t}
\)
と書けます。特に\(k=k_0\)周りしか波が存在しない場合、波は
\(\displaystyle
f(x,t)=A(x-v_g t)e^{ik_0 (x-v_p t)}
\)
と書けます。ここで、\(A(x)\)は波数\(k\ll k_0\)でしか値を持たないゆっくり振動する波です。また\(v_g, v_p\)はそれぞれ群速度、位相速度を表し、以下の式で表されます。
\(\displaystyle
v_g\equiv \omega'(k_0)=\frac{d\omega}{dk}\biggr|_{k=k_0},~~~v_p\equiv \frac{\omega(k_0)}{k_0}
\)

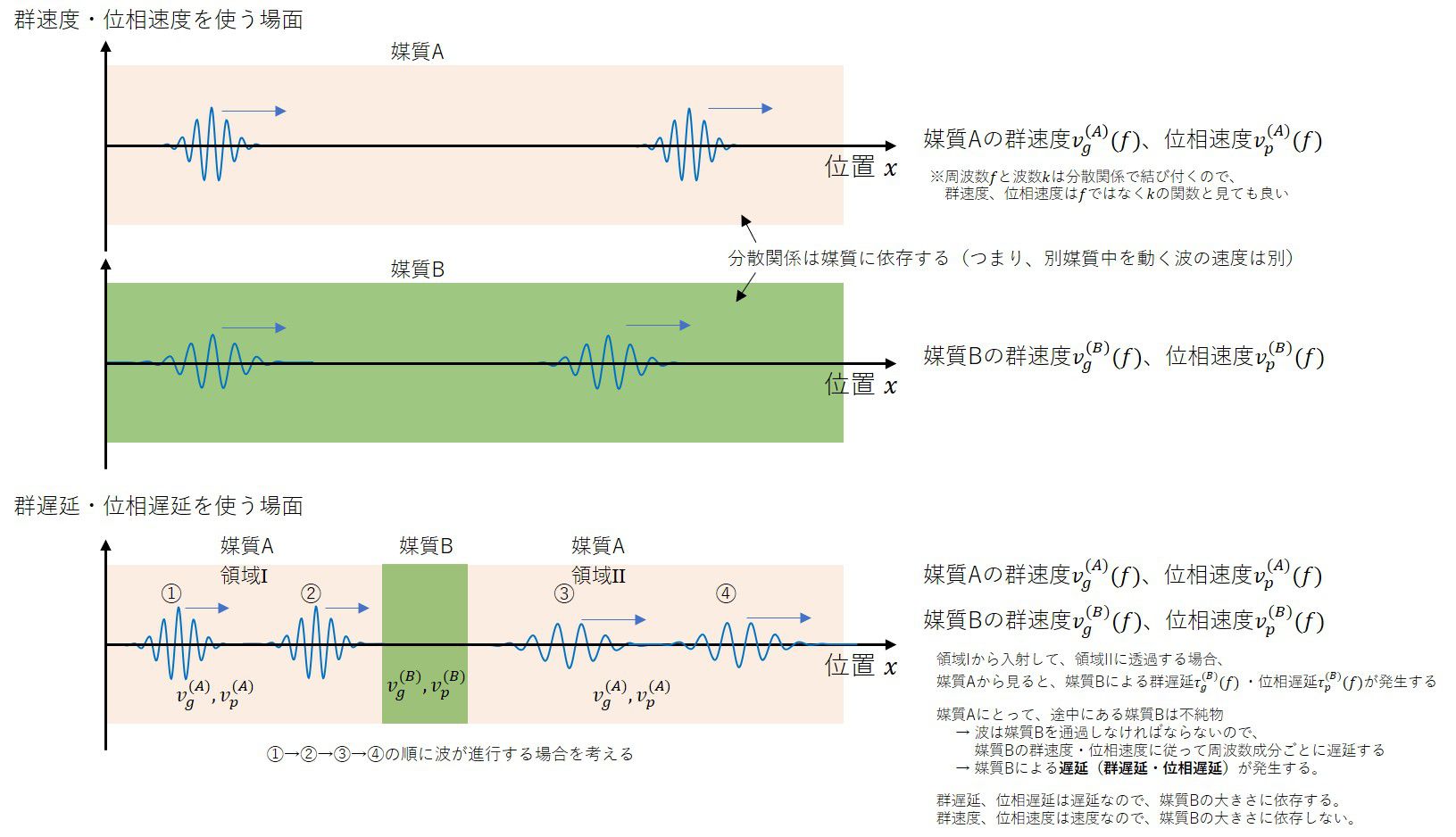
均一な媒質中の一部に存在する別の媒質の特徴が、インパルス応答\(G(k)\)で書かれるとします。
すると、別の媒質に入射する波\(f_0(x,t)\)が、透過すると波$g(x,t)$は
\(\displaystyle
g(x,t)\Bigr|_{t\to\infty}=|G_0|A\left(x- v_g t+\varphi’_0\right)
e^{ik_0 x -i\omega_0 t + i\varphi_0}
\)
と書けます。ここで、\(G(k)=|G(k)|e^{i\varphi(k)}\)であり、
\(\displaystyle
|G_0|\equiv G(k_0),~~\varphi_0\equiv \varphi(k_0),~~\varphi’_0\equiv \frac{d \varphi(k)}{d k}\biggr|_{k=k_0}
\)
と定義しています。
ある位置でしか波形を見ない場合、相互作用の影響は時間的な遅れとして観測され、
これらを群遅延、位相遅延と呼び、次の通り定義されます。
\(\displaystyle
\begin{align}
t_g&=\frac{1}{v_g}\varphi’_0 = -\frac{d\varphi(\omega)}{d\omega}\Bigr|_{\omega=\omega_0} \\
t_p&=\frac{1}{v_p}\varphi_0 = -\frac{\varphi(\omega_0)}{\omega_0}
\end{align}
\)

別の媒質に侵入すると、波の形が崩れてしまいます。その効果は\(\varphi”(k)\)で表現することができます。
\(A(x)=e^{-(x/a)^2}\)で書かれる場合、透過した波\(g(x,t)\)は
\(\displaystyle
g(x,t)\Bigr|_{t\to\infty}=|G_0| e^{ik_0x-i\omega_0 t +i\varphi_0} \cdot
\frac{a}{(a^2-2i\varphi”_0)^{1/2}}e^{-\frac{(x- v_g t+\varphi’_0)^2}{a^2-2i\varphi”_0}}
\)
と書かれ、波の形が崩れていることが分かります。