グリーン関数を用いて1次元のニュートンの運動方程式を解きます。
グリーン関数は非斉次微分方程式の特解を求める為に良く利用されます。
やっていることは、
微分方程式の満たす関数を、あたかも解いた風に書くこと
です。
なので実際、グリーン関数を使う、とは単なる式変形(微分方程式→積分方程式)をしているにすぎません。グリーン関数を本当に求め終わった時、はじめて解けた、と言えるのです。
物理現象では、グリーン関数が表現するのは「無限小時間に力が働く衝撃を受けた結果」を表現します。
どんな力も「複数の衝撃を積算したもの」と捉えることが出来ます。
衝撃に対する応答を考えてから、任意の力を衝撃の足し合わせと考え、問題を解きます。
すると、各々の力に対してその都度微分方程式を解いていくよりも
グリーン関数を求めた後の結果を足し合わせて任意の力に適応する、という考えの方が便利そうだと想像できます。
グリーン関数
微分方程式
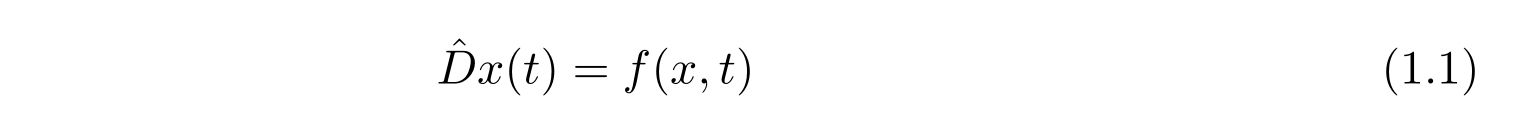
をグリーン関数を用いて解くことを考えます。
ここで、左辺の\(\hat{D}\)は演算子を表し、例えば
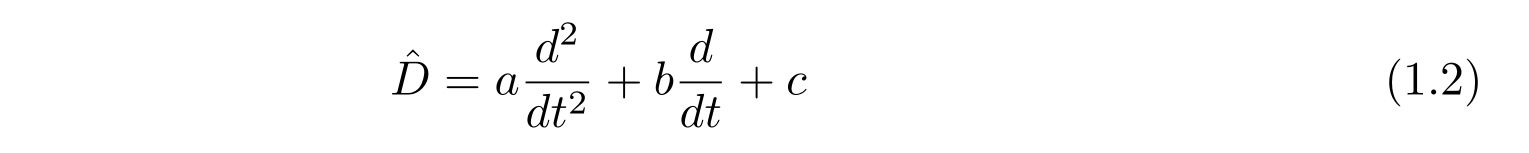
のような形です。
グリーン関数で解くとは、解を(一般解)+(特解)で書くときの特解を与える手段です。
特解なので、何かしらの境界条件の下でグリーン関数を求める訳です。
物理の問題では、”因果律”と呼ばれる、結果は原因の後の時間に起こる、ということを仮定した境界条件を採用します。
全ての演算子を左辺に移してしまいましたが、右辺に時間に関する微分演算子が入っていても問題ありません。
式(1.1)の形式的な解は、グリーン関数\(G(t,t’)\)を用いて
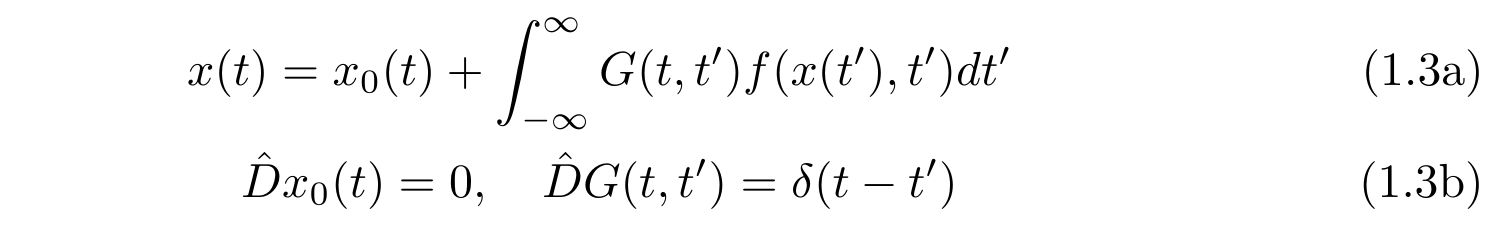
と、式(1.3a),(1.3b)を満たす解を用いて書くことが出来ます。
ここで、\(\delta(x)\)はディラックのデルタ関数です。
実際に解(1.3)は式(1.1)を満たすことを確かめます。
式(1.3)に左から演算子\(\hat{D}\)を作用させます。
ここで、\(\hat{D}\)は\(t\)に関する演算子なので、積分と交換できます。よって
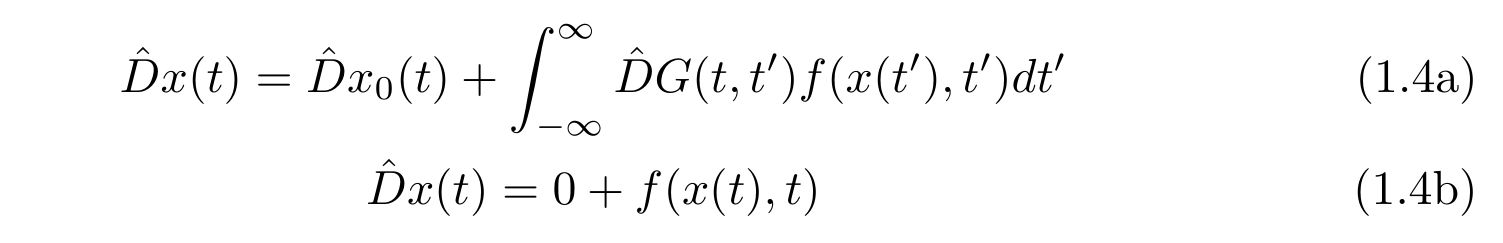
と変形でき、まさに解(1.3)は式(1.1)を満たす解として表されます。
重力下の質点
さて、質量\(m\)を持つ質点が、重力加速度\(g\)の重力下で運動する問題を考えます。運動方程式は
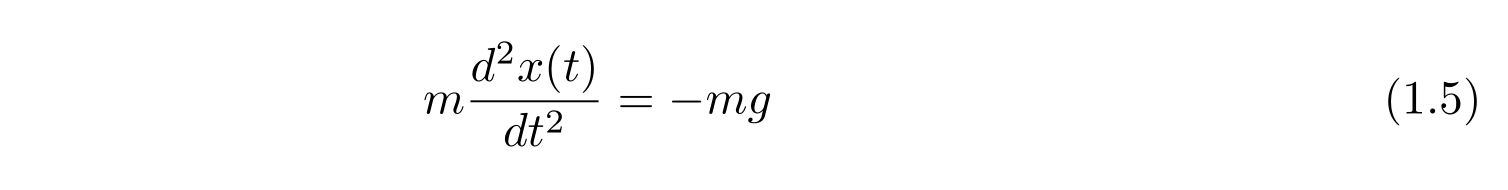
です。質量\(m\)で割って
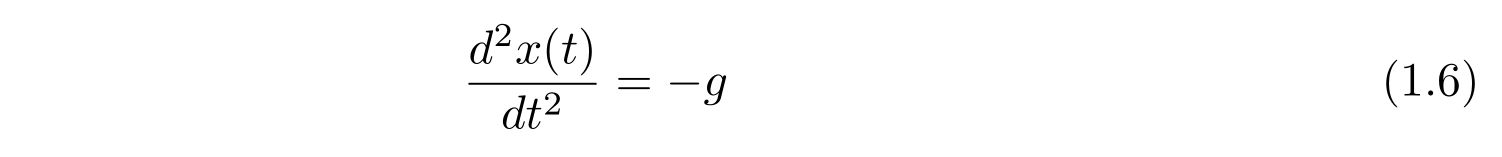
を得ます。
もちろん、この問題の解は
\(
\displaystyle x(t)=-\frac{1}{2}gt^2+at+b
\)
です。この問題はグリーン関数を用いて解く必要は全くありませんが、解析解が簡単に求められる練習問題として良いでしょう。
グリーン関数は単なる形式ですが、一般的な解法であり、非常に強力です。
しかし、こんな簡単な問題も解けないのであればお話になりません。
さて、式(1.6)の形式的な解は
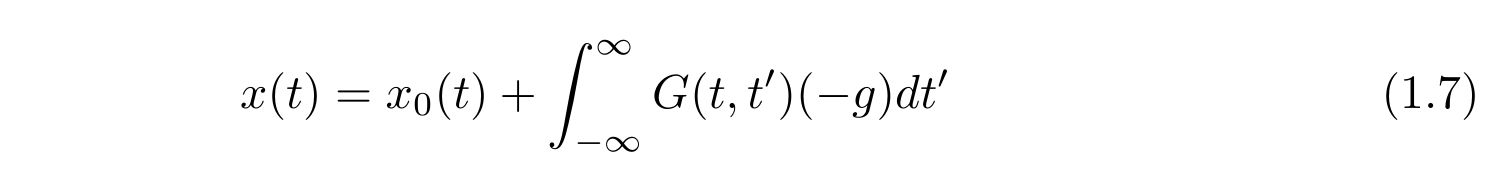
と書くことが出来ます。ここで、\(x_0(t), G(t,t’)\)は以下の微分方程式を満たします。

\(x_0(t)\)については簡単に解けてしまい、
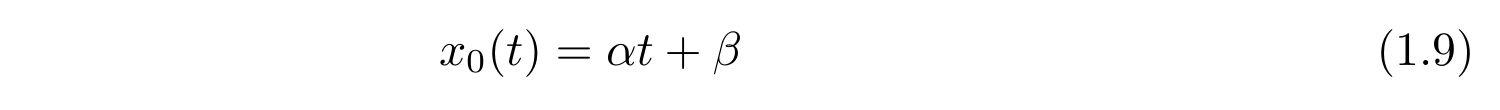
です。ここで、\(\alpha, \beta\)は\(x(t)\)の初期条件によって決まる定数です。
続いてグリーン関数の微分方程式を解きましょう。
方程式の右辺を見ますと、\(t= t’\)だけで変なことが起こっています。
ですが、\(t\ne t’\)であれば右辺は完全にゼロです。
すなわち、\(G(t,t’)\)は\(t\ne t’\)で、微分方程式

を満たしています。これは簡単に解けてしまい、
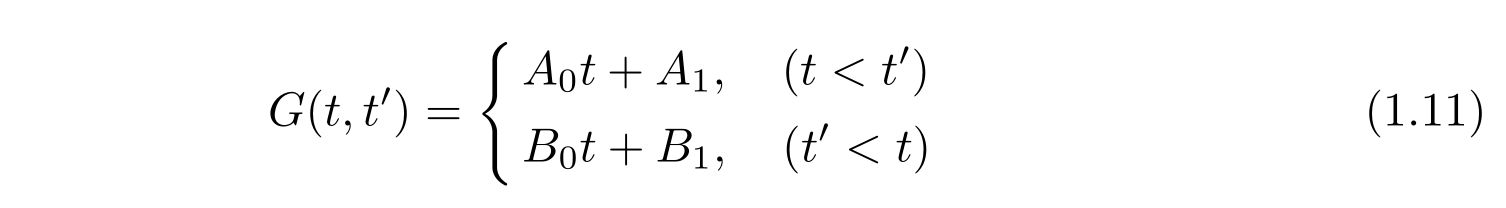
です。ここで、\(A_0, A_1, B_0, B_1\)を適当な定数としておきました。
これらの係数間には、とある関係式が成り立っています。それを調べましょう。
デルタ関数を発散する点を含んで積分すると定数1になることを利用します。
式(1.18)の下の式の両辺を時刻\(t=t”\)周りで積分します。
すなわち、微小な時間\(\varepsilon\)を用いて、
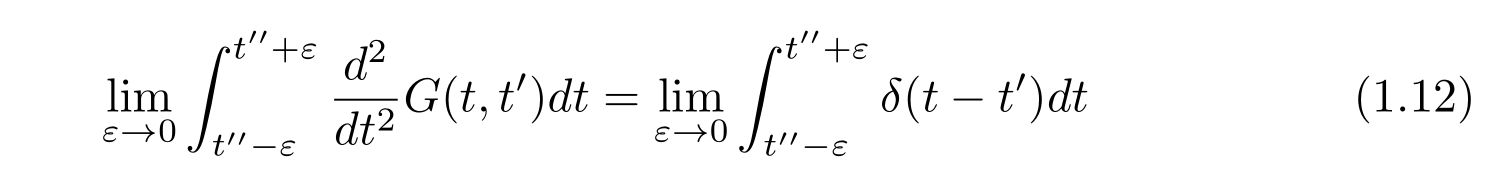
を計算します。
もしも、たまたま\(t”=t’\)であれば、積分を実行して
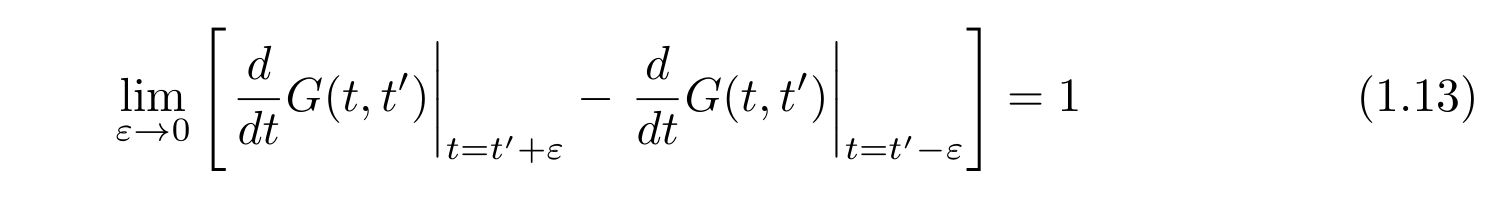
を得ます。これは、時刻\(t=t’\)周りでは、グリーン関数の導関数は、右から極限と左から極限は一致しないことを言っており、不連続になると言っています。
\(t”\ne t’\)であれば、この極限は一致し、グリーン関数の導関数は連続であるということを言っています。
式(1.11)を代入すれば、係数間の関係式
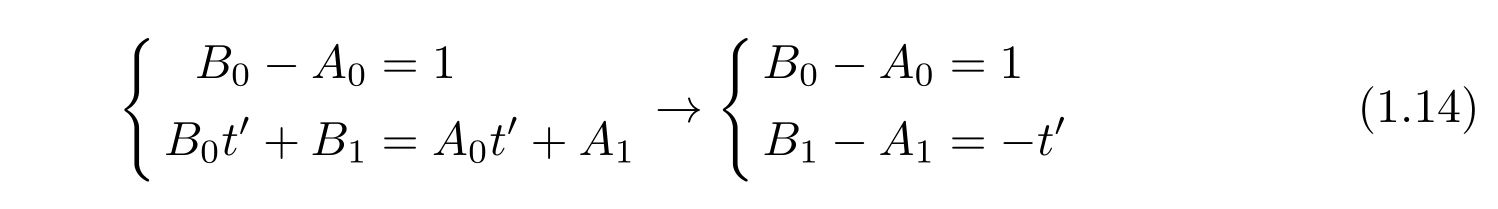
を得ます。
式(1.7)のグリーン関数を含む項は特解ですので、不明な定数は存在しません。
今、4つの未知の定数\(A_0, A_1, B_0, B_1\)に対して式の数は2つなので、全ての係数を決めるには2つ条件式が足りません。
そこで、境界条件を加えます。この条件は式(1.7)の解の形を見て決められます。
運動方程式を解こうとする場合、通常は物理的な要請から、ある時刻の運動はその時刻より過去の運動のみから決定される、という因果律が課されます(※1)。
さて、因果律を仮定すると、事が起こる時刻\(t=t’\)より前には何も起こらない、すなわち\(G(t,t’)=0\)を意味しており、\(A_0=A_1=0\)となります。よって、

を得ます。よって、グリーン関数
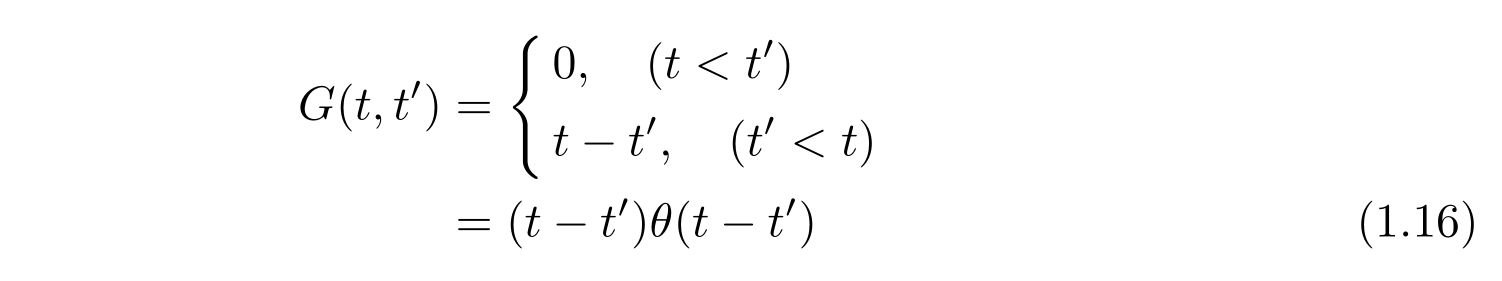
を得ます。ここで、\(\theta(x)\)はヘヴィサイド関数を表します。
グリーン関数(t’=5に固定)を書いてみるとこんな感じ。
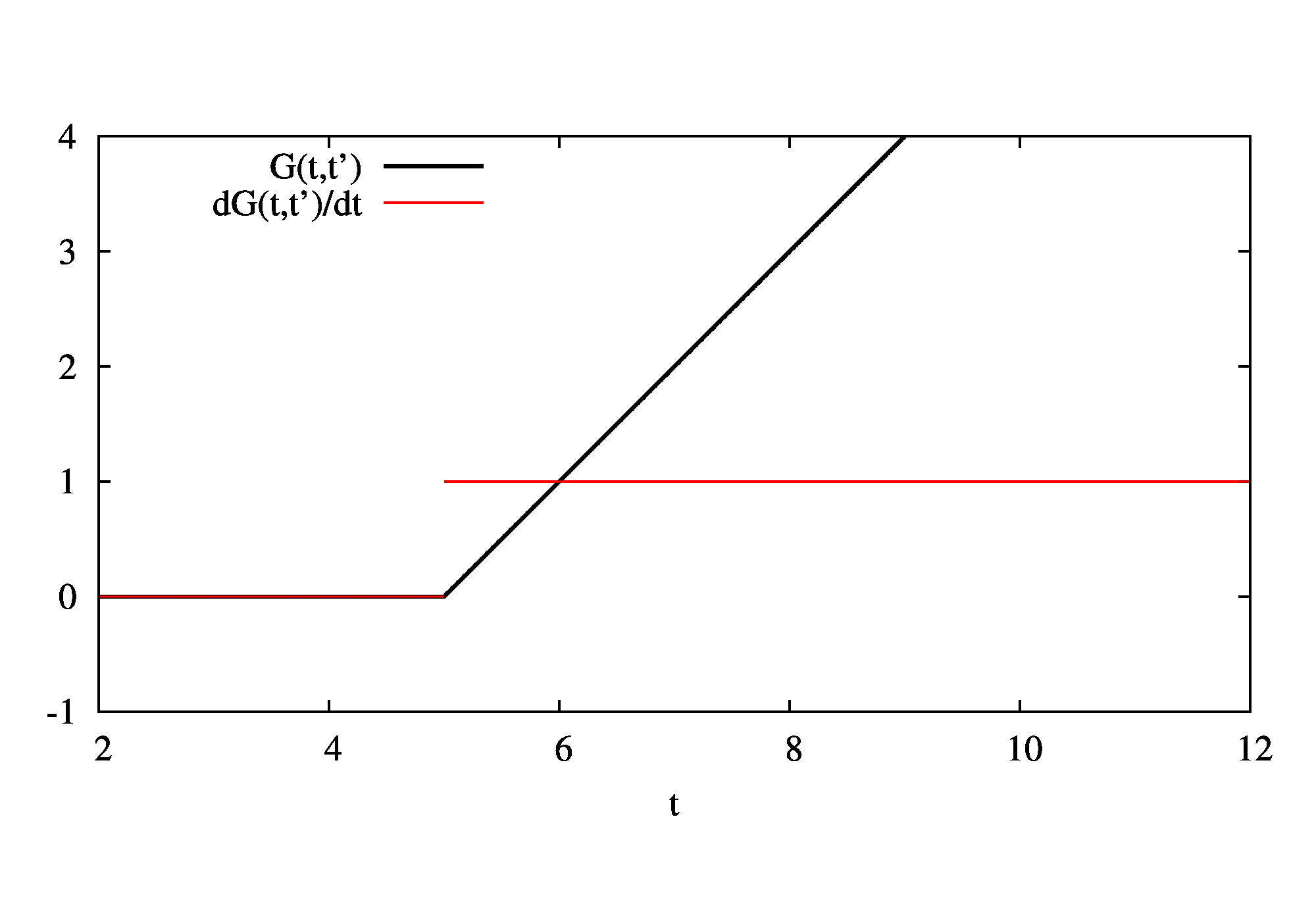
黒線がグリーン関数、赤線がその導関数です。導関数の右からと左からの極限の差がちょうどデルタ関数の積分、すなわち1になっていることが分かります。
これでグリーン関数が得られました。式(1.16)を使って式(1.7)の積分を計算すると、

を得ます。ここで、\(c\)は任意の値ではないことに注意してください。定まっている値です。
式(1.9)と式(1.17)の結果を代入すれば、運動方程式の解
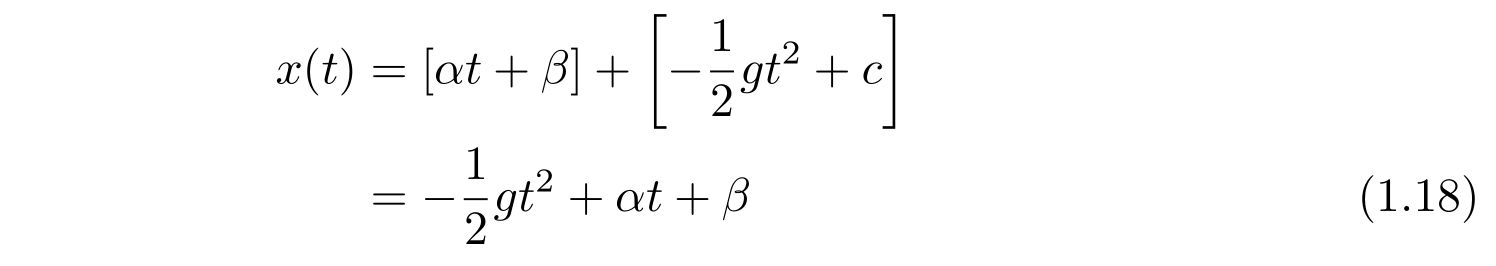
を得ます。ここで、\(\beta+c\)を改めて\(\beta\)と書きました。
この結果は本当の解に一致します。
重力化のばね
続いて、鉛直方向に置かれたばねと重力の問題を考えましょう。
ばね定数を\(k\)と置けば、運動方程式は
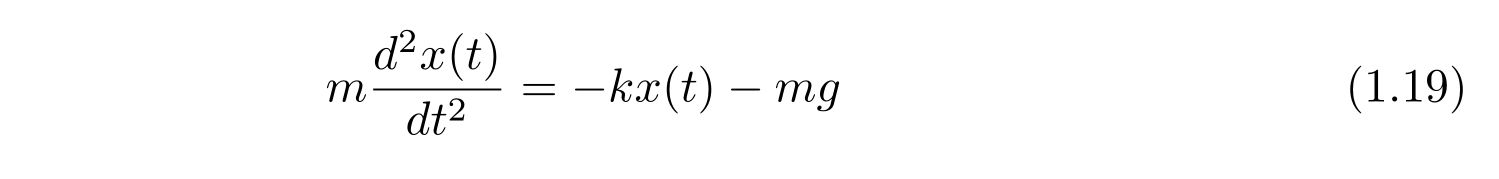
です。質量\(m\)で割り、\(\omega=\sqrt{k/m}\)と置くと、
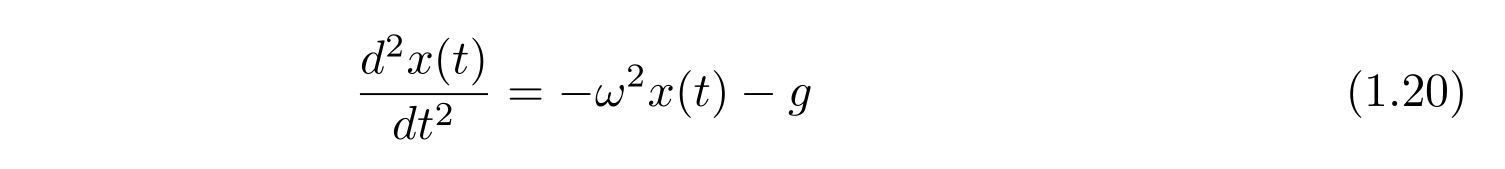
を得ます。
解は平衡点を中心とした振動運動です。平衡点\(x_0\)は力のつり合い
\(
-mg=kx_0~~~\to~~~x_0=-\frac{g}{\omega^2}
\)
から導くことが出来るので、
\(
\displaystyle x(t)=a\sin(\omega t +\varphi) -\frac{g}{\omega^2}
\)
です。これをグリーン関数を用いて導くことが出来れば目的達成です。
さて、グリーン関数の考え方として少なくとも2通りの方法が考えられます。
どちらの方法でも同じ解を与えるので、どちらをえらんでも構いません。
数学的に解きやすい方法を選ぶのが賢い方法です。
1つ目の選び方
微分方程式を
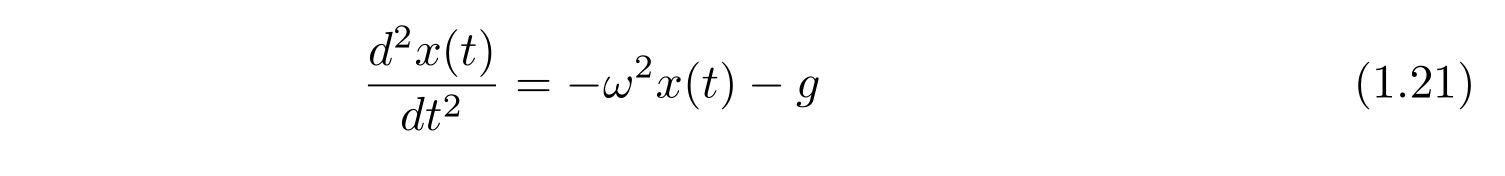
として考えます。
解を
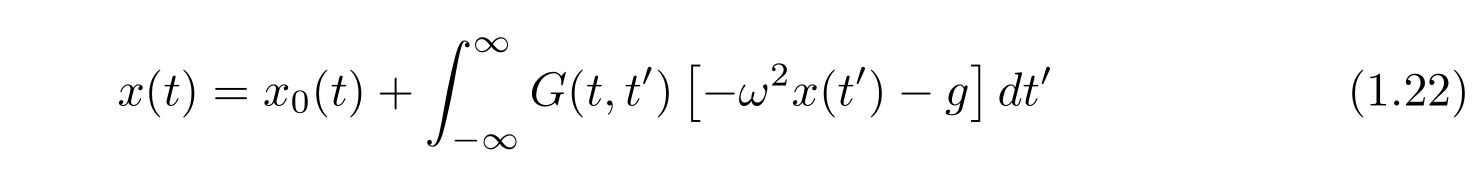
と考えるのです。\(x_0(t), G(t,t’)\)はそれぞれ
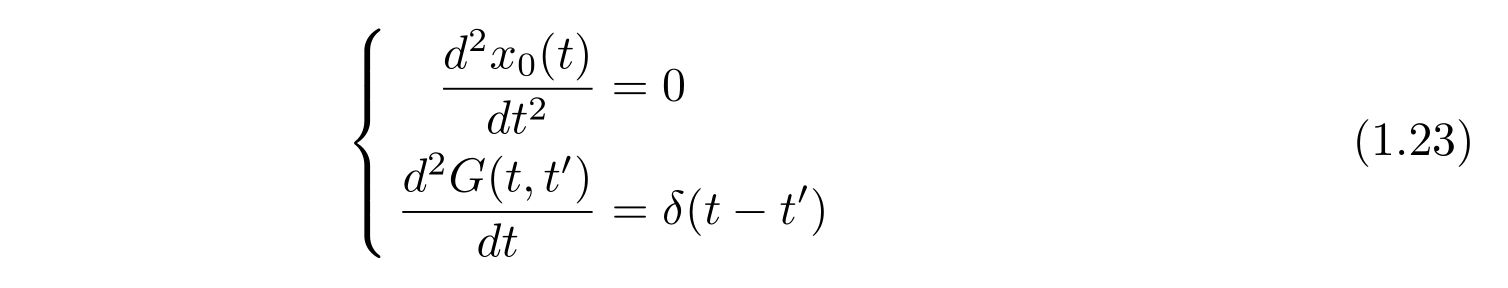
の微分方程式を満たします。式(1.9), 式(1.16)の結果を用いれば、容易に求められて、
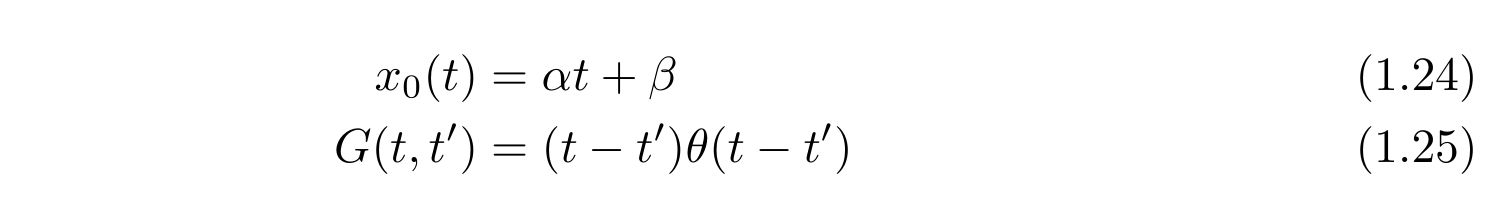
です。式(1.22)の積分部分は
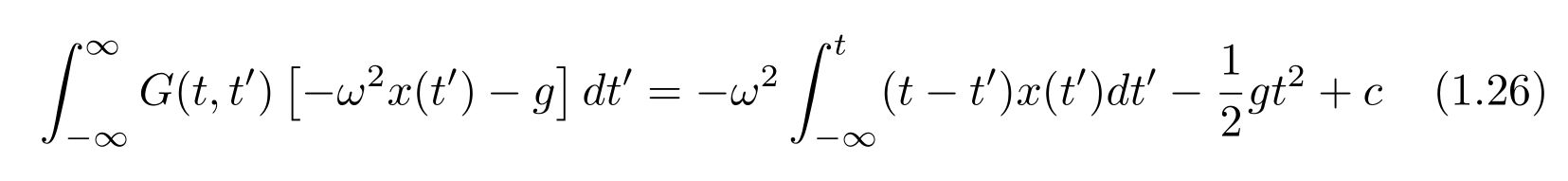
なので、解
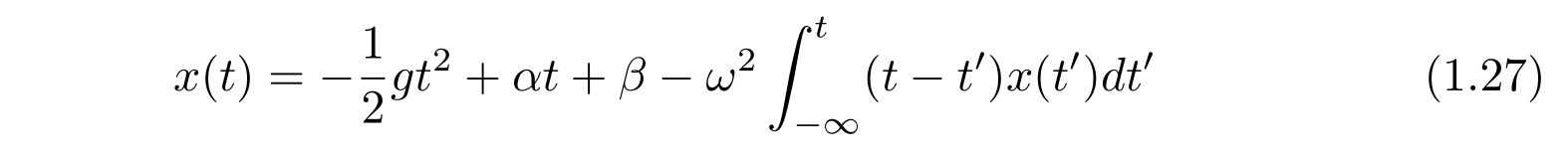
を得ます。
さて、あらわな形ではないものの、解が得られました。
式(1.27)を満たす\(x(t)\)を探さなければならないのですが、
正直なところ解を見つけられる気がしません。これは自己無撞着の方程式であり、
例えば散乱問題等のように、グリーン関数を得るのが難しい時などでこの形式にとどめておく方法がとられます。
あらわに求める事が出来ずとも、他の式へ代入が出来たり、摂動展開なんかに用いられるので、微分方程式の形式よりその後の計算が扱いやすいのです。
ただ、今の目的からそれてしまうので、ここではこれ以上は話しません。
2つ目の選び方
微分方程式を
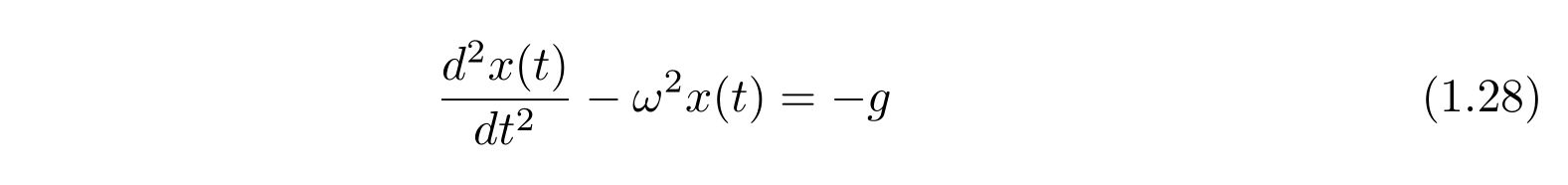
のように選びます。すると、解は
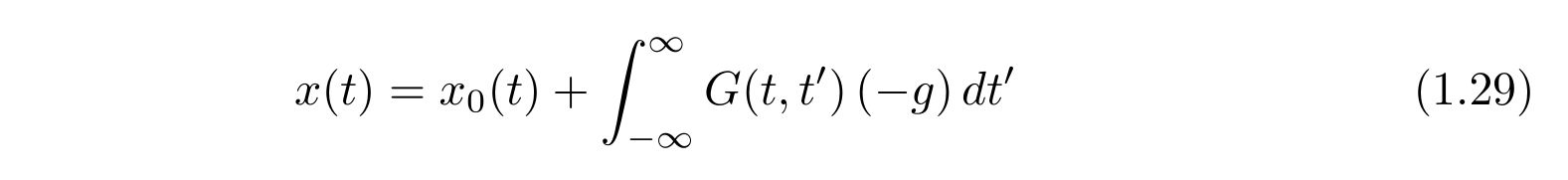
であり、\(x_0(t), G(t,t’)\)はそれぞれ
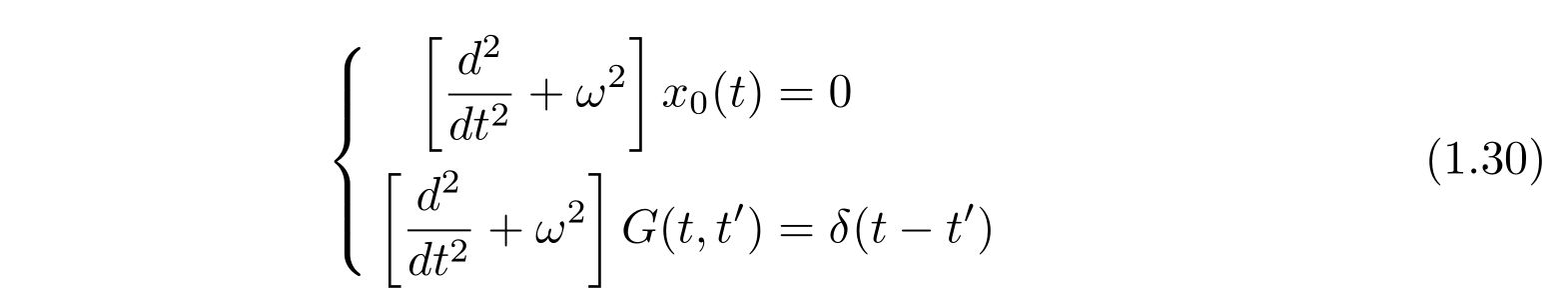
の微分方程式を満たします。
\(x_0(t)\)はただのばねの問題なので、
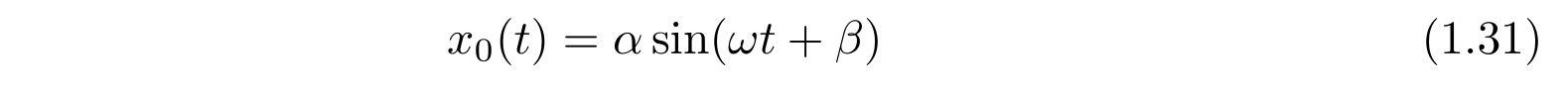
という解を得ます。一方、グリーン関数も\(t=t’\)を境に場合分けすると
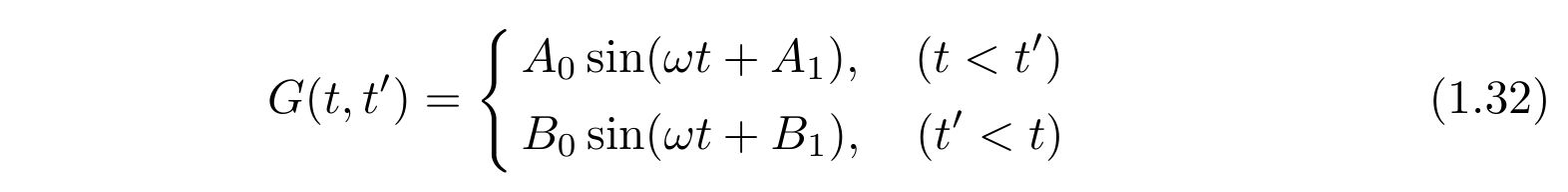
を得ます。時刻\(t=t”\)周りの微小時間で積分すれば、
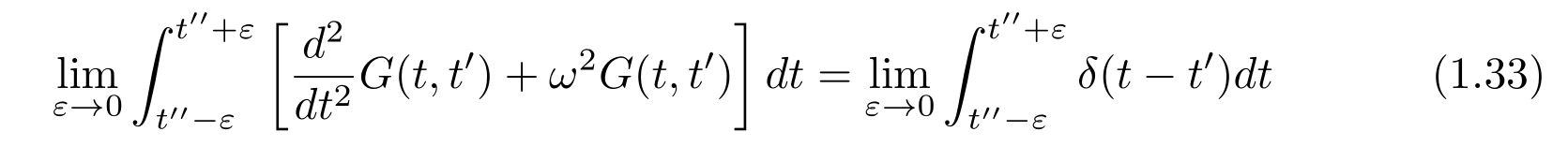
を得て、たまたま\(t”=t’\)であれば、
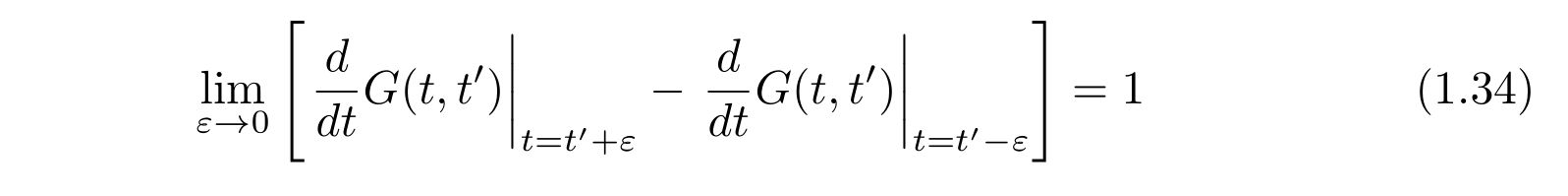
の関係式を得ます。ここで、グリーン関数自体はいかなる時刻でも右からと左から極限が一致するという事実をもちいました。
因果律を境界条件として使用すれば、係数は
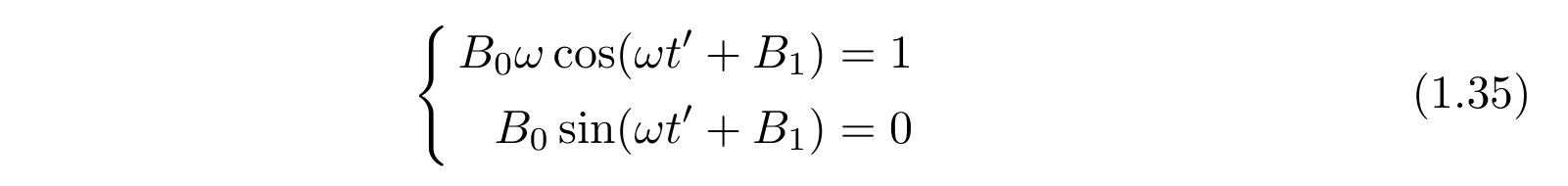
であるので、グリーン関数は
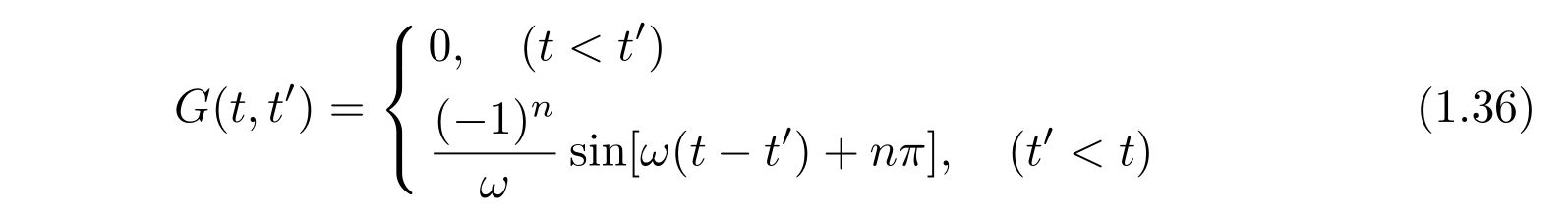
と求められます。ここで、\(n\)は三角関数の周期性からくる任意の整数です。具体的なグリーン関数(t’=5に固定)の格好はこんな感じ。

黒線がグリーン関数、赤線がその導関数です。導関数の右からと左からの極限の差がちょうどデルタ関数の積分、すなわち1になっていることが分かります。
式(1.29)の積分を計算すると
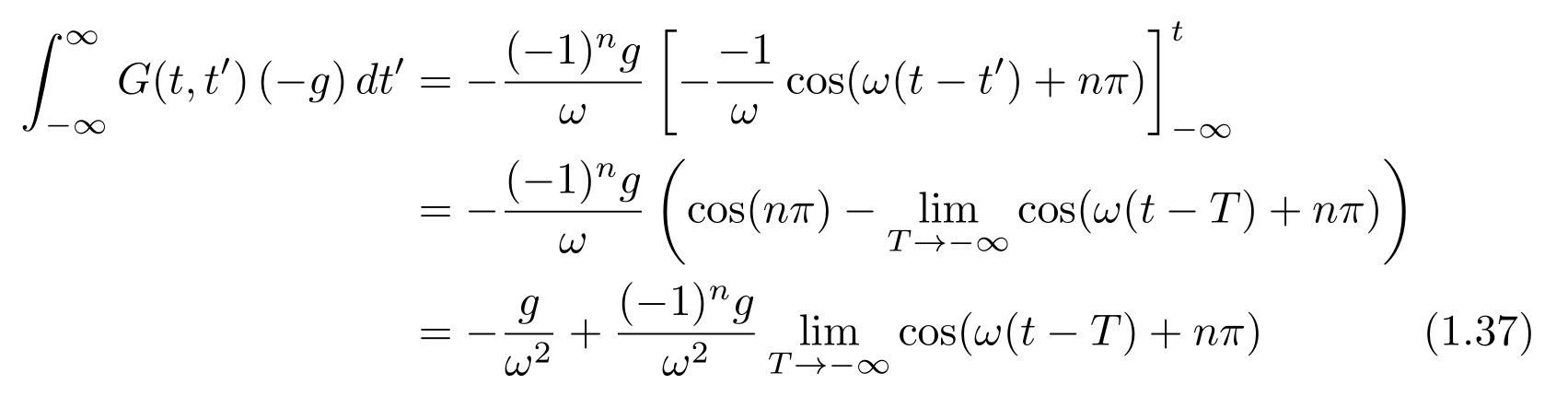
と求められます。三角関数を時刻無限に飛ばした時の値ですが、拡張リーマン・ルベーグの補題から得られる事実を用います(※2)。これによると、
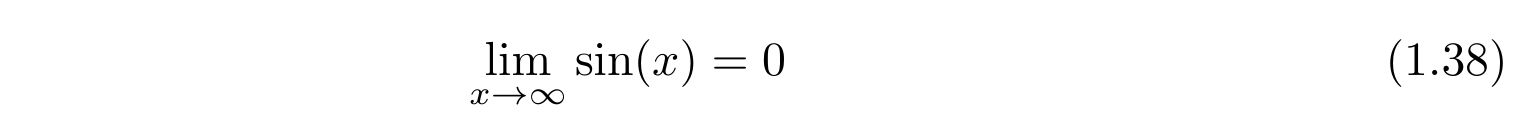
という事実が得られるので、式(1.37)の最後の項はゼロです。よって、
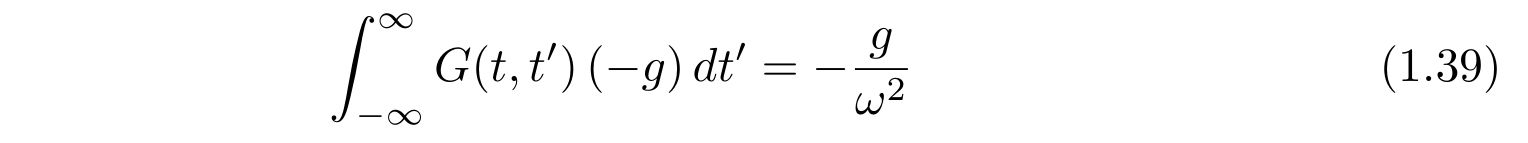
を得ます。
したがって、解
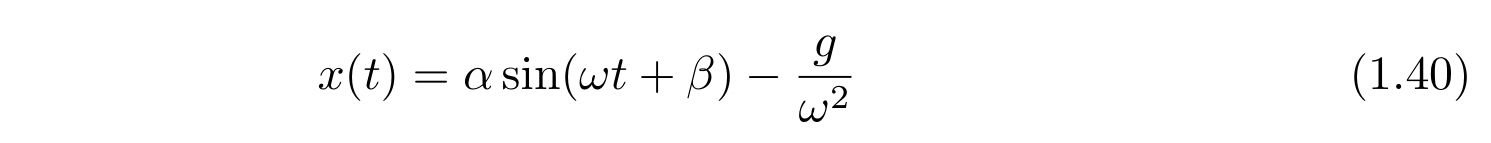
を得ます。これは求めたかった平衡点を中心に振動する運動です。
さて、1つ目の選び方で得た解(1.27)に解(1.42)を代入してみましょう。解(1.27)が本当にばねの問題なら、式は満たされるはずです。
式(1.27)の積分は

と計算できます。ここで、\(d\)を任意の定数ではない定数と置きました。
式(1.27)に代入すると、(RHS:right-hand side, 右辺)
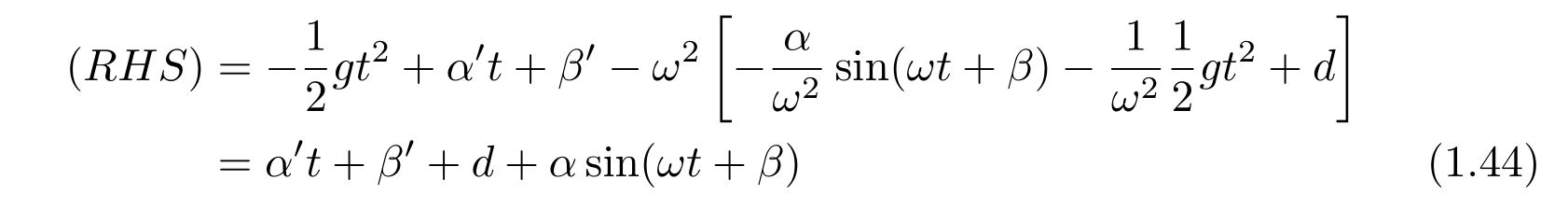
を得ますが、今、\(\alpha’, \beta’\)は自由に決めることが出来ます。
もしも\(\alpha’=0,~~\beta’+d=0\)となるように定数を決めれば、解(1.27)は式(1.42)で表される解と同じで、微分方程式(1.20)の解となっていることが分かります。
注釈
(※1) 因果律によるグリーン関数の境界条件は、妥当っぽく思われますが、人間が勝手にそうだろう、として経験的に与えている条件にすぎません。導くことは出来ない境界条件です。数学的には特解が何でも1つ与えられればいいので、時刻が未来であろうが特定の時間であろうが何でも構わないのです。
今回の場合は解きたい微分方程式の右辺が定数(重力のみ)という非常に特別な場合ですが、一般的にはグリーン関数を用いた特解の被積分関数には、左辺の解である\(x(t)\)が含まれます。
この時、因果律を仮定しないと、『ある時刻の運動を計算するために、その時刻より未来の運動を知らなければならない』という理解しがたい状況が生まれます。言い換えれば、『現時刻の運動は、未来の振る舞いが決定されているので、どんな力を新たに加えようとも決して運動を変えることは出来ない』となってしまい、非物理的に感じてしまいます。
もう一度言いますが、これは人間が「時間は必ず過去から未来に進む」という経験的に得られた事実を使用しているのであって、この根拠以外に因果律を採用する理由は存在しません。数学的に解こうとする際にはどんな条件でも構わないので、因果律を境界条件としても特解として正しい答えが得られるので良いのです。
位置に対する微分方程式である場合は、例えば位置が無限大でゼロである条件だったり、ある点で位置と微分が決まっていたり、漸近で特定の形を持っていなければならない、という条件が当てはめられます。
(※2)これいいんですかね、使って。あんまり考えてはいません。もしも時刻が負の∞ではなかったらと思うと不安で仕方ありません。都合がよかったので使いましたが…ダメな気がしないでもないです。
Thanks
アイキャッチ画像のフォントはmagicringを使用しています。
配布ページ
http://inatsuka.com/extra/magicring/
配布元のサークル様
森の中の猫の小屋 http://inatsuka.com/