ある関数の数値積分を考えます。
解析的に積分を行う事をまず考えましょう。1回の関数の評価で、全桁一致するからです。
解析的に計算
例えば,すぐには思いつかなそうな積分
\(
\displaystyle \int \sqrt{x}e^{-x^2} dx
\)
http://www.wolframalpha.com/input/?i=integral+sqrt(x)*exp(-x%5E2)
でも、wolfram alphaで計算させますと、不完全ガンマ関数を用いることで計算することが出来ることが分かります。
また、
森口繁一, 宇田川銈久, 一松信著『数学公式Ⅰ』、『数学公式Ⅱ』、『数学公式Ⅲ』岩波書店(1960)
にwolframでも答えてくれないような一般的な関数の積分も載っていますので、こちらも参照しましょう。
残念ながら解析的に積分出来ない場合、数値積分を行います。
ほとんどの数値積分法は、関数\(f(x)\)の積分を
\(
\displaystyle \int f(x) dx \approx \sum_{i} w_i f(x_i)
\)
と右辺の形で近似します。
ここで右辺に現れる、
あらかじめ決められた分点の位置\(x_i\)と
あらかじめ決められた重み\(w_i\)
をどのように決めるのか?で数値積分の良さが決まります。
上の例にあてはまらないものとして乱数を利用するモンテカルロ積分が挙げられます。
数値積分は大きく2つに分けられます。
- どんな位置の値でも関数値が得られる場合
- 特定の位置の値だけ関数値が得られる場合
です。
どんな位置の値でも関数値が得られる場合
とても簡単に実装、1-2桁程度合っていれば良い場合
モンテカルロ積分が簡単で、被積分関数が非連続性を持っていても、積分が存在すれば求めることが出来ます。
欠点としては、再現性が乱数に依存してしまう点でしょう。シード値を記録して置けばよいですが…。
良い乱数の発生方法として、メルセンヌツイスタと呼ばれる乱数の発生方法が良いそうです。
一様乱数を用いて1次元積分を行う場合、
\(
\displaystyle \int_a^b f(x)dx \approx \frac{b-a}{N}\sum_{i=1}^N f(x_i)+O(\frac{1}{\sqrt{N}})
\)
として計算できます。ここで\(x_i\)は位置\([a,b]\)に渡って発生される一様乱数です。
コードでは積分値をsとすると
s=0d0
do i=1,N
x=([0,1)の範囲で発生する乱数)*(b-a)+a
s=s+f(x)
enddo
s=s*(b-a)/dble(N)
で実装できます。
多重積分の場合、通常の積分法の収束が指数関数的に遅くなるので、モンテカルロ積分は良く使われます。
詳細はモンテカルロ積分をご覧ください。
モンテカルロ法 (Monte Carlo method)
確率密度関数からモンテカルロ積分まで
簡単に実装、2-4桁程度合っていれば良い場合
台形則による積分が良いでしょう。
区間\([a,b]\)で積分したい場合、区間を\(N+1\)点で分割すると
・等間隔の分点の場合
\(
\displaystyle \int_a^b f(x) dx \approx \frac{b-a}{N}\left(\frac{1}{2}[f(a)+f(b)]+\sum_{i=1}^{N-1} f(i\frac{b-a}{N}+a)\right)
\)
・非等間隔の分点の場合
\(
\displaystyle \int_a^b f(x) dx \approx
\frac{1}{2}\left[(x_1-x_0)f(x_0)+(x_N-x_{N-1})f(x_N)
+\sum_{i=1}^{N-1} (x_{i+1}-x_{i-1})f(x_i)\right]
\)
と求める事が出来ます。ここで、\(x_0=a,~x_N=b\)です。
s=0d0
do i=1,N
c=1d0
if(i.eq.1.or.i.eq.N)c=0.5d0
x=(i-1)*(b-a)/dble(N-1)+a
s=s+c*f(x)
enddo
s=s*(b-a)/(N-1)
3次元での台形則は以下のようなプログラムで実装できます。
s=0d0
do ix=1,Nx
cx=1d0
if(ix.eq.1.or.ix.eq.Nx)cx=0.5d0
x=(ix-1)*(xb-xa)/dble(Nx-1)+xa
do iy=1,Ny
cy=1d0
if(iy.eq.1.or.iy.eq.Ny)cy=0.5d0
y=(iy-1)*(yb-ya)/dble(Ny-1)+ya
do iz=1,Nz
cz=1d0
if(iz.eq.1.or.iz.eq.Nz)cz=0.5d0
z=(iz-1)*(zb-za)/dble(Nz-1)+za
s=s+cx*cy*cz*f(x,y,z)
enddo
enddo
enddo
s = s*((xb-xa)/dble(Nx-1))*((yb-ya)/dble(Ny-1))*((zb-za)/dble(Nz-1))
3,4桁以上の計算精度が欲しい時、台形則では間に合いません。
刻み幅を小さくすると精度は確実に上がりますが、刻み幅を1/10すると精度が1桁上がるだけなので、なかなか収束しません。
しかし、台形則も馬鹿にはできません。例えば、周期関数の1周期に渡る積分や、両端で定数に近づいていく積分の場合に、台形則はとんでもない精度をたたき出します(たしかガウス求積法と同じ精度まで上がると思いましたが、詳しい文献が見つけられないので参照はありません)。
この考えを元に考え出されたのが二重指数関数型数値積分です。端点特異性がある場合に特に強いため、学んでおいて損は無いでしょう。
[adsense1]
積分する関数に性質が見当たらないが、高い精度が欲しい場合
関数の形によって分点の取り方を自動的に決めてくれる適応型の自動積分が良いです。この種の積分で有名なのは、
NetlibにあるQUADPACK
http://www.netlib.org/quadpack/
(最速・高精度の数値積分, QUADPACKプログラム(1/2次元, 実/複素積分) -シキノート)、
もしくは
名古屋大学大型計算機センター、Numpacにあるaqnn9d
http://www2.itc.nagoya-u.ac.jp/center/ja/numpac/index.html
を参照してください。
QUADPACKはガウス-ルジャンドル求積法とガウス-クロンロッド求積法による適応型自動積分であり、
aqnn9dはニュートン・コーツ9点則に基づく適応型自動積分です。
おおよそ単精度ではaqnn9dの方が関数の評価回数が少なくて済み、倍精度以上ではQUADPACKの方が少なくて済みます。
この単精度/倍精度の違いは積分アルゴリズムそのものの特性です。
自動積分について、頒布されているfortranコードの良し悪しを最速・高精度の数値積分で比較したので、詳しいことを知りたい方はそちらをご覧ください。
また、刻み幅制御されたルンゲクッタ法による積分も良いでしょう。
定積分
\(
\displaystyle g(x)= \int_a^x f(x’)dx’
\)
を行うには、初期条件\(g(a)=0\)の下で、
\(
\displaystyle \frac{d g(x’)}{dx’} = f(x’)
\)
を点\(x\)まで上の微分方程式を解けば良いのです。
滑らかな関数(※1)であることが分かっている場合
積分区間内に特異性(※2)は無いとします。
この場合はチェビシェフ多項式による展開に基づくクレンショウ-カーティス(Clenshaw–Curtis)積分が優秀です。
定積分を
\(
\begin{align}
\displaystyle \int_{-1}^1 f(x) dx &\sim \sum_{k=0}^{n} \omega_k f(x_k)\\
x_k&=\cos\left(\frac{k\pi}{N}\right),\;\;\;k=0,1,\cdots,N\\
\omega_0 &=\omega_N =\frac{1}{N^2 -1} \\
\omega_s &=\omega_{N-s} = \frac{4}{n^2}\sum^{n/2}_{j=0}{\prime\prime }\frac{1}{1-4j^2}\cos\left(\frac{2j\pi s}{n}\right),\;\;\;s=0,1,\cdots,\frac{N}{2}
\end{align}
\)
ここで、\(\sum”\)は和の最初と最後の項に\(\frac{1}{2}\)を掛けることを意味します。
クレーンショー・カーチス数値積分則 Ooura’s Mathematical Software Packages
または
Clenshaw–Curtis求積法 シキノート、
最速・高精度の数値積分
をご覧下さい。
端点に特異性がある場合
計算区間内の途中に特異点は無く、計算区間の端点に特異性がある場合、変数変換型の数値積分である二重指数関数型数値積分が有効です。
具体的には例えば
\(
\displaystyle \int_0^1 \sqrt{x} dx
\)
や
\(
\displaystyle \int_{-1}^{1} x^{-0.8} dx
\)
の事です。これらの積分を行う際に二重指数関数型数値積分は非常に少ない分点数で非常に高精度の結果を返します。
重みと分点位置は以下の通り決められます。積分を
\(
\begin{align}
\int_{-1}^{1} f(x) dx &\approx \sum_{i=-N_-}^{N^+} w_i f(x_i),\\
x_i&=\tanh\left(\frac{\pi}{2}\sinh(ih)\right), \\
w_i&=\frac{h\frac{\pi}{2}\cosh(ih)}{\cosh^2\left(\frac{\pi}{2}\sinh(ih)\right)}
\end{align}
\)
として近似します。\(N−,N+\)は離散化誤差と打ち切り誤差が等しくなるように決められます。
\(N−,N+\)はプログラム上では、\(x_i\)がコンピュータの扱える桁数を超えず、\(w_i\)がアンダーフローを起こさない範囲で決められます。
詳しくは二重指数関数型数値積分 -シキノート
をご覧ください。
プログラム自体は大浦様による二重指数関数型数値積分公式の方が優秀なので、こちらを参照すると良いでしょう。
被積分関数が(特定の関数関数)×(多項式)の場合
被積分関数\(f(x)\)が(重み関数\(\omega(x)\))×(多項式\(g(x)\))で記述される特別な場合、ガウス求積法による数値積分が有効です。
多項式\(g(x)\)とは\(x^n/latexの足し算で書ける関数です。例えば[latex]x^4+3x^2+7x\)とかのことです。\(x^2+2\sqrt{x}\)とか、\(x\)の0以上の整数乗ではない項があってはいけません。
重み関数\(\omega(x)\)とは、特定の形をした関数の事です。例えば
\(\omega(x)=1~\to\) ガウス-ルジャンドル求積法、ガウス-ロバート求積法、ガウス-radau求積法
\(\omega(x)=x^n e^{-x}~\to\) ガウス-ラゲール求積法
\(\omega(x)=e^{-x^2}~\to\) ガウス-エルミート求積法
\(\omega(x)=\frac{1}{\sqrt{1-x^2}}~\to\) ガウス-チェビシェフ(第一種)求積法
\(\omega(x)=\sqrt{1-x^2}~\to\) ガウス-チェビシェフ(第二種)求積法
\(\omega(x)=(1-x)^\alpha (1+x)^\beta~\to\) ガウス-ヤコビ求積法
の形を数値積分したい場合、ガウス求積法を考えてみてはどうでしょうか。
上では省略しましたが、ガウス求積法を用いる際には積分区間も決まっています。しかし、これは簡単な変数変換によって書き換えることが出来ます。
例えば、ガウス-ルジャンドル求積法は区間\([-1,1]\)出なければ使うことはできませんが、変数変換
\(
\displaystyle \int_a^b f(x)dx=\frac{b-a}{2}\int_{-1}^{1}f(\frac{b-a}{2}x+\frac{a+b}{2}) dx
\)
の変換が出来るので、左辺を計算しようと思ったら右辺を計算しにいけばいいのです。
ガウス-ルジャンドル求積法 http://mathworld.wolfram.com/Legendre-GaussQuadrature.html
ガウス-radau求積法 http://mathworld.wolfram.com/RadauQuadrature.html
ガウス-ロバート求積法 http://mathworld.wolfram.com/LobattoQuadrature.html
ガウス-ラゲール求積法 http://mathworld.wolfram.com/Laguerre-GaussQuadrature.html
ガウス-エルミート求積法 http://mathworld.wolfram.com/Hermite-GaussQuadrature.html
ガウス-チェビシェフ求積法 http://mathworld.wolfram.com/ChebyshevQuadrature.html
ガウス-ヤコビ求積法 http://mathworld.wolfram.com/Jacobi-GaussQuadrature.html
ガウス求積法の原理・導出については
ガウス求積法の導出 シキノート
をご覧ください。
二重積分を行いたい場合
一番理解しやすい方法は直積を考えて計算する方法です。
「二重積分」を「一重積分した結果を一重積分する」という問題に焼直します。
すなわち、
\(
\displaystyle \int dx \int dy f(x,y)
\)
という問題は、
\(
\begin{align}
\int dx \int dy f(x,y)=\int dy\left[\int f(x;y) dx\right]
\end{align}
\)
と考えるのです。ここで、\(f(x;y)\)のセミコロンの意味は、
『\(f\)は\(x\)と\(y\)の変数だよ。だけど、今変数として注目したいのは\(x\)についてだけ。だから\(y\)は一応書いておくけど、今あらわな変数として扱わないよ。』
ということを示しています。
さて、計算を進めましょう。\([~~]\)内は今、固定したある\(y\)について\(x\)のみの変数なので、求積法の形にして
\(
\begin{align}
\int dy\left[\int f(x;y) dx\right]&\approx \int dy\left[\sum_i w^{(x)}_i f(x_i,y)\right]\\
&= \sum_i w^{(x)}_i \int f(x_i,y)dy \\
&\approx \sum_i w^{(x)}_i \sum_j w^{(y)}_j f(x_i,y_j)
\end{align}
\)
となります。ここで、\(w^{(x)}_i\)は\(x\)方向の\(i\)番目の分点の重みを表します。
これは、例えば被積分関数が\(x\)方向については端点特異性を持っていて、\(y\)方向については簡単な多項式で描けている、といった場合に別々の求積法を使うことで計算量を減らし、高精度の結果が得られるということを示しています。
表面積分を行いたい場合
表面積分
\(
\displaystyle \int_0^\pi d\theta \int_0^{2\pi} d\varphi f(\theta,\varphi) \sin\theta \approx 4\pi \sum_{i} w_i f(\theta_i, \varphi_i)
\)
を行う場合、Lebedev求積法かGaussian-quadrature(ガウス-ルジャンドル求積法と台形則の組み合わせ)が良いです。
lebedev求積法は、球面調和関数の直交性を利用した求積法で、\(f(\theta,\varphi)\)が最大\(l=131\)までの球面調和関数で展開されるのであれば、厳密な値を返すという積分法です。
fortranのプログラムはhttp://www.ccl.net/cca/software/SOURCES/FORTRAN/Lebedev-Laikov-Grids/Lebedev-Laikov.F
にあります。このプログラムと
program main
implicit none
integer::i,N
double precision,allocatable::x(:),y(:),z(:),w(:)
double precision::s
double precision,parameter::pi=dacos(-1d0)
double precision,external::f
N=146
allocate(x(1:N),y(1:N),z(1:N),w(1:N))
call LD0146(x,y,z,w,N)
s=0d0
do i=1,N
s=s+w(i)*f(x(i),y(i),z(i))
enddo
write(6,*)4d0*pi*s
stop
end program main
function f(x,y,z)
implicit none
double precision::x,y,z,f
f=x*x+y*y+z*z
return
end function f
を一緒にコンパイルしてください。プログラムでは\(\theta,\varphi\)での指定ではなく、\(x,y,z\)のデカルト座標系のものになっています。動かすと半径1の球面の立体角に関する積分、すなわち\(4\pi\cdot 1^2\)の値を返します。
3. Lebedev angular quadrature -Methods of Numerical Integration.
Gaussian-quadratureは、\(\theta\)方向についてはガウス-ルジャンドル求積法、\(\varphi\)方向については台形則により積分する、という方法です。良く使われるのでgaussian-quadratureと名前がついているようです。
\(\varphi\)方向で台形則が使われる理由は、\(\varphi\)方向について周期的であるため、台形則は非常に高精度の結果を与えるためです。
\(\theta\)方向でガウス-ルジャンドル求積法が用いられるのは、球面調和関数の\(m=0\)がルジャンドル多項式で展開されるためです。他の\(m\ne 0\)についてはルジャンドル多項式は完全系なので、その性質から計算されるのだろうという思惑だと思います。
lebedev求積法による計算は最大\(l=131\)の求積点と重みが知られていますが、これ以上の\(l\)に関してのlebedev求積点、重みに関する論文は見つけられませんでした。
もしも\(l=131\)以上が出てくることが分かっている場合、現状ではGaussian-quadratureによる求積が良いでしょう。
多次元(6,7次元以上)の積分を行いたい場合
この場合はモンテカルロ積分が良いです。
一様乱数によるD次元の積分は、
\(
\begin{align}
\displaystyle &\int_{x^{(1)}_{a}}^{x^{(1)}_{b}}\int_{x^{(2)}_{a}}^{x^{(2)}_{b}}\cdots\int_{x^{(D)}_{a}}^{x^{(D)}_{b}}
f(x^{(1)},x^{(2)},\cdots,x^{(D)})dx^{(D)}\cdots dx^{(2)} dx^{(1)}\\
&\approx
\frac{(x^{(1)}_{b}-x^{(1)}_{a})(x^{(2)}_{b}-x^{(2)}_{a})\cdots(x^{(N)}_{b}-x^{(N)}_{a})}{N}
\sum_{i=1}^N f(x^{(1)}_i,x^{(2)}_i,\cdots,x^{(D)}_i)
+O(\frac{1}{\sqrt{N}})
\end{align}
\)
と求める事が出来ます。
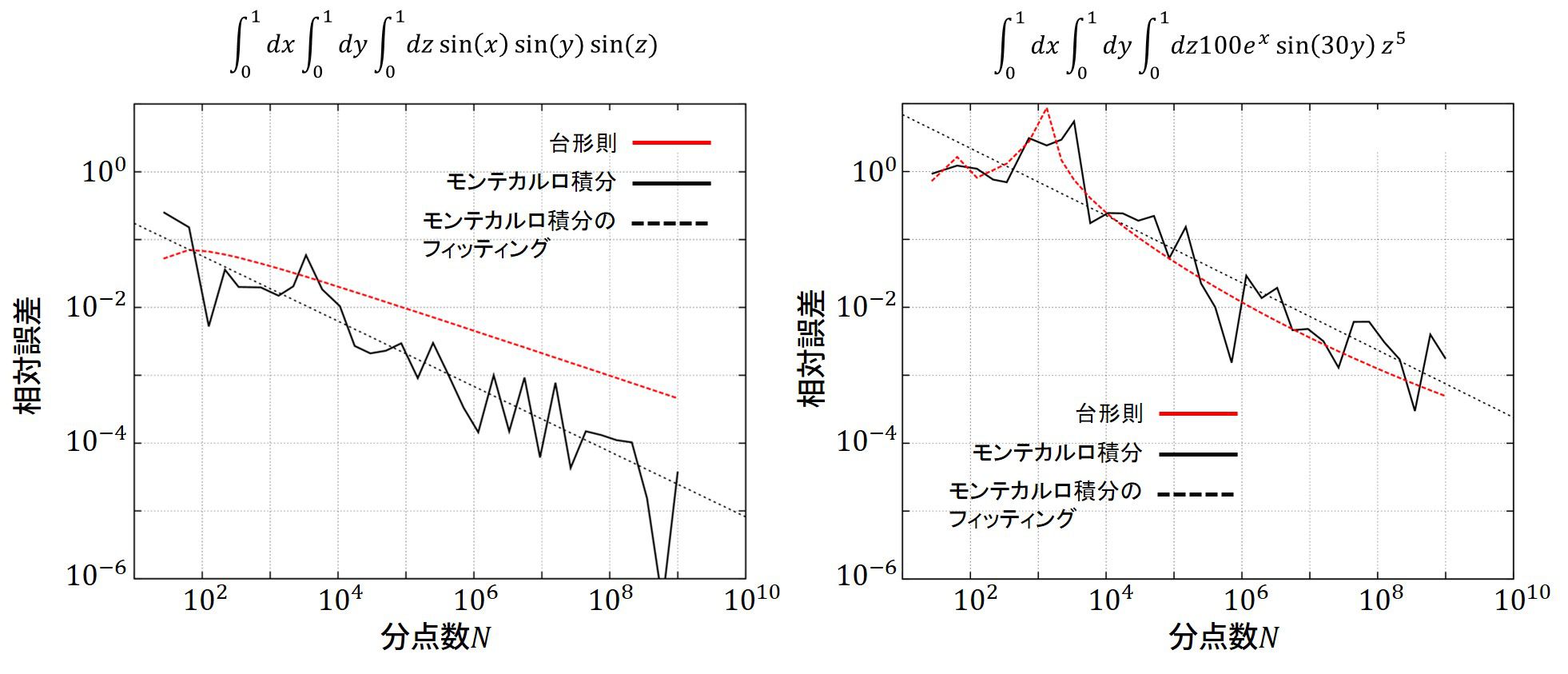
モンテカルロ積分の誤差はサンプル数にのみに依存します。
\(O(\frac{1}{\sqrt{N}})\)なので、サンプル数\(N\)を100倍に増やすと積分精度が\(\frac{1}{\sqrt{100}}=\frac{1}{10}\)、つまり1桁上がる事を意味しています。
一般的な数値積分法、例えば台形則を用いて1次元積分を\(N\)点で積分するとします。
すると、2次元の積分では\(N^2\)点、D次元では\(N^D\)点被積分関数を評価する必要があります。
台形則の組み合わせによる1次元当たりの積分の精度は\(N\cdot O(h^2)\sim O(\frac{1}{N})\)で決まるので、
1桁、積分精度を上げたいとすれば被積分関数の評価回数は\(10^{D}\)倍に増やさなければなりません。
しかしモンテカルロ積分では積分の精度は次元に依らずサンプル数にのみで決定されます。これは、
1桁、積分精度を上げたいとすれば被積分関数の評価回数は\(100\)倍に増やさなければならないことを意味しています。
台形則と比べるとおおよそ3重積分を解こうとする際に、モンテカルロ法の方が有利になる、ということが分かります。
[adsense2]
特定の\(x\)だけ関数値\(f(x)\)が得られる場合
”特定の\(x\)”が等間隔であったり、特に整然としていないと仮定します。
この場合は、
台形則による積分
もしくは
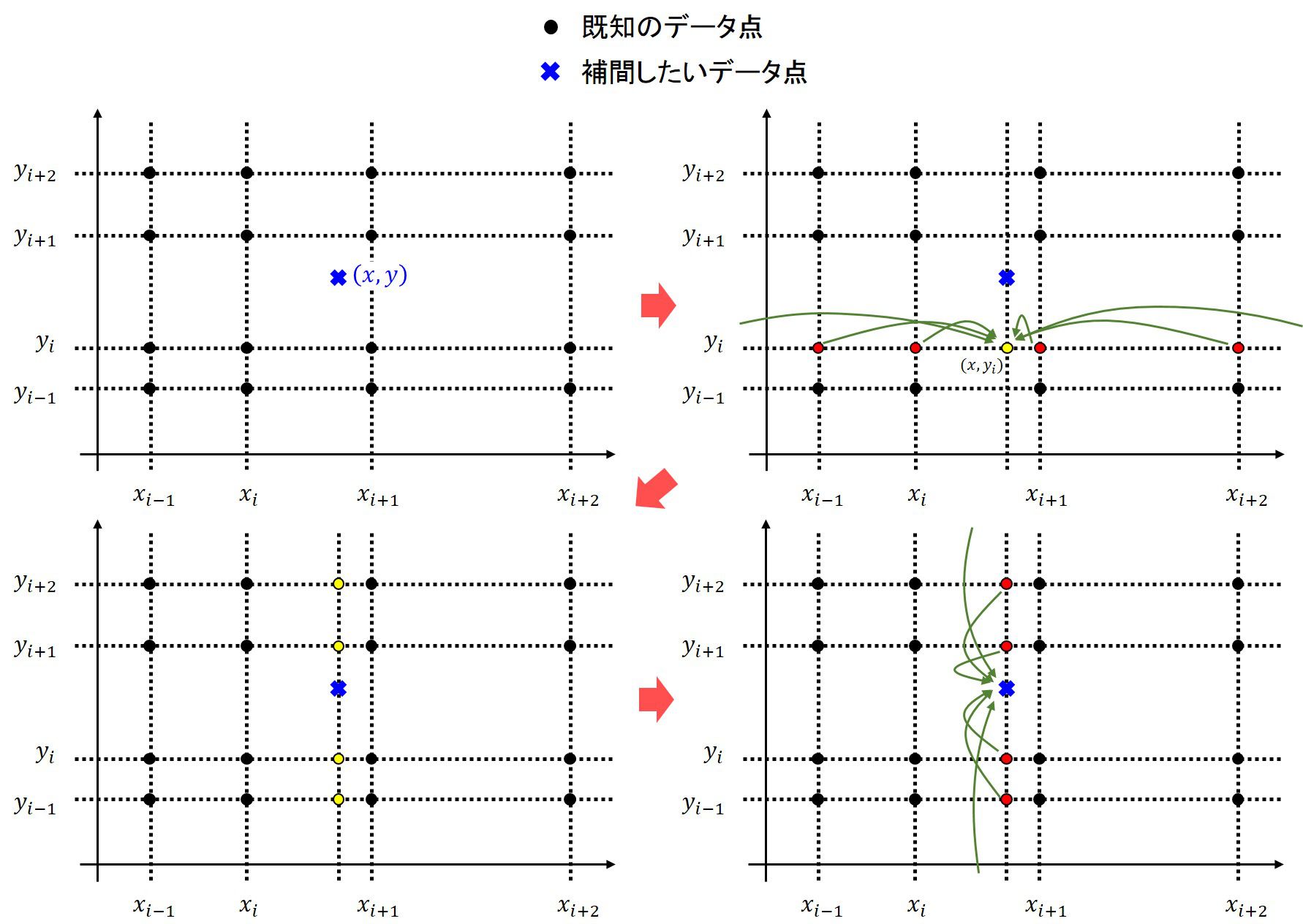
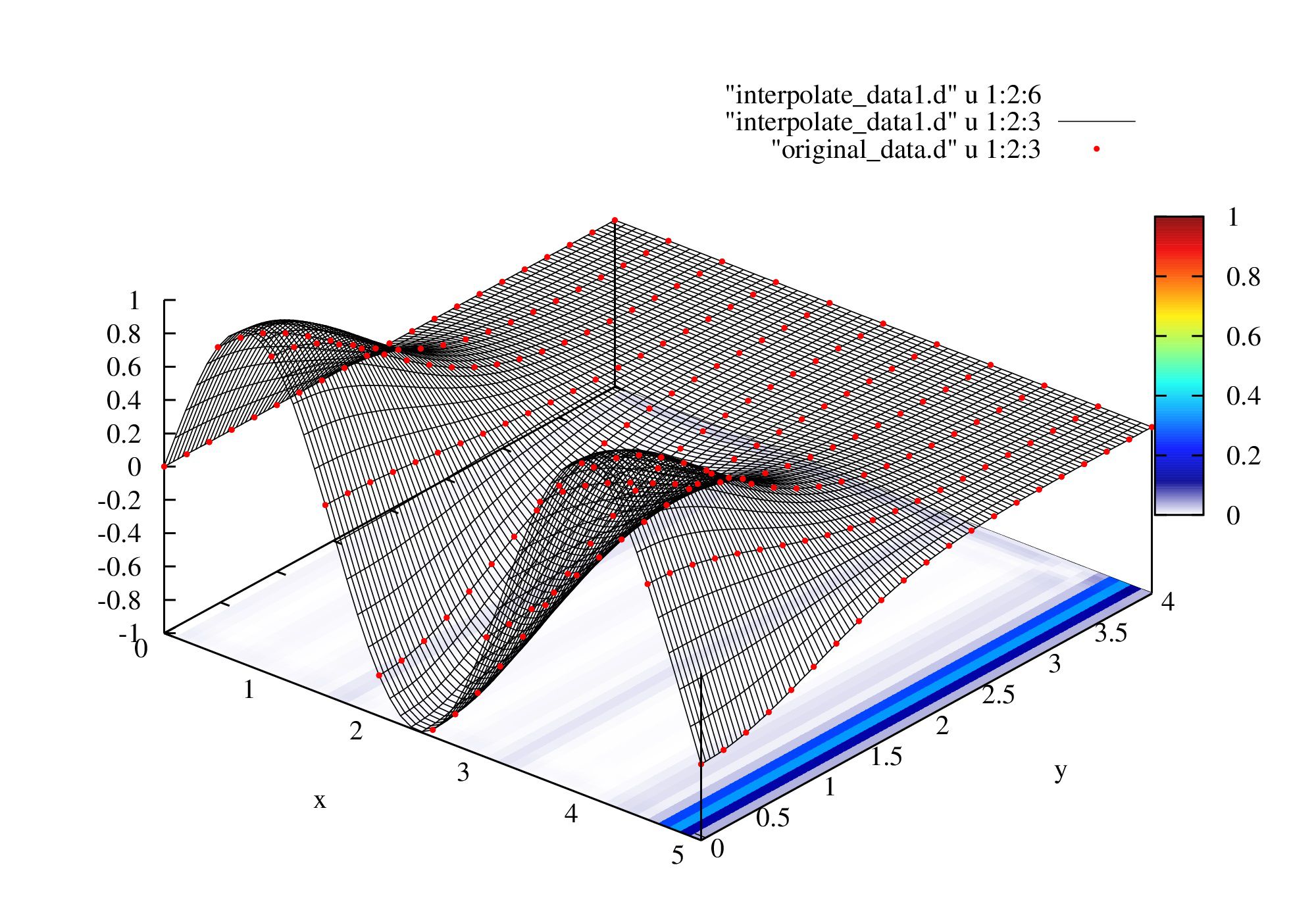
3次スプライン補間による積分
がどんな分点数、分点の間隔であっても、プログラムの変更をほとんどしないで計算できるので良いでしょう。
もしも分点が等間隔の場合で、データ配列の大きさが\(1,2,…,2N+1, (Nは整数)\)の場合はシンプソン則による計算でも良いでしょう。
また、分点が等間隔で、データの配列の大きさが\(1,2,…, 2^N+1(Nは整数)\)の場合はロンバーグ積分法が使えます。
3次スプライン補間による積分は
スプライン補間(1, 2次元) -シキノートに置いてあるc3spline_integralを用いると良いでしょう。
注釈
(※1)”滑らか”とは、
積分区間内の至る所で被積分関数の\(x\)のn階微分の右からの極限と左からの極限が一致すること、を意味します。
(※2)”特異性”とは、
積分区間のどこか一点でも被積分関数の\(x\)のn階微分の右からの極限と左からの極限が一致しない点がある、もしくは積分区間の端点で被積分関数の\(x\)のn階微分が無限大に発散する、ことを意味しています。