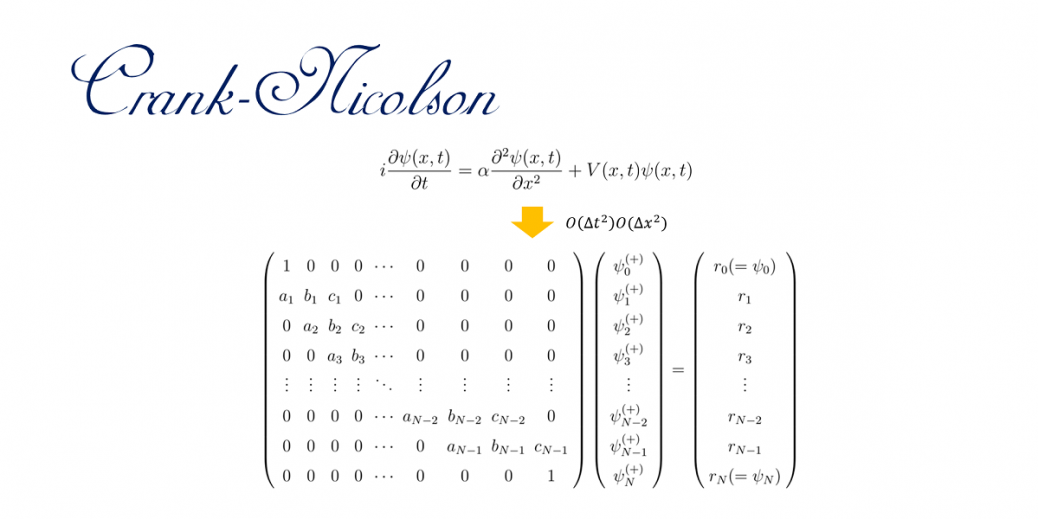
解きたい問題は以下の形の時間依存シュレーディンガー方程式です。
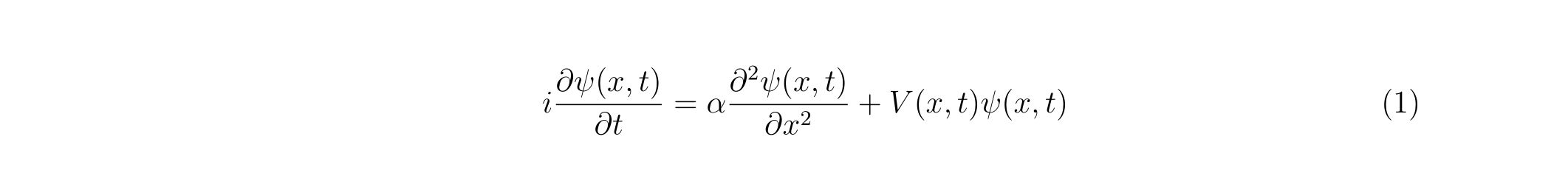
これをクランクニコルソン法という、微分を差分で近似する数値的な時間発展方法で求めていきます。
解法
※途中、式番号が抜けたり(例えば式15)、前後していますが仕様です。
時間を初期時刻\(t=0\)から\(t=\Delta t\)まで時間発展したいと考えます。
微分を差分で離散化しますが、時刻\(t=\frac{\Delta t}{2}\)だけ進んだ時刻からの前進差分をまず考えます。
すると、

と導けます。時間,空間に関して\(O(\Delta t),O(\Delta x^2)\)です。
続いて、時刻\(t=\Delta t\)から\(\frac{\Delta t}{2}\)との後進差分をまず考えますと

です。時間,空間に関して\(O(\Delta t),O(\Delta x^2)\)です。
式(2)と式(3)を足して2で割りますと、時間に関して中央差分を取っていることになりますので、次数が上がります。代入しますと、
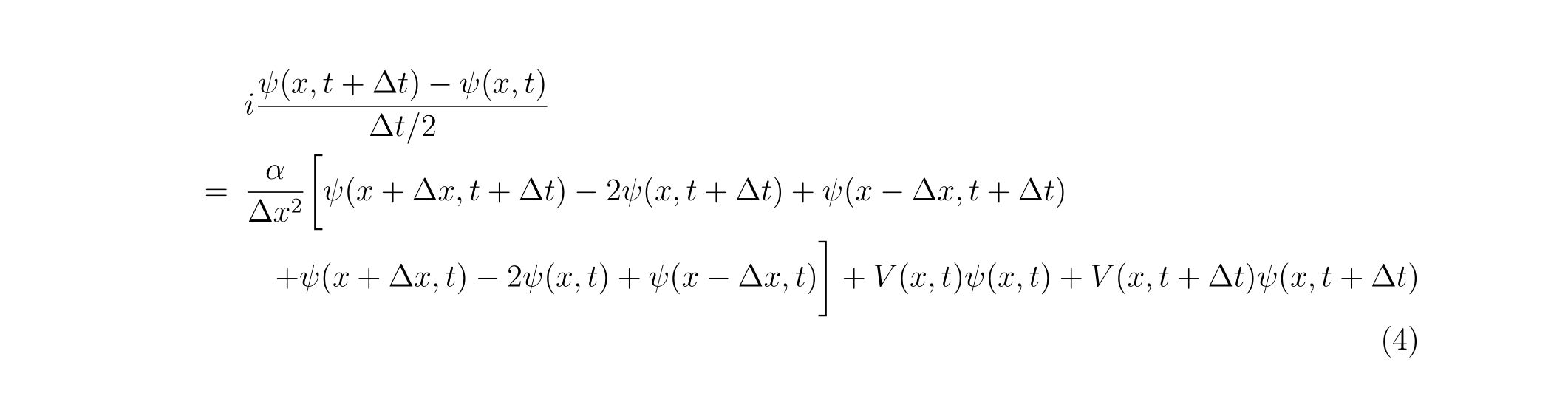
となります。時間,空間に関して\(O(\Delta t^2),O(\Delta x^2)\)です。
左辺に時刻\(t+\Delta t\)の波動関数をまとめますと、
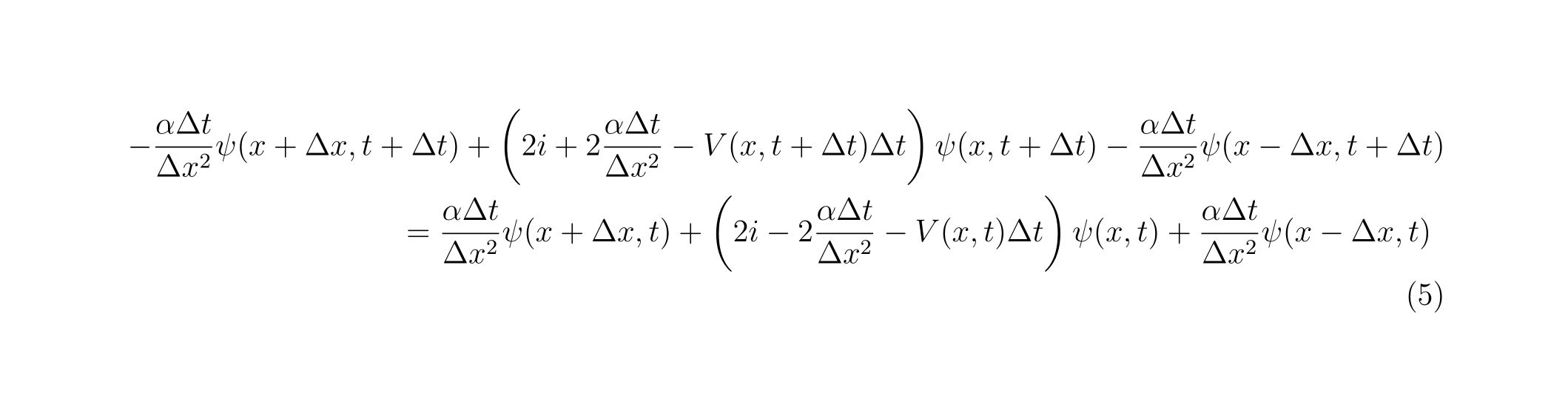
となります。これで離散化が出来ました。これがクランクニコルソン法です。
式が複雑なので、少し簡単にまとめます。
位置\(x\)を等間隔に離散化して、以下の通り離散化と記述を変えます。

この表記に倣いますと、離散化した時間依存シュレーディンガー方程式は簡潔に書けて
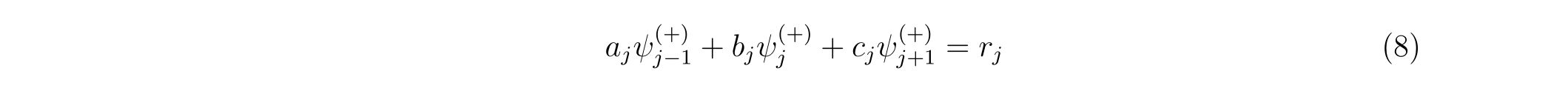
と書けます。
ここで、係数\(a,b,c,r\)は式(5)の各係数をまとめたものですが、境界条件によって多少異なります。
ここでは、固定端条件と周期境界条件の場合を特に考えてみましょう。
固定端条件の場合
固定端条件は両端での関数の値が時間によって変化しないとする条件です。数式で書けば
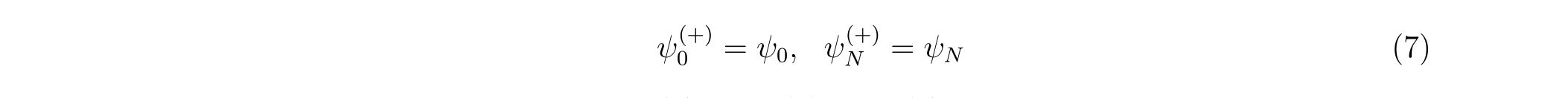
という条件が波動関数に課されます。この時、行列表式で式(8)を記述すれば、

と書き表すことが出来ます。ここで、\(\psi_0^{(+)},\psi_N^{(+)}\)に掛かる係数は境界条件を満たすように決定しています。行列の演算で知られているように、第1行目を\(a_1\)倍して第2行目を引き、第N行目を\(c_{N-1}\)倍して第N-1行目を引けばオレンジで四角く囲った枠内のみを計算すればよいことが分かります。
各々の係数の明らかな形は以下の通り得られます。

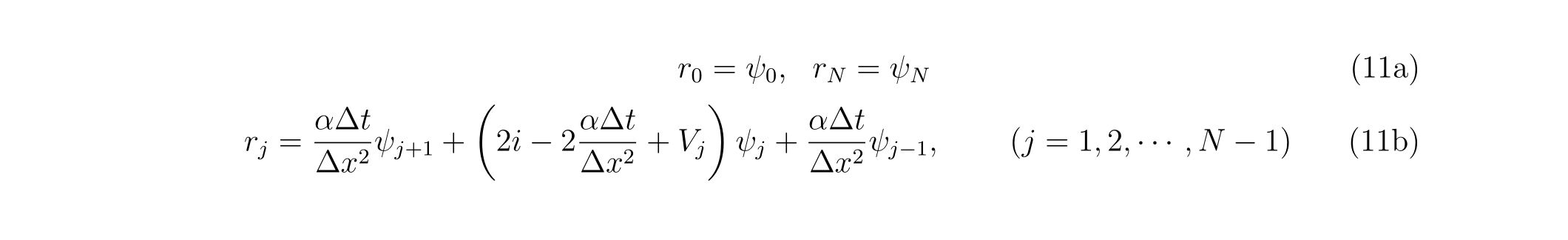
周期境界条件の場合
周期境界条件は両端での関数の値が等しく、その微分も等しいという条件です。数式で書けば
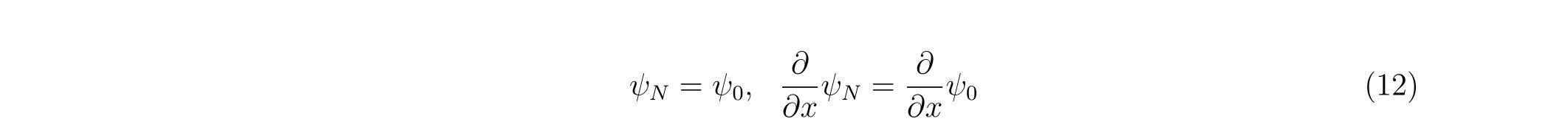
という条件が波動関数に課されます。この時、行列表式で式(8)を記述すれば、

と書き表すことが出来ます。ここで、\(\psi_N^{(+)}\)に掛かる係数は境界条件を満たすように決定しています。行列の演算で知られているように、第N行目は既に解けているのでこの要素を考える必要はありません。なので、オレンジで四角く囲った枠内のみを計算すればよいことが分かります。
各々の係数の明らかな形は以下の通り得られます。
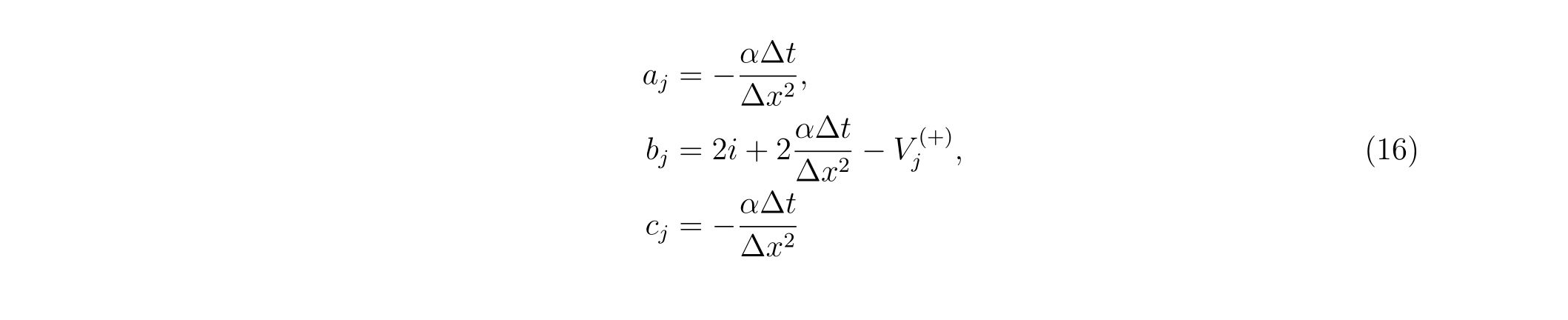
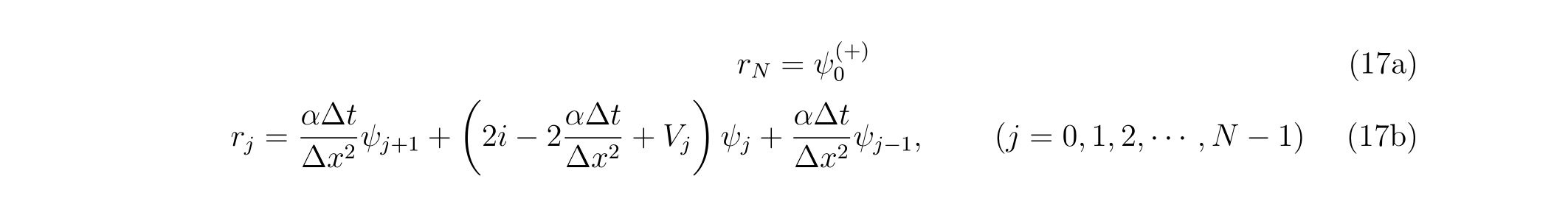
[adsense1]
三重対角行列の方程式の解法
さて、あとは式(9),(13)を数値的に解けば良いのです。
固有値問題ではありませんので、連立方程式を解けば良いのです。
固定端条件の式(9)を解くためのアルゴリズムはThomasのアルゴリズムと呼ばれる方法が一般的です。計算量のオーダーは\(O(N)\)です。
周期境界条件を含んだ三重対角行列の解法はLU分解を利用した方法[2]や、Sherman-morrison formulaという公式を利用した方法[3]があります。ここでは、擬コードが載せられている[2]を元に作成していきます。これも計算量のオーダーは\(O(N)\)ですが、固定端条件の場合よりも約二倍ほど計算量が多くなります。
メモとして書いておきますが、周期境界条件を含む5重対角行列の解法もありまして、[1]に見ることが出来ます。
フォン・ノイマンの安定性解析
これは、クランク=ニコルソン法のような線形変微分方程式を有限差分法で解く際に、数値的に安定なのか発散するのかを調べる手法です。
注意しなければならないのは、数値的に安定なので答えも正しい、という事ではない事です。
この解析により、有限差分を行う際に最低限満たさなければいけない空間の刻み幅と時間の刻み幅の条件が決定されます。
\(V(x)=0\)を考えます。
ざっくりと説明しますと、偏微分方程式における独立な解、すなわち固有の波数\(k\)で特徴づけられる解が発散しない条件から導かれます。
ある時刻の解が1ステップの時間発展をした時、複素数の増幅因子(amplification factor) \(\xi\)を伴って
\(
\begin{align}
\psi_j &= \xi^0 e^{ikj\Delta x}\\
&\downarrow \\
\psi^{(+)}_j &= \xi^1 e^{ikj\Delta x} \\
\end{align}
\)
で時間発展する、とします。時間発展によって、複素数の整数乗が掛かるのです。
もしも増幅因子の絶対値、すなわち\(|\xi|\)が1より小さければ、時間発展しても独立な解は収束するため、数値的に安定だと言えます。
しかし、\(|\xi|\)が1より大きければ、独立な解の時間発展が指数関数で発散していく事を意味するため、数値的に不安定になります。
この\(\xi\)を求めるためには、波数\(k\)をもつ固有モードの式を有限差分で書き表した式(ここでは式(5))に代入すれば求められます。kはいかなる値を持ち得ると考えます。
計算の結果、\(\xi\)は以下の通り求められます[3]。
\(
\begin{align}
\xi=\frac{1-2\beta \sin^2\left(\frac{k\Delta x}{2}\right)}{1+2\beta \sin^2\left(\frac{k\Delta x}{2}\right)} \\
\beta=\frac{\alpha}{i}\frac{\Delta t}{(\Delta x)^2}
\end{align}
\)
※検算はしていません。[3]を参照しました。
この式から分かることは、位置の間隔\(\Delta x\)が与えられたとき、いかなる\(\Delta t\)であっても\(|\xi|\lt 1\)を取るので、数値的に安定である、ということが分かります。
これはクランク=ニコルソン法(陰解法)の特徴となっており、数値的には安定な計算方法です。
詳細は[3]や[4]をご覧ください。
数値計算コード
数値計算コードは以下のように書けます。
以下のプログラムは下の例2を計算するプログラムです。
実用上は、固定端、周期境界のどちらかだけを使えばいいので、適宜消してください。
[adsense2]
実例
自由粒子
初期状態:ガウシアン型, 運動量を持つ波束が時間とともにどう発展していくか。
\(
\begin{align}
i\frac{\partial }{\partial t}\psi(x,t)&=-\frac{1}{2}\frac{\partial^2 }{\partial x^2}\psi(x,t) \\
\psi(x,t=0)&=\left(\frac{1}{\pi a^2}\right)^{1/4}\exp\left[-\frac{x^2}{2a^2}+ik_0 x\right]
\end{align}
\)
\(
\begin{align}
\psi(x,t)&=\frac{1}{\pi^{1/4}}\left(\frac{1}{a+it/a}\right)^{1/2}
\exp\left[-\frac{1}{2}\frac{(x-k_0 t)^2}{a^2+it}+i k_0 x -i\frac{k_0^2}{2} t\right]\\
|\psi(x,t)|^2&=\frac{1}{\pi^{1/2}}\left(\frac{1}{a^2+(t/a)^2}\right)^{1/2} \exp\left[-\frac{(x-k_0 t)^2}{a^2+(t/a)^2}\right]
\end{align}
\)
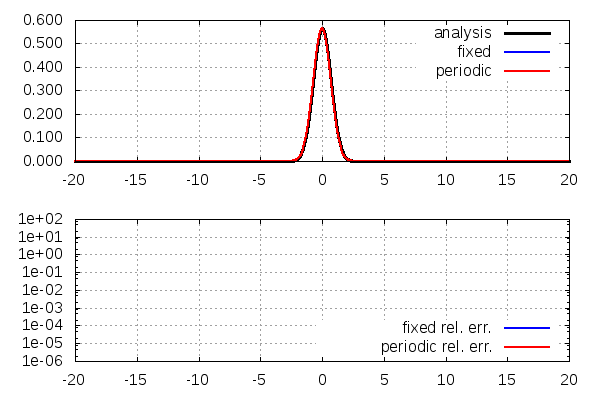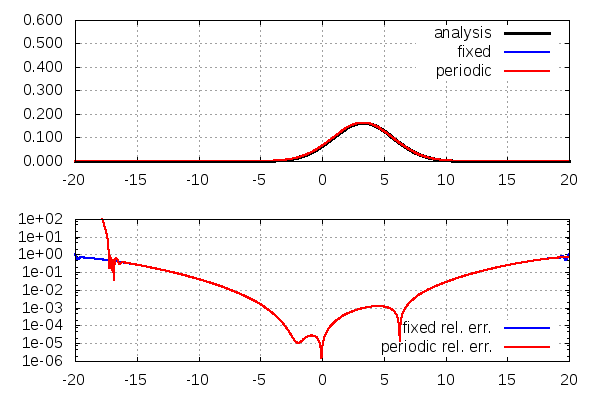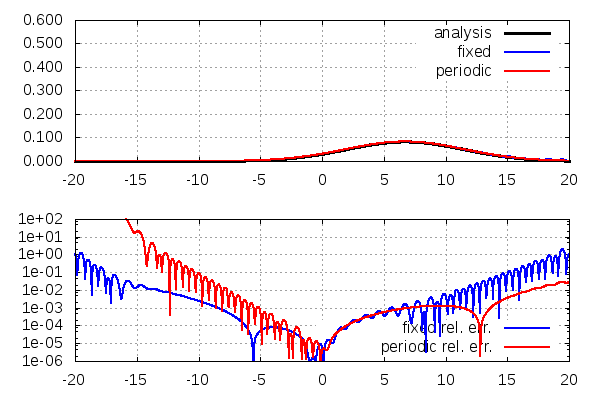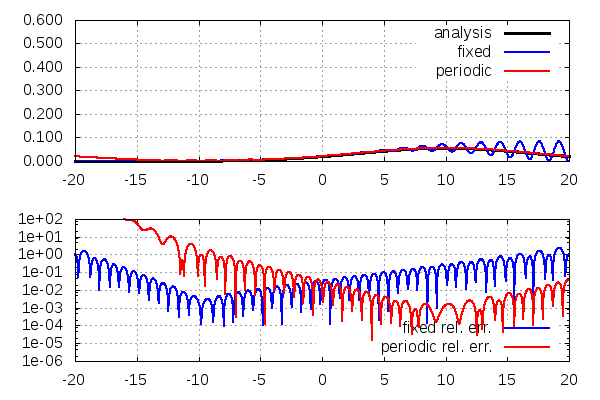
上:存在確率密度\(|\psi(x,t)|^2\)。黒→解析解、青→固定端条件の数値解、赤→周期境界条件の数値解
下:解析解との相対誤差\(|(|\psi(x,t)|^2-|f(x,t)|^2)/|f(x,t)|^2|\)。
gnuplotコードはこちら
調和振動子の固有状態の重ね合わせ
初期状態:調和振動子の基底状態+第一励起状態
\(
\begin{align}
i\frac{\partial }{\partial t}\psi(x,t)&=\left[-\frac{1}{2}\frac{\partial^2 }{\partial x^2}+\frac{1}{2}x^2\right]\psi(x,t) \\
\psi(x,t=0)&=\frac{1}{\sqrt{2}}\left[\frac{2^{1/2}}{\pi^{1/4}}xe^{-x^2/2}+\frac{1}{\pi^{1/4}}e^{-x^2/2}\right]
\end{align}
\)
\(
\displaystyle \psi(x,t)=\frac{1}{\sqrt{2}}\left[\frac{2^{1/2}}{\pi^{1/4}}xe^{-x^2/2}e^{-i\frac{3}{2}t}+\frac{1}{\pi^{1/4}}e^{-x^2/2}e^{-it/2}\right]
\)
gnuplotコードはこちら
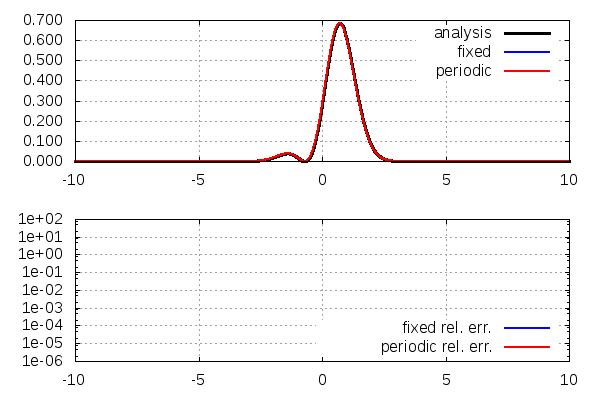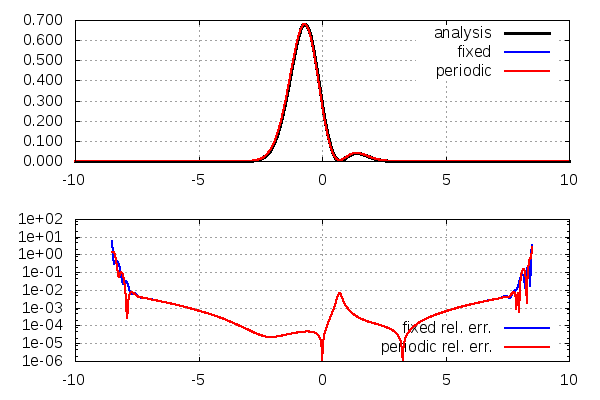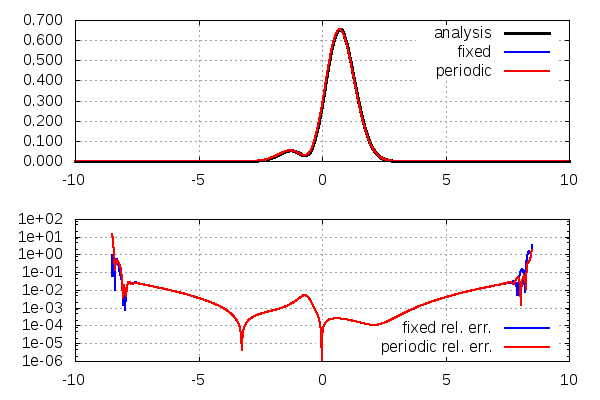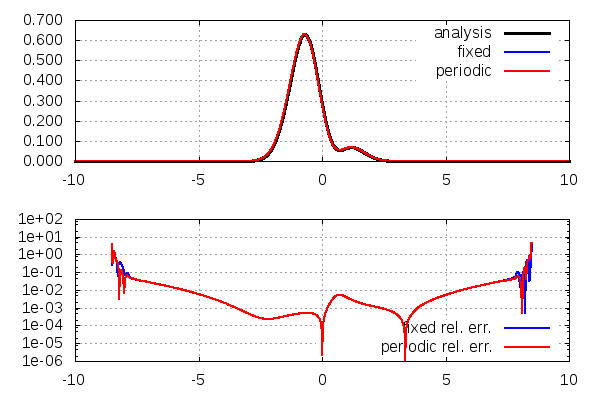
上:存在確率密度\(|\psi(x,t)|^2\)。黒→解析解、青→固定端条件の数値解、赤→周期境界条件の数値解
下:解析解との相対誤差\(|(|\psi(x,t)|^2-|f(x,t)|^2)/|f(x,t)|^2|\)。
参考文献
[1]Tomohiro Sogabe, New algorithms for solving periodic tridiagonal and periodic
pentadiagonal linear systems, Appl. Math. Comput. 202 (2008) 850-856
[2]A. A. Karawia, A computational algorithm for solving periodic pentadiagonal linear systems, Appl. Math. Comput. 174 (2006) 613–618
[3]Van Wijngaarden-Dekker-Brent法, William H. Press, Saul A. Teukolsky, William T. Vetterling, Brian P. Flannery著, 丹慶勝市ら訳(1993) 『Numerical Recipes in C [日本語版]C言語による数値計算のレシピ』 技術評論社
[4]フォン・ノイマンの安定性解析 -wikipedia