まとめ
関数

を求める問題を考えます。
\(f(x_0, y_0)=0\)を満たす\((x_0, y_0)\)が与えられている場合、\((x_1\equiv x_0+\Delta x, y_1\equiv y_0+\Delta y)\)を求めることを考えていきます。
まず、
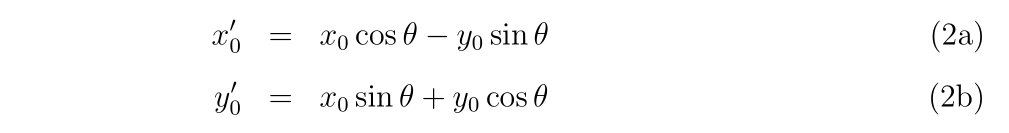
の変換を行い、初期値\((x_0, y_0)\)を\((x’_0, y’_0)\)に変換します。
ここで、\(\theta\)は定数で
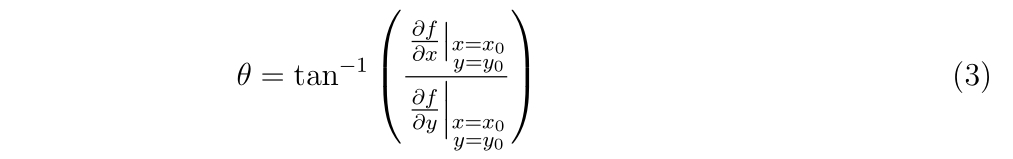
です。\((x’_0, y’_0)\)を新たな初期値として微分方程式
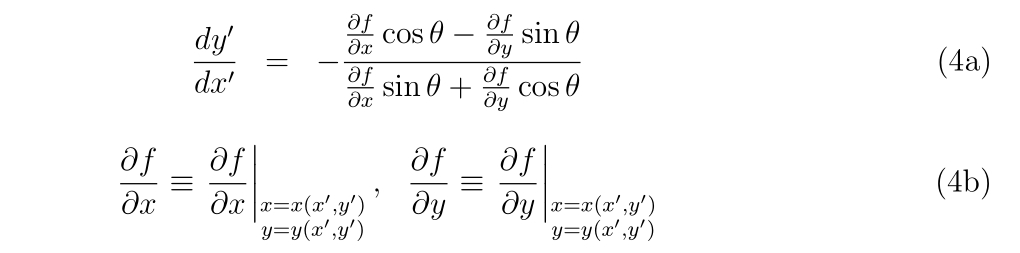
を解き、\(x_0′\)から微小距離\(h\)だけ発展させた\(x_1’\equiv x_0′ + h\)とその値\(y_1’\equiv y_0′ + \Delta y\)を求めます。
その後、逆変換
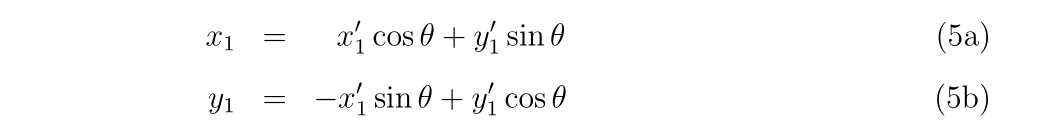
を経ることで\(f(x_1,y_1)=0\)を満たす\((x_1,y_1)\)の値を得ることができます。
導出
陰関数

を満たす\((x,y)\)を求めます。ある点\((x_0, y_0)\)において\(f(x_0, y_0)=0\)を満たすことが分かっている場合、
陰関数の全微分より、\((x_0, y_0)\)の近傍で
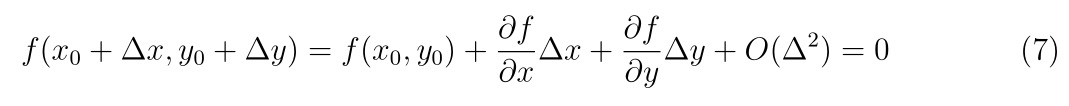
が満たされています。\(f(x_0,y_0)=0\)であり、\(\Delta x\approx \Delta y \to 0\)ならば、\(O(\Delta^2)\)の項を無視して
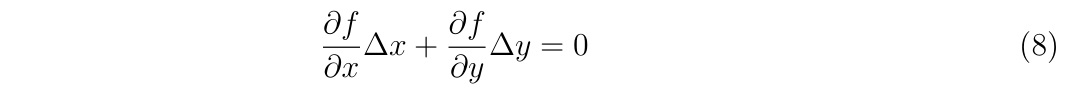
が成立する変化のみが許されます。両辺を\(\Delta x\)で割って、\(\Delta x\to 0\)の極限をとれば、
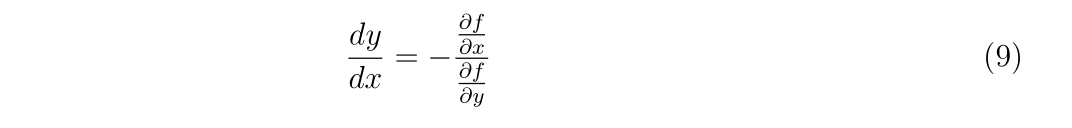
を得ます。すなわち、式(9)を何らかの手段、例えば数値計算で解けば等高線を得ることができます。
発散への対処
さて数値計算によって微分方程式(9)を解いて等高線を描く場合、\(y\)が\(x\)の一価関数になることはほとんどありません。
そのため、式(9)の右辺の分母がゼロになることがあり、微分が発散するため計算を行うことができなくなることがあります。言い換えれば、発散しない範囲しか計算できなくなるということです。
これを回避するためには様々な方法があると思いますが、例えば変数変換を適宜行いながら積分を実行していくことでこの問題を回避することができます。
発散を回避するためのアイデアは以下の通りです。
\(y\)を\(x\)の関数と見たとき、微分が発散するということは、分母がゼロになることを意味しています。
しかし、その点において90°回転させて\(y\)を\(x\)の関数としてみれば微分はゼロに等しいため、問題なく計算を進めることができます。
図示すれば以下の通りになります。
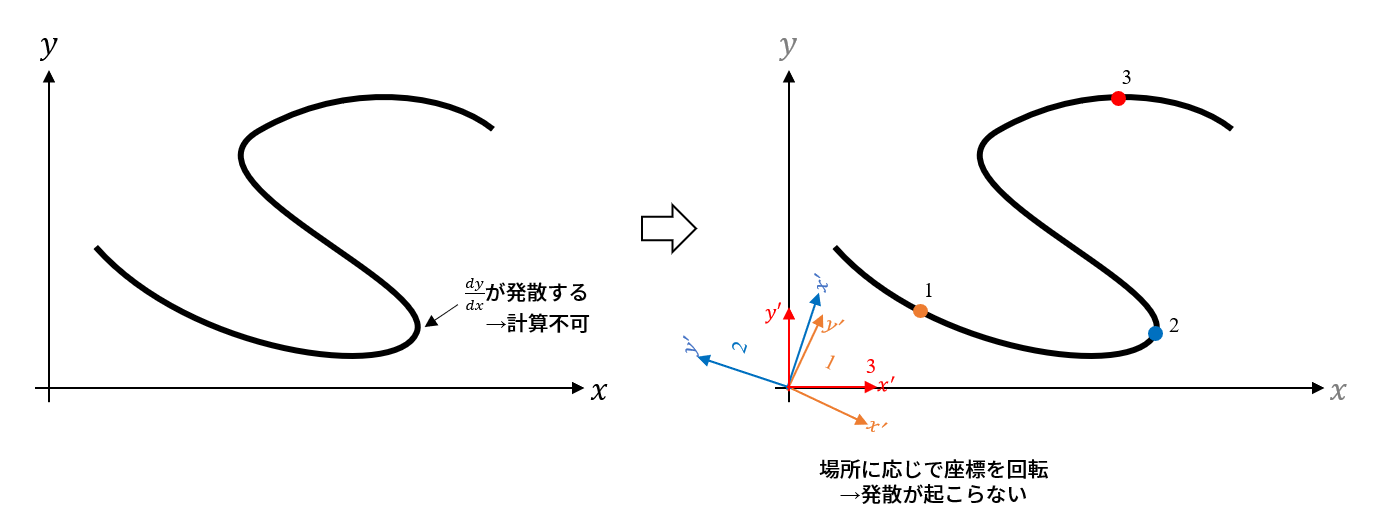
左図は座標を変化せずにそのままの関数ですが、右図のようにある点を計算したいときにその点近くの傾きと等しいように回転した座標から見るようにします。こうすることで発散を回避することができます。
これから変数変換について考えていきます。新たな変数\(x’, y’\)を用いて\(x=x(x’, y’),~y=y(x’, y’)\)(またはその逆関数)と書けているならば、

と書いても良いです。すなわち式(9)を解く代わりに\(x’\)と\(y’\)に関する方程式
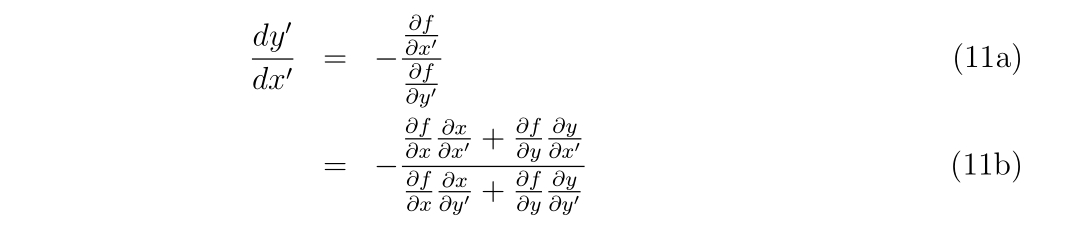
を解いても良いのです。具体的に変数変換
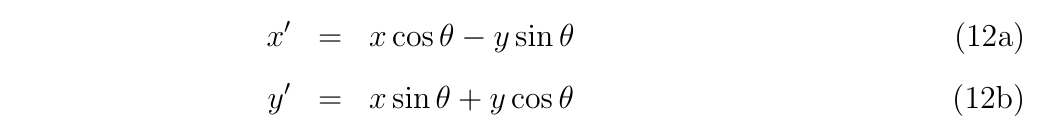

を考えます。これは座標を\(\theta\)回転させた座標系への変換です。もちろん、\(\theta=0\)のとき、\(x=x’, y=y’\)が成立し、恒等変換となります。微分方程式は
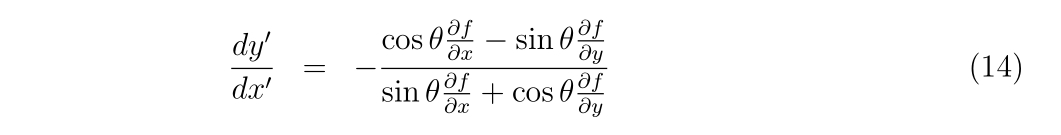
であり、\((x’, y’)\)の空間で解いていきます。
さて、回転角\(\theta\)は任意ですが、式(15)の右辺が発散しないような\(\theta\)を選ぶ必要があります。
また、数値計算を行う上では、傾きがほとんど0に近いほうが有利です。そのため、方針としては現在の傾きを計算し、その傾き分だけ逆方向に座標回転させることでこれを実現させます。
すなわち、
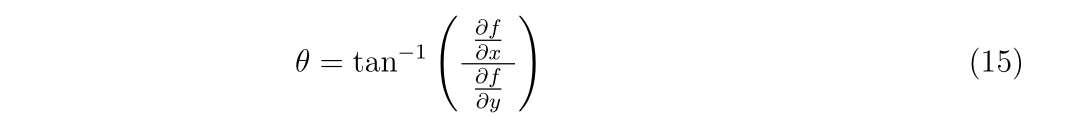
分だけ回転させます。現在の傾きと座標軸の傾きを一致させることで傾きがほとんどゼロの座標軸に回転させるのです。
プログラム
以下にプログラムを示します。
必要な情報は\(f(x,y)\)の\(x, y\)方向の偏微分\(\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}\)の解析解です。関数名”fx”, ”fy”にそれぞれを入力してください。
計算は刻み幅制御の陽的ルンゲクッタ法を用いています。
具体例
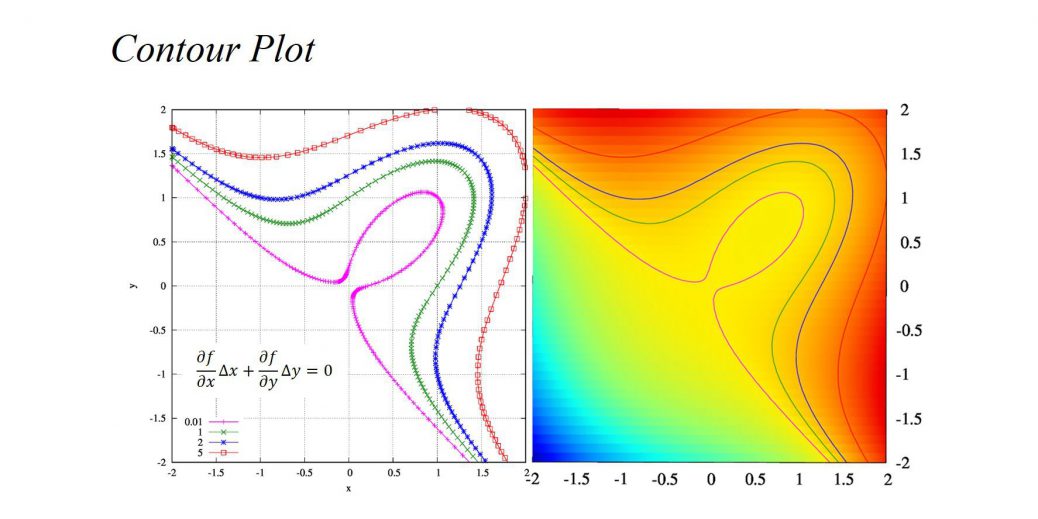
具体的に関数\(f(x,y)=x^3-2xy+y^3\)の等高線を考えていきましょう。
関数の値がそれぞれ、\(0.01,1,2,5\)に等しいときの等高線を考えます。
具体的な初期値は、
\(\displaystyle
f(-2,1.3657)\approx 0.01,~f(-2,1.4646)\approx 1,~f(-2,1.5568)\approx 2,~f(-2,1.7977)\approx 5
\)
とします。
具体的に解いたのが左の図です。
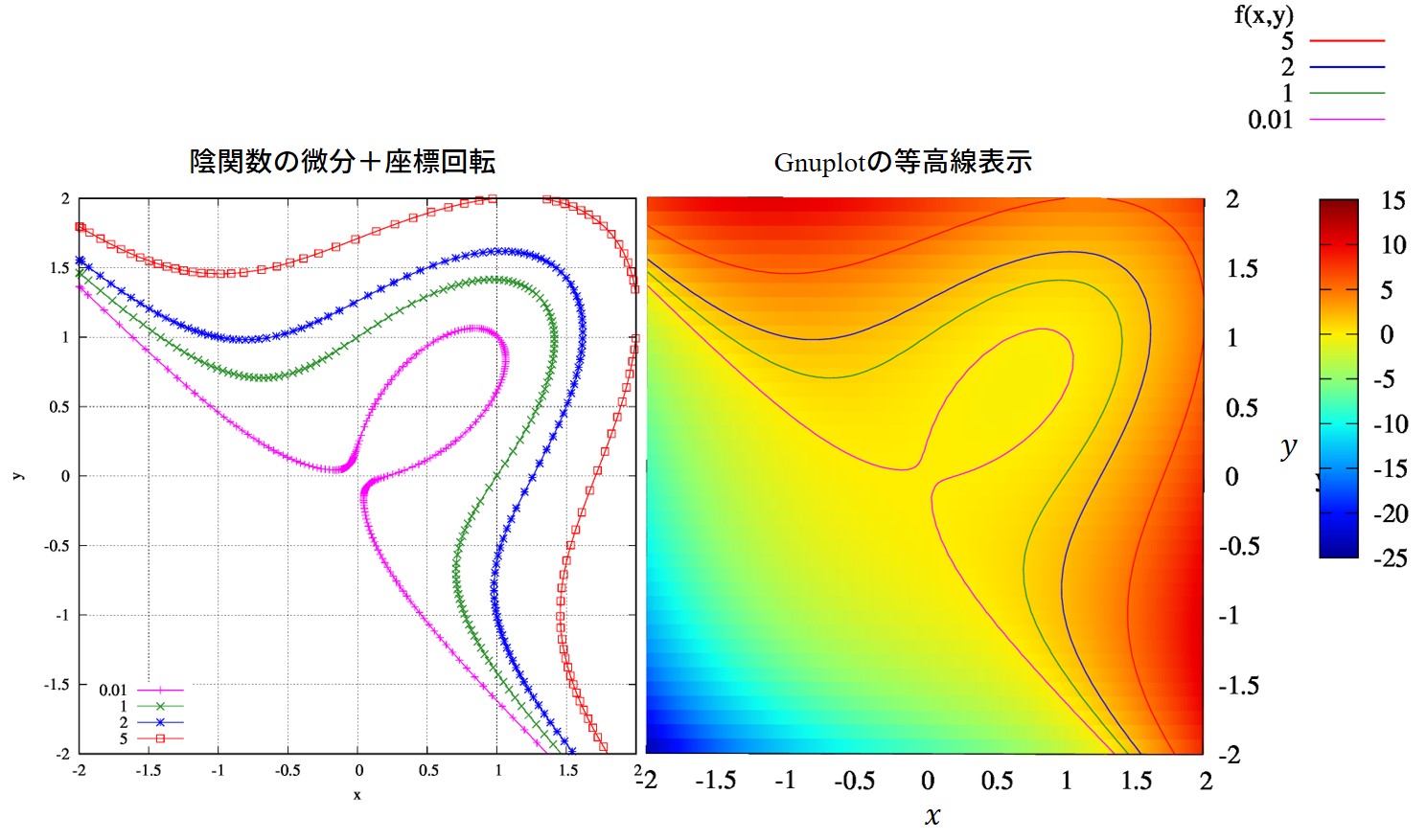
”正解”としたgnuplotの等高線表示の結果と同じ結果が得られました。座標回転がうまく働いているようですね。微分の発散を抑えるだけでなく、数値計算量も抑えられているようです。
刻み幅\(h\)が正である場合と負である場合で進む方向が変わります。
また計算の途中で分岐がある場合、どうなるかは保証できません。
また、閉じた等高線が複数ある場合、その全てを計算することは本稿のプログラムだけではできません。初期値を求める別のプログラムを作成する必要があります。
更に、等高線がある値に等しい量を計算することはできません。初期値の値に等しい等高線を引きます。
追記
調べ物をしていたら
照井章, 佐々木建昭著『27.代数関数の陰関数描画について』
http://www.kurims.kyoto-u.ac.jp/~kyodo/kokyuroku/contents/pdf/0941-27.pdf
という素晴らしい資料がありました。
この文献では2つの方法が紹介されており、
1.\(f(x,y_0)=0\)を解いて\(x=x_1,x_2,\cdots,x_n\)を解く
2.陰関数定理から求める
という方法です。資料では、1.の方法を採用していましたが、本稿の方法は2.の方法でした。
1.はもれなく等高線を見つけることができますので、考えられる結果を得たい場合によい方法です。
一方、2.は全てのゼロ点を見つけることができませんが、計算が早くできます。別の方法などで注目したい等高線が分かっている場合に良い方法でしょう。
効率的に解くためには、場合によって使い分けることが一番です。