正弦波ではない周期関数、三角波、矩形波等々の数式による表現です。
if文は使っていません。
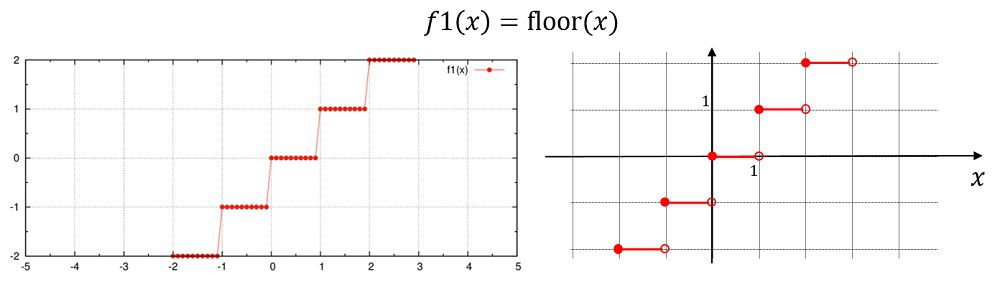
床関数\(floor(x)\)を主に用いています。
これらが唯一の作り方ではなく、最善の作り方でもありません。
非連続になる関数の場合の特定な関数の場合、中間の値を取るようにしています(フーリエ級数の収束より)。
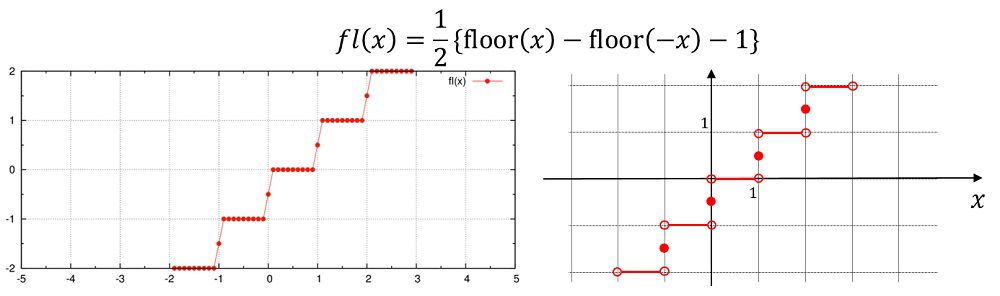
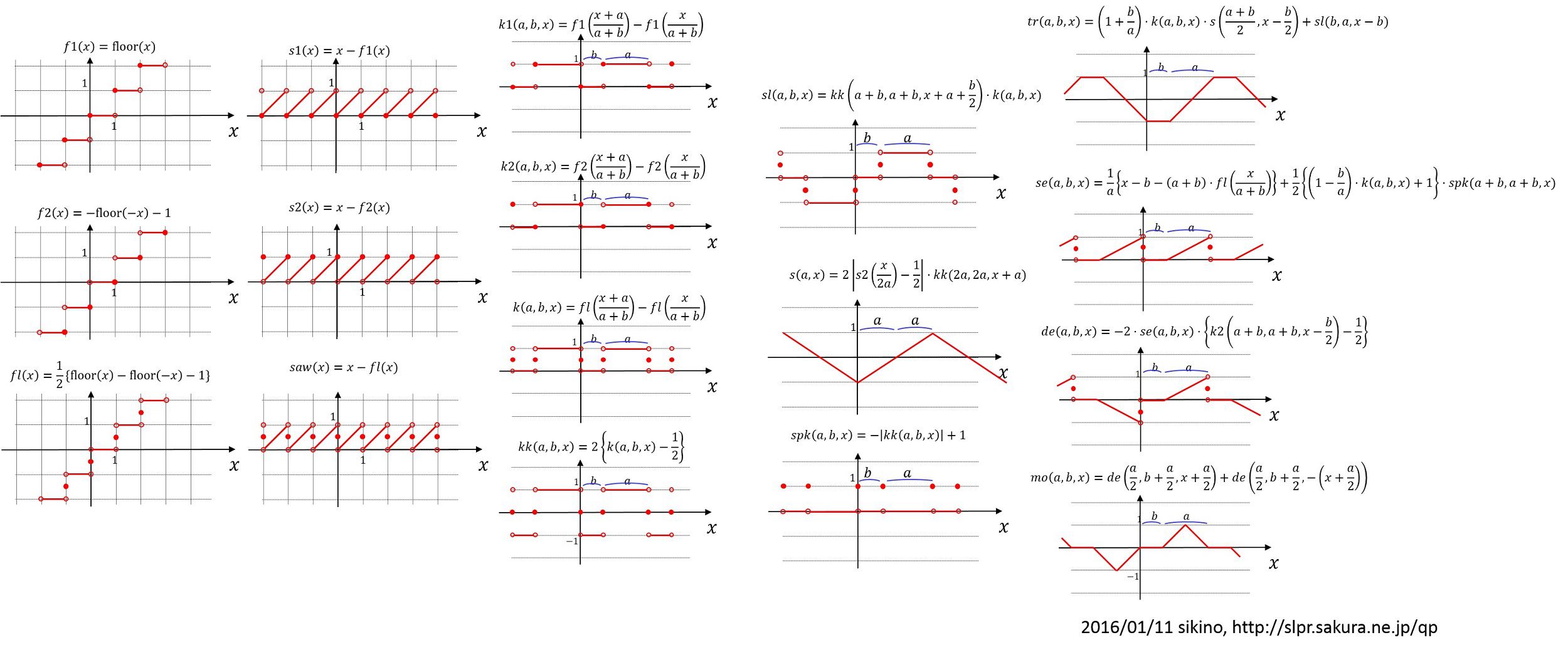
階段関数
——-
f1
——-
f2
——-
fl
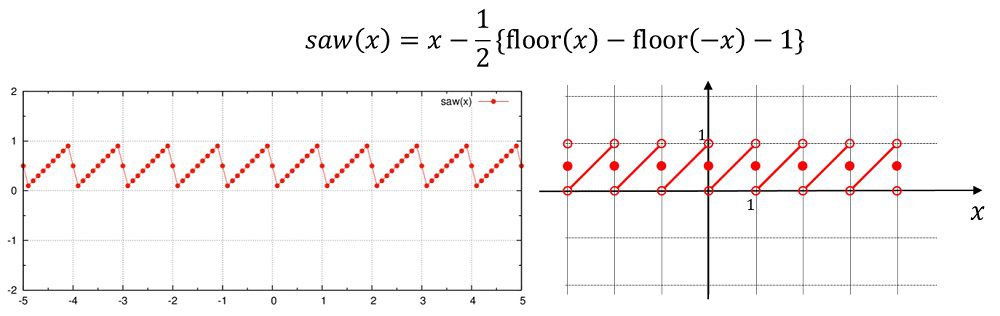
のこぎり波
s1
s2
saw
矩形波
k1,k2,k,ka,kb,kk
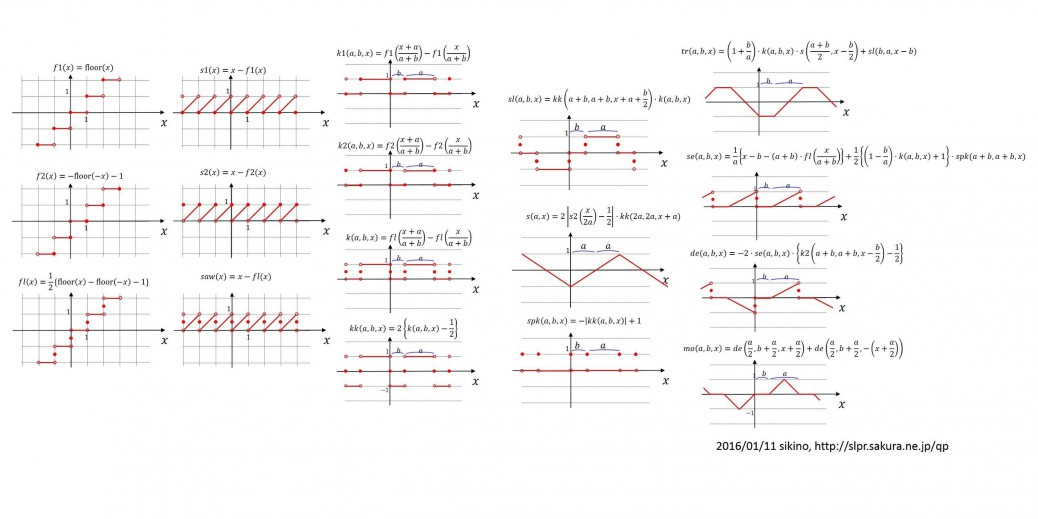
その他
sl,s,spk
tr,se,de,mo
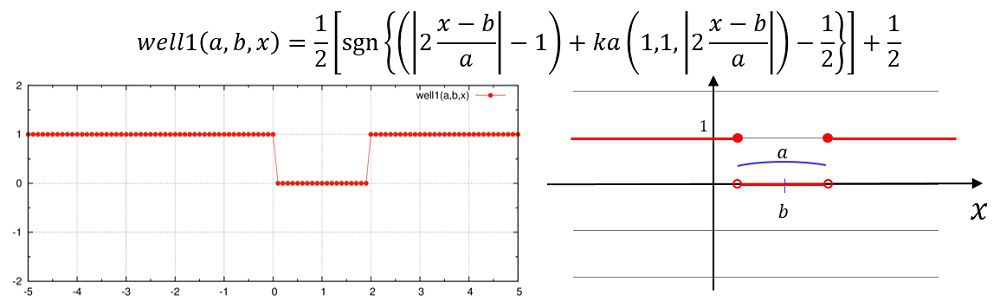
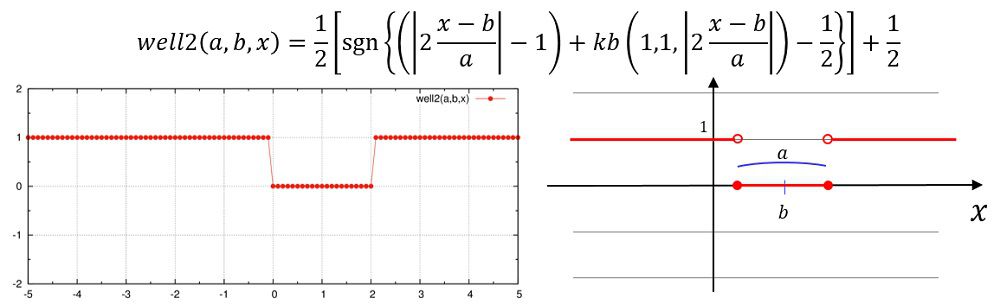
well1,well2
sl
s
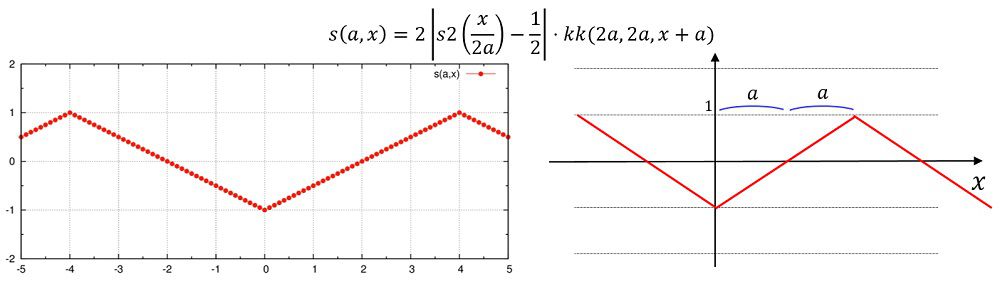
三角波は、\({\rm acos}(\cos(x))\)とも書けます。
spk
tr
se
de
mo
well1
well2
well
追記
\(\displaystyle
f(a,b,x) = sgn(abs(2*(x-b)/a)-1e0)
\)
でokです。aは井戸の幅、bは井戸の中心を示します。
まとめ
全てをまとめたgnuplotのコードは以下のものです。
set size ratio -1
set yr[-2:2]
set xr[-5:5]
set samples 101
set grid
set xtics 1
set ytics 1
set mxtics 2
set mytics 2
f1(x)=floor(x)
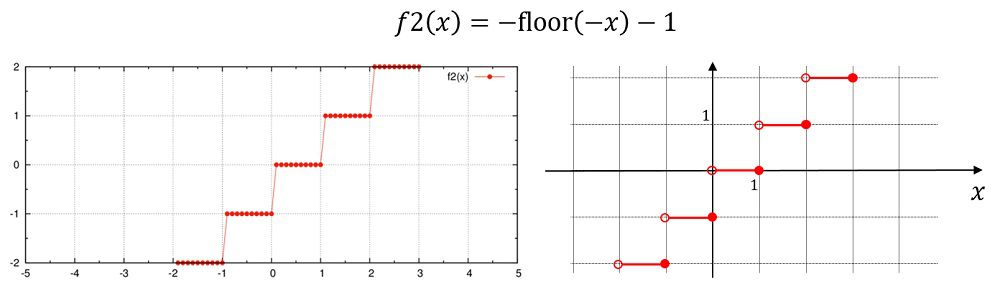
f2(x)=-floor(-x)-1e0
fl(x)=0.5e0*(floor(x)-floor(-x)-1e0)
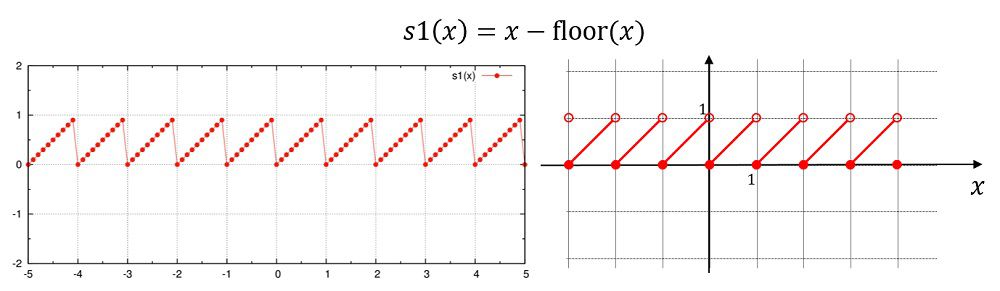
s1(x)=x-floor(x)
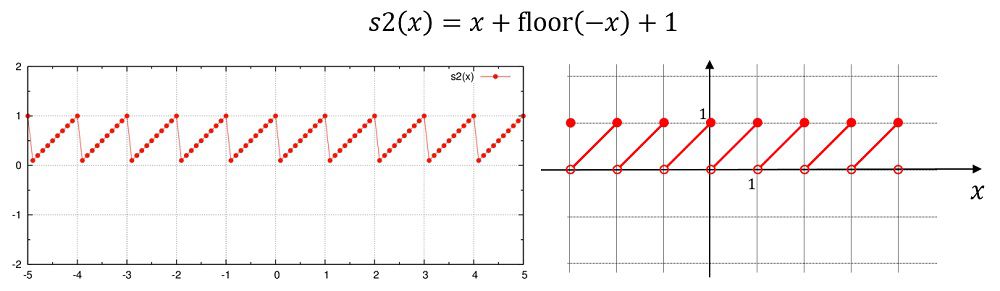
s2(x)=x+floor(-x)+1e0
saw(x)=x-0.5e0*(floor(x)-floor(-x)-1e0)
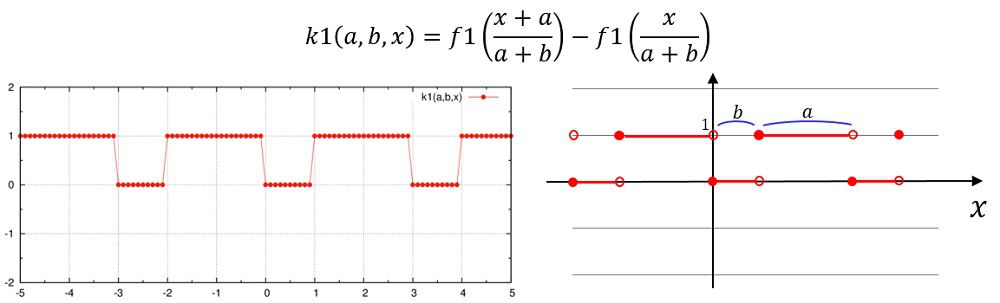
k1(a,b,x)=f1((x+a)/(a+b))-f1(x/(a+b))
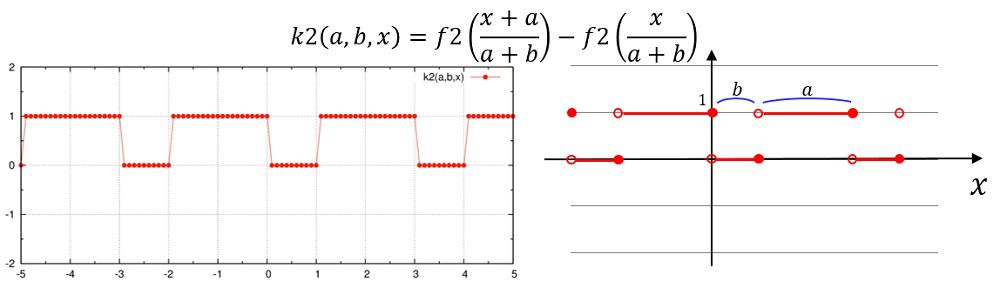
k2(a,b,x)=f2((x+a)/(a+b))-f2(x/(a+b))
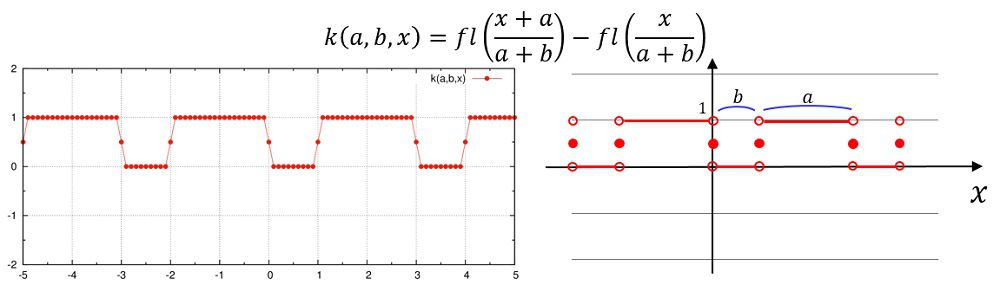
k(a,b,x)=fl((x+a)/(a+b))-fl(x/(a+b))
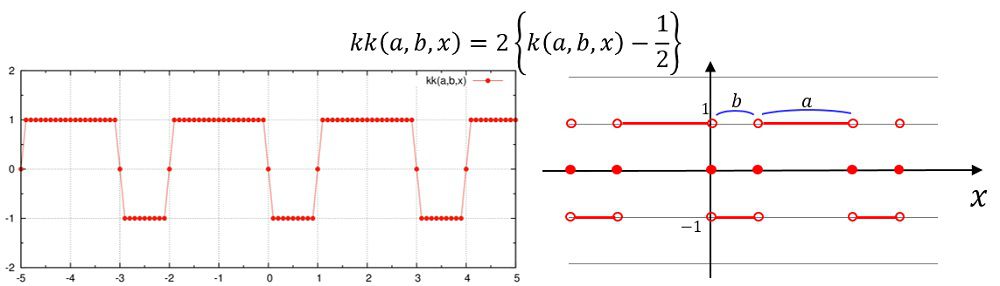
kk(a,b,x)=2e0*(k(a,b,x)-0.5e0)
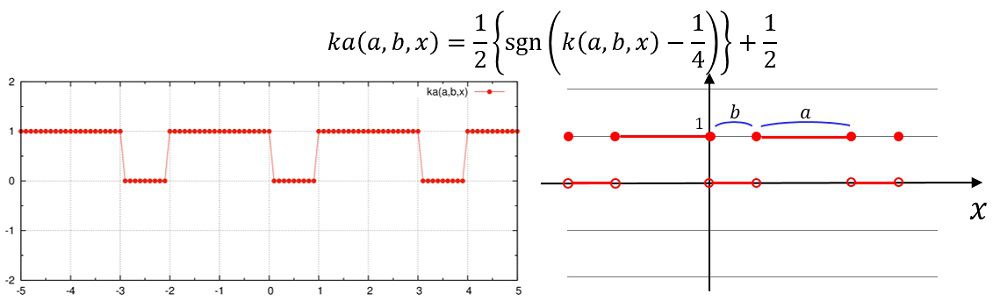
ka(a,b,x)=0.5e0*(sgn(k(a,b,x)-0.25e0))+0.5e0
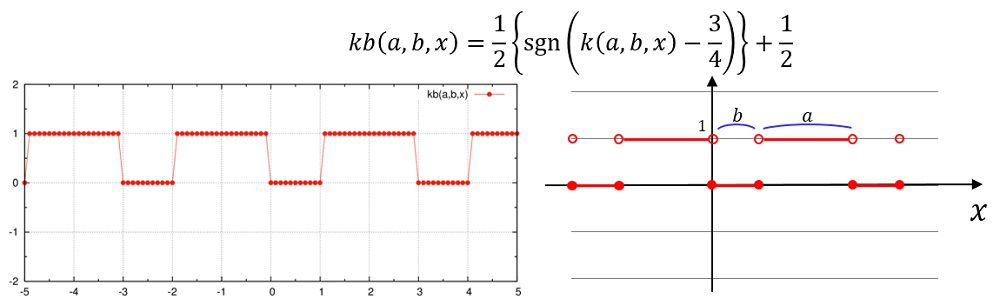
kb(a,b,x)=0.5e0*(sgn(k(a,b,x)-0.75e0))+0.5e0
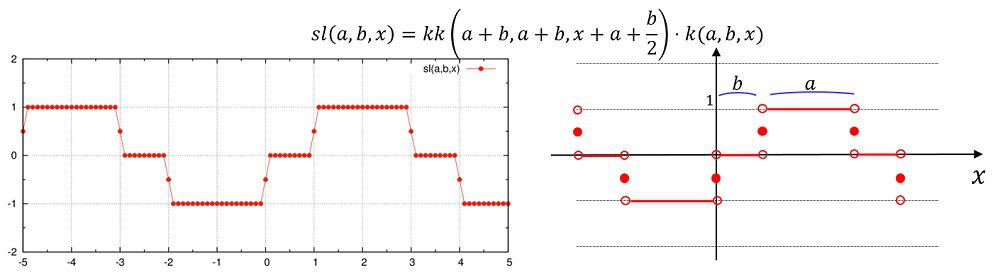
sl(a,b,x)=kk(a+b,a+b,x+0.5e0*b+a)*k(a,b,x)
s(a,x)=2e0*abs(s2(x/(a*2))-0.5e0)*kk(a*2e0,a*2e0,x+a)
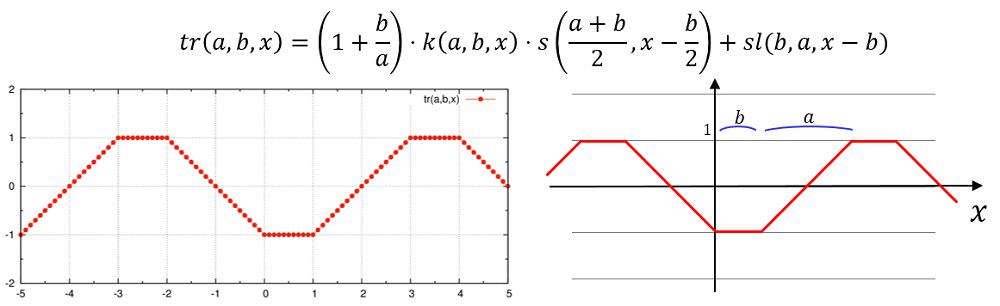
tr(a,b,x)=k(a,b,x)*s(0.5e0*(a+b),x-0.5e0*b)*(1e0+b/a)+sl(b,a,x-b)
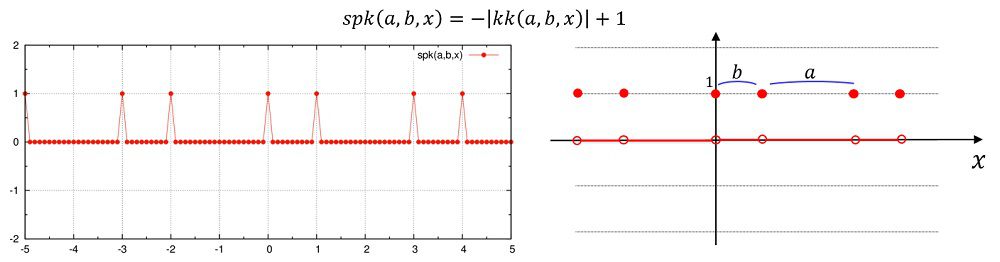
spk(a,b,x)=-abs(kk(a,b,x))+1e0
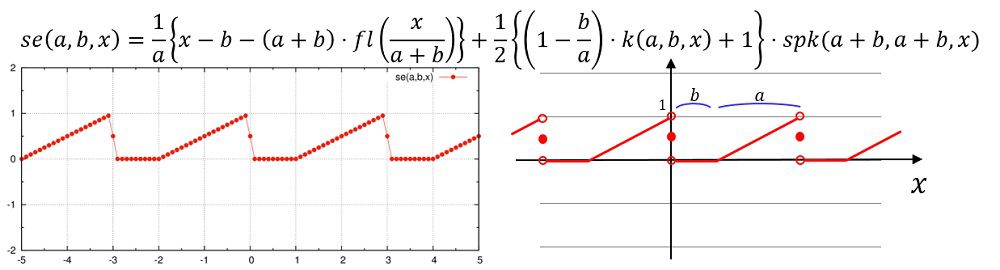
se(a,b,x)=(x-b-(a+b)*fl(x/(a+b)))/a*k(a,b,x)+0.5e0*(k(a,b,x)*(1e0-b/a)+1e0)*spk(a+b,a+b,x)
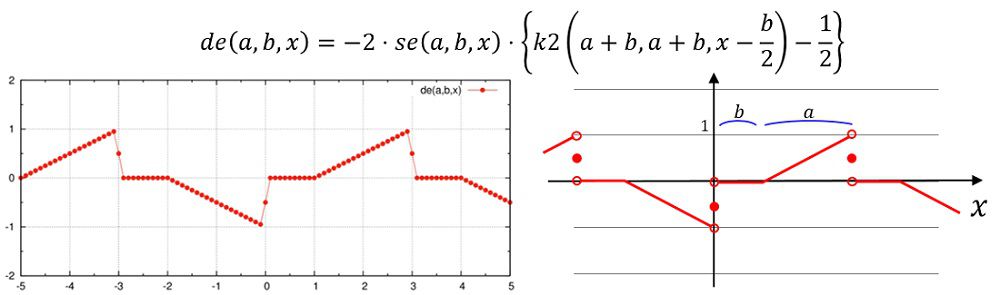
de(a,b,x)=-se(a,b,x)*2e0*(k2(a+b,a+b,x-0.5e0*b)-0.5e0)
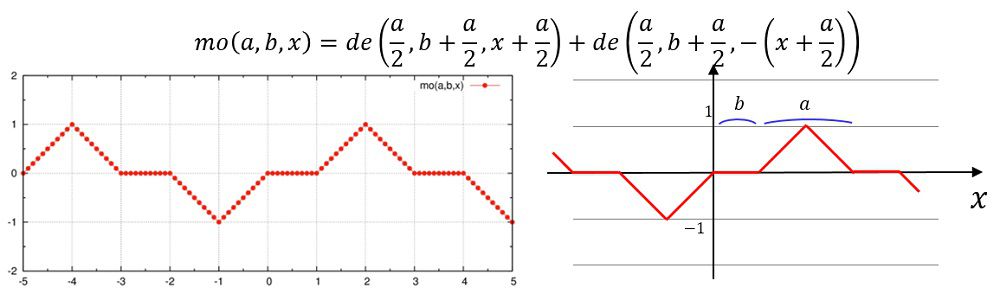
mo(a,b,x)=de(a*0.5e0,b+a*0.5e0,x+a*0.5e0)+de(a*0.5e0,b+a*0.5e0,-(x+a*0.5e0))
well1(a,b,x)=0.5e0*(sgn((abs(2e0*(x-b)/a)-1e0)+ka(1e0,1e0,abs(2e0*(x-b)/a))-0.5e0))+0.5e0
well2(a,b,x)=0.5e0*(sgn((abs(2e0*(x-b)/a)-1e0)+kb(1e0,1e0,abs(2e0*(x-b)/a))-0.5e0))+0.5e0
set yr[-2:2]
set xr[-5:5]
set samples 101
set grid
set xtics 1
set ytics 1
set mxtics 2
set mytics 2
f1(x)=floor(x)
f2(x)=-floor(-x)-1e0
fl(x)=0.5e0*(floor(x)-floor(-x)-1e0)
s1(x)=x-floor(x)
s2(x)=x+floor(-x)+1e0
saw(x)=x-0.5e0*(floor(x)-floor(-x)-1e0)
k1(a,b,x)=f1((x+a)/(a+b))-f1(x/(a+b))
k2(a,b,x)=f2((x+a)/(a+b))-f2(x/(a+b))
k(a,b,x)=fl((x+a)/(a+b))-fl(x/(a+b))
kk(a,b,x)=2e0*(k(a,b,x)-0.5e0)
ka(a,b,x)=0.5e0*(sgn(k(a,b,x)-0.25e0))+0.5e0
kb(a,b,x)=0.5e0*(sgn(k(a,b,x)-0.75e0))+0.5e0
sl(a,b,x)=kk(a+b,a+b,x+0.5e0*b+a)*k(a,b,x)
s(a,x)=2e0*abs(s2(x/(a*2))-0.5e0)*kk(a*2e0,a*2e0,x+a)
tr(a,b,x)=k(a,b,x)*s(0.5e0*(a+b),x-0.5e0*b)*(1e0+b/a)+sl(b,a,x-b)
spk(a,b,x)=-abs(kk(a,b,x))+1e0
se(a,b,x)=(x-b-(a+b)*fl(x/(a+b)))/a*k(a,b,x)+0.5e0*(k(a,b,x)*(1e0-b/a)+1e0)*spk(a+b,a+b,x)
de(a,b,x)=-se(a,b,x)*2e0*(k2(a+b,a+b,x-0.5e0*b)-0.5e0)
mo(a,b,x)=de(a*0.5e0,b+a*0.5e0,x+a*0.5e0)+de(a*0.5e0,b+a*0.5e0,-(x+a*0.5e0))
well1(a,b,x)=0.5e0*(sgn((abs(2e0*(x-b)/a)-1e0)+ka(1e0,1e0,abs(2e0*(x-b)/a))-0.5e0))+0.5e0
well2(a,b,x)=0.5e0*(sgn((abs(2e0*(x-b)/a)-1e0)+kb(1e0,1e0,abs(2e0*(x-b)/a))-0.5e0))+0.5e0
「三角波、のこぎり波、矩形波、その他の数式」への1件のフィードバック