program main
implicit none
integer::i,j,Nx,Ny,Mx,My
double precision::x,y,f,df,df2
double precision,allocatable::xdata(:),ydata(:),fdata(:,:),xa(:),ya(:),fa(:,:)
Nx=10
Ny=20
Mx=50
My=100
allocate(xdata(0:Nx),ydata(0:Ny),fdata(0:Nx,0:Ny))
allocate(xa(0:Mx),ya(0:My),fa(0:Mx,0:My))
xdata=0d0
ydata=0d0
fdata=0d0
xa=0d0
ya=0d0
fa=0d0
! original data
open(10,file='original_data.d')
write(10,'(A)')"# x y f(x,y)"
do i=0,Nx
do j=0,Ny
xdata(i)=dble(i)*0.5d0
ydata(j)=dble(j)*0.2d0
fdata(i,j)=sin(2d0*xdata(i))*exp(-0.5d0*ydata(j)**2)
write(10,*)xdata(i),ydata(j),fdata(i,j)
enddo
write(10,*)
enddo
close(10)
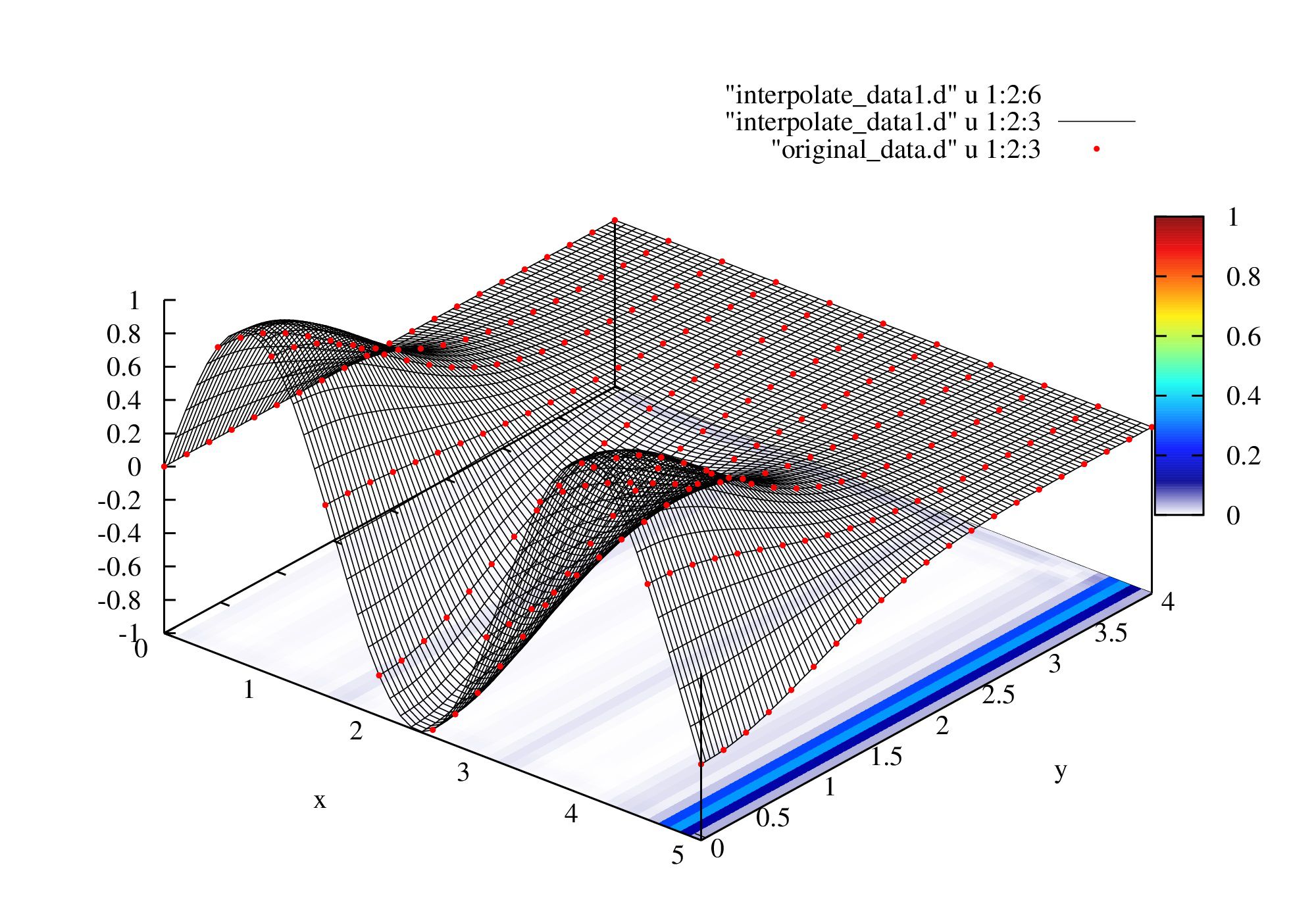
! Cubic-spline interpolation given position as point
open(10,file='interpolate_data1.d')
write(10,'(A)')"# x y f(x,y) df(x,y)/dx d^2f(x,y)/dx^2"
do i=0,Mx
do j=0,My
x=dble(i)*0.1d0
y=dble(j)*0.04d0
call c3spline2d1p(f,df,df2,x,y,Nx,Ny,fdata,xdata,ydata,1)
write(10,'(6e20.7e3)')x,y,f,df,df2,abs((f-sin(2d0*x)*exp(-0.5d0*y**2))/(f))
enddo
write(10,*)
enddo
close(10)
! Cubic-spline interpolation given position as array
do i=0,Mx
xa(i)=dble(i)*0.1d0
enddo
do j=0,My
ya(j)=dble(j)*0.04d0
enddo
open(10,file='interpolate_data2.d')
write(10,'(A)')"# x y f(x,y) "
call c3spline2d(fa,Mx,My,xa,ya,Nx,Ny,fdata,xdata,ydata)
do i=0,Mx
do j=0,My
write(10,'(3e20.7e3)')xa(i),ya(j),fa(i,j)
enddo
write(10,*)
enddo
close(10)
! 2d integration by spline interpolation
call c3spline2d_integral(s,Nx,Ny,xdata,ydata,fdata)
write(6,*)s
stop
end program main
subroutine c3spline2d1p(f,df,df2,x,y,Nx,Ny,fdata,xdata,ydata,key)
implicit none
integer,intent(in)::Nx,Ny,key
double precision,intent(in)::x,y,fdata(0:Nx,0:Ny),xdata(0:Nx),ydata(0:Ny)
double precision,intent(out)::f,df,df2
!
! key = 1 --> 1.interpolate y, 2.interpolate x | df = df/dx, df2 = d^2f/dx^2
! key = 2 --> 1.interpolate x, 2.interpolate y | df = df/dy, df2 = d^2f/dy^2
! key = 3 --> Average of key=1,2 | df = 0, df2=0
!
integer::i,j
double precision,allocatable::tfx(:),tfy(:)
double precision::p,q,dfdx,dfdy,dfdx2,dfdy2
allocate(tfx(0:Nx),tfy(0:Ny))
tfx=0d0; tfy=0d0
if(key.eq.1)then
do i=0,Nx
tfy(0:Ny)=fdata(i,0:Ny)
call c3spline1p(f,df,df2,y,Ny,tfy,ydata)
tfx(i)=f
enddo
call c3spline1p(f,df,df2,x,Nx,tfx,xdata)
elseif(key.eq.2)then
do j=0,Ny
tfx(0:Nx)=fdata(0:Nx,j)
call c3spline1p(f,df,df2,x,Nx,tfx,xdata)
tfy(j)=f
enddo
call c3spline1p(f,df,df2,y,Ny,tfy,ydata)
elseif(key.eq.3)then
do i=0,Nx
tfy(0:Ny)=fdata(i,0:Ny)
call c3spline1p(f,df,df2,y,Ny,tfy,ydata)
tfx(i)=f
enddo
call c3spline1p(p,dfdx,dfdx2,x,Nx,tfx,xdata)
do j=0,Ny
tfx(0:Nx)=fdata(0:Nx,j)
call c3spline1p(f,df,df2,x,Nx,tfx,xdata)
tfy(j)=f
enddo
call c3spline1p(q,dfdy,dfdy2,y,Ny,tfy,ydata)
f = (p+q)*0.5d0
df = 0d0
! df = dfdx
! df = dfdy
df2 = 0d0
! df2 = dfdx2
! df2 = dfdy2
endif
return
end subroutine c3spline2d1p
subroutine c3spline2d(f,Mx,My,x,y,Nx,Ny,fdata,xdata,ydata)
implicit none
integer,intent(in)::Nx,Ny,Mx,My
double precision,intent(in)::x(0:Mx),y(0:My)
double precision,intent(in)::fdata(0:Nx,0:Ny),xdata(0:Nx),ydata(0:Ny)
double precision,intent(out)::f(0:Mx,0:My)
integer::i,j
double precision,allocatable::tfx(:),tfy(:),gx(:),gy(:),gf(:,:)
allocate(tfx(0:Nx),tfy(0:Ny),gx(0:Mx),gy(0:My),gf(0:Nx,0:My))
tfx=0d0; tfy=0d0; gx=0d0; gy=0d0
do i=0,Nx
tfy(0:Ny)=fdata(i,0:Ny)
call c3spline(My,gy,y,Ny,tfy,ydata)
gf(i,0:My)=gy(0:My)
enddo
do j=0,My
tfx(0:Nx)=gf(0:Nx,j)
call c3spline(Mx,gx,x,Nx,tfx,xdata)
f(0:Mx,j)=gx(0:Mx)
enddo
return
end subroutine c3spline2d
subroutine c3spline(M,f,x,N,fdata,xdata)
implicit none
integer,intent(in)::N,M
double precision,intent(in)::x(0:M),fdata(0:N),xdata(0:N)
double precision,intent(out)::f(0:M) !,df(0:M),df2(0:M)
integer::i,j
double precision::t
double precision,allocatable::a(:),b(:),c(:),d(:)
allocate(a(0:N-1),b(0:N-1),c(0:N-1),d(0:N-1))
call spline_abcd(a,b,c,d,N,xdata,fdata)
do j=0,M
if(x(j).lt.xdata(0))then
t=x(j)-xdata(0)
f(j) = ((a(0)*t+b(0))*t+c(0))*t+d(0)
!df(j) =3d0*a(0)*t*t+2d0*b(0)*t+c(0)
!df2(j)=6d0*a(0)*t+2d0*b(0)
elseif(x(j).gt.xdata(N))then
t =x(j)-xdata(N-1)
f(j) = ((a(N-1)*t+b(N-1))*t+c(N-1))*t+d(N-1)
!df(j) =3d0*a(N-1)*t*t+2d0*b(N-1)*t+c(N-1)
!df2(j)=6d0*a(N-1)*t+2d0*b(N-1)
else
do i=0,N-1
if(x(j).ge.xdata(i).and.x(j).le.xdata(i+1))then
t=x(j)-xdata(i)
f(j) = ((a(i)*t+b(i))*t+c(i))*t+d(i)
!df(j) =3d0*a(i)*t*t+2d0*b(i)*t+c(i)
!df2(j)=6d0*a(i)*t+2d0*b(i)
exit
endif
enddo
endif
enddo
return
end subroutine c3spline
subroutine c3spline1p(f,df,df2,x,N,fdata,xdata)
implicit none
integer,intent(in)::N
double precision,intent(in)::x,fdata(0:N),xdata(0:N)
double precision,intent(out)::f,df,df2
integer::i
double precision::t
double precision,allocatable::a(:),b(:),c(:),d(:)
allocate(a(0:N-1),b(0:N-1),c(0:N-1),d(0:N-1))
call spline_abcd(a,b,c,d,N,xdata,fdata)
if(x.lt.xdata(0))then
t=x-xdata(0)
f = ((a(0)*t+b(0))*t+c(0))*t+d(0)
df =3d0*a(0)*t*t+2d0*b(0)*t+c(0)
df2=6d0*a(0)*t+2d0*b(0)
elseif(x.gt.xdata(N))then
t=x-xdata(N-1)
f= ((a(N-1)*t+b(N-1))*t+c(N-1))*t+d(N-1)
df =3d0*a(N-1)*t*t+2d0*b(N-1)*t+c(N-1)
df2=6d0*a(N-1)*t+2d0*b(N-1)
else
do i=0,N-1
if(x.ge.xdata(i).and.x.le.xdata(i+1))then
t=x-xdata(i)
f= ((a(i)*t+b(i))*t+c(i))*t+d(i)
df =3d0*a(i)*t*t+2d0*b(i)*t+c(i)
df2=6d0*a(i)*t+2d0*b(i)
exit
endif
enddo
endif
return
end subroutine c3spline1p
subroutine c3spline2d_integral(s,Nx,Ny,xdata,ydata,fdata)
implicit none
integer,intent(in)::Nx,Ny
double precision,intent(in)::fdata(0:Nx,0:Ny),xdata(0:Nx),ydata(0:Ny)
double precision,intent(out)::s
integer::i,j
double precision::t
double precision,allocatable::tfy(:),tfx(:)
allocate(tfx(0:Nx),tfy(0:Ny))
do j=0,Ny
tfx(0:Nx)=fdata(0:Nx,j)
call c3spline_integral(t,Nx,tfx,xdata)
tfy(j)=t
enddo
call c3spline_integral(s,Ny,tfy,ydata)
return
end subroutine c3spline2d_integral
subroutine c3spline_integral(s,N,fdata,xdata)
implicit none
integer,intent(in)::N
double precision,intent(in)::fdata(0:N),xdata(0:N)
double precision,intent(out)::s
integer::i
double precision::t
double precision,allocatable::a(:),b(:),c(:),d(:)
allocate(a(0:N-1),b(0:N-1),c(0:N-1),d(0:N-1))
call spline_abcd(a,b,c,d,N,xdata,fdata)
s=0d0
do i=0,N-1
t=xdata(i+1)-xdata(i)
s=s+0.25d0*a(i)*t**4 + (b(i)/3d0)*t**3 + 0.5d0*c(i)*t**2 + d(i)*t
enddo
return
end subroutine c3spline_integral
subroutine spline_abcd(a,b,c,d,N,xdata,fdata)
implicit none
integer,intent(in)::N
double precision,intent(out)::a(0:N-1),b(0:N-1),c(0:N-1),d(0:N-1)
double precision,intent(in)::xdata(0:N),fdata(0:N)
integer::i,j
double precision,allocatable::l(:),mu(:),h(:),alpha(:),z(:)
allocate(h(0:N-1),alpha(1:N-1))
do i=0,N-1
h(i)=xdata(i+1)-xdata(i)
enddo
do i=1,N-1
alpha(i)=3d0*(fdata(i+1)-fdata(i))/h(i)-3d0*(fdata(i)-fdata(i-1))/h(i-1)
enddo
allocate(l(0:N-1),mu(0:N-1),z(0:N-1))
l=0d0; mu=0d0; z=0d0
l(0)=1d0
do i=1,N-1
l(i)=2d0*(xdata(i+1)-xdata(i-1))-h(i-1)*mu(i-1)
mu(i)=h(i)/l(i)
z(i)=(alpha(i)-h(i-1)*z(i-1))/l(i)
enddo
b(N-1)=z(N-1)
c(N-1)=(fdata(N)-fdata(N-1))/h(N-1)-h(N-1)*(2d0*b(N-1))/3d0
a(N-1)=-b(N-1)/(3d0*h(N-1))
d(N-1)=fdata(N-1)
do j=N-2,0,-1
b(j)=z(j)-mu(j)*b(j+1)
c(j)=(fdata(j+1)-fdata(j))/h(j)-h(j)*(b(j+1)+2d0*b(j))/3d0
a(j)=(b(j+1)-b(j))/(3d0*h(j))
d(j)=fdata(j)
enddo
return
end subroutine spline_abcd

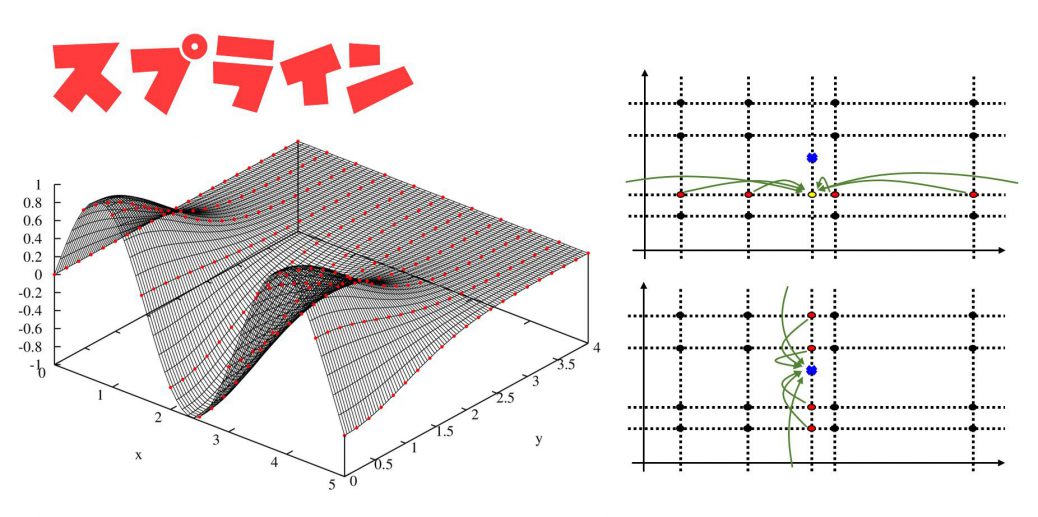
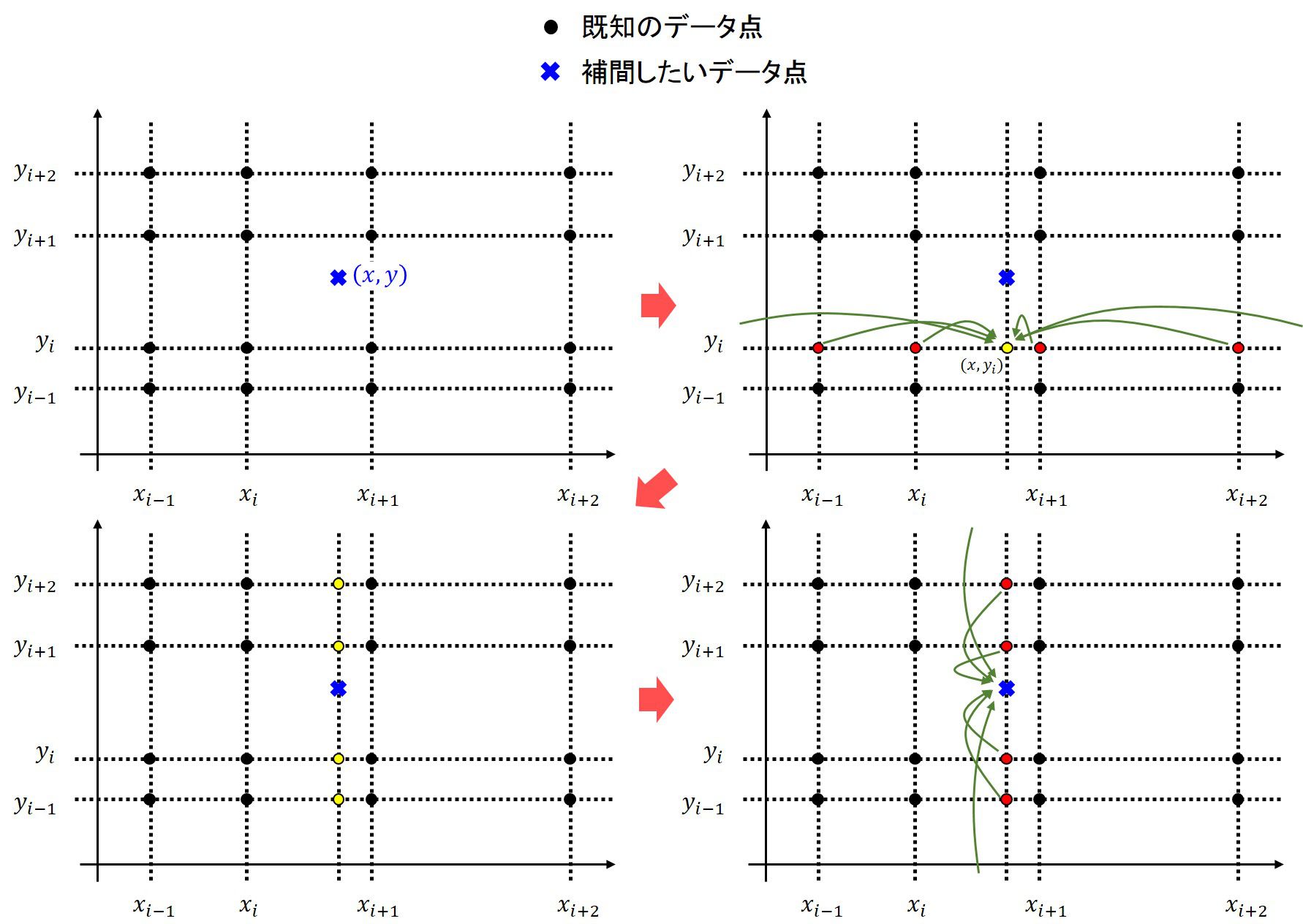
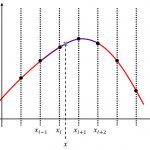


2次元スプライン補間の導出を参考にさせていただきました.
記事でデータ点の端の二階微分値を0にする理由がわからないとおっしゃっていましたが,
これは材料力学の梁(はり*)のたわみ計算に近いものと理解しました.
梁のたわみ計算にもスプライン曲線と似た考え方が登場するのですが,
このとき,二階微分値は梁にかかるモーメントに相当します.
そのため,梁の両端にモーメントをかけると不自然に曲がってしまうように,
スプライン曲線もデータ点の端の二階微分値を0にしないと
不自然な形になってしまうのではないかと考えます.
*あるいは宙に浮かんだ棒を考えてください.
ご参考になれば幸いです.
コメントありがとうございます。
たしかに、物理的な視点を加えればそのような解釈が可能ですね。
スプライン補間をある特定の物理的な現象(二階微分がゼロである境界条件を満たす現象)に施す場合ならば、二階微分がゼロで補間する方法は妥当な境界条件であり、その通りだと思いました。
しかし、
1.スプライン補間の考えそれ自体に物理現象は関係ない点
2.例えば周期境界条件を満たすような物理現象を記述する関数を補間する際には適切ではない点
が説明できません。
にもかかわらず、よく見るスプライン補間の説明では、データ点の端の二階微分値を0にするというのが通例となっています。
その意味でなぜ二階微分がゼロの境界条件が採用されているのか分からない、と記述しました。
二階微分値を0に置く物理現象が多いので採用しているのかな、と思っています。
大変分かりやすく素晴らしい記事でした、ありがとうございます。
境界条件に関してですが、この記事で紹介されているものの他にも、様々なパターンがあるようです。両端で2階微分が0という条件を課したものは特にnatural splineやsimple splineと呼ばれているようです。他にも両端の1階微分の係数を与えるclamped splineや、周期境界条件を課すようなperiodic splineなど色々あるようです。
同じデータでも、この境界条件の取り方でスプライン曲線は変わりますので、状況に応じて使い分ける必要がありますね。色々比較してみると興味深いかと思います。
コメントありがとうございます。
なるほど!キーワードで検索したところ、たくさん出てきました。私の調べが足りなかったようで、ご指摘ありがとうございます。
固定端だと数値計算的に三重対角行列になるので、最も簡単に解けるから教育的にも良いのかな?と考えていました。
特に端が重要になる場合は使い分ける必要がありますね。
プログラム勉強中に出会い、素晴らしいサイトに感動しております。
subroutine spline_abcd中のl, mu, zの部分はどのような仕組み(アルゴリズム)なのでしょうか?大変恐縮なのですが、お教え頂ければ幸いです。
この部分は、三重対角行列の解法で『TDMA(Tri-Diagonal Matrix Algorithm)』または『Thomasのアルゴリズム』と呼ばれています。
googleの検索で、『三重対角行列 TDMA』と調べれば出てくるかと思います。
この記事を書いたのが少し前なのであまり覚えていませんが、私もどこかの擬コードを元に作成したか、
今回の場合に特化させている段階で途中の値をl,mu,zという変数で置いていたか、どちらかと思います。
私のページでは、クランク・ニコルソン法(https://slpr.sakura.ne.jp/qp/tdse-crank-nicolson/)で三重対角行列を使っています。
その中に以下の似たコードがありました。
x(1)=r(1)/u
do j=2,n
w(j)=c(j-1)/u
u=b(j)-a(j)*w(j)
x(j)=(r(j)-a(j)*x(j-1))/u
enddo
spline_ancdの中のzが上のコードのxに対応しているような感じです。
早速のお返事ありがとうございます。TDMAを調べ簡単なプログラムを組んで勉強させていただきました。Sikinote様のwebsiteは非常に勉強になります。このようなサイトを作ってくださりありがとうございます。