program main
implicit none
integer::i,j,Nx,Ny,Mx,My
double precision::x,y,f,df,df2
double precision,allocatable::xdata(:),ydata(:),fdata(:,:),xa(:),ya(:),fa(:,:)
Nx=10
Ny=20
Mx=50
My=100
allocate(xdata(0:Nx),ydata(0:Ny),fdata(0:Nx,0:Ny))
allocate(xa(0:Mx),ya(0:My),fa(0:Mx,0:My))
xdata=0d0
ydata=0d0
fdata=0d0
xa=0d0
ya=0d0
fa=0d0
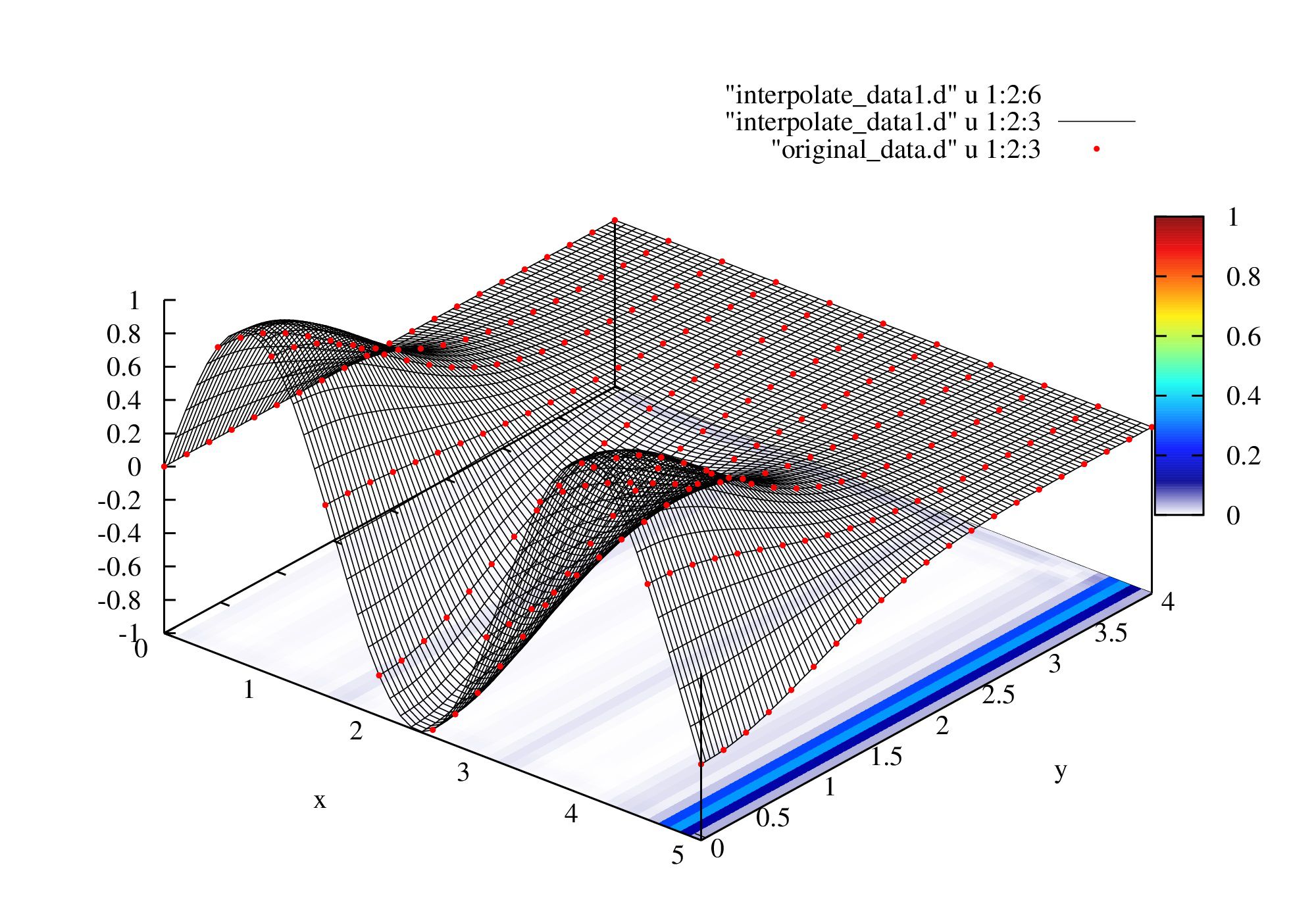
! original data
open(10,file='original_data.d')
write(10,'(A)')"# x y f(x,y)"
do i=0,Nx
do j=0,Ny
xdata(i)=dble(i)*0.5d0
ydata(j)=dble(j)*0.2d0
fdata(i,j)=sin(2d0*xdata(i))*exp(-0.5d0*ydata(j)**2)
write(10,*)xdata(i),ydata(j),fdata(i,j)
enddo
write(10,*)
enddo
close(10)
! Cubic-spline interpolation given position as point
open(10,file='interpolate_data1.d')
write(10,'(A)')"# x y f(x,y) df(x,y)/dx d^2f(x,y)/dx^2"
do i=0,Mx
do j=0,My
x=dble(i)*0.1d0
y=dble(j)*0.04d0
call c3spline2d1p(f,df,df2,x,y,Nx,Ny,fdata,xdata,ydata,1)
write(10,'(6e20.7e3)')x,y,f,df,df2,abs((f-sin(2d0*x)*exp(-0.5d0*y**2))/(f))
enddo
write(10,*)
enddo
close(10)
! Cubic-spline interpolation given position as array
do i=0,Mx
xa(i)=dble(i)*0.1d0
enddo
do j=0,My
ya(j)=dble(j)*0.04d0
enddo
open(10,file='interpolate_data2.d')
write(10,'(A)')"# x y f(x,y) "
call c3spline2d(fa,Mx,My,xa,ya,Nx,Ny,fdata,xdata,ydata)
do i=0,Mx
do j=0,My
write(10,'(3e20.7e3)')xa(i),ya(j),fa(i,j)
enddo
write(10,*)
enddo
close(10)
! 2d integration by spline interpolation
call c3spline2d_integral(s,Nx,Ny,xdata,ydata,fdata)
write(6,*)s
stop
end program main
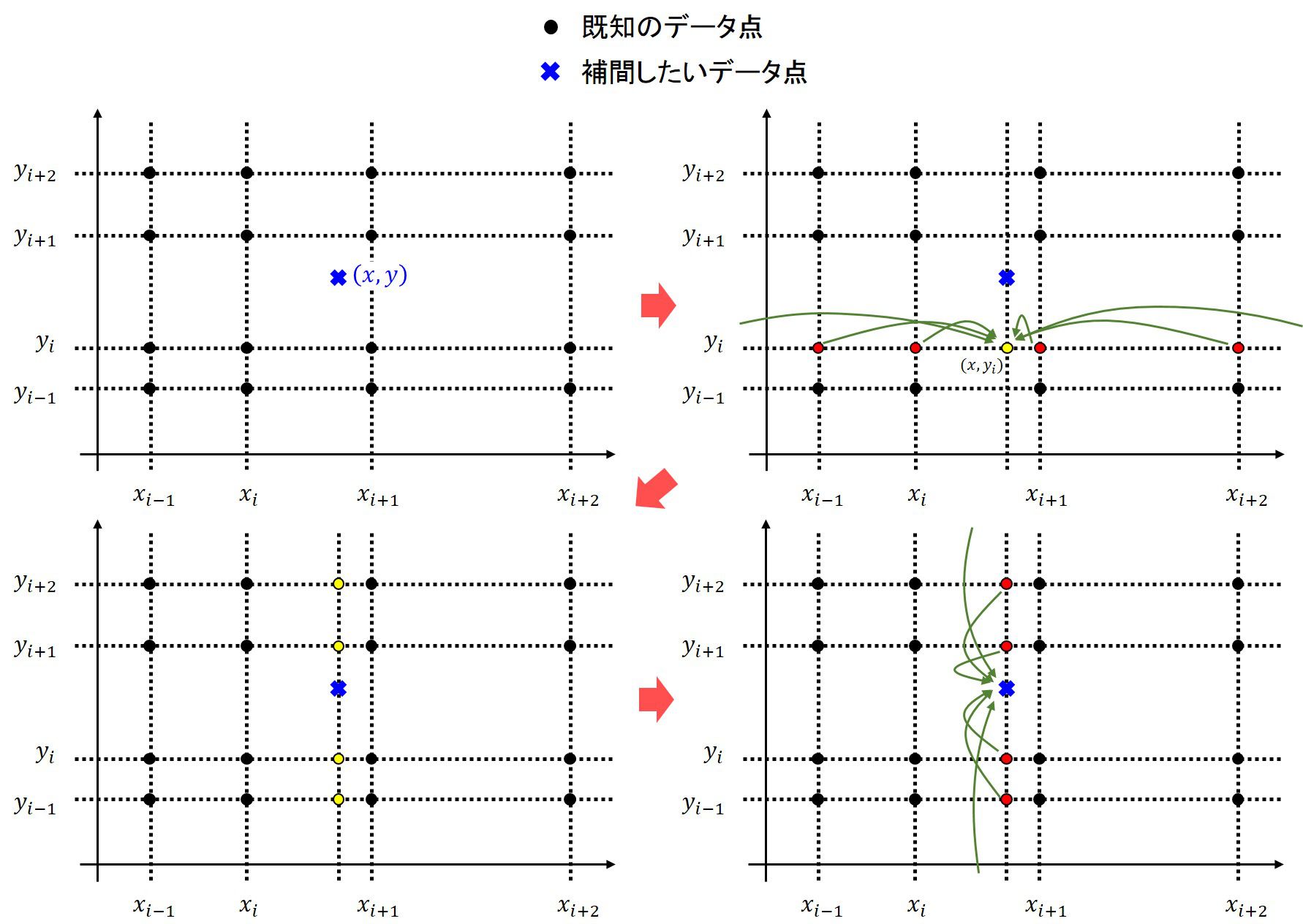
subroutine c3spline2d1p(f,df,df2,x,y,Nx,Ny,fdata,xdata,ydata,key)
implicit none
integer,intent(in)::Nx,Ny,key
double precision,intent(in)::x,y,fdata(0:Nx,0:Ny),xdata(0:Nx),ydata(0:Ny)
double precision,intent(out)::f,df,df2
!
! key = 1 --> 1.interpolate y, 2.interpolate x | df = df/dx, df2 = d^2f/dx^2
! key = 2 --> 1.interpolate x, 2.interpolate y | df = df/dy, df2 = d^2f/dy^2
! key = 3 --> Average of key=1,2 | df = 0, df2=0
!
integer::i,j
double precision,allocatable::tfx(:),tfy(:)
double precision::p,q,dfdx,dfdy,dfdx2,dfdy2
allocate(tfx(0:Nx),tfy(0:Ny))
tfx=0d0; tfy=0d0
if(key.eq.1)then
do i=0,Nx
tfy(0:Ny)=fdata(i,0:Ny)
call c3spline1p(f,df,df2,y,Ny,tfy,ydata)
tfx(i)=f
enddo
call c3spline1p(f,df,df2,x,Nx,tfx,xdata)
elseif(key.eq.2)then
do j=0,Ny
tfx(0:Nx)=fdata(0:Nx,j)
call c3spline1p(f,df,df2,x,Nx,tfx,xdata)
tfy(j)=f
enddo
call c3spline1p(f,df,df2,y,Ny,tfy,ydata)
elseif(key.eq.3)then
do i=0,Nx
tfy(0:Ny)=fdata(i,0:Ny)
call c3spline1p(f,df,df2,y,Ny,tfy,ydata)
tfx(i)=f
enddo
call c3spline1p(p,dfdx,dfdx2,x,Nx,tfx,xdata)
do j=0,Ny
tfx(0:Nx)=fdata(0:Nx,j)
call c3spline1p(f,df,df2,x,Nx,tfx,xdata)
tfy(j)=f
enddo
call c3spline1p(q,dfdy,dfdy2,y,Ny,tfy,ydata)
f = (p+q)*0.5d0
df = 0d0
! df = dfdx
! df = dfdy
df2 = 0d0
! df2 = dfdx2
! df2 = dfdy2
endif
return
end subroutine c3spline2d1p
subroutine c3spline2d(f,Mx,My,x,y,Nx,Ny,fdata,xdata,ydata)
implicit none
integer,intent(in)::Nx,Ny,Mx,My
double precision,intent(in)::x(0:Mx),y(0:My)
double precision,intent(in)::fdata(0:Nx,0:Ny),xdata(0:Nx),ydata(0:Ny)
double precision,intent(out)::f(0:Mx,0:My)
integer::i,j
double precision,allocatable::tfx(:),tfy(:),gx(:),gy(:),gf(:,:)
allocate(tfx(0:Nx),tfy(0:Ny),gx(0:Mx),gy(0:My),gf(0:Nx,0:My))
tfx=0d0; tfy=0d0; gx=0d0; gy=0d0
do i=0,Nx
tfy(0:Ny)=fdata(i,0:Ny)
call c3spline(My,gy,y,Ny,tfy,ydata)
gf(i,0:My)=gy(0:My)
enddo
do j=0,My
tfx(0:Nx)=gf(0:Nx,j)
call c3spline(Mx,gx,x,Nx,tfx,xdata)
f(0:Mx,j)=gx(0:Mx)
enddo
return
end subroutine c3spline2d
subroutine c3spline(M,f,x,N,fdata,xdata)
implicit none
integer,intent(in)::N,M
double precision,intent(in)::x(0:M),fdata(0:N),xdata(0:N)
double precision,intent(out)::f(0:M) !,df(0:M),df2(0:M)
integer::i,j
double precision::t
double precision,allocatable::a(:),b(:),c(:),d(:)
allocate(a(0:N-1),b(0:N-1),c(0:N-1),d(0:N-1))
call spline_abcd(a,b,c,d,N,xdata,fdata)
do j=0,M
if(x(j).lt.xdata(0))then
t=x(j)-xdata(0)
f(j) = ((a(0)*t+b(0))*t+c(0))*t+d(0)
!df(j) =3d0*a(0)*t*t+2d0*b(0)*t+c(0)
!df2(j)=6d0*a(0)*t+2d0*b(0)
elseif(x(j).gt.xdata(N))then
t =x(j)-xdata(N-1)
f(j) = ((a(N-1)*t+b(N-1))*t+c(N-1))*t+d(N-1)
!df(j) =3d0*a(N-1)*t*t+2d0*b(N-1)*t+c(N-1)
!df2(j)=6d0*a(N-1)*t+2d0*b(N-1)
else
do i=0,N-1
if(x(j).ge.xdata(i).and.x(j).le.xdata(i+1))then
t=x(j)-xdata(i)
f(j) = ((a(i)*t+b(i))*t+c(i))*t+d(i)
!df(j) =3d0*a(i)*t*t+2d0*b(i)*t+c(i)
!df2(j)=6d0*a(i)*t+2d0*b(i)
exit
endif
enddo
endif
enddo
return
end subroutine c3spline
subroutine c3spline1p(f,df,df2,x,N,fdata,xdata)
implicit none
integer,intent(in)::N
double precision,intent(in)::x,fdata(0:N),xdata(0:N)
double precision,intent(out)::f,df,df2
integer::i
double precision::t
double precision,allocatable::a(:),b(:),c(:),d(:)
allocate(a(0:N-1),b(0:N-1),c(0:N-1),d(0:N-1))
call spline_abcd(a,b,c,d,N,xdata,fdata)
if(x.lt.xdata(0))then
t=x-xdata(0)
f = ((a(0)*t+b(0))*t+c(0))*t+d(0)
df =3d0*a(0)*t*t+2d0*b(0)*t+c(0)
df2=6d0*a(0)*t+2d0*b(0)
elseif(x.gt.xdata(N))then
t=x-xdata(N-1)
f= ((a(N-1)*t+b(N-1))*t+c(N-1))*t+d(N-1)
df =3d0*a(N-1)*t*t+2d0*b(N-1)*t+c(N-1)
df2=6d0*a(N-1)*t+2d0*b(N-1)
else
do i=0,N-1
if(x.ge.xdata(i).and.x.le.xdata(i+1))then
t=x-xdata(i)
f= ((a(i)*t+b(i))*t+c(i))*t+d(i)
df =3d0*a(i)*t*t+2d0*b(i)*t+c(i)
df2=6d0*a(i)*t+2d0*b(i)
exit
endif
enddo
endif
return
end subroutine c3spline1p
subroutine c3spline2d_integral(s,Nx,Ny,xdata,ydata,fdata)
implicit none
integer,intent(in)::Nx,Ny
double precision,intent(in)::fdata(0:Nx,0:Ny),xdata(0:Nx),ydata(0:Ny)
double precision,intent(out)::s
integer::i,j
double precision::t
double precision,allocatable::tfy(:),tfx(:)
allocate(tfx(0:Nx),tfy(0:Ny))
do j=0,Ny
tfx(0:Nx)=fdata(0:Nx,j)
call c3spline_integral(t,Nx,tfx,xdata)
tfy(j)=t
enddo
call c3spline_integral(s,Ny,tfy,ydata)
return
end subroutine c3spline2d_integral
subroutine c3spline_integral(s,N,fdata,xdata)
implicit none
integer,intent(in)::N
double precision,intent(in)::fdata(0:N),xdata(0:N)
double precision,intent(out)::s
integer::i
double precision::t
double precision,allocatable::a(:),b(:),c(:),d(:)
allocate(a(0:N-1),b(0:N-1),c(0:N-1),d(0:N-1))
call spline_abcd(a,b,c,d,N,xdata,fdata)
s=0d0
do i=0,N-1
t=xdata(i+1)-xdata(i)
s=s+0.25d0*a(i)*t**4 + (b(i)/3d0)*t**3 + 0.5d0*c(i)*t**2 + d(i)*t
enddo
return
end subroutine c3spline_integral
subroutine spline_abcd(a,b,c,d,N,xdata,fdata)
implicit none
integer,intent(in)::N
double precision,intent(out)::a(0:N-1),b(0:N-1),c(0:N-1),d(0:N-1)
double precision,intent(in)::xdata(0:N),fdata(0:N)
integer::i,j
double precision,allocatable::l(:),mu(:),h(:),alpha(:),z(:)
allocate(h(0:N-1),alpha(1:N-1))
do i=0,N-1
h(i)=xdata(i+1)-xdata(i)
enddo
do i=1,N-1
alpha(i)=3d0*(fdata(i+1)-fdata(i))/h(i)-3d0*(fdata(i)-fdata(i-1))/h(i-1)
enddo
allocate(l(0:N-1),mu(0:N-1),z(0:N-1))
l=0d0; mu=0d0; z=0d0
l(0)=1d0
do i=1,N-1
l(i)=2d0*(xdata(i+1)-xdata(i-1))-h(i-1)*mu(i-1)
mu(i)=h(i)/l(i)
z(i)=(alpha(i)-h(i-1)*z(i-1))/l(i)
enddo
b(N-1)=z(N-1)
c(N-1)=(fdata(N)-fdata(N-1))/h(N-1)-h(N-1)*(2d0*b(N-1))/3d0
a(N-1)=-b(N-1)/(3d0*h(N-1))
d(N-1)=fdata(N-1)
do j=N-2,0,-1
b(j)=z(j)-mu(j)*b(j+1)
c(j)=(fdata(j+1)-fdata(j))/h(j)-h(j)*(b(j+1)+2d0*b(j))/3d0
a(j)=(b(j+1)-b(j))/(3d0*h(j))
d(j)=fdata(j)
enddo
return
end subroutine spline_abcd