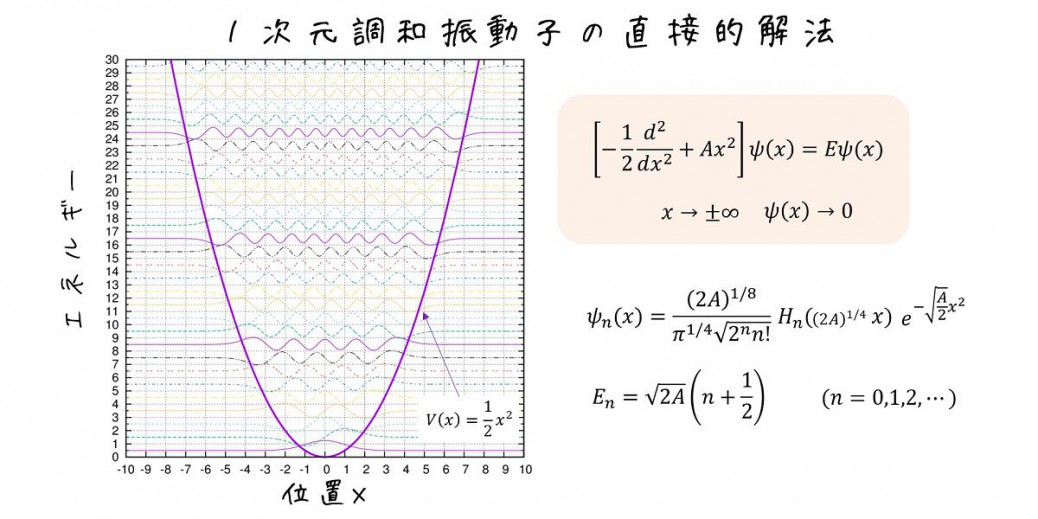
1次元調和振動子の良く知られた解法は3種類あります。
- 昇降演算子を利用し\(\hat{a}\psi(x)=0\)から求める方法
- 微分方程式を境界条件の下、直接解く方法
- ハイゼンベルグ方程式から解く方法
です。ここでは直接的に解く2番目の方法を紹介します。
対象にする微分方程式は一次元調和振動子の原子単位系での表現
\(
\displaystyle \left[-\frac{1}{2}\frac{d^2}{dx^2}+Ax^2\right]\psi(x)=E\psi(x)
\)
です。ここでAは正の実数です。
この微分方程式を境界条件\(\left. \psi(x)\right|_{x\to \pm\infty}=0\)の下で解きます。
まとめますと、エネルギー\(E_n\)と固有関数\(\psi_n(x)\)は、
\(
\begin{align}
E_n&=\sqrt{2A}\left(n+\frac{1}{2}\right)\\
\psi_n(x)&=\frac{\left(2A\right)^{1/8}}{\pi^{1/4}\sqrt{2^n n!}}H_n( {\scriptsize (2A)^{1/4}}x)\exp\left(-\sqrt{\frac{A}{2}} x^2\right)\;\;\;\; (n=0,1,2,\cdots)
\end{align}
\)
です。
導出
両辺を\(-2\)を掛けて式変形して
\(
\displaystyle \left[\frac{d^2}{dx^2}-2Ax^2+2E\right]\psi(x)=0
\)
常套手段ですが、この微分方程式を満たすべき関数\(\psi(x)\)の漸近形を考えます。
何とか解ける部分だけを解いていこうという方針です。
漸近での解
もしも\(x\to \infty\)だったならば、上式の\(2E\)の項は定数であるため、\(-2Ax^2\)と比べて無視できるようになるはずです。
ただし、微分の項\(\frac{d^2}{dx^2}\)は比較することはできないため無視はしないで置いておきます。
つまり、関数\(\psi(x)\)は\(x\to \infty\)の漸近で
\(
\displaystyle \left[\frac{d^2}{dx^2}-2Ax^2\right]\psi(x)=0
\)
の形の微分方程式を満足しなければなりません。
式変形して
\(
\displaystyle \frac{d^2}{dx^2}\psi(x)=2Ax^2\psi(x)
\)
関数を2回微分したら\(x^2\times\)(自分自身)が出てくる、という性質を持つ関数は
\(
\displaystyle \psi(x)= C \exp(Bx^2)
\)
という形で掛けそうです。実際にこの形の2階微分は
\(
\begin{align}
\frac{d\psi}{dx}&=C\cdot 2Bx \exp(Bx^2) \\
\frac{d^2\psi}{dx^2}&=C\cdot 2B(1+2Bx^2)\exp(Bx^2) \\
&\sim C\cdot 4B^2x^2\exp(Bx^2)
\end{align}
\)
です。今、2階微分で括弧内に定数”1”が出てきていますが、\(x\to \infty\)の漸近を考えているのでこの定数は\(2Bx^2\)と比較して無視されるはずです。よって最後の式変形をしています。
漸近での微分方程式に代入すると、
\(
\begin{align}
\frac{d^2}{dx^2}\psi(x)&=2Ax^2\psi(x) \\
C 4B^2x^2\exp(Bx^2)&=2Ax^2 C \exp(Bx^2) \\
2C(2B^2-A)x^2\exp(Bx^2)&=0
\end{align}
\)
上記の方程式は\(x\)の値に依らず常に満たされなければなりません。
よって、\(2C=0\)もしくは\(2B^2-A=0\)である必要があります。
\(C=0\)の解は波動関数が至る所でゼロである自明な解です。なので物理的には適しません。
※漸近でゼロであるだけで漸近じゃないところではokなんじゃないの?という疑問が出てきますが、\(C=0\)の場合、漸近で\(\psi(x)=0\)であり、その微分\(\frac{d\psi}{dx}=C 2Bx \exp(Bx^2)\)もゼロです。波動関数は全領域に渡って滑らかに続いていなければならないため、いつまでたっても波動関数はゼロです。ということは、存在確率がゼロ、有限にはならないつまらない解なのです。通常、\(x\to \infty\)の漸近で\(\psi(x)=0\)という条件は入れますが、その微分\(\frac{d\psi}{dx}\)もゼロという条件は入れません。
なので物理的に意味のある解は
\(
\begin{align}
2B^2-A=0 \\
\to B=\pm \sqrt{\frac{A}{2}}
\end{align}
\)
というBでなければなりません。よって波動関数\(\psi(x)\)は漸近で2つの解の線形結合として書かれ、
\(
\displaystyle \psi(x)= C_1 \exp\left(-\sqrt{\frac{A}{2}} x^2\right)+C_2 \exp\left(\sqrt{\frac{A}{2}}x^2\right)
\)
という形で記述できます。
しかし、境界条件\(\left. \psi(x)\right|_{x\to \pm\infty}=0\)を満たさなければならない場合、係数\(C_2=0\)である必要があります。よって波動関数の漸近形は
\(
\displaystyle \psi(x)= C\exp\left(-\sqrt{\frac{A}{2}} x^2\right)
\)
と求められます。
漸近ではないところの解
漸近では波動関数は
\(
\displaystyle \psi(x)= C\exp\left(-\sqrt{\frac{A}{2}} x^2\right)
\)
という形を満たさなければならないことが分かりました。残りは漸近ではない場所の解です。
定数変化法を使います。定数をxに依存する関数として全領域に渡る波動関数を
\(
\displaystyle \psi(x)= f(x)\exp\left(-\sqrt{\frac{A}{2}} x^2\right)
\)
と仮定します。この操作は\(\psi(x)\)に関する方程式から\(f(x)\)に関する微分方程式に焼直す操作です。
全領域に渡る波動関数の満たすべき微分方程式は
\(
\displaystyle \left[\frac{d^2}{dx^2}-2Ax^2+2E\right]\psi(x)=0
\)
なので、これに代入します。
計算過程で出てくる文字を減らすために、\(B=-\sqrt{\frac{A}{2}}\)として、\(B\)で記述していきます。
\(
\begin{align}
&\left[\frac{d^2}{dx^2}-2Ax^2+2E\right]\psi(x)= \\
&\;\;\;\;\;\;\;\left\{\frac{d^2f}{dx^2}+4Bx\frac{df}{dx}+(4B^2-2A)x^2+(2B+2E)f\right\}e^{Bx^2}=0
\end{align}
\)
と求める事ができ、\((4B^2-2A)=0\)を利用すると、\(f(x)\)の満たすべき微分方程式は、
\(
\displaystyle \frac{d^2f}{dx^2}+4Bx\frac{df}{dx}+(2B+2E)f=0
\)
と求まります。
この微分方程式の解はエルミートの微分方程式と呼ばれる形をしています。
エルミートの微分方程式は
\(
\displaystyle \frac{d^2 H(x)}{dx^2}-2x\frac{dH(x)}{dx}+2nH(x)=0
\)
の微分方程式を満たす直交多項式です[1]。
そのままエルミートの微分方程式を今回の問題に適応することはできません。なぜならば1階微分の係数が違っているからです。
なので変数変換により、\(x=\alpha y\)とおいて、一階微分の係数\(4B\)をちょうど\(-2\)にする定数\(\alpha\)を探しましょう。
\(
\begin{align}
\frac{d}{dx}&=\frac{dy}{dx}\frac{d}{dy}=\frac{1}{\alpha}\frac{d}{dy}\\
\frac{d^2}{dx^2}&=\frac{1}{\alpha^2}\frac{d^2}{dy^2}
\end{align}
\)
を代入して、
\(
\displaystyle \frac{1}{\alpha^2}\frac{d^2 f(x)}{dy^2}+4By\frac{df(x)}{dy}+(2B+2E)f(x)=0
\)
xとyが混在しているので気持ち悪いです。\(f(x)\to f(y)\)とおきましょう。そして最後に求められたyを用いたf(y)をxの式f(x)に焼直します。
両辺に\(\alpha^2\)を掛けると
\(
\displaystyle \frac{d^2 f(y)}{dy^2}+4B\alpha^2 y\frac{df(y)}{dy}+(2B+2E)\alpha^2 f(y)=0
\)
です。今、一階微分の係数を\(-2\)にする定数\(\alpha\)を探していました。
なので、
\(
\begin{align}
4B\alpha^2&=-2 \\
\alpha&=\pm\sqrt{-\frac{1}{2B}}=\pm\left(\frac{1}{2A}\right)^{1/4}
\end{align}
\)
となります。ここの\(\alpha\)のプラスマイナスはどちらでもいいです。
プラスに取ることにすれば、\(f(y)\)についての微分方程式は、
\(
\displaystyle \frac{d^2 f(y)}{dy^2}-2 y\frac{df(y)}{dy}-\left(\frac{B+E}{B}\right) f(y)=0
\)
であるため、エルミートの微分方程式の形になりました。
エルミートの微分方程式は\(f(y)\)に掛かる項、すなわち\(-\left(\frac{B+E}{B}\right)\)の部分が\(2n\), (\(n=0,1,2,\cdots\))である時だけ解を満たします。
よって、
\(
\begin{align}
-\frac{B+E}{B}&=2n\\
E=E_n&=-2B(n+\frac{1}{2})\\
&=\sqrt{2A}(n+\frac{1}{2})\;\;\; (n=0,1,2,\cdots)
\end{align}
\)
を満たすエネルギー\(E=E_n(n=0,1,2,\cdots)\)でなければ解は存在しません。
その時の解\(f(y)\)も\(n\)で番号付けされて、
\(
f(y)=H_n(y)\;\;\; (n=0,1,2,\cdots)
\)
と記述され、右辺はエルミート多項式と呼ばれます。
エルミート多項式\(H_n(y)\)は
\(
\begin{align}
H_0(y)&= 1\\
H_1(y)&= 2y\\
H_2(y)&= 4y^2-2\\
H_3(y)&= 8y^3-12y\\
H_4(y)&= 16y^4-48y^2+12\\
H_5(y)&= 32y^5-160y^3+120y\\
H_6(y)&= 64y^6-480y^4+720y^2-120\\
\ldots
\end{align}
\)
と言う関数です。三項漸化式
\(
H_n(y)=2yH_{n-1}(y)-2(n-1)H_{n-2}(y)
\)
を用いて\(n=2\)以上のエルミート多項式は記述されます。
以上より微分方程式を満たす解とエネルギーは、整数(\(n=0,1,2,\cdots\))で番号付けされた解を持つことが分かりました。
\(y\)を変数変換に従い\(x\)に戻します。
\(
\begin{align}
x&=\alpha y \\
&\alpha=\left(\frac{1}{2A}\right)^{1/4}
\end{align}
\)
なので、
\(H_n(y)=H_n(x/\alpha)\)
です。
漸近形での波動関数と合わせて、本当に求めたかった解\(\psi(x)\)は、
\(
\begin{align}
\displaystyle \psi(x) &= f(x)\exp\left(-\sqrt{\frac{A}{2}} x^2\right) \\
&=C H_n(x/\alpha)\exp\left(-\sqrt{\frac{A}{2}} x^2\right)
\end{align}
\)
であることが分かりました。定数\(C\)の自由度がありますが、これは物理的に合った条件を用いてなされます。
おさらい
解きたかった問題は
\(
\displaystyle \left[-\frac{1}{2}\frac{d^2}{dx^2}+Ax^2\right]\psi(x)=E\psi(x)
\)
を境界条件\(\left. \psi(x)\right|_{x\to \pm\infty}=0\)の下で解くことでした(A>0)。
この微分方程式を何とか解くために、まず\(x\to \pm\infty\)で解の満たすべき形を考えました。
その後、全領域で境界条件を満たす解を定数変化法によって求めました。
計算の結果、微分方程式の解は与えられた適当なエネルギー\(E\)に対していつも存在するわけではなく、特別な\(E=E_n\)で番号付けされた値でなければ解が存在しないことが分かりました。
\(n\)番目のエネルギー\(E_n\)と関数\(\psi_n(x)\)は、
\(
\begin{align}
E_n&=\sqrt{2A}\left(n+\frac{1}{2}\right) \\
&\psi_n(x)= C_n H_n(x/\alpha)\exp\left(-\sqrt{\frac{A}{2}} x^2\right) \\
&\;\;\;\;\alpha=\left(2A\right)^{-1/4}
\end{align}
\)
です。与えられた条件下では規格化までは追求していないのでここでお仕舞いですが、規格化を考えてみましょう。
規格化
波動関数\(\psi_n(x)\)を規格直交化(正規直交化とも言う)します。
規格化は、全空間での存在確率
\(
\displaystyle \int_{-\infty}^{\infty}|\psi(x)|^2dx
\)
を1にすること。
直交化は異なる状態間をかけ合わせて積分した時ゼロになること・・・すなわち内積をゼロにします。
\(
\displaystyle \int_{-\infty}^{\infty}\psi_m^*(x)\psi_n(x)dx=C\cdot\delta_{mn}
\)
ここで\(C\)は任意の定数で、\(\delta_{mn}\)はクロネッカーのデルタを表します。
両方を考慮すると、規格直交化とは、
\(
\displaystyle \int_{-\infty}^{\infty}\psi_m^*(x)\psi_n(x)dx=\delta_{mn}
\)
を満たすように係数を決定します。
実際に波動関数を代入すると、
\(
\begin{align}
\int_{-\infty}^{\infty}\psi_m^*(x)\psi_n(x)dx&= C_m^*C_n \int_{-\infty}^{\infty} H_m(x/\alpha)H_n(x/\alpha)\exp\left(-\sqrt{2A} x^2\right)dx
\end{align}
\)
変数変換を行います。
\(
\begin{align}
x&=\alpha y \\
&\alpha=\left(\frac{1}{2A}\right)^{1/4}
\end{align}
\)
より、
\(
\begin{align}
& C_m^*C_n \int_{-\infty}^{\infty} H_m(x/\alpha)H_n(x/\alpha)\exp\left(-\sqrt{2A} x^2\right)dx \\
&= C_m^*C_n \int_{-\infty}^{\infty} H_m(y)H_n(y)\exp\left(-\sqrt{2A}\alpha^2y^2\right)\cdot \alpha dy \\
&= C_m^*C_n\alpha \int_{-\infty}^{\infty} H_m(y)H_n(y)\exp\left(-y^2\right) dy \\
\end{align}
\)
ここで、エルミート多項式の特性を使います。エルミート多項式の関係式の中に、
\(
\displaystyle \int_{-\infty}^{\infty} H_m(x)H_n(x)\exp\left(-y^2\right) dx=2^n n!\sqrt{\pi}\delta_{mn}
\)
という関係式があります。
なので、これを使うと、
\(
\displaystyle \int_{-\infty}^{\infty}\psi_m^*(x)\psi_n(x)dx=C_m^*C_n\alpha 2^n n!\sqrt{\pi}\delta_{mn}
\)
と求められます。今、\(({\mbox 右辺})=\delta_{mn}\)にしたいので、係数について、
\(
\begin{align}
C_m^*C_n\alpha 2^n n!\sqrt{\pi}\delta_{mn}&=\delta_{mn} \\
(C_m^*C_n\alpha 2^n n!\sqrt{\pi}-1)\delta_{mn}&=0
\end{align}
\)
にするように\(C_n\)を決定すればよいことになります。
クロネッカーのデルタより、\(m=n\)以外の時は係数に依らずゼロになるため、自明です。
なので、\(m=n\)の時,
\(
\begin{align}
|C_n|^2\alpha 2^n n!\sqrt{\pi}&=1\\
\to |C_n|&=\sqrt{\frac{1}{\sqrt{\pi}2^n n!\alpha}} \\
C_n&=\frac{1}{\sqrt{\alpha}\pi^{1/4}\sqrt{2^n n!}}\cdot \exp(i\theta)
\end{align}
\)
と規格化定数が求められます。位相\(\exp(i\theta)\)の任意性がありますが、この位相に特に意味は無く、自由に選べます。よって、式が簡単になる\(\theta=0\)を取ることにします。
以上の結果から、規格直交化された波動関数は\(\psi_n(x)\)は、
\(
\begin{align}
\psi_n(x)&=\frac{1}{\sqrt{\alpha}\pi^{1/4}\sqrt{2^n n!}}H_n(x/\alpha)\exp\left(-\sqrt{\frac{A}{2}} x^2\right)\\
\alpha&=\left(2A\right)^{-1/4}
\end{align}
\)
となります。\(\alpha\)を使わず、\(A\)だけで表せば、
\(
\displaystyle \psi_n(x)=\frac{\left(2A\right)^{1/8}}{\pi^{1/4}\sqrt{2^n n!}}H_n( {\scriptsize (2A)^{1/4}}x)\exp\left(-\sqrt{\frac{A}{2}} x^2\right)
\)
です。
参考文献
[1]小野寺嘉孝著「物理のための応用数学」裳華房 p.71