計算例
具体的に適当なポテンシャルの形を考えて解いてみましょう。
プログラムは
時間依存しないシュレーディンガー方程式と変分原理 1/2
にあります。
おさらいですが、間接法による変分原理は、
- 固有値の上限を与える(変分原理によるエネルギー固有値は必ず厳密なエネルギー固有値よりも大きくなる)
- 基底関数の数を増やすほど精度は上がる(完全系の場合)
ということを想定しています。
そして、時間依存しないシュレーディンガー方程式と変分原理 1/2 (計算手法の説明)
では、これから束縛状態のみを考えるので、sin関数系の場合の変分原理について計算を行っていきました。
上に想定した変分原理の想定は、
正しい境界条件の下で誤差なく行列要素が求められ、誤差なく対角化が行われた
場合にのみ成り立ちます。sin関数系の場合の境界条件は固定端条件、つまり区間[a,b]で
\(
\psi(x=a)=\psi(x=b)=0
\)
ということです。
ここでは、解析的な解が存在する
について比較していきます。
シュレーディンガー方程式は全て原子単位系(\(m=1, \hbar=1\))で考え、
\(
\displaystyle \left[-\frac{1}{2}\frac{d^2}{dx^2}+V(x)\right]\psi(x)=E\psi(x)
\)
の形を考えます。
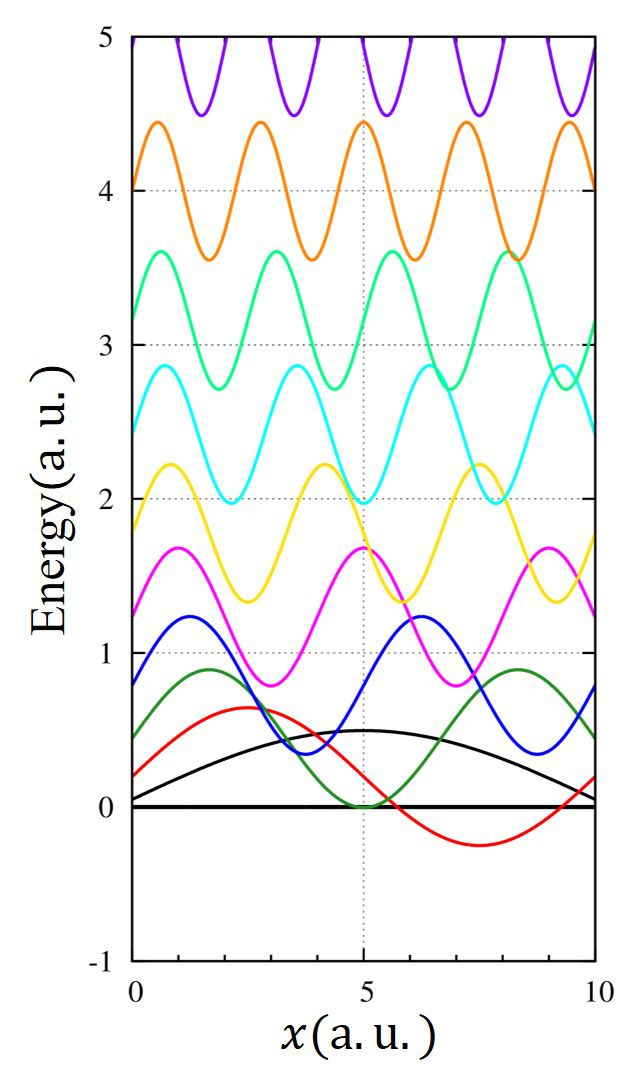
無限に深い井戸型ポテンシャル
ポテンシャル
\(
V(x)=\left\{
\begin{eqnarray}
0 \hspace{2em}&(& 0\lt x \lt L,)\\
\infty \hspace{2em}&(& x\le 0 \ or\ L\le x)
\end{eqnarray}
\right.
\)
※井戸の区間が\([a,b]\)であっても変数変換\(y=x-a,\;\;L=b-a\)によって上記ポテンシャルの形に変換されます。
固有値
\(
\displaystyle E_n=\frac{(n+1)^2\pi^2}{2 L^2},\;\;(n=0,1,2,\cdots)
\)
固有関数
\(
\psi_n(x)=\left\{
\begin{eqnarray}
\sqrt{\frac{2}{L}}\sin\left(\frac{(n+1)\pi}{L}(x+\frac{L}{2})\right) &(& 0\lt x \lt L,)\\
0 \hspace{6em}&(& x\le 0 \ or\ L\le x)
\end{eqnarray}
\right.
\)
解法
区間\(0\lt x \lt L,\)ではシュレーディンガー方程式の\(V(x)=0\)の解、sin,cosの形をしてなければなりません。
また、\(\psi(x=0)=0,\;\psi(x=L)=0\)では境界条件より、波動関数の値はゼロです。
よって、解はsin,cosの形で、そのゼロ点がちょうど\(x=0,x=L\)にくるような関数となります。
数値計算解と解析解との比較
数値計算の設定:
Gauss-Lobatto求積法の次数(Ngl):12
計算区間(a,b):[0,\(\pi\)]
基底関数の数(N):200
エネルギー固有値
| 量子数\(n\) | 数値計算解 | 解析解 |
|---|---|---|
| 0 | 0.5000000000000000 | 0.5000000000000000 |
| 1 | 2.0000000000000000 | 2.0000000000000000 |
| 2 | 4.5000000000000000 | 4.5000000000000000 |
| 3 | 8.0000000000000000 | 8.0000000000000000 |
| 4 | 12.5000000000000000 | 12.5000000000000000 |
| … | ||
| 10 | 60.500000000000000 | 60.500000000000000 |
| 20 | 220.50000000000000 | 220.50000000000000 |
| 30 | 480.50000000000000 | 480.50000000000000 |
| 40 | 840.50000000000000 | 840.50000000000000 |
| 50 | 1300.5000000000000 | 1300.5000000000000 |
考察
行列は元々対角です。なので、対角化する前から対角行列です。
誤差は入りようがありません。
三角量子井戸
ポテンシャル
\(
V(x)=\left\{
\begin{eqnarray}
\infty \hspace{2em}&(& x\lt 0)\\
\alpha x \hspace{2em}&(& 0 \lt x)
\end{eqnarray}
\right.
\)
固有値
\(
\displaystyle E_n=-\left(\frac{\alpha^2}{2}\right)^{1/3}a_n
\)
ここで、\(a_n\)はAiry関数[4]のゼロ点です。
固有関数
\(
\displaystyle \psi_n(x)=C\cdot \text{Ai}\left(\left(\frac{2}{\alpha^2}\right)^{1/3}(\alpha x-E_n)\right)
\)
※積分区間がエアリー関数のゼロ点から無限までであり、これは解析的に実行できません。なので規格化定数をあらわに書くことはできません。
解法
区間\(0\lt x \lt \infty,\)ではシュレーディンガー方程式の\(V(x)=\alpha x\)の解、Airy関数の形をしてなければなりません。
また、\(\psi(x=0)=0, \psi(x\to \infty)=0\)の境界条件を満たします。
よって、解はAiry関数の形で、\(x\)が漸近で減衰していく方の解(\(Ai(x),Bi(x)\)のAiの方)で、そのゼロ点がちょうど\(x=0\)にくるような関数となります。
数値計算解と解析解との比較
数値計算の設定:
Gauss-Lobatto求積法の次数(Ngl):12
計算区間(a,b):[0,60]
基底関数の数(N):200
\(\alpha\):1
エネルギー固有値
| 量子数\(n\) | 数値計算解 | 解析解 |
|---|---|---|
| 0 | 1.8557572021449626 | 1.8557570814892386 |
| 1 | 3.2446077578572123 | 3.2446076240031596 |
| 2 | 4.3816713853293896 | 4.3816712392861303 |
| 3 | 5.3866139387958034 | 5.3866137807905003 |
| 4 | 6.3052631766282223 | 6.3052630065857747 |
| … | ||
| 10 | 10.8669422991860358 | 10.8669420487522821 |
| 20 | 16.8461591354108187 | 16.8461586901918032 |
| 30 | 21.8969186983512394 | 21.8969179157570224 |
| 40 | 26.4182318860569758 | 26.4182304793452509 |
| 50 | 30.5803380635310234 | 30.5803354172938597 |
考察
上記計算では基底状態から励起状態までほとんど精度が変わっていません。
また、変分原理が想定したとおり、全ての数値計算解は、厳密な解よりも高い結果を与えています。
厳密な解よりも高い結果を与えていることから、
行列要素は高精度で計算されているが、基底関数が足らない、もしくは計算区間が足らない
事が考えられます。
精度がなぜ良くないのかを考えましょう。
\(x=0\)の境界条件は\(\sin\)関数で良く表現されます。が、\(x\to\infty\)側は指数関数で減少していきます。
(一次の)指数関数で減衰していくことを\(\sin\)関数系ではうまく表現できないのではないか、と思います。
実際、Airy関数の指数関数での減衰は漸近で
\(
\displaystyle \frac{e^{-\frac{2}{3}x^{3/2}}}{x^{1/4}}
\)
と表されます。
この後、調和ポテンシャルとクーロンポテンシャルの場合も考えますが、
調和ポテンシャル(漸近で\(\exp(-x^2)\)、基底状態の精度14,15桁)
↓
三角量子井戸(漸近でおおよそ\(\exp(-x^{2/3})\)、基底状態の精度7,8桁)
↓
クーロンポテンシャル(漸近で\(\exp(-x)\)、基底状態の精度2,3桁)
の順に精度が悪くなっていきます。
指数関数的な減衰が早い≒無限に深い量子井戸
を意味するはずなので、恐らくこうなのではと思います。
調和ポテンシャル
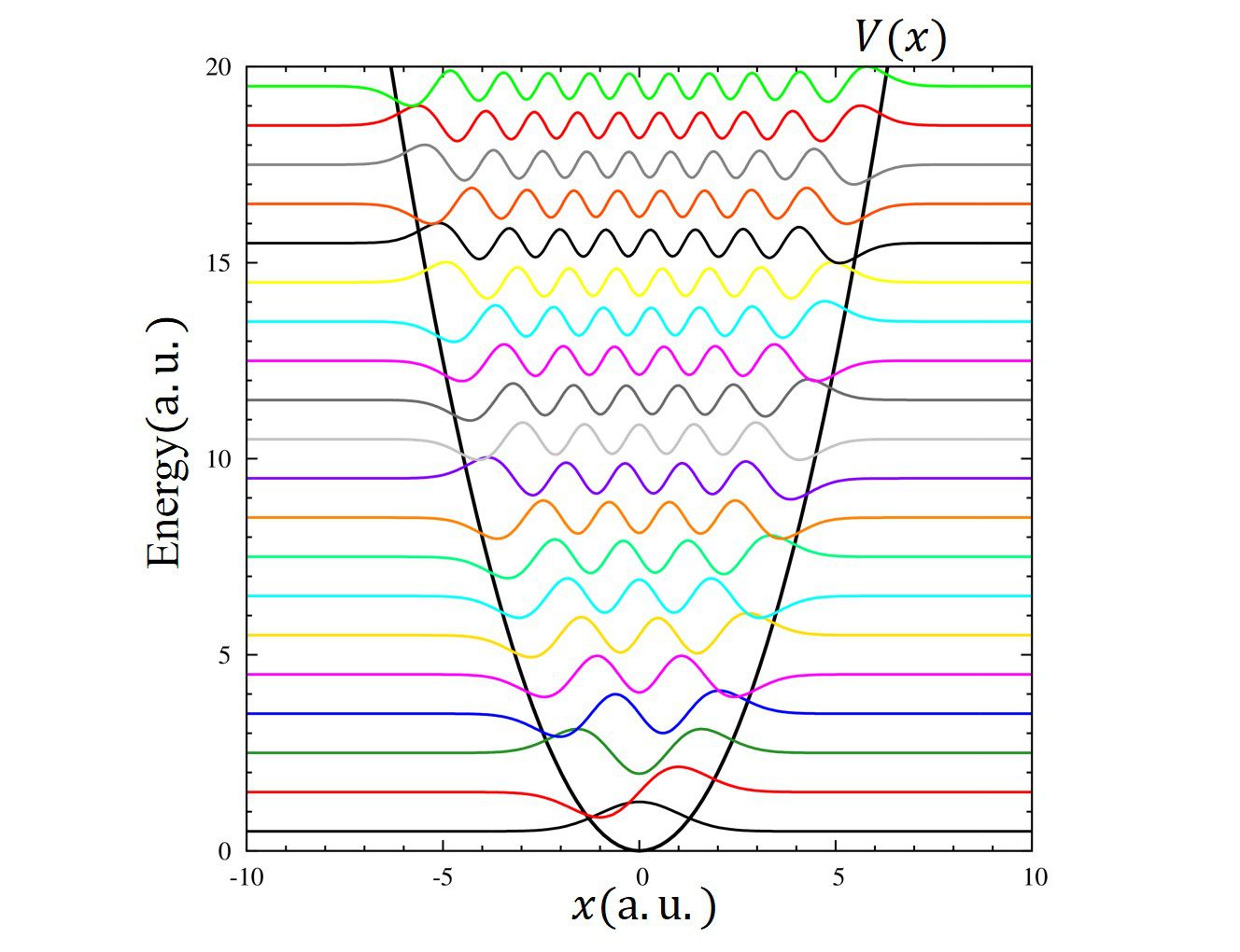
\(
\displaystyle V(x)=\frac{1}{2}x^2
\)
固有値
\(
\displaystyle E_n=n+\frac{1}{2},\;\;(n=0,1,2,\cdots)
\)
固有関数
\(
\displaystyle \psi_n(x)=\frac{\pi^{-1/4}}{\sqrt{2^n n!}}e^{-\frac{x^2}{2}} H_n\left(x\right)
\)
ここで\(H_n(x)\)はエルミート多項式を表します。
解法
数値計算解と解析解との比較
数値計算の設定:
Gauss-Lobatto求積法の次数(Ngl):12
計算区間(a,b):[-30,30]
基底関数の数(N):200
| 量子数\(n\) | 数値計算解 | 解析解 |
|---|---|---|
| 0 | 0.5000000000000038 | 0.5 |
| 1 | 1.5000000000000340 | 1.5 |
| 2 | 2.4999999999998268 | 2.5 |
| 3 | 3.4999999999996776 | 3.5 |
| 4 | 4.4999999999999165 | |
| … | ||
| 10 | 10.4999999999999680 | 10.5 |
| 20 | 20.4999999999997691 | 20.5 |
| 30 | 30.5000000000065015 | 30.5 |
| 40 | 40.5000064794500432 | 40.5 |
| 50 | 50.5426649449273313 | 50.5 |
考察
変分原理の典型的な傾向を見せています。というのは高い励起状態になればなるほど精度が悪くなっているためです。
高励起状態になるにつれて精度が悪くなっていくのは基底関数が足らない為でしょう。計算区間に関してはポテンシャルは境界で高いまま(\(V(a)=V(b)=450\))であり、求められたエネルギー固有値の値\(E_{50}\approx 50\)と比べても十分大きいです。なので、計算区間は足りています。
また、変分原理の固有値の上限を与えるに関しては必ずしも満たしているわけでは無いことに気が付きます。これは行列要素を求める際の誤差や丸め誤差に起因するものであると考えられます。なので、原理が破られているのではなく、数値計算上の問題に起因しています。\(n=30,40,50\)では厳密解よりも大きな値を与えています。これは、数値計算上の誤差よりも変分原理の原理的な値の方が大きくなっているためです。
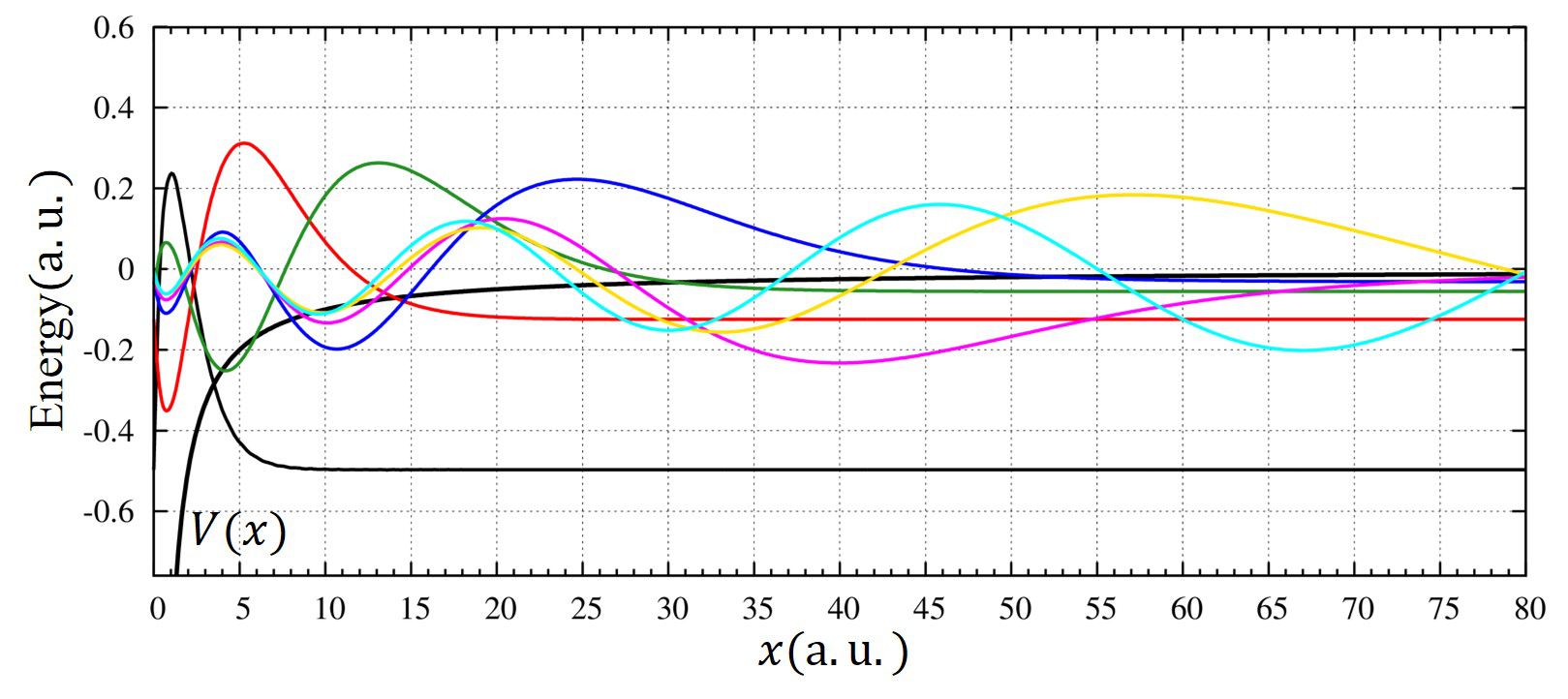
F.モースによるポテンシャル[3]

\(
\displaystyle V(x)=A\left(e^{-2\alpha x}-2e^{-\alpha x}\right)
\)
固有値
\(
\displaystyle E_n=-A\left[1-\frac{\alpha}{\sqrt{2A}}\left(n+\frac{1}{2}\right)\right]^2
\)
ここで、\(n\)は正の整数で、ゼロから始まり、
\(
\displaystyle\frac{\sqrt{2A}}{\alpha}\gt n+\frac{1}{2}
\)
を満足する最大値\(n_{\text{max}}\)まで。
固有関数
\(
\begin{align}
\psi(x)&=e^{-\xi/2} \xi^s w(\xi) \\
& w(\xi)=F(-n,2s+1,\xi) \\
& \xi=\frac{2\sqrt{2A}}{\alpha}e^{-\alpha x} \\
& s=\frac{\sqrt{-2E}}{\alpha}
\end{align}
\)
ここで\(F(a,b,x)\)は合流型超幾何関数です。
この問題では離散スペクトルは有限個だけ存在します。もしも
\(
\displaystyle\frac{\sqrt{2A}}{\alpha}\gt n+\frac{1}{2}
\)
であれば、離散スペクトルは一般に存在しません。
解法
[3]を参照してください
数値計算解と解析解との比較
数値計算の設定:
Gauss-Lobatto求積法の次数(NGL):12
計算区間(a,b):[-3,80]
基底関数の数(N):200
\(A\):5
\(\alpha\):1
エネルギー固有値
| 量子数\(n\) | 数値計算解 | 解析解 |
|---|---|---|
| 0 | –3.5437173567132851 | -3.5438611699158100 |
| 1 | –1.3814252908344455 | -1.3815835097474309 |
| 2 | –0.2185797147047042 | -0.2193058495790518 |
| 3 | -0.0049226123802256 | – |
| 4 | 0.0081675032299395 | – |
| … | ||
| 10 | 0.0527783252864115 | – |
| 20 | 0.2666761210195411 | – |
| 30 | 0.6404251854103465 | – |
| 40 | 1.1703593933291645 | – |
| 50 | 1.8543552927405405 | – |
考察
厳密解は3つしか存在しません。この3つの状態に対しては数値計算解の方が厳密解よりも大きくなり、想定通りです。
しかし精度があまり良くありません。これはポテンシャルが\(V(x\to\infty)=0\)であり、波動関数が速やかにゼロに向かわないためだろうと考えられます。
また、基底状態でもあまり良い結果が得られていません。上記ポテンシャルの閉じ込めが強くなく、多くの基底関数が必要となり、数値計算で用いた200個では十分ではないのでしょう。
4つ目の解に注目しましょう。厳密解は存在しないのに数値計算ではあたかも解が存在するように見えます(\(E\le 0\))。また、変分原理は上限を与えるため、4つ目の解が存在すると考えてしまうかもしれません。しかし、これは違います。明らかにするために4つ目の解の波動関数の形(青色の線)を拡大してみますと、
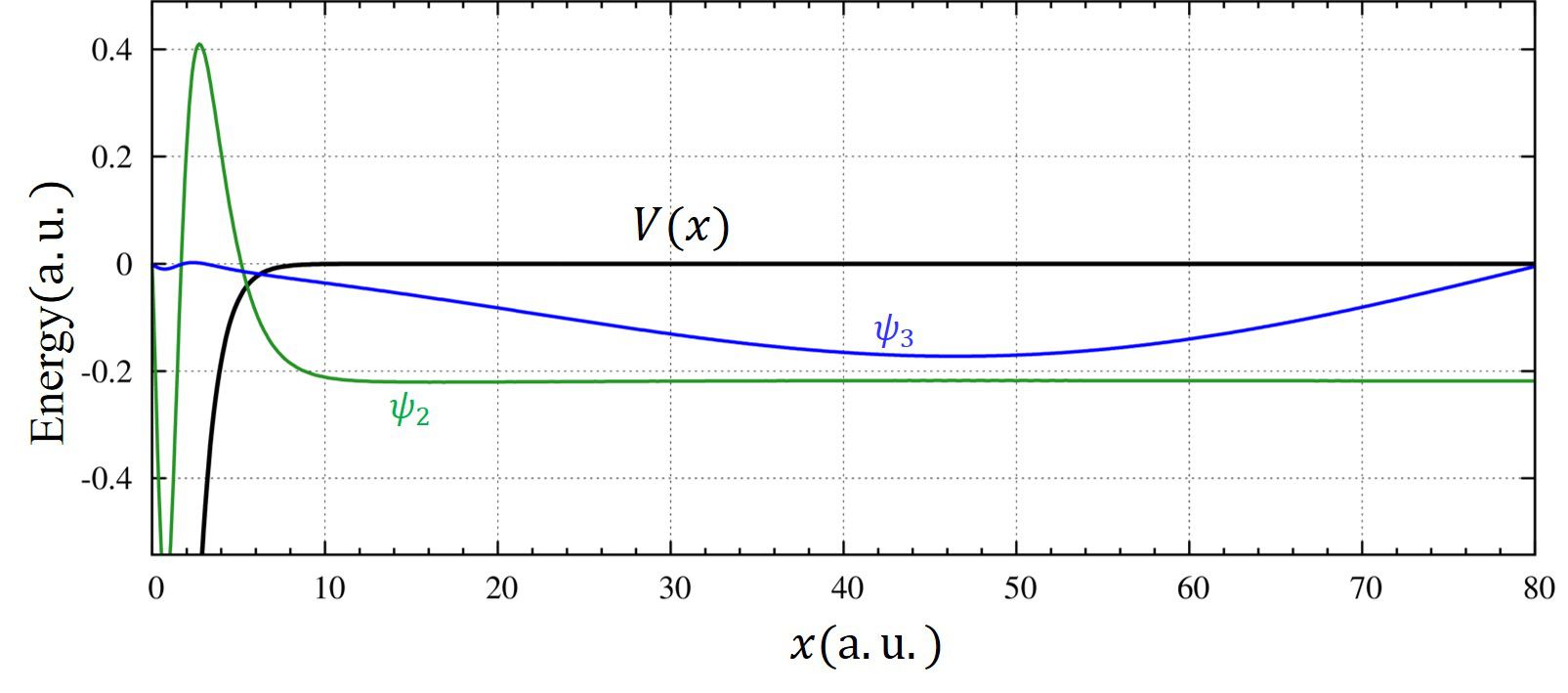
となり、物理的に意味を成していないことが分かります。なぜなら、波動関数は\(x\to\infty\)に向かうにつれて徐々に小さくなっていかなければなりません。もしもこれが正しければ、\(x=80\)で節を持っている解ということになり、これは束縛状態の解としては適しません。
エネルギー固有値だけを考えては求められないものだったということですね。
さらに、束縛状態以上ではすべて連続状態です。それにもかかわらず\(E\gt 0\)でも離散的に固有値が得られているのは基底関数に固定端の境界条件を課しているためです。これらに物理的な意味は無いので評価する際には気を付けましょう。
\(1/(\cosh^2)\)型ポテンシャル[3]
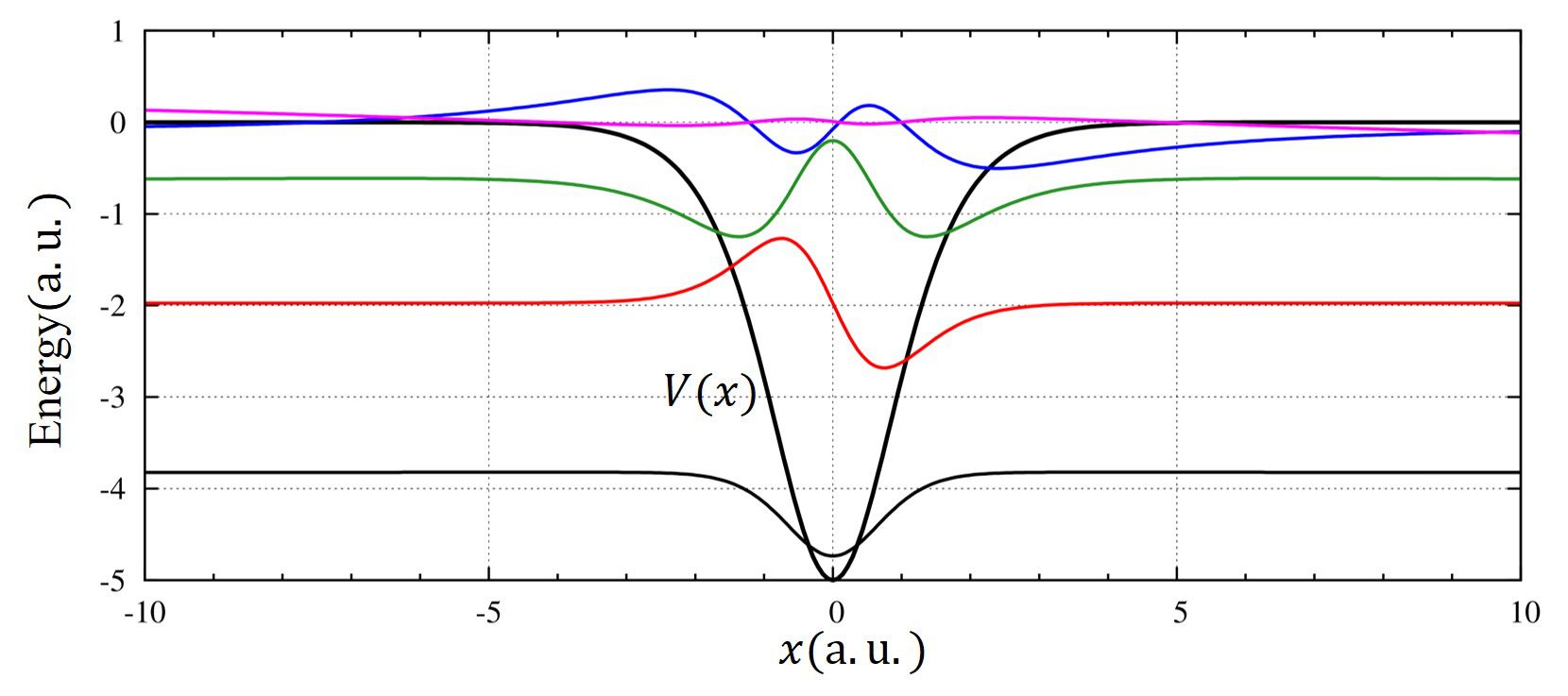
\(
\displaystyle V(x)=-\frac{V_0}{\cosh^2 \alpha x}
\)
固有値
\(
\displaystyle E_n=-\frac{\alpha^2}{8}\left[-(1+2n)+\sqrt{1+\frac{8V_0}{\alpha^2}}\right]^2
\)
で、\(n\)は
\(
\displaystyle n\lt s = \frac{1}{2}\left(-1+\sqrt{1+\frac{8V_0}{\alpha^2}}\right)
\)
から有限個の準位が決まります。
固有関数
\(
\begin{align}
\psi(x)&=(1-\xi^2)^{\xi/2}F\left[\varepsilon-s, \varepsilon+s+1, \varepsilon+1, \frac{1-\xi}{2}\right]\\
& \varepsilon=\frac{\sqrt{-2E}}{\alpha}\\
& \xi=\tanh \alpha x
\end{align}
\)
ここでの\(F(a,b,c,x)\)は超幾何関数です。
解法
[3]を参照してください
数値計算解と解析解との比較
数値計算の設定:
Gauss-Lobatto求積法の次数(NGL):12
計算区間(a,b):[-30,30]
基底関数の数(N):200
エネルギー固有値
| 量子数\(n\) | 数値計算解 | 解析解 |
|---|---|---|
| 0 | –3.8286053565505553 | -3.885009803959261 |
| 1 | –1.9750293441823026 | -1.9750294118777854 |
| 2 | –0.6459145040771800 | -0.7050490197963089 |
| 3 | –0.0750649726143545 | -0.0750686277148326 |
| 4 | 0.0076704714372625 | – |
| … | ||
| 10 | 0.1139873400292487 | – |
| 20 | 0.4849841979196881 | – |
| 30 | 1.1689850012563472 | – |
| 40 | 2.1388129318397651 | – |
| 50 | 3.3888397726738235 | – |
考察
エネルギー固有値の上限を確かに与えています。そのほかはおおよそF.モースによるポテンシャルと同じような結果を与えています。
精度に関して、エネルギー固有値の精度は\(n=0,2\)の時、1~2桁程度の精度ですが、\(n=1,3\)の時、は6~7桁一致と著しく精度が上がっています。計算区間を変えたりしたのですが、この傾向は変わりません。
なぜなのか…詳しくは分かりません。偶関数、奇関数の問題だと思います。すなわち、奇関数の場合はなにか\(x\gt 0\)の領域に誤差があっても同じ量の誤差で\(x\lt 0\)で打ち消し合ってくれるのですが、偶関数の場合は打ち消し合いが起きないのではないか、ということです。
ただ、これが行列要素の精度からくるものなのかは詳しく見ていないので分かりません…
クーロンポテンシャル(動径方向, \(l=0\))
ポテンシャル
\(
\displaystyle V(x)=-\frac{1}{x}
\)
※ここでは、一階微分の存在しない形にした時のシュレーディンガー方程式を考えています。
固有値
\(
\displaystyle E_n=-\frac{1}{2n^2},\;\;(n=1,2,\cdots,)
\)
です。
固有関数
\(
\begin{align}
\psi(x)=C \cdot e^{-x/n} x^l L_{n-1}^{(1)}(x)
\end{align}
\)
ここで,\(C\)は規格化定数, \(L_n^k(x)\)はラゲール倍多項式[5]で
\(
\begin{align}
L_0^k(x)&=1 \\
L_1^k(x)&=-x+k+1 \\
L_2^k(x)&=\frac{1}{2}[x^2-2(k+2)x+(k+1)(k+2)] \\
L_3^k(x)&=\frac{1}{6}[-x^3+3(k+3)x^2-3(k+2)(k+3)x+(k+1)(k+2)(k+3)]
\end{align}
\)
です。もちろん規格化定数をあらわに決めることが出来ますが、通常、この問題は3次元のシュレーディンガー方程式を解いた時の動径方向として出てくるので、その時の規格化は
\(
\displaystyle \int_0^\infty x^2 \psi(x)^2 dx =1
\)
で規格化されます。しかし、本稿の規格化は\(\displaystyle \int_0^\infty \psi(x)^2 dx =1\)
で規格化しているので、エネルギー固有値のみの比較を行います。
解法
\(x=0, x\to infty\)の漸近形を考えて、本当の解を
(\(x=0\)の漸近形)×(\(x=\infty\)の漸近形)×(未知関数)
と仮定します。これをシュレーディンガー方程式に代入すると未知関数がラゲール陪多項式だと分かります。
数値計算解と解析解との比較
数値計算の設定:
Gauss-Lobatto求積法の次数(NGL):12
計算区間(a,b):[0,80]
基底関数の数(N):200
エネルギー固有値
| 量子数\(n\) | 数値計算解 | 解析解 |
|---|---|---|
| 1 | –0.4970775696080274 | -0.5000000000000000 |
| 2 | -0.1246297940063756 | -0.1250000000000000 |
| 3 | –0.0554455545682885 | -0.0555555555555556 |
| 4 | –0.0312035408553899 | -0.0312500000000000 |
| 5 | –0.0199704293764349 | -0.0200000000000000 |
| 6 | –0.0134298208377274 | -0.0138888888888889 |
| 7 | –0.0068151982214300 | -0.0102040816326531 |
| 8 | 0.0018616612074302 | -0.0078125000000000 |
| … | ||
| 10 | 0.0251247065596211 | -0.0050000000000000 |
| 20 | 0.2439421094228725 | -0.0012500000000000 |
考察
クーロンポテンシャルの場合、\(x=\infty\)では波動関数は指数関数で減衰していきます。
このため、減衰がゆっくりになってしまい、sin関数でうまく表現できないために精度が落ちているのだと推測できます。
また、計算区間を十分に大きく取ると励起状態の表現はうまくいきますが、反対に基底状態の表現ができなくなります。なぜなら、多くの区間で波動関数はゼロですが、\(x=0\)の近傍だけに大きなピークを持つため、sin関数ではうまく表現できません。その兆候は上の数値計算でも見えてます。基底状態は2桁程度ですが、量子数の増加と共に1桁くらい精度が上がっています。
クーロンの場合、ラゲール関数を基底関数としてとる方が良いでしょう。
参考文献
[1]P. J. Davis, P. Rabinowitz著, 森正武訳, 「計算機による数値積分法」, Gauss-Lobatto求積法 p.88
[2]P. J. Davis, P. Rabinowitz著, 森正武訳, 「計算機による数値積分法」, ゼロ点に挟まれる区間の積分 p.131
[3]ランダウ=リフシッツ,「量子力学1」第3刷, p81-84
[4]Abramowitz and Stegun, HANDBOOK OF MATHEMATICAL FUNCTIONS, p.446,478 http://people.math.sfu.ca/~cbm/aands/page_446.htm
Airy関数のゼロ点は
エアリー関数 Ai, Bi(ゼロ点)-Keisan
より22桁の精度で求めたものを用いています。
ちなみにそれらの値(Airy関数のゼロ点)は、
1 -4.087949444130970616637
2 -5.52055982809555105913
3 -6.78670809007175899878
4 -7.944133587120853123138
10 -13.6914890352107179283
20 -21.2248299436420969552
30 -27.58838780988244481195
40 -33.28488468190140187962
50 -38.52880830509424882263
です。ゼロ点を0,1,2,…と、今回の計算の都合上0からインデックスを付けています。
もしかすると最後の1~2桁はあってないかもしれませんが、本稿では16桁まであっていればいいので、問題ありません。
[5]
Associated Laguerre Polynomial -wolfram mathworld式(22)-(25)