微分方程式なら任せろーバリバリバリー
ルンゲ=クッタ法ってもともとどういうもの?理論は?刻み幅\(h\)を自動的に制御する方法について知りたい方は、ルンゲ=クッタ法の系統的扱いと刻み幅制御へどうぞ。
4次ルンゲ=クッタ法は微分方程式を数値的に解く手段です。
ルンゲ=クッタ法が良く使われる理由は、ひとえにプログラムの実装のしやすさです。ルンゲクッタ法は非常に良い!というアルゴリズムではありませんが、他の方法よりもシンプルで、プログラムに組み込みやすいのです。
”4次”は問題の解の関数をテイラー展開した場合、4次までは一致するように作られた、という意味です。
例えば微分方程式
\(
\displaystyle \frac{dy}{dx}=g(x,y)
\)
を考えます。
数値計算では初期値(例えばx=0の時、y=1など)を決めて、そこからxをhだけ増やし、微分方程式というルールに従って関数\(y(0+h),y(0+h+h),y(0+h+h+h),\cdots\)を作り上げていきます。
この時、4次ルンゲ=クッタ法で求められる答えの関数というのは
\(
\displaystyle y(x+h)=y(x)+hg(x,y)+\frac{h^2}{2!}\frac{dg}{dx}+\frac{h^3}{3!}\frac{d^2g}{dx^2}+\frac{h^4}{4!}\frac{d^3g}{dx^3}+O(h^5)
\)
という関数になります。
\(
g(x,y)=-xy
\)
(ただし、初期条件\(x=0\)で\(y=1\))
である場合、微分方程式の解析解は
\(
\displaystyle y=e^{-x^2/2}
\)
であるため、4次ルンゲ=クッタ法によって導かれる答えは、
\(
\displaystyle y(x+h)=y(x)\left[1-hx+\frac{h^2}{2}(x^2-1)+\frac{h^3}{6}(-x^3+3x)+\frac{h^4}{24}(x^4-6x^2+3)\right]+O(h^5)
\)
となります。
本題に入りましょう。
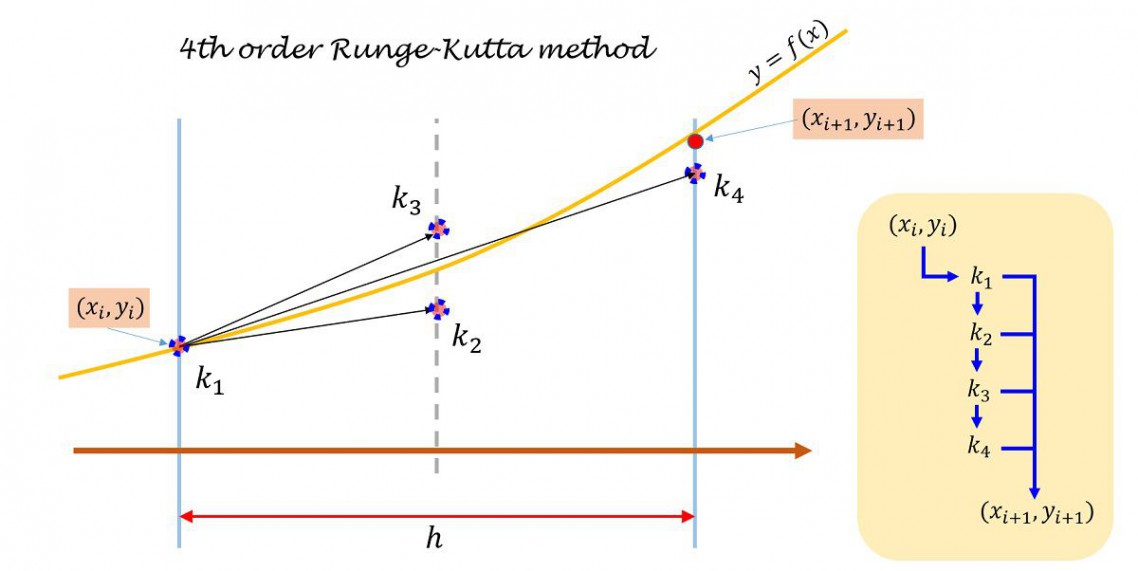
4次ルンゲ=クッタ法は6つのステップが必要となります。
初期値を\((x_0,y_0)\)と書くと、(\(y_0=y(x_0)\)です。)
- \((x_0,y_0)\)より\(k_a\)を求める
- \(k_a\)より\(k_b\)を求める
- \(k_b\)より\(k_c\)を求める
- \(k_c\)より\(k_d\)を求める
- \(k_a,k_b,k_c,k_d\)より\(y(x_0+h)\)を求める
- \((x_0+h,y(x_0+h))\)を初期値だと思って手順1に戻る。
という感じです。
3章:連立ルンゲ・クッタ法による微分方程式の解を参考にすると、数値計算での4次ルンゲ=クッタ法の計算スキームは以下のようになります。
解きたい微分方程式を連立1次微分方程式の形で書くと一般的にはこう書けます。
———
\(
\begin{eqnarray}
\left\{
\begin{aligned}
\frac{dy_1}{dx} &= f_1(x,y_1,y_2,\cdots,y_N) \\
\frac{dy_2}{dx} &= f_2(x,y_1,y_2,\cdots,y_N) \\
&\vdots \\
\frac{dy_N}{dx} &= f_N(x,y_1,y_2,\cdots,y_N) \\
\end{aligned}
\right.
\end{eqnarray}
\)
———
まず係数\(k_a\)を求めます。
———
\(
\begin{eqnarray}
\left\{
\begin{aligned}
k_{a1} &= hf_1(x,y_1,y_2,\cdots,y_N) \\
k_{a2} &= hf_2(x,y_1,y_2,\cdots,y_N) \\
&\vdots \\
k_{aN} &= hf_N(x,y_1,y_2,\cdots,y_N) \\
\end{aligned}
\right.
\end{eqnarray}
\)
———
次に\(k_b\)。
———
\(
\begin{eqnarray}
\left\{
\begin{aligned}
k_{b1} &= hf_1(x+\frac{h}{2},y_1+\frac{k_{a1}}{2},y_2+\frac{k_{a2}}{2},\cdots,y_N+\frac{k_{aN}}{2}) \\
k_{b2} &= hf_2(x+\frac{h}{2},y_1+\frac{k_{a1}}{2},y_2+\frac{k_{a2}}{2},\cdots,y_N+\frac{k_{aN}}{2}) \\
&\vdots \\
k_{bN} &= hf_N(x+\frac{h}{2},y_1+\frac{k_{a1}}{2},y_2+\frac{k_{a2}}{2},\cdots,y_N+\frac{k_{aN}}{2}) \\
\end{aligned}
\right.
\end{eqnarray}
\)
———
そして\(k_c\)。
———
\(
\begin{eqnarray}
\left\{
\begin{aligned}
k_{c1} &= hf_1(x+\frac{h}{2},y_1+\frac{k_{b1}}{2},y_2+\frac{k_{b2}}{2},\cdots,y_N+\frac{k_{bN}}{2}) \\
k_{c2} &= hf_2(x+\frac{h}{2},y_1+\frac{k_{b1}}{2},y_2+\frac{k_{b2}}{2},\cdots,y_N+\frac{k_{bN}}{2}) \\
&\vdots \\
k_{cN} &= hf_N(x+\frac{h}{2},y_1+\frac{k_{b1}}{2},y_2+\frac{k_{b2}}{2},\cdots,y_N+\frac{k_{bN}}{2}) \\
\end{aligned}
\right.
\end{eqnarray}
\)
———
最後に\(k_d\)。
———
\(
\begin{eqnarray}
\left\{
\begin{aligned}
k_{d1} &= hf_1(x+h,y_1+k_{c1},y_2+k_{c2},\cdots,y_N+k_{cN}) \\
k_{d2} &= hf_2(x+h,y_1+k_{c1},y_2+k_{c2},\cdots,y_N+k_{cN}) \\
&\vdots \\
k_{dN} &= hf_N(x+h,y_1+k_{c1},y_2+k_{c2},\cdots,y_N+k_{cN}) \\
\end{aligned}
\right.
\end{eqnarray}
\)
———
最後に求めた\(k_a,k_b,k_c,k_d\)を使って\(x+h\)でのそれぞれの関数の値を導きます。、
———
\(
\begin{eqnarray}
\left\{
\begin{aligned}
x &= x+h \\
y_{1} &= y_{1}+(k_{a1}+2k_{b1}+2k_{c1}+k_{d1})/6 \\
y_{2} &= y_{2}+(k_{a2}+2k_{b2}+2k_{c2}+k_{d2})/6 \\
&\vdots \\
y_{N} &= y_{N}+(k_{aN}+2k_{bN}+2k_{cN}+k_{dN})/6 \\
\end{aligned}
\right.
\end{eqnarray}
\)
———
となります。
4次ルンゲ=クッタ法のプログラム
実際に例題を解きましょう。
2つの例題を解きます。
[adsense1]
1階微分方程式
1つ目は
\(
\displaystyle \frac{dy}{dx}=-y\sin{x}
\)
です。
一般解は
\(
y=Ae^{\cos{x}}
\)
であり、初期条件\(x=0,y=2\)として解けば解析解は
\(
y=2e^{\cos{x}-1}
\)
です。これを4次ルンゲ=クッタ法を用いて解くには、以下のプログラムで実現できます。
program main
implicit none
integer::i,N,step,Nmax
double precision::x,h
double precision,allocatable::y(:)
external::grk
!==============
h=1.d-3
Nmax=20000
step=200
N=1
!==============
x=0d0
allocate(y(1:N))
y(1)=2d0
write(10,*)x,y(1)
do i=1,Nmax
call rk4(grk,N,x,h,y)
if(mod(i,step).eq.0)then
write(10,*)x,y(1)
endif
enddo
stop
end program main
subroutine grk(N,x,y,f)
implicit none
integer,intent(in)::N
double precision,intent(in)::x,y(1:N)
double precision,intent(out)::f(1:N)
f(1)=-y(1)*sin(x)
return
end subroutine grk
!===================================
subroutine rk4(grk,N,x,h,y)
implicit none
integer,intent(in)::N
double precision,intent(in)::h
double precision,intent(inout)::x,y(1:N)
external::grk
!
! N --> Number of 1st order differential equation
! x --> Variable
! h --> Step size
! y --> Solution
!
! sikinote(https://slpr.sakura.ne/jp/qp)
! 2020/04/22
!
integer::i,j
double precision,allocatable::tmp(:),K(:,:),f(:)
double precision::tx,c(1:4)
c(1:4)=(/0d0,0.5d0,0.5d0,1d0/)
allocate(tmp(1:N),K(1:N,0:4),f(1:N))
tmp=0d0
K=0d0
f=0d0
do j=1,4
do i=1,N
tmp(i) = y(i) + K(i,j-1)*c(j)
enddo
tx = x+c(j)*h
call grk(N,tx,tmp,f)
do i=1,N
K(i,j) = h*f(i)
enddo
enddo
x = x+h
do i=1,N
y(i) = y(i) + (K(i,1)+K(i,4))/6d0+(K(i,2)+K(i,3))/3d0
enddo
return
end subroutine rk4
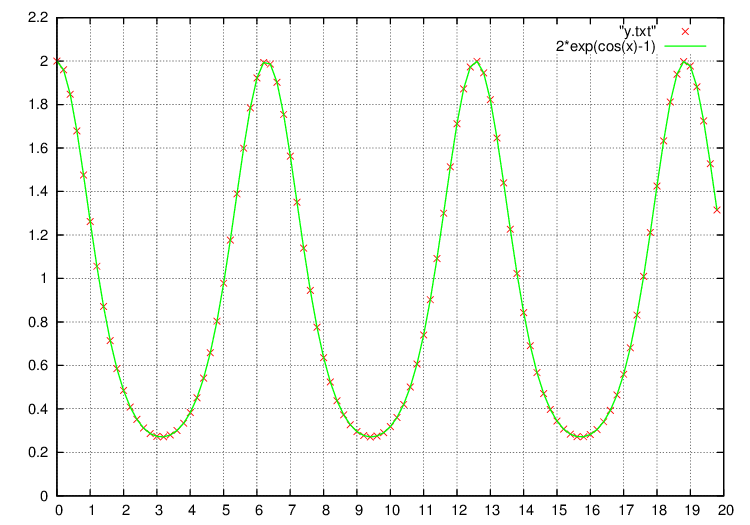
解いて、gnuplotで
plot “fort.10”
で数値計算解(赤点)と解析解(緑線)と共に出力すると、こんなグラフが得られます。
連立1階微分方程式
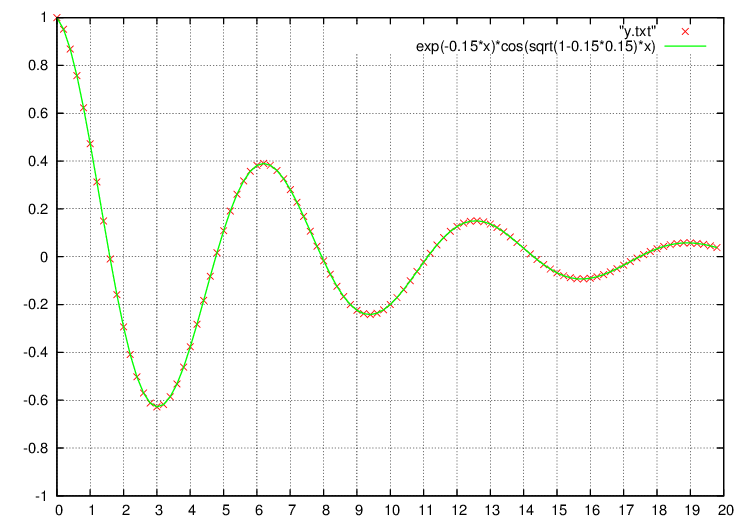
もう一つの例題は微分方程式
\(
\displaystyle \frac{d^2y}{dx^2}+2\gamma \frac{dy}{dx}+y=0
\)
を解きます。これは物理の世界ではバネの減衰振動を表す運動方程式で(詳しくは減衰振動へ。)、\(0\lt\gamma\lt1\)の場合、解は
\(
y(x)=Ae^{-\gamma x}\cos(x\sqrt{1-\gamma^2}-\alpha)
\)
となります。
\(\gamma=0.15\), 初期条件を今、
\(
\begin{eqnarray}
\left\{
\begin{aligned}
\left.y\right|_{x=0} &= 1 \\
\left.\frac{dy}{dx}\right|_{x=0} &= -0.15 \\
\end{aligned}
\right.
\end{eqnarray}
\)
とすると、解析解は
\(
y(x)=e^{-\gamma x}\cos{(x\sqrt{1-0.15^2})}
\)
となります。
プログラムで計算する際は、まず連立1次微分方程式に焼きなおす必要があります。すなわち、
\(
\begin{eqnarray}
\left\{
\begin{aligned}
\frac{dy}{dx}&=v \\
\frac{dv}{dx}&=-2\gamma v -y \\
\end{aligned}
\right.
\end{eqnarray}
\)
として解けばいいわけです。
その時の変更するべき場所は少しで、mainとrkfdの一部を変えればおしまいです。
変えた場所をコメントで
!+—+
を入れたので確認してください。
program main
implicit none
integer::i,N,step,Nmax
double precision::x,h
double precision,allocatable::y(:)
external::grk
!==============
h=1.d-3
Nmax=20000
step=200
N=2 ! +-------+
!==============
x=0d0
allocate(y(1:N))
y(1)=1d0
y(2)=-0.15d0 ! +-------+
write(10,*)x,y(1),y(2) ! +-------+
do i=1,Nmax
call rk4(grk,N,x,h,y)
if(mod(i,step).eq.0)then
write(10,*)x,y(1),y(2) ! +-------+
endif
enddo
stop
end program main
subroutine grk(N,x,y,f)
implicit none
integer,intent(in)::N
double precision,intent(in)::x,y(1:N)
double precision,intent(out)::f(1:N)
f(1)=y(2)
f(2)=-0.3d0*y(2)-y(1) ! +-------+
return
end subroutine grk
!===================================
subroutine rk4(grk,N,x,h,y)
implicit none
integer,intent(in)::N
double precision,intent(in)::h
double precision,intent(inout)::x,y(1:N)
external::grk
!
! N --> Number of 1st order differential equation
! x --> Variable
! h --> Step size
! y --> Solution
!
! sikinote(https://slpr.sakura.ne/jp/qp)
! 2020/04/22
!
integer::i,j
double precision,allocatable::tmp(:),K(:,:),f(:)
double precision::tx,c(1:4)
c(1:4)=(/0d0,0.5d0,0.5d0,1d0/)
allocate(tmp(1:N),K(1:N,0:4),f(1:N))
tmp=0d0
K=0d0
f=0d0
do j=1,4
do i=1,N
tmp(i) = y(i) + K(i,j-1)*c(j)
enddo
tx = x+c(j)*h
call grk(N,tx,tmp,f)
do i=1,N
K(i,j) = h*f(i)
enddo
enddo
x = x+h
do i=1,N
y(i) = y(i) + (K(i,1)+K(i,4))/6d0+(K(i,2)+K(i,3))/3d0
enddo
return
end subroutine rk4
gnuplotで数値計算解(赤点)と解析解(緑線)のグラフを書くとこうでなります。
[adsense2]