ニュートン法に関するお話です。
”ニュートン法”と呼ばれる方法は
２種類（1．初期値近傍の極値を求めるニュートン法、2. ゼロ点を求めるためのニュートン法）
があるようですが、ここでは1. 初期値近傍の極値を求める方のニュートン法についてのお話です。

まとめ

ベクトル\(\mathbf{x}=(x_1, x_2, \cdots, x_N)\)で指定される実数値関数\(f(\mathbf{x})\)の極値を求める事を考えます。
ここで、初期値近傍の点\(\mathbf{x}=\mathbf{x}^{(0)}\)が分かっている時、その近傍にある\(f(\mathbf{x})\)の極小値を与える\(\mathbf{x}=\mathbf{a}\)は適当な反復計算を行い、
\begin{equation}
\mathbf{a}=\lim_{k\to\infty}\mathbf{x}^{(k)}
\end{equation}
で与えられます。極値を求めるニュートン法を用いる場合、\(\mathbf{x}^{(k)}\)は漸化式として与えられ、
\begin{align}
\mathbf{x}^{(k+1)}&=\mathbf{x}^{(k)}+\mathbf{d}^{(k)} \\
\mathbf{d}^{(k)}&=-\left[H f\bigl(\mathbf{x}^{(k)}\bigr)\right]^{-1}\cdot \left[\nabla f\bigl(\mathbf{x}^{(k)}\bigr)\right]
\end{align}
として逐次的に与えられます。ここで、\(H f(\mathbf{x}), \nabla f\bigl(\mathbf{x}\bigr)\)は関数\(f(\mathbf{x})\)のヘッセ行列、傾き(Gradient)を表し、
\begin{equation}
\hat{H}f=
\begin{pmatrix}
\frac{\partial^2 f}{\partial x_1^2} & \frac{\partial^2 f}{\partial x_1 \partial x_2} &\cdots &\frac{\partial^2 f}{\partial x_1 \partial x_n} \\
\frac{\partial^2 f}{\partial x_2 \partial x_1} & \frac{\partial^2 f}{\partial x_2^2} &\cdots & \frac{\partial^2 f}{\partial x_2 \partial x_n} \\
\vdots & \vdots &\ddots & \vdots \\
\frac{\partial^2 f}{\partial x_n \partial x_1} & \frac{\partial^2 f}{\partial x_n \partial x_2} &\cdots &\frac{\partial^2 f}{\partial x_n^2} \\
\end{pmatrix}
,~~\nabla f=
\begin{pmatrix}
\frac{\partial f}{\partial x_1} \\
\frac{\partial f}{\partial x_2} \\
\vdots \\
\frac{\partial f}{\partial x_n}
\end{pmatrix}
\end{equation}
で与えられます。

特に\(f\)が\(x, y\)の２変数関数\(f(x,y)\)であるならば、
\begin{align}
\begin{pmatrix}
x^{(k+1)} \\
y^{(k+1)}
\end{pmatrix}
&=
\begin{pmatrix}
x^{(k)} \\
y^{(k)}
\end{pmatrix}
-\frac{1}{f_{xx}f_{yy}-f_{xy}f_{yx}}
\begin{pmatrix}
f_{yy} & -f_{xy} \\
-f_{yx} & f_{xx}
\end{pmatrix}
\begin{pmatrix}
f_x \\
f_y
\end{pmatrix}
\end{align}
ここで、
\begin{equation}
\hat{H}f
=
\begin{pmatrix}
f_{xx} & f_{xy} \\
f_{yx} & f_{yy}
\end{pmatrix}
,~~
\nabla f=
\begin{pmatrix}
f_x \\
f_y
\end{pmatrix}
\end{equation}
です。ここで、\(f_p\equiv\frac{\partial f}{\partial p}, ~f_{pq}\equiv\frac{\partial^2 f}{\partial p\partial q}, (p, q=x,y)\)と書きました。
微分を差分で近似するとします。\(x, y\)方向の刻み幅を\(h=h_x=h_y\)とすればそれぞれの偏微分は点\((x,y)\)近傍の7点を用いて
\begin{align}
f_x &= \frac{f(x+h, y) – f(x-h, y)}{2h} +O(h^2)\\
f_y &= \frac{f(x, y+h) – f(x, y-h)}{2h} +O(h^2)\\
f_{xx} &= \frac{f(x+h, y) – 2f(x, y)+ f(x-h, y)}{h^2} +O(h^2)\\
f_{xy} &=f_{yx}= \frac{1}{2h^2}\bigl[f(x+h, y) + f(x-h, y) + f(x, y+h) \\
&\hspace{1em}+ f(x, y-h)-2f(x,y)-f(x+h,y+h)-f(x-h,y-h)\bigr]+O(h^2) \\
f_{yy} &= \frac{f(x, y+h) – 2f(x, y)+ f(x, y-h)}{h^2} +O(h^2)
\end{align}
と書けます[2]。

導出

詳しくは述べませんが、1次元の問題における極小値を求めるニュートン法くらいは導いておきましょう。
多次元の場合は拡張すれば良く、考え方は変わりません。多次元では他の文献、例えば[1]を参考にして下さい。

関数\(f(x)\)を\(x=x^{(k)}\)周りでテイラー展開を行えば、
\begin{equation}
f(x)=f\bigl(x^{(k)}\bigr)+f’\bigl(x^{(k)}\bigr)\bigl(x-x^{(k)}\bigr)+\frac{1}{2}f^{\prime\prime}\bigl(x^{(k)}\bigr)\bigl(x-x^{(k)}\bigr)^2+O(\Delta^3)
\end{equation}
となります。ここで、\(\Delta=|x-x^{(k)}|\)とおきました。
今、欲しい解\(a\)は関数\(f(x)\)の極値なので、
\(\frac{df}{dx}=0\)を満たす\(x\)を探せばよいのです。よって、両辺を\(x\)で微分して、
\begin{align}
\frac{df(x)}{dx}=f’\bigl(x^{(k)}\bigr)+f^{\prime\prime}\bigl(x^{(k)}\bigr)\bigl(x-x^{(k)}\bigr)+O(\Delta^2)
\end{align}
を得ます。これが\(0\)になる\(x\)が解\(a\)なので、
\begin{equation}
\left. \frac{df(x)}{dx}\right|_{x=a}=f’\bigl(x^{(k)}\bigr)+f^{\prime\prime}\bigl(x^{(k)}\bigr)\bigl(a-x^{(k)}\bigr)+O(\Delta^2) = 0
\end{equation}
となります。今、\(O(\Delta^2)\)を無視すれば得られる解\(a\)は近似解\(a\approx x^{(k+1)}\)となるので、
\begin{equation}
f’\bigl(x^{(k)}\bigr)+f^{\prime\prime}\bigl(x^{(k)}\bigr)\bigl(x^{(k+1)}-x^{(k)}\bigr) = 0 \\
\end{equation}
を解いて
\begin{equation}
x^{(k+1)} = x^{(k)}-\frac{f’\bigl(x^{(k)}\bigr)}{f^{\prime\prime}\bigl(x^{(k)}\bigr)}
\end{equation}
となります。…ここまで来てしまうとニュートン・ラフソン法と同じですね。関数値がゼロになる点を探すのか、導関数値がゼロになる点を探すのかの違いなだけです。
多次元だと行列になってしまいシンプルではない形になり難しく見えますが、１次元では非常に単純です。

問題は1階(傾き)、2階導関数(ヘッセ行列)をどのように求めるかです。厳密な値が無い場合は近似的にしか得るしかありません。基本的にこれらの計算量は膨大になります。
最も簡単な方法は微分を差分に置き換えてしまうことですが、差分は余り良い方法とは言えません。

厳密なヘッセ行列は、例えば自動微分の考えで得ることが出来ます。例えば、Hyper-dual numbersによる二階偏微分の計算を参考にして得ることが出来ます。

また、引数が複素数で計算結果が実数で返ってくる関数\(f(z)\)の最小値を求めたいのであれば、\(z=x+iy\)として、\(f(x,y)\)の二変数関数としてその極致を探せば良いです。

2次元のプログラム

ここでは2次元の問題に限り、傾き、ヘッセ行列を差分で近似した場合のプログラムを記述します。

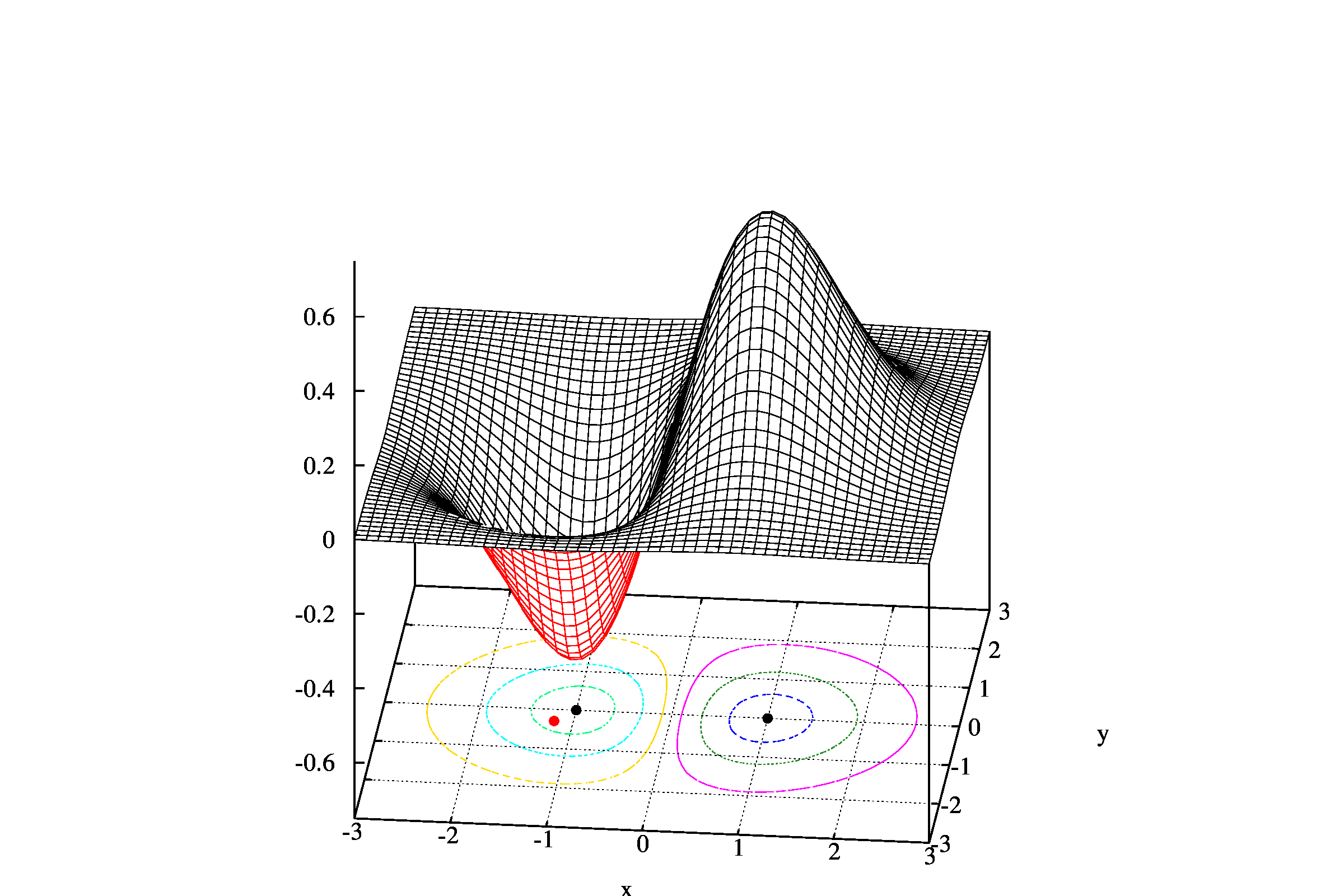
下のプログラムは関数
\begin{equation}
f(x,y)=x e^{-(x^2+y^2)/2}
\end{equation}
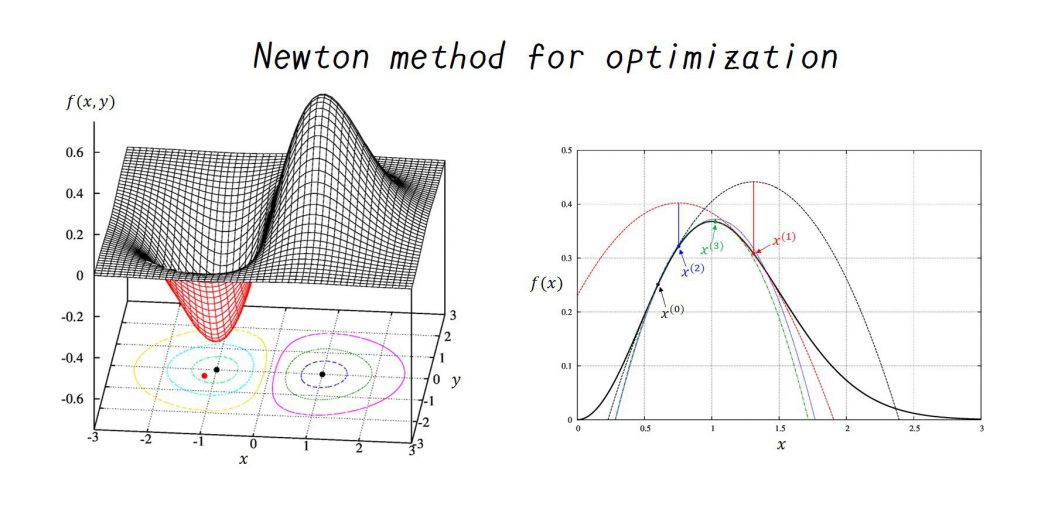
の、点\((x_0, y_0)=(-1.2, -0.3)\)近傍にある極値を求めるプログラムです。
グラフで示せば、以下の通りになります。
この関数の極値は黒点、初期値は赤点で示しています。

以下に実行例を示します。

1行目1,2,3列目はそれぞれ\(x,y\)の初期値, 関数\(f(x,y)\)の値を示しています。
また、2行目1,2,3,4列目は求まった\(x,y\)の値, 関数\(f(x,y)\)の値、そして収束に至るまでに行った繰り返しの回数を示しています。

参考文献

[1]塩浦昭義, 数理計画法 第13回
[2]Abramowitz and Stegun, “Handbook of Mathematical Functions”, http://people.math.sfu.ca/~cbm/aands/page_883.htm, http://people.math.sfu.ca/~cbm/aands/page_884.htm

Tweet