複素関数論のメモです。
微分
コーシー・リーマンの関係式(まとめ)
複素関数がコーシー・リーマンの関係式を満たすと、その複素関数は通常の変数通りに微分することが出来ます。複素数\(z=x+iy\)を引数に持つ複素関数\(f(z)=f(x+iy)\)が、実数値関数\(u(x,y), v(x,y)\)を用いて
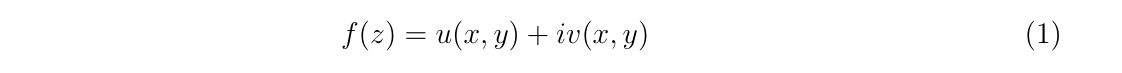
と書けているとき、コーシー・リーマンの関係式
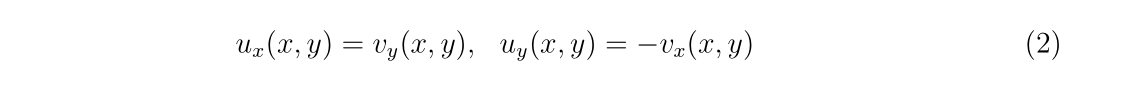
を満たすならば、\(f(z)\)は正則関数と呼ばれます。ここで、
\(f_x(x,y)=\frac{\partial f}{\partial x}, f_y(x,y)=\frac{\partial f}{\partial y}\)を意味します。式(2)を満たす場合、複素関数\(f(z)\)の複素数\(z\)による微分は
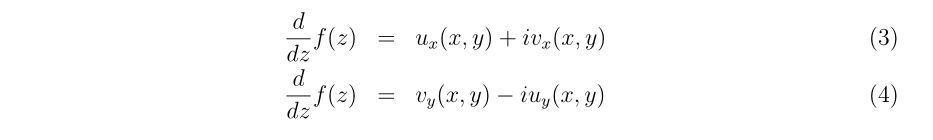
と書くことができ、式(3), (4)は同じ値となります。
コーシー・リーマンの関係式(導出)
複素関数の引数の数は1つであり、それは複素数です。すなわち1変数関数です。故に、複素関数の微分を定義しようとすれば、
\begin{align}
\frac{df(z)}{dz}
\end{align}
という量は1つに定まるはずです。しかし実数の空間で生活している我々には、1つの複素数を実部と虚部に分けて考えてしまう癖のようなものがあります。そのせいで、複素関数は平面に記述される関数であり、実部方向と虚部方向をそれぞれ独立に考えることが出来る2変数関数だと勘違いしてしまいますが、そうではありません。
すなわち、2変数の実数値関数と1変数の複素関数は全く異なる関数であり、同じ様に扱ってはいけません。しかし、我々は1次元上に複素数を表現する方法を持っておらず、本来、1変数の複素関数を2変数の実数値関数のように表現しなければイメージすることが出来ません。この場合、複素関数の表現に何らかの制約がかかることがイメージできるでしょう。その制約が正則である、という条件であり、コーシー・リーマンの関係式なのです。
では実際に本来1変数関数の複素関数を実軸と虚軸という、あたかも2変数関数のように拡張して考えて、微分を考えてみましょう。
前提として、複素関数の微分
\begin{align}
\frac{df(z)}{dz}
\end{align}
は一意に定まるとします。この下で2変数関数として\(f(z)=f(x,y)\)を拡張した場合、微分したい点への近づき方が二通りあることに気が付きます。それは、\(x\)方向と\(y\)方向ということです。2変数関数であれば、偏微分の事です。どんな方向から近づいても微分値は一意に定まると考えているので、両結果は等しくなければなりません。
微分は実数値関数と同様に差分の極限として定義して、
\begin{align}
\frac{df(z)}{dz}\equiv \lim_{\Delta z\to 0}\frac{f(z+\Delta z)-f(z)}{\Delta z}
\end{align}
と書けるとします。ここで、\(\Delta z = \Delta x+i\Delta y\)を意味しており、\(\Delta x, \Delta y\)は実数です。
点\(z=(x, y)\)に実数軸に沿って近づく場合、\(\Delta y=0\)を考えればよいので、微分は差分の極限として
\begin{align}
\frac{df(z)}{dz}=\lim_{\Delta x\to 0}\frac{f(x+\Delta x,y)-f(x,y)}{\Delta x}
\end{align}
と書かれます。ここで\(h\)は実数です。また、虚数軸に沿って近づく場合\(\Delta x=0\)を考えればよいので、
\begin{align}
\frac{df(z)}{dz}=\lim_{\Delta y\to 0}\frac{f(x,y+\Delta y)-f(x,y)}{i\Delta y}
\end{align}
と書かれるはずです。複素関数の微分は一意に決まることから、二つの近づき方を考えたとしても一致していなければなりません。複素関数が\(f(z)=u(x,y)+iv(x,y)\)と実部と虚部があらわに分離されて書かれていたとするならば、
\begin{align}
&\lim_{\Delta x\to 0}\frac{f(x+\Delta x,y)-f(x,y)}{\Delta x}\
&=\lim_{\Delta x\to 0}\frac{[u(x+\Delta,y)+iv(x+\Delta,y)]-[u(x,y)+iv(x,y)]}{\Delta x} \
&=\lim_{\Delta x\to 0}\frac{[u(x+\Delta,y)-u(x,y)]+i[v(x+\Delta,y)-v(x,y)]}{\Delta x} \
&=\frac{\partial u}{\partial x}+i\frac{\partial v}{\partial x} \
\end{align}
と書けます。また、虚軸方向は
\begin{align}
&\lim_{\Delta y\to 0}\frac{f(x,y+\Delta y)-f(x,y)}{i\Delta y}\
&=\lim_{\Delta y\to 0}\frac{[u(x,y+\Delta y)+iv(x,y+\Delta y)]-[u(x,y)+iv(x,y)]}{i\Delta y} \
&=\lim_{\Delta y\to 0}\frac{-i[u(x,y+\Delta y)-u(x,y)]+[v(x,y+\Delta y)-v(x,y)]}{\Delta y} \
&=-i\frac{\partial u}{\partial y}+\frac{\partial v}{\partial y}
\end{align}
と書くことが出来ます。
両者はもともと同じものであるとしてきましたから、実部と虚部で比較します。
すると、
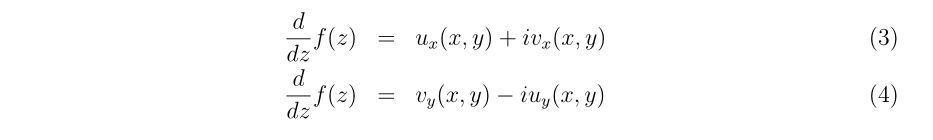
という関係式が導けるという訳です。これがコーシー・リーマンの関係式と呼ばれるもので、1変数関数の複素関数を実部、虚部という2変数関数に無理矢理拡張した場合に現れる条件です。
複素関数の微分が定義できるとき、複素関数の実部虚部は、この関係式を満たしていなければなりません。ある範囲においてすべての点で複素関数の微分が定義できることを、正則であると言ったり、滑らかである、解析的であると言います。
”複素関数の滑らか”は通常の”滑らか”と意味が異なることに注意しましょう。通常は不連続点が無いことを指しますが、複素関数の場合はそれ以上の制約(コーシー・リーマンの関係式)を含んでいます。
また、ここでは述べませんが、複素関数は1度微分できると何回でも微分することが出来ます。
さらに微分が定義できる正則関数であれば定義域を超えた領域へ関数が拡張できる場合があります。これが解析接続と呼ばれるテクニックです。コーシー・リーマンの関係式を制約として今まで捉えてきたのですが、この制約があるからこそまだ見ぬ定義域外をこの関係式を手掛かりに関数を拡張できるのです。
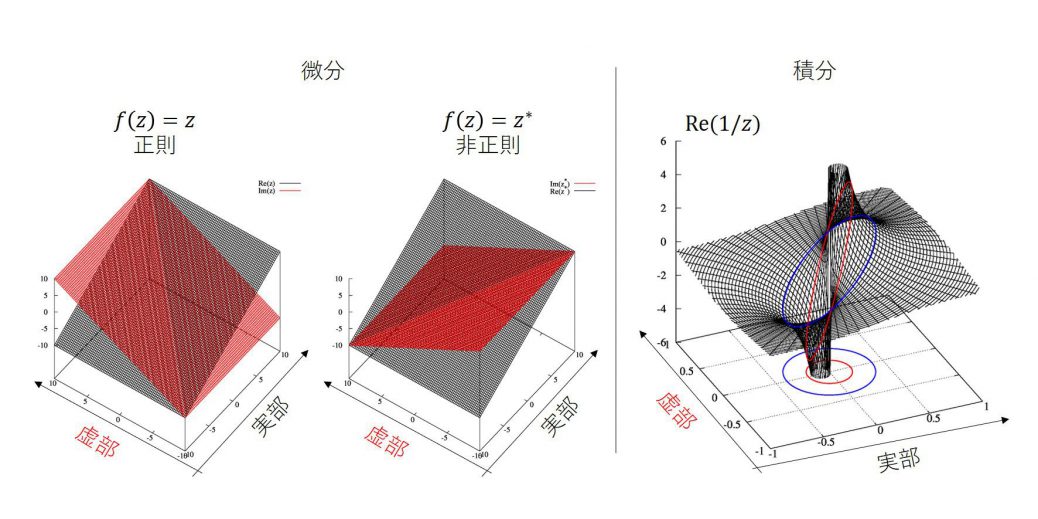
例として、究極的に滑らかそうに見えるけど微分できない関数を上げましょう。
\begin{align}
f(z)=z=x+iy
\end{align}
はコーシー・リーマンの関係式を満たすため、複素関数として微分が定義でき、正則です。しかし、その複素共役を取った関数
\begin{align}
f(z)=z^*=x-iy
\end{align}
はコーシー・リーマンの関係式を満たさないため、複素関数として微分が定義できず、正則ではありません。近づき方によって微分の値が変わってしまうのです。
通常の微分が可能という意味を明確にするため、例を挙げます。\(f(z)\)が\(z\)の多項式で書かれている場合、微分は
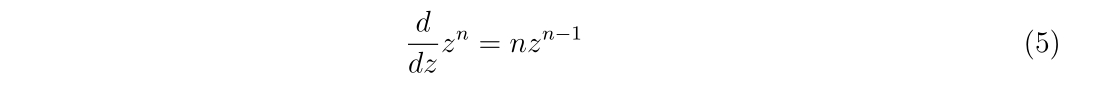
として求める事が出来ます。通常と同じですね。これは、複素数の成分を持たない場合には実軸上で考えたものと同等になるので、実数軸上の微分を自然に拡張したようになっています。
積分
特異点周りの積分
端的にまとめます。
点\(a\)を囲うように複素平面上の閉じた積分経路の方向を\(C\)で指定するとします。\(z\)の多項式で表現される関数\(f(z)=(z-a)^n\)の積分は、
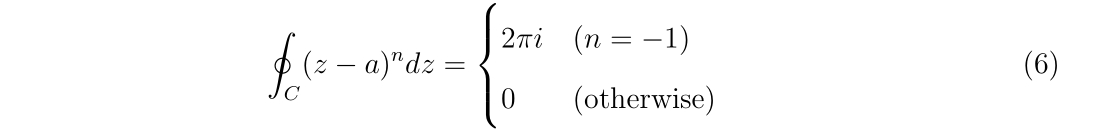
となります。点\(a\)の周りを反時計回りに1周回る場合、\(C\)はパラメータ\(t\)を用いて\(z(t)\)と書くと、
\begin{align}
z(t)=a+re^{it},~(0\le t \le 2\pi)
\end{align}
と書けます。\(r\)は積分経路の半径を意味します。式(6)の計算をすれば、
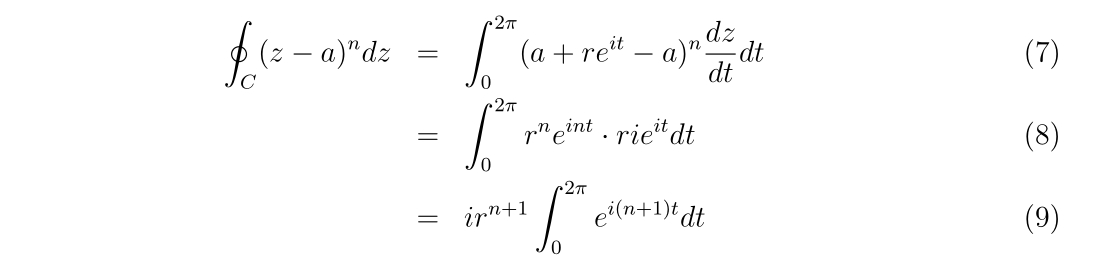
となります。\(n=-1\)の時、右辺の積分は\(2\pi\)に等しい事は明らかです。それ以外の\(n\ne -1\)ならば、
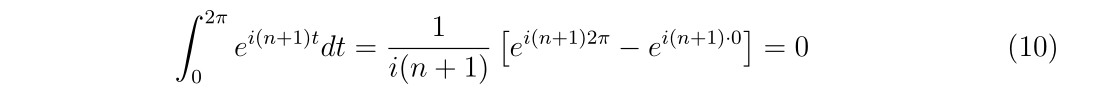
となります。よって、
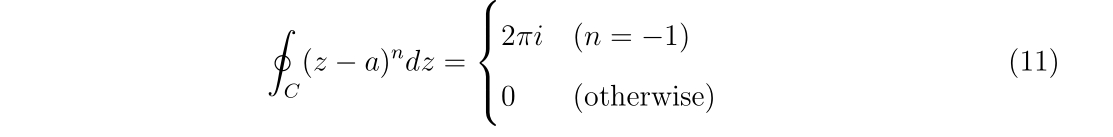
が導かれます。
留数定理
一つ前の、ある点周りの積分をもう少し一般的に考えましょう。\(z=a\)を中心とした閉曲線に沿った複素関数\(f(z)\)の複素積分\(\oint_C f(z)dz\)は

と書けます。ここで\(\text{Res}[f,a]\)は留数と呼ばれる量です。これから留数について述べていきます。
\(\text{Res}[f,a]\)は、\(f(z)\)が点\(a\)周りで
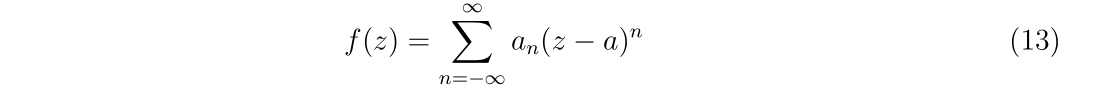
とローラン展開出来るとします。この時、\(a_{-1}\)を留数と呼びます。すなわち、
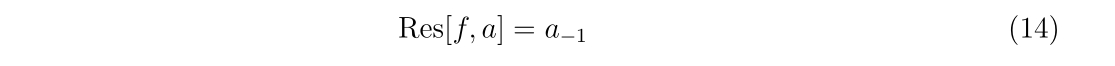
を意味します。
では、留数を実際に求めていきましょう。\(f(z)\)が点\(a\)周りでローラン展開可能な場合、\(n\)の下限が重要になります。下限を極の位数\(k\)と表現します。\(k\)は、
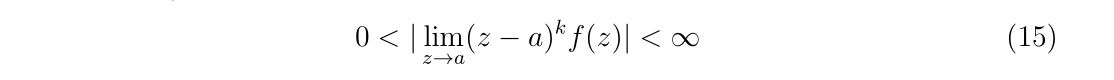
を満たすときの値として定義できます。
もし、関数\(f(z)\)が\(z=a\)で\(k\)位の極であれば、\(z=a\)周りで

と展開できます。
留数は\(a_{-1}\)なので、\(a_{-1}\)について式変形を行っていけば、

と計算できます。
参考文献
原惟行、松永秀章著、『複素解析入門』(第3刷2010, 初版2007)