2体のケプラー問題を数値的に解きます。
ここでは、適切な変換をして求めるのではなく、刻み幅制御されたプログラムで無理やり計算します。
そして、
陽的解法であるルンゲ=クッタ=フェールベルグ法
と
陰的解法であるルンゲ=クッタ=ガウス=ルジャンドル法
の離心率に対する計算量の違いを調べてみます。
Kepler問題
二次元で二体の問題を考えます。運動方程式は
\(
\begin{align}
\frac{d^2 x}{dt^2}&=-\frac{x}{(x^2+y^2)^{3/2}} \\
\frac{d^2 y}{dt^2}&=-\frac{y}{(x^2+y^2)^{3/2}}
\end{align}
\)
\(t=[0,20],~~x(0)=1-e,~~x'(0)=0,~~y(0)=0,~~y'(0)=\sqrt{\frac{1+e}{1-e}}\)
です。ここで、\(e\)は離心率を表します。
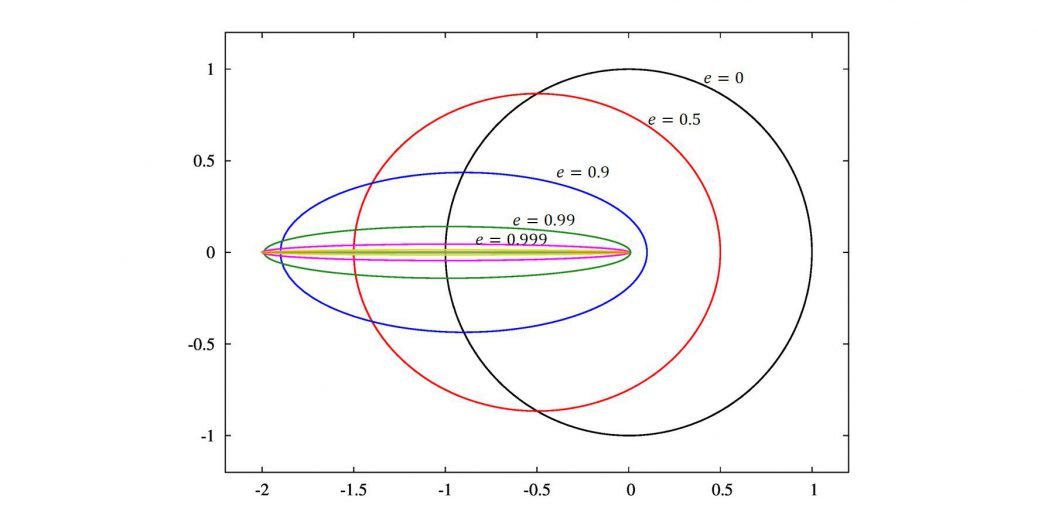
この問題に対する解は良く知られていて、
\(
\displaystyle (x+e)^2+\frac{y^2}{1-e^2}=1
\)
で表され、
\(
0\le e\lt 1
\)
の時、楕円となります。
関数の評価回数の離心率の依存性
楕円の軌道を持つ範囲において、
計算は離心率\(e\)が1に近づくほど難しくなります。
なぜなら、原点付近を通過する際に、質点の導関数の変化が大きくなるからです。
使用したプログラムの説明は
陽的解法はhttps://slpr.sakura.ne.jp/qp/runge-kutta-ex/
陰的解法はhttps://slpr.sakura.ne.jp/qp/irkgl-program/
です。実際のプログラムも置いておきます。
さて、計算速度の評価ですが、関数が何回評価されたかで比較します。
念の為、陰的解法はLU分解もあるので単純な比較は難しいことを注記しておきます。
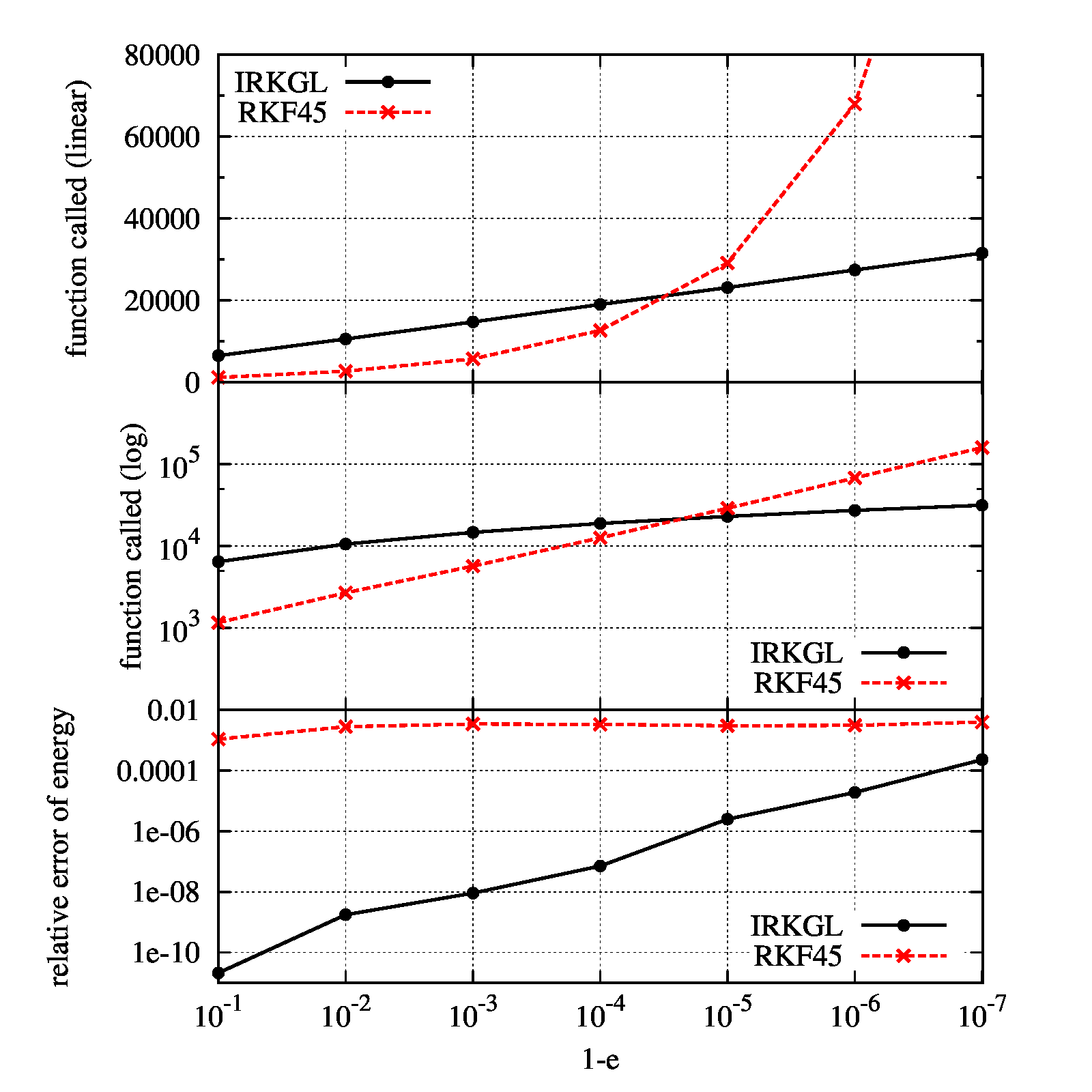
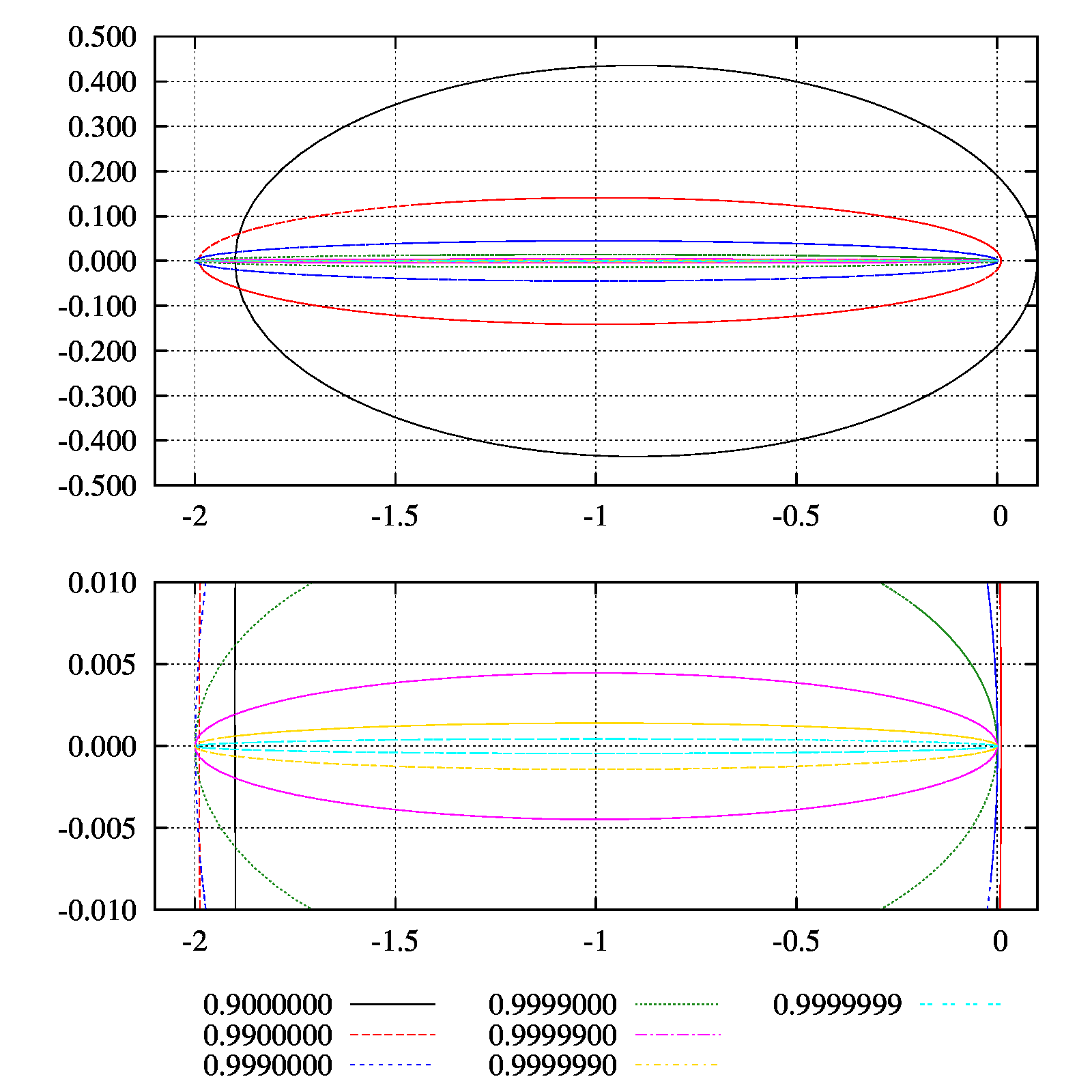
図の一番上は関数の評価回数の離心率依存性を表しています。縦軸は評価回数、横軸は\(1-e\)を表します。真ん中の図は一番上と同じですが、軸を対数にとっています。一番下は、\(t=20\)まで計算した時に\(t=0\)の初期エネルギーとの相対誤差\(|(E(t=20)-E(t=0))/E(t=0)|\)を表しています。
特徴的な振る舞いは、離心率に対して陰的解法の評価回数は線形の振る舞い、陽的解法は指数で振る舞っている点です。
これは、質点が原点の近くを通るような問題の際に違いが際立つ事を示しています。
また、エネルギーの保存に関しても陰的解法の方が良いことが分かるでしょう。
一応注意しておきますが、ここでいう陰的解法はルンゲ=クッタ=ガウス=ルジャンドル法の振る舞いです。一般的な陰的解法については話していないことに注意してください。
プログラム
implicit none
integer::count
end module GBL
program main
use GBL
implicit none
integer::N,Ns,istep,ih0,Jup,info,ih,i,Nx,iJac,j,cirk,cerk
double precision::h,h0,err0,eta0,tol,xa,xb,tx,e
double precision::y1,y2,y3,y4,eneirk,eneerk
integer,allocatable::ipiv(:),epiv(:)
double precision,allocatable::x(:),y(:),Rtol(:),Atol(:)
double precision,allocatable::Jmat(:,:),errJ(:,:),z0(:),Jac(:,:)
double precision,external::egrk
external::grk
N=4 ! Number of 1st order ODEs
allocate(y(1:N),Rtol(1:N),Atol(1:N))
y=0d0; Rtol=0d0; Atol=0d0
Nx=2
allocate(x(1:Nx))
x=0d0
!------------ Initial set up ------------
Ns=N*3 ! Ns=N*s, s means s-stage IRK.
allocate(ipiv(1:Ns),epiv(1:N))
allocate(Jmat(1:Ns,1:Ns),errJ(1:N,1:N),z0(1:Ns),Jac(1:N,1:N))
ipiv=0; epiv=0; Jmat=0d0; errJ=0d0; Jup=0; ih=0
ih0=0; z0=0d0; eta0=0d0; h0=0d0; err0=0d0; iJac=0; Jac=0d0
!----------------------------------------
xa=0d0 ! Initial value of x
xb=20d0 ! End value of x
do i=1,Nx ! Separate equal interval x.
x(i)=(i-1)*(xb-xa)/dble(Nx-1)+xa
enddo
do j=1,7
if(j.eq.1)e=0.9d0
if(j.eq.2)e=0.99d0
if(j.eq.3)e=0.999d0
if(j.eq.4)e=0.9999d0
if(j.eq.5)e=0.99999d0
if(j.eq.6)e=0.999999d0
if(j.eq.7)e=0.9999999d0
y1=1d0-e ! Initial values at x of y_1
y2=0d0 ! Initial values at x of y_2
y3=0d0 ! Initial values at x of y_1
y4=sqrt((1d0+e)/(1d0-e)) ! Initial values at x of y_2
tol=1d-4 ! Tolerance
Rtol(1:N)=tol ! Relative tolerance
Atol(1:N)=tol ! Absolute tolerance
! Imxplicit method
y(1)=y1; y(2)=y2; y(3)=y3; y(4)=y4; h=1d-6; count=0
istep=0
do i=2,Nx
info=0
tx=x(i-1)
do while(info.le.0)
call irkgl(istep,grk,N,tx,h,x(i),y,info,Atol,Rtol &
,ih,z0,ih0,h0,eta0,err0,Jup,ipiv,Jmat,epiv,errJ,iJac,Jac)
if(j.eq.4)write(21,'(7e25.15e3)')tx,y(1),y(2),y(3),y(4),h,&
0.5d0*(y(2)**2+y(4)**2) - 1d0/(sqrt(y(1)**2+y(3)**2))
enddo
h=h0
enddo
eneirk = 0.5d0*(y(2)**2+y(4)**2) - 1d0/(sqrt(y(1)**2+y(3)**2))
cirk=count
write(6,*)cirk
! Explicit method
y(1)=y1; y(2)=y2; y(3)=y3; y(4)=y4; h=1d-6; count=0
info=0
do i=2,Nx
info=-1
tx=x(i-1)
do while(info.le.0)
call drkf45(egrk,tx,h,N,y,x(i),info,tol)
if(j.eq.4)write(22,'(7e25.15e3)')tx,y(1),y(2),y(3),y(4),h, &
0.5d0*(y(2)**2+y(4)**2) - 1d0/(sqrt(y(1)**2+y(3)**2))
enddo
enddo
eneerk = 0.5d0*(y(2)**2+y(4)**2) - 1d0/(sqrt(y(1)**2+y(3)**2))
cerk = count
write(6,*)cerk
write(30,*)e,cirk,count,eneirk,eneerk
enddo
stop
end program main
subroutine grk(N,x,y,f)
use GBL
implicit none
integer,intent(in)::N
double precision,intent(in)::x,y(1:N)
double precision,intent(out)::f(1:N)
! Write right-hand-side of 1st order ODEs
f(1)=y(2)
f(2)=-y(1)/((y(1)**2+y(3)**2)**1.5d0)
f(3)=y(4)
f(4)=-y(3)/((y(1)**2+y(3)**2)**1.5d0)
count=count+1
return
end subroutine grk
!=====================================
subroutine irkgl(istep,grk,Neq,x,h,xend,y,info,Atol,Rtol &
,ih,z0,ih0,h0,eta0,err0,Jup,ipiv,Jmat,epiv,errJ,iJac,Jac)
implicit none
integer,parameter::s=3
integer,intent(in)::Neq
integer,intent(inout)::istep,info,Jup,ipiv(1:Neq*s),epiv(1:Neq)
double precision,intent(in)::xend,Atol(1:Neq),Rtol(1:Neq)
double precision,intent(inout)::x,h,y(1:Neq)
integer,intent(inout)::ih0,ih,iJac
double precision,intent(inout)::z0(1:Neq*s),h0,eta0,err0
double precision,intent(inout)::Jmat(1:Neq*s,1:Neq*s),errJ(1:Neq,1:Neq)
double precision,intent(inout)::Jac(1:Neq,1:Neq)
external::grk
!
! Implicit Runge-Kutta method based on
! the Gauss-Legendre 3-stage 6-order
!
! Properties of this routine:
! 1. A-stable
! 2. Symplectic
! 3. Symmetric
! 4. Step size control
! Note, Gauss-Legendre IRK method is Symplectic
! even if we change the step size.
!
! Meaning of parameters
! istep : Number of IRK step
! grk : Right hand Side of ODEs
! Neq : Number of 1st-order ODEs
! x : Integral parameter (automatically updated)
! h : Step size (automatically updated)
! xend : End point of the x range
! y : Values of ODEs
! info : Information of the IRK process
! Atol : Absolute tolerance
! Rtol : Relative tolerance
!
! Other parameters are work parameters,
! referenced for istep >= 1
! ***0 : Previous parameters
! Jmat : LU decomposited J' (= I-hAJ) matrix
! ipiv : Pivot information for Jmat
! errJ : LU decomposited (I-h\gamma J) matrix
! epiv : Pivot information for errJ
! Jup : Decide the update of Jmat and errJ,
! Jup = 0 --> No update
! Jup = 1 --> Update
! Jac : Jacobian matrix of the grk function
! iJac : Decide the update of Jac,
! iJac = 0 --> No update when Jup=1
! iJac = 1 --> Update when Jup=1
!
! How to use?
! 1. Call this routine with istep = 0 and info = 0.
! 2. Call and Loop this routine while info <= 0.
!
! ==== Example =====
! istep=0
! info=0
! do while(info.le.0)
! call irk(istep,grk,Neq,x,h,xend,y,info,Atol,Rtol &
! ,ih,z0,ih0,h0,eta0,err0,Jup,ipiv,Jmat,epiv,errJ,iJac,Jac)
! enddo
! ==================
!
! After starting computation with istep=0,
! you must not touch WORK parameters.
!
!
! istep = 0 : when you start computation,
! set WORK parameters like ;
! ih = 0
! z0(1:Ns) = 0d0
! ih0 = 0
! h0 = 0d0
! eta0 = 0d0
! err0 = 0d0
! Jup = 0
! ipiv(1:Ns) = 0
! Jmat(1:Ns,1:Ns) = 0d0
! epiv(1:Neq) = 0
! errJ(1:Neq,1:Neq) = 0d0
! iJac = 0
! Jac(1:Neq,1:Neq) = 0d0
!
! Author : sikino
! URL : http://slpr.sakura.ne.jp/qp/
! Date : 2019/01/14 (yyyy/mm/dd)
! 2019/01/21 keep Jacobian matrix
! 2019/01/22 did Something
! 2019/01/23 initial value estimation
!
double precision::tx,th
double precision,allocatable::ty(:),tz0(:)
integer,parameter::kmax=7 ! Newton iteration limit
double precision,parameter::hmin=1d-13,hmax=1d0
integer::kexit,Ns,key,FLAG,Newt
double precision::theta,err,fac,del,del1,del2,teta0,th0
if(istep.le.-1)then
write(6,*)"**** Error, unexpected istep"
stop
endif
Ns=Neq*s
if(abs(h).ge.hmax)then
h=sign(1d0,h)*hmax
endif
if(h.ge.abs(xend-x))h=xend-x
FLAG=1
if(abs(x-xend).le.hmin)then
info=1
FLAG=0
endif
if(istep.eq.0)then
ipiv=0; epiv=0; Jmat=0d0; errJ=0d0; Jup=0; ih=0
ih0=0; z0=0d0; eta0=0d0; h0=0d0; err0=0d0; iJac=0; Jac=0d0
call discrete_h(h,ih,th,hmin,hmax)
h=th
ih0 = ih+1
Jup = 1
iJac = 1
else
endif
key=0
allocate(ty(1:Neq),tz0(1:Ns))
ty=0d0; tz0=0d0
do while(FLAG.eq.1)
if(ih.ne.ih0)then
Jup=1
endif
tx=x
ty(1:Neq)=y(1:Neq)
tz0(1:Ns)=z0(1:Ns)
teta0 = eta0
th0=h0
call dirk6(istep,grk,Neq,tx,h,ty,Jup &
,tz0,th0,teta0,ipiv,Jmat,epiv,errJ,Atol,Rtol &
,err,kmax,kexit,Newt,theta,iJac,Jac)
! Even if the step is fail, ipiv,Jmat,epiv,errJ are updated if Jup=1.
if(Jup.eq.1)then
Jup=0
endif
if(kexit.eq.1)then
! Change step size
!fac = 0.9d0*(2d0*kmax+1d0)/(2d0*kmax+dble(Newt-1))
fac = 0.95d0*(2d0*kmax+1d0)/(2d0*kmax+dble(Newt))
if(err.ge.1d-30)then
if(istep.eq.0)then
del = fac*((1d0/err)**(0.33d0)) !(27)
else
del1 = fac*((1d0/err)**(0.33d0)) !(27)
del2 = del1*(h/h0)*((err0/err)**(0.33d0)) !(27)
del = del1
if(del2.lt.del)del=del2
if(del.gt.1d0)then
del=del1
else
del=del2
endif
endif
else
del=100d0
endif
elseif(kexit.eq.2)then
del=0d0
else
write(6,*)" **** detect unexpected kexit"
stop
endif
! Accept or Reject
if(err.le.1d0.or.key.eq.1)then
FLAG=0 ! This step with h is accepted
x=x+h
y(1:Neq)=ty(1:Neq)
z0(1:Ns)=tz0(1:Ns)
h0=h
ih0=ih
eta0=teta0
err0=err
iJac = 1
Jup=1
! Don't update Jacobian for next step
if(Newt.le.2.or.theta.lt.1d-3)Jup=0
!if(Newt.le.1.or.theta.lt.1d-3)Jup=0
endif
if(del.le.0.1d0)then
!function changes dramatically.
h=0.1d0*h
elseif(del.ge.4d0)then
!function changes loosely.
h=4d0*h
else
!function changes moderately.
h=del*h
endif
if(abs(h).ge.hmax)then
h=sign(1d0,h)*hmax
elseif(abs(h).lt.hmin)then
h=sign(1d0,h)*hmin
key=1
endif
! Step size alignment
if(abs(xend-x).le.abs(h))then
h=xend-x
Jup=1
if(abs(h).le.hmin)then
info=1
FLAG=0
endif
else
call discrete_h(h,ih,th,hmin,hmax)
h=th
endif
if(h.le.0d0.and.xend-x.ge.0d0)then
info=1
FLAG=0
elseif(h.ge.0d0.and.xend-x.le.0d0)then
info=1
FLAG=0
endif
if(key.eq.1)then
write(6,'(A,f10.5,A,f10.5)')"Strange point between ",x-h," and ",x
info=-9
endif
enddo
istep=istep+1
return
end subroutine irkgl
subroutine dirk6(istep,grk,Neq,x,h,y,Jup &
,z0,h0,eta0,ipiv,Jmat,epiv,errJ,Atol,Rtol &
,err,kmax,kexit,Newt,theta,iJac,Jac)
implicit none
integer,parameter::s=3
integer,intent(in)::istep,Neq,Jup,kmax
integer,intent(out)::kexit,Newt
double precision,intent(in)::h,Atol(1:Neq),Rtol(1:Neq)
double precision,intent(inout)::x,y(1:Neq),z0(1:Neq*s),h0,eta0
double precision,intent(out)::err,theta
integer,intent(inout)::ipiv(1:Neq*s),epiv(1:Neq),iJac
double precision,intent(inout)::Jmat(1:Neq*s,1:Neq*s),errJ(1:Neq,1:Neq)
double precision,intent(inout)::Jac(1:Neq,1:Neq)
external::grk
!
! istep >= 0
!
! Input
! Jup = 0 : Don't update Jacobian
! = 1 : Update Jacobian
! Output
! kexit = 1 : Newton iteration converge.
! = 2 : Newton iteration didn't converge.
!
! Below parameters have meaning when kexit = 1.
! Newt : Number of Newton iteration till converge.
! theta : Convergion rate, \theta < 1.
! err : Estimated err, if err < 1, satisfied required tol.
!
integer::i,j,k,n,m,p,q,Ns,info
double precision,parameter::kappa=5d-2
double precision,parameter::Uround=5d-16
double precision,parameter::sq15=sqrt(15d0)
! Real eigenvalue of A matrix in butcher table for Gauss-Legendre
double precision,parameter::gamma=0.215314423116112178244733530380696d0
double precision::a(1:s,1:s),c(1:s),d(1:s),d2(1:s),dc(1:s)
double precision::c12,c23,c31,xc1,xc2,xc3,xx,omega
double precision::x0,tx
double precision,allocatable::z(:),y0(:),dy(:),f(:),tf(:),ty(:),tf0(:)
double precision,allocatable::w(:,:),w0(:,:),e(:)
double precision::Ntol,sc,sdz,sdz0,tmp,eta
Ns=Neq*s
allocate(z(1:Ns))
z=0d0
! 3-stage Gauss-Legendre
c(1:3)=(/0.5d0-0.1d0*sq15, 0.5d0, 0.5d0+0.1d0*sq15/)
a(1,1:3)=(/5d0/36d0, 2d0/9d0-sq15/15d0, 5d0/36d0-sq15/30d0/)
a(2,1:3)=(/5d0/36d0+sq15/24d0, 2d0/9d0, 5d0/36d0-sq15/24d0/)
a(3,1:3)=(/5d0/36d0+sq15/30d0, 2d0/9d0+sq15/15d0, 5d0/36d0/)
d(1:3)=(/5d0/3d0,-4d0/3d0,5d0/3d0/)
d2(1:3)=(/-15d0-10d0*sqrt(5d0/3d0),12d0,-15d0+10d0*sqrt(5d0/3d0)/)
dc(1:3)=(/(5d0+sq15)*10d0/3d0, -40d0/3d0 ,(5d0-sq15)*10d0/3d0/)
if(istep.eq.0)then
z(1:Ns)=0d0
else
allocate(dy(1:Neq))
dy=0d0
do n=1,Neq
do j=1,s
dy(n)=dy(n)+d(j)*z0((n-1)*s+j)
enddo
enddo
! Lagrange interpolation
omega=h/h0
c12=1d0/(c(1)-c(2))
c23=1d0/(c(2)-c(3))
c31=1d0/(c(3)-c(1))
do n=1,Neq
do p=1,s
xx=1d0+omega*c(p)
xc1=xx-c(1)
xc2=xx-c(2)
xc3=xx-c(3)
z((n-1)*s+p)=&
-z0((n-1)*s+1)*xc2*xc3*(c12*c31)*xx/c(1) &
-z0((n-1)*s+2)*xc3*xc1*(c12*c23)*xx/c(2) &
-z0((n-1)*s+3)*xc1*xc2*(c31*c23)*xx/c(3) &
-dy(n)
enddo
enddo
deallocate(dy)
endif
if(Jup.eq.1)then
! LU decomposition of J' matrix
if(iJac.eq.1)then
call Jacobian(Neq,x,y,grk,Jac)
iJac=0
endif
do m=1,Neq
do n=1,Neq
do q=1,s
do p=1,s
Jmat(s*(n-1)+p,s*(m-1)+q) = - h*Jac(n,m)*a(p,q)
enddo
enddo
enddo
enddo
do n=1,Neq
do m=1,Neq
errJ(n,m) = - h*gamma*Jac(n,m)
enddo
enddo
do i=1,Ns
Jmat(i,i) = 1d0 + Jmat(i,i)
enddo
do i=1,Neq
errJ(i,i) = 1d0 + errJ(i,i)
enddo
! LU factorization for main part of IRK
call dgetrf(Ns,Ns,Jmat,Ns,ipiv,info)
! LU factorization for estimate error
call dgetrf(Neq,Neq,errJ,Neq,epiv,info)
endif
allocate(f(1:Ns),tf(1:Neq),ty(1:Neq),w(1:Ns,1:1))
f=0d0; tf=0d0; ty=0d0; w=0d0
!===============================
Ntol=sqrt(Rtol(1))
!if(0.03d0.le.Ntol)Ntol=0.03d0
!if(1d-12.le.Ntol)Ntol=1d-12
if(1d-12.le.Ntol)Ntol=1d-12
!if(1d-6.le.Ntol)Ntol=1d-6
!===============================
sdz0=0d0 ! Initialize
! Simple Newton iteration
kexit=0
do k=1,kmax
do j=1,s
tx = x + c(j)*h
do n=1,Neq
ty(n) = y(n) + z((n-1)*s+j)
enddo
call grk(Neq,tx,ty,tf)
do n=1,Neq
f((n-1)*s+j) = tf(n)
enddo
enddo
w(1:Ns,1:1)=0d0
do n=1,Neq
do p=1,s
do j=1,s
w((n-1)*s+p,1) = w((n-1)*s+p,1) + a(p,j)*f((n-1)*s+j)
enddo
w((n-1)*s+p,1) = z((n-1)*s+p) - h*w((n-1)*s+p,1)
enddo
enddo
! Solve J' \delta z = - w
do i=1,Ns
w(i,1) = - w(i,1)
enddo
call dgetrs('N',Ns,1,Jmat,Ns,ipiv,w,Ns,info)
! --> Now, w is \Delta z
! z^{(k+1)} = z^{(k)} + Delta z
do i=1,Ns
z(i) = z(i) + w(i,1)
enddo
sdz=0d0
do i=1,Ns
sdz = sdz + w(i,1)**2
enddo
sdz=sqrt(sdz)
! Stop iteration criteria
if(istep.eq.0.and.k.eq.1)then
! Do nothing
kexit=0
elseif(istep.eq.0.and.k.ge.2)then
if(sdz0-sdz.lt.0d0)then
! Convergion rate > 1, must change small step size.
kexit=2
elseif(sdz0*sdz**(kmax-k+1).gt.kappa*Ntol*(sdz0-sdz)*sdz0**(kmax-k))then
! Rough convergion estimation fail, must change small step size.
kexit=2
elseif(sdz*sdz.lt.kappa*Ntol*(sdz0-sdz))then
! Good behavior. Iteration finish.
kexit=1
endif
elseif(istep.ge.1.and.k.eq.1)then
tmp = Uround
if(eta0.gt.tmp)tmp=eta0
tmp=tmp**0.8d0
if(tmp*sdz.lt.kappa*Ntol)then
kexit=1
endif
elseif(istep.ge.1.and.k.ge.2)then
if(sdz0-sdz.lt.0d0)then
! Convergion rate > 1, must change small step size.
kexit=2
elseif(sdz0*sdz**(kmax-k+1).gt.kappa*Ntol*(sdz0-sdz)*sdz0**(kmax-k))then
! Rough convergion estimation fail, must change small step size.
kexit=2
elseif(sdz*sdz.lt.kappa*Ntol*(sdz0-sdz))then
! Good behavior. Iteration finish.
kexit=1
endif
else
write(6,*)" *****Unexpected parameters"
stop
endif
if(kexit.ne.0)exit
sdz0 = sdz
enddo
!
! 0 < \eta < \infty --> Good.
! if \eta ~ 0, good behavior
! -\infty < \eta < -1, --> Bad.
! Error increase as iteration increase.
!
if(k.eq.kmax+1.or.kexit.eq.2.or.kexit.eq.0)then
! Did not converge k_max iteration.
kexit=2
eta=100d0
Newt=kmax
err=100d0
theta=1000d0 ! Convergion ratio, \theta ~ 0 is Good.
! h0, z0, x, y are don't updated
return
else
! (sdz0-sdz) > 0
if(k.eq.1)then
! No sdz0 case.
eta = Uround
if(eta0.gt.eta)eta=eta0
eta = eta**0.8d0
theta = 100d0 ! Here, \theta cannot evaluate because k=1.
else
if(sdz0.eq.sdz)then
! z does not change --> converge enough.
eta = Uround
theta = 0d0 ! \theta=0.
else
! General case.
eta = sdz/(sdz0-sdz)
theta = sdz/sdz0
endif
endif
Newt = k
endif
deallocate(w)
x0=x
allocate(y0(1:Neq))
y0(1:Neq)=y(1:Neq)
! Update x and y(1:Neq)
x=x+h
do n=1,Neq
do j=1,s
y(n) = y(n) + d(j)*z((n-1)*s+j)
enddo
enddo
! Error estimation
allocate(w(1:Neq,1:1),w0(1:Neq,1:1),tf0(1:Neq),e(1:Neq))
w=0d0; w0=0d0; tf0=0d0; e=0d0
do n=1,Neq
do j=1,s
w(n,1) = w(n,1) + dc(j)*z((n-1)*s+j)
enddo
enddo
w0(1:Neq,1:1)=w(1:Neq,1:1)
call dgetrs('N',Neq,1,errJ,Neq,epiv,w,Neq,info)
do n=1,Neq
e(n)=w(n,1)
enddo
err=0d0
do n=1,Neq
sc=abs(y0(n))
if(abs(y(n)).gt.y0(n))sc=abs(y(n))
sc=Atol(n)+sc*Rtol(n)
err=err+(e(n)/sc)**2
enddo
err=sqrt(err/dble(Neq))
if(err.ge.1d0)then
call grk(Neq,x0,y0,tf0)
do n=1,Neq
ty(n) = y0(n) + e(n)
enddo
call grk(Neq,x0,ty,tf)
do n=1,Neq
w(n,1) = w0(n,1) + gamma*h*(tf(n)-tf0(n))
enddo
call dgetrs('N',Neq,1,errJ,Neq,epiv,w,Neq,info)
do n=1,Neq
e(n)=w(n,1)
enddo
err=0d0
do n=1,Neq
sc=abs(y0(n))
if(abs(y(n)).gt.y0(n))sc=abs(y(n))
sc=Atol(n)+sc*Rtol(n)
err=err+(e(n)/sc)**2
enddo
err=sqrt(err/dble(Neq))
endif
z0(1:Ns)=z(1:Ns)
h0=h
eta0=eta
return
end subroutine dirk6
subroutine discrete_h(h,ih,th,hmin,hmax)
implicit none
double precision,intent(in)::h,hmin,hmax
integer,intent(out)::ih
double precision,intent(out)::th
double precision::dx,hmin1,hmax1
integer,parameter::imax=200
hmin1=0.10d0*hmin
hmax1=1d0*hmax
dx=(log10(hmax1)-log10(hmin1))/dble(imax)
do ih=0,imax
th=10d0**(-ih*dx+log10(hmax1))
if(th.le.abs(h))exit
enddo
if(h.lt.0d0)th=-th
return
end subroutine discrete_h
subroutine Jacobian(Neq,x,y,fxy,Jac)
implicit none
integer,intent(in)::Neq
double precision,intent(in)::x,y(1:Neq)
double precision,intent(out)::Jac(1:Neq,1:Neq)
external::fxy
integer::n,m
double precision::dy
double precision,parameter::delta=2d-8
double precision,allocatable::f0(:),f1(:),ty(:)
allocate(f0(1:Neq),f1(1:Neq),ty(1:Neq))
f0=0d0; f1=0d0; ty=0d0
call fxy(Neq,x,y,f0)
do m=1,Neq
ty(1:Neq) = y(1:Neq)
dy=sqrt(abs(y(m)))
if(dy.lt.1d0)dy=1d0
dy=delta*dy
ty(m) = ty(m)+dy
call fxy(Neq,x,ty,f1)
do n=1,Neq
Jac(n,m) = (f1(n)-f0(n)) / dy
enddo
enddo
return
end subroutine Jacobian
!=========================================
function egrk(N,x,y,s)
use GBL
implicit none
integer,intent(in)::N,s
double precision,intent(in)::x
double precision,intent(in)::y(1:N)
double precision::egrk
! Solve
! d^2 y(1) / dt^2 = - 0.5 * y(1)
egrk=0d0
if(s.eq.1)then
egrk = y(2)
elseif(s.eq.2)then
egrk = -y(1)/((y(1)**2+y(3)**2)**1.5d0)
elseif(s.eq.3)then
egrk = y(4)
elseif(s.eq.4)then
egrk = -y(3)/((y(1)**2+y(3)**2)**1.5d0)
else
write(6,*)"***Error grk"; stop
endif
if(s.eq.1)count=count+1
return
end function egrk
!===============================
subroutine drkf45(grk,x,h,N,y,xbound,info,tol)
! if h < hmin, propagate forcibly with warning.
!
!-----------------
!info = -9 (maybe path the discontinue points)
! = 0 (Running now)
! = 1 (x reach xbound)
!-----------------
!
implicit none
integer,intent(in)::N
double precision,intent(in)::xbound,tol
double precision,intent(inout)::x,h,y(1:N)
integer,intent(inout)::info
double precision,external::grk
integer::i,j,FLAG,key
double precision::R,delta,tx,Sy,err
double precision,allocatable::tmp(:),K(:,:)
double precision,parameter::hmin=1d-14,hmax=0.5d0
integer,parameter::s=6
double precision::a(1:s,1:s),b1(1:s),b2(1:s),c(1:s),Rc(1:s)
c(1:6)=(/0d0, 0.25d0, 0.375d0,&
0.9230769230769230769230769230769230769231d0, 1d0, 0.5d0/)
a(1:6,1:6)=0d0
a(1,1:6)=(/0d0, 0d0, 0d0, 0d0, 0d0, 0d0/)
a(2,1:6)=(/0.25d0, 0d0, 0d0, 0d0, 0d0, 0d0/)
a(3,1:6)=(/0.09375d0, 0.28125d0, 0d0, 0d0, 0d0, 0d0/)
a(4,1:6)=(/0.8793809740555302685480200273099681383705d0, &
-3.277196176604460628129267182521620391443d0, &
3.320892125625853436504324078288575329995d0, 0d0, 0d0, 0d0/)
a(5,1:6)=(/2.032407407407407407407407407407407407407d0,-8d0, &
7.173489278752436647173489278752436647173d0, &
-0.2058966861598440545808966861598440545809d0, 0d0, 0d0/)
a(6,1:6)=(/-0.2962962962962962962962962962962962962963d0,2d0, &
-1.381676413255360623781676413255360623782d0, &
0.4529727095516569200779727095516569200780d0,-0.275d0,0d0/)
b2(1:6)=(/0.1185185185185185185185185185185185185185d0, 0.d0,&
0.5189863547758284600389863547758284600390d0, &
0.5061314903420166578061314903420166578061d0, &
-0.18d0, 0.03636363636363636363636363636363636363636d0/)
b1(1:6)=(/0.1157407407407407407407407407407407407407d0, 0d0,&
0.5489278752436647173489278752436647173489d0, &
0.5353313840155945419103313840155945419103d0, -0.2d0, 0d0/)
Rc(1:6)=(/0.002777777777777777777777777777777777777778d0,0d0, &
-0.02994152046783625730994152046783625730994d0, &
-0.02919989367357788410419989367357788410420d0, 0.02d0, &
0.03636363636363636363636363636363636363636d0/)
key=0
allocate(tmp(1:N),K(1:s,1:N))
tmp=0d0; K=0d0
if(abs(h).ge.hmax)then
h=sign(1d0,h)*hmax
endif
if(h.ge.abs(xbound-x))h=xbound-x
FLAG=1
if(abs(x-xbound).le.hmin)then
info=1
FLAG=0
endif
do while(FLAG.eq.1)
tx=x
do j=1,s
tx=x+c(j)*h
tmp(1:N)=y(1:N)
do i=1,j-1
tmp(1:N)=tmp(1:N)+K(i,1:N)*a(j,i)
enddo
do i=1,N
K(j,i)=h*grk(N,tx,tmp,i)
enddo
enddo
!step 4
R=0d0
do i=1,N
R=R+(Rc(1)*K(1,i)+Rc(3)*K(3,i)+Rc(4)*K(4,i)+Rc(5)*K(5,i)+Rc(6)*K(6,i))**2d0
enddo
R=abs(dsqrt(R/dble(N))/h)
Sy=0d0
do i=1,N
Sy=Sy+(y(i)*y(i))
enddo
Sy=dsqrt(Sy)
if(Sy.ge.1d0)then
err=tol*Sy
else
err=tol
endif
!step 5
if(R.le.err.or.key.eq.1)then
x=x+h
y(1:N)=y(1:N)+b1(1)*K(1,1:N)+b1(3)*K(3,1:N)+b1(4)*K(4,1:N)+b1(5)*K(5,1:N)
FLAG=0
endif
!step 6
! Avoid zero deviding.
if(R.ge.1d-20)then
delta=(err/(2d0*R))**0.25d0
else
delta=4d0
endif
!step 7
if(delta.le.0.1d0)then
!function changes dramatically.
h=0.1d0*h
elseif(delta.ge.4d0)then
!function changes loosely.
h=4d0*h
else
!function changes moderately.
h=delta*h
endif
!step 8
if(abs(h).ge.hmax)then
h=sign(1d0,h)*hmax
elseif(abs(h).lt.hmin)then
h=sign(1d0,h)*hmin
key=1
endif
!step 9
if(abs(xbound-x).le.abs(h))then
h=xbound-x
if(abs(h).le.hmin)then
info=1
FLAG=0
endif
end if
if(h.le.0d0.and.xbound-x.ge.0d0)then
info=1
FLAG=0
elseif(h.ge.0d0.and.xbound-x.le.0d0)then
info=1
FLAG=0
endif
enddo
if(key.eq.1)then
write(6,'(A,f10.5,A,f10.5)')"Strange point between ",x-h," and ",x
info=-9
endif
deallocate(tmp,K)
return
end subroutine drkf45
きっかけ
きっかけとしてはtwitterで流れてきまして、やってみよう、と思いました。
RKFにもってこいの題材だよ。(みょんみょん度とかは無視してください() pic.twitter.com/VWouH7IhWZ
— みーくん | itmz153 (@math153arclight) 2018年11月6日