ホロノミックな束縛を受けている質点の運動を考えます。
ホロノミックな束縛とは、
”束縛条件が一般化座標と時間のみで決まる方程式によって解析的に表現できるもの”
です。空気抵抗のない単振り子などは、半径(一般化座標)が一定という条件のみで決まるので、ホロノミックな束縛に相当します。
ラグランジュの方程式を基本として考えていきます。
スタートはラグランジアン、ゴールは運動方程式を立てる事です。
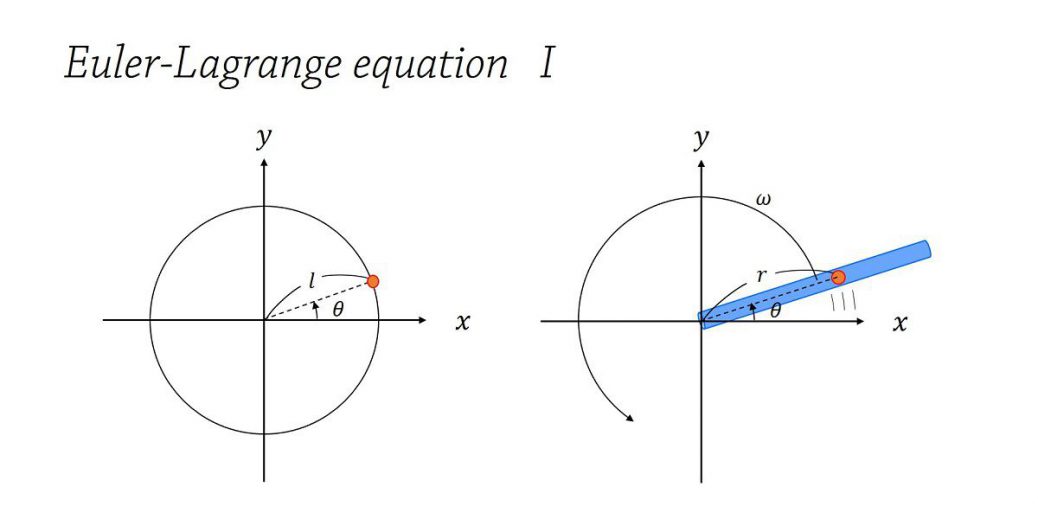
2次元平面上に束縛されている質点
1つの質量を持った質点が、ある軌道上しか動けない運動に対する運動方程式を導きましょう。
ある軌道上しか動けないという条件は、時刻\(t\)における質点の位置\((x,y)\)が、関数\(f(x,y,t)=0\)を満たす動きしか許されないということで表現することが出来ます。
束縛条件を含めた実効的なラグランジアンは, 未定乗数\(\lambda(t)\)を用いて
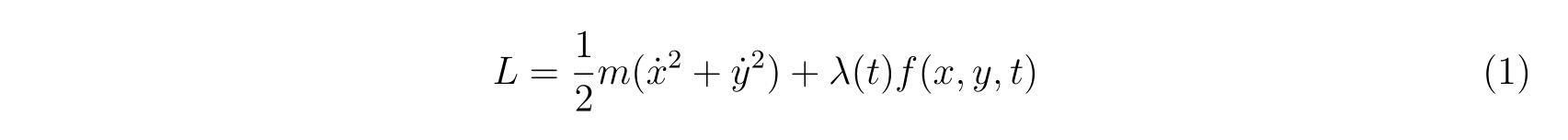
と書けます。ラグランジュの方程式

に代入すれば運動方程式
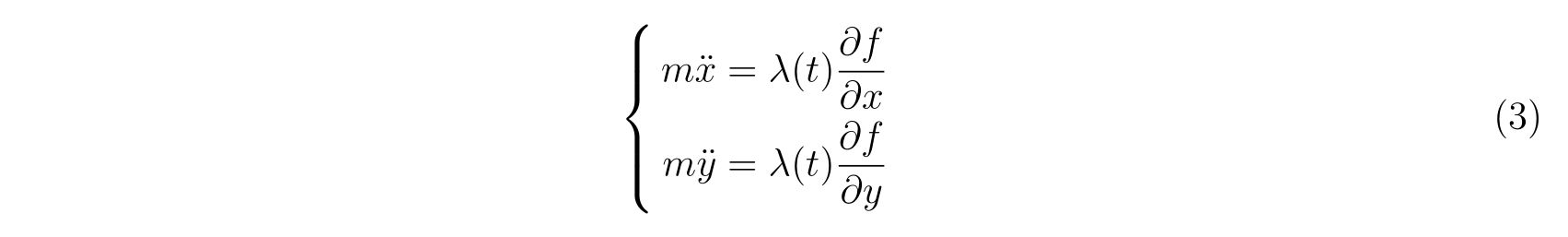
を得ます。
円に束縛されている運動
運動が半径\(l\)の円に束縛されている場合、束縛条件は
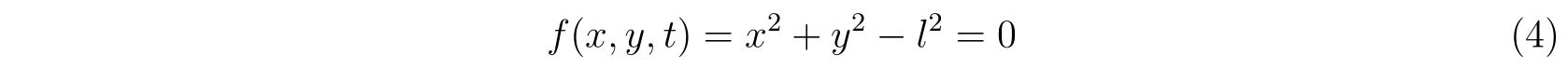
として表現されます。もちろん、\(f(x,y,t)=\sqrt{x^2+y^2}-l=0\)としても構いません。運動は束縛条件の形には依らないからです。
式(3)に代入すると、運動方程式
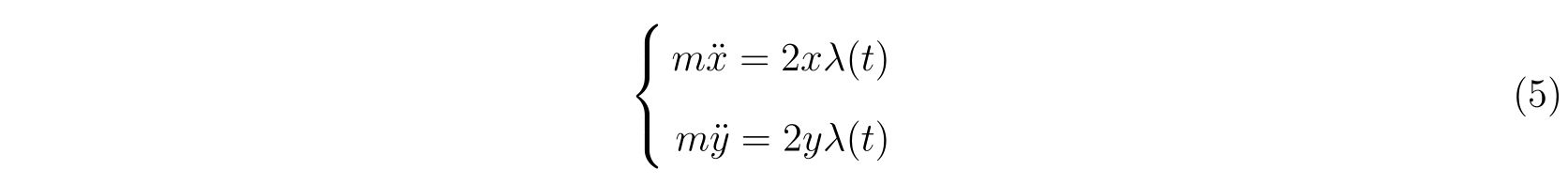
を得ます。方程式(3),(4),(5)の3本の方程式に対して未知の関数は\(x(t),y(t),\lambda(t)\)の3つなので、方程式を立てて\(x(t),y(t)\)を求めることが出来ます。
式(5)の第1式に\(x\)、第2式に\(y\)を掛けて両式を引くと
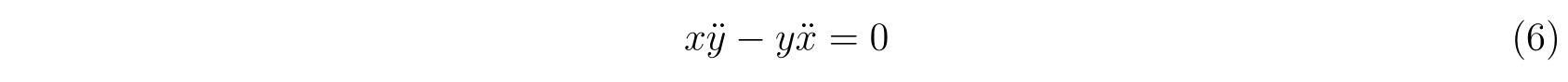
です。変形すれば
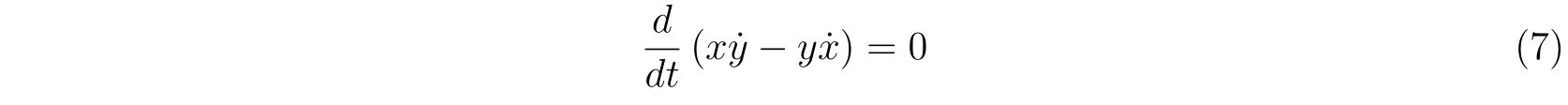
を得ます。どういう解き方でも構わないのですが、半径\(l\)が変わらないことから極座標
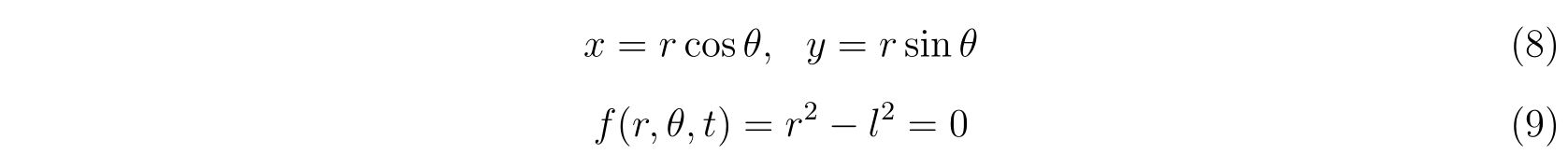
を用いることを考えます。すると、式(7)は
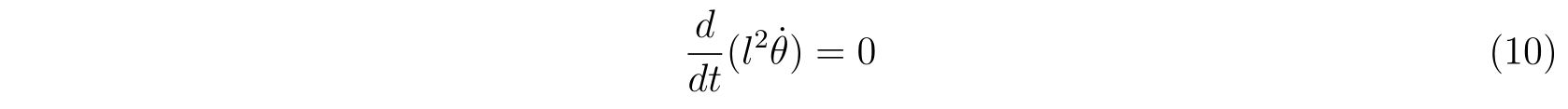
と書けます。よって

ここで、\(\omega,\theta_0\)は初期条件から来まる定数です。よって、解
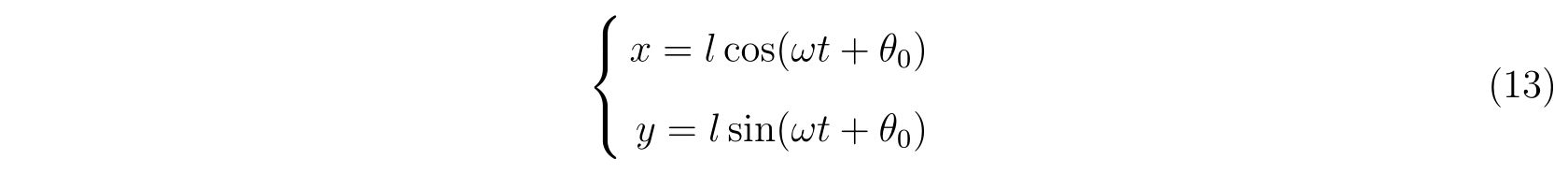
を得ます。ちなみに、\(\lambda(t)\)は

です。
角周波数\(\omega\)で等速回転する筒に入れられた質点が描く軌道
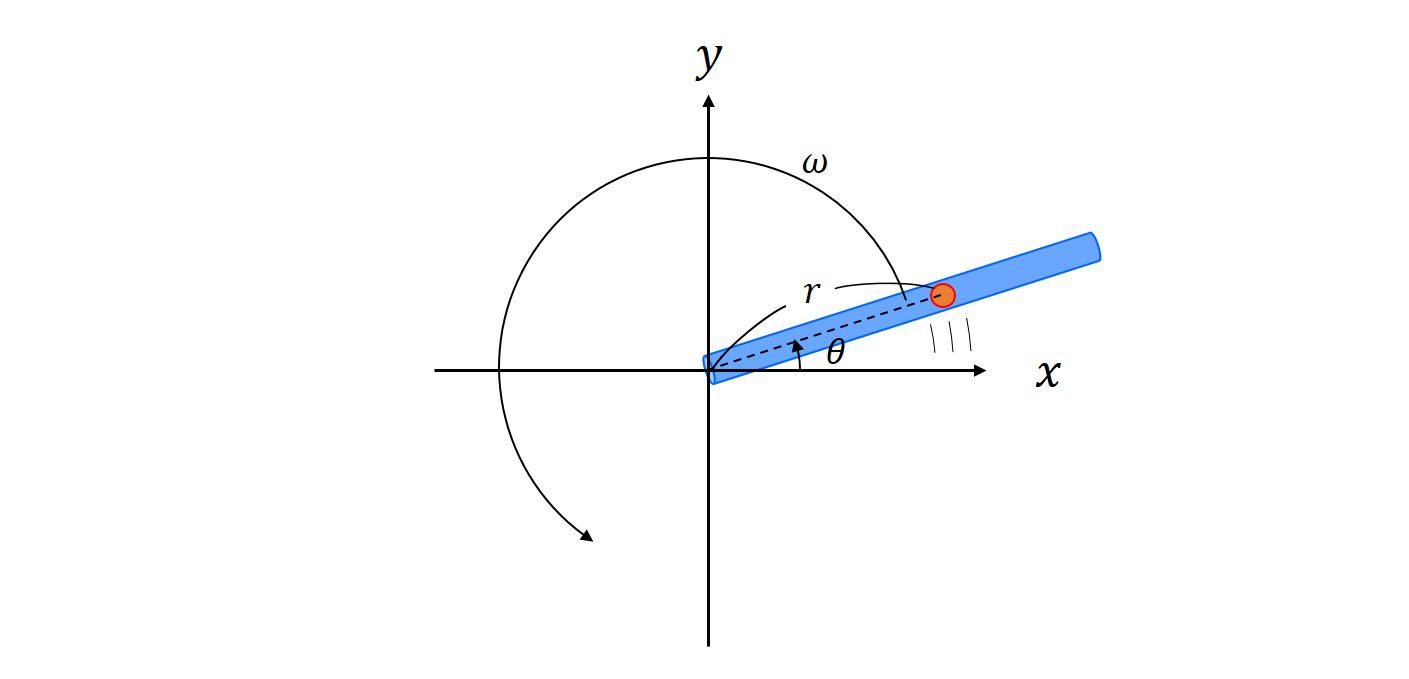
続いて、ホロノミックな束縛条件が時間\(t\)に依存する問題を考えてみましょう。
そこで、角周波数\(\omega\)で等速回転する筒に入れられた質点の軌道を考えます。
極座標表示の方が扱いやすいので、極座標で考えていきます。
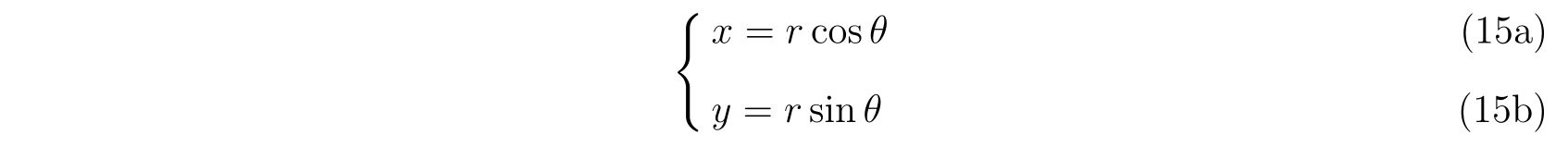
ホロノミックな束縛条件を含めた実効的なラグランジアンは、デカルト座標系のラグランジアンから出発して
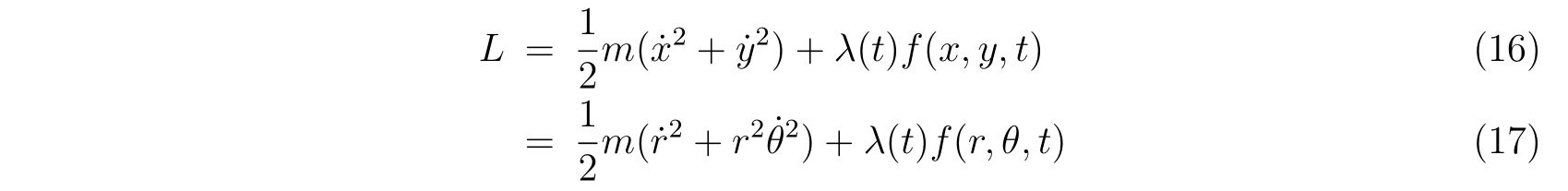
を得ます。ここで、\(\lambda(t)\)は未定乗数を表します。
計算していけば、運動方程式
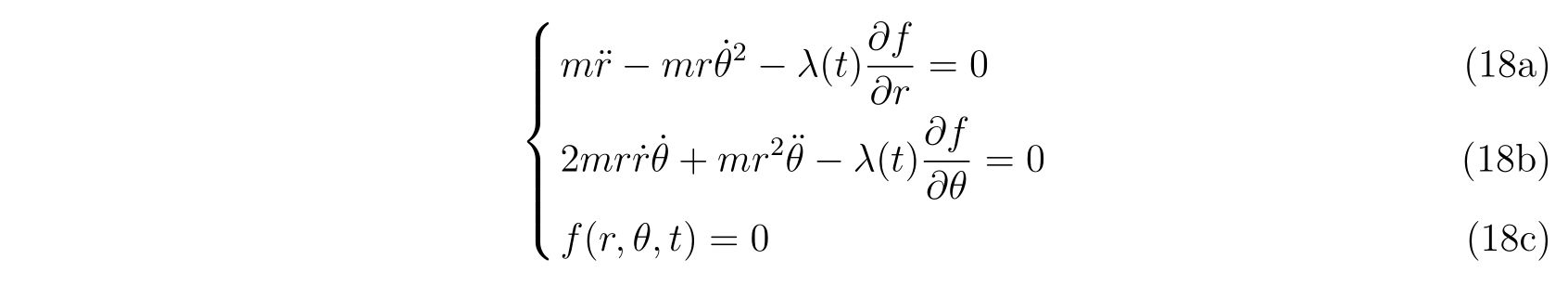
を得ます。方程式(18a),(18b),(18c)の3本の方程式に対して未知の関数は\(r(t),\theta(t),\lambda(t)\)の3つなので、方程式を立てて\(x(t),y(t)\)を求めることが出来ます。
角周波数\(\omega\)で等速回転する筒を表現する関数を考えてみましょう。
筒の上の任意の点\((x,y)\)は、
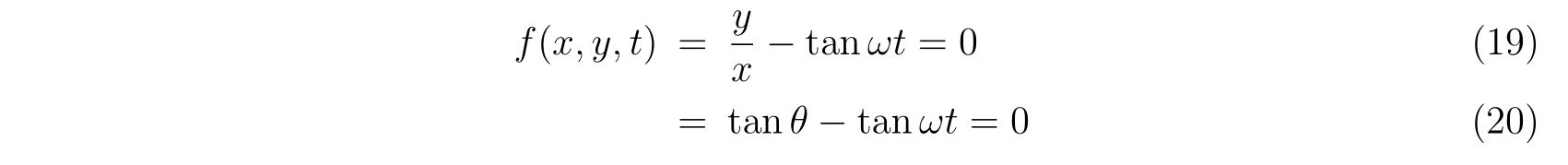
と書くことで表現することが出来ます。よって、束縛条件から
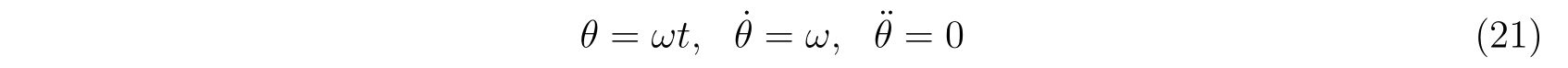
という関係式を得ます。式(21)を運動方程式(18)に代入すれば、
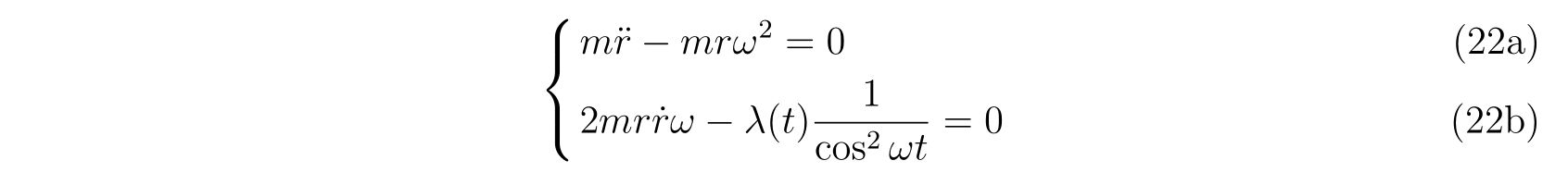
を得ます。式(22a)を解けば、
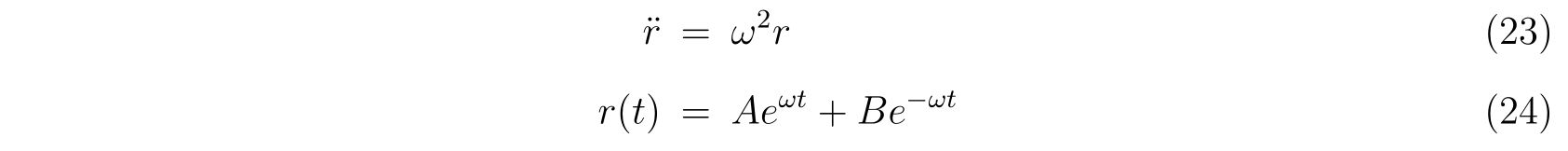
であるので、解
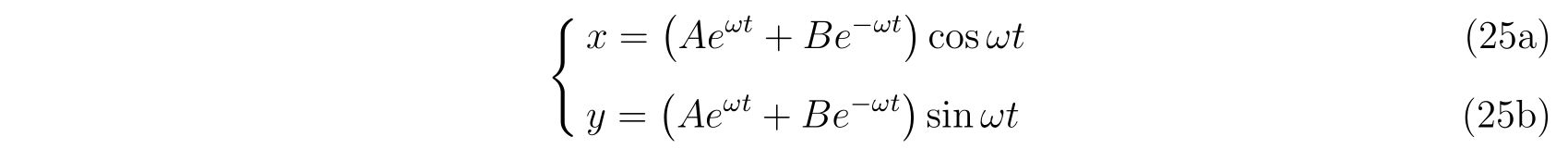
を得ます。ここで、\(A,B\)は初期条件から決まる定数です。
実際に解いてみると、こんなグラフが得られます。
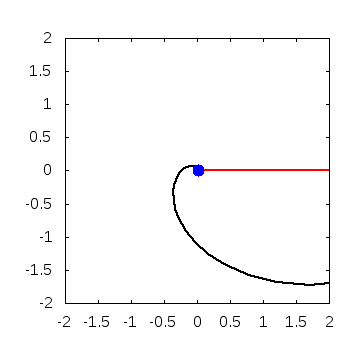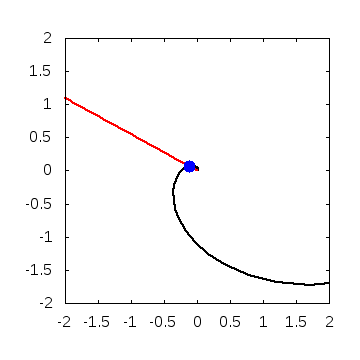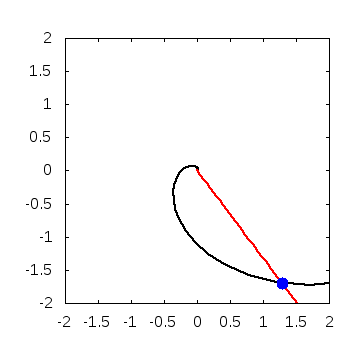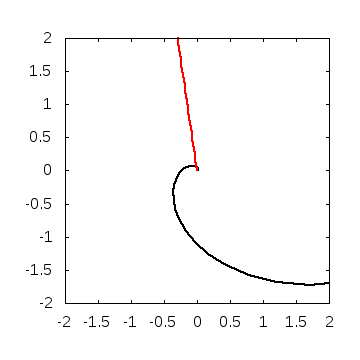
・パラメータ
\(A=0.01, B=0, w=2\)
このページはここで終わりです。
続いて、ポテンシャルが加わる問題である単振り子と束縛条件を考えていきます。
次のリンク
束縛条件下の運動 – ホロノミックな束縛と非保存力
参考文献
田辺行人、品田正樹著『理・工基礎 解析力学』 裳華房