Hyper-dual numbersによる二階偏微分の計算

Hyper-dual numbersと呼ばれる、実数を拡張した考えを導入すると導関数が計算できます。

あらかじめ、引数がHyper-dual numbersである時の数々の関数の定義を実装しておけば、その関数の組み合わせで作られる関数の一階導関数、二階導関数のほぼ厳密な答えを得ることが出来ます。
この考えに従う関数の微分方法は、Forward型の自動微分と呼ばれます。

Dual number
1. Dual numberと導関数
Hyper-dual numbers
参考文献

Dual number

Dual numberという考えがあります[2,3,5]。

これは実数を拡張する、という考えで複素数に似た考え方です。

良く知られている実数の拡張方法の一つは、複素数です。
通常の実数に\(i^2=-1\)を満たす\(i\)という数を付加するのが複素空間です。

拡張の方法は何も\(i\)だけではありません。
例えば、\(\epsilon^2=0, (\epsilon\ne 0)\)を満たす\(\epsilon\)という数を付加することもできます。

この\(\epsilon\)は複素数ではありません。
複素平面上でこの性質を満たす数は無いことからも、この\(\epsilon\)を追加するということは新しい方向への数の拡張です。
実際、複素平面上で\(\epsilon^2=0, (\epsilon\ne 0)\)を満たす数があるのかを探しても
\(
\begin{align}
(a+ib)^2=a^2-b^2+i2ab=0
\end{align}
\)
であるので、これを満たすのは\(a=b=0\)しか存在せず、複素平面上の数ではないことが分かります。

そんな新しい方向\(\epsilon\)の平面で定義された数をDual number(二重数、または双対数)と呼びます。

二重数\(a\)は実数部と非実数部から構成されており、
\(
a=a_0+a_1\epsilon
\)
と書くことが出来ます。ここで、\(a_0, a_1\)は実数であり、 \(\epsilon\)は、虚数単位\(i\)に倣って二重数単位とでも名付けておきましょう。

Dual numberと導関数

二重数は関数の導関数と大きな関係がある事を示しましょう。
テーラー展開を行います。
関数\(f\)の\(x\)周りの展開は刻み幅\(\Delta\)を用いて
\(\displaystyle
f(x+\Delta)=f(x)+f'(x) \Delta+\frac{1}{2!}f^{\prime\prime}(x)\Delta^2+\cdots
\)
と記述することが出来ます。もし仮に\(\Delta\)が純非実数だとしましょう。すなわち、\(\Delta=h\epsilon\)とします。ここで、\(h\)は実数です。テーラー展開の式に代入すれば、
\(
\begin{eqnarray}
f(x+h\epsilon)&=& f(x)+f'(x) h\epsilon+\frac{1}{2!}f^{\prime\prime}(x){h}^2\epsilon^2+\cdots \\
&=& f(x)+f'(x) h\epsilon
\end{eqnarray}
\)
となるわけです。注記しますが、上の式は\(h\)の1次で打ち切っているのではなく、厳密にイコールが成り立っています。
この式が言っているのは、関数\(f(a), (a\text{は二重数})\)を計算し、その非実数部を\(h\)で割ると関数の導関数になっているということです。

二重数の非実数部を取り出す関数\(\text{Dual}\)を定義します。
すると、導関数は
\(\displaystyle
f'(x)=\frac{1}{h}\text{Dual}(f(x+h\epsilon))
\)
として得られます。
言葉で書けば、二重数空間に拡張した\(f(x+h\epsilon)\)を計算すると、その非実数部に導関数が現れる、ということです。

二重数のプログラムはJeffrey Fikeさんによる[4]にありますので、そちらをご参考ください。

Hyper-dual numbers

さて、ここまでで二重数の概念を簡単に説明し、新しい実数の拡張を行いました。
Dual Numberのままでは高階導関数は得られません。なぜなら、導関数の二次以降は二重数の性質\(\epsilon^2=0\)によってゼロになるからです。

そこで、若干工夫します。
Dual Numberを二種類用意することで二階微分を得ることが出来ます[2,3]。
すなわち、
\(\begin{gather}
a=a_0+a_1\epsilon_1+a_2\epsilon_2+a_3\epsilon_1\epsilon_2\\
\epsilon_1^2=\epsilon_2^2=(\epsilon_1\epsilon_2)^2=0,~\epsilon_1\ne 0,~~\epsilon_2\ne 0,~~\epsilon_1\epsilon_2 \ne 0
\end{gather}
\)
と実数を拡張します。この様に拡張した数\(a\)をHyper-dual numbersと呼びます[2,3]。

Hyper-dual numbersの演算

Hyper-dual numbersである
\(
\begin{align}
a&=a_0+a_1\epsilon_1+a_2\epsilon_2+a_3\epsilon_1\epsilon_2\\
b&=b_0+b_1\epsilon_1+b_2\epsilon_2+b_3\epsilon_1\epsilon_2
\end{align}
\)
を用意します。和、積、商はそれぞれ
\(
\begin{align}
a+b&=(a_0+b_0)+(a_1+b_1)\epsilon_1+(a_2+b_2)\epsilon_2+(a_3+b_3)\epsilon_1\epsilon_2\\
ab&=a_0b_0+(a_0b_1+a_1b_0)\epsilon_1+(a_0b_2+a_2b_0)\epsilon_2+(a_0b_3+a_1b_2+a_2b_1+a_3b_0)\epsilon_1\epsilon_2\\
\frac{1}{a}&=\frac{1}{a_0}-\frac{a_1}{a_0^2}\epsilon_1-\frac{a_2}{a_0^2}\epsilon_2+\left(-\frac{a_3}{a_0^2}+\frac{2a_1a_2}{a_0}\right)\epsilon_1\epsilon_2
\end{align}
\)
と定義されます[2]。任意の関数は
\(
f(x)=f(x_0)+x_1f'(x_0)\epsilon_1+x_2f'(x_0)\epsilon_2
+\left(x_3f'(x_0)+x_1x_2f^{\prime\prime}(x_0)\right)\epsilon_1\epsilon_2
\)
として計算することが出来ます。なので、この結果から\(\epsilon_1\epsilon_2\)の係数として関数の二階微分が得られます。

Hyper-dual numbersのプログラム

実際にプログラムを組みましょう。
Hyper-dual numbersの型を持つ変数はFortran90では定義できません。
なので、構造体を利用して自分で型と、演算を定義します。

Fortran90のプログラムは以下の通りになるかと思います。
基本的な四則演算、基本的な初等関数のHyper-dual numbersの演算をモジュールとして書いています。

▼ここクリックでこの場に展開

module Hyperdualmod
implicit none

type Hyperdual
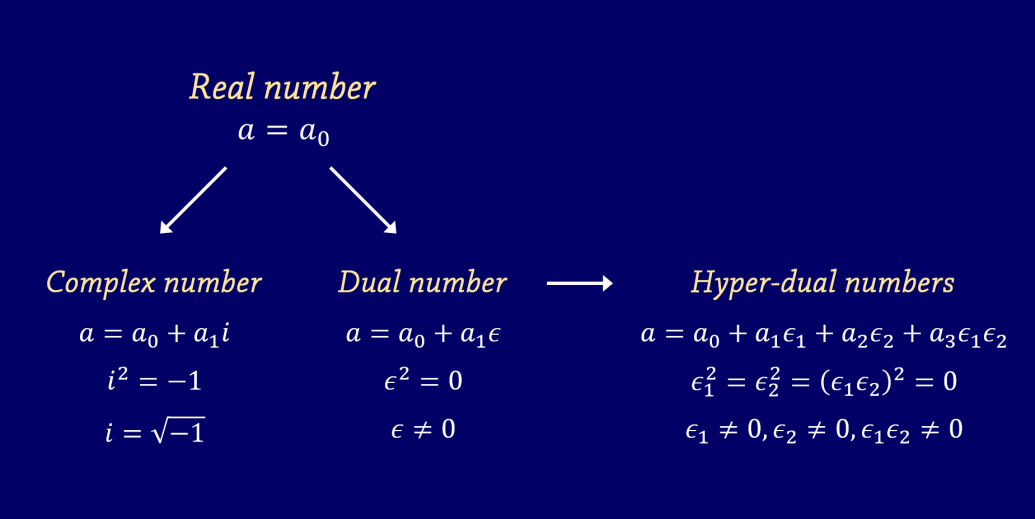
! x = x0 + x1 e1 + x2 e2 + x3 e1 e2
double precision::x0
double precision::x1
double precision::x2
double precision::x3
end type Hyperdual

! Equal =
interface assignment (=)
module procedure Equal_HH
module procedure Equal_HD
end interface assignment (=)

! Unary operator +, -
interface operator (+)
module procedure Plus_HH
end interface operator (+)
interface operator (-)
module procedure Minus_HH
end interface operator (-)

! Addition operator +
interface operator (+)
module procedure Add_HH
module procedure Add_HD
module procedure Add_DH
end interface operator (+)

! Subtraction operator -
interface operator (-)
module procedure Sub_HH
module procedure Sub_HD
module procedure Sub_DH
end interface operator (-)

! Multiply operator -
interface operator (*)
module procedure Mul_HH
module procedure Mul_HD
module procedure Mul_DH
module procedure Mul_HI
module procedure Mul_IH
end interface operator (*)

! Division operator
interface operator (/)
module procedure Div_HH
module procedure Div_HD
module procedure Div_DH
end interface operator (/)

! Power operator
interface operator (**)
module procedure Pow_HI
module procedure Pow_HH
module procedure Pow_HD
module procedure Pow_DH
end interface operator (**)

! Equal logical
interface operator (.eq.)
module procedure eq_HH
module procedure eq_HD
module procedure eq_DH
module procedure eq_HI
module procedure eq_IH
end interface operator (.eq.)

! Not equal logical
interface operator (.ne.)
module procedure ne_HH
module procedure ne_HD
module procedure ne_DH
module procedure ne_HI
module procedure ne_IH
end interface operator (.ne.)

! Less than logical
interface operator (.lt.)
module procedure lt_HH
module procedure lt_HD
module procedure lt_DH
module procedure lt_HI
module procedure lt_IH
end interface operator (.lt.)

! Less or equal logical
interface operator (.le.)
module procedure le_HH
module procedure le_HD
module procedure le_DH
module procedure le_HI
module procedure le_IH
end interface operator (.le.)

! Greater than logical
interface operator (.gt.)
module procedure gt_HH
module procedure gt_HD
module procedure gt_DH
module procedure gt_HI
module procedure gt_IH
end interface operator (.gt.)

! Greater than or equal
interface operator (.ge.)
module procedure ge_HH
module procedure ge_HD
module procedure ge_DH
module procedure ge_HI
module procedure ge_IH
end interface operator (.ge.)

! abs
interface abs
module procedure abs_H
end interface abs

! int
interface int
module procedure int_H
end interface int

! nint
interface nint
module procedure nint_H
end interface nint

! real
interface real
module procedure real_H
end interface real

! sign
interface sign
module procedure sign_HH
module procedure sign_HD
module procedure sign_DH
end interface sign

! sin
interface sin
module procedure sin_H
end interface sin

! cos
interface cos
module procedure cos_H
end interface cos

! tan
interface tan
module procedure tan_H
end interface tan

! sqrt
interface sqrt
module procedure sqrt_H
end interface sqrt

! log
interface log
module procedure log_H
end interface log

! log10
interface log10
module procedure log10_H
end interface log10

! exp
interface exp
module procedure exp_H
end interface exp

! sinh
interface sinh
module procedure sinh_H
end interface sinh

! cosh
interface cosh
module procedure cosh_H
end interface cosh

! tanh
interface tanh
module procedure tanh_H
end interface tanh

! acos
interface acos
module procedure acos_H
end interface acos

! asin
interface asin
module procedure asin_H
end interface asin

! atan
interface atan
module procedure atan_H
end interface atan

! atan2
interface atan2
module procedure atan2_H
end interface atan2

contains
subroutine Equal_HH(res, inp)
implicit none
type(Hyperdual),intent(out) :: res
type(Hyperdual),intent(in) :: inp
res%x0 = inp%x0
res%x1 = inp%x1
res%x2 = inp%x2
res%x3 = inp%x3
end subroutine Equal_HH
subroutine Equal_HD(res, inp)
implicit none
type(Hyperdual),intent(out) :: res
double precision,intent(in) :: inp
res%x0 = inp
res%x1 = 0d0
res%x2 = 0d0
res%x3 = 0d0
end subroutine Equal_HD

!---------------------------------------

function Plus_HH(t1) result (t2)
type(Hyperdual),intent(in) :: t1
type(Hyperdual) :: t2
t2%x0 = t1%x0
t2%x1 = t1%x1
t2%x2 = t1%x2
t2%x3 = t1%x3
end function Plus_HH
function Minus_HH(t1) result (t2)
type(Hyperdual),intent(in) :: t1
type(Hyperdual) :: t2
t2%x0 = -t1%x0
t2%x1 = -t1%x1
t2%x2 = -t1%x2
t2%x3 = -t1%x3
end function Minus_HH

!---------------------------------------

function Add_HH(t1,t2) result (t3)
type(Hyperdual), intent(in) :: t1,t2
type(Hyperdual) :: t3
t3%x0 = t1%x0 + t2%x0
t3%x1 = t1%x1 + t2%x1
t3%x2 = t1%x2 + t2%x2
t3%x3 = t1%x3 + t2%x3
end function Add_HH
function Add_HD(t1,t2) result (t3)
type(Hyperdual), intent(in) :: t1
double precision,intent(in) :: t2
type(Hyperdual) :: t3
t3%x0 = t1%x0 + t2
t3%x1 = t1%x1
t3%x2 = t1%x2
t3%x3 = t1%x3
end function Add_HD
function Add_DH(t1,t2) result (t3)
double precision,intent(in) :: t1
type(Hyperdual), intent(in) :: t2
type(Hyperdual) :: t3
t3%x0 = t1 + t2%x0
t3%x1 = t2%x1
t3%x2 = t2%x2
t3%x3 = t2%x3
end function Add_DH

!---------------------------------------

function Sub_HH(t1,t2) result (t3)
type(Hyperdual), intent(in) :: t1,t2
type(Hyperdual) :: t3
t3%x0 = t1%x0 - t2%x0
t3%x1 = t1%x1 - t2%x1
t3%x2 = t1%x2 - t2%x2
t3%x3 = t1%x3 - t2%x3
end function Sub_HH
function Sub_HD(t1,t2) result (t3)
type(Hyperdual), intent(in) :: t1
double precision,intent(in) :: t2
type(Hyperdual) :: t3
t3%x0 = t1%x0 - t2
t3%x1 = t1%x1
t3%x2 = t1%x2
t3%x3 = t1%x3
end function Sub_HD
function Sub_DH(t1,t2) result (t3)
double precision,intent(in) :: t1
type(Hyperdual), intent(in) :: t2
type(Hyperdual) :: t3
t3%x0 = t1 - t2%x0
t3%x1 = t2%x1
t3%x2 = t2%x2
t3%x3 = t2%x3
end function Sub_DH

!---------------------------------------

function Mul_HH(t1,t2) result (t3)
type(Hyperdual), intent(in) :: t1,t2
type(Hyperdual) :: t3
t3%x0 = t1%x0 * t2%x0
t3%x1 = t1%x0 * t2%x1 + t1%x1 * t2%x0
t3%x2 = t1%x0 * t2%x2 + t1%x2 * t2%x0
t3%x3 = t1%x0 * t2%x3 + t1%x1 * t2%x2 &
+ t1%x2 * t2%x1 + t1%x3 * t2%x0
end function Mul_HH
function Mul_HD(t1,t2) result (t3)
type(Hyperdual), intent(in) :: t1
double precision,intent(in) :: t2
type(Hyperdual) :: t3
t3%x0 = t1%x0 * t2
t3%x1 = t1%x1 * t2
t3%x2 = t1%x2 * t2
t3%x3 = t1%x3 * t2
end function Mul_HD
function Mul_DH(t1,t2) result (t3)
double precision,intent(in) :: t1
type(Hyperdual), intent(in) :: t2
type(Hyperdual) :: t3
t3%x0 = t1 * t2%x0
t3%x1 = t1 * t2%x1
t3%x2 = t1 * t2%x2
t3%x3 = t1 * t2%x3
end function Mul_DH
function Mul_HI(t1,t2) result (t3)
type(Hyperdual), intent(in) :: t1
integer ,intent(in) :: t2
type(Hyperdual) :: t3
t3%x0 = t1%x0 * t2
t3%x1 = t1%x1 * t2
t3%x2 = t1%x2 * t2
t3%x3 = t1%x3 * t2
end function Mul_HI
function Mul_IH(t1,t2) result (t3)
integer ,intent(in) :: t1
type(Hyperdual), intent(in) :: t2
type(Hyperdual) :: t3
t3%x0 = t1 * t2%x0
t3%x1 = t1 * t2%x1
t3%x2 = t1 * t2%x2
t3%x3 = t1 * t2%x3
end function Mul_IH

!-----------------------------------------

function Div_HH(t1,t2) result (t3)
type(Hyperdual), intent(in) :: t1,t2
type(Hyperdual) :: s2, t3
double precision:: u2
s2%x0 = 1d0/t2%x0
u2 = s2%x0 * s2%x0
s2%x1 = - t2%x1 * u2
s2%x2 = - t2%x2 * u2
s2%x3 = (- t2%x3 + 2d0 * t2%x1 * t2%x2 * s2%x0) * u2
t3%x0 = t1%x0 * s2%x0
t3%x1 = t1%x0 * s2%x1 + t1%x1 * s2%x0
t3%x2 = t1%x0 * s2%x2 + t1%x2 * s2%x0
t3%x3 = t1%x0 * s2%x3 + t1%x1 * s2%x2 &
+ t1%x2 * s2%x1 + t1%x3 * s2%x0
end function Div_HH
function Div_HD(t1,t2) result (t3)
type(Hyperdual), intent(in) :: t1
double precision,intent(in) :: t2
type(Hyperdual) :: t3
double precision :: s2
s2 = 1d0/t2
t3%x0 = t1%x0 * s2
t3%x1 = t1%x1 * s2
t3%x2 = t1%x2 * s2
t3%x3 = t1%x3 * s2
end function Div_HD
function Div_DH(t1,t2) result (t3)
double precision,intent(in) :: t1
type(Hyperdual), intent(in) :: t2
type(Hyperdual) :: s2, t3
double precision :: u2
s2%x0 = 1d0/t2%x0
u2 = s2%x0 * s2%x0
s2%x1 = - t2%x1 * u2
s2%x2 = - t2%x2 * u2
s2%x3 = (- t2%x3 + 2d0 * t2%x1 * t2%x2 * s2%x0) * u2
t3%x0 = t1 * s2%x0
t3%x1 = t1 * s2%x1
t3%x2 = t1 * s2%x2
t3%x3 = t1 * s2%x3
end function Div_DH

!--------------------------

function Pow_HI(t1,t2) result (t3)
type(Hyperdual),intent(in) :: t1
integer,intent(in) :: t2
integer :: i, m
type(Hyperdual) :: t3
t3 = 1d0
m = abs(t2)
do i=1,m
t3 = t3*t1
enddo
if(t2 .lt. 0) t3 = 1d0/t3
end function Pow_HI
function Pow_HH(t1,t2) result (t3)
type(Hyperdual),intent(in) :: t1, t2
type(Hyperdual) :: t3, v4
v4 = log_H(t1)
t3 = exp_H(t2*v4)
end function Pow_HH
function Pow_DH(t1,t2) result (t3)
double precision,intent(in) :: t1
type(Hyperdual), intent(in) :: t2
double precision :: v4
type(Hyperdual) :: t3
v4 = log(t1)
t3 = exp_H(t2*v4)
end function Pow_DH
function Pow_HD(t1,t2) result (t3)
type(Hyperdual), intent(in) :: t1
double precision,intent(in) :: t2
type(Hyperdual) :: t3
double precision,parameter :: tol=1d-30
double precision :: tx, p1, p2
tx = t1%x0
if(abs(tx) .lt. tol) then
if(tx .ge. 0d0) then
tx = tol
else
tx = -tol
endif
endif
p1 = t2*(tx**(t2-1d0))
p2 = t2*(t2-1d0)*(tx**(t2-2d0))
t3%x0 = (t1%x0)**t2
t3%x1 = t1%x1 *p1
t3%x2 = t1%x2 *p1
t3%x3 = t1%x3 *p1 + t1%x1 * t1%x2 *p2
end function Pow_HD

!---------------------------------

! .eq.
logical function eq_HH(lhs, rhs)
type(Hyperdual),intent(in)::lhs, rhs
eq_HH = lhs%x0 == rhs%x0
end function eq_HH
logical function eq_HD(lhs, rhs)
type(Hyperdual),intent(in)::lhs
double precision,intent(in)::rhs
eq_HD = lhs%x0 == rhs
end function eq_HD
logical function eq_DH(lhs, rhs)
double precision,intent(in)::lhs
type(Hyperdual),intent(in)::rhs
eq_DH = lhs == rhs%x0
end function eq_DH
logical function eq_HI(lhs, rhs)
type(Hyperdual),intent(in)::lhs
integer,intent(in)::rhs
eq_HI = lhs%x0 == rhs
end function eq_HI
logical function eq_IH(lhs, rhs)
integer,intent(in)::lhs
type(Hyperdual),intent(in)::rhs
eq_IH = lhs == rhs%x0
end function eq_IH

!------------------------

! .ne.
logical function ne_HH(lhs, rhs)
type(Hyperdual),intent(in)::lhs, rhs
ne_HH = lhs%x0 /= rhs%x0
end function ne_HH
logical function ne_HD(lhs, rhs)
type(Hyperdual),intent(in)::lhs
double precision,intent(in)::rhs
ne_HD = lhs%x0 /= rhs
end function ne_HD
logical function ne_DH(lhs, rhs)
double precision,intent(in)::lhs
type(Hyperdual),intent(in)::rhs
ne_DH = lhs /= rhs%x0
end function ne_DH
logical function ne_HI(lhs, rhs)
type(Hyperdual),intent(in)::lhs
integer,intent(in)::rhs
ne_HI = lhs%x0 /= rhs
end function ne_HI
logical function ne_IH(lhs, rhs)
integer,intent(in)::lhs
type(Hyperdual),intent(in)::rhs
ne_IH = lhs /= rhs%x0
end function ne_IH

!-------------------

! .lt.
logical function lt_HH(lhs, rhs)
type(Hyperdual),intent(in)::lhs, rhs
lt_HH = lhs%x0 < rhs%x0
end function lt_HH
logical function lt_HD(lhs, rhs)
type(Hyperdual),intent(in)::lhs
double precision,intent(in)::rhs
lt_HD = lhs%x0 < rhs
end function lt_HD
logical function lt_DH(lhs, rhs)
double precision,intent(in)::lhs
type(Hyperdual),intent(in)::rhs
lt_DH = lhs < rhs%x0
end function lt_DH
logical function lt_HI(lhs, rhs)
type(Hyperdual),intent(in)::lhs
integer,intent(in)::rhs
lt_HI = lhs%x0 < rhs
end function lt_HI
logical function lt_IH(lhs, rhs)
integer,intent(in)::lhs
type(Hyperdual),intent(in)::rhs
lt_IH = lhs < rhs%x0
end function lt_IH

!-------------------

!.le.
logical function le_HH(lhs, rhs)
type(Hyperdual),intent(in)::lhs, rhs
le_HH = lhs%x0 <= rhs%x0
end function le_HH
logical function le_HD(lhs, rhs)
type(Hyperdual),intent(in)::lhs
double precision,intent(in)::rhs
le_HD = lhs%x0 <= rhs
end function le_HD
logical function le_DH(lhs, rhs)
double precision,intent(in)::lhs
type(Hyperdual),intent(in)::rhs
le_DH = lhs <= rhs%x0
end function le_DH
logical function le_HI(lhs, rhs)
type(Hyperdual),intent(in)::lhs
integer,intent(in)::rhs
le_HI = lhs%x0 <= rhs
end function le_HI
logical function le_IH(lhs, rhs)
integer,intent(in)::lhs
type(Hyperdual),intent(in)::rhs
le_IH = lhs <= rhs%x0
end function le_IH

!-------------------

! .gt.
logical function gt_HH(lhs, rhs)
type(Hyperdual),intent(in)::lhs, rhs
gt_HH = lhs%x0 > rhs%x0
end function gt_HH
logical function gt_HD(lhs, rhs)
type(Hyperdual),intent(in)::lhs
double precision,intent(in)::rhs
gt_HD = lhs%x0 > rhs
end function gt_HD
logical function gt_DH(lhs, rhs)
double precision,intent(in)::lhs
type(Hyperdual),intent(in)::rhs
gt_DH = lhs > rhs%x0
end function gt_DH
logical function gt_HI(lhs, rhs)
type(Hyperdual),intent(in)::lhs
integer,intent(in)::rhs
gt_HI = lhs%x0 > rhs
end function gt_HI
logical function gt_IH(lhs, rhs)
integer,intent(in)::lhs
type(Hyperdual),intent(in)::rhs
gt_IH = lhs > rhs%x0
end function gt_IH

!----------------------------

! .ge.
logical function ge_HH(lhs, rhs)
type(Hyperdual),intent(in)::lhs, rhs
ge_HH = lhs%x0 >= rhs%x0
end function ge_HH
logical function ge_HD(lhs, rhs)
type(Hyperdual),intent(in)::lhs
double precision,intent(in)::rhs
ge_HD = lhs%x0 >= rhs
end function ge_HD
logical function ge_DH(lhs, rhs)
double precision,intent(in)::lhs
type(Hyperdual),intent(in)::rhs
ge_DH = lhs >= rhs%x0
end function ge_DH
logical function ge_HI(lhs, rhs)
type(Hyperdual),intent(in)::lhs
integer,intent(in)::rhs
ge_HI = lhs%x0 >= rhs
end function ge_HI
logical function ge_IH(lhs, rhs)
integer,intent(in)::lhs
type(Hyperdual),intent(in)::rhs
ge_IH = lhs >= rhs%x0
end function ge_IH

!------------------------------

! Absolute
function abs_H(t1) result (t2)
type(Hyperdual),intent(in)::t1
type(Hyperdual)::t2
if(t1%x0 .ge. 0d0) then
t2%x0 = t1%x0
t2%x1 = t1%x1
t2%x2 = t1%x2
t2%x3 = t1%x3
else
t2%x0 = -t1%x0
t2%x1 = -t1%x1
t2%x2 = -t1%x2
t2%x3 = -t1%x3
endif
end function abs_H

! Int
function int_H(t1) result (t2)
type(Hyperdual),intent(in)::t1
integer :: t2
t2 = int(t1%x0)
end function int_H

! Nearest int
function nint_H(t1) result (t2)
type(Hyperdual),intent(in)::t1
integer :: t2
t2 = nint(t1%x0)
end function nint_H

! Real
function real_H(t1) result (t2)
type(Hyperdual),intent(in)::t1
double precision::t2
t2 = t1%x0
end function real_H

! Sign
function sign_HH(t1,t2) result (t3)
type(Hyperdual),intent(in)::t1, t2
type(Hyperdual)::t3
double precision::ssign
if(t2%x0 .lt. 0d0) then
ssign = -1d0
else
ssign = 1d0
endif
t3 = ssign*t1
end function sign_HH
function sign_HD(t1,t2) result (t3)
type(Hyperdual),intent(in)::t1
double precision,intent(in) :: t2
type(Hyperdual)::t3
double precision::ssign
if(t2 .lt. 0d0) then
ssign = -1d0
else
ssign = 1d0
endif
t3 = ssign*t1
end function sign_HD
function sign_DH(t1,t2) result (t3)
double precision,intent(in) :: t1
type(Hyperdual),intent(in)::t2
type(Hyperdual)::t3
double precision :: ssign
if(t2%x0 .lt. 0d0) then
ssign = -1d0
else
ssign = 1d0
endif
t3 = ssign*t1
end function sign_DH

! sin
function sin_H(t1) result (t2)
type(Hyperdual),intent(in)::t1
type(Hyperdual)::t2
double precision::df0, df1, df2
df0 = sin(t1%x0)
df1 = cos(t1%x0)
df2 = -df0
t2%x0 = df0
t2%x1 = t1%x1 * df1
t2%x2 = t1%x2 * df1
t2%x3 = t1%x3 * df1 + t1%x1 * t1%x2 * df2
end function sin_H

! cos
function cos_H(t1) result (t2)
type(Hyperdual),intent(in)::t1
type(Hyperdual)::t2
double precision::df0, df1, df2
df0 = cos(t1%x0)
df1 = -sin(t1%x0)
df2 = -df0
t2%x0 = df0
t2%x1 = t1%x1 * df1
t2%x2 = t1%x2 * df1
t2%x3 = t1%x3 * df1 + t1%x1 * t1%x2 * df2
end function cos_H

! tan
function tan_H(t1) result (t2)
type(Hyperdual),intent(in)::t1
type(Hyperdual)::t2
double precision::df0, df1, df2
df0 = tan(t1%x0)
df1 = 1d0 + df0*df0
df2 = 2d0 * df0 * df1
t2%x0 = df0
t2%x1 = t1%x1 * df1
t2%x2 = t1%x2 * df1
t2%x3 = t1%x3 * df1 + t1%x1 * t1%x2 * df2
end function tan_H

! sqrt
function sqrt_H(t1) result (t2)
type(Hyperdual),intent(in)::t1
type(Hyperdual)::t2
double precision::df0, df1, df2
df0 = sqrt(t1%x0)
df1 = 1d0/(2*df0)
df2 = -2d0*df1*df1*df1
t2%x0 = df0
t2%x1 = t1%x1 * df1
t2%x2 = t1%x2 * df1
t2%x3 = t1%x3 * df1 + t1%x1 * t1%x2 * df2
end function sqrt_H

! log
function log_H(t1) result (t2)
type(Hyperdual),intent(in)::t1
type(Hyperdual)::t2
double precision::df0, df1, df2
df0 = log(t1%x0)
df1 = 1d0/t1%x0
df2 = -df1*df1
t2%x0 = df0
t2%x1 = t1%x1 * df1
t2%x2 = t1%x2 * df1
t2%x3 = t1%x3 * df1 + t1%x1 * t1%x2 * df2
end function log_H

! log10
function log10_H(t1) result (t2)
type(Hyperdual),intent(in)::t1
type(Hyperdual)::t2
double precision::df0, df1, df2
df0 = log10(t1%x0)
df1 = 1d0/(log(10d0)*t1%x0)
df2 = -df1/(t1%x0)
t2%x0 = df0
t2%x1 = t1%x1 * df1
t2%x2 = t1%x2 * df1
t2%x3 = t1%x3 * df1 + t1%x1 * t1%x2 * df2
end function log10_H

! exp
function exp_H(t1) result (t2)
type(Hyperdual),intent(in)::t1
type(Hyperdual)::t2
double precision::df0, df1, df2
df0 = exp(t1%x0)
df1 = df0
df2 = df1
t2%x0 = df0
t2%x1 = t1%x1 * df1
t2%x2 = t1%x2 * df1
t2%x3 = t1%x3 * df1 + t1%x1 * t1%x2 * df2
end function exp_H

! sinh
function sinh_H(t1) result (t2)
type(Hyperdual),intent(in)::t1
type(Hyperdual)::u1, u2, t2
u1 = exp(t1)
u2 = exp(-t1)
t2 = 0.5d0*(u1-u2)
end function sinh_H

! cosh
function cosh_H(t1) result (t2)
type(Hyperdual),intent(in)::t1
type(Hyperdual)::u1, u2, t2
u1 = exp(t1)
u2 = exp(-t1)
t2 = 0.5d0*(u1+u2)
end function cosh_H

! tanh
function tanh_H(t1) result (t2)
type(Hyperdual),intent(in)::t1
type(Hyperdual)::u1, u2, t2
u1 = exp(t1)
u2 = exp(-t1)
t2 = (u1-u2)/(u1+u2)
end function tanh_H

! acos
function acos_H(t1) result (t2)
type(Hyperdual),intent(in)::t1
type(Hyperdual)::t2
double precision::df0, df1, df2
df0 = acos(t1%x0)
df1 = -1d0/sqrt(1d0 - t1%x0*t1%x0)
df2 = df1*df1*df1 * t1%x0
t2%x0 = df0
t2%x1 = t1%x1 * df1
t2%x2 = t1%x2 * df1
t2%x3 = t1%x3 * df1 + t1%x1 * t1%x2 * df2
end function acos_H

! asin
function asin_H(t1) result (t2)
type(Hyperdual),intent(in)::t1
type(Hyperdual)::t2
double precision::df0, df1, df2
df0 = asin(t1%x0)
df1 = 1d0/sqrt(1d0 - t1%x0*t1%x0)
df2 = df1*df1*df1 * t1%x0
t2%x0 = df0
t2%x1 = t1%x1 * df1
t2%x2 = t1%x2 * df1
t2%x3 = t1%x3 * df1 + t1%x1 * t1%x2 * df2
end function asin_H

! atan
function atan_H(t1) result (t2)
type(Hyperdual),intent(in)::t1
type(Hyperdual)::t2
double precision::df0, df1, df2
df0 = atan(t1%x0)
df1 = 1d0/(1.0d0 + t1%x0*t1%x0)
df2 = -2d0*t1%x0*df1*df1
t2%x0 = df0
t2%x1 = t1%x1 * df1
t2%x2 = t1%x2 * df1
t2%x3 = t1%x3 * df1 + t1%x1 * t1%x2 * df2
end function atan_H

! atan2
function atan2_H(t1, t2) result (t3)
type(Hyperdual),intent(in)::t1, t2
type(Hyperdual)::t3
double precision::a, b, c, d, e, f, g, h
double precision::df0, r2, fx, fy
!y0 y1 y2 y3
a = t1%x0; b = t1%x1; c = t1%x2; d = t1%x3
!x0 x1 x2 x3
e = t2%x0; f = t2%x1; g = t2%x2; h = t2%x3
r2 = a*a + e*e
fx = -e/r2
fy = a/r2
df0 = atan2(a,e)
t3%x0 = df0
t3%x1 = f*fx + b*fy
t3%x2 = g*fx + c*fy
t3%x3 = h*fx + d*fy + (f*c+g*b)*(fx-fy)*(fx+fy) - 2d0*(f*g+b*c)*fx*fy
end function atan2_H
end module Hyperdualmod

上のモジュールと下のメインプログラムを一緒にコンパイルすることにより、関数の二階微分が得られます。

例として
2変数関数
\(\displaystyle
f(x,y)=\frac{\text{ln}(xy^2)e^x}{\sqrt{\sin^3{x}+\sin^3{y}}}
\)
の偏微分
\(\begin{align}
\frac{\partial f}{\partial x},~~\frac{\partial f}{\partial y},~~\frac{\partial^2 f}{\partial x\partial y}
\end{align}
\)
を得ることを考えます。
\(
f(x+1\epsilon_1,y+1\epsilon_2)
\)
を計算すると
\(
f(x+1\epsilon_1,y+1\epsilon_2)=a_0+a_1\epsilon_1+a_2\epsilon_2+a_3\epsilon_1\epsilon_2
\)
のように実数係数\(a_0, a_1, a_2, a_3\)が得られます。
すると、
\(
\begin{align}
\frac{\partial f}{\partial x}=a_1 \\
\frac{\partial f}{\partial y}=a_2 \\
\frac{\partial^2 f}{\partial x\partial y} =a_3
\end{align}
\)
として偏微分が得られます。
ちなみに、二階微分が欲しい場合は
\(
f(x+1\epsilon_1+1\epsilon_2, y)
\)
を考えると
\(
\begin{align}
\frac{\partial f}{\partial x}=a_1 \\
\frac{\partial f}{\partial x}=a_2 \\
\frac{\partial^2 f}{\partial x^2} =a_3
\end{align}
\)
として得られます。\(a_1,~a_2\)はどちらを採用しても構いません。

プログラムでは変数の型Hyperdualを持つ入力変数を\(\text{xH,yH}\),出力を\(\text{rH}\)と置いています。

program main
use Hyperdualmod
implicit none
type(Hyperdual)::xH,yH,rH

xH%x0 = 0.3d0 ! real part
xH%x1 = 1d0 ! unreal part \epsilon_1
xH%x2 = 0d0 ! unreal part \epsilon_2
xH%x3 = 0d0 ! unreal part \epsilon_1\epsilon_2

yH%x0 = 0.4d0 ! real part
yH%x1 = 0d0 ! unreal part \epsilon_1
yH%x2 = 1d0 ! unreal part \epsilon_2
yH%x3 = 0d0 ! unreal part \epsilon_1\epsilon_2

write(6,'(4f23.16)')xH%x0,xH%x1,xH%x2,xH%x3
write(6,'(4f23.16)')yH%x0,yH%x1,yH%x2,yH%x3

rH = log(xH*yH**2)*exp(xH)/sqrt(sin(xH)**3+cos(yH)**3)
!rH = asin(2d0*xH)*acos(yH)/atan(xH*yH)
!rH = xH**yH

write(6,'(4f23.16)')rH%x0,rH%x1,rH%x2,rH%x3

stop
end program main

ヘッセ行列

二階偏微分の計算が出来たので、ヘッセ行列が簡単に計算できます。
ルーチンを作れば、以下の通りになるかと思います。
下のプログラムは3変数関数
\(\displaystyle
f(x,y,z)=\exp(xy)\tan(z)
\)
の\(x=-2,~y=3,~z=1\)におけるヘッセ行列を計算します。

program main
use Hyperdualmod
implicit none
integer::N
double precision::x,y,z,f
double precision,allocatable::nabla(:),Hesse(:,:)
double precision,allocatable::w(:)
external::func

N=3

allocate(nabla(1:N),Hesse(1:N,1:N))
nabla=0d0
Hesse=0d0
allocate(w(1:N))
w=0d0

x = -2d0
y = 3d0
z = 1d0
w(1) = x
w(2) = y
w(3) = z
call Hessian(N,w,func,nabla,Hesse)

f=exp(x*y)*tan(z)
write(6,'(1e24.16)')nabla(1)
write(6,'(1e24.16)')y*f
write(6,'(1e24.16)')nabla(2)
write(6,'(1e24.16)')x*f
write(6,'(1e24.16)')nabla(3)
write(6,'(1e24.16)')exp(x*y)/(cos(z)**2)
write(6,'(3e24.16)')Hesse(1,1:3)
write(6,'(3e24.16)')f*y**2, f*(1+x*y), f*y/(cos(z)*sin(z))
write(6,'(3e24.16)')Hesse(2,1:3)
write(6,'(3e24.16)')f*(1+x*y), x**2*f, f*x/(cos(z)*sin(z))
write(6,'(3e24.16)')Hesse(3,1:3)
write(6,'(3e24.16)')f*y/(cos(z)*sin(z)), f*x/(cos(z)*sin(z)), f*2d0/(cos(z)**2)

stop
end program main

subroutine func(N,x,f)
use Hyperdualmod
implicit none
integer::N
type(Hyperdual),intent(in)::x(1:N)
type(Hyperdual),intent(out)::f

f = exp(x(1)*x(2))*tan(x(3))

return
end subroutine func

subroutine Hessian(N,x,func,nabla,Hesse)
use Hyperdualmod
implicit none
integer,intent(in)::N
double precision,intent(in)::x(1:N)
double precision,intent(out)::nabla(1:N)
double precision,intent(out)::Hesse(1:N,1:N)
external::func

integer::i,j,k
type(Hyperdual),allocatable::xH(:)
type(Hyperdual)::rH

allocate(xH(1:N))
do i=1,N
xH(i)%x0 = 0d0
xH(i)%x1 = 0d0
xH(i)%x2 = 0d0
xH(i)%x3 = 0d0
enddo

do i=1,N
xH(i)%x0 = x(i)
xH(i)%x3 = 0d0
enddo

do i=1,N
do k=1,N
xH(k)%x1 = 0d0
xH(k)%x2 = 0d0
enddo
xH(i)%x1 = 1d0
xH(i)%x2 = 1d0

call func(N,xH,rH)
nabla(i) = rH%x1
Hesse(i,i) = rH%x3
enddo

do i=1,N
do j=i+1,N
do k=1,N
xH(k)%x1 = 0d0
xH(k)%x2 = 0d0
enddo
xH(i)%x1 = 1d0
xH(i)%x2 = 0d0
xH(j)%x1 = 0d0
xH(j)%x2 = 1d0
call func(N,xH,rH)
Hesse(i,j) = rH%x3
Hesse(j,i) = Hesse(i,j)
enddo
enddo

return
end subroutine Hessian

Hyperdual.f90にモジュールを入れ、メインプログラムをmain.f90に入れたとすると、以下の結果を得ます。

> gfortran Hyperdual.f90 main.f90
> ./a.out
0.1158128336233602E-01
0.1158128336233602E-01
-0.7720855574890680E-02
-0.7720855574890680E-02
0.8491012233306163E-02
0.8491012233306162E-02
0.3474385008700806E-01 -0.1930213893722670E-01 0.2547303669991849E-01
0.3474385008700806E-01 -0.1930213893722670E-01 0.2547303669991849E-01
-0.1930213893722670E-01 0.1544171114978136E-01 -0.1698202446661233E-01
-0.1930213893722670E-01 0.1544171114978136E-01 -0.1698202446661233E-01
0.2547303669991849E-01 -0.1698202446661233E-01 0.2644793608458059E-01
0.2547303669991849E-01 -0.1698202446661233E-01 0.2644793608458058E-01

実行結果の奇数行目はHyper-dual Numberによる計算結果、偶数行目は解析解を表します。
また、6行目までは一階微分、7行目以降はヘッセ行列を表します。

参考文献

[1]関数
\(\displaystyle
f(x,y)=\frac{\text{ln}(xy^2)e^x}{\sqrt{\sin^3{x}+\sin^3{y}}}
\)
の偏微分\(\frac{\partial^2 f}{\partial x\partial y}\)
の計算
https://www.wolframalpha.com/input/?i=D%5Bln(x*y%5E2)*e%5E(x)%2Fsqrt(sin%5E3(x)%2Bcos%5E3(y)),+y,x%5D

[2]Jeffrey A. Fike and Juan J. Alonso,~”The Development of Hyper-Dual Numbers for Exact Second-Derivative Calculations”, 49th AIAA Aerospace Sciences Meeting(2011)
http://adl.stanford.edu/hyperdual/fike_aiaa-2011-886_slides.pdf,
J. A. Fike and J. J. Alonso. The Development of Hyper-Dual Numbers for Exact Second Derivative Calculations. AIAA paper 2011-886, 49th AIAA Aerospace Sciences Meeting, January 4-7, 2011.http://adl.stanford.edu/hyperdual/Fike_AIAA-2011-886.pdf

[3]JeffreyA.Fike,~”Derivative Calculations Using Hyper-Dual Numbers”, Sandia National Laboratories (2016)
https://www.osti.gov/servlets/purl/1368722

[4]Jeffrey Fike, Aerospace Design Lab, http://adl.stanford.edu/hyperdual/

[5]松本佳彦, 新しい数をつくる, (2018) http://ymatz.net/assets/docs/20180629-jtpa-slide-mod

（更新停止）

Hyper-dual numbersによる二階偏微分の計算