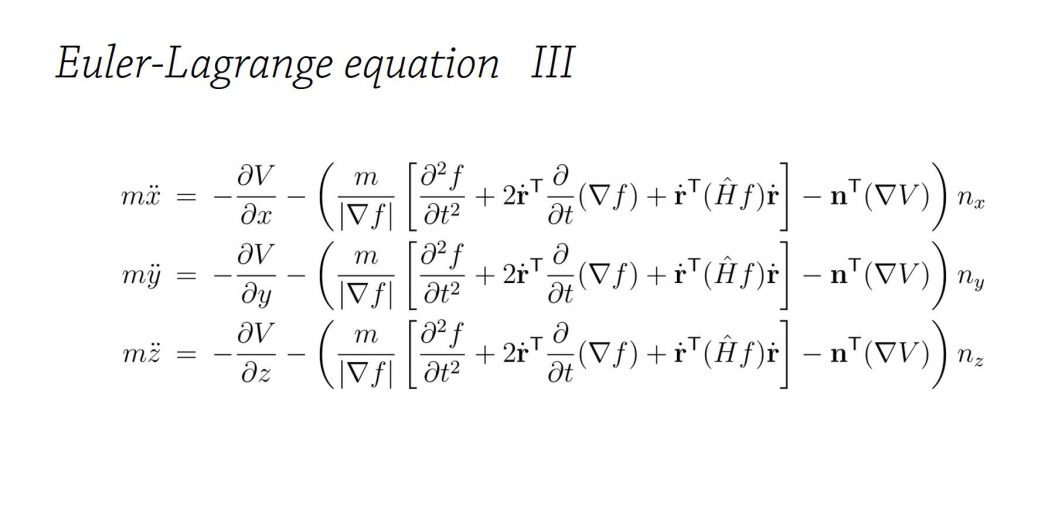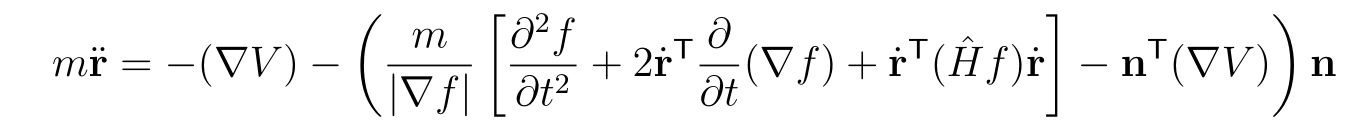このページは
束縛条件下の運動 – ホロノミックな束縛と非保存力
の続きです。
拘束がある場合の2次元の運動
ラグランジュの方程式を解く際に適切な座標変換が見付からず自由度が落とせない場合を考えます。その時の運動方程式は
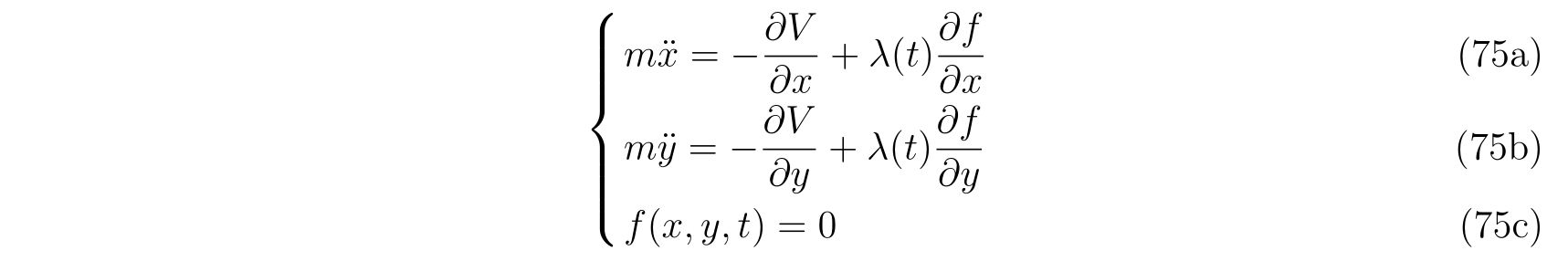
の形で止まります。式(75)において、未知の関数は\(x(t), y(t), \lambda(t)\)の3つであり、条件式は3つなので解くことは出来るはずです。
方針は、式(75)から\(\lambda(t)\)を消去すれば良いのです。
束縛条件\(f(x,y,t)=0\)が成立する点\(x=x_0, y=y_0\)周りで、微小時間\(\Delta t\)の変化を考えます。
点\((x_0, y_0)\)まわりでテーラー展開すれば、
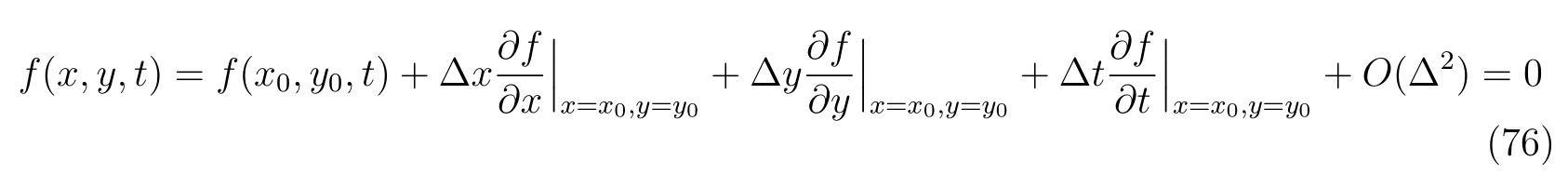
を得ます。よって
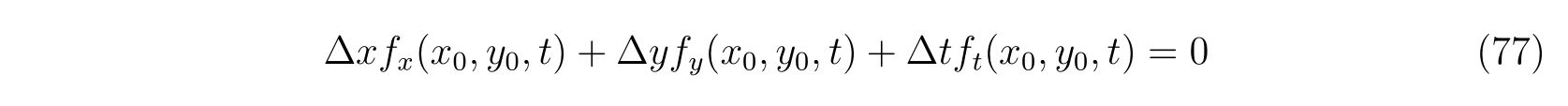
が満たされる変化でなければなりません。すなわち、\(x,y\)の時間変化は式(77)をいつも満たしていなければならないのです。両辺を\(\Delta t\)で割って極限をとれば、
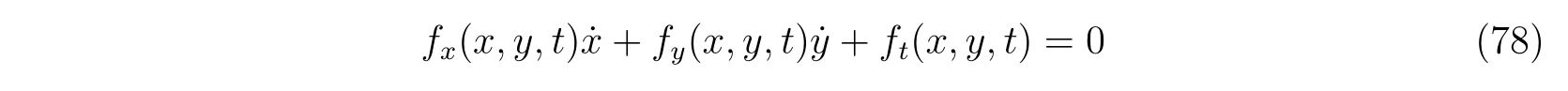
が成立することが分かります。式(75)を書きかえれば、
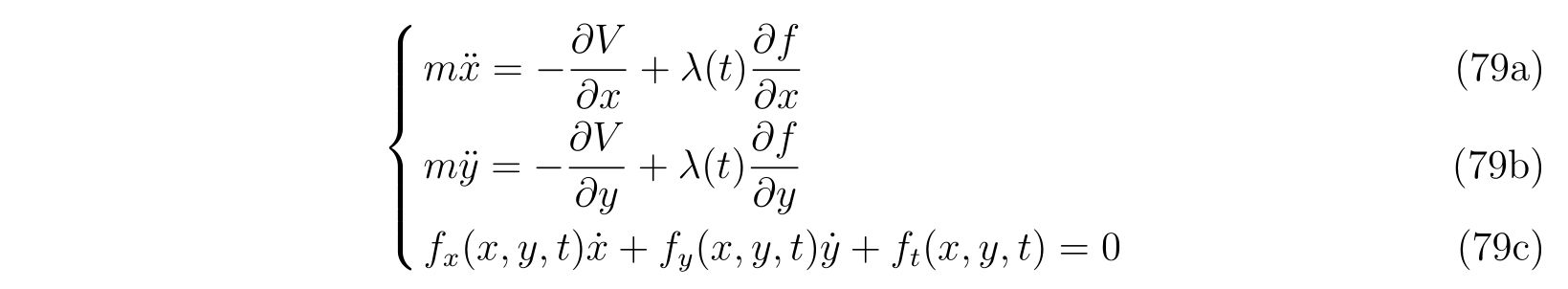
を得ます。式(79c)もまた時間変化しても成立し続けなければなりません。よって、左辺の時間微分を取れば、
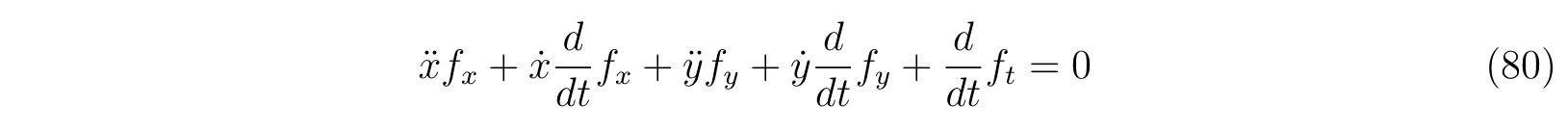
を得ます。整理して

を得ます。ここで関係式
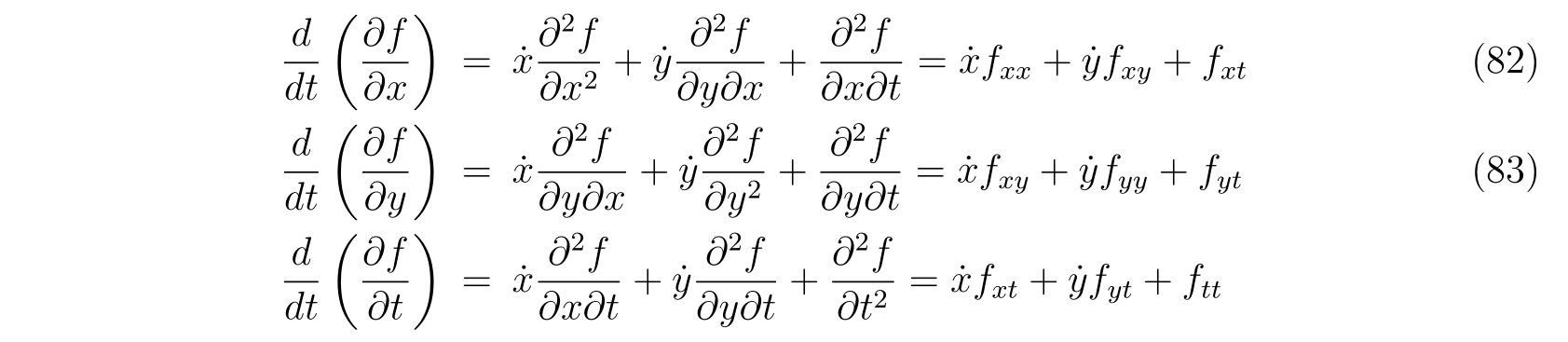
を用いました。式(79a), (79b)から未定乗数\(\lambda(t)\)を消去すれば
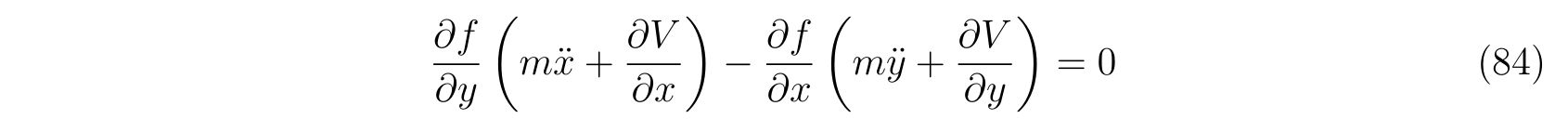
を得ます。よって、式(81)と式(84)から連立方程式
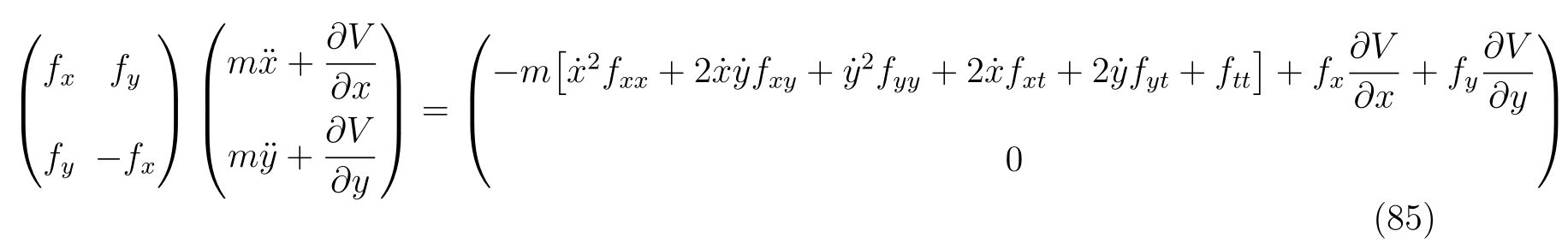
を立てることが出来ます。これをあらわに解けば、運動方程式
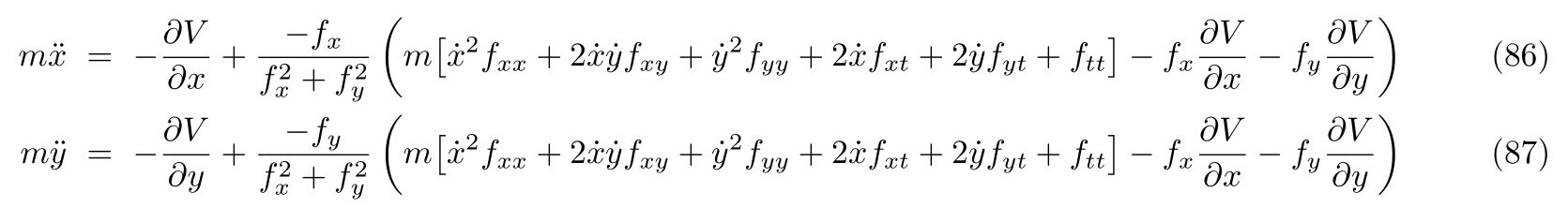
を得ます。ここで、式(86), (87)の右辺の\(-\frac{\partial V}{\partial x}, -\frac{\partial V}{\partial y}\)は\(x, y\)方向の保存力であり、右辺の残りの項は束縛条件によって決まる束縛力であることが分かります。
拘束がある場合の3次元の運動
スカラー関数\(f\)で表される拘束がある条件のもとで, 運動方程式
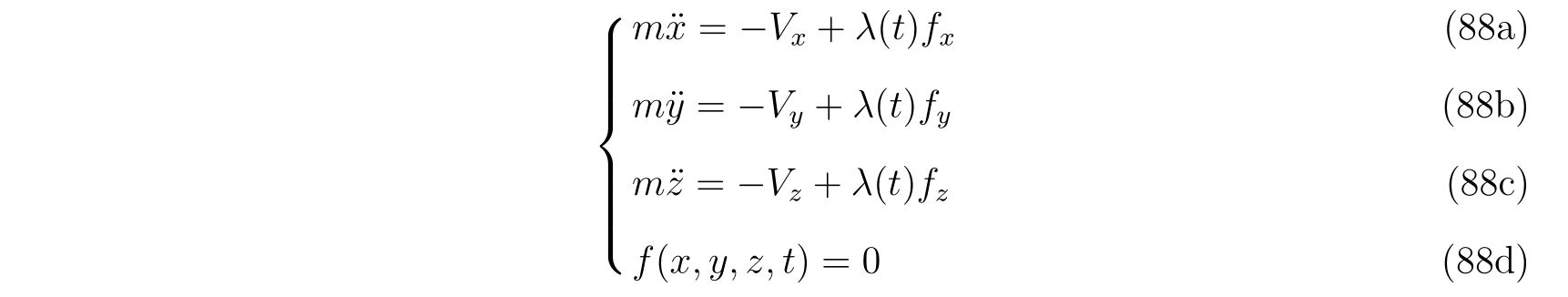
またはベクトル表記で
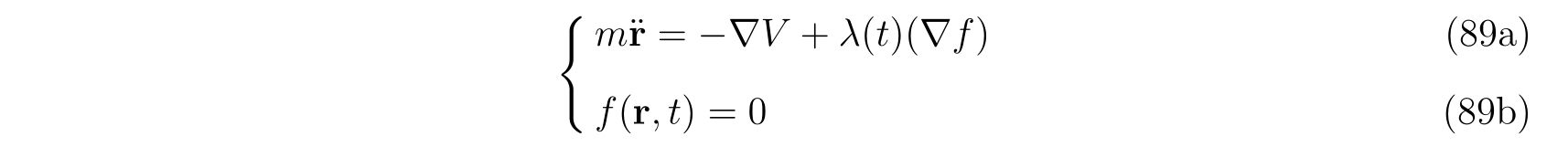
について考えます。ここで表記を略すために
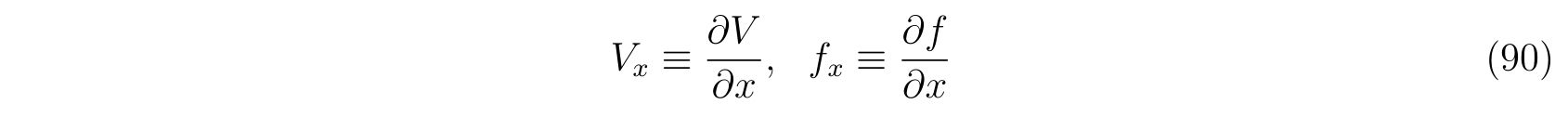
の略記を用いました(\(y, z\)方向についても同様)。
また、\(\nabla\)はナブラ演算子で、
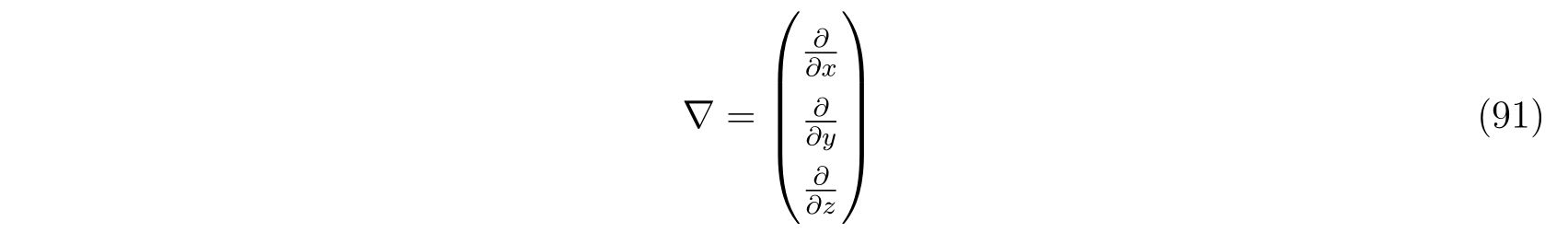
です。2次元の場合と同様に、式(88d)の時間微分から
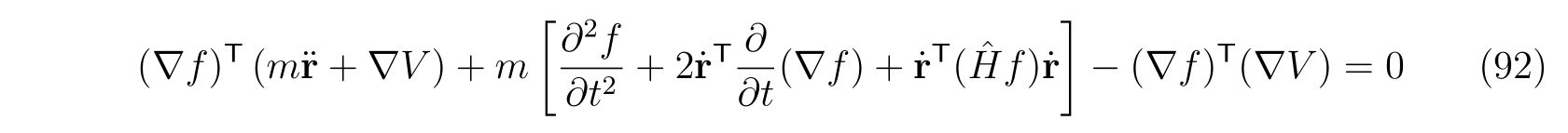
が導けます。ここで、\(\hat{H}f\)は関数\(f\)のヘッセ行列であり、
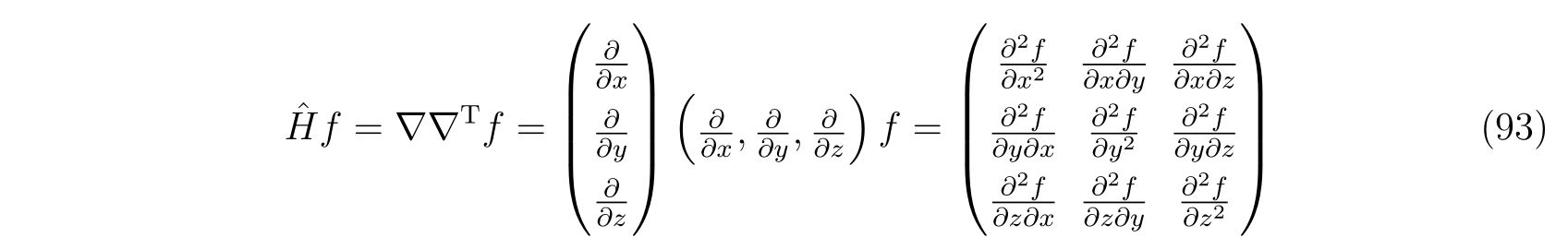
を表します。式(92)は、式(81)を3次元に拡張した形になっています。
式(88a),(88b),(88c)から未定乗数を消去すると従属な3つの関係式
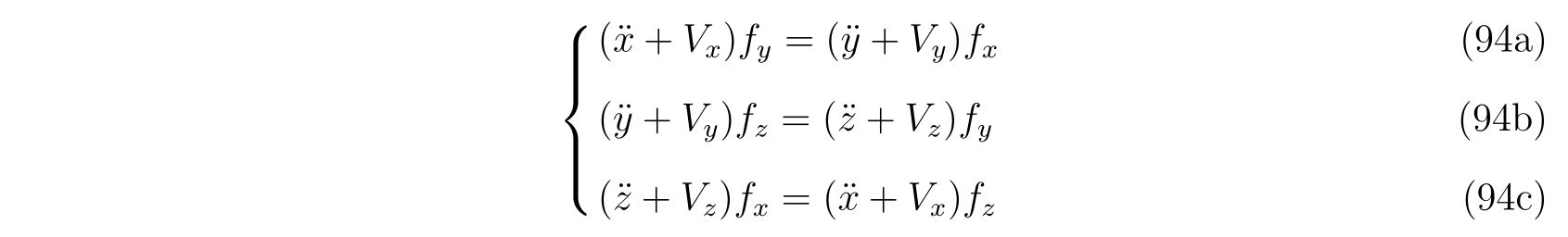
を得ることが出来ます。この3式で独立なのは2つです。
独立な式として式(94a)と式(94b)を選ぶことにし、式(92)と共に書けば、連立方程式

を得ます。この式をあらわに解けば、運動方程式
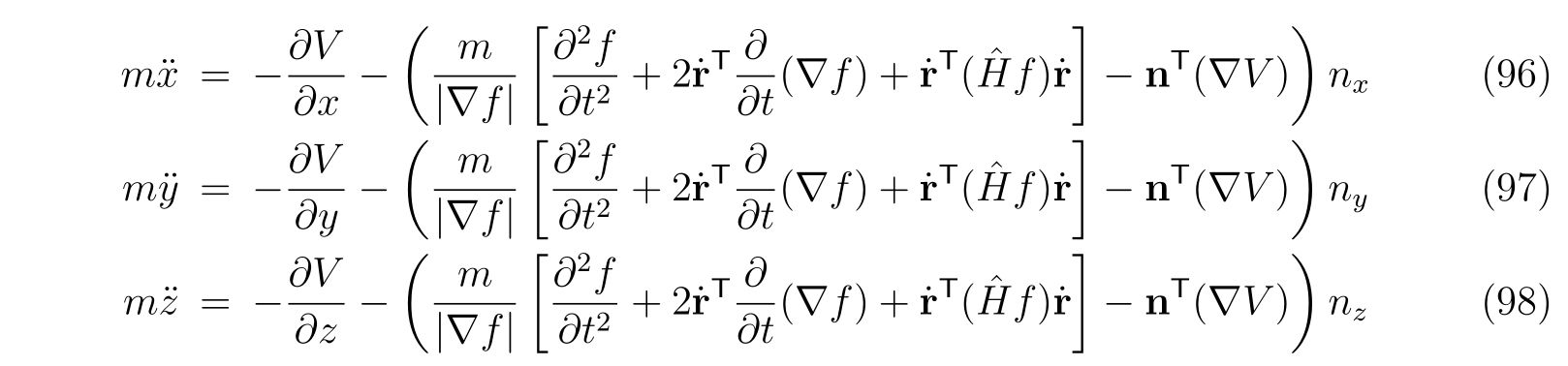
を得ることが出来ます。ここで、\(n_x, n_y, n_z\)は壁の法線ベクトル\(\mathbf{n}=\frac{\nabla f}{|\nabla f|}\)の\(x,y,z\)成分です。偏微分ではないことに注意してください。
単振り子の例
ここでは単振り子を例に挙げ、式(86)に代入した時本当に振り子を表す方程式になっているのか、また束縛条件の選び方に依らず、同じ運動を記述しているのかを例に挙げます。
保存力は重力で
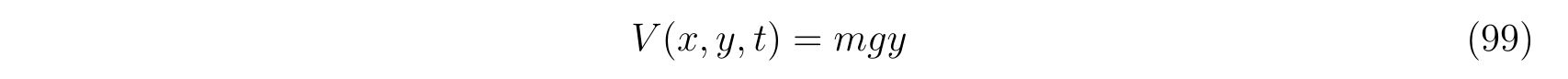
を考えます。
考える束縛条件は
\(
f(x,y,t)=x^2+y^2-l^2=0
\)
と
\(
f(x,y,t)=\sqrt{x^2+y^2}-l=0
\)
です。
束縛条件1
束縛条件として
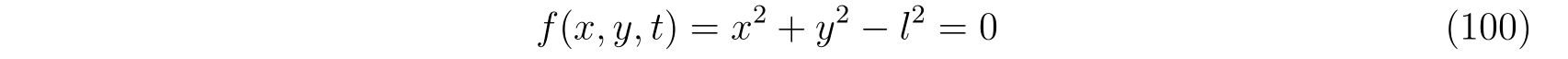
を考えます。この束縛条件に対する偏微分を計算して、
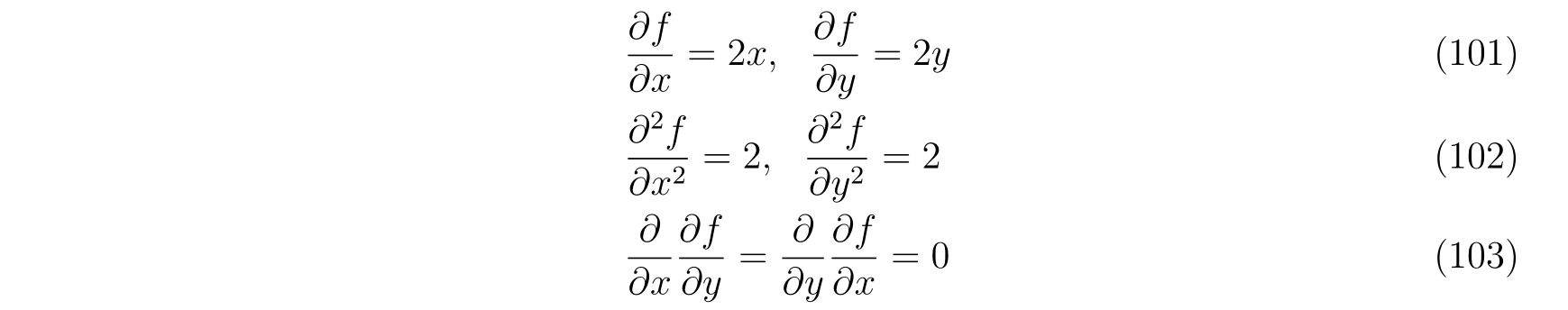
を得ます。これを式(86), (87)に代入すれば、
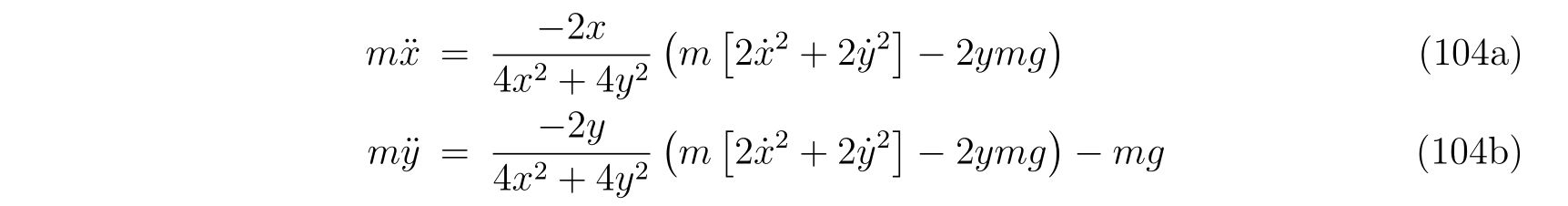
であり、整理すれば
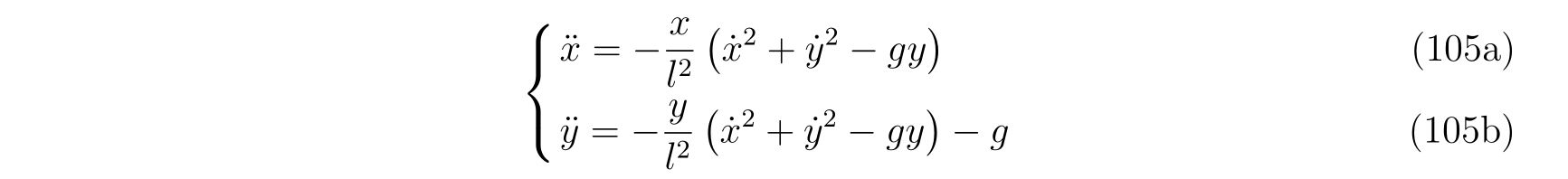
を得ます。
束縛条件2
束縛条件として
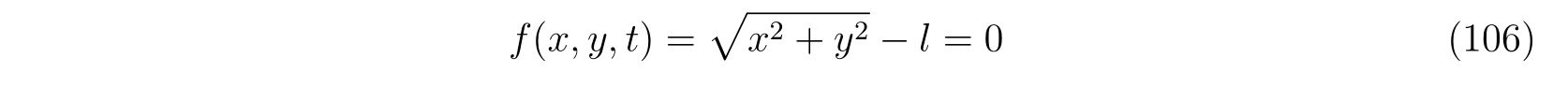
を考えます。この束縛条件に対する偏微分を計算して、
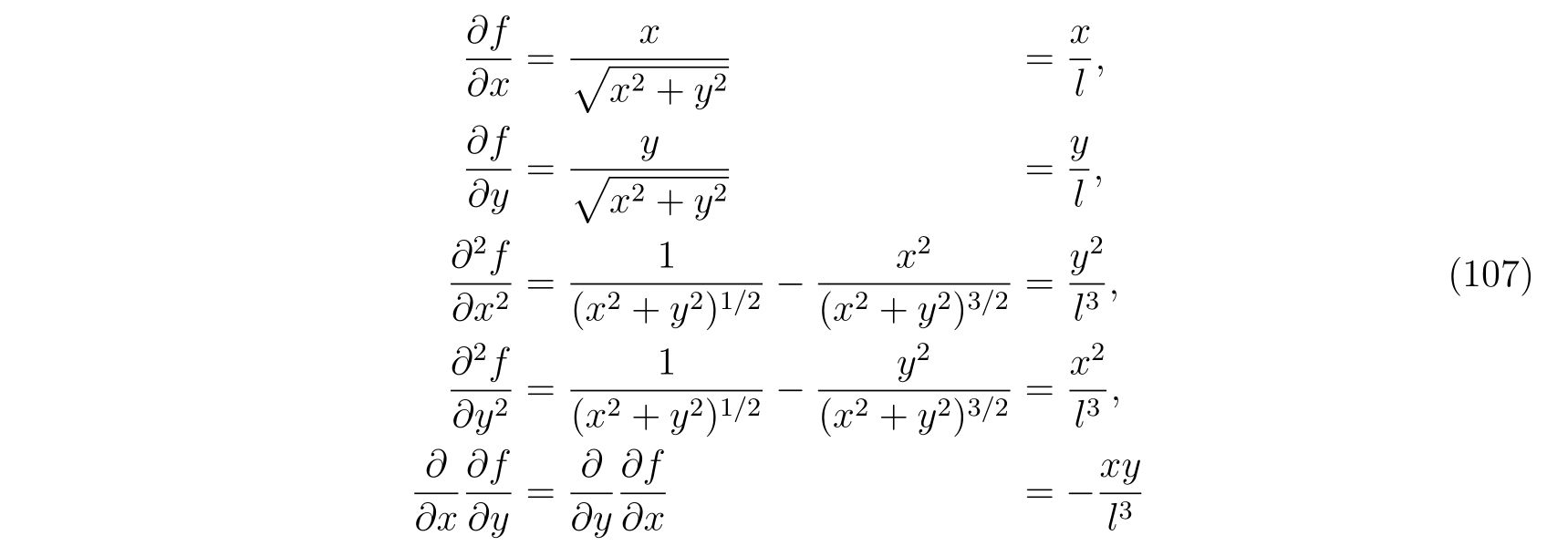
を得ます。これを式(86), (87)に代入すれば、
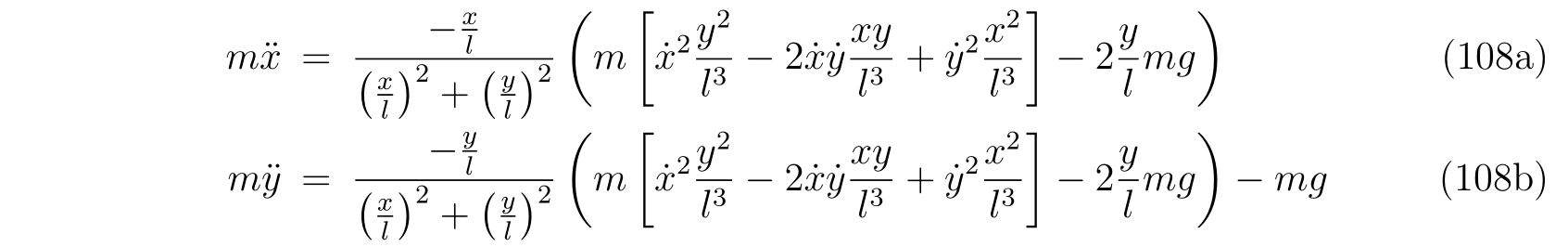
であり、整理すれば
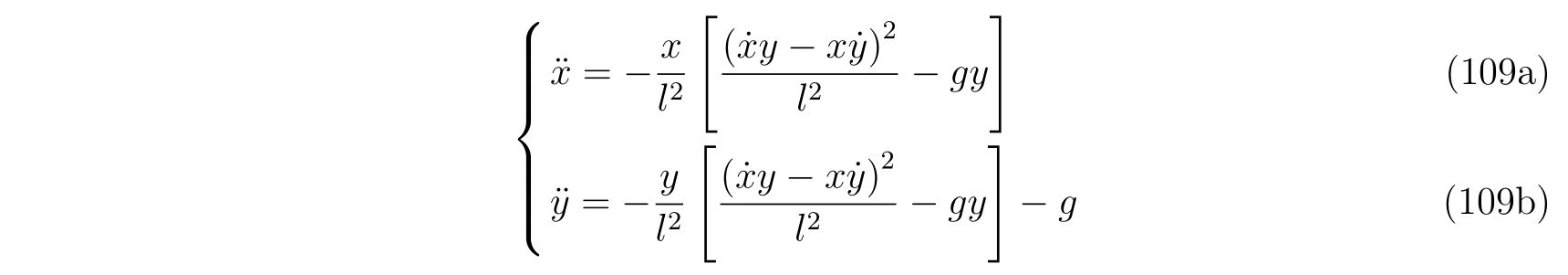
を得ます。
考察
同じ束縛条件なので、式(105)と(109)の示す運動は同じになるはずです。
それを示すには、2式の差異である

を示せればよい、ということです。そのために拘束力に対して座標変換

を考えます。右辺と左辺をそれぞれ計算すれば、
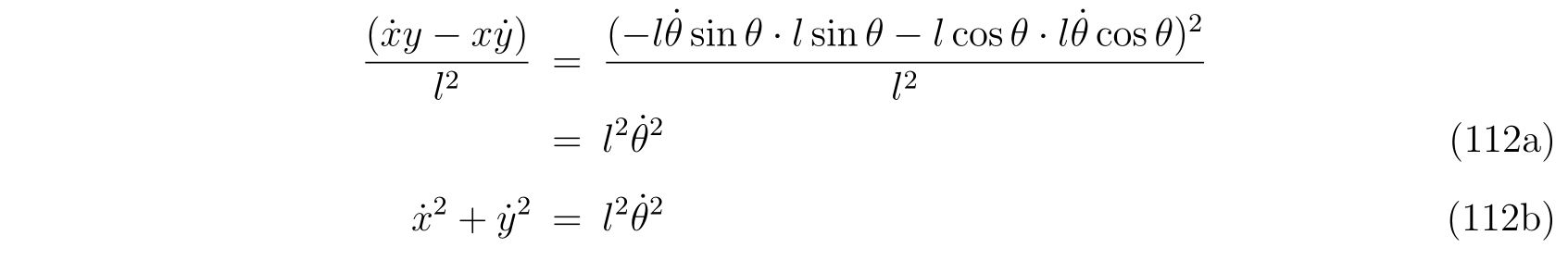
となり、同じ運動を記述していることが分かります。
Fortran90によるプログラム
Fortran90で2次元平面を動く質点の束縛運動のプログラムを作ります。
そのプログラムは
https://slpr.sakura.ne.jp/qp/supplement_data/constraint.tar.gz
に置いてあります。
一応補足しておきますが、初期状態の位置は\(f(x, y, t)=0\)を満たすx,yでなければなりませんし、初期速度も\(f(x, y, t)=0\)の傾きと一致していなければなりません。
上の条件を満たさずとも何も警告は出さず、計算自体は行われますが、その計算は束縛運動ではなくなります。
上のプログラムの中で、変更すると思われるのは以下の2つです。
1. fp2d
2. fw2d
1. fp2dは、ポテンシャル\(V(x,y)\)を記述しており、デフォルトのプログラムでは、重力による位置エネルギー
\(
V(x,y)=mgy
\)
に設定しています。
2. fw2dは、束縛条件\(f(x,y, t)=0\)を記述しており、デフォルトのプログラムでは、
\(
f(x,y,t)=y – [2(cos(1.5*x)-1) + 0.1x^2]=0
\)
に設定しています。
もしも非保存力を入れたい場合は、grkの最後の方を変更してください。
数値計算では、
時間発展は刻み幅制御の陽的ルンゲクッタ、
gradient, Hesse行列、束縛条件に関する時間の二階微分は、Hyper-dual numbersを利用してほぼ厳密な値を得ています。
! Author : sikino
! Date : 2019/10/12 (yyyy/mm/dd)
! URL : http://slpr.sakura.ne.jp/qp/constraint-condition3/
use Parameters
use Hyperdualmod
implicit none
integer::i,N,info,Nt
double precision::t,h,tol,ta,tb
double precision,allocatable::x(:),tgrid(:)
external::grk
double precision::E,Ek,Ep
N=4
allocate(x(1:N))
! Time range [ta, tb]
ta = 0d0
tb = 30d0
! Divide time range equally among Nt
Nt = 201
! Tolerance of the RK method
tol=1d-8
! Initial condition
x(1)=0d0 ! x (ta)
x(2)=4d0 ! x'(ta)
x(3)=0d0 ! y (ta)
x(4)=0d0 ! y'(ta)
! Time grid
allocate(tgrid(1:Nt))
do i=1,Nt
tgrid(i) = (i-1)*(tb-ta)/dble(Nt-1)+ta
enddo
do i=2,Nt
info = 0
t = tgrid(i-1)
h = (tgrid(i) - t)*0.1d0
do while(info.le.0)
call drkf45(grk,t,h,N,x,tgrid(i),info,tol)
enddo
! Kinetic energy
Ek = 0.5d0*mass*(x(2)**2+x(4)**2)
! Potential energy
Ep = mass*g*x(3)
! Total energy
E = Ek + Ep
write(10,'(8e25.10e3)')t,x(1),x(2),x(3),x(4),E,Ek,Ep
enddo
stop
end program main
subroutine fp2d(N,xH,fH)
use Parameters, only:mass, g
use Hyperdualmod
implicit none
integer,intent(in)::N
type(Hyperdual),intent(in)::xH(1:N)
type(Hyperdual),intent(out)::fH
! Potential
type(Hyperdual)::x,y,t
x = xH(1)
y = xH(2)
t = xH(3)
! If conservative force,
! fH doesn't depend on the time.
!-----------------------------
fH = mass * g * y
return
end subroutine fp2d
subroutine fw2d(N,xH,fH)
use Hyperdualmod
implicit none
integer,intent(in)::N
type(Hyperdual),intent(in)::xH(1:N)
type(Hyperdual),intent(out)::fH
! Wall of the function
type(Hyperdual)::x,y,t
x = xH(1)
y = xH(2)
t = xH(3)
!-----------------
fH = y - (2d0*(cos(1.5d0*x)-1d0) + 0.1d0*x*x)
! fH = (y-5d0)**2 + x**2 - 25d0
return
end subroutine fw2d
デフォルトのまま計算すると、fort.10に以下の出力が現れます。アニメーションは、同じファイルに入っているanime.pltで実行できます。
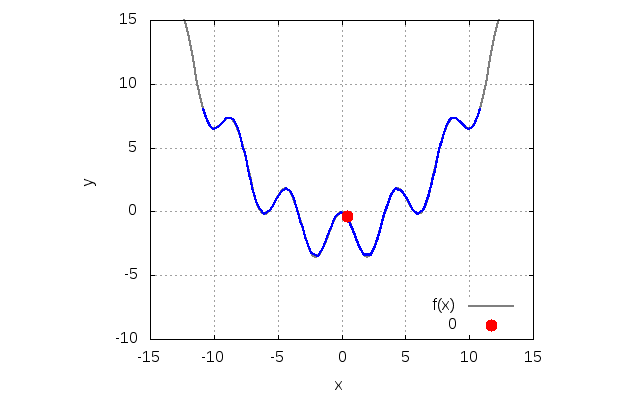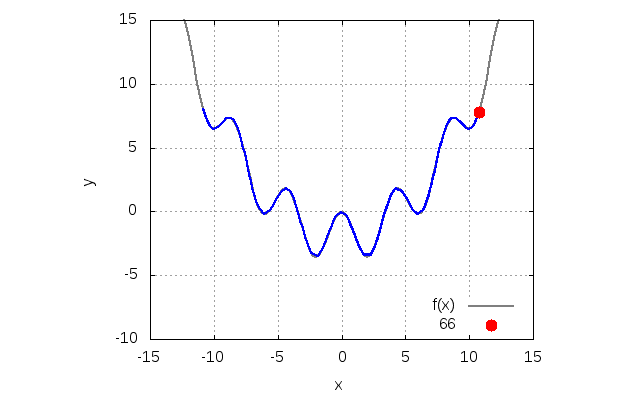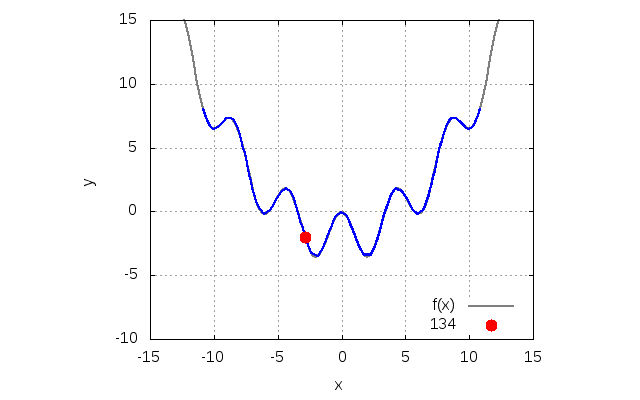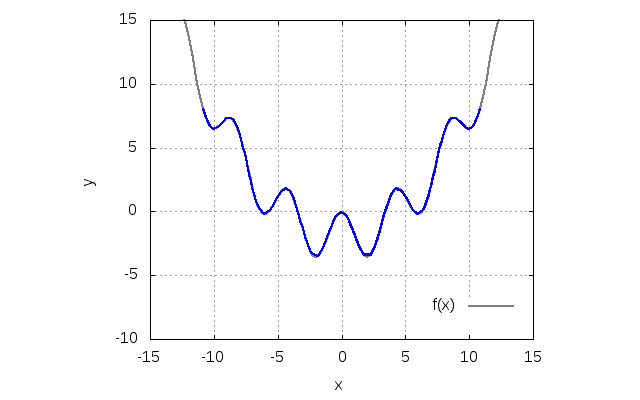
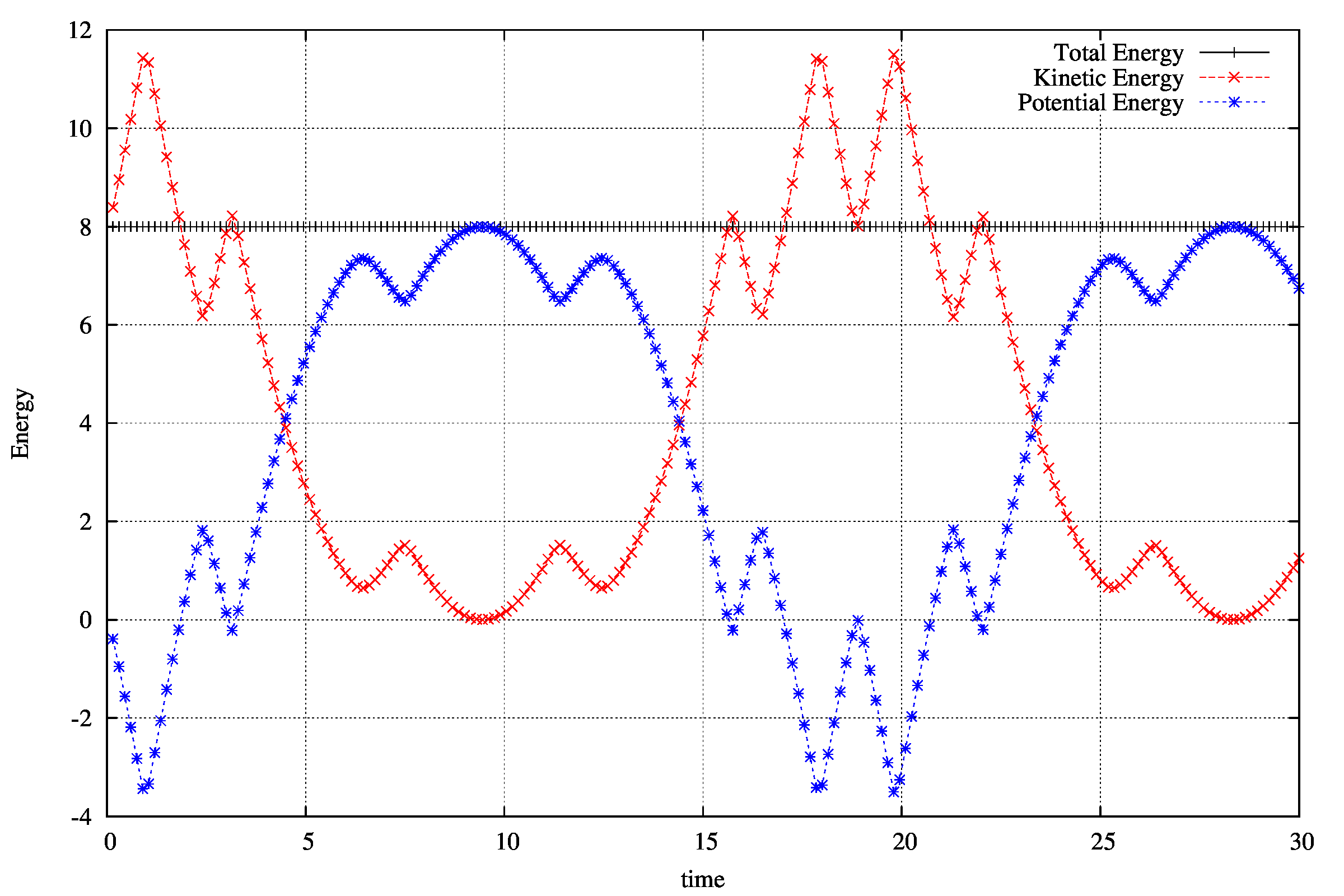
エネルギーは計算の範囲ではほとんどありません。全力学的エネルギーは、計算時間内でおおよそ5桁目が変化していました。
参考文献
6. 振り子 -物理学の見つけ方
9. 自由な座標 -物理学の見つけ方