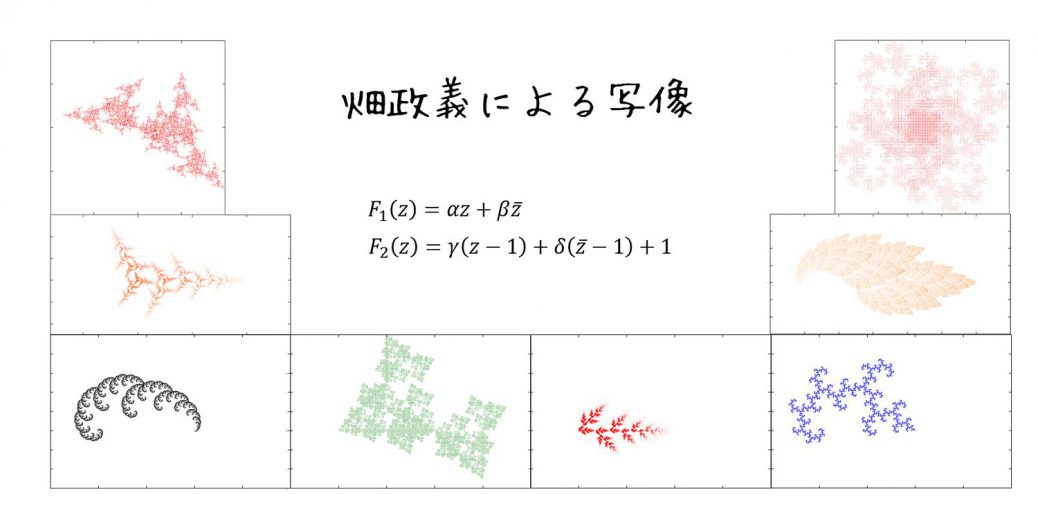
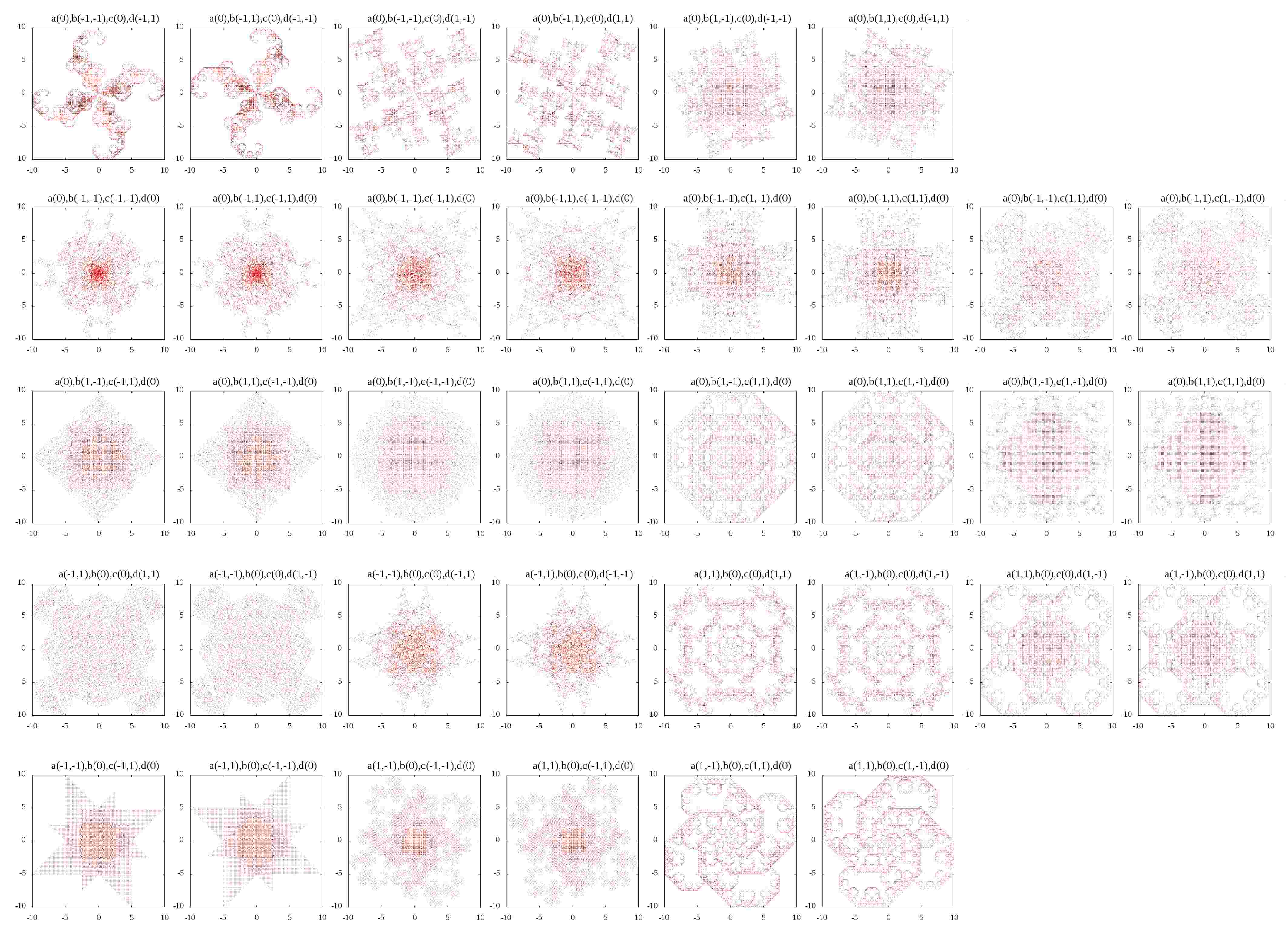
畑政義による写像によって得られる点の集合は、簡単な式で書かれるにもかかわらず、その綺麗さに惹きつけられます
このページでは、畑政義による写像の定義、fortranコード、図を掲載します。
序
ある日、こんなツイートを見ました。
畑政義の写像です。
この写像は4つのパラメーターを変えるだけで本当にたくさんのパターンを見ることができます。#数学GIF pic.twitter.com/EaE0BD7QvI— 数学GIF画像bot (@math_gif) 2016年11月6日
とても綺麗で感動しました。また、
パラメーター参考にして綺麗なものも描きました。畑政義写像です。 pic.twitter.com/uYPaHQwW3C
— あすなろ (@snowy_tree) 2016年11月6日
というツイートに触発されました。自分でも作ってみよう、と。
畑政義による写像の数式
畑政義によって考えられた写像は、簡単な数式で綺麗な図が得られます。
このページでは畑政義の写像で得られる画像の”綺麗さ”を主とします。
畑政義による写像の数式は論文[1]より、
\(
\begin{align}
F_1(z)&=\alpha z+\beta \bar{z} \\
F_2(z)&=\gamma (z-1)+\delta (\bar{z}-1)+1
\end{align}
\)
です(\(\alpha,\beta,\gamma,\delta\)は複素定数,\(\bar{z}\)は\(z\)の複素共役を意味します)。
ある1点に対して写像を行うと、\(F_1,F_2\)によっての2つ点に写像されます。
ある1点からスタートして、\(n\)回作用させていきます。\(n\)回作用させた結果、最後に得られる点の数は\(2^n\)点になります。
具体的にどういう風に計算をすればいいかといいますと
1.初期値\(z_0\)を用意
2.値\(F_1(z_0),F_2(z_0)\)を計算
3.値\(F_1(F_1(z_0)),F_1(F_2(z_0)),F_2(F_1(z_0)),F_2(F_2(z_0))\)を計算
4…
という具合に計算していくのです。そうして得られた最後の複素数の組を複素平面上に打っていくのです。
fortranコードはこちら。重複して計算するのが嫌なので少し工夫しています。
implicit none
integer,parameter::N=12
integer::i
complex(kind(0d0))::a,b,c,d,z0,h(1:2**N)
a=dcmplx(0.7d0,0.2d0)
b=dcmplx(0.0d0,0.0d0)
c=dcmplx(0d0,0d0)
d=dcmplx(2d0/3d0,0d0)
z0=dcmplx(1d0,0d0)
h=dcmplx(0d0,0d0)
call hatamap(N,a,b,c,d,z0,h)
do i=1,2**N
write(10,'(2f10.6)')h(i)
enddo
stop
end program main
subroutine hatamap(N,a,b,c,d,z0,h)
implicit none
integer,intent(in)::N
complex(kind(0d0)),intent(in)::a,b,c,d,z0
complex(kind(0d0)),intent(out)::h(1:2**N)
integer::i,j,k,l,m
complex(kind(0d0))::z,F,h0(1:2**N)
external::F
h=dcmplx(0d0,0d0); h0=dcmplx(0d0,0d0)
h(1)=z0; h0(1:2**N)=h(1:2**N)
do j=1,N
k=1-2**(N-j)
l=1-2**(N-j+1)
do i=1,2**j
if(mod(i,2).eq.1)l=l+2**(N-j+1)
k=k+2**(N-j)
m=mod(i+1,2)+1
h(k)=F(m,a,b,c,d,h0(l))
enddo
h0(1:2**N)=h(1:2**N)
enddo
return
end subroutine hatamap
function F(n,a,b,c,d,z)
implicit none
integer,intent(in)::n
complex(kind(0d0)),intent(in)::a,b,c,d,z
complex(kind(0d0))::F
if(n.eq.1)then
F=a*z+b*conjg(z)
elseif(n.eq.2)then
F=c*(z-1d0)+d*(conjg(z)-1d0)+1d0
else
write(6,*)"***error"; stop
endif
return
end function F
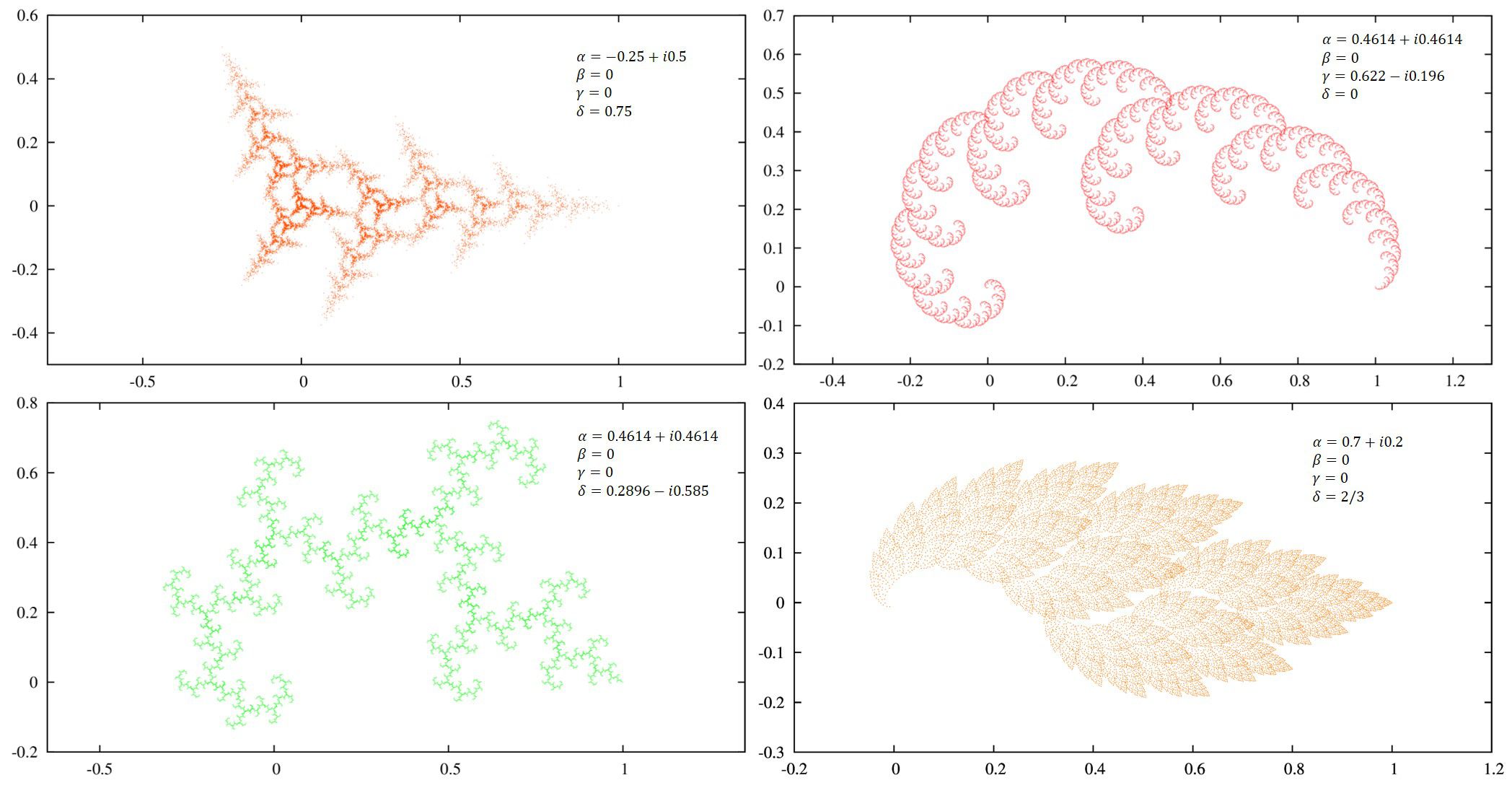
さて、プログラムが正しく動いていることを確かめるため、論文のパラメータで写像を再現してみます。
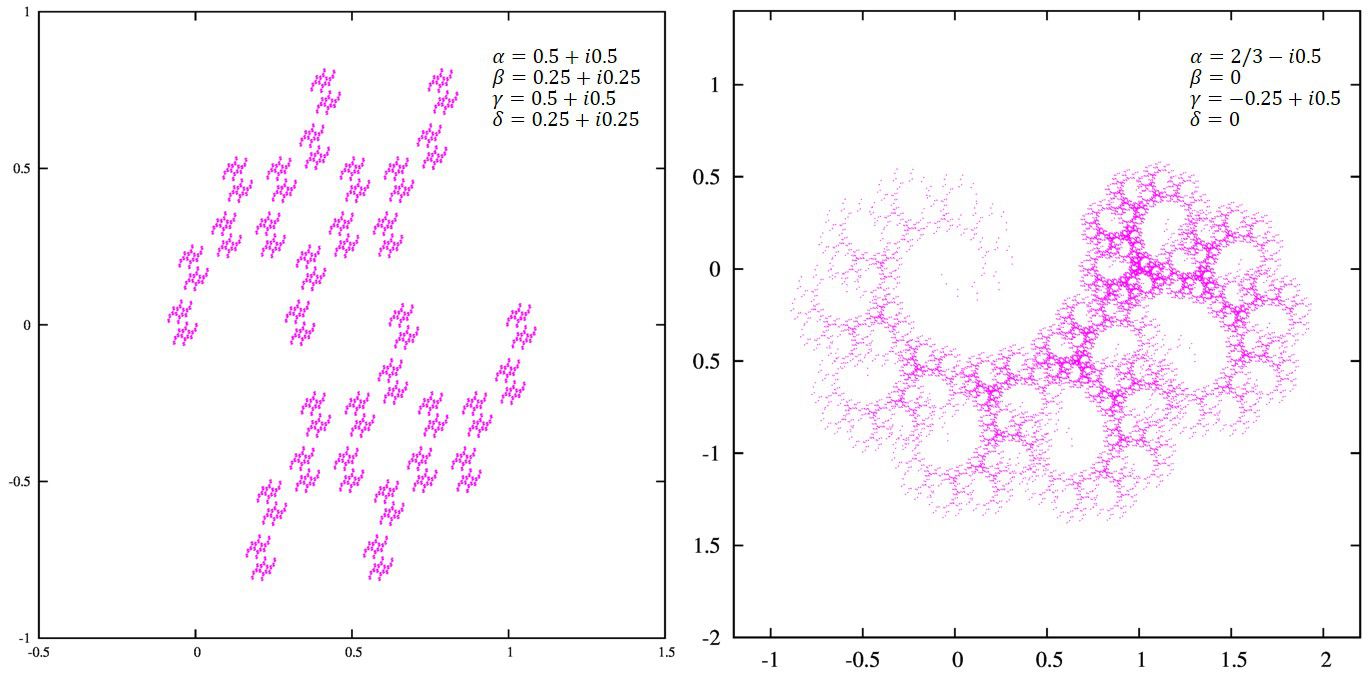
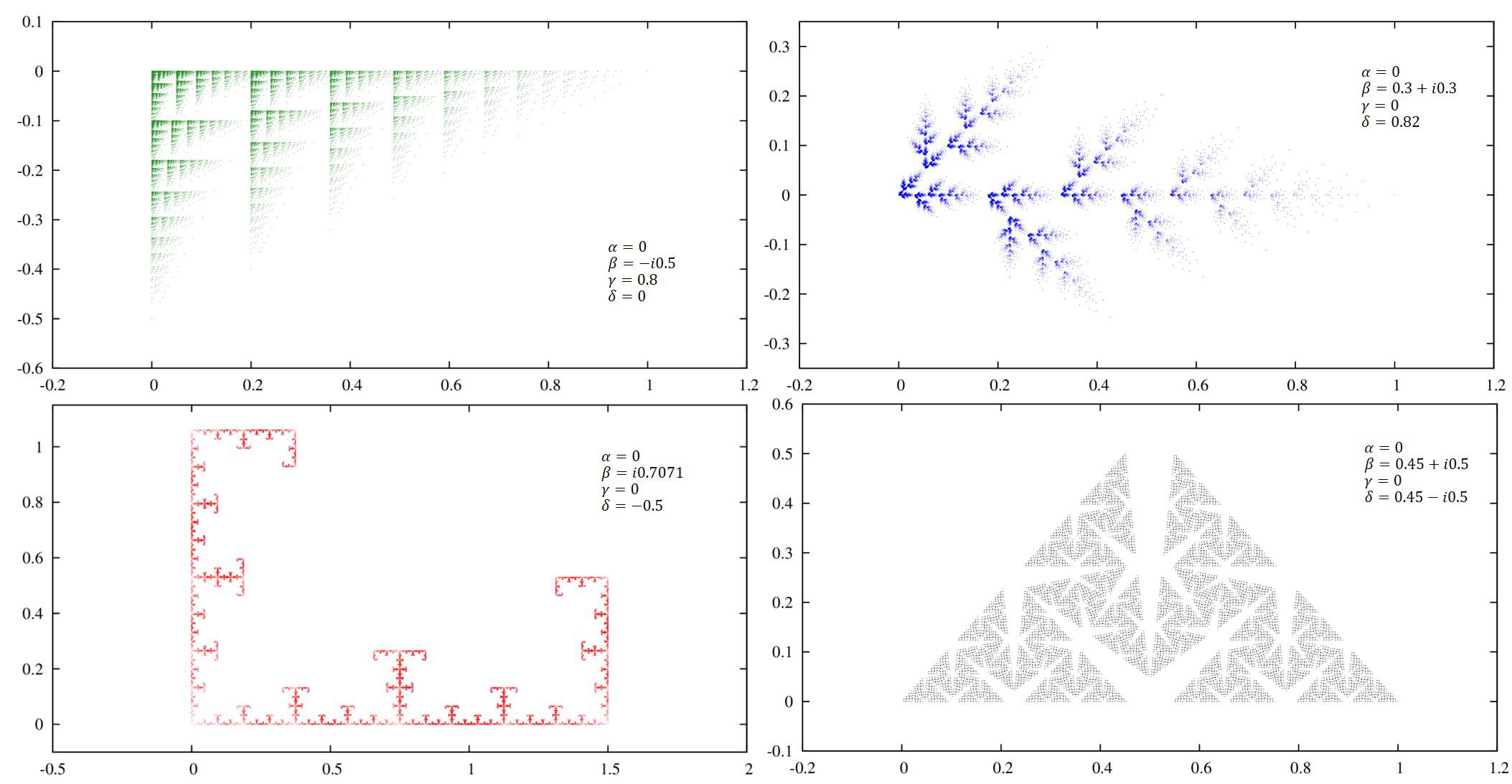
論文[1]では\((\alpha,\beta,\gamma,\delta)\)のセットとして描いています。
論文[1]ではこんな感じに紹介されています。
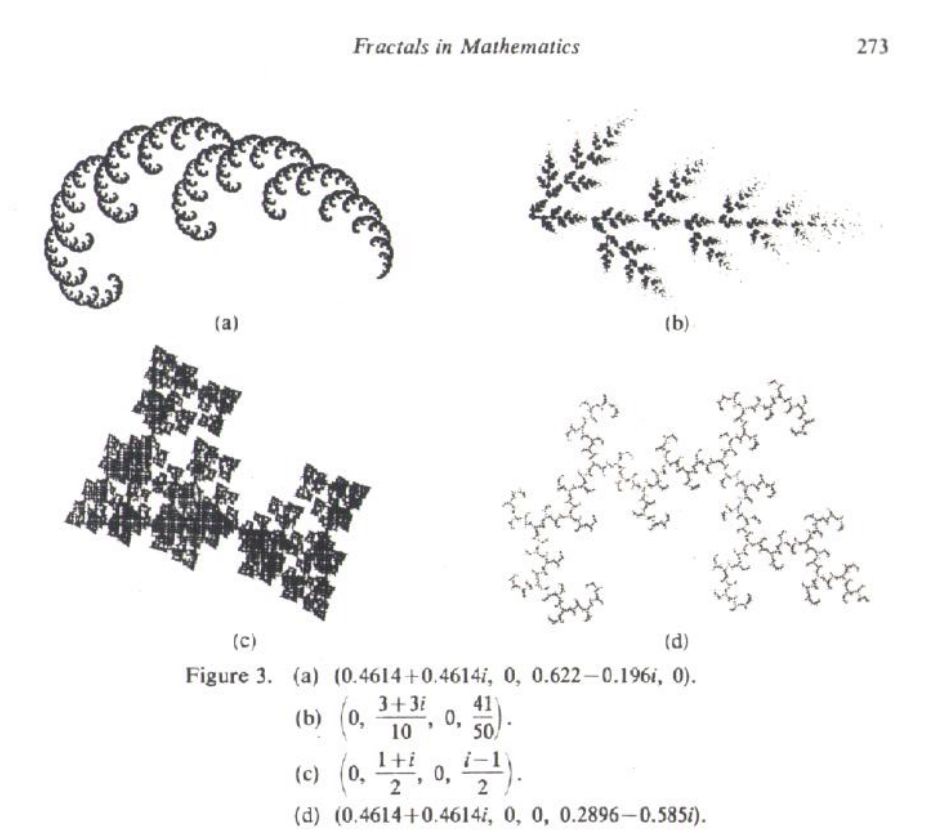
私のプログラムでは、
(左上) \((0.4614+i0.4614, 0, 0.622-i0.196, 0)\)
(右上) \( (0, 0.3+i0.3, 0, 41/50)\)
(左下) \((0, 0.5+i0.5, 0, -0.5+i0.5)\)
(右下) \((0.4614+i0.4614, 0, 0, 0.2896-i0.585)\)
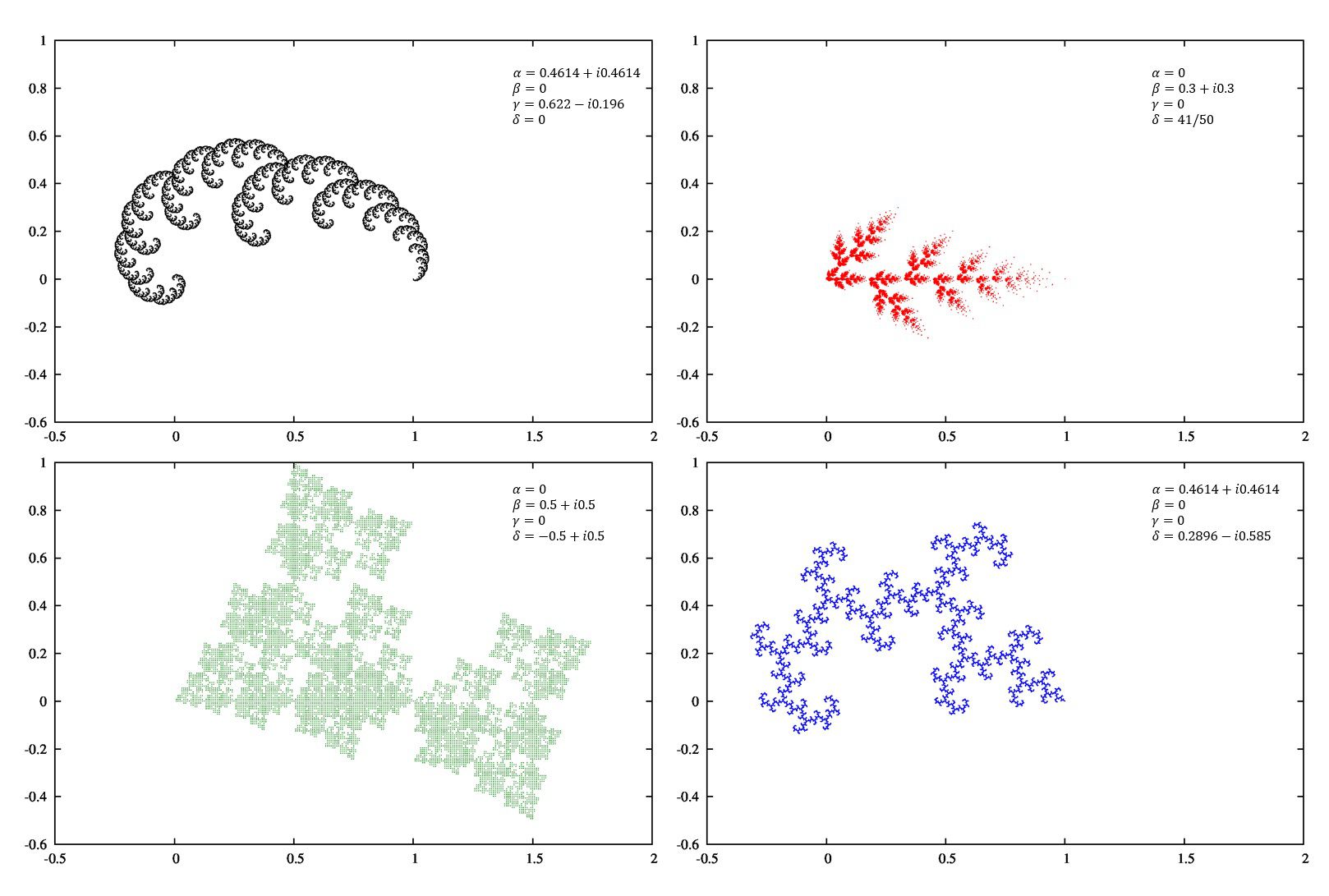
となり、ちゃんと正しく計算されていることが分かります。綺麗ですね。
[adsense1]
代表的なパラメータ
さて綺麗な画像を得るために探さなければならないパラメータは\(\alpha,\beta,\gamma,\delta,z_0\)の全部で5つ。各々複素定数なので、実部と虚部で合計10個のパラメータをいじって綺麗な画像を探さなければなりません。これは多いです。
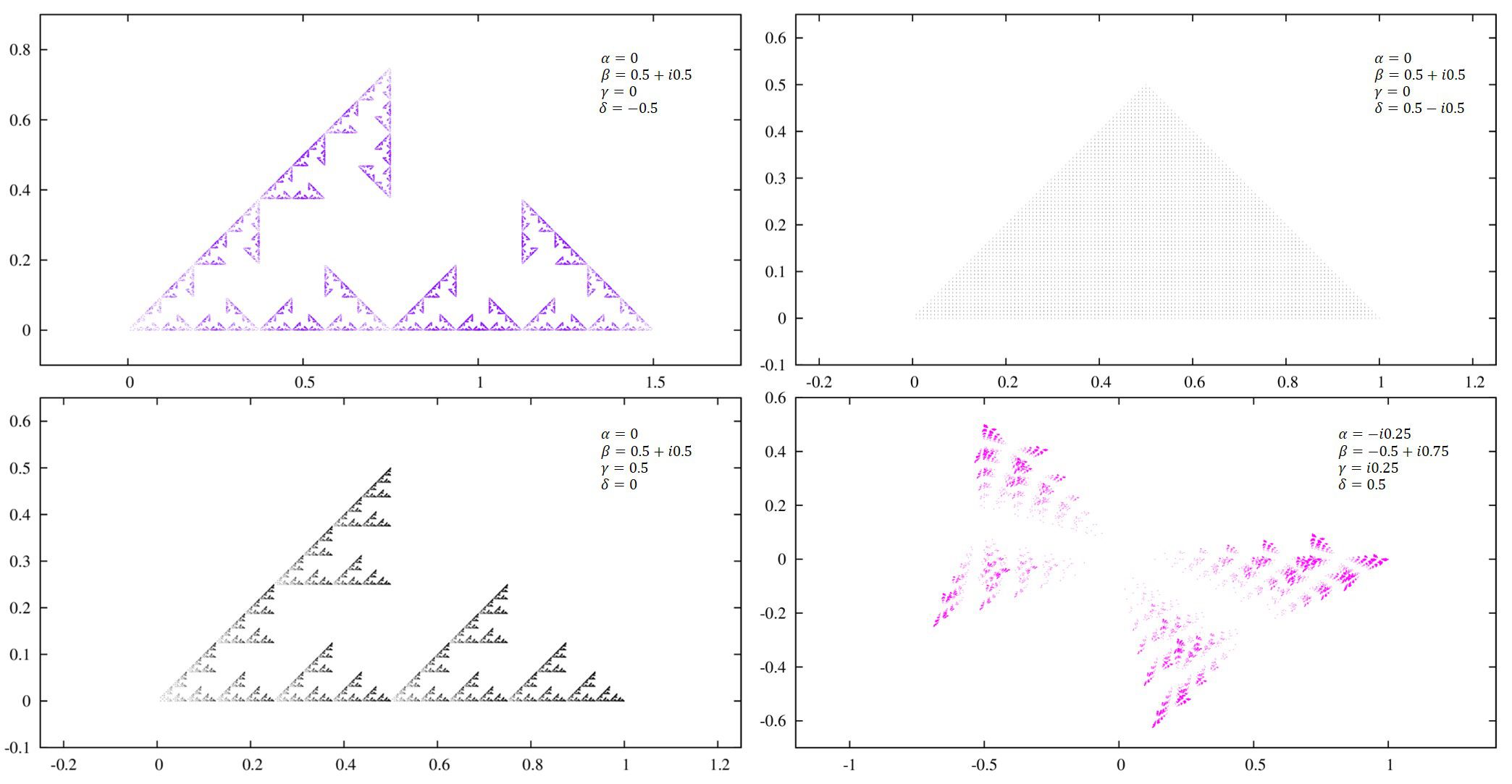
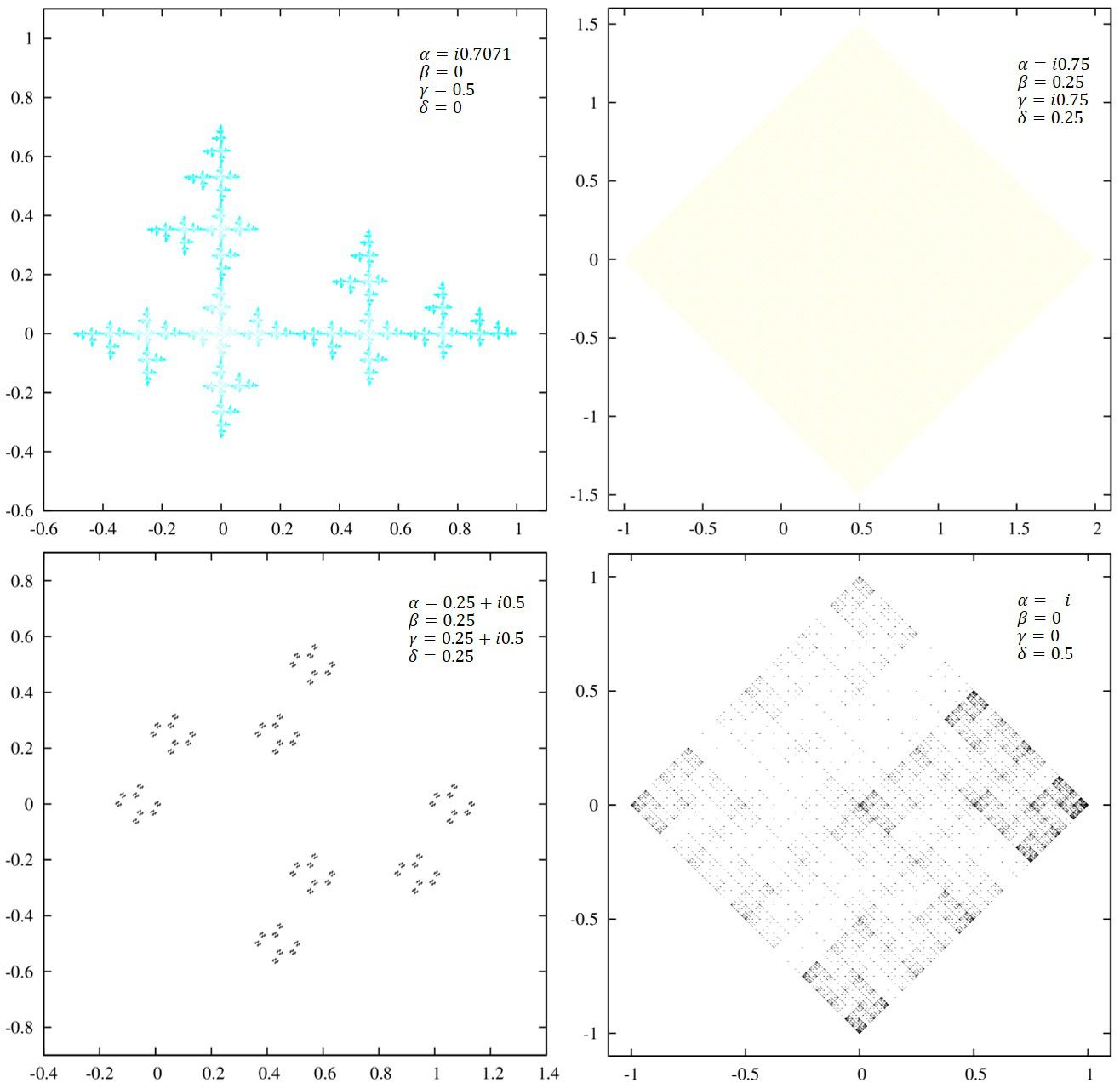
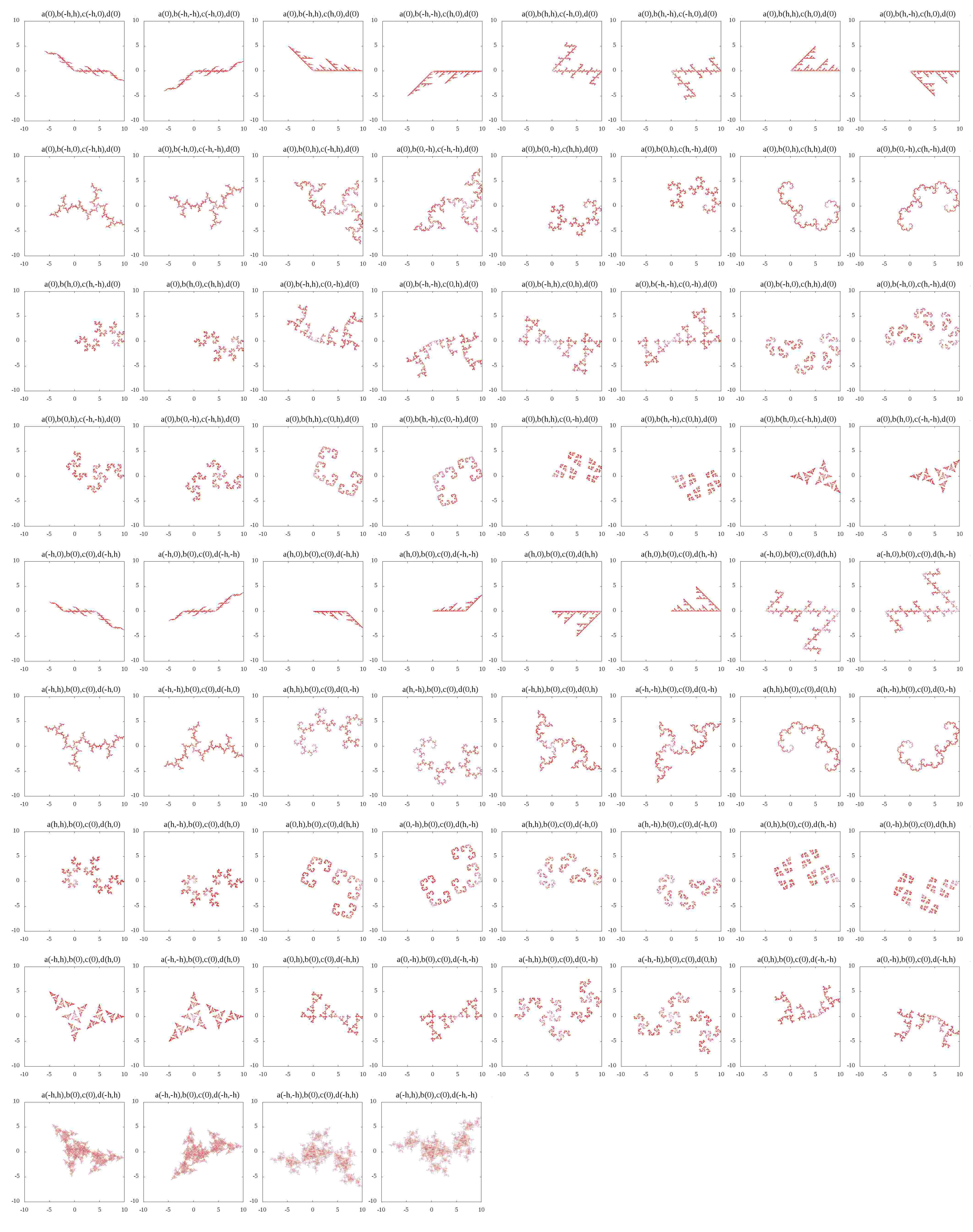
まずは[2],[3],[4]に掲載されているパラメータで計算を行って見ましょう。
ずらっと並べます。
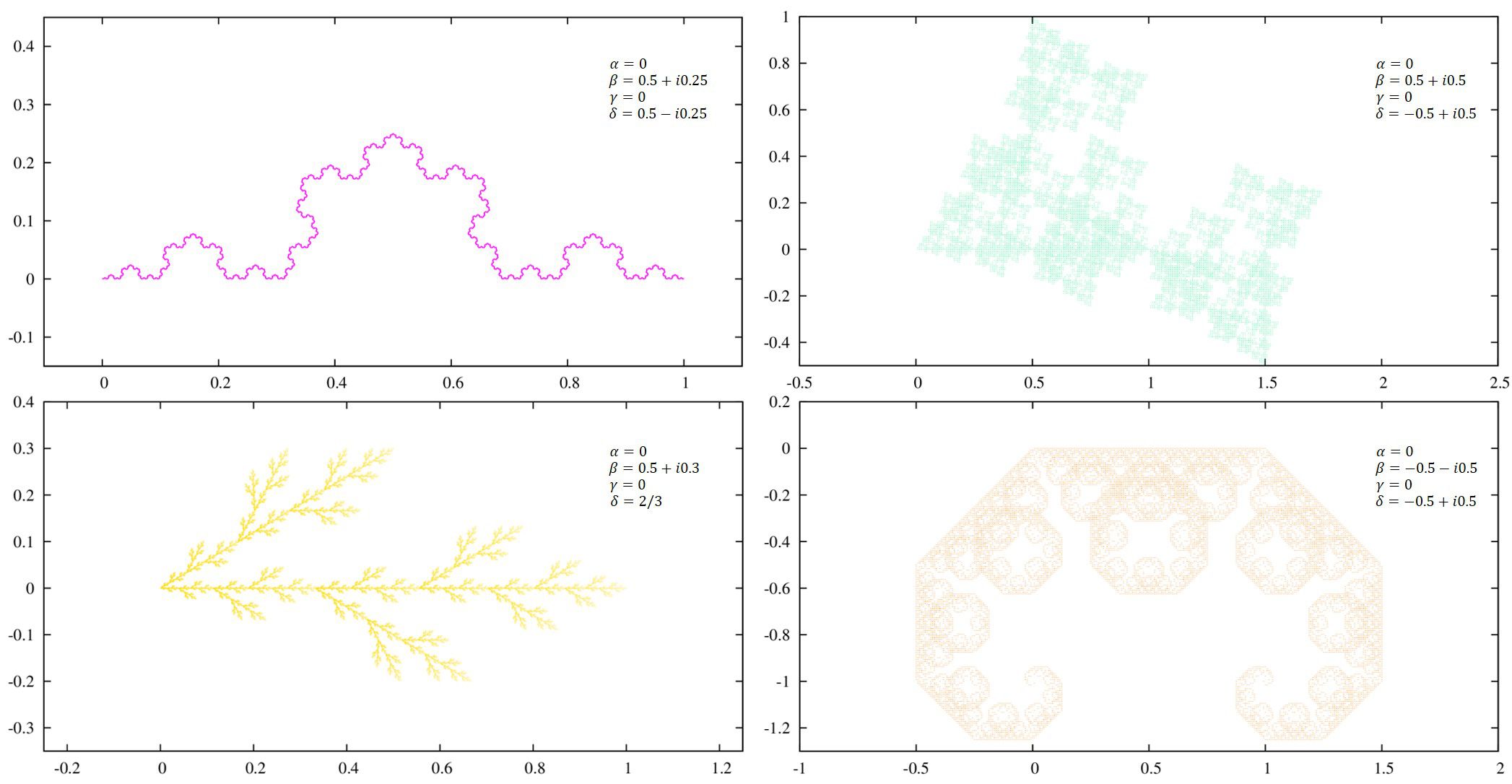
[adsense2]
パラメータを予想する
さて、綺麗な画像として紹介されているのは大体\(\alpha,\beta,\gamma,\delta\)のうち2つがゼロであり、\(0,\pm0.25,\pm 0.5, \pm0.75, \pm1\)のどれかです。この組み合わせだけでも甚大で、
\( _4C_2\times 9^8=258 280 326\)通りの組み合わせがあります。
2億個の画像を見てこれは綺麗、これは違うを判断することはできません。
注記しておきますが、写像を作る際に\(\alpha,\beta,\gamma,\delta\)の絶対値が1以下である必要はありません。
この条件は恐らく指数関数の発散を最低限防ぐためという予想だと思います。
おおよその傾向として以下の推測が出来ました。
\(\kappa, \lambda\)を\(\alpha,\beta,\gamma,\delta\)のゼロではないどれかだとすると、
- \({\rm Re}{\kappa}={\rm Re}{\lambda}=0\)の時、つまらない画像になる
- \({\rm Im}{\kappa}={\rm Im}{\lambda}=0\)の時、つまらない画像になる
- \(\kappa=0\)または\(\lambda=0\)はつまらない画像になる
- \(\alpha=\beta=0\)または\(\gamma=\delta=0\)はつまらない画像になる
だと感覚的にわかったので、これらを除外します。
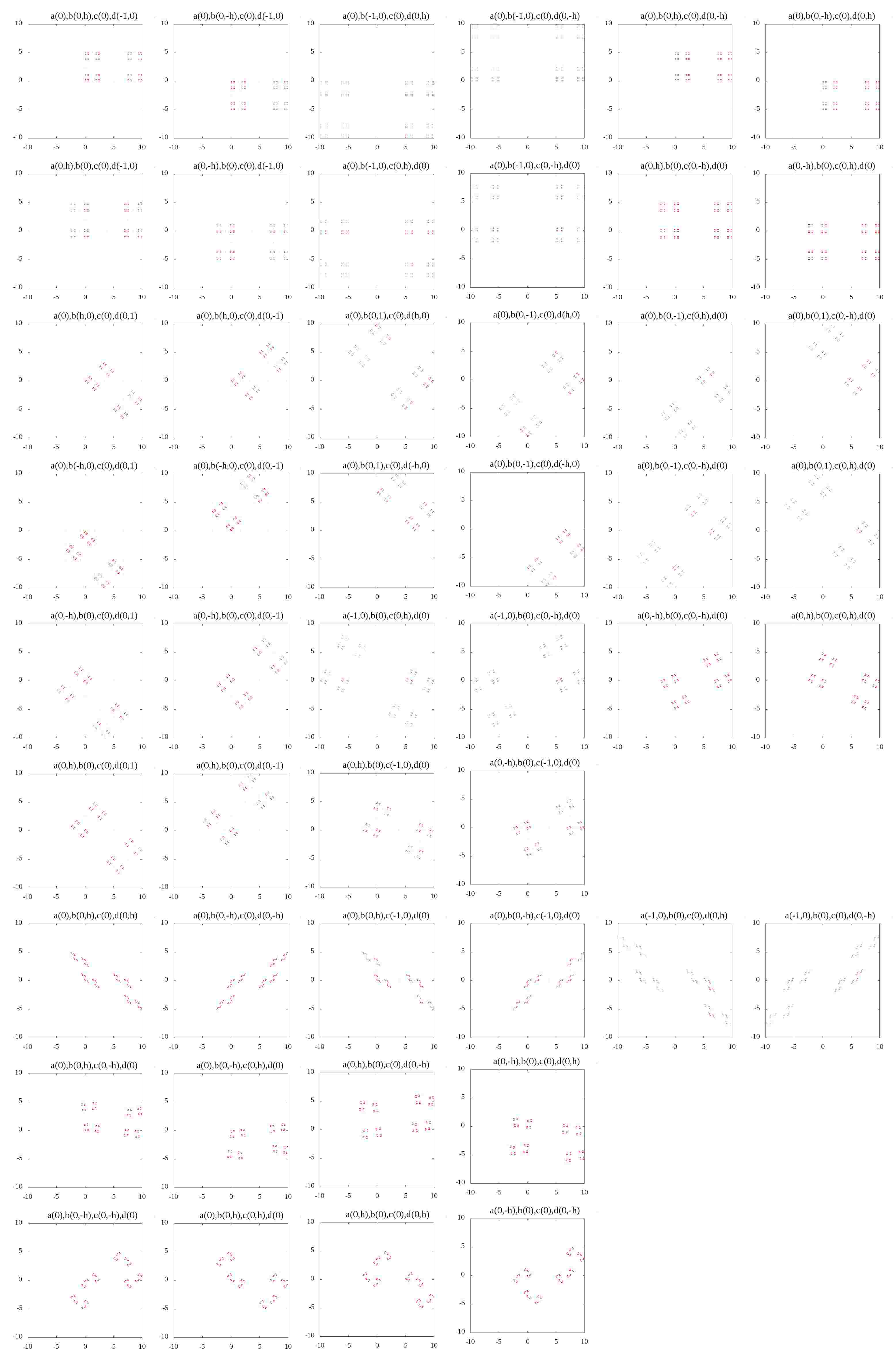
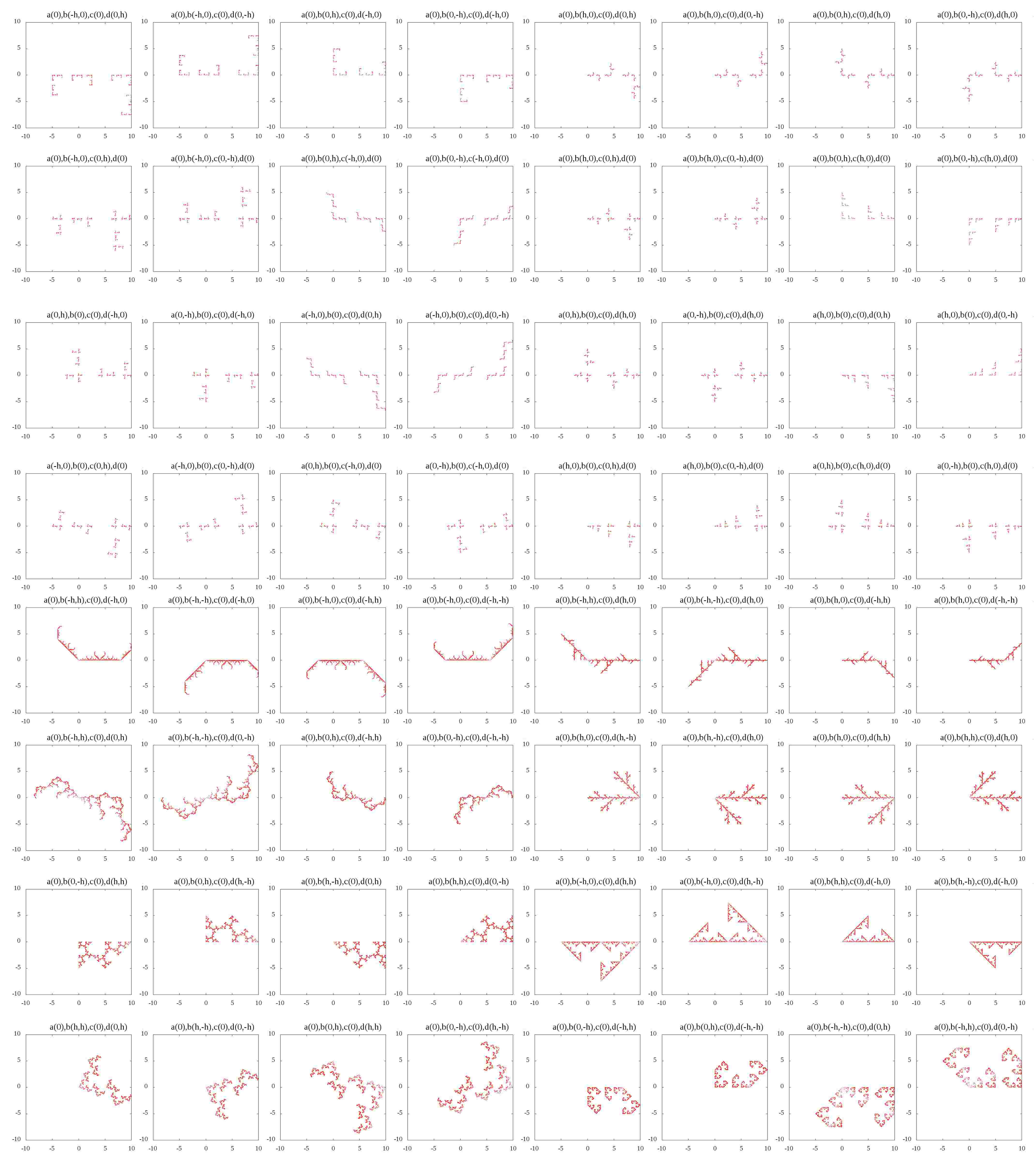
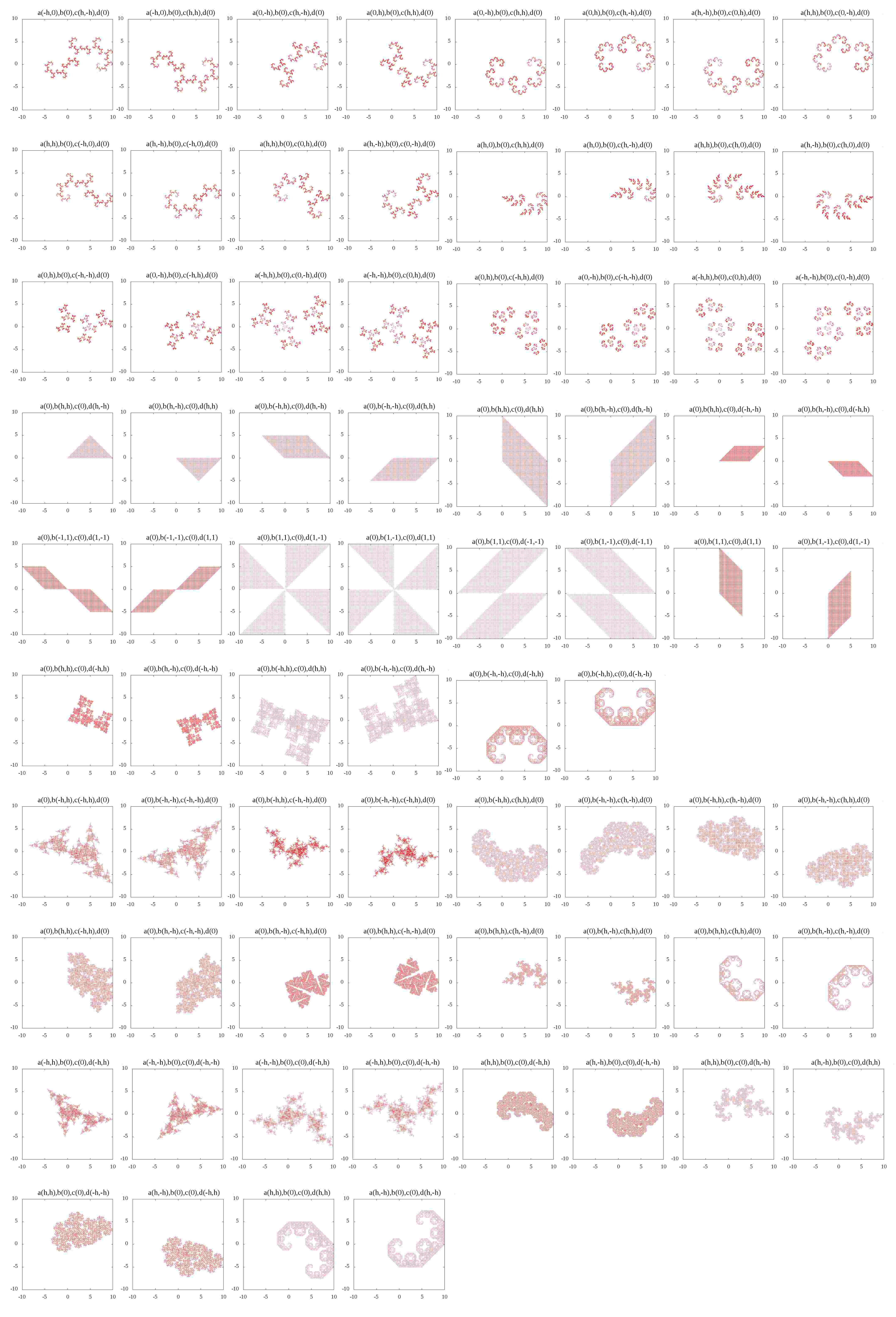
さらに、\(0,\pm 0.5, \pm1\)のみを考えて僕自身が綺麗だと思う画像のみを集めてみました。
都合上、\(h=0.5\)と置いています。
また、範囲を固定するために点の撮りうる最大の値を固定してあります。
考察
簡単に分かったことがあります。図の傾向は0.5の数や1の数に密接に関係しているようです。
ここで考えている4つのパラメータは、\(\kappa, \lambda\)のそれぞれ実部、虚部です。
ここで、この4つのパラメータを\((i,j,k,l)\)の組と考えましょう。括弧内の順番は特に関係なく、4つのパラメータの内どれか、を意味するとします。
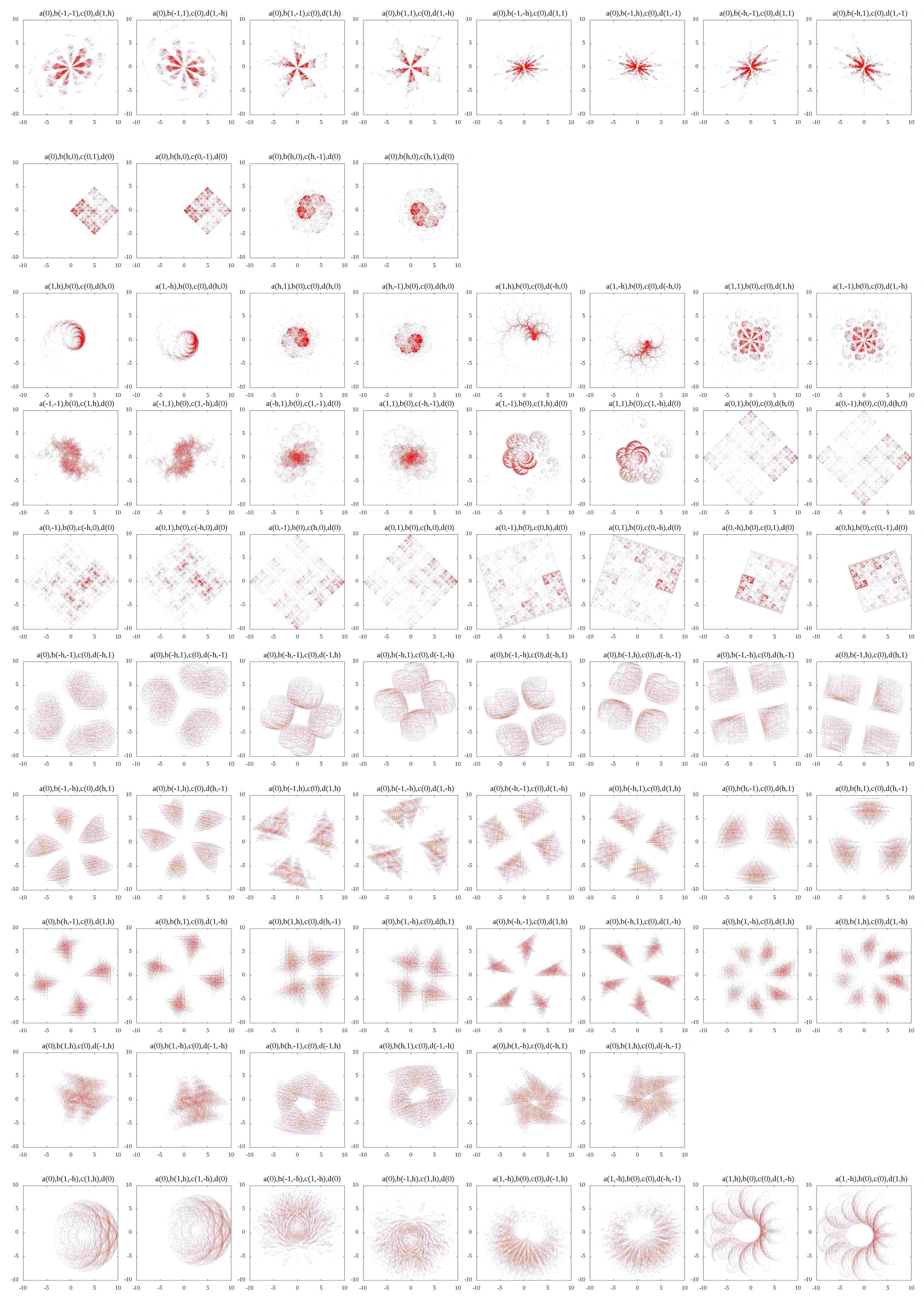
例えば、初めの方にある、長方形の頂点に点が置かれたような図が得られるとき、4つのパラメータの組は\((0,0,\pm 1,\pm h)\)の組み合わせが多いことに気が付きます。
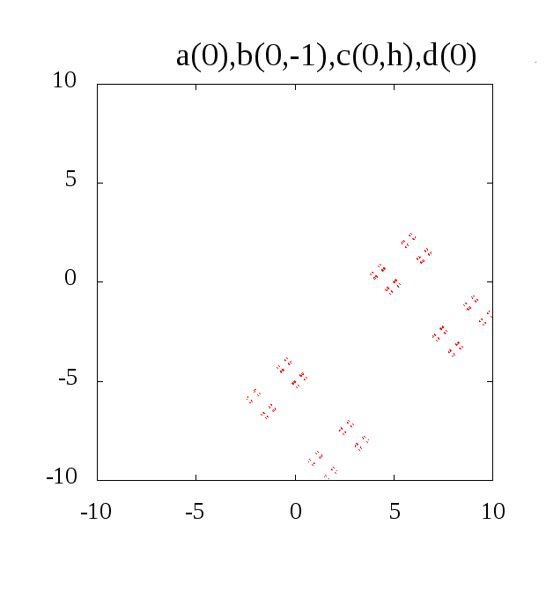
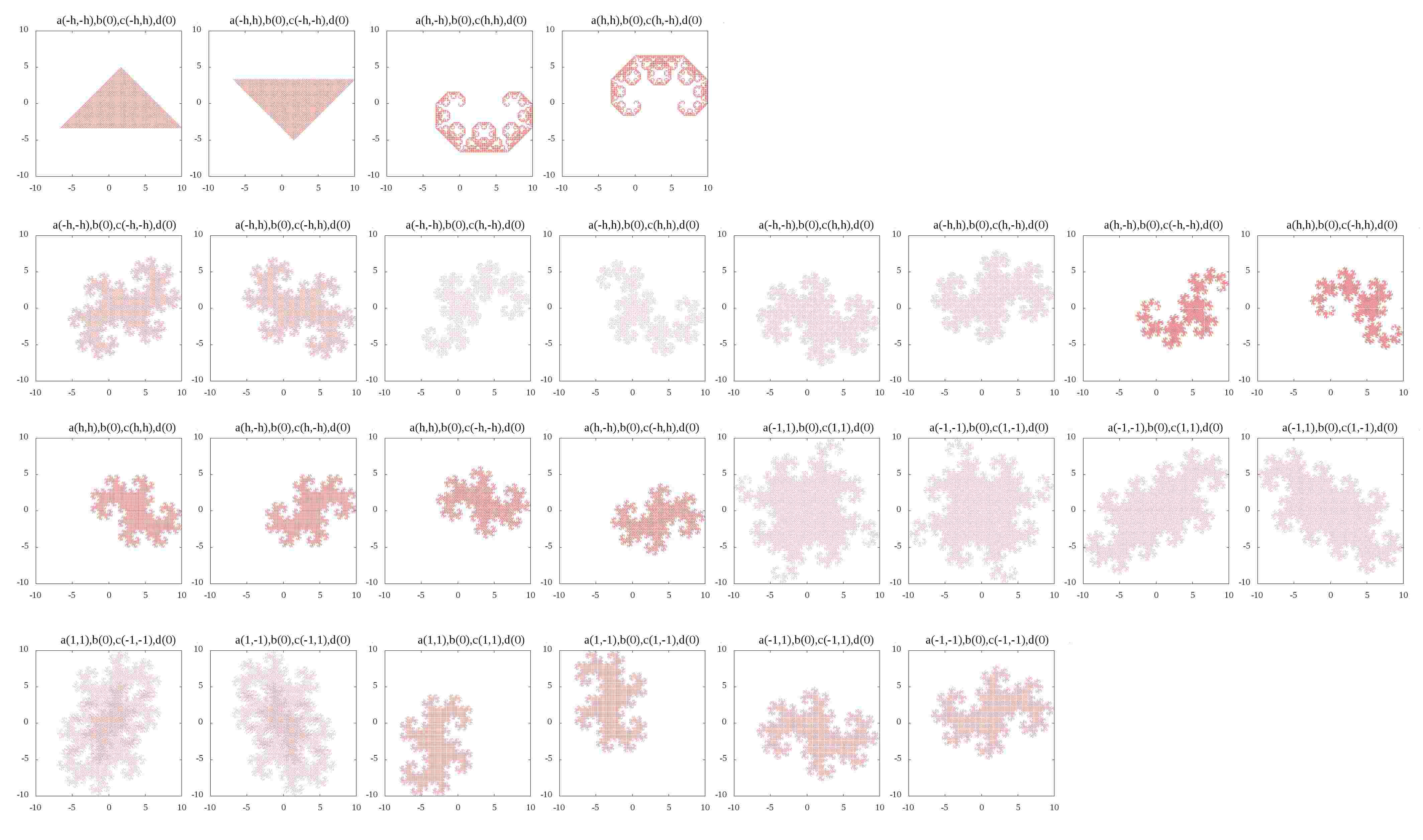
続いて、これぞフラクタルだ、と思わせる形は\((\pm h, \pm h, \pm h, \pm h)\)、

最後の方の紋様のような模様では\((\pm 1, \pm 1, \pm 1, \pm 1)\)で埋められているようです。
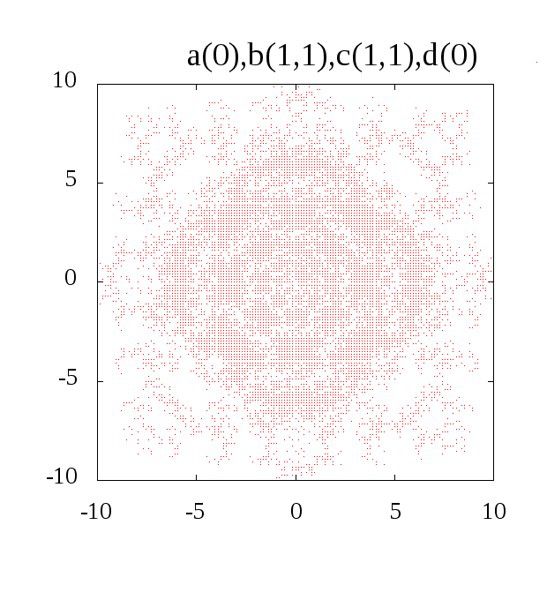
恐らく、フラクタル的な雰囲気を持つ画像は、\(\kappa, \lambda\)の各々の値が有限で、絶対値が1とか、そんな時に出てくるのではないでしょうか。
今回調べた範囲のは、\(\alpha,\beta,\gamma,\delta\)のうち2つがゼロ、しかも0.5刻みしか許さないという非常に強い条件を入れた範囲です。
これだけでも膨大な数になることが、上の画像の量を見ただけで分かるでしょう。
本来は\(\alpha,\beta,\gamma,\delta\)がゼロではなくて良く、0.5刻みである必要もなく、実数ですから、今回調べたのはごくごく一部です。
綺麗な画像の定義があいまいなのもいけませんね。どうにかしてみたいものです。
また、同じく@snowy_treeさんが、
.@sig_colon 101選作りました。パラメーターで知りたいのあればどうぞ. pic.twitter.com/XGDZIATJVN
— あすなろ (@snowy_tree) 2016年11月20日
という綺麗なパラメータを集めたgifを公開してくれました。凄く綺麗なパラメータがたくさんあります!
とんでもなく綺麗な写像を見てみたいものです。
参考文献
[1]Dimensión, Análisis Multifractal y Aplicaciones
内の「3. Fractals in Mathematics (Hata)」
※中を見ると掲載されている元の論文はPatterns and Waves pp.259-278(1986)という論文のようです。
畑さんは、写像を拡張し統一的に扱おうとしたようです。なので、畑さんがこの写像を1から全て作った、というのは語弊があるかと思います。
[2]カオス #3,#6,#10,#11,#12,#13,#14,#15,#27畑政義写像 -主にコーディング
Web上で畑政義による写像が書けるサイトがありますので紹介いたします。
[2]畑政義写像で遊ぼう -救済に紹介されています。
(Play with Hata-map / 畑政義写像で遊ぼう)
[3]畑政義写像(1) -閃光的網站・弛緩複合体 Blog
※1. ただし、若干異なっています。
n回繰り返した時のみの写像の集まりのはずですが、どうやらn回に至るまでの点もプロットしているようです。n+1回繰り返しても似た画像しか出てこないのでまぁ、問題ないと思いますが…。
※2. また、どちらも上下が逆さまになっています。時々この上の二つで作成した値を私のプログラムに入れても再現できない場合があります。これに起因する問題なのか、別の要因なのかははっきりしません。