最速・高精度の数値積分

無償で公開されている1次元数値積分コードで優秀なルーチンは何か？を見つけます。

何よりも早さが足りない人へ。
言語はFortranです。

まとめ

QUADPACK(ルーチン名dqag, key=2,6)
http://www.netlib.org/quadpack/
が広い場合で使えて優秀です。しかもパブリックドメイン！
直ぐ使えるように私が変更を加えたQUADPACKプログラムが下の方にあります。

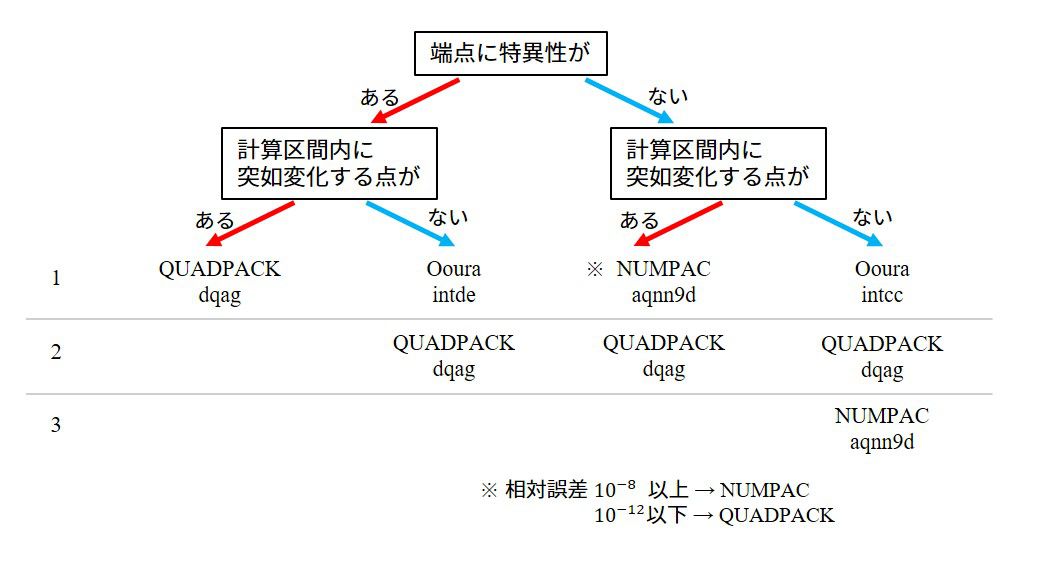
もう少し問題に対して最適化をしたければ以下のチャートに従ってください。

この一長一短は非常に極端です。
被積分関数に特定の性質があるのであればその方法を使うべきです。
特定の積分範囲、被積分関数が(重み関数)×(多項式)で表現されるのであれば、ガウス求積法が最速で高精度です。
被積分関数が端点で特異性(例えば端点で$x^{-1/2}$)を持つのであれば二重指数関数型数値積分が最速で高精度です。

ここでは、無償公開されている自動積分コードのみを比較します。
使っている手法が実行したい積分とマッチすれば自動積分は最善の方法です。

比較するコードは以下のものです。

比較コード
パッケージ or 作成者（ルーチン名）	積分戦略	積分の手法
NUMPAC(aqnn9d) http://www2.itc.nagoya-u.ac.jp/center/ja/numpac/	適応型	ニュートン・コーツ9点則
NUMPAC(rombgd) http://www2.itc.nagoya-u.ac.jp/center/ja/numpac/	非適応型	ロンバーグ積分
Ooura(intcc) http://www.kurims.kyoto-u.ac.jp/~ooura/intcc-j.html	非適応型	クレンショウ-カーティス積分
Ooura(intde) http://www.kurims.kyoto-u.ac.jp/~ooura/index-j.html	非適応型	二重指数関数型数値積分
QUADPACK(dqag,key=2) http://people.sc.fsu.edu/~jburkardt/f_src/quadpack/quadpack.html	適応型	7-15点ガウス-ルジャンドル、ガウス-クロンロッド求積法
QUADPACK(dqag,key=6) http://people.sc.fsu.edu/~jburkardt/f_src/quadpack/quadpack.html	適応型	30-61点ガウス-ルジャンドル、ガウス-クロンロッド求積法
Sikino(romberg) https://slpr.sakura.ne.jp/qp/nc-integral/	非適応型	ロンバーグ積分
Sikino(de) https://slpr.sakura.ne.jp/qp/de-fourmula/	非適応型	二重指数関数型数値積分
Sikino(rkf451) https://slpr.sakura.ne.jp/qp/runge-kutta-ex/	適応型	ルンゲ-クッタ-フェールベルグ法による積分

　適応型というのは、被積分関数の形に依って分点を増やす減らすを決める自動積分法です。
非適応型というのは、被積分関数の形に依らず分点を増やす減らすを決める自動積分法です。

[adsense1]

ライセンスについて

各プログラムの利用条件に関して注記しておきます。
私の理解であるので、解釈に間違いがあるかもしれません。最終的な判断は個人の判断にお任せします。

NetlibにあるQUADPACK
http://www.netlib.org/quadpack/
パブリックドメイン。Fortran数値積分用のパッケージ。
著作権表示無しに、商用非商用問わず複製、利用、改変、配布して良いもの。
ただし、所有権や人格権などを侵してはならない。

私がNetlibにあるQUADPACKをfortran90用に改変したものを置いておきます。下のQUADPACKプログラムへ。

people.sc.fsu.eduにあるQUADPACK
GNU LGPLライセンス。Fortran数値積分用のパッケージ。

! Licensing:
!
! This code is distributed under the GNU LGPL license.

とあり、http://people.sc.fsu.edu/~jburkardt/f_src/quadpack/quadpack.html
にコードがあります。こちらの方が使うまでが簡単ですが、ライセンスがあることが面倒。

NUMPAC

NUMPACを利用した論文には，NUMPAC利用の記述を記載してください。
また，著者から修正プログラムの提供があったときには置き換えてください。
NUMPAC邦文マニュアル – XML

とあります。著作権表示や複製、利用、改変、配布に関する記述は無いので、これらをするべきではありません。

Ooura’s Mathematical Software Packages
プログラムのreadmeの中に

copyright
Copyright(C) 1996 Takuya OOURA (email: ooura@mmm.t.u-tokyo.ac.jp).
You may use, copy, modify this code for any purpose and
without fee. You may distribute this ORIGINAL package.

とあります。翻訳すれば、
”著作権はTakuya OOURAにあります。どんな目的に対しても無償でコードを使用、複製、改変して良いです。そしてオリジナルパッケージを配布して良いです。”
とあります。
例えば上の説明にあてはまらないため、許諾なしに改変したものを配布してはいけません

本サイト(シキノート)のプログラム
私のは最終的な出版物や何かに、私の著作権表示、利用した旨を記述してもらえれば商用非商用であっても複製、利用、改変、配布して良いです。
論文に使用した場合、表示は要りません。
改変したものを配布したい場合、著作権、責任は改変を行ったものにあります。また、オリジナルのコードはシキノートにあることを注記してください。オリジナルのコード、また改変したものについてもそれによって生じた責任は負いません。

すなわち本当に自由に使えるのはNetlibで公開されているQUADPACKだけです。

比較方法

Kahaner’s 21 test problemsより、問題を抜粋して比較します。
Kahaner’s 21 test problemsとは21個のベンチマーク用の問題で、全て解析解が存在するものです。
これが解けたら大した数値積分プログラムだ！ということです。
被積分関数に特異性や発散などを含んでいる問題です。

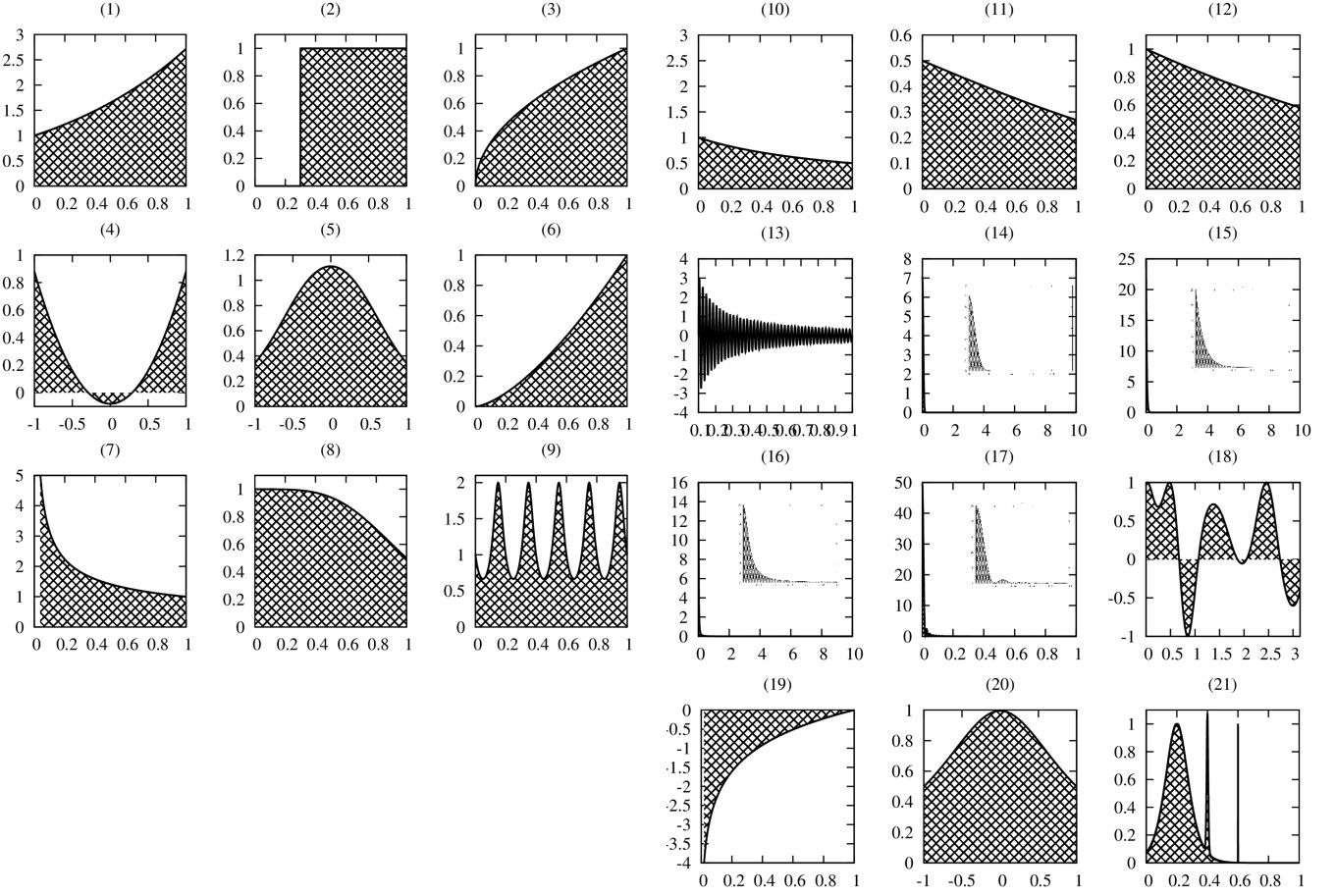
より、以下の10問を選んで比較します。問題の抜粋は私が独断で選びました。

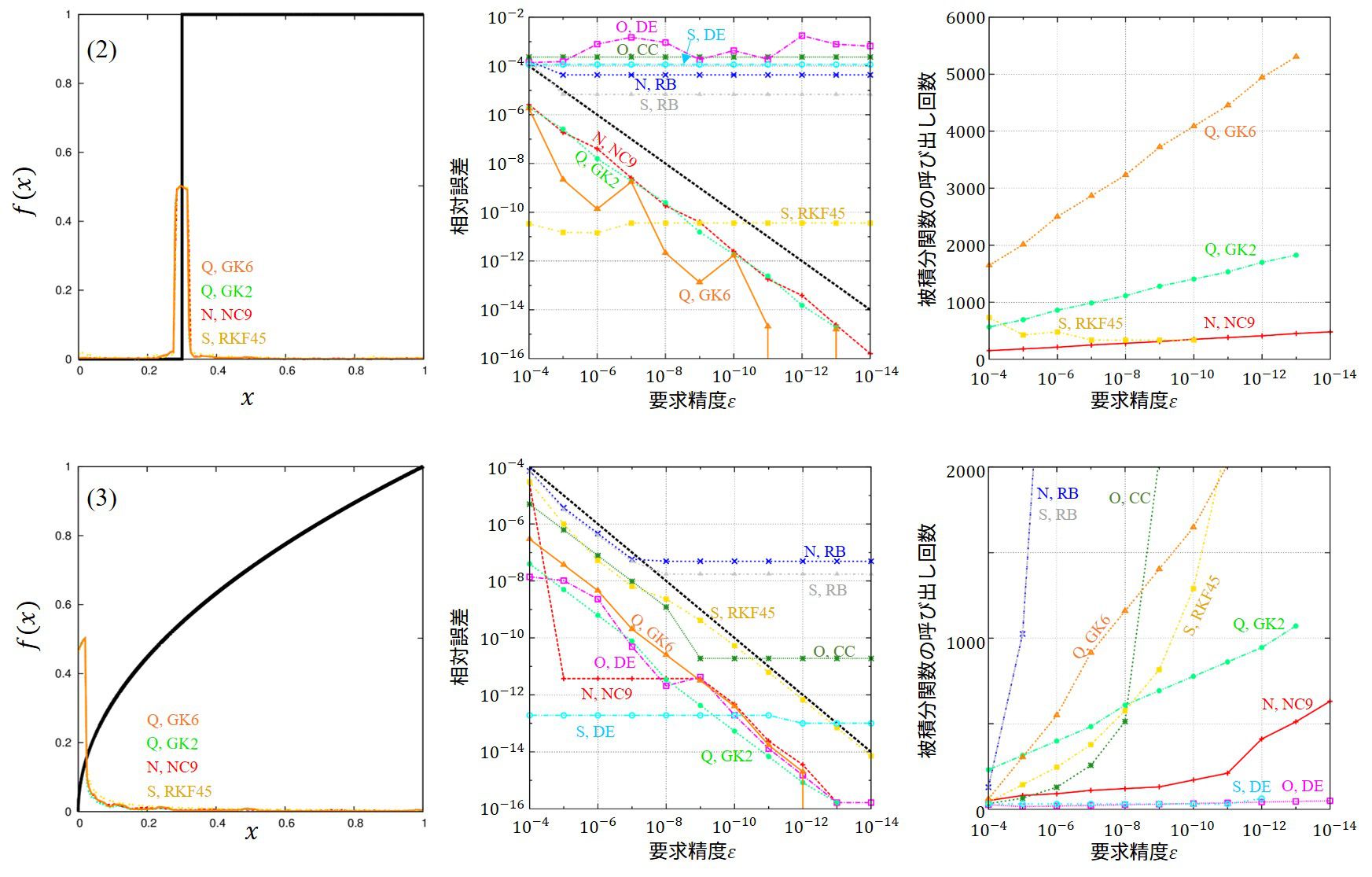
結果

計算結果を並べます。比較は、

積分プログラムに積分区間と精度を要求し、その精度に達したか？
要求精度を実現するまでに被積分関数が評価された回数

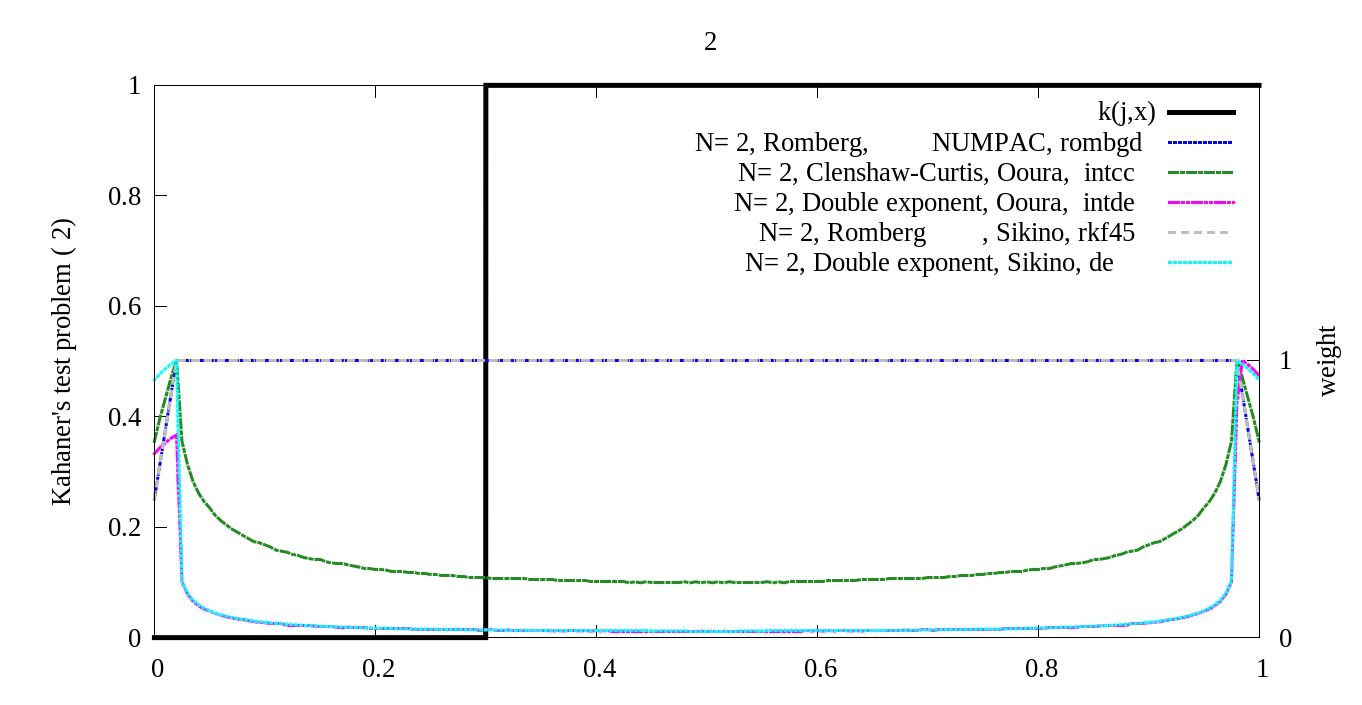
を比較します。また、適応型の積分手法に対して、実際にどの点が評価されているかを知りたかったため、
実際に評価された点達に対し矩形波で畳み込みを行い、最大値を１にするように規格化し比較しました。
これが左から１枚目の画像です。
2枚目は、真値との相対誤差を要求精度$\varepsilon$の関数として、
3枚目は、要求精度が達成された場合の被積分関数の評価回数です。
3枚目が一番重要な情報です。

この問題(2),(3)は被積分関数に不連続性、特異性がある場合の問です。
(2)の有効な手法は適応型の数値積分法であることが分かります。シンプルな問題ですが、大域的に精度を決める自動積分では3-4桁程度にとどまり、全く計算できていません。
(3)は左の端点で一回微分が発散する関数です。最も有効な手法は変数変換型の数値積分、二重指数関数型数値積分法で、次いで適応型の積分法です。一回微分が発散が意味するのは、テーラー展開による誤差評価で、誤差項が発散することを意味しています。

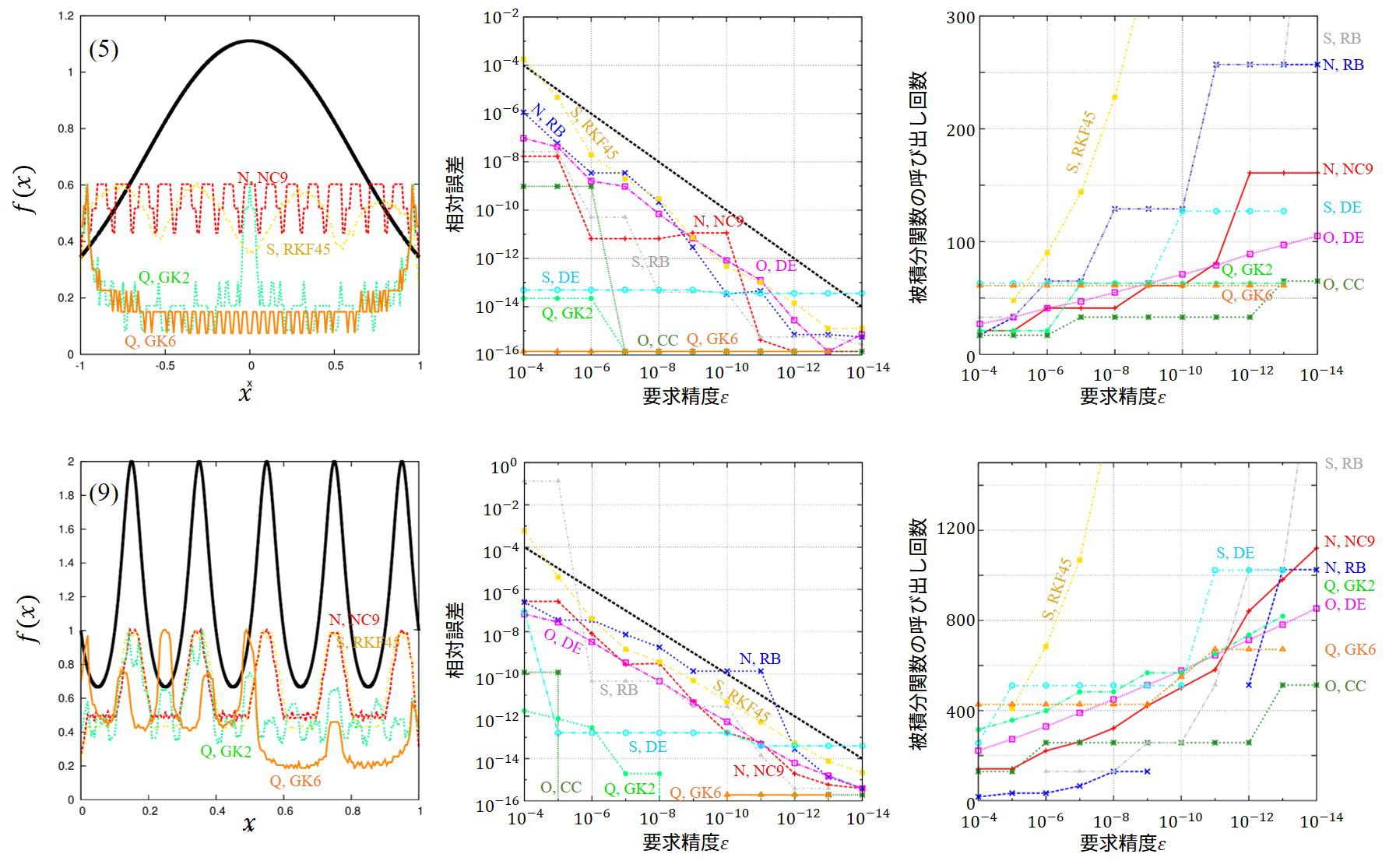
(3)はラグランジュ補間が難しい関数です。ラグランジュ補間が難しい場合、チェビシェフ多項式による補間が有効です。
(9)は振動型の関数です。sin(x)のテーラー展開が難しいように、これもチェビシェフ多項式による補間が有効です。

(13)は早く振動する関数です。関数に節の数が多いため次数の高い手法が必要、もしくは分割するしかありません。
(14)は振動型の関数です。sin(x)のテーラー展開が難しいように、これもチェビシェフ多項式による補間が有効です。

(17)はx=0回りだけに値が存在します。適応型でなければ、局在部分を評価するために要らない部分を増やさなければならない無駄が生じてしまいます。
(18)は程々の振動型の関数です。チェビシェフ多項式による補間が有効です。

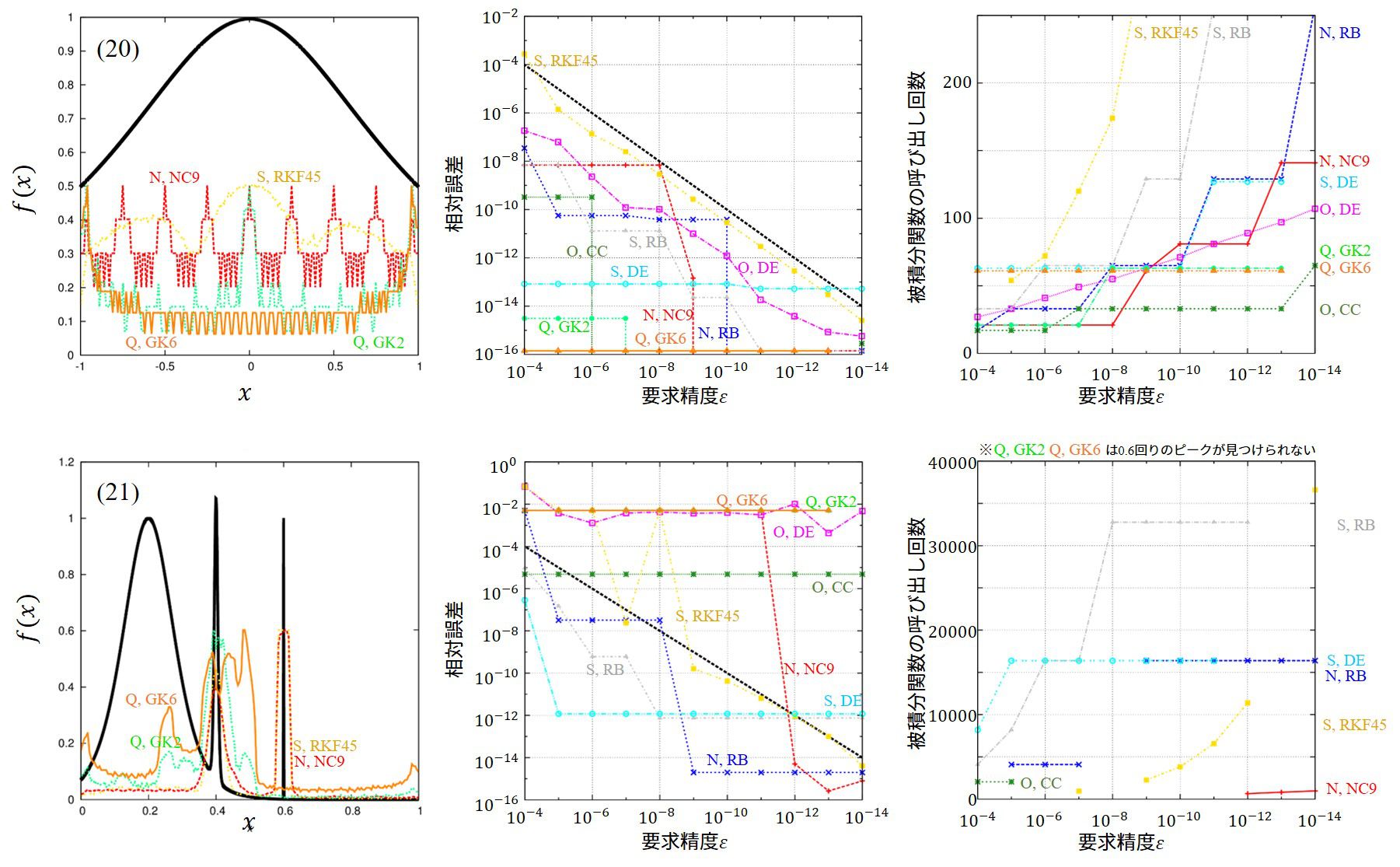
(20)はローレンツ型の関数です。ローレンツ型はラグランジュ補間ではうまく補間されません。
(21)は突如値が大きくなる地点が存在する関数です。うまく変化する点を見つけないと的外れな計算結果になります。

ちなみに

二重指数関数型数値積分が有効な例として
$
\displaystyle \int_0^{1}\sin(1/\sqrt{x})/\sqrt{x}
$
という例題が挙げられます。難しい事には変わりませんが二重指数関数型数値積分だけが出来るのではないことをここに注記しておきます。

二重指数関数型数値積分の凄いところは、適当に作った私のプログラムでさえ有名な積分プログラムと張り合えるという点でしょう。

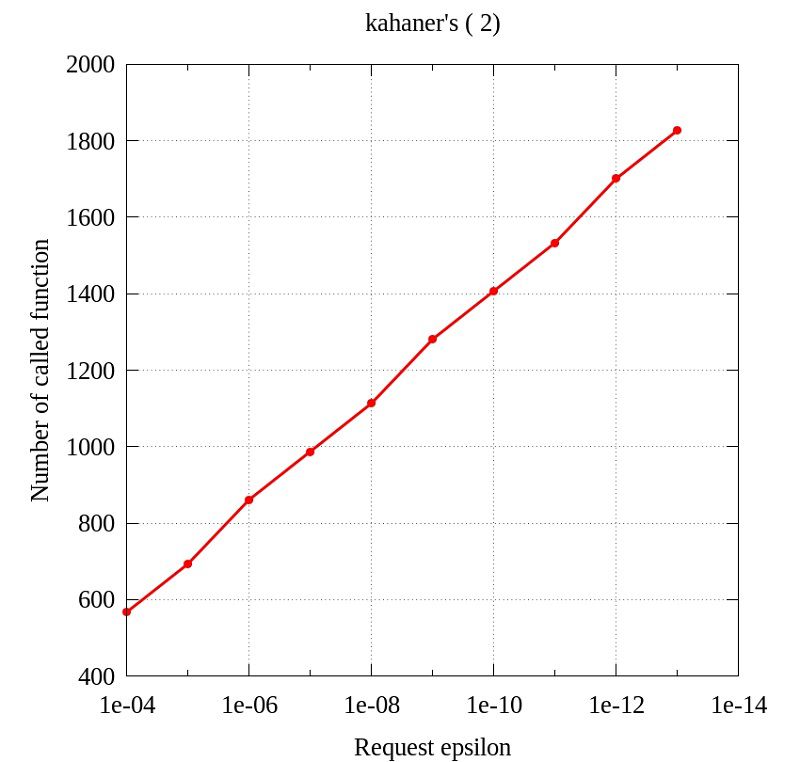
非適応型の数値積分法の重みは被積分関数の形に依存しないで決まることを確認しておきましょう。いつでもこんな感じの重みになります。

まとめです。

問題番号	被積分関数の特徴	最も有効な積分法	次いで有効な積分法
(2)	不連続性	NUMPAC(aqnn9d)	QUADPACK(dqag, key=2)
(3)	端点特異性	Ooura(intde)	NUMPAC(aqnn9d)
(5)	ローレンツ	Ooura(intcc)	QUADPACK(dqag, key=6)
(9)	振動関数	Ooura(intcc)	QUADPACK(dqag, key=6)
(13)	高振動	Ooura(intcc)	QUADPACK(dqag, key=6)
(14)	局在	NUMPAC(aqnn9d)	Ooura(intcc)
(17)	局在、振動	Ooura(intcc)	QUADPACK(dqag, key=6)
(18)	振動	Ooura(intcc)	QUADPACK(dqag, key=6)
(20)	ローレンツ	Ooura(intcc)	QUADPACK(dqag, key=6)
(21)	突如変化する関数	NUMPAC(aqnn9d)	NUMPAC(rombgd)

ある精度で積分の問題を解きたい時に、最高のパフォーマンスを出したければ以下のチャートに従うと良いと思います。ライセンスの問題を含めて、QUADPACKが優秀でしょう。

QUADPACKのkey=2がよいか、key=6がよいかは良く分かりません。上の表にはkey=6が優秀に見えますが、$\sqrt{x}$の積分などでは圧倒的にkey=2が優秀だからです。

QUADPACKプログラム

私が手を加えているので、オリジナルと比較し相違点が生じるかもしれません。
また、使用するにあたっては、私の作成したものと同様、元にしたものが私の物である、と表示さえしていただければ、商用非商用問わず複製、利用、改変、配布してくださって結構です。ただし、責任は負いません。
問題ないと思いますが、もし公開しているプログラムに著作権的にダメな点があればお知らせください。判明次第、ページを非公開にし、早急に対応いたします。

1次元実積分

Quadpackのコード
https://slpr.sakura.ne.jp/qp/supplement_data/quadpack_dqag.f90
と
プログラムのサンプルコード

program main
implicit none
integer::ier
double precision::a,b,s,eps,g
external::g

a=0d0
b=1d0
eps=1d-12

call dqag_k2(g,a,b,eps,s,ier)
write(6,*)s,ier
! ier = 0 : success
! ier > 0 : fail

call dqag_k6(g,a,b,eps,s,ier)
write(6,*)s,ier

stop
end program main

function g(x)
implicit none
double precision::g,x

g=sqrt(x)

return
end function g

g　　：　被積分関数$g(x)$
a,b　：　積分区間$[a,b]$
eps　：　要求する相対誤差
s　　：　$g(x)$の数値積分値
ier　：　ier=0 成功、収束した。
　　　　　ier>0 失敗、収束しなかった。

本来のquadpackには色々な引数がありますが、それを省略するためにdqag_k2、dqag_k6というサブルーチンを挟んでいます。これはquadpack_dqag.f90の中に入っているので参照してください。
dqag_k2は7-15点ガウス-ルジャンドル、ガウス-クロンロッド求積法を用いた適応型の数値積分法です。
dqag_k6は30-61点ガウス-ルジャンドル、ガウス-クロンロッド求積法を用いた適応型の数値積分法です。

コンパイルと実行は

$ gfortran quadpack_dqag.f90 main.f90
$ ./a.out
0.66666666666666718 0
0.66666666666666796 0
$

でokです。積分値が0の時、相対誤差の条件は満たされないためier=2が返ってきます。
問題に応じて無視するかどうか決めてください。

もしも値が存在するはずなのにier=1が帰ってくるようであれば、サブルーチンdqag_k2、dqag_k6の中のlimitの値を増やしてください。こんなふうに。

ier=1
epsabs=-1d0
!limit=200
limit=1000
lenw=limit*4

1次元複素積分

2017/11/02 追記)
複素平面上の点$a=(a_x,a_y)$から、$b=(b_x,b_y)$に至る経路を直線で結ぶ、複素関数$g(z)$の線積分は以下のコードです。

ただし、多価関数は不可能です。偏角の範囲はfortran90では$[-\pi\lt \theta \le \pi]$出なければなりません。

Quadpackのコード
https://slpr.sakura.ne.jp/qp/supplement_data/quadpack_cqag.f90
と
プログラムのサンプルコード

program main
implicit none
integer::ier
double precision::eps
complex(kind(0d0))::a,b,s
complex(kind(0d0)),external::g

a=dcmplx(0d0,0d0)
b=dcmplx(1d0,1d0)
eps=1d-12

call cqag_sk(g,a,b,eps,s,2,ier)
write(6,*)s,ier

stop
end program main

function g(z)
implicit none
complex(kind(0d0))::g
complex(kind(0d0)),intent(in)::z

g=1d0/sqrt(z)

return
end function g

2次元実積分

2018/01/03追）
wolfram alphaによる解析解
http://www.wolframalpha.com/input/?i=%5Cint_%7B0%7D%5E2+%5Cint_%7B0%7D%5E1+sin(x)cos(10y%5E2)+dxdy+10digits
$
\displaystyle \int_{0}^2 dy \int_{0}^1 dx sin(x)cos(10y^2) \approx 0.09975138562
$

Quadpackのコード
https://slpr.sakura.ne.jp/qp/supplement_data/quadpack_dqag2d.f90
と
プログラムのサンプルコード

program main
implicit none
integer::ier,key
double precision::eps
double precision::xa,xb,ya,yb,s
double precision,external::g,h

xa=0d0
xb=1d0
ya=0d0
yb=2d0
eps=1d-8
key=2

call dqag_sk2d(h,xa,xb,ya,yb,eps,s,ier,key)
write(6,*)s,ier

stop
end program main

function h(x,y)
implicit none
double precision::h
double precision,intent(in)::x,y

h=sin(x)*cos(y*y*10d0)

return
end function h

2次元複素積分

2018/01/03追）
wolfram alphaによる解析解
http://www.wolframalpha.com/input/?i=int+from+1%2Bsqrt(-1)+to+3+int+from+-2%2Bsqrt(-1)+to+5+of+exp(-sqrt(x)*y)+dx+dy
$
\displaystyle \int_{1+i}^3 dy \int_{-2+i}^5 dx e^{-\sqrt{x}y} \approx -3.41684-2.47923i
$

Quadpackのコード
https://slpr.sakura.ne.jp/qp/supplement_data/quadpack_cqag2d.f90
と
プログラムのサンプルコード

program main
implicit none
integer::ier,key
double precision::eps
complex(kind(0d0))::xa,xb,ya,yb,s
complex(kind(0d0)),external::g

xa=dcmplx(-2d0,1d0)
xb=dcmplx(5d0,0d0)
ya=dcmplx(1d0,1d0)
yb=dcmplx(3d0,0d0)
eps=1d-6

key=6
call cqag_sk2d(g,xa,xb,ya,yb,eps,s,key,ier)
write(6,*)s,ier

stop
end program main

function g(x,y)
implicit none
complex(kind(0d0))::g
complex(kind(0d0)),intent(in)::x,y

g=exp(-sqrt(x)*y)

return
end function g

3次元実積分

2018/01/30追）
https://slpr.sakura.ne.jp/qp/supplement_data/quadpack_dqag3d.f90

integrate{sin(x)*cos(y*z)*z,{x,1,3},{y,2,4},{z,0,1}} -wolfram alpha
$
\displaystyle \int_1^3 \int_2^4 \int_0^1 \sin(x) \cos(y z) z dz dy dx \approx -0.450 920 512 214 481 28…
$

program main
implicit none
integer::ier,key
double precision::xa,xb,ya,yb,za,zb,s,eps
double precision,external::f

xa=1d0
xb=3d0
ya=2d0
yb=4d0
za=0d0
zb=1d0
key=3
eps=1d-8
call dqag_sk3d(f,xa,xb,ya,yb,za,zb,eps,s,ier,key)

write(6,*)s

stop
end program main

function f(x,y,z)
implicit none
double precision::f,x,y,z

f=sin(x)*cos(y*z)*z

return
end function f

[adsense2]

ベンチマーク用プログラム

自分の持っているプログラムのベンチマークを行いたい場合のプログラムを公開します。

▼ここクリックでこの場に展開

積分プログラムを用意し、以下のプログラムと一緒にコンパイルしてください。
積分のサブルーチンは

call dqag_k2(func,x0(j),x1(j),tol,s,ier)

で呼び出しています。各々の用いたいルーチンの形に合わせて引数を調節してください。

module GBL
implicit none
integer::eqn,count
end module GBL

program main
use GBL
implicit none
integer,parameter::N=10
integer::j,k,k0,ier
double precision::x0(1:N),x1(1:N),tol,s
character(128)::fname
double precision,external::sol,func

tol=1d-12
x0(1:N)=(/0d0,0d0,-1d0,0d0,0.1d0,0d0, 0.01d0,0d0,-1d0,0d0/)
x1(1:N)=(/1d0,1d0, 1d0,1d0,1d0,10d0,1d0,3.1415927d0,1d0,1d0/)

write(fname,'(A,i0,A)')"errcount.d"
open(100,file=trim(fname))

k0=4
do j=1,N
do k=k0,13
tol=10d0**(-dble(k))
eqn=j

count=0
call dqag_k2(func,x0(j),x1(j),tol,s,ier)
write(100,'(3e30.17e3,i10)')tol,s,sol(j),count

enddo
write(100,*)
enddo

stop
end program main

function sol(n)
implicit none
integer,intent(in)::n
double precision::sol,s

if(n.eq.1)s=0.7d0
if(n.eq.2)s=2d0/3d0
if(n.eq.3)s=1.58223296372967293312d0
if(n.eq.4)s=1.15470066904371304341d0
if(n.eq.5)s=0.0090986452565692970698d0
if(n.eq.6)s=0.500000211166100039341d0
if(n.eq.7)s=0.112139569626709460839885d0
if(n.eq.8)s=0.8386763233809718250439d0
if(n.eq.9)s=1.564396444069049773091d0
if(n.eq.10)s=0.2108027355005492773756d0

sol=s

return
end function sol

function func(x)
use GBL
implicit none
double precision,intent(in)::x
double precision::func,t

if(eqn.eq.1)then
func=x/0.3d0
if(func.ge.1d0)then
func=1d0
else
func=0d0
endif
elseif(eqn.eq.2)then
func=sqrt(x)
elseif(eqn.eq.3)then
func=1d0/(x*x*x*x+x*x+0.9d0)
elseif(eqn.eq.4)then
func=2d0/(2d0+sin(31.4159d0*x))
elseif(eqn.eq.5)then
func=sin(314.159d0*x)/(3.14159d0*x)
elseif(eqn.eq.6)then
t=50d0*3.14159d0*x*x
if(t.le.700d0)then
func=sqrt(50d0)*exp(-t)
else
func=0d0
endif
elseif(eqn.eq.7)then
t=50d0*3.14159d0*x
func=50d0*(sin(t)/t)**2
elseif(eqn.eq.8)then
func=cos(cos(x)+3d0*sin(x)+2d0*cos(2d0*x)+3d0*sin(2d0*x)+3d0*cos(3d0*x))
elseif(eqn.eq.9)then
func=1d0/(x*x+1.005d0)
elseif(eqn.eq.10)then
t=0d0
t=t+1d0/((cosh(10d0*(x-0.2d0)))**2)
t=t+1d0/((cosh(100d0*(x-0.4d0)))**4)
t=t+1d0/((cosh(1000d0*(x-0.6d0)))**6)
func=t
elseif(eqn.eq.11)then
func=sin(1d0/sqrt(x))/sqrt(x)
endif

count=count+1

return
end function func

上のプログラムを実行すると、ファイル”errcount.d”が生成されます。この状態で、下のgnuplotのコード(例えばファイル名”count.plt”に記述)

j=$0
knum(n) = (n==1 ? 2 :\
(n==2 ? 3 :\
(n==3 ? 5 :\
(n==4 ? 9 :\
(n==5 ? 13 :\
(n==6 ? 14 :\
(n==7 ? 17 :\
(n==8 ? 18 :\
(n==9 ? 20 :\
(n==10 ? 21 :\
999 ))))))))))

set format x "%2.0e"
set format y "%g"
set log xr

set yl "Number of called function"
set xl "Request epsilon"
set title sprintf("kahaner's (%2d)",knum(j))
set xr[1e-14:1e-4] reverse

set grid
unset key
set size ratio 1

plot "errcount.d" every :::j-1::j-1 u 1:(abs(($$2-$$3)/$$3) < $$1 ? $$4 : 1/0) w lp lw 3 ps 1 pt 7 lc 2 ti " Quadpack , kahaner, dqag "

をgnuplot上で

call "count.plt" 1

とやると3枚目の画像がプロットされます。引数1は私が選んだ問題のインデックスをあわらし、1~10までの値を入れることが出来ます。quadpack, k=2の場合は

という画像が得られます。

参考文献

QUADPACK Netlibhttp://www.netlib.org/quadpack/
QUADPACK_DOUBLE Numerical Integration http://people.sc.fsu.edu/~jburkardt/f_src/quadpack_double/quadpack_double.html
NUMPAC http://www2.itc.nagoya-u.ac.jp/center/ja/numpac/
Ooura’s Mathematical Software Packages http://www.kurims.kyoto-u.ac.jp/~ooura/i
シキノート https://slpr.sakura.ne.jp/qp/nc-integral/

kahaner’s 21 test problemに関して
Takemitsu Hasegawa, Susumu Hibino, Yohsuke Hosoda and Ichizo Ninomiya,
“An extended doubly-adaptive quadrature method based on the combination of the Ninomiya and the FLR schemes”

幸谷智紀、鈴木千里 “補外法に基づく数値積分法の実装と性能評価”

（更新停止）

最速・高精度の数値積分

まとめ

もくじ