1次元時間依存シュレーディンガー方程式を確実に解くことを目的とします。
本稿の方針は
計算時間が掛かってもいいので、高精度に解く
ことを主眼においています。対象とする問題は、
ポテンシャルに空間的、時間的に不連続な点があっても高精度に解く
事を目的とします。
ポテンシャルが滑らかで、変なことが起こらないのならば、空間や時間を離散化して解く
クランク=ニコルソン法による時間発展が簡単で優秀な方法です。
本稿では導出する過程では\(N\)次元の問題として扱っていますが、プログラムは1次元の問題のみです。
方針
空間に関する積分を適応型数値積分、時間に関する積分を適応刻み幅陽的ルンゲ=クッタ法で行います。
時間依存しないシュレーディンガー方程式は適応型数値積分であるQUADPACKを使うことで求められます。
詳しくはこちらへ。
解法
原子単位系における時間依存シュレーディンガー方程式は
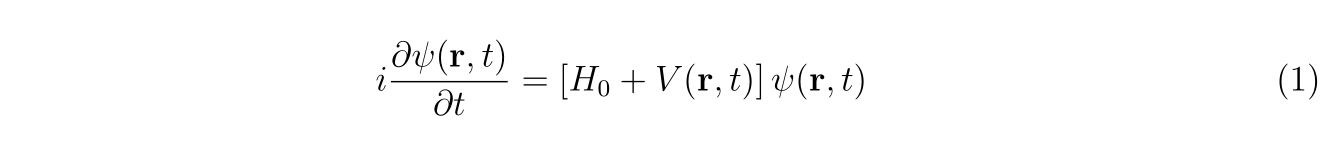
として書けます。
波動関数を
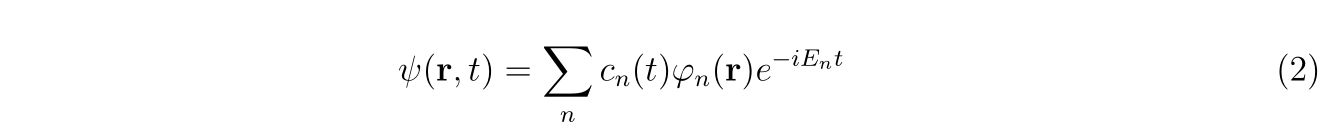
のように展開します。ここで、基底関数\(\varphi_n(\mathbf{r})\)はハミルトニアン\(H_0\)の固有関数で、以下の固有値問題
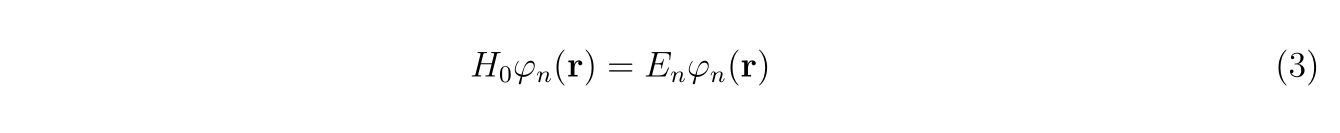
の固有値\(E_n\)に属する固有関数です。
この固有関数は以下の通り規格化されているとします。
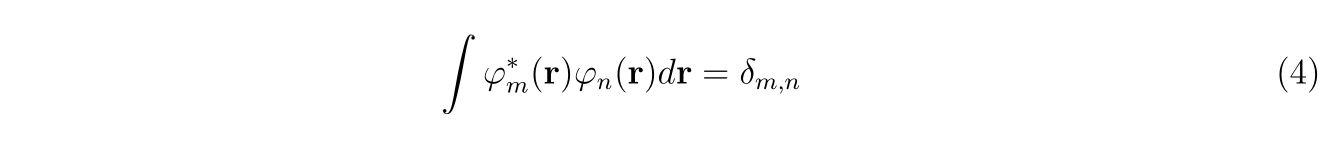
関数で展開するのはハミルトニアンに含まれる空間に対する二階微分を解析的に行い、消す為です。
式(1)に代入すると、
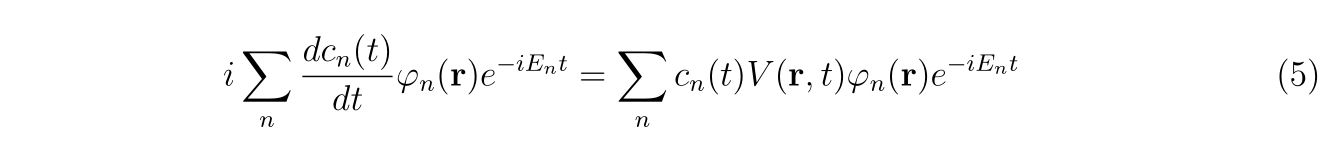
となり、左から\(\varphi^*_m(\mathbf{r})\)を掛けて全空間で積分すると
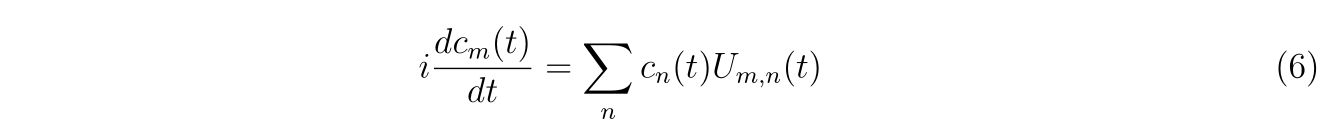
という式が得られます。ここで、\(U_{m,n}(t)\)を
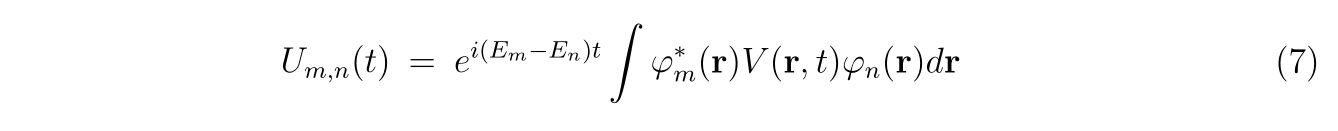
と書きました。
この\(U_{m,n}(t)\)は
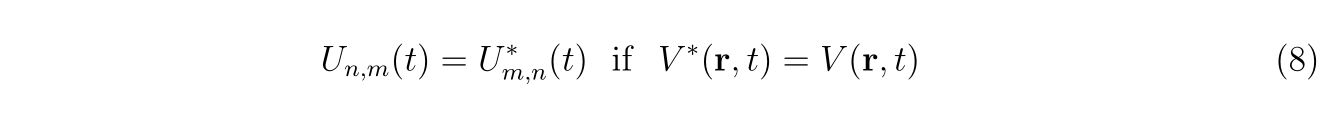
の性質を満たします。すなわち、ポテンシャル\(V(\mathbf{r},t)\)が実数値関数であれば、\(U_{m,n}(t)\)はエルミート行列となります。行列形式で書くとすれば、
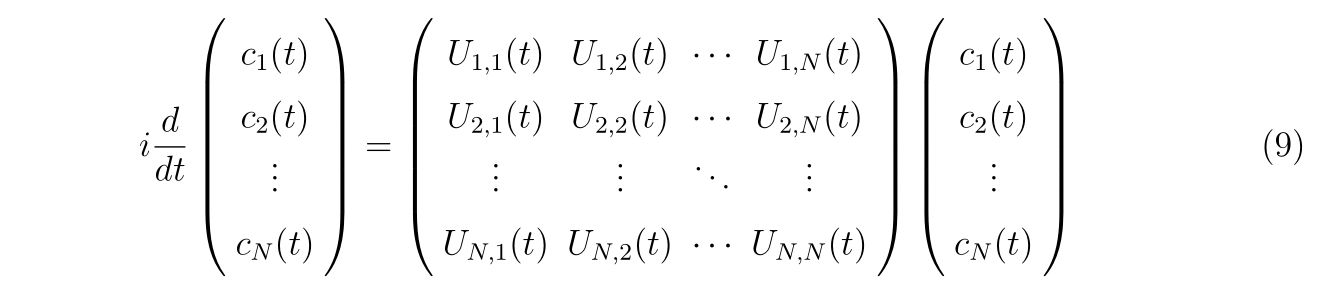
と表せられます(補遺1)。
ここでは行列形式で書いても見やすくなるだけで、今回は使わないので、式(6)を高精度に解くことに集中します。
高精度に解くために
この問題を解くために高精度に求めなければならない重要な部分は
- 空間に対する積分
\(\displaystyle
\int \varphi^*_m(\mathbf{r})f(\mathbf{r})\varphi_n(\mathbf{r})d\mathbf{r}
\)
と - 時間に対する積分(連立微分方程式)
\(\displaystyle
\frac{d c_m(t;c_1,~\cdots,c_{N})}{dt}=F_m(t;c_1,~\cdots,c_{N})
\)
という箇所を、不連続箇所があっても高精度に求める手法を使えばよい訳です。
空間に関してはQUADPACKによる適応型の数値積分, 時間に関しては刻み幅制御のルンゲ=クッタ法を用いることで対処します。
各々の詳細は以下のページをご覧ください。
最速・高精度の数値積分
ルンゲクッタ法の説明と刻み幅制御
ここまで確実に解けると仮定すると、精度の不安は基底関数の数だけに依存します。
基底関数の数を積めば積むほど精度が高い計算が出来ますが、計算時間が莫大になります。
ここは計算機の性能と折り合いをつけるしかありません。
ここから考える数値計算上の基底関数\(\varphi_n(x)\)は計算区間の端でゼロになるsin基底関数で、区間[x_a,x_b]で定義され、
\(\displaystyle
\varphi_n(x)=\sqrt{\frac{2}{x_b-x_a}}\sin\left(n\pi\frac{x-x_a}{x_b-x_a}\right)
\)
です。これは、固有値問題
\(\displaystyle
-\frac{1}{2}\frac{d^2}{dx^2}\varphi_n(x)=E_n\varphi_n(x),~~E_n = \frac{1}{2}\left(\frac{n\pi}{x_b-x_a}\right)^2
\)
境界条件
\(\varphi_n(x_a)=\varphi_n(x_b)=0\)
の元での解となっています。
さて、定式化は終わりましたので、あとはプログラムして解くだけです。
莫大な計算時間
問題は計算時間が膨大にかかりすぎる事です。
計算時間を評価してみます。
・次元数を\(D\)
・1次元辺りの基底関数の数は\(N\)
・合計\(N^D\)元1次連立微分方程式を解く
・1つの連立微分方程式の右辺を計算するのに\(N^D\)個の積分
・適応刻み幅ルンゲクッタ法を\(N_{t}\)回繰り返す
・適応刻み幅ルンゲクッタ法は時間1ステップ辺り\(5\)回評価
・積分は空間の分点数\(N_{\mathbf{r}}^D\)回に比例
・ポテンシャルが対称行列であることを利用すれば\(1/2\)倍
・CPU個数を\(N_{\mathrm{cpu}}\)とし、完璧に並列計算が行われれば\(1/N_{\mathrm{cpu}}\)倍
・関数を1回呼び出すのに必要な時間を\(t_f\)
であるので、全計算時間(関数が評価される回数に比例する、と考える)は
\(\frac{5}{2N_{\mathrm{cpu}}}\times N^D_{\mathbf{r}}N_{t}N^{2D}t_f\)と求められます。
現実的な量で計算時間を見積もってみます。
10[原子単位]秒の時間発展を区間20[原子単位]メートルで計算することを考えます。
\(D=1,~ N_{\mathbf{r}}=1000,~N_{t}=2000,~N=50,~N_{\mathrm{cpu}}=1\)とすると、\(1.25\times 10^{10}\)回関数を呼び出さなければなりません。
手持ちのノートパソコン(1.9GHz、1コア使用)で、\(2.5\times 10^8\)回の関数\(f(x)=\sin(x)\)の呼び出しに掛かるCPU時間を測ると約7[cpu秒]かかりました。
ということは、関数を1回呼び出すのにかかる時間\(t_f\)は約\(3\times 10^{-8}\)秒です。
よって、\(1.25\times 10^{10}\)回の関数の呼び出しだけで約400秒、すなわち8分かかります。
現実には他の処理も入るので、8分は絶対にかかる、という事です。
仮にCPUが10個あれば40秒、CPU速度が倍程度の物を使えば20秒位になるでしょうか。
まぁまぁ受け入れられる時間になります。
2次元を計算しようと思ったら基底関数が二乗、かつ空間の分点も二乗になるので、CPUが10個,4GHz近くのCPUを使えても\(20\times 1000\times 50=1000000\)秒程度、すなわち11日です。
11日の計算は現実的ではありません。
二乗で効いてくる基底関数の数を減らすか、空間の積分の精度を犠牲にする、CPUを増やす等の対策をしなければなりません。
また、ここで示した時間は最低かかる時間ですので、実際に動かすのであればこれ以上は確実にかかるでしょう。関数の中の関数を呼び出す等の操作があれば倍々に増えていくのです。
計算量を減らす工夫
ポテンシャルが変わらない場合、\(U_{m,n}(t)\)の積分は、前の時刻と値が変わらないのでいちいち計算するのは無駄です。
数値的に”ポテンシャルが変わっていない”という情報を取り出すことが出来れば、この無駄を排除することが出来ます。
”ポテンシャル関数が変わっていない”というのはどうすれば評価できるのでしょうか?
私が考えたのは、Quadpackの自動積分を行う時に評価された引数の点における関数の値が全て一致すれば関数が変わっていない、と判断するという評価方法です。
実際にこれはうまく行きまして、ポテンシャルが一度だけ切り替わる、という問題に対して計算時間が
1085[CPU sec] → 25[CPU sec]
にまで減少しました。約1/50の計算時間になりました。
先ほどの11日で~と言っていたのはこの工夫をし無ければ、ですので、ポテンシャルの変化が殆どない問題に限れば1時間程度で計算が終わる、ということです。
もちろん、ポテンシャルが変化し続ける場合も試しましたが、変化はほぼありません。
83[CPU sec] → 84[CPU sec]
程度になりました。
この場合は2次元の例で出した通り、11日間掛かる推測です。
初期状態の準備
式(6)を解こうとしても初期条件が与えられなければ数値的に解くことは出来ません。
初期条件で良く使われるのは、1)解析的な解を与える場合と 2)系の固有状態を与える場合の2種類があります。
-
解析的な解を与える場合
この場合、時間発展を考える場合、上記の時間発展方法ではsin関数基底に射影して係数\(c_n(t)\)を求めなければなりません。
時刻\(t=t_a\)で初期状態\(\psi(x,t_a)\)が解析的に与えられた場合、係数\(c_n(t)\)は、
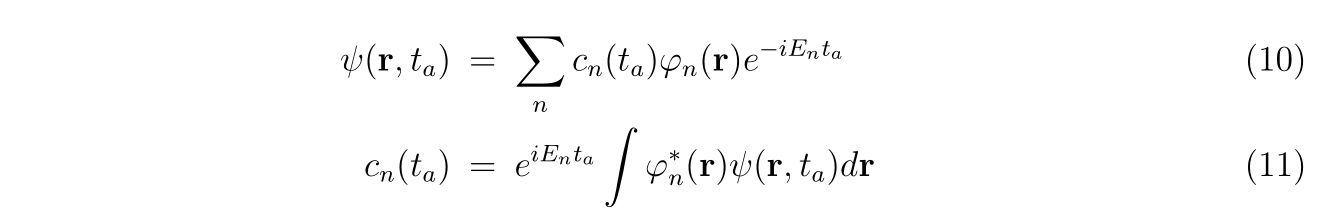
として与えられます。 -
系の固有状態を与える場合
この場合は時刻\(t_a\)のポテンシャル中の時間依存しないシュレーディンガー方程式
\(\displaystyle
\left[H_0 + V(\mathbf{r},t_c)\right]\phi_n(\mathbf{r})=E’_n\phi_n(\mathbf{r})
\)
を実際に解かなければなりません。
そのためには、時間発展に使う基底と同じ基底\(\varphi_n(\mathbf{r})\)で展開し、対角化するのが賢い方法です。
すなわち、

として展開し、ハミルトニアンを行列表示にし、対角化して固有値、固有ベクトルを得ればいいのです。
計算の解析
計算結果を解析するにあたり、ある時刻の固有関数系の基底にどの位存在確率があるかという情報が良く使われます。
初期状態で利用した固有状態の存在確率を調べましょう。
今、求めたいのは時刻\(t_c\)のポテンシャル中の固有関数で展開した時の係数\(a_m(t)\)を求める事です。
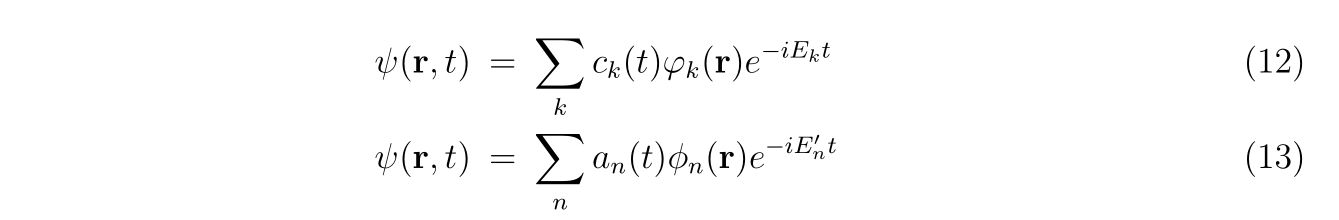
ここで、\(\phi_n(\mathbf{r})\)は時刻\(t_c\)のポテンシャル中の固有関数であり、

を満たしています。また、\(\varphi_n(\mathbf{r})\)は数値計算を行う際の基底関数であり、
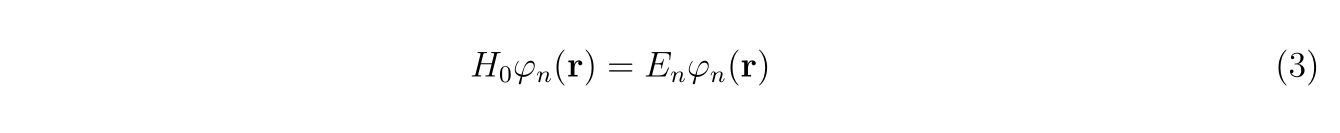
を満たしています。
任意の時刻\(t\)における波動関数を

として表したいので、\(a_n(t)\)について求めていけば、
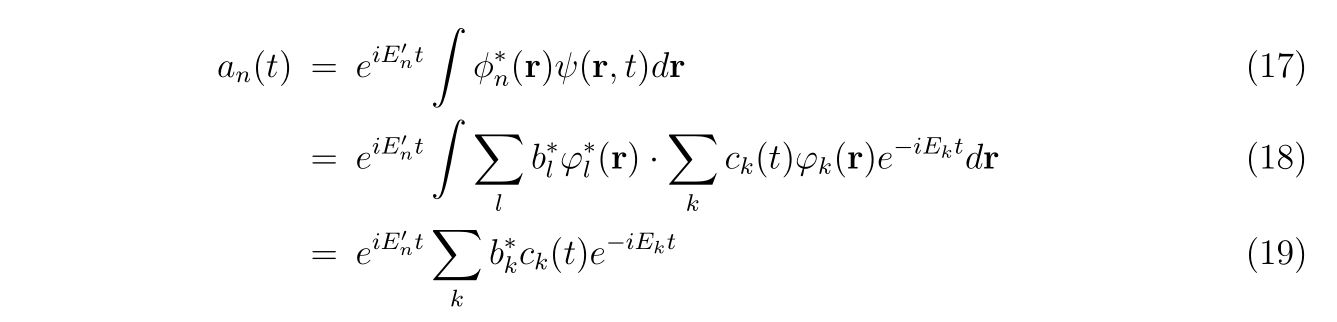
という関係式を導くことが出来ます。
数値計算プログラム
プログラムは以下のリンクにあります。
https://slpr.sakura.ne.jp/qp/supplement_data/highprecision_1Dtdsetise.tar.gz
そのままのプログラムでは、以下の設定となっています。
プログラムの利用に関してはhttps://slpr.sakura.ne.jp/qp/about/をお読みください。
解凍すると、4つのファイル(main.f90, integrate.f90,anime.plt,anime_project.plt)が入っています。計算パラメータの設定は、main.f90に入っているので各自調整してください。
繰り返しますが、全て原子単位系です。デフォルトでは、
計算時間の範囲\([ta,tb]\) … \([-5, 20]\)秒
出力時間枚数\(Nt\) … \(100\)枚
1ステップ当りの時間積分の精度\(\mathrm{RKeps}\) … \(10^{-5}\)
1ステップ当りの時間の最小刻み幅\(\mathrm{hmin}\) … \(10^{-4}\)
※理想は最小刻み幅は倍精度ならば\(10^{-14}\)程度が良いと思いますが、時間変化するポテンシャルを計算しようとする時、いつまでも最小刻み幅で進む時間がたまにあります。こういう時間はさっさと抜け出たいので、それを考慮して設定できるようにしています。
位置空間の範囲\([xa,xb]\) … \([-10, 10]\)
出力時の分点数\(Nx\) … 200点
時間積分の精度\(\mathrm{QPeps}\) … \(10^{-6}\)
初期状態を時間依存しないシュレーディンガー方程式を解くか、解析解で与えるかiname … “tise”
inameが”tise”の場合、どの時刻\(t_{ini}\)の固有状態を使うか … \(t_a\)
基底関数の数\(N\) … \(30\)個
計算に用いるスレッド数\(N{\mathrm{cpu}}\) … 1つ
空間積分の分点数を強制的に増やすか否かQPforce … 0
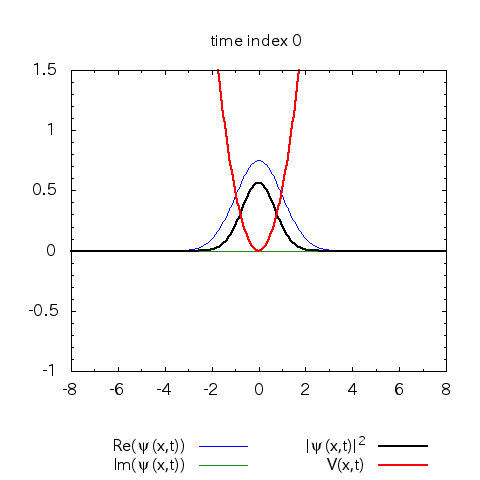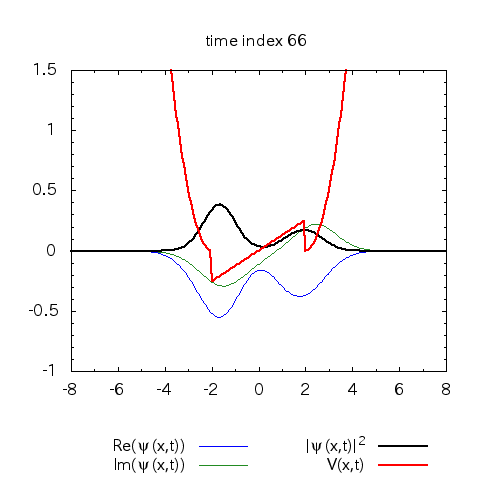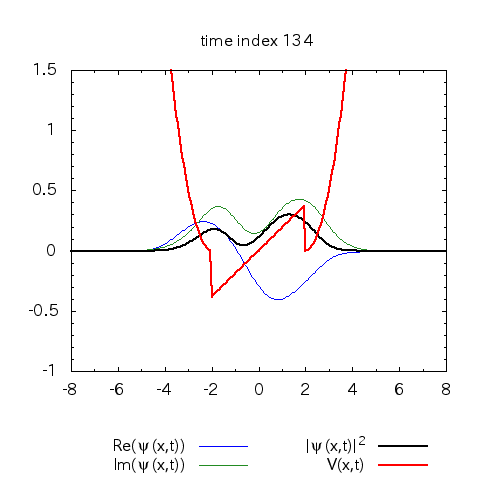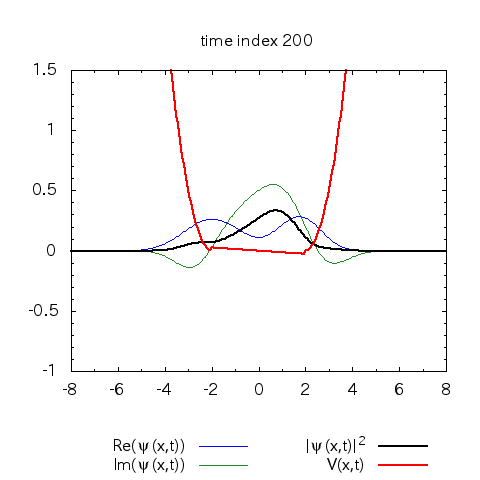
初期状態波動関数… 時間依存しないシュレーディンガー方程式の基底状態
ポテンシャル\(
\begin{eqnarray}
V(x,t)=\left\{
\begin{aligned}
0.5 x^2 (t\lt 0)\\
0.1 x^2 (t\ge 0)
\end{aligned}
\right.
\end{eqnarray}\)
で解くプログラムとなっています。
lapackと、必要があればopemMPを使います。
./a.out
もしくは、gfortranでlapackにリンクしてintegrate.f90 main.f90を一緒にコンパイル、実行してください。
実行後、以下のファイルを生成します。
- wf_***.d
波動関数の各時刻におけるデータです。時間順にwf_0.d(初期状態), wf_1.d, wf_2.d,…という風に指定された等間隔の時刻で出力します。アウトプットのファイル数はNtで指定した数です。 - project_ratio.d
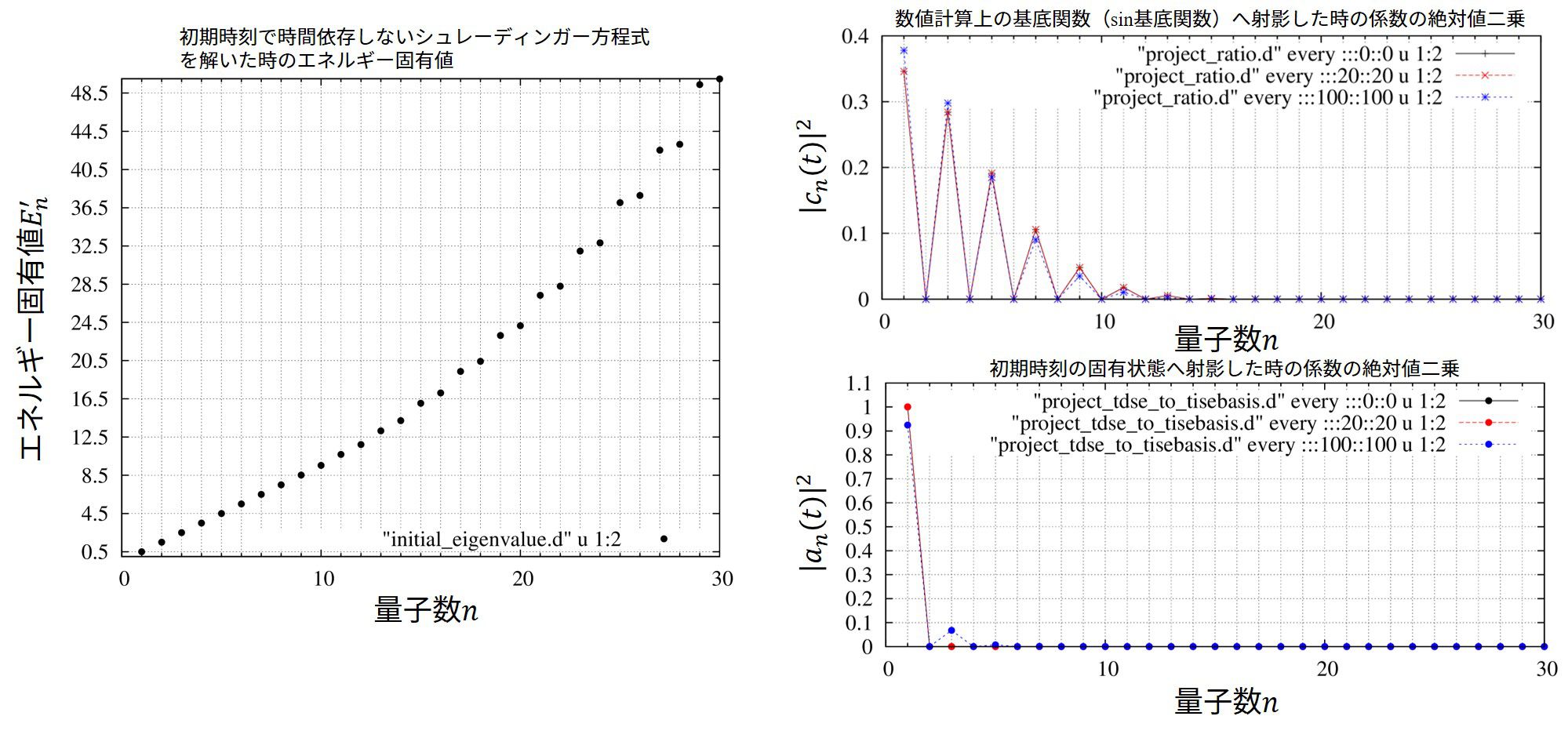
各時刻でのsin関数基底への射影した際の式(2)の係数\(c_n(t)\)の絶対値二乗を出力します。最も高い状態が振幅を持ってしまう場合、基底数が足りていないことを示しています。\( |c_n(t)|^2\)の事です。 - unitarity.d
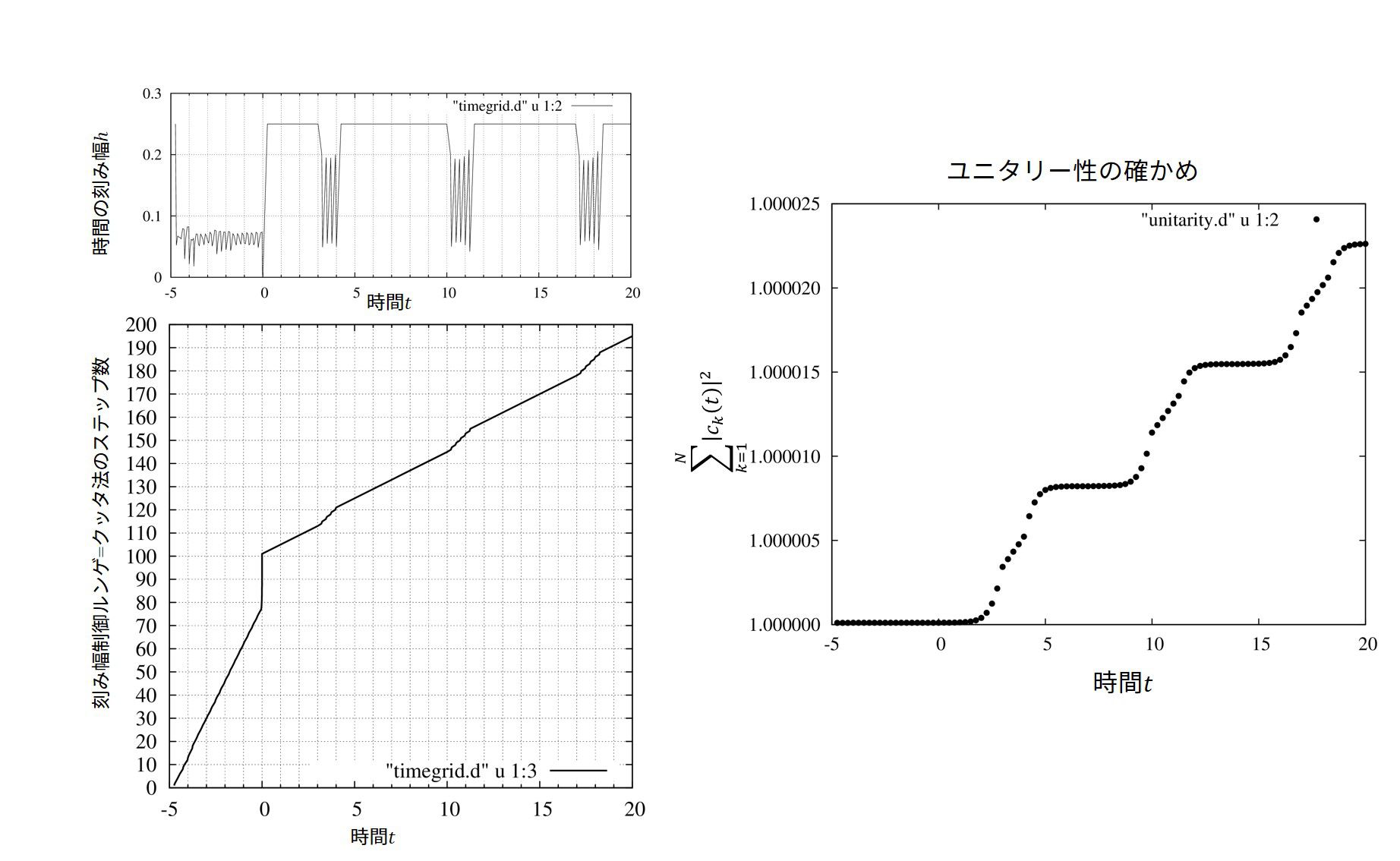
ユニタリー性を確認します。要は数値計算の発散とかで全計算区間内の存在確率が変化していないか見るためのものです。\(\sum_{n=1}^N |c_n(t)|^2\)の事です。 - timerange.d
時間グリッドを確認します。物理的な意味は無く、どの時間で計算負荷が大きいかを見るためのものです。 - timeindex_correspondence.d
時間インデックス(wf.***.dの***の値と、原子単位系の時刻の変換)を出力します。
もしも初期状態を時間依存しないシュレーディンガー方程式を解いて準備していた場合、以下のファイルを追加で出力します。
- initial_eigenvalue.d
初期状態のエネルギー固有値を出力します。式(14)の\(E’_n\)です。 - project_tdse_to_tisebasis.d
各時刻における初期状態の固有状態に射影した時の係数の絶対値の二乗を出力します。式(13)の係数\(a_n(t)\)の絶対値二乗である\(|a_n(t)|^2\)を出力します。
波動関数をgnuplot上でアニメーションとして見たい場合、同封してあるファイル”anime.plt”をgnuplot上でloadすれば良いです。
また、gifアニメが欲しい場合、
とすれば、波動関数と時間依存しないシュレーディンガー方程式を解いた時の基底関数への係数の絶対値二乗を共に出力します。
実行例
デフォルトの設定で計算を行います。
実行すると
0 / 100 1.0000000000
10 / 100 1.0000001064
20 / 100 1.0000001082
30 / 100 1.0000012466
40 / 100 1.0000079960
50 / 100 1.0000082264
60 / 100 1.0000114047
70 / 100 1.0000154242
80 / 100 1.0000154993
90 / 100 1.0000193449
1.948[CPU sec]
$
という文が出力されます。
左の/100とは、今計算が100枚中枚まで終わった、ということを示しており、枚数は変数Ntに対応しています。
右の1に近い数字は、全空間の存在確率を表しており、計算が発散しないかどうかを確認できます。これはルンゲクッタ法の要求精度\(RKeps\)に大きく依存します。
最後のCPUsecは計算に要したCPU時間であり、1コアではおおよそ実時間と同一です。なので、この計算は約2秒で終わる、ということです。ちなみにCPUは1.9GHzの物です。
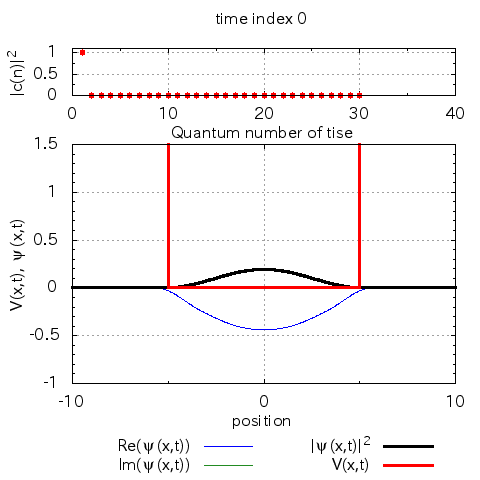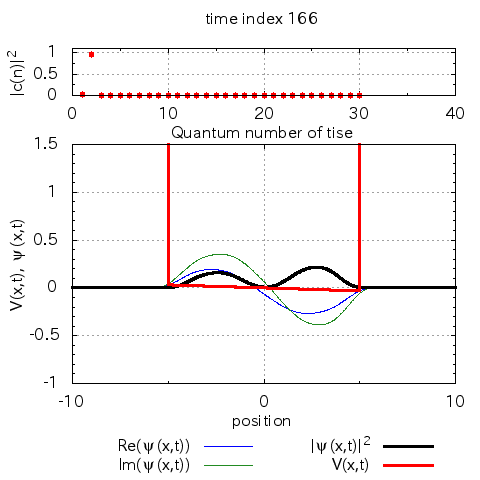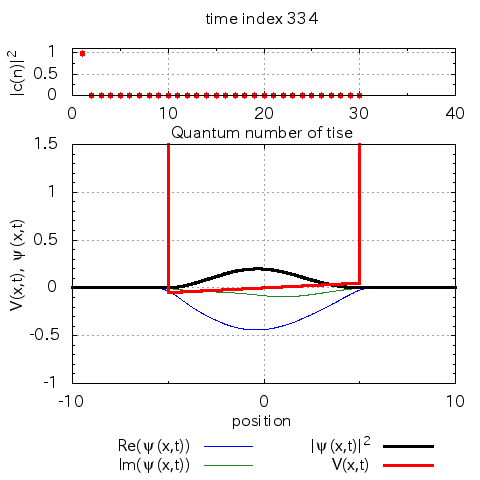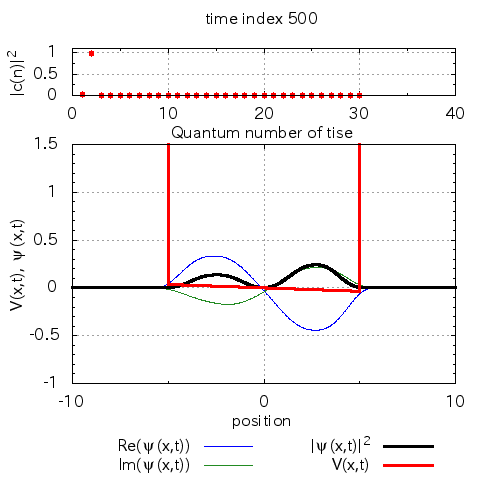
anime_project.pltによってgifアニメを生成すると、以下のgifアニメが得られます。
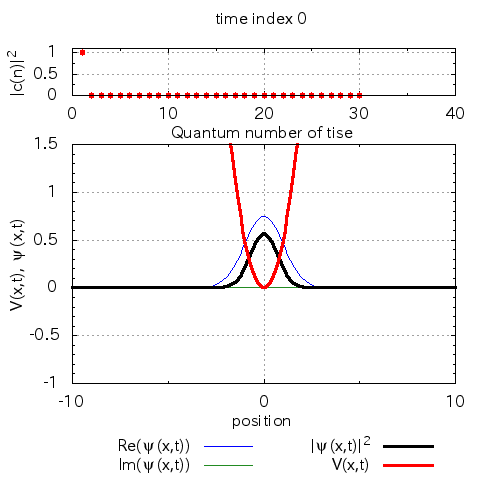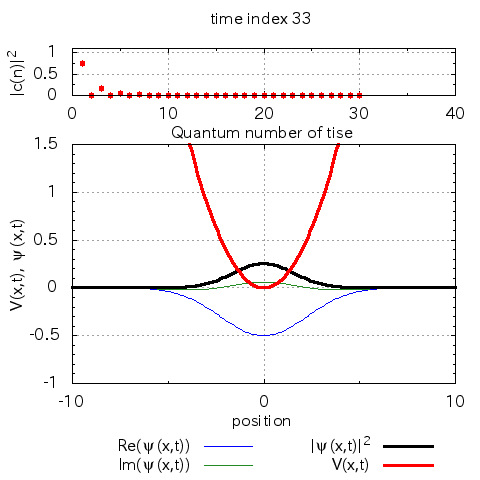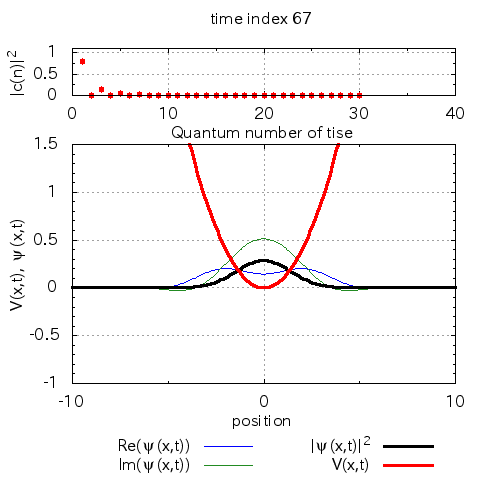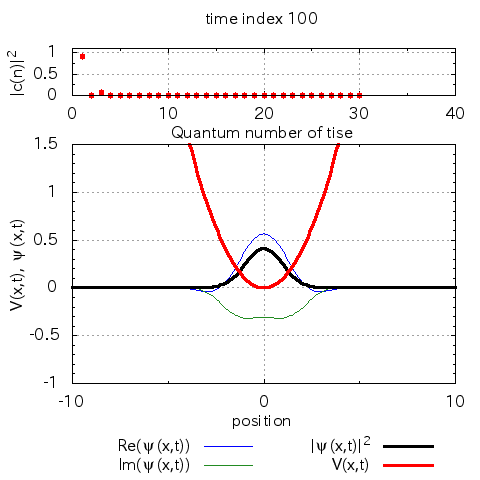
計算例
ポテンシャルによる反射

※この上図の縦軸は数値計算上の基底である\(\varphi_n(x)\)への射影した時の係数の絶対値二乗です。
ラビ周波数
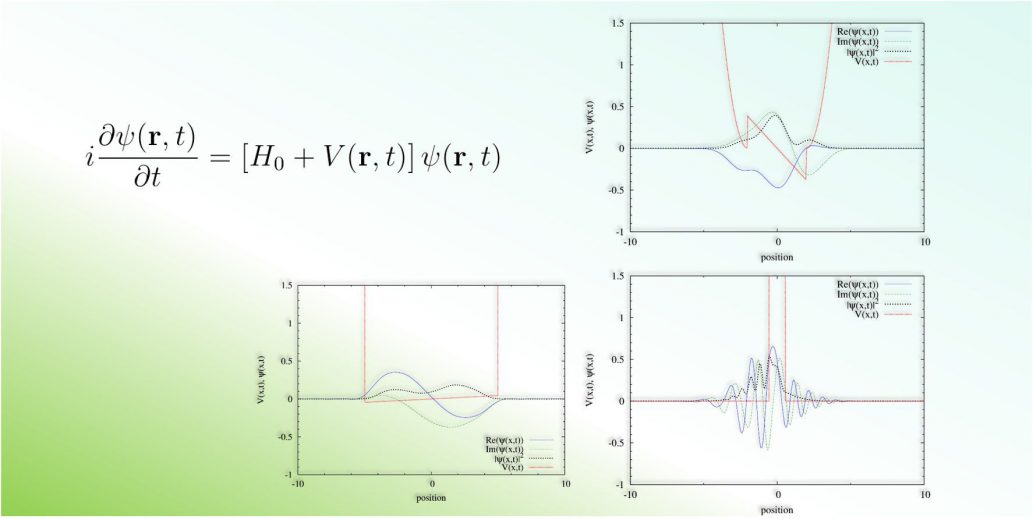
基底状態と第一励起状態の間の周波数でポテンシャルを揺らしています。
意地悪なポテンシャル
補遺1
もし仮に、\(U_{m,n}(t)\)が時間によって変化しないのであれば、
\(\displaystyle
\frac{\partial \mathbf{x}}{\partial t}=\mathbf{A}\mathbf{x}
\)
の形の微分方程式であるので、指数関数の解を仮定して\(\mathbf{A}\)を対角化、その固有値固有ベクトルを求めて、線形結合で表現すればokです(線形代数II/連立線形微分方程式等にあるのでそちらを参照してください)。



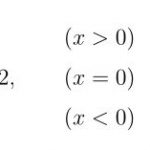
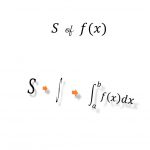
いつも勉強させていただいております。
U_{m,n}(t)の積分についてお聞きしたいのですが、
もしV(x, t)がV(x, t) = X(x)T(t)と
変数分離の形で書けた場合、
U_{m,n}(t) = exp[i(Em – En)t] ∫φ*m(x) V(x, t) φn(x) dx
= exp[i(Em – En)t] T(t)∫φ*m(x) X(x) φn(x) dx
となって、Vが時間に依存する場合でも、
積分は一度だけ行えばよいという理解で
問題ないでしょうか。
確かにその通りですね。
変数分離で書けている場合、積分の計算は1度で良いです。