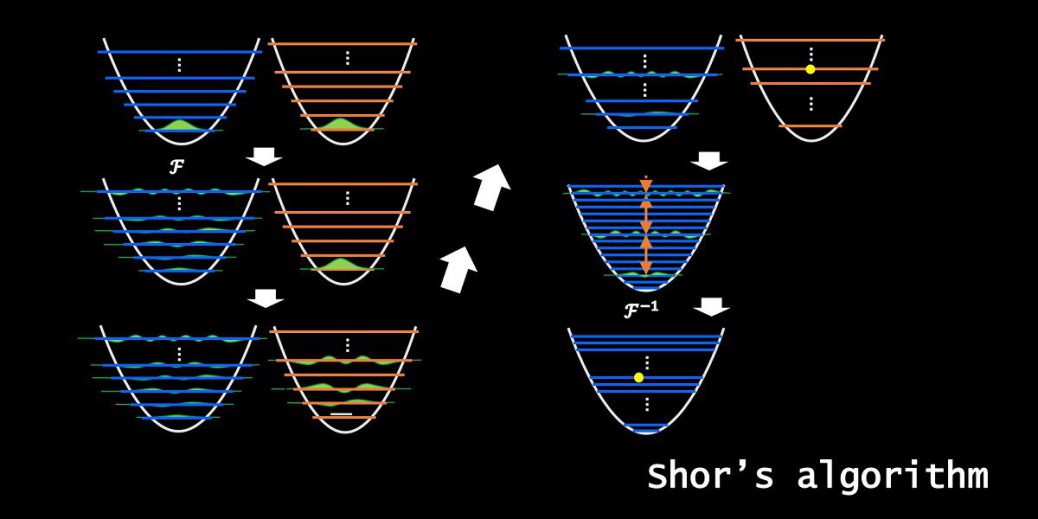
量子コンピュータを使用する素因数分解アルゴリズム

量子コンピュータを使うと素因数分解が高速にできる。

が、実際はどうやって素因数分解をするんでしょう？
そして具体的に何が高速化するんでしょう？これを知るのが本稿の目的です。

素因数分解アルゴリズム(古典的)
実際のアルゴリズム(量子的)
最大公約数を求めるアルゴリズム(古典)

素因数分解アルゴリズム

量子的に高速に出来るのであれば、そのアイデア自体は古典的に考えられるはずです。

素因数分解する古典的アルゴリズムは以下のように記述されます。
\(m\)を素因数分解したい数とし、\(x\)をmと互いに素な整数(\(\text{gcd}(x,m)=1\)を満たす数)と表記します。

ここで、\(\text{gcd}(a,b)\)は、\(a\)と\(b\)の最大公約数(greatest common divisor)を出力する関数です。

\(a(=0,1,\cdots )\)を引数として、関数\(f_m(a)=x^a~ \text{mod}~ m\)を計算

\(f_m(a)\)の周期\(r\)を見つける。実は\(f_m(a)\)は周期\(r\)の周期関数(周期\(r\)は実際に計算してみるまで分からない。数式で表せば、\(f_n(a)=f_n(a+r)\))。

周期\(r\)が判明したら、\(p=\text{gcd}(x^{r/2}+1,m),~q=\text{gcd}(x^{r/2}-1,m)\)を計算

\(p,q\)は\(m\)の素因数となっている

という風に素因数分解を行うことが出来ます。

具体的に\(m=21\)を素因数分解してみましょう。\(m\)と互いに素な整数として、\(x=11\)を選びます。
実際に横軸に\(a\)をとり、関数\(f_m(a)\)を計算すると以下のようになります。

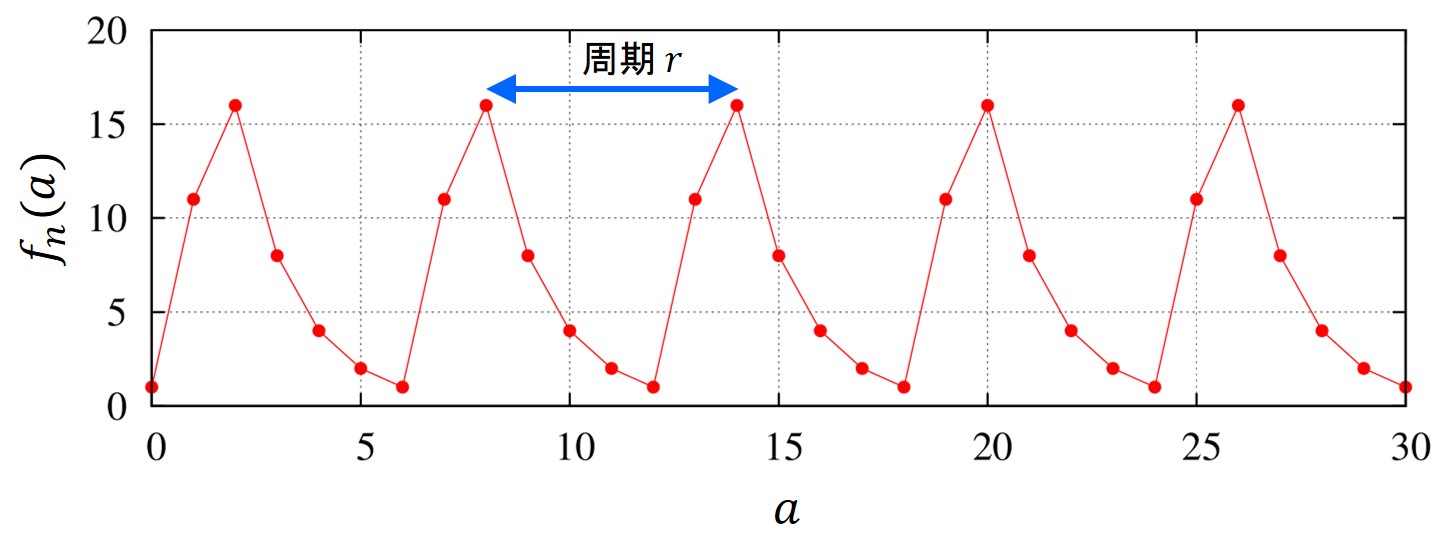
この計算結果を見ますと、周期\(r\)が6だと分かります。

周期が\(6\)が分かったので、\(p=\text{gcd}(x^{r/2}+1,m),~q=\text{gcd}(x^{r/2}-1,m)\)を計算します。すると、
\(
\begin{align}
p&=\text{gcd}(x^{r/2}+1,m)=\text{gcd}(11^{6/2}+1,21)=3 \\
q&=\text{gcd}(x^{r/2}-1,m)=\text{gcd}(11^{6/2}-1,21)=7
\end{align}
\)
と分かります。\(21\)は\(3\times 7\)と書けるので、素因数分解を行うことが出来ました。

さて、量子的に素因数分解を行う場合、上のアルゴリズムはShorのアルゴリズムと呼ばれます。
上の計算は、

最大公約数を求めるアルゴリズム(Euclidの互除法, 計算量\(O(\text{log} n)\))
周期\(r\)を見つけるアルゴリズム(
古典的:\(O(\exp[(\text{log}n)^{1/3}(\text{ln}\text{ln}n)^{2/3}])\),
量子的:\(O((\text{log}n)^{2}(\text{log}\text{log}n)(\text{log}\text{log}\text{log}n))\)

です。最も時間が掛かる部分は、周期\(r\)を見つける部分で、これを見つけるために量子コンピュータを用いるのです。Shorのアルゴリズムは、この部分だけ量子コンピュータを使うのです。

量子的に高速に計算する、という部分は、
\(f_m(a)\)の周期\(r\)を見つける
という部分です。

実際のアルゴリズム

ここで紹介するモデルは、量子ビット(キュービット)を出さないで説明するものです。

キュービットの考えはShorのアルゴリズムの本質ではなく、実現できるか？の部分で重要です。
すなわち、ある状態を指定するために
・１つの系で、非常に高い量子番号に属する状態まで制御する（\(1[つの系]\times N[量子状態]\)）
ではなく、
・複数の系で、基底状態と１つの励起状態を制御する（\(Q[つの系]\times 2[量子状態]\)）
の方が現実で実現しやすいという考えです。

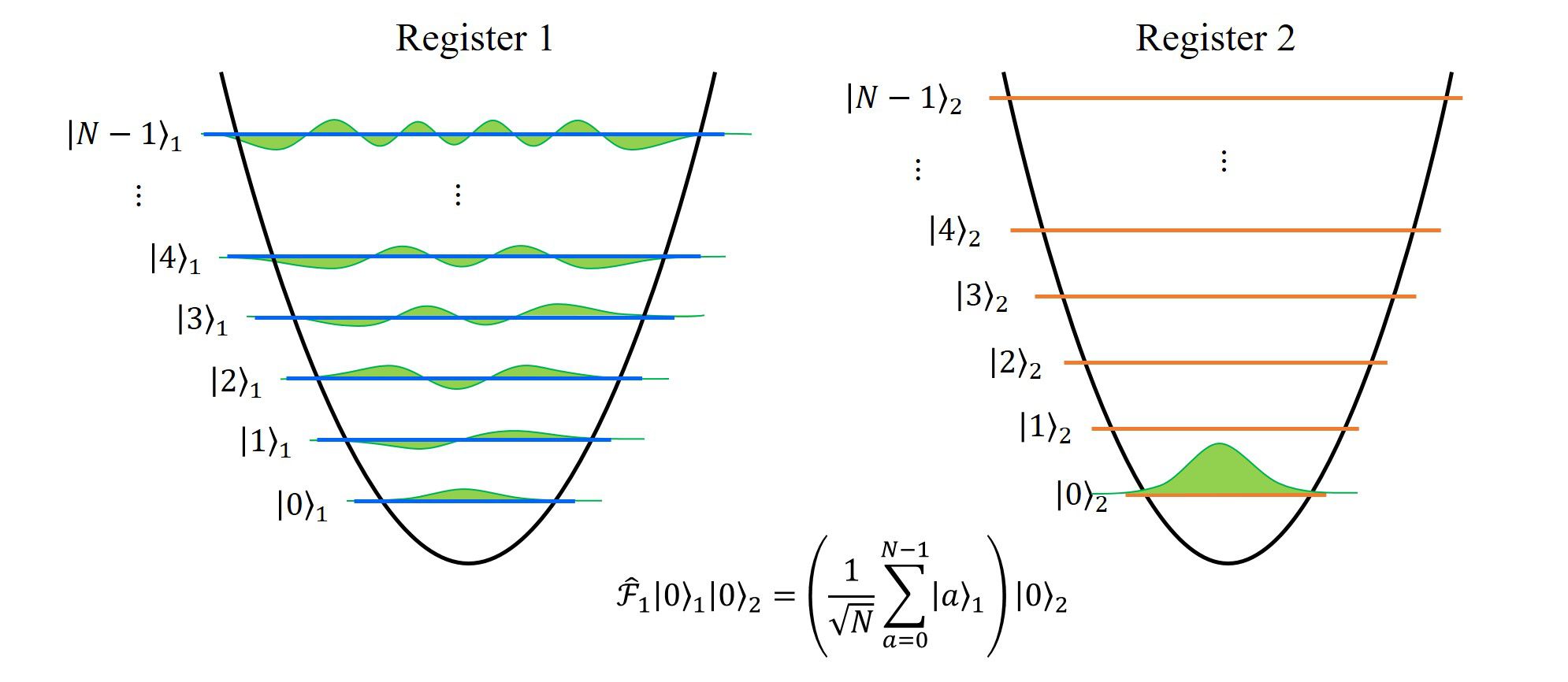
1. 初期状態の準備

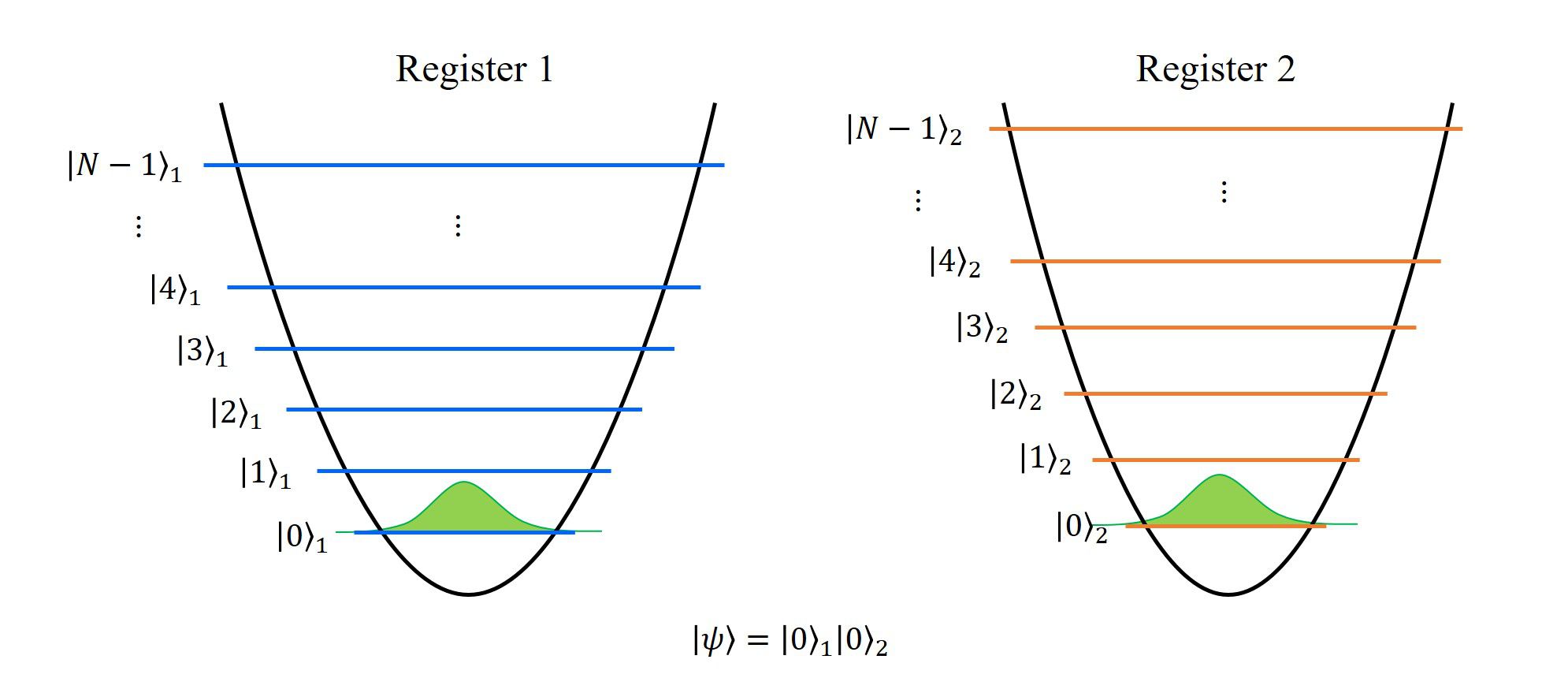
2つの系（２つの記憶素子、レジスタ）を用意し、初期状態として各々の基底状態を表します。
この時点で、２つの系は独立に存在するもので、系同士に相互作用や、もつれ等は存在しません。

図示すると、上の図のようになり、左はレジスタ1, 右はレジスタ2の量子状態を表していて、それぞれ、基底状態であることを表しています。

2. レジスタ1の状態に量子フーリエ変換を施す

レジスタ1に量子フーリエ変換を施すことで、レジスタ1の全状態の確率振幅を等確率にします。
量子フーリエ変換は量子状態に対して施す変換で、

\(
\begin{align}
\mathcal{F}|a\rangle&=\frac{1}{\sqrt{N}}\sum_{b=0}^{N-1}e^{-2\pi i a b/N}|b\rangle \\
\mathcal{F}^{-1}|a\rangle&=\frac{1}{\sqrt{N}}\sum_{a=0}^{N-1}e^{2\pi i a b/N}|a\rangle
\end{align}
\)

で定義します。基底状態\(|0\rangle\)に対して量子フーリエ変換を施すと、考えたい全励起状態を等確率にすることが出来ます。
\(
\begin{align}
\mathcal{F}|0\rangle&=\frac{1}{\sqrt{N}}\sum_{b=0}^{N-1}e^{-2\pi i 0 b/N}|b\rangle \\
&=\frac{1}{\sqrt{N}}\sum_{b=0}^{N-1}|b\rangle
\end{align}
\)
量子フーリエ変換を作用させると、上図のようになります。

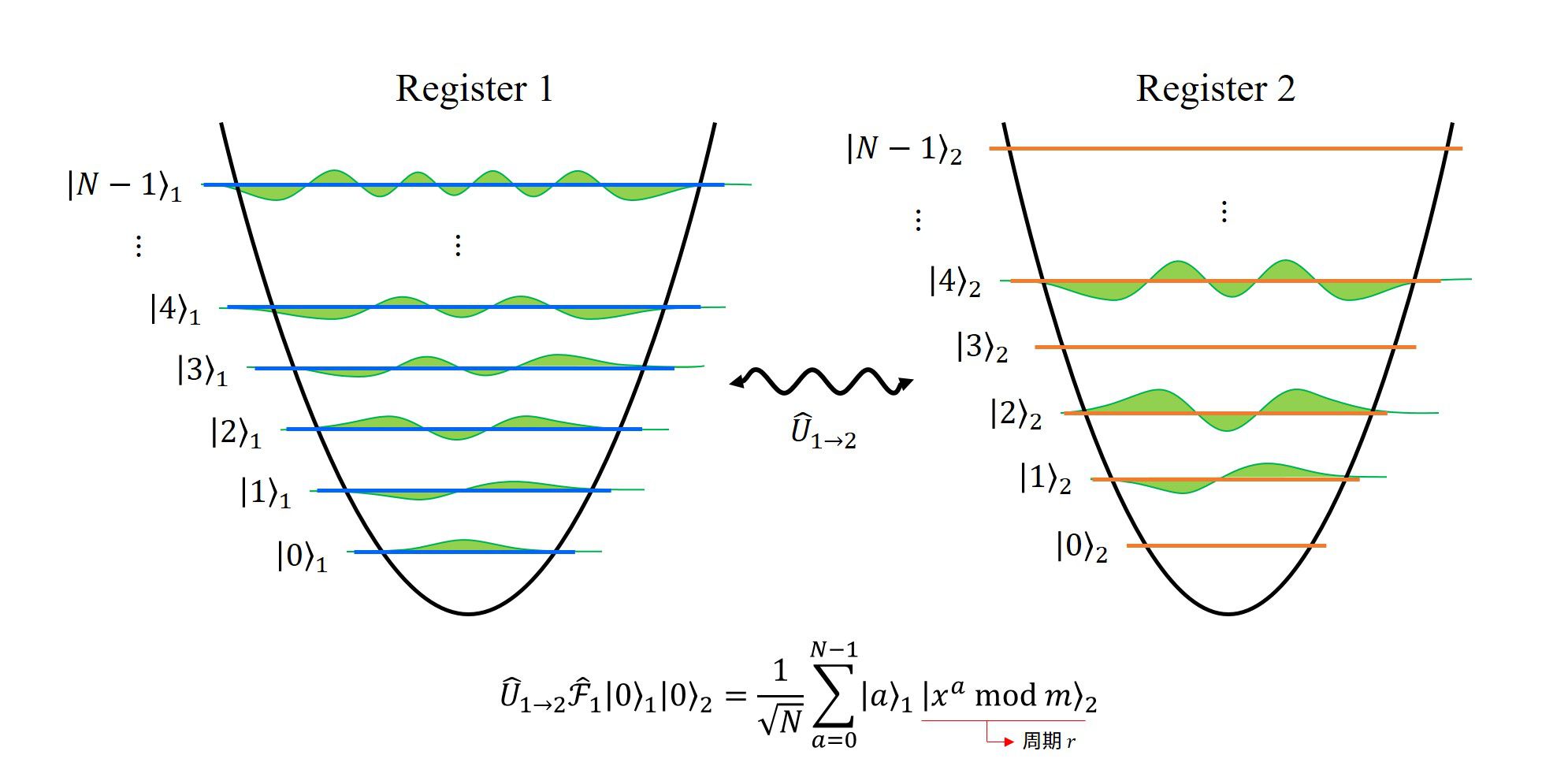
3. レジスタ2に、レジスタ1を元にした関数を作用させる

レジスタ2に、レジスタ1を参照して計算した結果をレジスタ2に出力する、という演算を行います。
この操作を行うことで、レジスタ1と2をもつれさせます（もつれ、という言葉が正しいかは分かりません。ですが、言いたいことはレジスタ1と2を結びつける、という操作を行います）。

この演算を行う事が出来る装置があるかはわかりませんが、あると仮定します。この　”あるかどうか分からない演算を行う装置”　はオラクル（神託装置）といいます。

このオラクルを用いて、レジスタ1の量子数\(a\)の値を引数として、レジスタ2の量子状態を\(|f_m(a)\rangle\)にしていきます。

この作用を\(\hat{U}_{1\to2}\)という演算子で表すと、レジスタ1の結果をレジスタ2に格納するので、

\(
\begin{align}
\hat{U}_{1\to2} \hat{\mathcal{F}}_1|0\rangle_1|0\rangle_2
&=\frac{1}{\sqrt{N}}\sum_{a=0}^{N-1}\hat{U}_{1\to2}|a\rangle_1|0\rangle_2 \\
&=\frac{1}{\sqrt{N}}\sum_{a=0}^{N-1}|a\rangle_1|x^a~ \text{mod}~ m\rangle_2
\end{align}
\)

4. レジスタ2を観測する

レジスタ2を観測し、レジスタ2の量子数を知ります。
この観測は以下の2つの影響を系に与えます。

・レジスタ2の量子状態を確定させる
・レジスタ1が取り得る量子状態に制限を加える

1回の”観測”の操作はただ１点だけを与えますが、数式上扱いづらいです。
なので、数式では何度も観測を行った時に得られる期待値を数式で表すと分かりやすくなります。
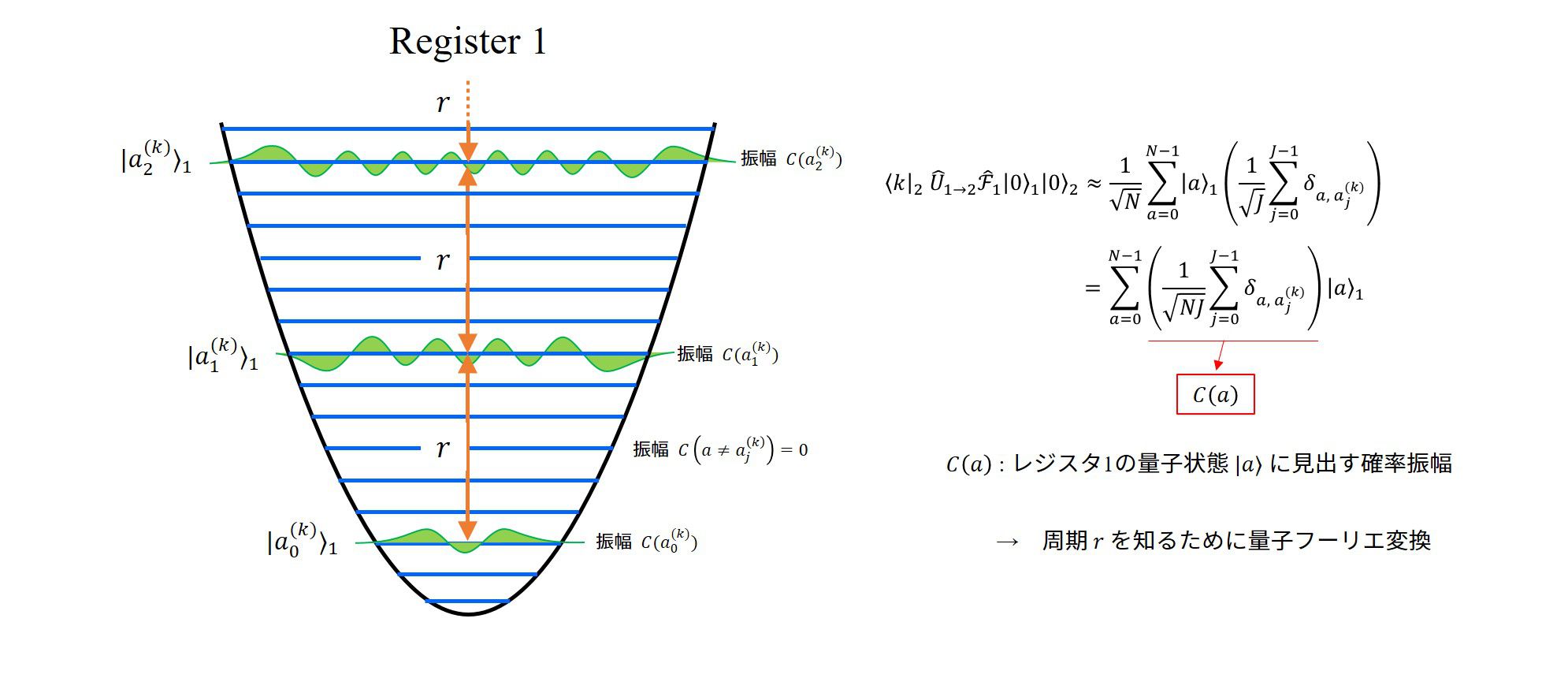
レジスタ2の状態を量子数\(k\)の状態に見出す確率を知るために、左から\(\langle k|_2\)を作用させます。
すると、以下のように式変形をすることが出来ます。

\(
\begin{align}
\langle k|\hat{U}_{1\to 2} \hat{\mathcal{F}}_1|0\rangle_1|0\rangle_2
&=\frac{1}{\sqrt{N}}\sum_{a=0}^{N-1}|a\rangle_1|x^a ~\text{mod}~ m\rangle_2 \\
&\approx\frac{1}{\sqrt{N}}\sum_{a=0}^{N-1}|a\rangle_1\langle k|x^a ~\text{mod}~ m\rangle_2 \\
&=\frac{1}{\sqrt{N}}\sum_{a=0}^{N-1}|a\rangle_1\left(\frac{1}{\sqrt{J}}\sum_{j=0}^J \delta_{a,a_j^{(k)}}\right)
\end{align}
\)
ここで、\(a_j^{(k)}\)は、
\(k=x^{a_{j}^{(k)}}~ \text{mod} ~m,~~(j=0,1,\cdots,J-1)\)を満たす\(J\)個の\(a\)です。

この観測により、レジスタ1の状態を特定の状態を\(|a_j^{(k)}\rangle,~~(j=0,1,\cdots, J-1)\)のみ存在させることになります。レジスタ1のとれる状態は周期的で周期\(r\)をもち、
\(
\displaystyle a_j^{(k)}=a_0^{(k)}+j\cdot r,~~(j=0,1,\cdots, J-1)
\)
という形で表すことが出来ます。

レジスタ1の状態を図示するとこのようになっているはずです。

係数をまとめると分かりやすくなります。
単なる式変形ですが、状態に適当な係数が掛かった状態の重ね合わせで表現されるので、なじみ深い形…だと私は思います。
\(
\begin{align}
\langle k|\hat{U}_{1\to 2} \hat{\mathcal{F}}_1|0\rangle_1|0\rangle_2
\approx=\sum_{a=0}^{N-1}\left(\frac{1}{\sqrt{NJ}}\frac{1}{\sqrt{J}}\sum_{j=0}^{J-1} \delta_{a,a_j^{(k)}}\right)|a\rangle_1
\end{align}
\)

5. レジスタ1を量子フーリエ変換する

レジスタ1の状態に対して量子フーリエ変換を行うことで、レジスタ1の持つ周期を知ることが出来ます。

量子フーリエ変換を行う前は量子の属する状態そのものに周期\(r\)の情報は含まれていませんが、量子フーリエ変換を行った後は量子数そのものに周期\(r\)に関係する値が含まれるようになります。

実際に観測を行うと、

\(
\begin{align}
\hat{\mathcal{F}}^{-1}_1\langle k|\hat{U}_{1\to 2} \hat{\mathcal{F}}_1|0\rangle_1|0\rangle_2
&\approx\sum_{a=0}^{N-1}\left(\frac{1}{\sqrt{NJ}}\frac{1}{\sqrt{J}}\sum_{j=0}^J \delta_{a,a_j^{(k)}}\right)\hat{\mathcal{F}}^{-1}_1|a\rangle_1 \\
&=\sum_{b=0}^{N-1}\left(\frac{1}{N\sqrt{J}}\sum_{j=0}^{J-1} e^{2\pi i a_j^{(k)}b/N}\right)|b\rangle_1 \\
&=\sum_{b=0}^{N-1}\left[\frac{1}{N\sqrt{J}}e^{2\pi i a_0^{(k)}b/N}\sum_{j=0}^{J-1} e^{2\pi i jrb/N}\right]|b\rangle_1
\end{align}
\)

レジスタ1の量子数\(b’\)に見出す確率は、左から\(\langle b’|_1\)を作用させて絶対値の２乗をとると分かります。

まず、左から\(\langle b’|_1\)を作用させると、
\(
\begin{align}
C'(b’)=\langle b’|_1\hat{\mathcal{F}}^{-1}_1\langle k|\hat{U}_{1\to 2} \hat{\mathcal{F}}_1|0\rangle_1|0\rangle_2
&\approx\frac{1}{N\sqrt{J}}e^{2\pi i a_0^{(k)}b’/N}\sum_{j=0}^{J-1} e^{2\pi i jrb’/N}
\end{align}
\)
となります。確率は上記\(C'(b)\)の値の絶対値の2乗で与えられるので(表記を\(b’\to b\)に変更)、
\(
\begin{align}
|C'(b)|^2&=\left|\frac{1}{N\sqrt{J}}e^{2\pi i a_0^{(k)}b/N}\sum_{j=0}^{J-1} e^{2\pi i jrb/N}\right|^2 \\
&=\frac{1}{N^2 J}\left|\sum_{j=0}^{J-1} e^{2\pi i jrb/N}\right|^2
\end{align}
\)
となります。確率密度は
\(
\displaystyle \left|\sum_{j=0}^{J-1} e^{i(2\pi jrb/N)}\right|
\)
に依存します。この形は離散フーリエ変換の場合に似ています。
つまり、この項が大きくなる時の状態がレジスタ1の量子状態として観測されることが期待され、
観測される状態とは、\(j\)が変化しても位相が一致しているとき、すなわち

\(2\pi rb/N=2\pi \times (整数)\)

を満たすような\(r\)の時に存在確率密度が大きくなる、ということになります。
整数をsと表記すると、

\(rb/N= s~\to~ b/N= s/r\)

と表されます。

6. レジスタ1の観測

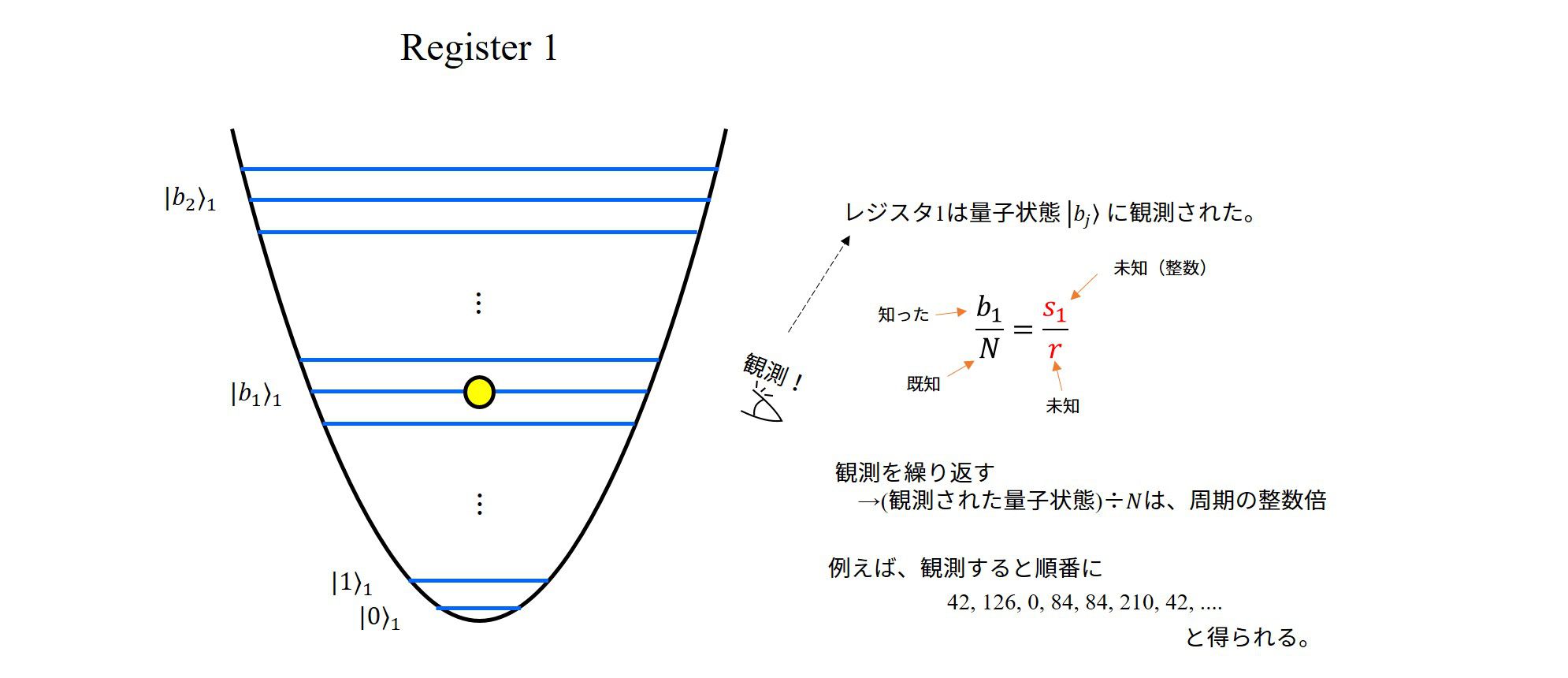
確率密度分布は\(b=a_0^{(k)}+j\cdot r\)の量子状態を中心に分布しますが、あくまで、確率分布ですので、観測を行った場合は若干ずれた所に見出したりします。

実際にレジスタ1の観測を行った際に得られた量子数を\(A\)とします。すると、関係式

\(\frac{A}{N}\approx \frac{s}{r}\)

が近似的に成立していると考えることが出来ます。
今、左辺は完全に分かっている量ですが、右辺の分子・分母は整数を持つ、ということくらいしかわかりません。これを求めるために連分数展開を用います。

7. 連分数展開によって周期\(r\)を見つける

レジスタ1の観測によって得られた状態の量子数を\(A\)とします。今、
\(\displaystyle
\frac{A}{N}=\frac{s}{r}
\)
ここで、\(A\)は観測された量子数、
\(N\)はレジスタの全量子状態数、
\(s (\lt N)\)は任意の整数、
\(r\)は求めたい周期です。

これから行いたい操作は、\(\frac{A}{N}\)の分子分母を出来るだけ小さい数にする、という作業を行いたいのです。
これは単純に割るだけで済む話ではありません。なぜなら、\(\frac{A}{N}\)は綺麗に割り切れる数ではない可能性があるからです。

例えば、\(k=184, N=243\)という値であった場合、直感的に\(\frac{184}{243}\approx \frac{3}{4}\)だということが分かります。

これを機械的に行うためには連分数展開を利用します。
連分数展開とは、ある実数\(x\)を整数\(a_n\)を用いて以下のように展開することです。
\(\displaystyle
x=a_0+\frac{1}{a_1+\frac{1}{a_2+\frac{1}{\cdots}}}
\)

ここで、\(a_n~(n=0,1\cdots)\)は、
\(
\begin{align}
&a_0=\lfloor x \rfloor,~~b_0=\frac{1}{x-a_0} \\
&a_n=\lfloor b_{n-1} \rfloor,~~b_n=\frac{1}{b_{n-1}-a_n}
\end{align}
\)
と得られます。ここで\(\lfloor x \rfloor\)はガウスの記号で、実数の整数部分を表しています。
\(x\)が有理数であれば、連分数展開は有限の項数で終わります。

連分数展開後、\(x\)の分数による近似は
\(\displaystyle
x\approx\frac{d_n}{r_n}
\)
ここで、
\(
\begin{align}
& d_0=a_0,~d_1=1+a_0a_1,~d_n=a_n d_{n-1}+d_{n-2},\\
& r_0=1,~r_1=a_1,~r_n=a_n r_{n-1}+r_{n-2},
\end{align}
\)
として順々に求める事が出来ます。
また、連分数の打切りに関しては定理

「\(\frac{q}{p}\)を\(\left|\frac{q}{p}-x\right|\lt \frac{1}{2q^2}\)を満たす任意の有理数とする時、\(\frac{q}{p}\)は\(x\)の近似分数である。さらに、その近似分数は\(p,q\)の最大公約数は1である。」

を用いて、条件式\(\left|\frac{q}{p}-x\right|\lt \frac{1}{2q^2}\)から決めます。

連分数展開によって分子・分母を出力するプログラムはこんな感じで実装できます。

▼ここクリックでこの場に展開

最大公約数を求めるアルゴリズム(古典)

最大公約数を求めるアルゴリズムはEuclidのアルゴリズムと呼ばれ、他のアルゴリズムと比べても早く終わります。そのプログラムは以下で実装できます。

function gcd(a,b)
implicit none
integer,intent(in)::a,b
integer::gcd
!compute the greatest common divisor
integer::x,r

x=a
gcd=b
r=mod(x,gcd)
do while( r .gt. 0)
x=gcd
gcd=r
r=mod(x,gcd)
enddo

return
end function gcd

参考文献

Elisa Bäumer, Jan-Grimo Sobez, Stefan Tessarini, Shor’s Algorithm
https://qudev.phys.ethz.ch/content/QSIT15/Shors%20Algorithm.pdf

C. P. ウィリアムズ、S. H. クリアウォータ著、西野哲郎、新井隆、渡邉昇訳「量子コンピューティング」(springer, 2000)

（更新停止）

量子コンピュータを使用する素因数分解アルゴリズム

素因数分解アルゴリズム