\begin{align}
\int_{-\infty}^{\infty}\frac{1}{x}e^{-ikx}dx =-\pi i ~\text{sgn}(k)
\end{align}
※ただし、\(x=0\)での値は定義しない。また、\(\text{sgn}(x)\)は符号関数
数値計算による上式の確かめはexp(-ikx)/x の無限区間に渡る積分を数値的に計算したい。をご覧ください。
その他フーリエ変換
ヘヴィサイド関数のフーリエ変換
1のフーリエ変換
\(x\)のフーリエ変換
\(1/x\)のフーリエ変換 ← 今ここ
\(1/(x^n)\)のフーリエ変換
実軸上の積分は複素平面の上から近づいた値と下から近づいた値の平均をとって定めるとします。すなわち、
\(
\begin{align}
&\int_{-\infty}^{\infty}\frac{1}{x}e^{-ikx}dx \nonumber \\
&=\lim_{\varepsilon\to +0} \frac{1}{2}\left[\int_{-\infty}^{\infty}\frac{1}{x+i\varepsilon}e^{-ikx}dx +\int_{-\infty}^{\infty}\frac{1}{x-i\varepsilon}e^{-ikx}dx \right]
\end{align}
\)
で表されると仮定します。
そして、第1項、第2項をそれぞれ計算していきます。
\(
\displaystyle \lim_{\varepsilon\to +0}\int_{-\infty}^{\infty}\frac{1}{x\pm i\varepsilon}e^{-ikx}dx
\)
を計算するにあたり、複素x平面上の漸近で収束する半径が\(k\)の符号によって異なるので場合分けをしてます。
\(k\gt 0\)の時
まず、\(\varepsilon\)の符号が正である場合を考えます。
この実軸上の積分は実軸への近づき方を指定して
\(
\begin{align}
\lim_{\varepsilon\to +0} \int_{-\infty}^{\infty}\frac{1}{x+i\varepsilon}e^{-ikx}dx =
\left[\int_{-\infty}^{-\varepsilon’}+\int_{\Gamma_+}+\int_{\varepsilon’}^{\infty}\right]\frac{e^{ikx}}{x}dx
\end{align}
\)
です。ここで、\(\int_{\Gamma_+}\)は特異点周りを複素平面上半面を通る経路です。
この積分を計算するために閉路積分を考えます。すなわち、以下の図の左側のように回った積分を考えます。

すると、この閉経路に対して、
\(
\begin{align}
\oint \frac{e^{-ikx}}{x}dx&=
\lim_{R\to\infty}\left[\int_{-R}^{-\varepsilon’}+\int_{\Gamma_+}+\int_{\varepsilon’}^{R}+\int_{\Gamma’}\right]
\frac{e^{ikx}}{x}dx\\
&=\lim_{\varepsilon\to +0} \int_{-\infty}^{\infty}\frac{1}{x+i\varepsilon}e^{-ikx}dx+\lim_{R\to\infty}\int_{\Gamma’}\frac{e^{-ikx}}{x}dx
\end{align}
\)
が成立します。今、閉経路内に特異点が一つ存在し、負の方向に回っているので、左辺\(\oint \frac{e^{-ikx}}{x}dx=-2\pi i\)です。また、大きく外側を回る経路\(\Gamma’\)の積分はゼロです。よって、
\(
\begin{align}
\lim_{\varepsilon\to +0}\int_{-\infty}^{\infty}\frac{1}{x+i\varepsilon}e^{-ikx}dx =-2\pi i.
\end{align}
\)
が示されます。
また、特異点を下に回る積分(図の左の経路)では、閉経路内に特異点は存在しないので、\(\oint \frac{e^{-ikx}}{x}dx=0\)です。なので、
\(
\begin{align}
\lim_{\varepsilon\to +0}\int_{-\infty}^{\infty}\frac{1}{x-i\varepsilon}e^{-ikx}dx =0.
\end{align}
\)
と導けます。
\(k\lt 0\)の時
まず、\(\varepsilon\)の符号が正である場合を考えます。
kが正の時と異なる点は、漸近で収束する領域が複素x平面の上半面であるという点です。
図の左のような閉経路を考えます。
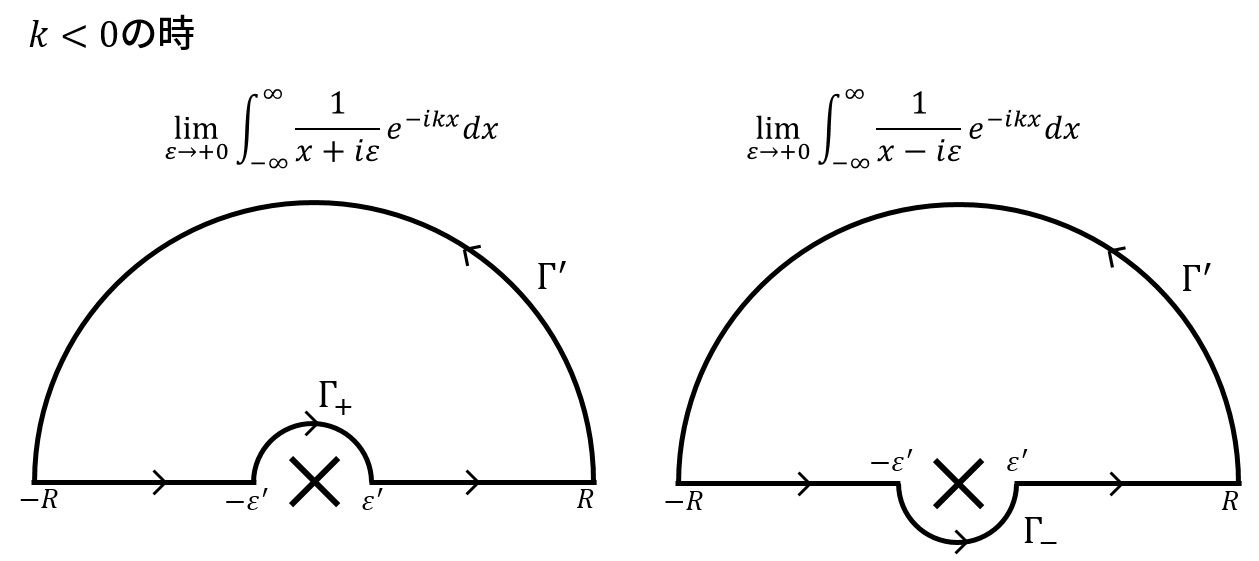
同様に計算を行うと
\(
\begin{align}
\oint \frac{e^{-ikx}}{x}dx&=
\lim_{R\to\infty}\left[\int_{-R}^{-\varepsilon’}+\int_{\Gamma_+}+\int_{\varepsilon’}^{R}+\int_{\Gamma’}\right]
\frac{e^{ikx}}{x}dx\\
&=\lim_{\varepsilon\to +0} \int_{-\infty}^{\infty}\frac{1}{x+i\varepsilon}e^{-ikx}dx+\lim_{R\to \infty}\int_{\Gamma’}\frac{e^{-ikx}}{x}dx
\end{align}
\)
今、閉経路内に特異点を含まないので、左辺\(\oint \frac{e^{-ikx}}{x}dx=0\)、また遠方ではゼロに近づくので、\(\int_{\Gamma’}\frac{e^{ikx}}{x}dx=0\)です。よって、
\(
\begin{align}
\lim_{\varepsilon\to +0}\int_{-\infty}^{\infty}\frac{1}{x+i\varepsilon}e^{-ikx}dx =0.
\end{align}
\)
また、特異点周りを正方向に回る場合、閉経路内に特異点を含むので、
\(
\begin{align}
\lim_{\varepsilon\to +0}\int_{-\infty}^{\infty}\frac{1}{x-i\varepsilon}e^{-ikx}dx =2\pi i.
\end{align}
\)
となります。
\(k= 0\)の時
\(k=0\)では被積分関数は漸近で収束しません。なので漸近で大きく回った時の値がゼロになりません。
ここからは誤解を恐れずに計算します。
今求めたい積分は
\(
\int_{-\infty}^{\infty}\frac{1}{x}e^{-i0x}dx =\int_{-\infty}^{\infty}\frac{1}{x}dx
\)
です。実軸上の積分がこのページで書いた
\(
\begin{align}
&\int_{-\infty}^{\infty}\frac{1}{x}e^{-ikx}dx \nonumber \\
&=\lim_{\varepsilon\to +0} \frac{1}{2}\left[\int_{-\infty}^{\infty}\frac{1}{x+i\varepsilon}e^{-ikx}dx +\int_{-\infty}^{\infty}\frac{1}{x-i\varepsilon}e^{-ikx}dx \right]
\end{align}
\)
で定義されているのだとすれば、
\(
\begin{align}
\int_{-\infty}^{\infty}\frac{1}{x}dx =\lim_{\varepsilon\to +0} \frac{1}{2}\left[\int_{-\infty}^{\infty}\frac{1}{x+i\varepsilon}dx +\int_{-\infty}^{\infty}\frac{1}{x-i\varepsilon}dx \right]
\end{align}
\)
です。簡単のため、特異点を含まない閉経路を取れば第1項は
\(
\begin{align}
\lim_{R\to \infty}
\left[\int_{-R}^{-\varepsilon’}+\int_{\Gamma_+}
+\int_{\varepsilon’}^{R}+\int_{\Gamma’} \right]\frac{1}{x}dx =\oint \frac{1}{x}dx=0
\end{align}
\)
なので、
\(
\begin{align}
\lim_{\varepsilon\to +0} \int_{-\infty}^{\infty}\frac{1}{x+i\varepsilon}dx +\int_{\Gamma’} \frac{1}{x}dx =0
\end{align}
\)
となります。外側を回る経路\(\Gamma’\)を通った積分は
\(
\begin{align}
\int_{\Gamma’} \frac{1}{x}dx &=\int_0^\pi \frac{1}{re^{i\theta}}ire^{i\theta} d\theta \\
&=\pi i
\end{align}
\)
と計算できてしまうので、代入すれば
\(
\begin{align}
\lim_{\varepsilon\to +0} \int_{-\infty}^{\infty} \frac{1}{x+i\varepsilon} dx=-\pi i
\end{align}
\)
となります。また、同様にして
\(
\begin{align}
\lim_{\varepsilon\to +0} \int_{-\infty}^{\infty} \frac{1}{x-i\varepsilon} dx=\pi i
\end{align}
\)
を得ます。
よって、実軸上の積分の式に代入すれば
\(
\begin{align}
\int_{-\infty}^{\infty}\frac{1}{x}dx =\lim_{\varepsilon\to +0} \frac{1}{2}\left[(-\pi i) +\pi i \right] =0
\end{align}
\)
を得ます。すなわち、フーリエ変換後の\(k=0\)の値はゼロということです。
計算結果のまとめ
以上をまとめると、3つの関係式
\(
\begin{eqnarray}
\lim_{\varepsilon\to +0} \int_{-\infty}^{\infty}\frac{e^{-ikx}}{x+i\varepsilon}dx =
\left\{
\begin{aligned}
-2\pi i~~~(k\gt 0)\\
0~~~(k\lt 0)
\end{aligned}
\right.
\end{eqnarray}
\)
\begin{eqnarray}
\lim_{\varepsilon\to +0} \int_{-\infty}^{\infty}\frac{e^{-ikx}}{x-i\varepsilon}dx =
\left\{
\begin{aligned}
0~~~(k\gt 0)\\
2\pi i~~~(k \lt 0)
\end{aligned}
\right.
\end{eqnarray}
\)
\(
\begin{align}
\int_{-\infty}^{\infty}\frac{1}{x}e^{-i0x}dx=0
\end{align}
\)
を得ることが出来ました。
これを実軸上の積分の式に代入すると、
\(
\begin{align}
\int_{-\infty}^{\infty}\frac{1}{x}e^{-ikx}dx =-\pi i ~\text{sgn}(k)
\end{align}
\)
となります。ここで、\(\text{sgn}(x)\)は符号関数で、
\(
\begin{eqnarray}
\text{sgn}(x) =
\left\{
\begin{aligned}
-1~~~(x\lt 0)\\
0~~~(x=0) \\
1~~~(x\gt 0)
\end{aligned}
\right.
\end{eqnarray}
\)
で定義される関数です。