今まではゼロインする距離を固定した時の比較を行ってきましたが、
通常軌道を見て適正ホップだ、とか決定するかと思います。
この条件ならば上下幅を一定にしなければ適切な比較とは言えないと思ったのでその場合の結果です。
また、山のフィールドで
斜面の下から上に向かって打つとき、
斜面の上から下へ向かって打つとき
の着弾点は上にずれることを示します。
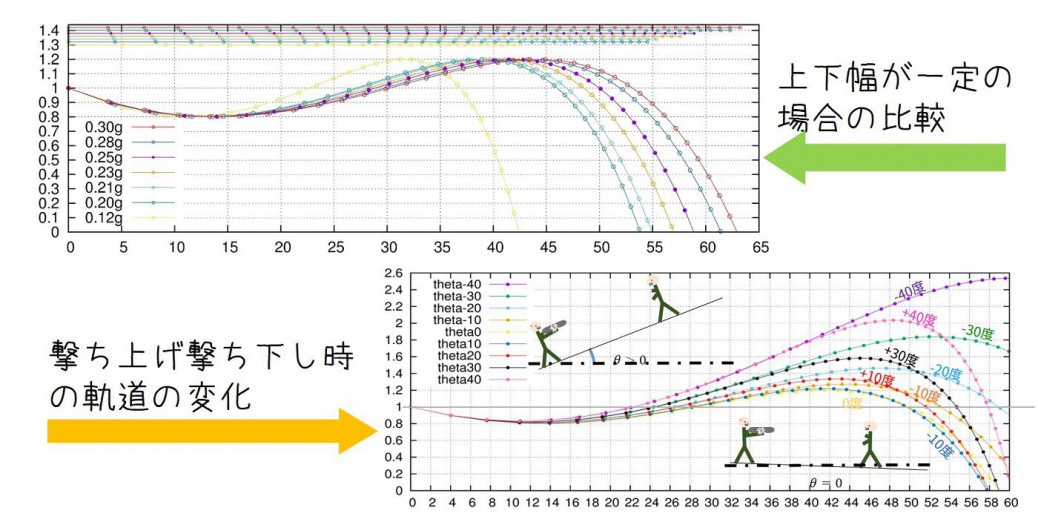
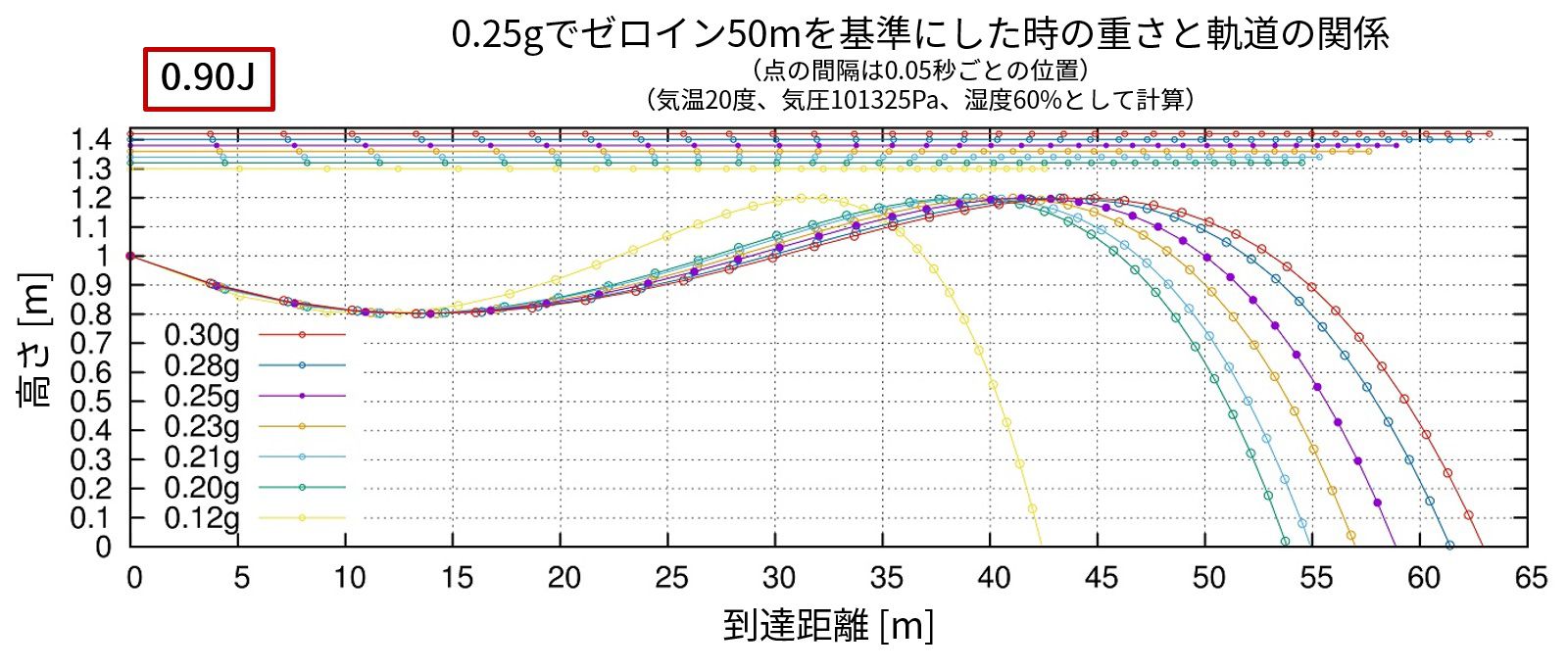
上下幅が一定の時の軌道
弾道の上下の幅を、0.25gのBB弾で0.9Jで射出した時の弾道の上下幅を基準にして重さを変えた時、弾道がどうなるかを計算すると以下の通りになります。
変更するBB弾の重さは販売されているものを基準とし、
0.12g, 0.20g, 0.21g, 0.23g, 0.25g, 0.28g, 0.30g
にしています。
グラフ中の点は0.05秒ごとの位置をプロットしており、図中の上の数本の線は水平距離のみを見た時のものです。
静止画では
のようになります。
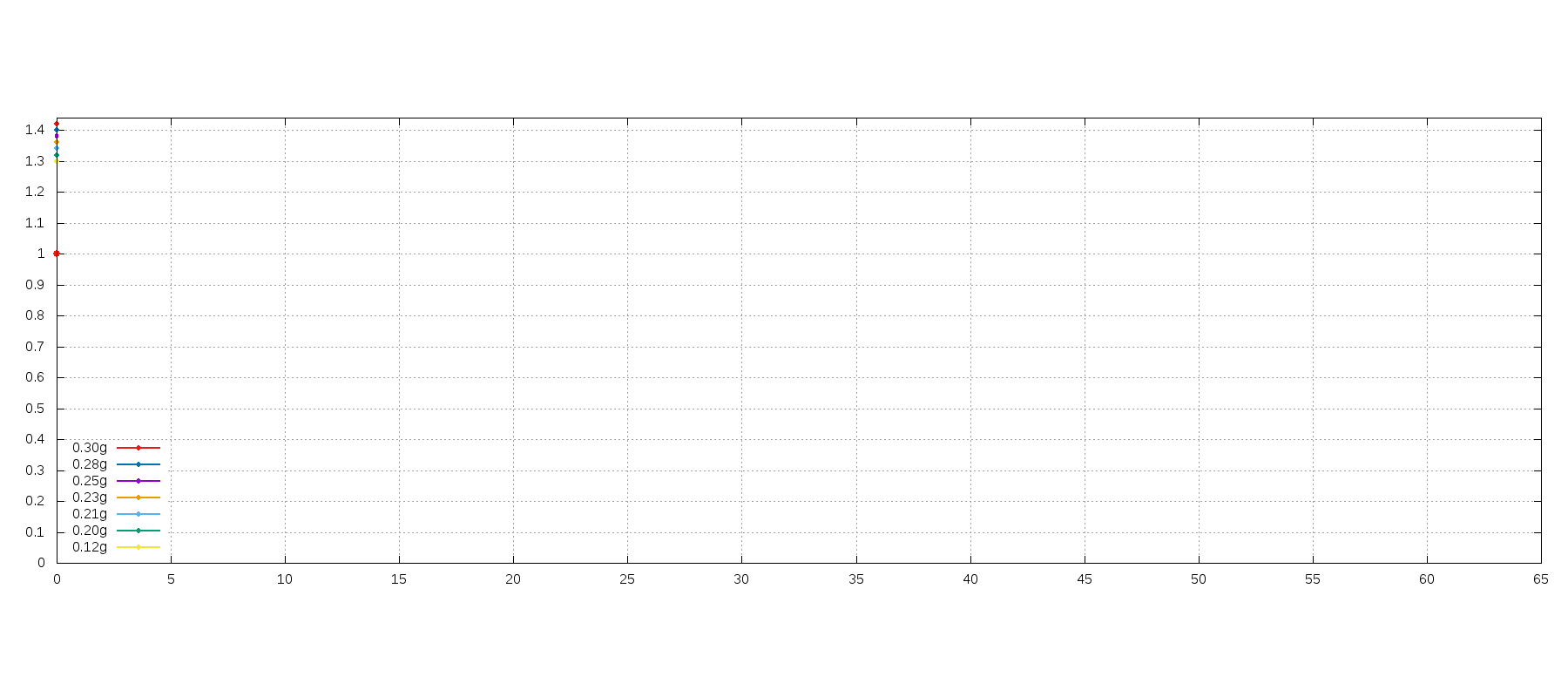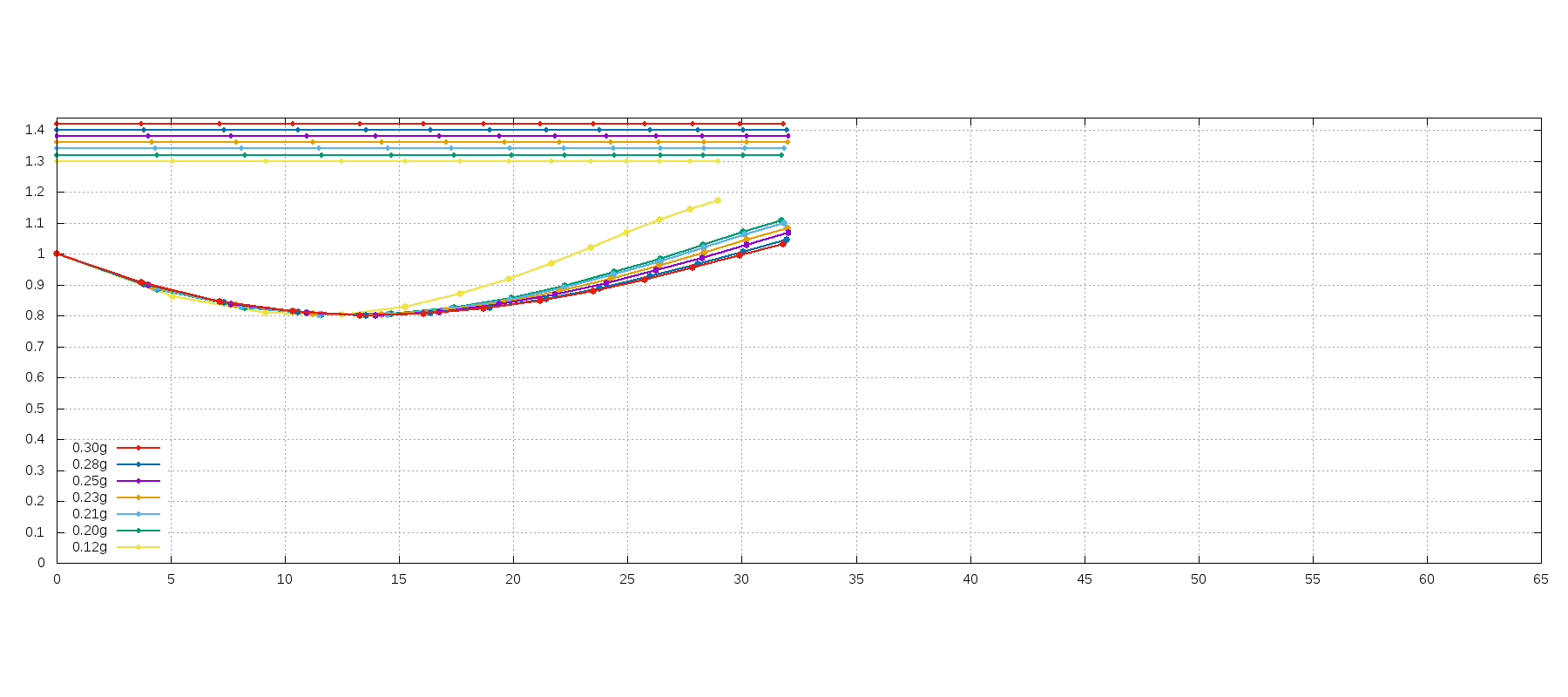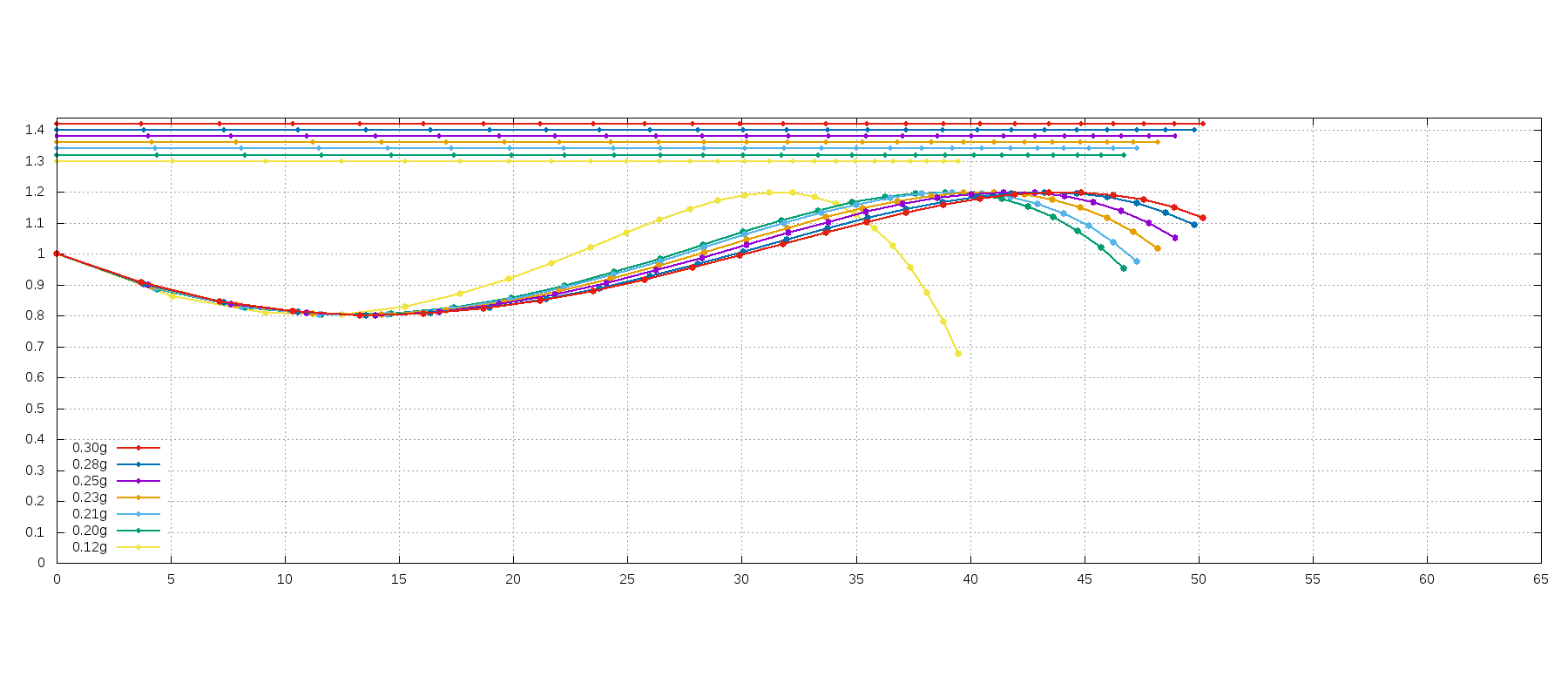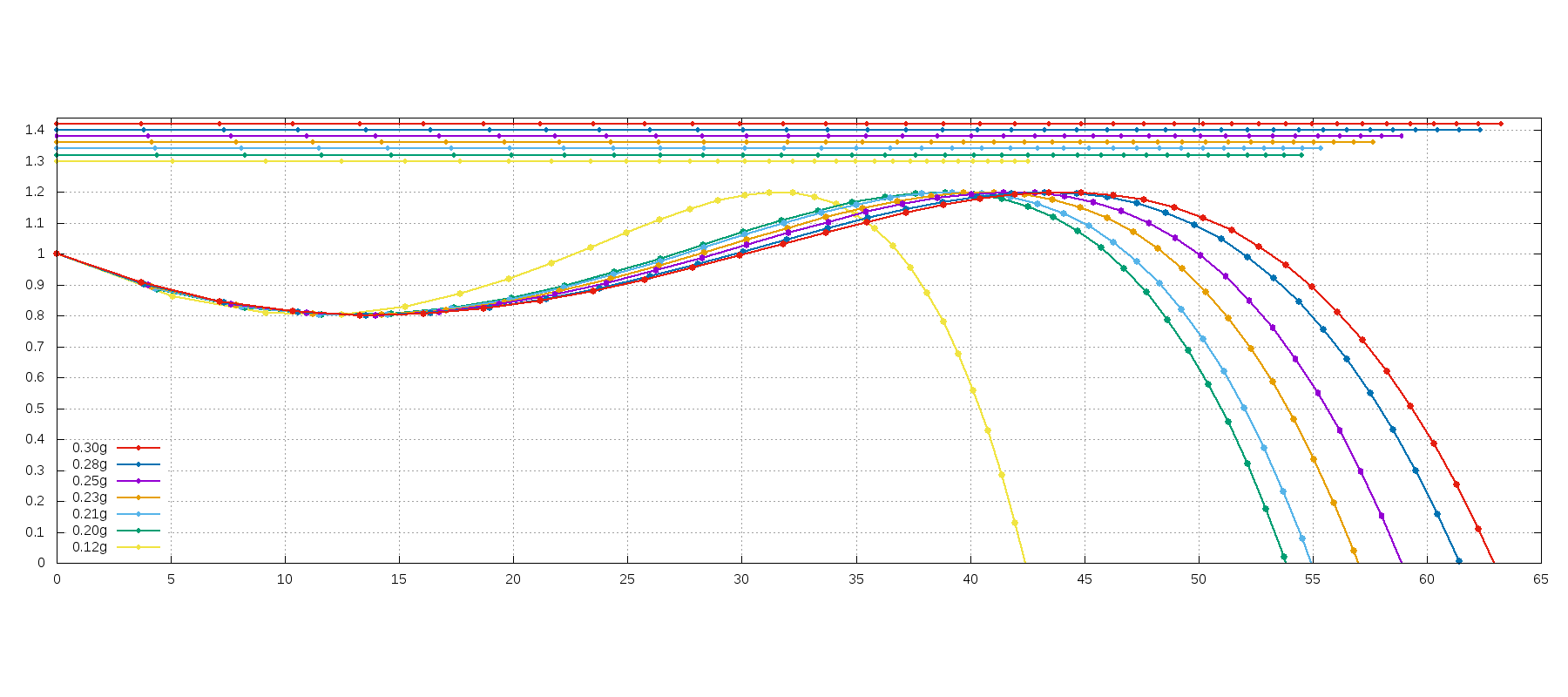
飛距離に対して到達速度は0.12g以外ではほとんど変わりません。
30m付近でおおよそ同じ時間に到達していることが分かります。
それ以降は重いほど早く到達し、かつ遠くまで飛んでいることが分かるかと思います。
やはり銃が許す限り、BB弾は重ければ重いほど良い、ということです。
撃ち上げ、撃ち下し時の軌道のずれについて
山のフィールドにおいて、斜面下から上、または上から下に向かって撃つ時、軌道はどう変わるのでしょうか。
答えは、照準よりも上に飛んでいきます。
以下の画像の状況を考えます。
エネルギーは0.90J, 重さは0.25gを考えます。
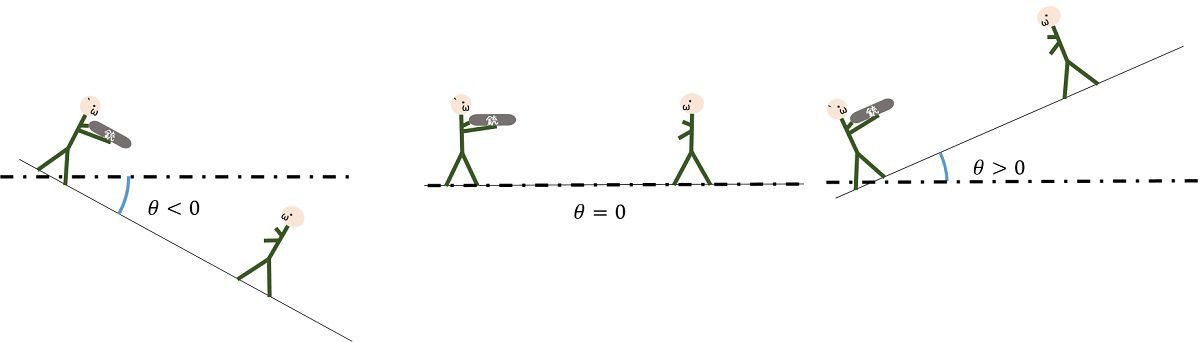
下から上に向かって打つときの角度を正にとって\(+\theta\)
上から下に向かって打つときの角度を負にとって\(-\theta\)と表すことにします。
また、平坦な場所でゼロイン50mで最小の振れ幅になる軌道で比較します。
それぞれの角度\(\theta\)の向きで射出した後、撃った角度\(\theta\)で座標を回転させて主観的な視点で見た時にどうなるかを考えます。
すると、以下の結果を得ます。
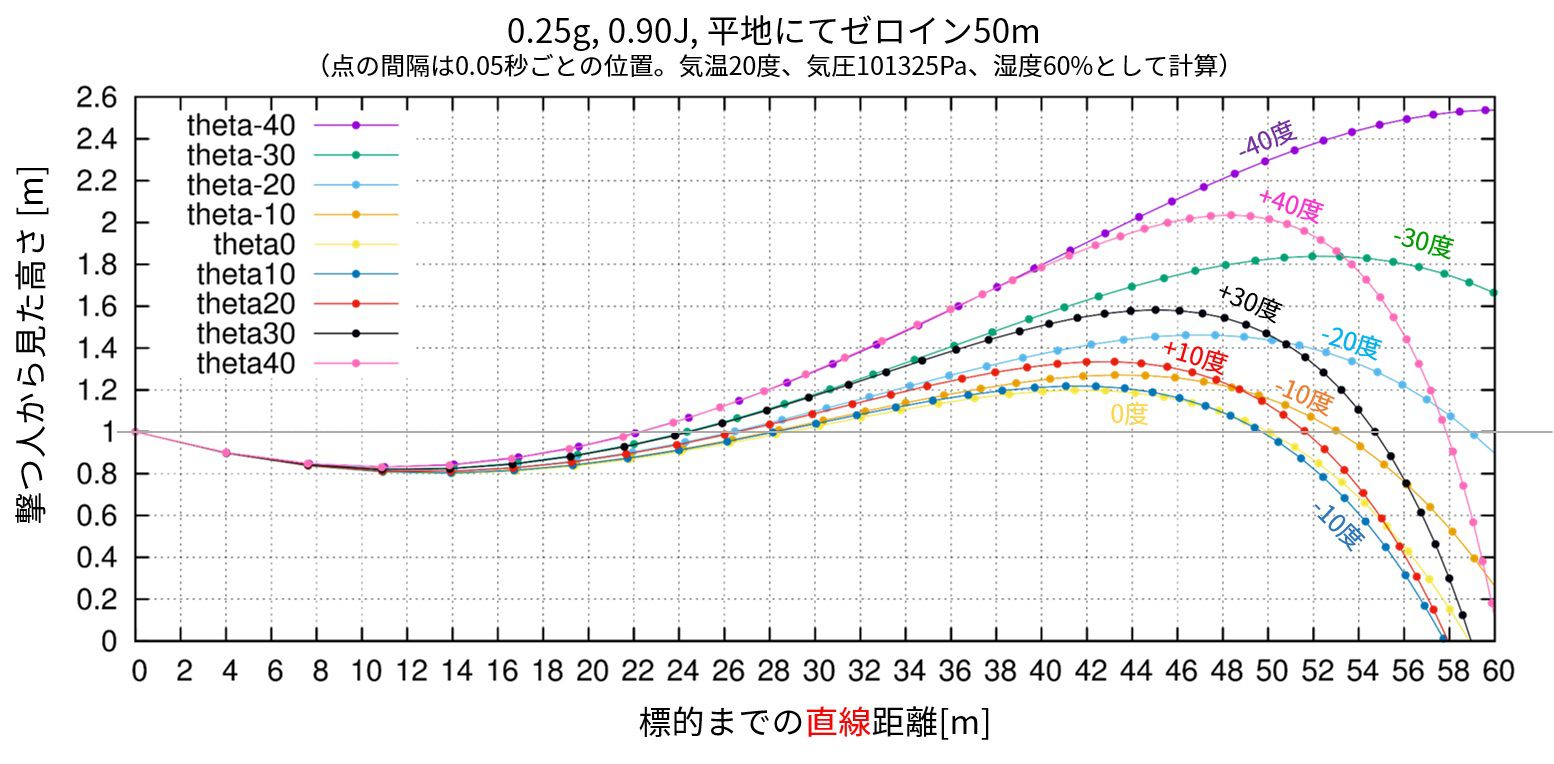
横軸は水平の距離ではなく、その角度で見た時の相対的な距離です。
\(\theta=0\)の時とそれぞれの角度の時を比較すると、角度をつける場合はほとんどの場合で上向きにずれることが分かります。
すなわち、角度がある時はシューティングレンジで合わせた照準よりも上に着弾するのです。
何故でしょうか。ちゃんと理由があります。
上向きにでも下向きにでも、角度があって撃つとき、BB弾に掛かる見かけ上の重力が減少します。
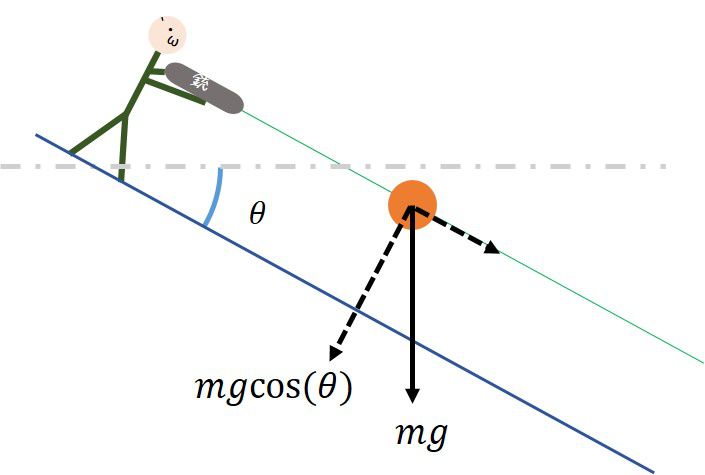
なので角度がある時は重力が小さく感じるので、角度が無いところで調節した時よりも上の方に飛んでいくことになります。
なので、山のフィールドで斜面があるときは、若干下方向を、すなわち相手の膝や腰辺りを狙えばいいのです。
