近頃SNSやインターネットでよく見る言葉、「位相速度」「群速度」。
元ネタや原理を分かった気になって使っている方、多いのではないでしょうか。
せっかくなので調べてみました!!!
(数式で殴りに殴ったものを以下のページに書きました。真面目に詳細を知りたい方はこちらをどうぞ。)
https://slpr.sakura.ne.jp/qp/group-phase-velocity-delay/
- そもそも「位相速度」「群速度」って何?
- 学会騒然。ある波数近傍だけ値を持つ場合にテーラー展開!?
- 位相速度はどうやって!?驚きの仮定
- 簡単だと思いました?注意です!
- いろいろなところに群速度に関する議論が!
- 最後に
- Note
そもそも「位相速度」「群速度」って何?
なにはともあれwikipedia!!
関連するキーワードをササッと知るには強い味方です。
「位相速度」「群速度」を調べるとこのように説明されていました。
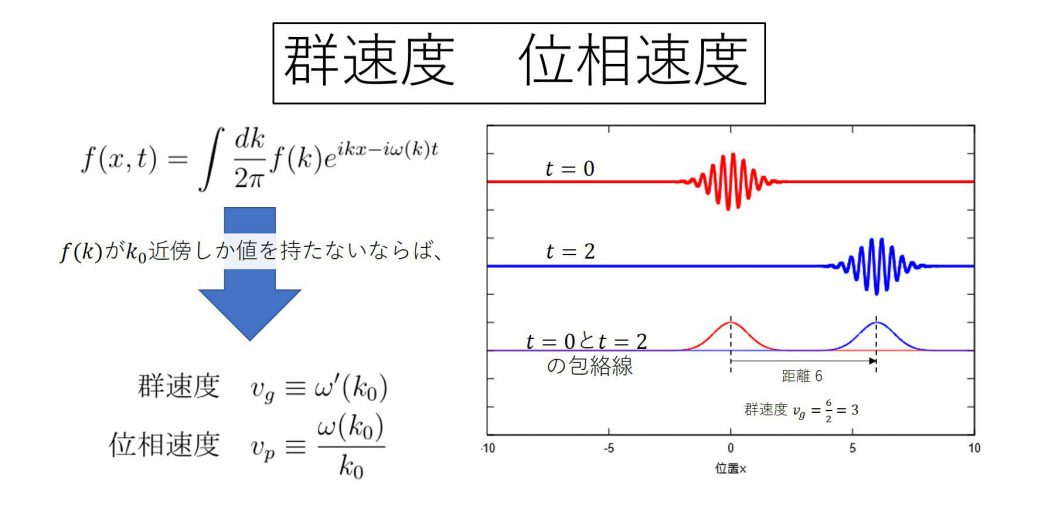
群速度(ぐんそくど、英: group velocity)とは、複数の波を重ね合わせた時にその全体(波束)が移動する速度のことである。
位相速度(いそうそくど、英語: phase velocity)は、位相、すなわち波の山や谷の特定の位置が移動する速度のことである。
どうやら、波束や波の速度を表現する際に都合が良い言葉なようです。
波束とは何なのでしょう…?また変な言葉が出てきました。wikipediaの出番です!!
波束(はそく、英: wave packet, wave train)は、局所的に存在する波うち/波動であり、移動する1個の波動の塊のようにふるまう。
うーん、つまり一回だけ波打って、ある程度まとまった波みたいなものですかね。
水面に水が一滴だけ落ちたときに発生する波みたいなものでしょう。
具体的にどういう意味なのでしょうか。気になりますよね!
皆さんも群速度、位相速度の導出が気になったら「tweet」、お願いします!
学会騒然。ある波数近傍だけ値を持つ場合にテーラー展開!?
角周波数が波数の関数として書けている場合、分散関係があるといいます。
つまり、角周波数\(\omega\)が波数\(k\)に依存して\(\omega=\omega(k)\)と書けている場合、波形のほとんどは
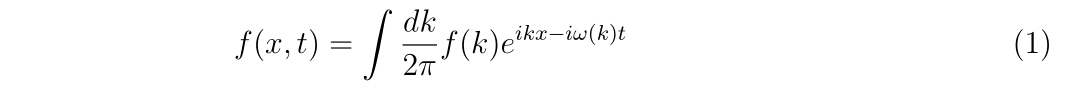
とように書けます!!
本来、位置\(x\)と時間\(t\)で書ける関数は、\(k\)と\(w\)の二重積分で表現されなければなりませんが、分散関係のおかげで\(\omega\)が強制的に決まってしまうので、一重積分で良くなるのですね!
うーん、とても嬉しい!!!!
…でも、あまりに一般的過ぎて分かりませんね。
しかし!!
応用で重要なのは、ゆっくり振動する包絡線と早く振動する波の掛け算で表されていることが多いのです。
つまり、これから考える波が持つ波数は、\(k= k_0\)の周りしか値を持たないのです。ここで、早く振動する波の波数を\(k_0\)と置きました。
\(k_0=5\)の場合、これから考えていく\(f(k)\)はこんな感じの特徴を持っています!ババン!
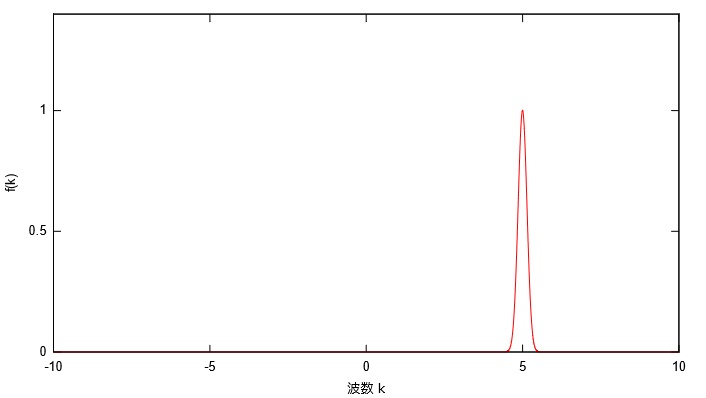
こんな特徴を持つのならば、\(k=k_0\)以外ではどうせ\(f(k)\to 0\)となるので、考えてもしょうがないっていう近似が使えそうですよね。
そ こ で !
波数\(k=k_0\)周りでいろいろテーラー展開して使用していきます。つまり、\(k=k_0\)の近傍さえ合っていれば、\(k_0\)以外でどんな振る舞いになろうとも\(f(k)\)がゼロになるので大丈夫でしょう!ということです。
早速、分散関係についてテーラー展開を行うと
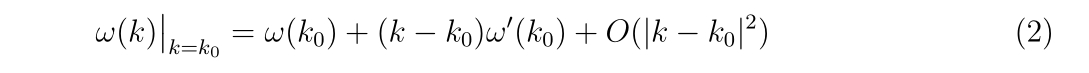
となります。式を簡単に書くために\(\omega'(k_0)\equiv \frac{d\omega}{dk}\bigr|_{k=k_0}\)と置きました。
計算を進めると、
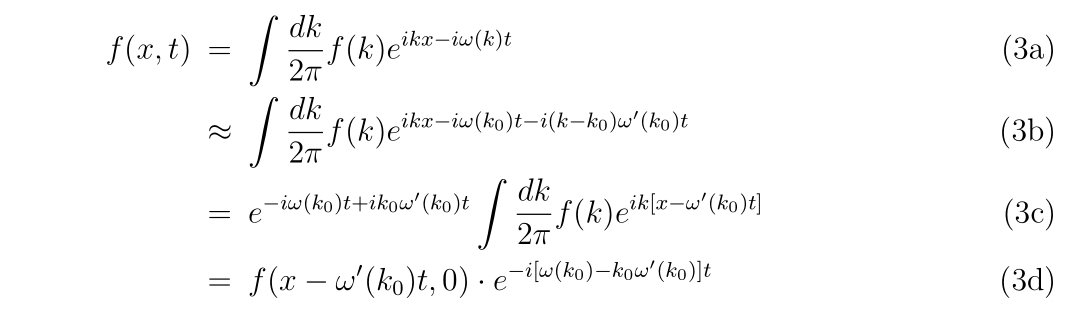
より、
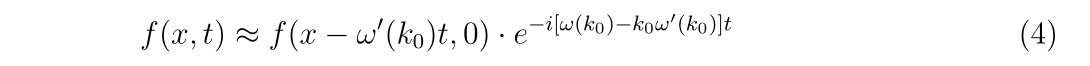
のように書けます。つまり、式(4)が言っていることは、
時刻\(t\)の波形とは、初期状態\(t = 0\)の波形 \(f(x,0)\)を\(\omega'(k_0)t\)だけ平行移動させた波に、時間だけに依存する位相に関する変化分 \(e^{−i[\omega(k_0)−k_0 \omega'(k_0)]t}\)が掛け合わされたもの、と表すことができる。と言っています。
以上から、初期状態の波が時刻\(t\)に至るまでの速度は\(\omega'(k_0)\)で決まることが分かり、これは
群速度
と呼ばれます!!
位相速度はどうやって!?驚きの仮定
さて、ここまでで群速度が求まりましたが、位相速度が求められていません。
そこで、もう少し具体的な波の形を定義しましょう。
波が、
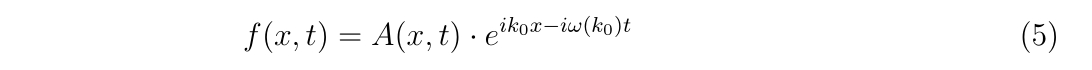
と書けている場合を想定します。ここで、振幅\(A(x,t)\)は実数値関数で波の包絡線を表しています。また\(A(x,t)\)の変化は \(k_0\) に比べて非常にゆっくり変化しているものとします。
つまり、
今まで考えてきた仮定が全部使える
んですね!
式(5)に代入しますと
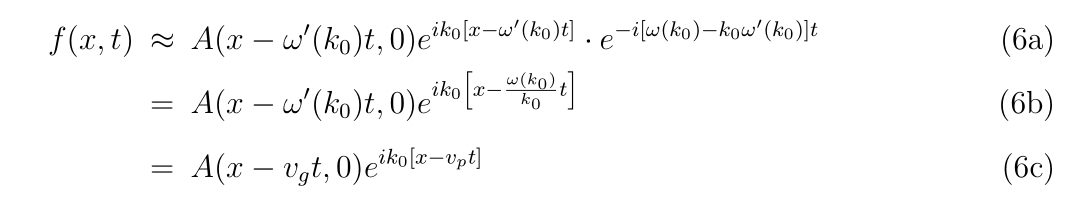
となります。つまり、振幅の変化はいつも初期状態の単なる平行移動として表現することができ、位相の変化も簡単に表せられます。
そこで、振幅が平行移動する速度を群速度\(v_g\)、位相が平行移動していく速度を位相速度 \(v_p\) として定義すると、 式(6c) よりそれぞれ
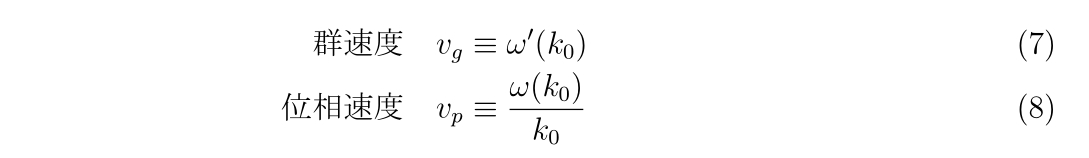
と定義してしまうのが良さそうです!
簡単だと思いました?注意です!
注意しなければならないのは、群速度と位相速度の概念は、
振幅と位相を記述する部分がはっきりと区別できるような状況でなければ、定義できない
ということです!振幅部が早く振動していたら、これまでの議論が使えなくなることに注意しましょう。
その場合、群速度と位相速度の概念が変わってしまうので、意味をなさなくなってしまいます。
いろいろなところに群速度に関する議論が!
様々なところにリンクがあります。やはり皆、群速度の概念を理解するのに苦労しているようですね。
「yam@広島大」物理化学Monographシリーズ ”3. 物体の速度と物質波の速度 -E=hνの本質の理解-”
最後に
いかがでしたか?気に入ったなら是非、記事の下にある「like!」ボタンや「tweet」して皆さんに共有して下さいね!
それでは皆さん、良い物理ライフを!
Note
本記事の大枠の構成はいかがでしたか? -ニコニコ大百科を参照しています。