角度に依存して色を付ける(gnuplot)

gnuplotです。
gnuplotで、関数、もしくはデータでsplotすると3列目のデータに依存してカラーリングがされます。新たに4列目にデータを加え、splotをする時に

splot "test.d" u 1:2:3:4 w pm3d

とすると、4列目に従ったカラーリングがされます。

データの場合

例えば、以下のデータ(球面調和関数$l=1,m=0$)を持っていたとします。
(ここにテキストデータ”y10.d”(500kB)を置きました。)
1列目:$\sin{\theta}\cos{\phi}\cdot Y_{l,m}$, 2列目:$\sin{\theta}\sin{\phi}\cdot Y_{l,m}$, 3列目:$\cos{\theta}\cdot Y_{l,m}$, 4列目：$\theta$, 5列目：$\phi$
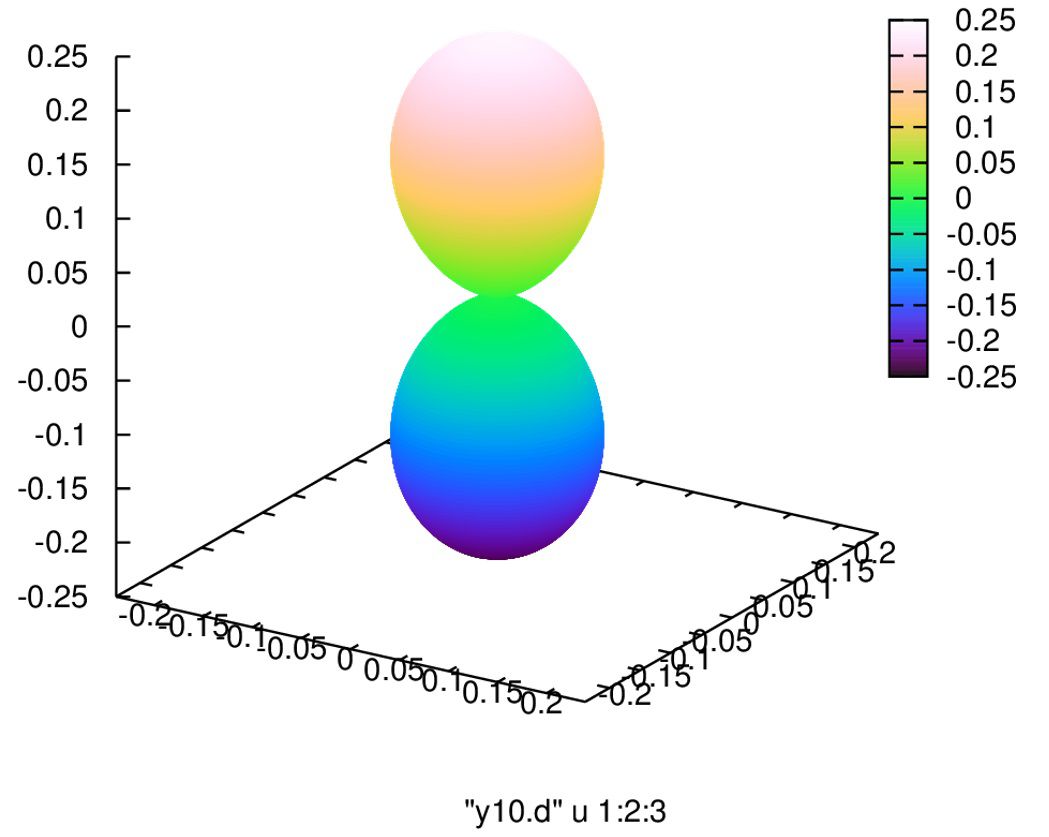
そのまま出力する場合、以下のようなスクリプトで、以下の画像が取得できるはずです。

set pm3d
set pm3d depthorder
unset sur
set view equal xyz
set ticslevel 0
splot "y10.d" u 1:2:3

これを角度$\theta$に依存させて、形は変えずに色を付けましょう。
splotするときに、カラーを4列目に沿って付けるとすれば、

splot "y10.d" u 1:2:3:4 w pm3d

であり、もしも角度$\phi$に依存させて描くのであれば

splot "y10.d" u 1:2:3:5 w pm3d

でokです。実際に書いて、出力するとそれぞれ以下のような画像が出力されます。

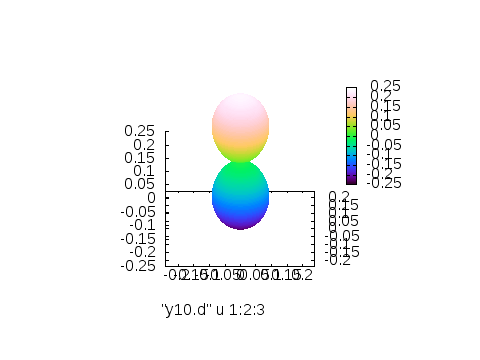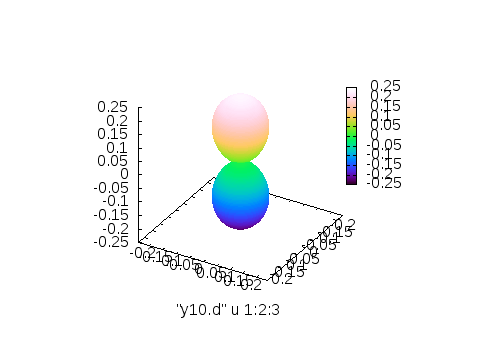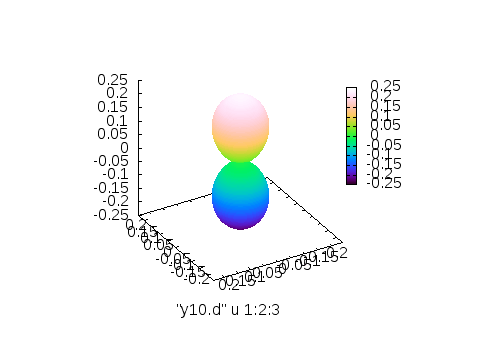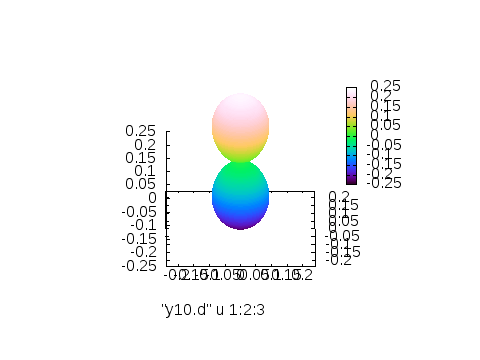
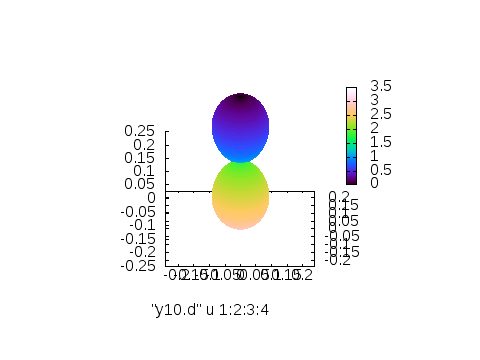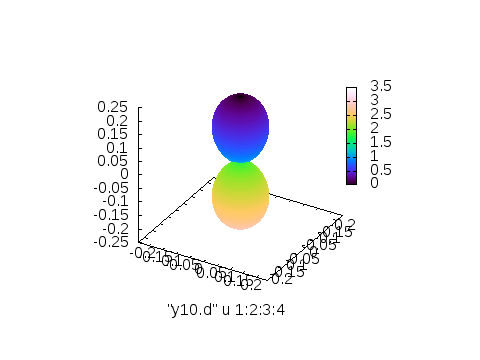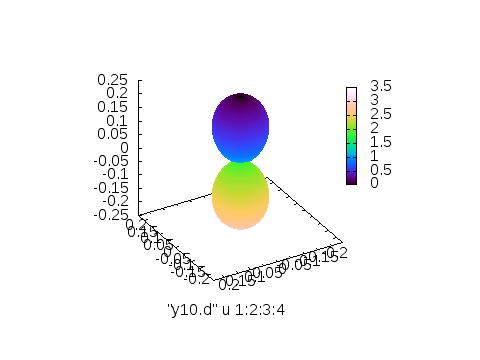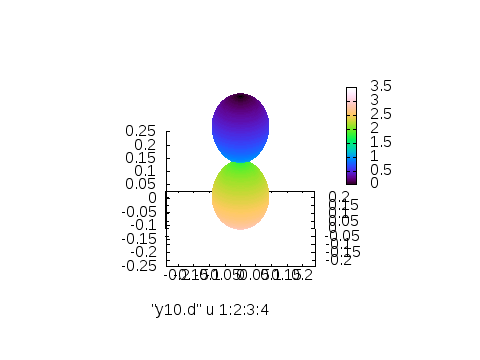
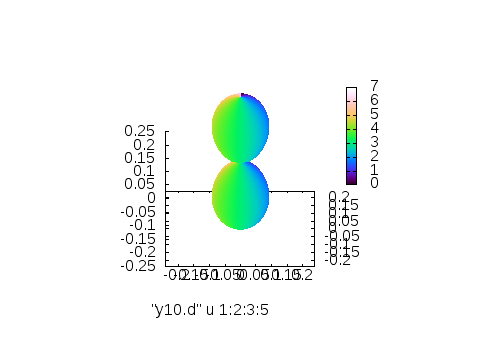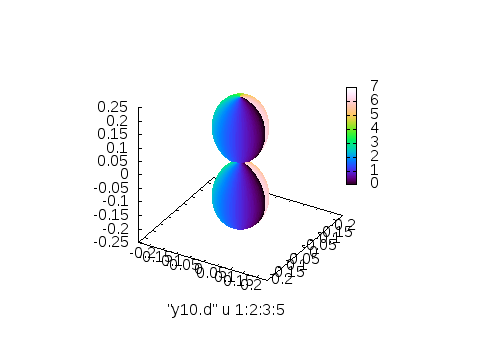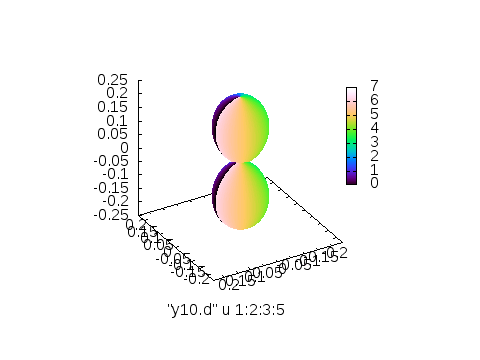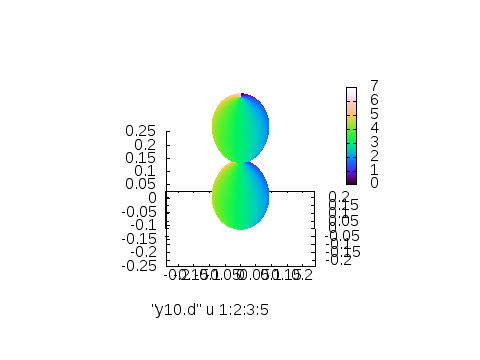
※左から3列目($Y_{l,m}$の値)に従って付けたカラー、4列目$\theta$に従って付けたカラー、5列目$\phi$に従って付けたカラー
となります。

※球面調和関数の出力に関して
球面調和関数は球面座標で$\theta,\phi$の関数$Y_{l,m}(\theta,\phi)$です。
ただし、今出力したい座標はデカルト座標($x,y,z$)です。デカルト座標で球面座標で記述される画像を得たい場合は単位ベクトル$\; \vec{r}/|\vec{r}|\;$に球面座標の関数を掛ければよいのです。
よって
$
\displaystyle Y_{l,m}(\theta,\phi)\cdot \frac{\vec{r}}{|\vec{r}|}
$
を表示すればよい、すなわちgnuplot上では($r=1$の場合)、
1列目に $x\;\;\to \;\; \sin{\theta}\cos{\phi}\cdot Y_{l,m}(\theta,\phi)$
2列目に $y\;\;\to \;\; \sin{\theta}\sin{\phi}\cdot Y_{l,m}(\theta,\phi)$
3列目に $z\;\;\to \;\; \cos{\theta}\cdot Y_{l,m}(\theta,\phi)$
を表示させればokです。

多価関数の場合

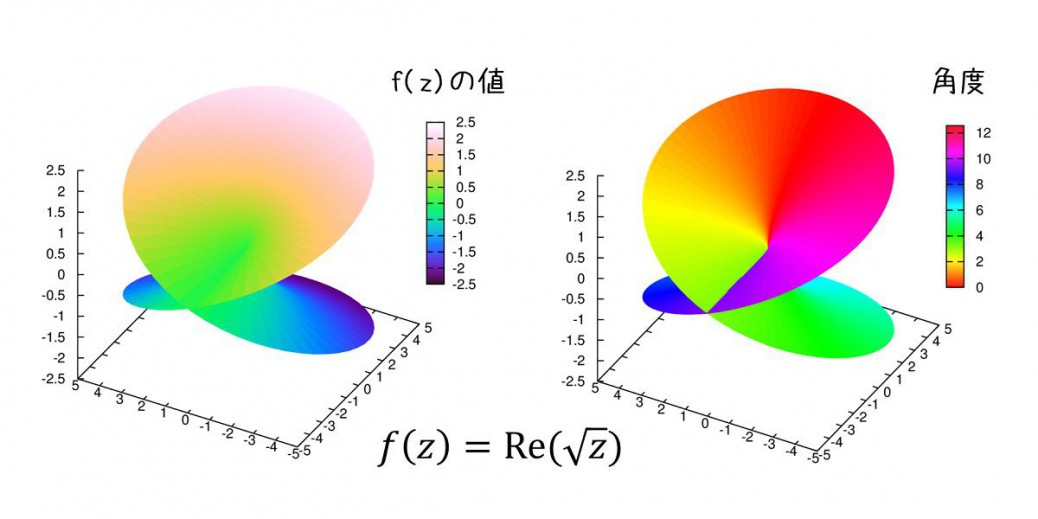
続いて、多価関数として有名なリーマン面を出力します。
通常のリーマン面(3列目の高さがカラーの基準)を表示させるには

set pm3d depthorder
set parametric
set ur[0.01:5]
set vr[0:4*pi]
i={0,1}
splot u*cos(v),u*sin(v),real(sqrt(u)*exp(i*0.5*v))

とすれば下にある、左側の画像が得られます。角度に依存したカラーリングをしたい場合、以下のスクリプトでokです。

set isosamples 150
set pm3d depthorder

set table "param1.d"
set parametric
set ur[0.01:5]
set vr[0:4*pi]
i={0,1}
splot u,v,real(sqrt(u)*exp(i*0.5*v))
unset table

set table "param2.d"
plot "param1.d" u ($1*cos($2)):($1*sin($2)):3:($2) w vector
unset table

splot "param2.d" u 1:2:3:4 w pm3d

データでは無く、解析的な関数を直接、別の列を基準にして色付け、出力させることはできないようです。なので、関数を数値的なファイルに出力させるコマンド

set table "data.d"
...(ここに数値的に出力させたいグラフをプロット)
unset table

を書いて出力を行わせています。

また、角度を出力させるので周期的なカラーリングが良いと思います。色相環を元に下のカラーマップを使うといいでしょう。

set palette defined(0"#ff0000",1"#ff8000",2"#ffff00",3"#80ff00",4"#00ff00",5"#00ff80",6"#00ffff",7"#0080ff",8"#0000ff",9"#8000ff",10"#ff00ff",11"#ff0080",12"#ff0000")

上のスクリプトを実行すると右図のように、角度に依存したカラーリングがされます。

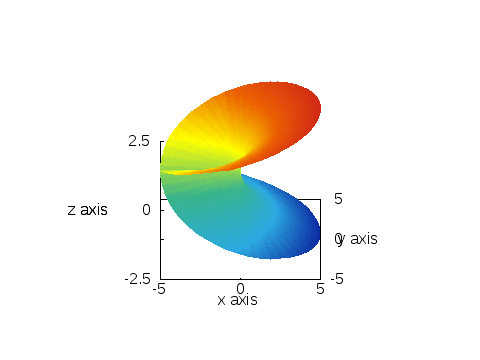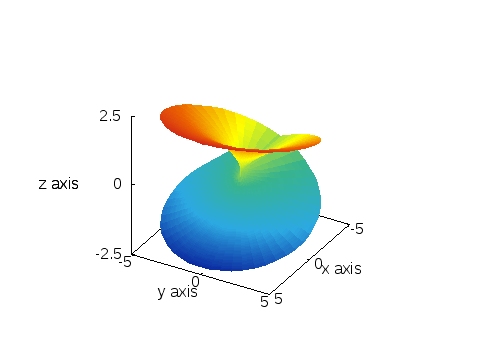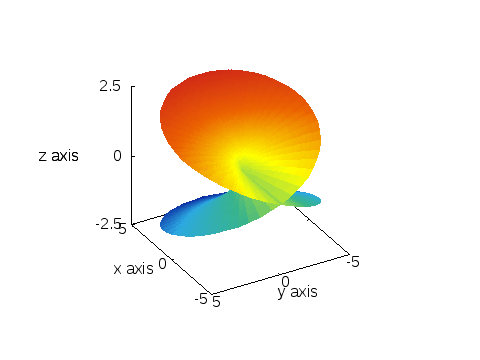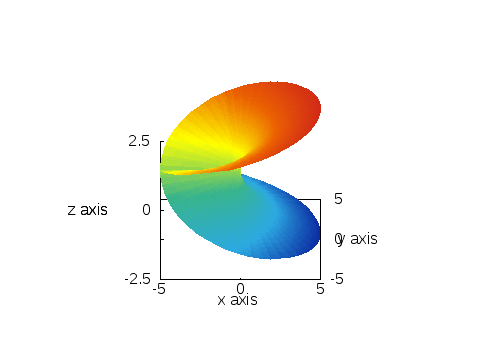
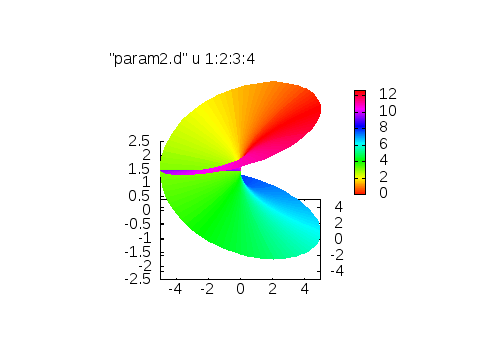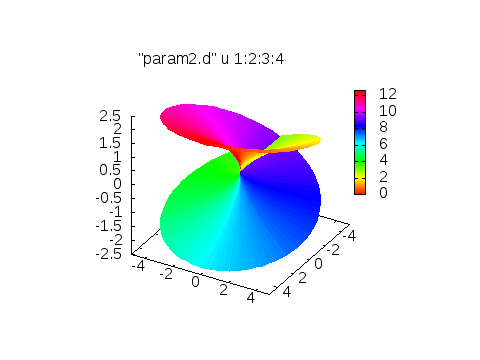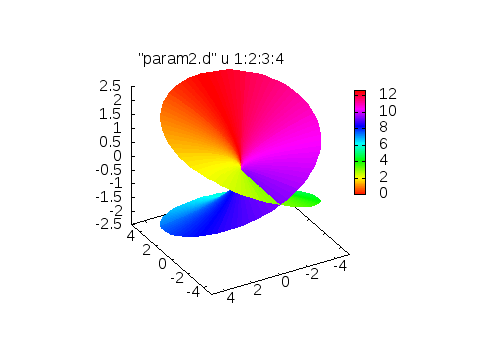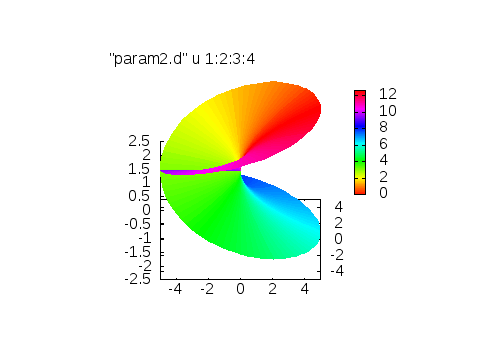
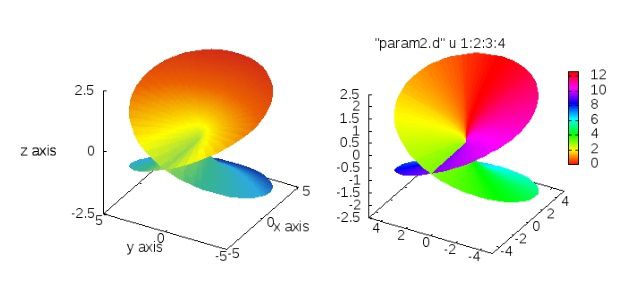
※Riemann面について
Riemann面は
$
f(z)=Re(\sqrt{z})
$
で表される多価関数です。
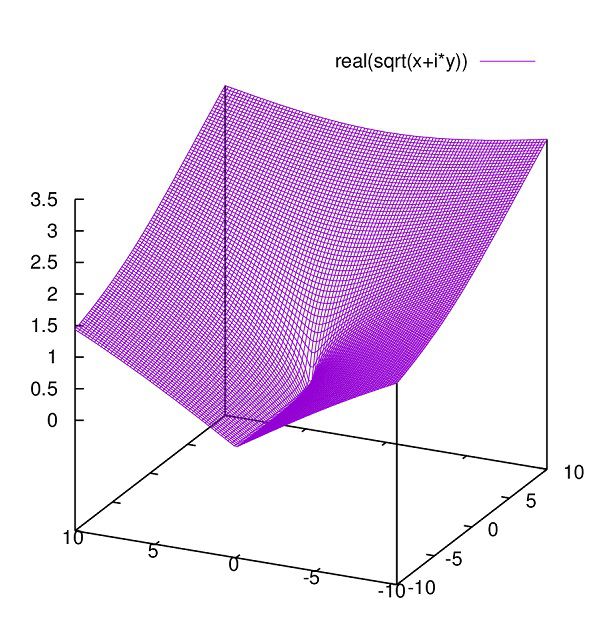
gnuplotで単純に考えて上のグラフをプロットしようとすると、

i={0,1}
splot real(sqrt(x+i*y))

で良いはずですが、これを実際にプロットするとこうなります。

本来は多価関数なのですが、それゆえに上記方法ではgnuplotでは記述されません。
極座標を用いて以下のように考えます。
$
\begin{align}
f(z)&=\sqrt{z} \\
&=\sqrt{r}e^{i\frac{1}{2}\theta} (0\le \theta\lt 4\pi)\\
\end{align}
$
であるため、gnuplotでは媒介変数表示u,vを用いて
$(x,y,z)=(u\cos{v},u\sin{v},\sqrt{u}e^{i\frac{1}{2}v})$
$(u:0\sim \infty, v:0\sim 4\pi)$
とすればいいのです。