クイックソートが速いのは分かっていますが、コーディングの仕方によって速度は変わります。
本稿では、ネット上で公開されているどのクイックソートが早いのか調べていきます。
最も早いクイックソートはNUMPACのプログラムでした。
比較プログラム
比較するプログラムはネット上で公開されているクイックソート+αです。
対象は、倍精度実数をソートするプログラム、です。
1. 再帰を用いたクイックソート(f90)
t-nissieの日記: 【電脳】Fortranで書いたクイックソート
implicit none
double precision,intent(inout)::a(*)
integer,intent(in)::first,last
!
! Original
! https://gist.github.com/t-nissie/479f0f16966925fa29ea
!
double precision::x,t
integer::i,j
x = a((first+last)/2)
i = first
j = last
do
do while (a(i) < x)
i=i+1
end do
do while (x < a(j))
j=j-1
end do
if (i >= j) exit
t = a(i)
a(i) = a(j)
a(j) = t
i=i+1
j=j-1
end do
if (first < i-1) call quicksort1(a, first, i-1)
if (j+1 < last) call quicksort1(a, j+1, last)
return
end subroutine quicksort1
2. 再帰を用いないクイックソート(f90)
[Fortran]再帰を使わないquicksortその2 -fortran66の日記
※ただし、私が割と変えていますので、オリジナルそのものではないということを注記しておきます。この変更によって、実行速度はほぼほぼ変わらないことは確認しています。
implicit none
integer,intent(in)::n
double precision,intent(inout)::x(1:n)
integer,allocatable::ix(:),iw(:)
!
! Original
! http://d.hatena.ne.jp/fortran66/20120415/1334423664
!
integer :: i, j, kk0, kk1, k0, k1, ix0, ix1, l, nx
double precision :: tmp
allocate(ix(n),iw(n))
ix=0
iw=0
if (n < 2) return
ix(1) = 1
ix(2) = n
nx = 2
do while(nx.ne.0)
l = 0
do j = 1, nx - 1, 2
kk0 = ix(j)
kk1 = ix(j + 1)
k0 = kk0 + 1
k1 = kk1
do while(k0 <= k1)
do ix0 = k0, k1 ! L
if (x(ix0) > x(kk0)) exit
end do
do ix1 = k1, k0, -1 ! R
if (x(ix1) < x(kk0)) exit
end do
if (ix0 >= ix1) exit
tmp = x(ix0) !swap
x(ix0) = x(ix1)
x(ix1) = tmp
k0 = ix0 + 1
k1 = ix1 - 1
end do
tmp = x(kk0) ! CSHIFT(x(kk0:ix1), 1)
do i = kk0, ix1 - 1
x(i) = x(i + 1)
end do
x(ix1) = tmp
if (kk0 < ix1 - 1) then ! L
l = l + 1
iw(l) = kk0
l = l + 1
iw(l) = ix1 - 1
end if
if (kk1 > ix0) then ! R
l = l + 1
iw(l) = ix0
l = l + 1
iw(l) = kk1
end if
end do
nx = l
ix(1:nx) = iw(1:nx)
end do
return
end subroutine quicksort2
3. Netlibのクイックソートdsort.f
https://www.netlib.org/slatec/src/dsort.f
SUBROUTINE DSORT (DX, DY, N, KFLAG)
C***BEGIN PROLOGUE DSORT
C***PURPOSE Sort an array and optionally make the same interchanges in
C an auxiliary array. The array may be sorted in increasing
C or decreasing order. A slightly modified QUICKSORT
C algorithm is used.
C***LIBRARY SLATEC
C***CATEGORY N6A2B
C***TYPE DOUBLE PRECISION (SSORT-S, DSORT-D, ISORT-I)
C***KEYWORDS SINGLETON QUICKSORT, SORT, SORTING
C***AUTHOR Jones, R. E., (SNLA)
C Wisniewski, J. A., (SNLA)
C***DESCRIPTION
C
C DSORT sorts array DX and optionally makes the same interchanges in
C array DY. The array DX may be sorted in increasing order or
C decreasing order. A slightly modified quicksort algorithm is used.
C
C Description of Parameters
C DX - array of values to be sorted (usually abscissas)
C DY - array to be (optionally) carried along
C N - number of values in array DX to be sorted
C KFLAG - control parameter
C = 2 means sort DX in increasing order and carry DY along.
C = 1 means sort DX in increasing order (ignoring DY)
C = -1 means sort DX in decreasing order (ignoring DY)
C = -2 means sort DX in decreasing order and carry DY along.
C
C***REFERENCES R. C. Singleton, Algorithm 347, An efficient algorithm
C for sorting with minimal storage, Communications of
C the ACM, 12, 3 (1969), pp. 185-187.
C***ROUTINES CALLED XERMSG
C***REVISION HISTORY (YYMMDD)
C 761101 DATE WRITTEN
C 761118 Modified to use the Singleton quicksort algorithm. (JAW)
C 890531 Changed all specific intrinsics to generic. (WRB)
C 890831 Modified array declarations. (WRB)
C 891009 Removed unreferenced statement labels. (WRB)
C 891024 Changed category. (WRB)
C 891024 REVISION DATE from Version 3.2
C 891214 Prologue converted to Version 4.0 format. (BAB)
C 900315 CALLs to XERROR changed to CALLs to XERMSG. (THJ)
C 901012 Declared all variables; changed X,Y to DX,DY; changed
C code to parallel SSORT. (M. McClain)
C 920501 Reformatted the REFERENCES section. (DWL, WRB)
C 920519 Clarified error messages. (DWL)
C 920801 Declarations section rebuilt and code restructured to use
C IF-THEN-ELSE-ENDIF. (RWC, WRB)
C***END PROLOGUE DSORT
C .. Scalar Arguments ..
INTEGER KFLAG, N
C .. Array Arguments ..
DOUBLE PRECISION DX(*), DY(*)
C .. Local Scalars ..
DOUBLE PRECISION R, T, TT, TTY, TY
INTEGER I, IJ, J, K, KK, L, M, NN
C .. Local Arrays ..
INTEGER IL(21), IU(21)
C .. External Subroutines ..
! EXTERNAL XERMSG
C .. Intrinsic Functions ..
INTRINSIC ABS, INT
C***FIRST EXECUTABLE STATEMENT DSORT
NN = N
IF (NN .LT. 1) THEN
! CALL XERMSG ('SLATEC', 'DSORT',
! + 'The number of values to be sorted is not positive.', 1, 1)
RETURN
ENDIF
C
KK = ABS(KFLAG)
IF (KK.NE.1 .AND. KK.NE.2) THEN
! CALL XERMSG ('SLATEC', 'DSORT',
! + 'The sort control parameter, K, is not 2, 1, -1, or -2.', 2,
! + 1)
RETURN
ENDIF
C
C Alter array DX to get decreasing order if needed
C
IF (KFLAG .LE. -1) THEN
DO 10 I=1,NN
DX(I) = -DX(I)
10 CONTINUE
ENDIF
C
IF (KK .EQ. 2) GO TO 100
C
C Sort DX only
C
M = 1
I = 1
J = NN
R = 0.375D0
C
20 IF (I .EQ. J) GO TO 60
IF (R .LE. 0.5898437D0) THEN
R = R+3.90625D-2
ELSE
R = R-0.21875D0
ENDIF
C
30 K = I
C
C Select a central element of the array and save it in location T
C
IJ = I + INT((J-I)*R)
T = DX(IJ)
C
C If first element of array is greater than T, interchange with T
C
IF (DX(I) .GT. T) THEN
DX(IJ) = DX(I)
DX(I) = T
T = DX(IJ)
ENDIF
L = J
C
C If last element of array is less than than T, interchange with T
C
IF (DX(J) .LT. T) THEN
DX(IJ) = DX(J)
DX(J) = T
T = DX(IJ)
C
C If first element of array is greater than T, interchange with T
C
IF (DX(I) .GT. T) THEN
DX(IJ) = DX(I)
DX(I) = T
T = DX(IJ)
ENDIF
ENDIF
C
C Find an element in the second half of the array which is smaller
C than T
C
40 L = L-1
IF (DX(L) .GT. T) GO TO 40
C
C Find an element in the first half of the array which is greater
C than T
C
50 K = K+1
IF (DX(K) .LT. T) GO TO 50
C
C Interchange these elements
C
IF (K .LE. L) THEN
TT = DX(L)
DX(L) = DX(K)
DX(K) = TT
GO TO 40
ENDIF
C
C Save upper and lower subscripts of the array yet to be sorted
C
IF (L-I .GT. J-K) THEN
IL(M) = I
IU(M) = L
I = K
M = M+1
ELSE
IL(M) = K
IU(M) = J
J = L
M = M+1
ENDIF
GO TO 70
C
C Begin again on another portion of the unsorted array
C
60 M = M-1
IF (M .EQ. 0) GO TO 190
I = IL(M)
J = IU(M)
C
70 IF (J-I .GE. 1) GO TO 30
IF (I .EQ. 1) GO TO 20
I = I-1
C
80 I = I+1
IF (I .EQ. J) GO TO 60
T = DX(I+1)
IF (DX(I) .LE. T) GO TO 80
K = I
C
90 DX(K+1) = DX(K)
K = K-1
IF (T .LT. DX(K)) GO TO 90
DX(K+1) = T
GO TO 80
C
C Sort DX and carry DY along
C
100 M = 1
I = 1
J = NN
R = 0.375D0
C
110 IF (I .EQ. J) GO TO 150
IF (R .LE. 0.5898437D0) THEN
R = R+3.90625D-2
ELSE
R = R-0.21875D0
ENDIF
C
120 K = I
C
C Select a central element of the array and save it in location T
C
IJ = I + INT((J-I)*R)
T = DX(IJ)
TY = DY(IJ)
C
C If first element of array is greater than T, interchange with T
C
IF (DX(I) .GT. T) THEN
DX(IJ) = DX(I)
DX(I) = T
T = DX(IJ)
DY(IJ) = DY(I)
DY(I) = TY
TY = DY(IJ)
ENDIF
L = J
C
C If last element of array is less than T, interchange with T
C
IF (DX(J) .LT. T) THEN
DX(IJ) = DX(J)
DX(J) = T
T = DX(IJ)
DY(IJ) = DY(J)
DY(J) = TY
TY = DY(IJ)
C
C If first element of array is greater than T, interchange with T
C
IF (DX(I) .GT. T) THEN
DX(IJ) = DX(I)
DX(I) = T
T = DX(IJ)
DY(IJ) = DY(I)
DY(I) = TY
TY = DY(IJ)
ENDIF
ENDIF
C
C Find an element in the second half of the array which is smaller
C than T
C
130 L = L-1
IF (DX(L) .GT. T) GO TO 130
C
C Find an element in the first half of the array which is greater
C than T
C
140 K = K+1
IF (DX(K) .LT. T) GO TO 140
C
C Interchange these elements
C
IF (K .LE. L) THEN
TT = DX(L)
DX(L) = DX(K)
DX(K) = TT
TTY = DY(L)
DY(L) = DY(K)
DY(K) = TTY
GO TO 130
ENDIF
C
C Save upper and lower subscripts of the array yet to be sorted
C
IF (L-I .GT. J-K) THEN
IL(M) = I
IU(M) = L
I = K
M = M+1
ELSE
IL(M) = K
IU(M) = J
J = L
M = M+1
ENDIF
GO TO 160
C
C Begin again on another portion of the unsorted array
C
150 M = M-1
IF (M .EQ. 0) GO TO 190
I = IL(M)
J = IU(M)
C
160 IF (J-I .GE. 1) GO TO 120
IF (I .EQ. 1) GO TO 110
I = I-1
C
170 I = I+1
IF (I .EQ. J) GO TO 150
T = DX(I+1)
TY = DY(I+1)
IF (DX(I) .LE. T) GO TO 170
K = I
C
180 DX(K+1) = DX(K)
DY(K+1) = DY(K)
K = K-1
IF (T .LT. DX(K)) GO TO 180
DX(K+1) = T
DY(K+1) = TY
GO TO 170
C
C Clean up
C
190 IF (KFLAG .LE. -1) THEN
DO 200 I=1,NN
DX(I) = -DX(I)
200 CONTINUE
ENDIF
RETURN
END
4. NUMPACのクイックソート(sortdk.f)
SORTPACK(SORTxK,SORTxy,SRTVxz) (スカラー又はベクトルデータの内部ソーティング)
5. ヒープソート
fortran90によるヒープソートとバブルソート -シキノート
implicit none
integer,intent(in) :: n
double precision,intent(inout) :: x(1:n)
integer ::i,k,j,l
double precision :: t
if(n.le.0)then
write(6,*)"Error, at heapsort"; stop
endif
if(n.eq.1)return
l=n/2+1
k=n
do while(k.ne.1)
if(l.gt.1)then
l=l-1
t=x(L)
else
t=x(k)
x(k)=x(1)
k=k-1
if(k.eq.1) then
x(1)=t
exit
endif
endif
i=l
j=l+l
do while(j.le.k)
if(j.lt.k)then
if(x(j).lt.x(j+1))j=j+1
endif
if (t.lt.x(j))then
x(i)=x(j)
i=j
j=j+j
else
j=k+1
endif
enddo
x(i)=t
enddo
return
end subroutine heapsort
以上の5つのプログラムを比較していきます。
メインプログラムはこちら↓
implicit none
integer::i,n
double precision,allocatable::x(:),x0(:),data(:)
double precision::d
real::t0,t1
integer::j,Nt
integer::k,Nk
Nt=100
allocate(data(0:4))
do k=4,24
n=nint(10**(k*0.25d0))
allocate(x(1:n),x0(1:n))
data(0:4)=0d0
do j=1,Nt
call pre_random
do i=1,n
call random_number(d)
x0(i)=d
enddo
x=x0
call cpu_time(t0)
call heapsort(n,x)
call cpu_time(t1)
data(0)=data(0)+(t1-t0)
x=x0
call cpu_time(t0)
call quicksort1(x,1,n)
call cpu_time(t1)
data(1)=data(1)+(t1-t0)
x=x0
call cpu_time(t0)
call quicksort2(n,x)
call cpu_time(t1)
data(2)=data(2)+(t1-t0)
x=x0
call cpu_time(t0)
call dsort(x,x,n,1)
call cpu_time(t1)
data(3)=data(3)+(t1-t0)
x=x0
call cpu_time(t0)
call sortdk(n,x,0)
call cpu_time(t1)
data(4)=data(4)+(t1-t0)
enddo
write(6,*)k
write(10,*)n,data(0:4)/dble(Nt)
deallocate(x,x0)
enddo
stop
end program
subroutine pre_random
! sikinote
! Date : 2015/03/15
! : 2015/09/07
!
!How to use?
!===================
!call random_number(a)
!===================
! random_number produce
! value between 0~1
!
implicit none
integer::seedsize,c
integer,allocatable::seed(:)
!In fortran90, seed is array.
! To get seedsize, use below.
call random_seed(size=seedsize)
!Allocate seed array.
allocate(seed(1:seedsize))
!Get system time.
call system_clock(count=c)
!Substitute "seed" using system time.
seed=c
!seed=2
!Set "seed" to produce random number obey to system time.
call random_seed(put=seed)
return
end subroutine pre_random
コンパイルは
で行いました。
結果
結果を示します。
横軸にデータ数、縦軸にソートに掛かった時間を示しました。
”ソートに掛かった時間”とは、同じデータ数でソートを100回繰り返した時の1回当たりの時間です。
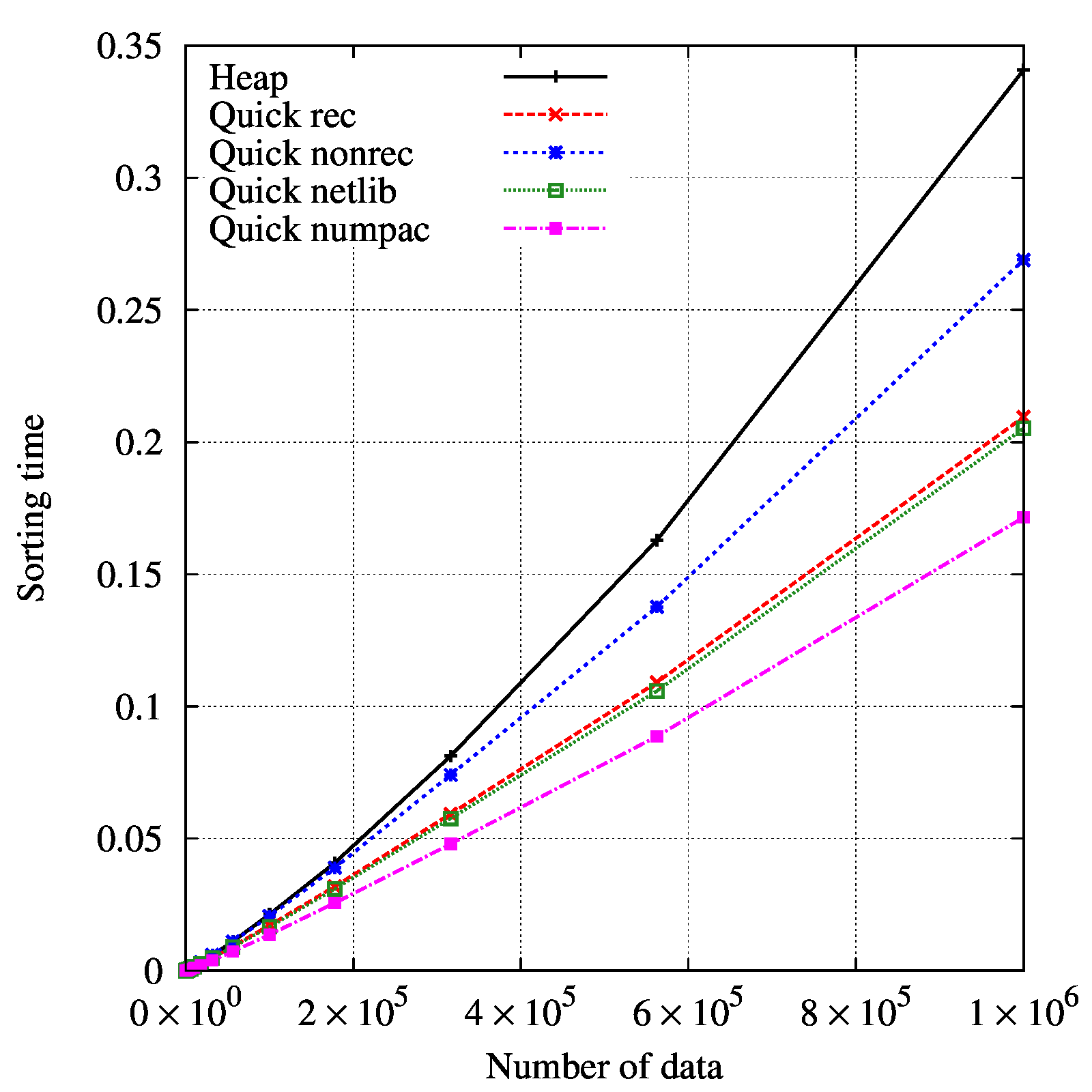
それぞれ、
赤線:再帰有りクイックソート
青線:再帰無しクイックソート
緑線:Netlibのクイックソート
紫線:NUMPACのクイックソート
黒線:ヒープソート
です。
最も早いのがNUMPAC, 最も遅いのがヒープソートだと分かりました。
ヒープソートもクイックソートも大体\(O(n\log n)\)ですので、グラフの傾きは両者でほとんど変わりません。再帰有りの方が遅い、という結果は面白いです。
先入観で”再帰は遅い”と考えていたのですが、そんなことはありませんでした。
続いて、同じデータを対数で見てみると以下の通りです。
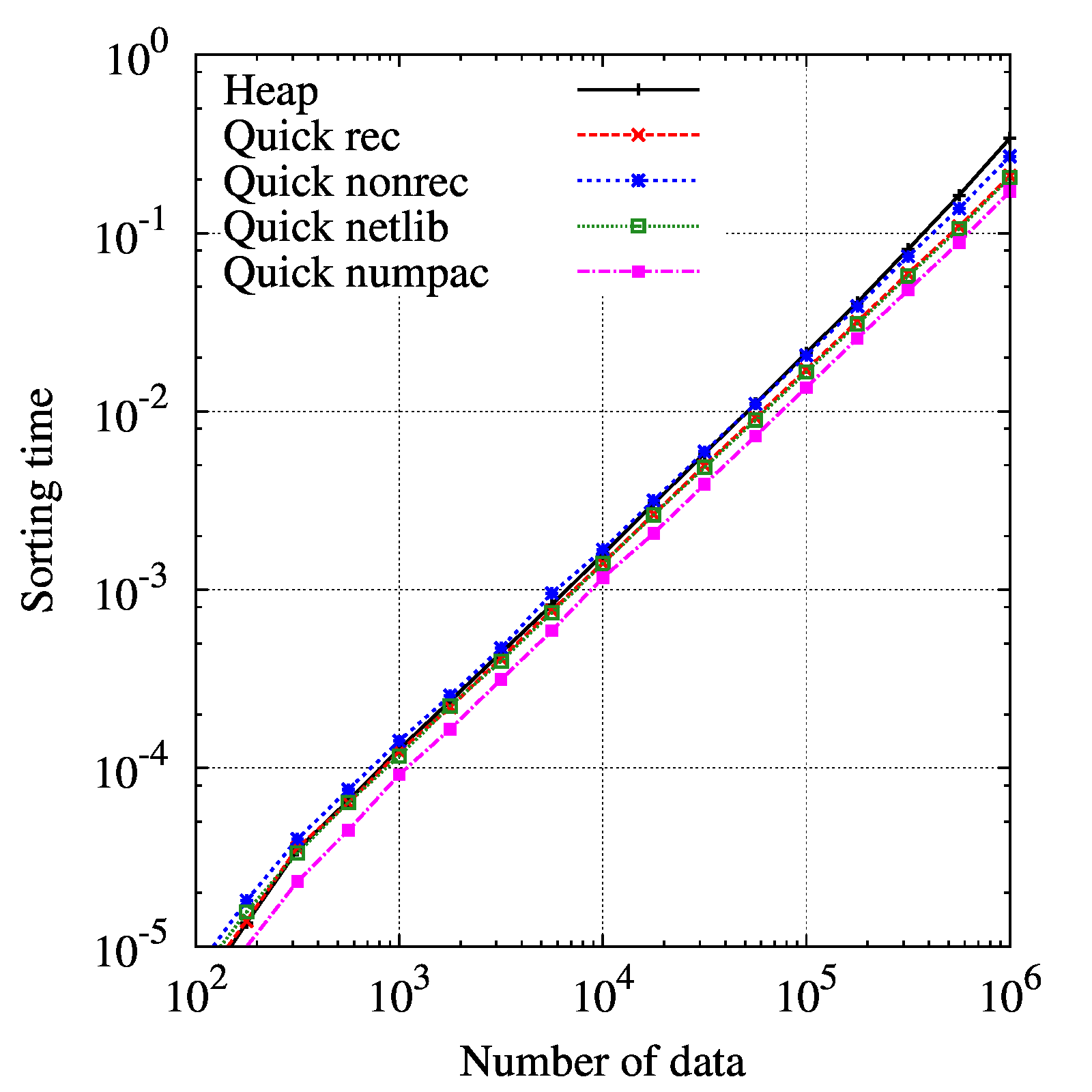
走査したデータサイズの範囲では変化は有りません。更に大規模になれば、違いが見えてくるかもしれません。