問題：以下の積分を数値的に計算せよ。
\( \displaystyle
-\frac{1}{2\pi i}\int_{-\infty}^{\infty} \frac{e^{-ikx}}{x}dx,~~(kは任意の実数)
\)

1/xのフーリエ変換である
\( \displaystyle
\int_{-\infty}^{\infty} \frac{e^{-ikx}}{x}dx,~~(kは任意の実数)
\)
を数値的に計算します。

この積分値は一意には決まりません。
複素関数論によると、この積分値は\(x=0\)周りに存在する特異点を上周りに迂回して積分するか、下周りに迂回して積分するか、で答えが異なります。

特異点を上周りに回る場合、答えは
\(
\begin{eqnarray}
\lim_{\varepsilon\to +0} \int_{-\infty}^{\infty}\frac{e^{-ikx}}{x+i\varepsilon}dx =
\left\{
\begin{aligned}
-2\pi i~~~(k\gt 0)\\
0~~~(k\lt 0)
\end{aligned}
\right.
\end{eqnarray}
\)
であり、特異点を下周りに回る場合、
\(
\begin{eqnarray}
\lim_{\varepsilon\to +0} \int_{-\infty}^{\infty}\frac{e^{-ikx}}{x-i\varepsilon}dx =
\left\{
\begin{aligned}
0~~~(k\gt 0)\\
2\pi i~~~(k \lt 0)
\end{aligned}
\right.
\end{eqnarray}
\)
となります。
私が疑問に思うのは、積分すると本当にステップ状の関数が現れるのか？ということです。にわかには信じられません。

ここでは、上を回った時の計算にのみ注目します。
答えに出てくる係数を減らしたいため、被積分関数
\( \displaystyle
-\frac{1}{2\pi i}\int_{-\infty}^{\infty} \frac{e^{-ikx}}{x}dx
\)
を考えます。

数値計算方法

さて、問題を整理しましょう。今取り組む問題は、

問題：以下の積分を数値的に計算せよ。
\( \displaystyle
-\frac{1}{2\pi i}\int_{-\infty}^{\infty} \frac{e^{-ikx}}{x}dx,~~(kは任意の実数)
\)
です。読み取れる情報は

・始点は、実軸上のマイナス無限大
・終点は、実軸上のプラス無限大
・\(x=0\)に特異点が存在する

という情報です。これらは理由なく勝手に変えてはいけません。
被積分関数が収束するならば、xがどんなに大きくても無限遠まで振動していきますが、フレネル積分のように積分結果は収束することを期待しましょう。

さて、\(x=0\)に特異点があるために、実軸上のマイナス無限からプラス無限まで積分していこうとすると\(x=0\)を通過しようとする時に無限大になるため、オーバーフローします。
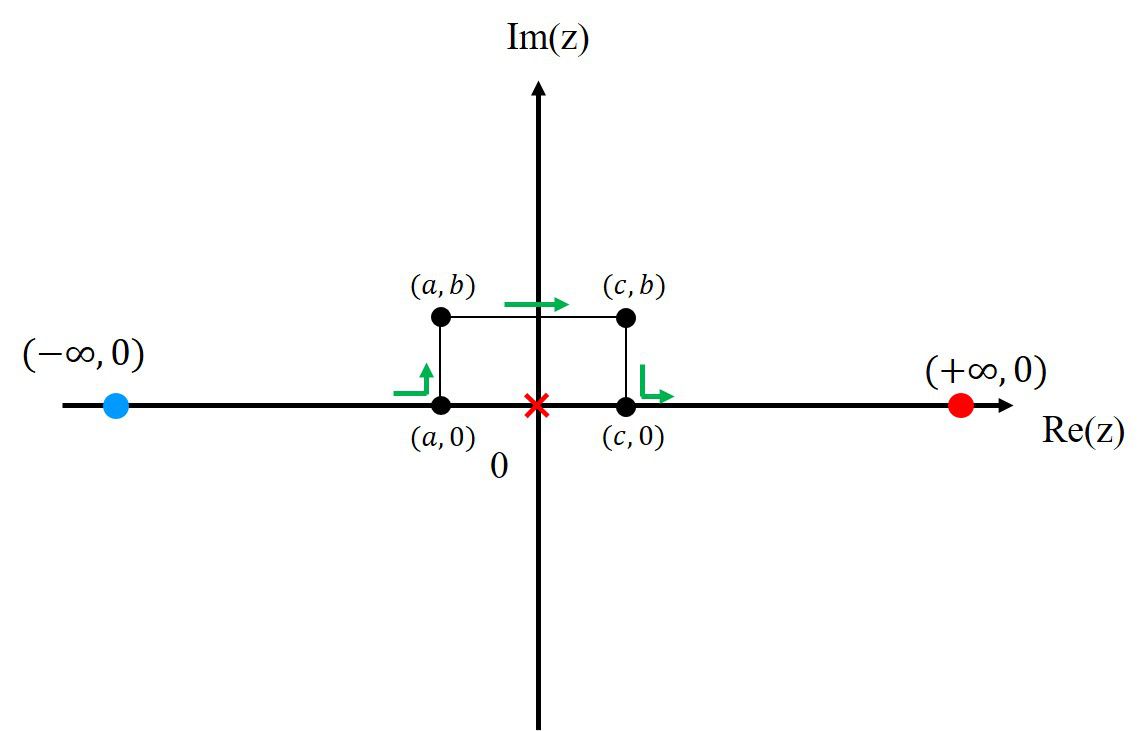
ということで、積分経路を特異点周りで迂回します。

始点と終点は決められていますが、積分経路の指定はありませんので何も問題ありません。
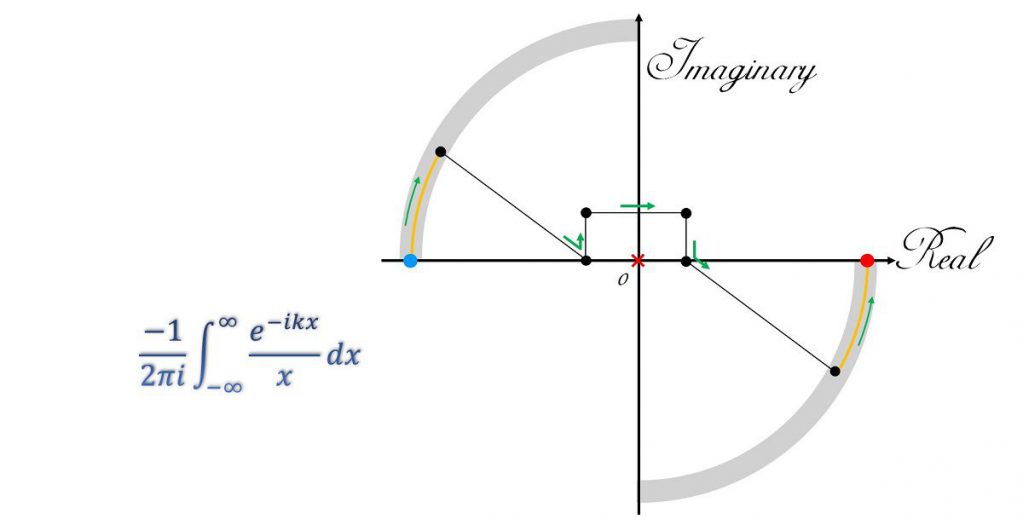
積分経路は以下の図のように取ります。

このようにとると、積分経路上に特異点はないですので計算することが出来ます。
始点と終点は十分大きい値、ここでは(±2000,0)という値にします。

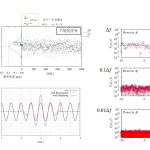
横軸をkとして、積分を計算すると以下のようになります。

複素関数論から、特異点を複素平面上方を迂回した場合に得られる解は
\(
\begin{eqnarray}
\lim_{\varepsilon\to +0} -\frac{1}{2\pi i}\int_{-\infty}^{\infty}\frac{e^{-ikx}}{x+i\varepsilon}dx =
\left\{
\begin{aligned}
1~~~(k\gt 0)\\
0~~~(k\lt 0)
\end{aligned}
\right.
\end{eqnarray}
\)
です。数値計算によって得られた解は、\(k\lt 0\)で値0, \(k\gt 0\)で値1であるので、数値的にも正しそうです。
しかし、厳密にそれぞれの値になっているわけではないことに気が付きます。なぜならば、\(k=0\)周りでは値は収束していないように見えます。
この原因は始点と終点としてとった、大きい値(±2000,0)が十分ではない事を意味しています。kが小さいと、被積分関数の\(\exp(-ikx)\)による振動はゆっくりになるため、収束が遅くなっている、と考えられます。

ジョルダンの補題の利用

この振動を無くすためには被積分関数が漸近領域で収束するように積分経路を変えればいいのです。

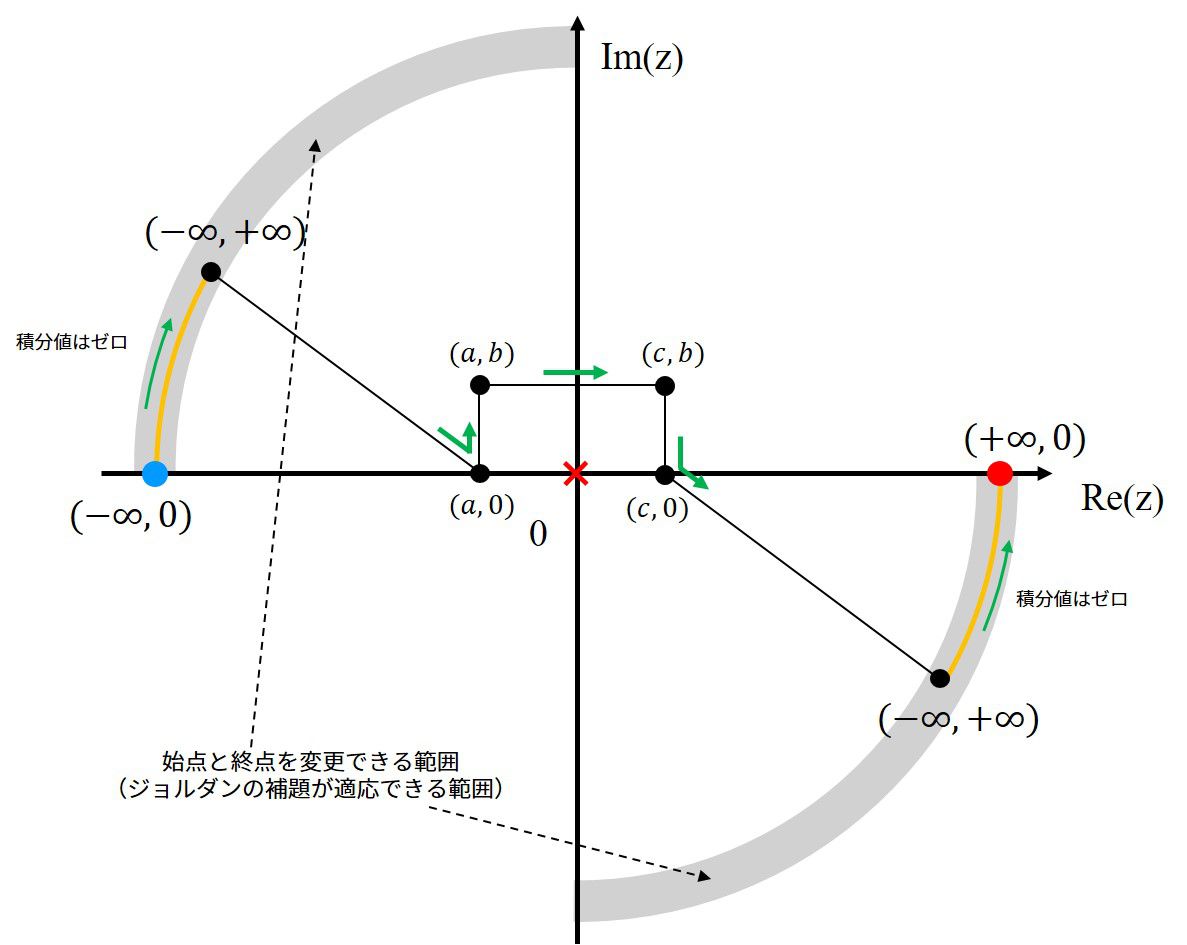
始点と終点は変わりません。図は\(k\)が負の時の経路です。

経路の取り方は無数にあり、上の経路は一つ前の計算で選んだ経路を出来る限り変更しないように経路をとっているだけにすぎません。

ジョルダンの補題を利用すれば、被積分関数が収束する領域であれば積分の寄与はゼロなので、数値的に積分する場合の視点、終点を複素平面上へ移すことが出来ます。
この考えの下実際に計算すると積分結果はこうなります。

綺麗なエッジが作られました。これならば解析解と数値解が一致した、と言えるでしょう。複素平面上の数値計算は一筋縄ではいかないことが実感できました。

数値計算プログラム

プログラムは以下のものを用いています。

数値積分はquadpackのガウス=ルジャンドル求積法の自動積分コードを複素関数用に変更して用いています。
実際に使用しているquadpackコードは以下のもので、
https://slpr.sakura.ne.jp/qp/supplement_data/quadpack_cqag.f90
これと、下のはmainプログラムです。

オリジナルのquadpackコードは
http://www.netlib.org/quadpack/（パブリックドメイン）です。

Tweet