弦を考えます。弦は重さ\(M\), 長さ\(L\), ばね定数\(K\)を持ちます。
この弦を波動方程式に頼らないで定式化しましょう。
波動方程式は、2次元の波動のうち、1次元分の方向を\(y=y(x, t)\)として表現するため、x軸にとって多価関数となる弦を表現することが出来ません。物性物理学等で格子の振動を考える場合は、結晶を構成する原子が平衡位置から殆ど動かないのでこういった問題は起こりません(起こったとしても無視される位少ないので、大多数の振る舞いを考える場合には問題になりません)。
よって多次元の問題を考えるには波動方程式を元にして考えるのは不適切です。そのため、弦を単なる連成振動として考えて、完全に2次元の問題として扱いたいと思います。
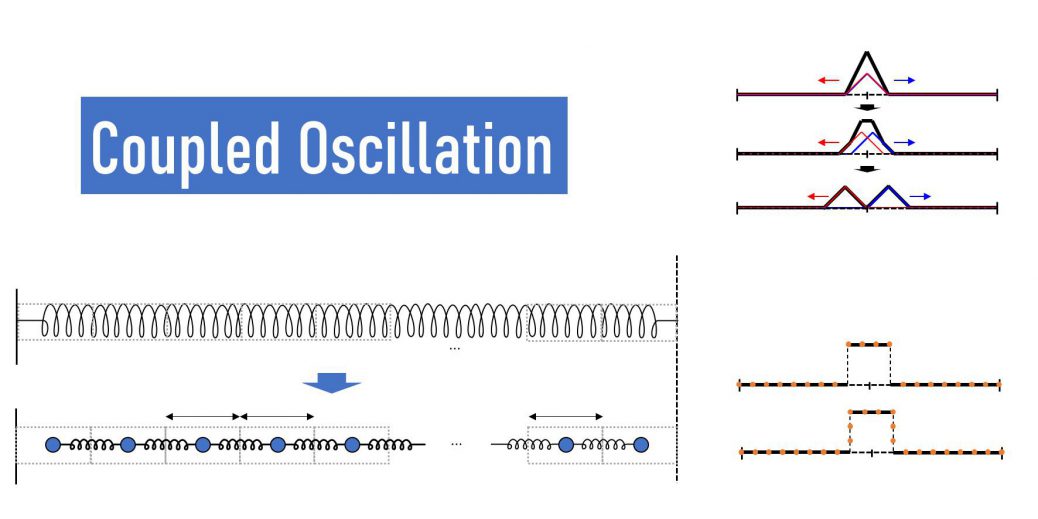
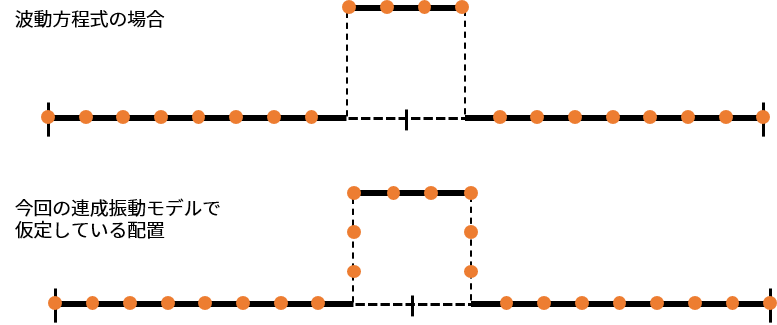
図のような連成振動のモデルを考えます。
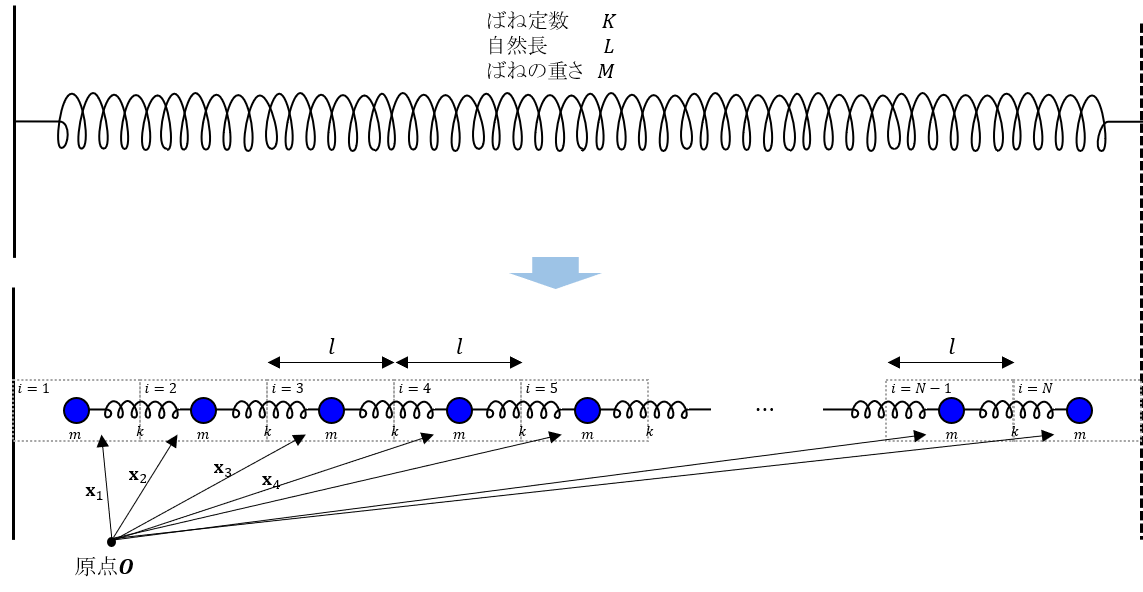
質量\(m\)を持つ\(i\)番目の質点が、位置ベクトル\(\mathbf{x}_i\)で指定され、隣り合う質点との間が、ばね定数\(k\)、自然長\(l\)を持つ理想的なばねで繋がれているとします\((i=1,2,\cdots, N)\)。この時、運動方程式を立てると
\begin{eqnarray}
m\frac{d^2 \mathbf{x}_i}{dt^2}&=&
+k(|\mathbf{x}_{i+1}-\mathbf{x}_{i}|-l) \frac{\mathbf{x}_{i+1}-\mathbf{x}_{i}}{|\mathbf{x}_{i+1}-\mathbf{x}_{i}|}
-k(|\mathbf{x}_{i}-\mathbf{x}_{i-1}|-l)\frac{\mathbf{x}_i-\mathbf{x}_{i-1}}{|\mathbf{x}_i-\mathbf{x}_{i-1}|}
\end{eqnarray}
となります。全く同じですが、見通しをよくするため式変形すれば、
\begin{eqnarray}
m\frac{d^2 \mathbf{x}_i}{dt^2}&=& k\Bigl[A_i \mathbf{x}_{i+1}-\bigl(A_i+A_{i-1}\bigr)\mathbf{x}_{i}+A_{i-1} \mathbf{x}_{i-1}\Bigr]
\end{eqnarray}
と表せます。ここで、
\begin{equation}
A_i = \frac{|\mathbf{x}_{i+1}-\mathbf{x}_{i}|-l}{|\mathbf{x}_{i+1}-\mathbf{x}_{i}|},~~(i=1,\cdots, N, A_N = 0)
\end{equation}
と置きました。
さて、こうしたモデルを考えた時に、連成振動として考えた\(N\)分割した1つ1つの小さいばね(”ミクロなばね”と名づけます)とその弦を1つにみなした時の大きなばね(”マクロなばね”と名づけます)の間の関係式を考えましょう。
仮定として、等間隔に分割し、弦の密度は一様であるとします。
この条件の下で、
マクロなばねの重さ\(M\), 自然長\(L\), ばね定数\(K\)
と
ミクロなばねの重さ\(m\), 自然長\(l\), ばね定数\(k\)
の間の関係式を導出します。
結論として、マクロとミクロなばねの間に成り立つ関係は
\begin{eqnarray}
L&=&N l \\
M&=&N m \\
K &=& k/N
\end{eqnarray}
となります。
自然長
自然長\(L\)の弦を\(N\)分割するので、
\begin{equation}
L=N l
\end{equation}
の関係があります。
重さ
重さ\(M\)の弦を\(N\)分割するので、
\begin{equation}
M=N m
\end{equation}
と書けます。
ばね定数
最後にばね定数の関係を考えましょう。この関係は、弾性エネルギーを考えることで導くことができます。
マクロなばねとして全体を見た場合に長さ\(D\)だけ縮んだ時に蓄えられる弾性エネルギーと
同じだけ縮んだ時にミクロな\(N\)個のばねに蓄えられる弾性エネルギーが同じであってほしいと要請します。すなわち、ミクロなばねの縮みの合計がマクロなばねの縮み\(D\)に等しいとすると、
\begin{equation}
D=N d
\end{equation}
と書けます。
実は、大胆な過程をしないとマクロなばねとミクロなばねの関係を求めることが出来ません。
なぜなら、マクロなばねはいつでも線形応答をするかのように現在考えていますが、ミクロなばねでは場所ごとに違っても良いという様に定式化しています。なのでもともと無理な話なのです。
ではどうやって妥当な関係式を導出すればよいかといえば、ばねが非常にゆっくり運動が行われるときを仮定するのです。ゆっくり動くときの振る舞いは全てのばねが同じ動きをするとして差し支えないでしょう。そうして定式化します。
よって、
\begin{eqnarray}
\frac{1}{2}K D^2 &=& N\cdot \frac{1}{2} k d^2 \nonumber \\
\to ~~ K &=& k/N
\end{eqnarray}
という関係式が導けます。
あとは数値計算を行うだけです。陽的ルンゲクッタ法で解いたプログラムを以下に示します。
https://slpr.sakura.ne.jp/qp/supplement_data/wave_particles.tar.gz
実行は、
$ ./a.out
でokだと思います。初期状態や、重さや自然長はinputファイルを見てください。
実行後、動画をgnuplot上で出力したければ、
$ call "movie.plt" 100
としてください。100は表示する時間ステップを表します。この引数の値の最大はinputファイルの中のNtまでです。
数値計算結果
実際に数値計算を行う条件として、自然長や重力があると波動方程式と若干異なる振る舞いになってしまうので、対応を見る上ではなくしています。すなわち、自然長\(L=0\)、重力\(g=0\)として計算します。
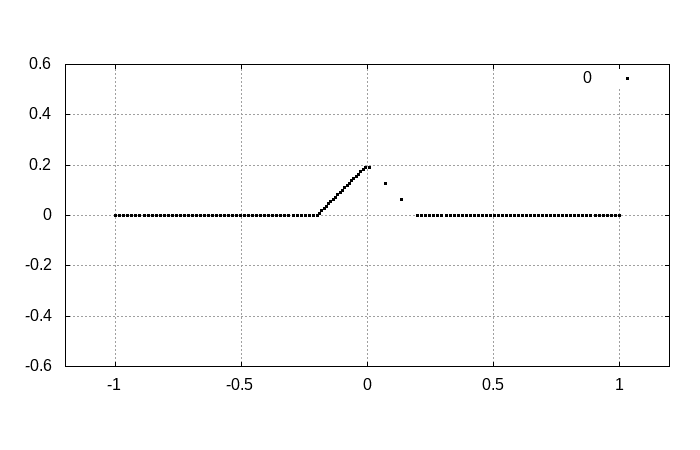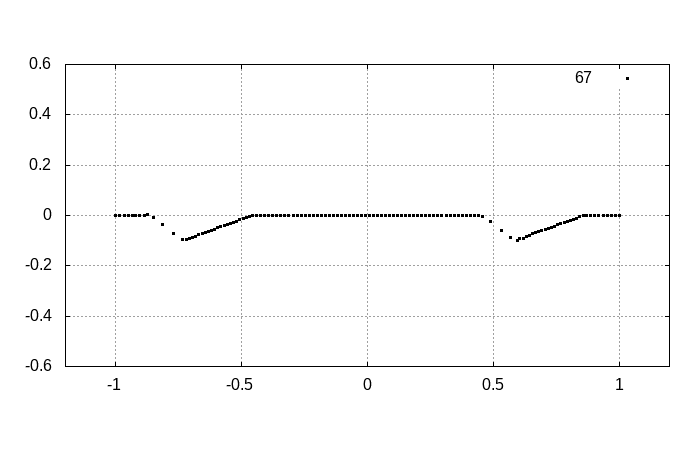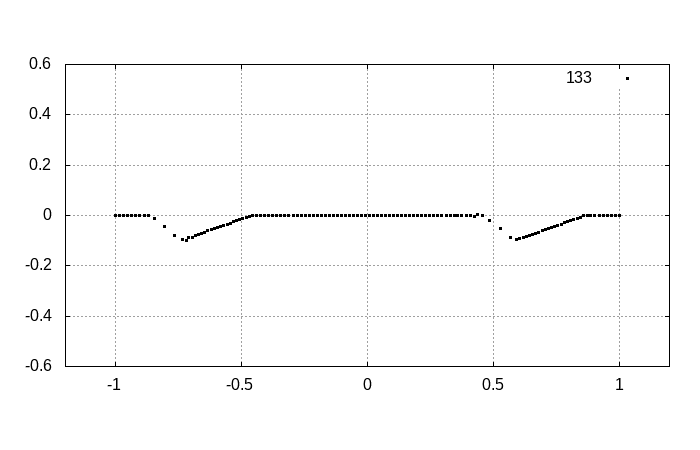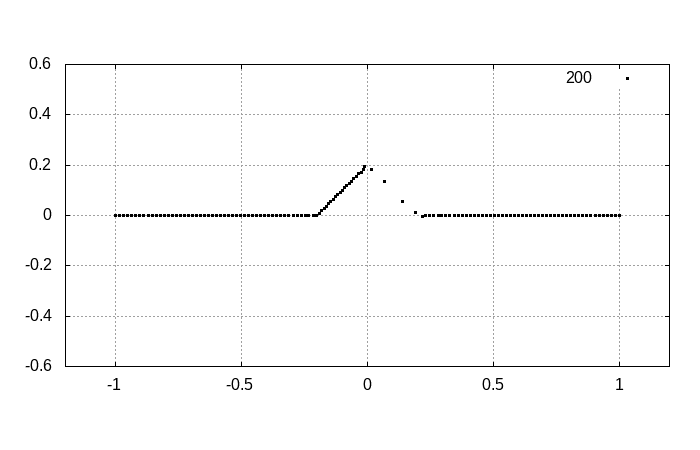
三角パルス
三角形の波がパルス状に存在するとします。
そして初期状態として、初速度がゼロであることを仮定しましょう。
この場合、波動方程式の考察から、
同じ関数であらわされる右向きの波\(f(x-vt)\)と左向きの波\(f(x+vt)\)の重ね合わせとして書かれることが分かっています。すなわち、解\(y=y(x,t)\)は
\begin{equation}
y(x,t)=f(x-vt)+f(x+vt)
\end{equation}
と書かれます。図で表せば以下のように時間発展していくことが期待されます。
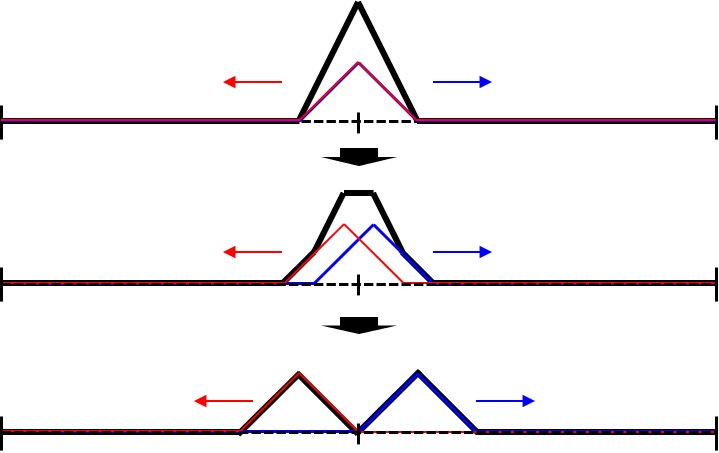
これが本稿の連成振動モデルで実際にそうなっているのかを確かめるのは良い問いかけでしょう。
実際に連成振動を数値的に解くと以下の通りになります。
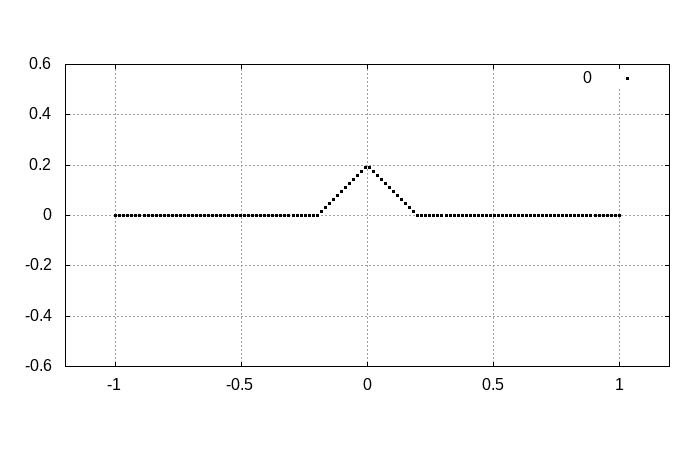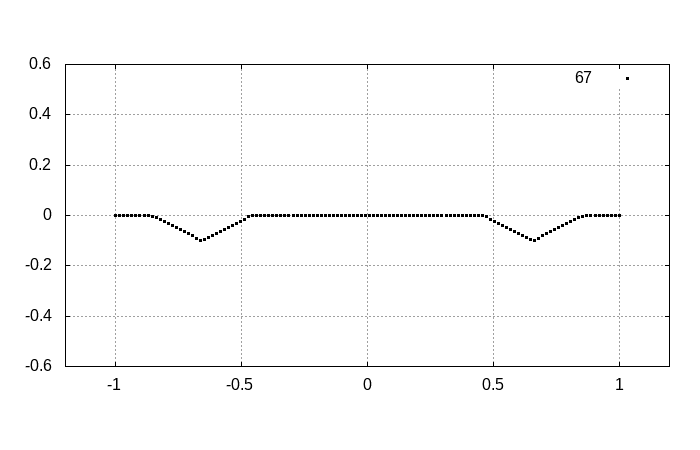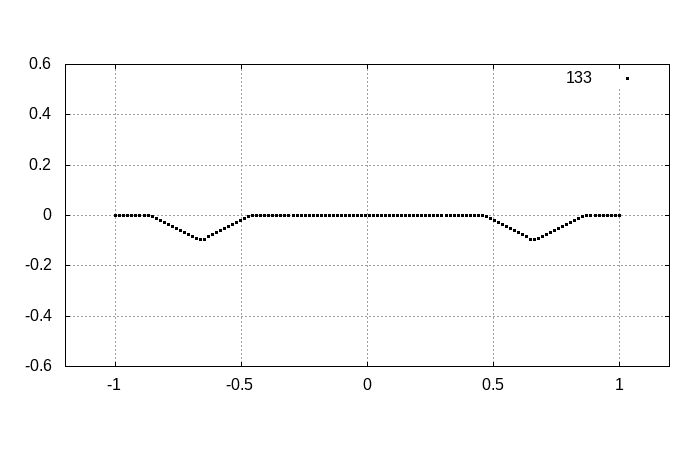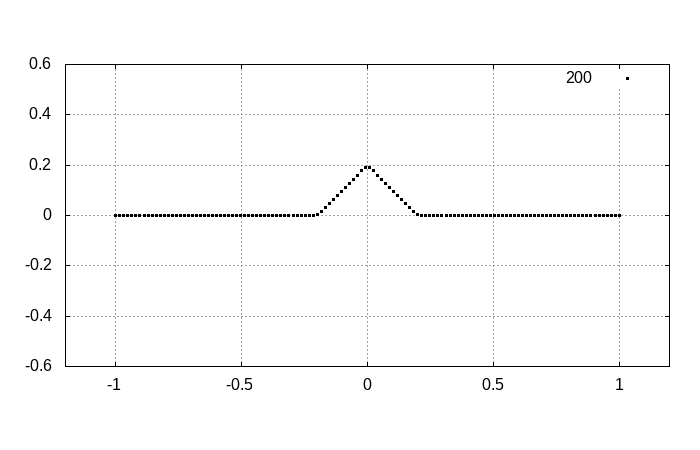
ゆっくりと時間発展を見ていくと

となります。明らかに右向きに進む波と左向きに進む波として分離します。分離した結果から、初期状態がそれらの波の重ね合わせで表現されていたことが分かるでしょう。
矩形パルス
矩形パルスを考えてみます。実際に数値計算をするとこんな感じです。

結局右向きと左向きの重ね合わせとしてあらわされることも確認できますが、決して単純なそれらの足し合わせで書かれているわけではないことがわかります。この振る舞いは、波動方程式に対応するように連成振動モデルを作っていないことから由来します。波動方程式としてあらわした二階微分の偏微分方程式の場合は多価関数をとることができません。なので縦に弦が伸びる場合、間に質点を置くことができないので質点の位置がいきなり飛ぶことになります。しかし、連成振動モデルではその制約をして初期状態を準備しているわけではありませんのでその違いが出て来ます。図で表せば、以下のようになります。
両者の違いがあるので、波動方程式の結論である
\begin{equation}
y(x,t)=f(x-vt)+f(x+vt)
\end{equation}
が成り立っていない、と解釈することができます。
三角形の波
端まで三角形のパルスであった場合にどのように振る舞うかを見てみましょう。特に面白い振る舞いがあるわけではなく、上のパルスの、右向きと左向きの波の重ね合わせで説明ができるので、単にシミュレーション結果を載せるだけにとどめます。実際に計算してみると以下のようになります。
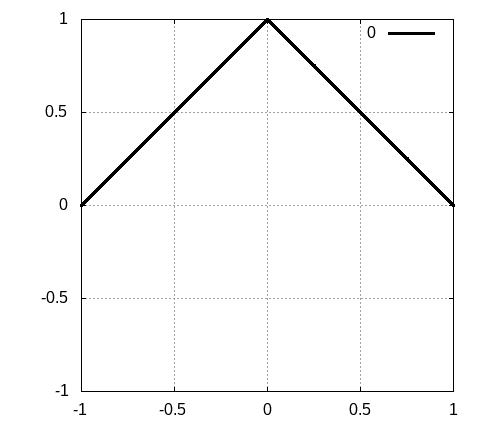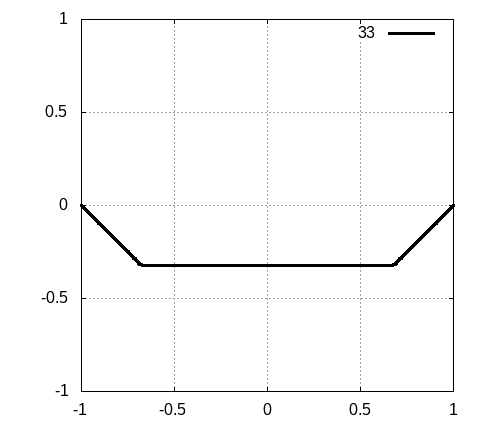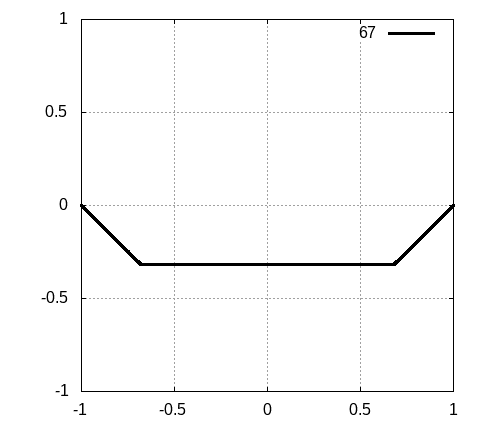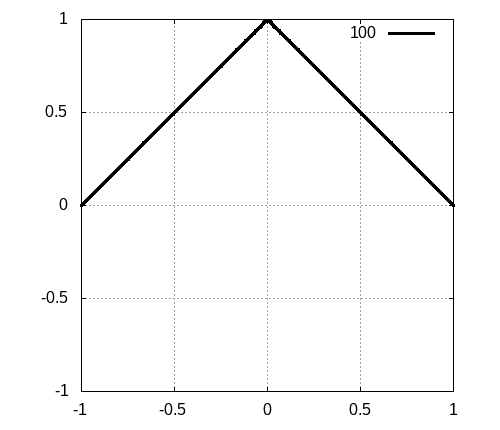
星形
初期状態が星型である場合も見てみましょう。振る舞いも同じです。
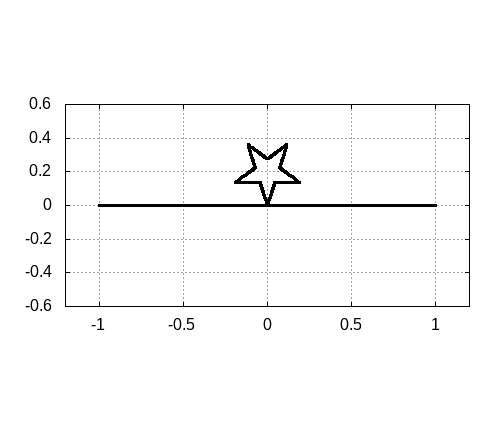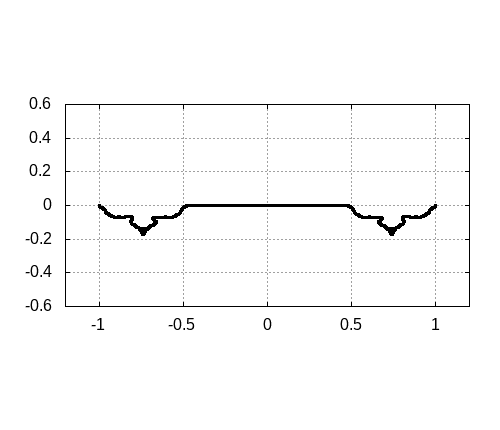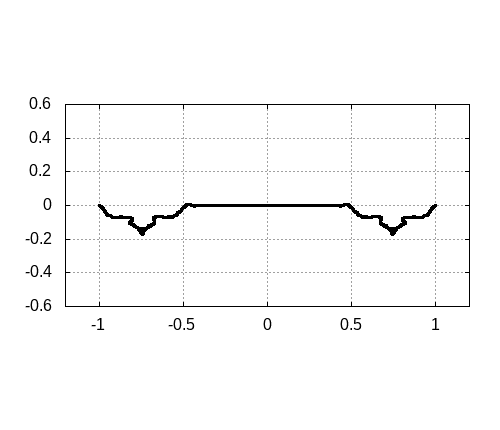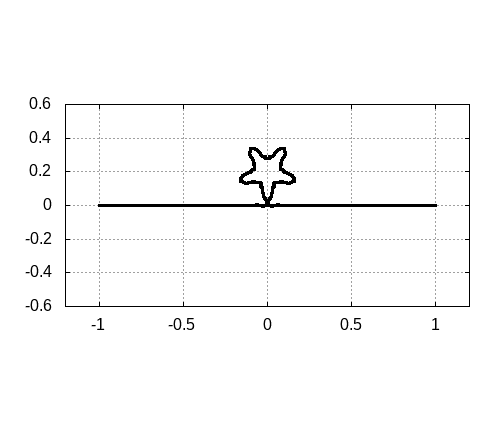
注意点としては、実際にこの振る舞いは起こりえないことに注意しておきましょう。なぜなら、本当の弦で行った場合、重なる場所があると弦の衝突が起こります。しかし、この連成振動モデルでは計算上、衝突は起こりません。
偏りがある三角形のパルス
偏りがある場合も波動方程式では記述することができません。こんな感じの初期状態です。

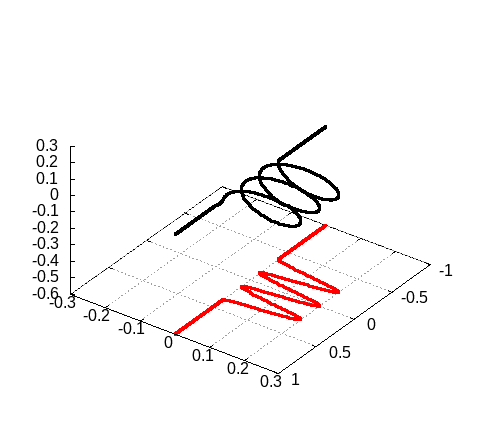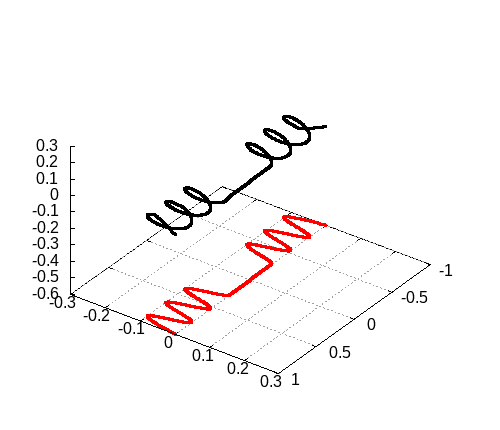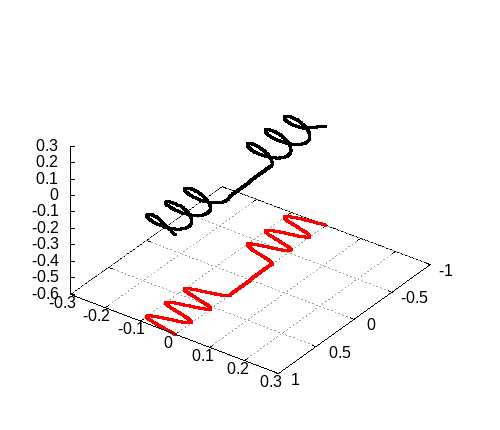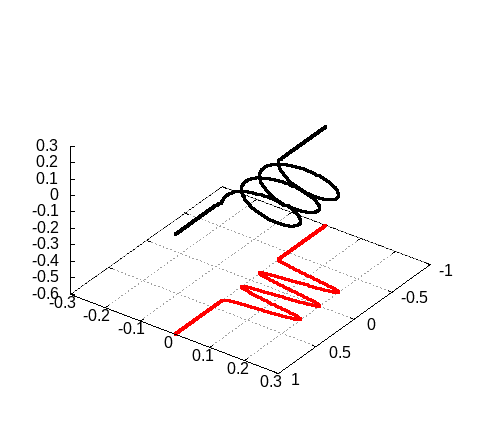
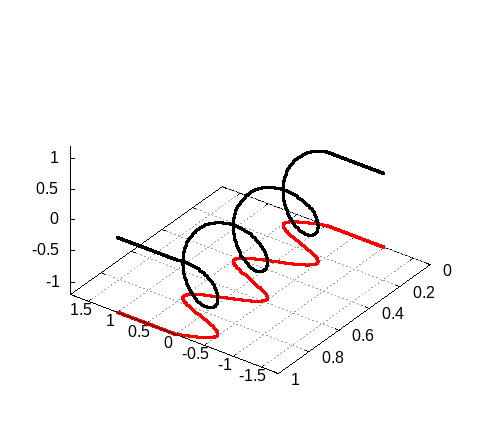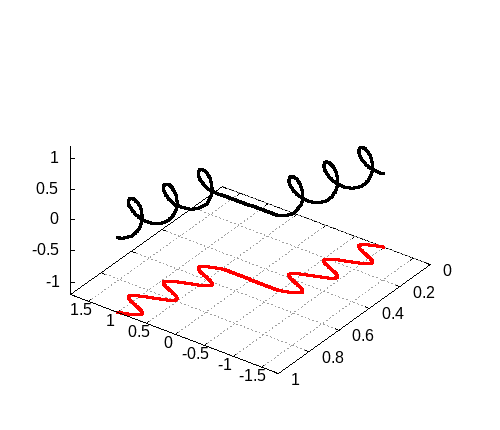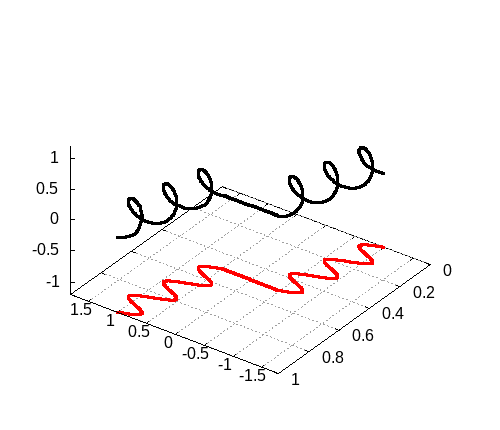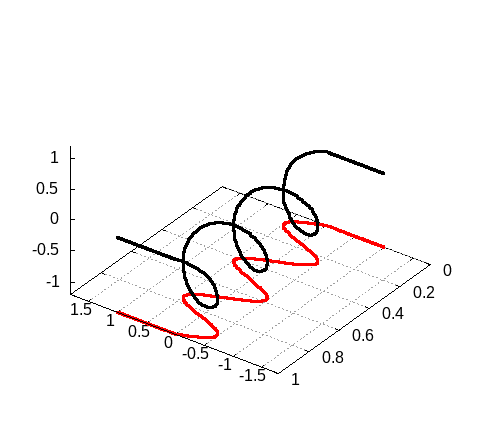
3次元の場合
3次元の場合も載せておきます。ふるまい自体はそんなに変わるわけではないので、シミュレーション結果を載せるだけにとどめておきます。