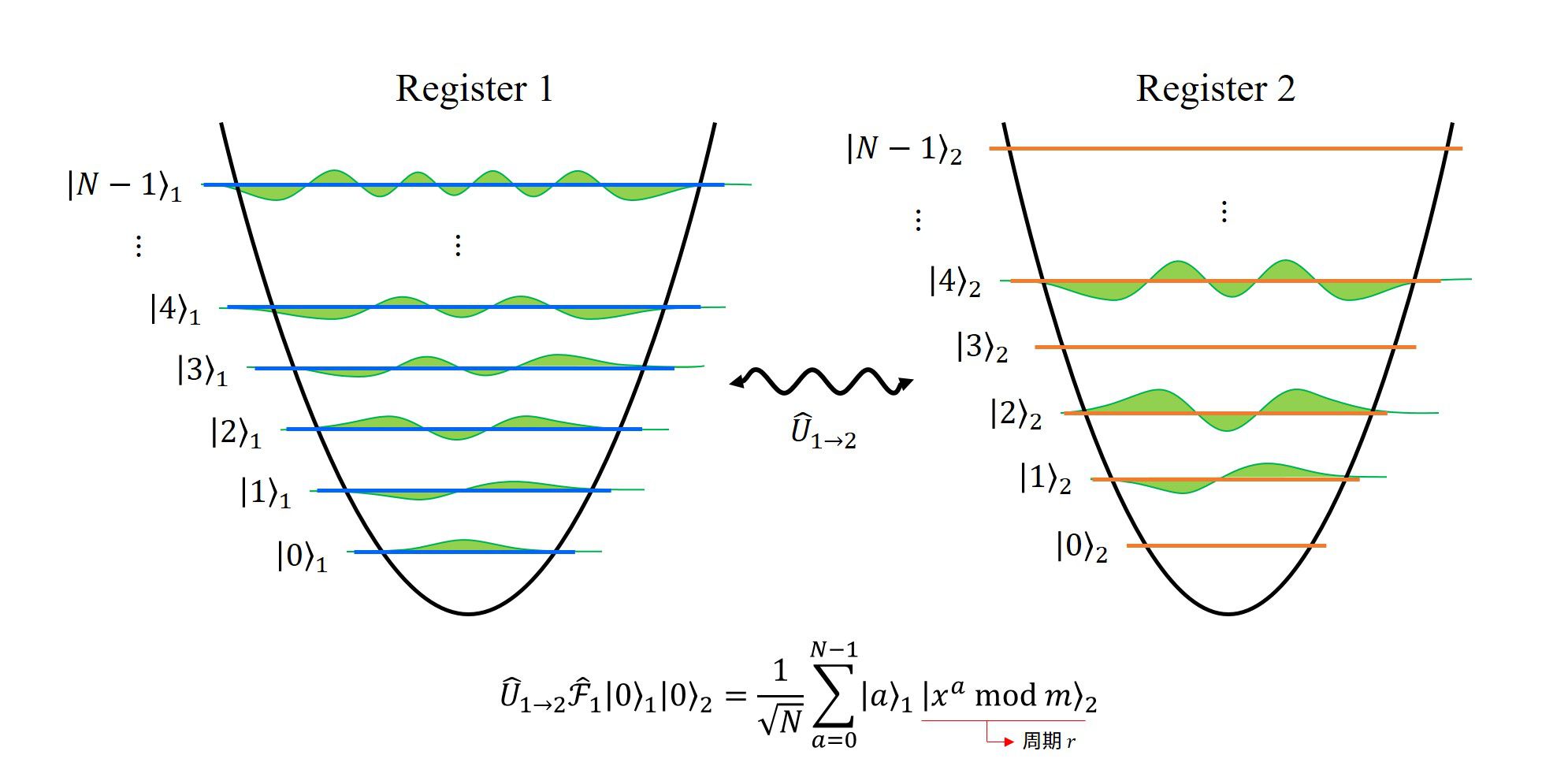
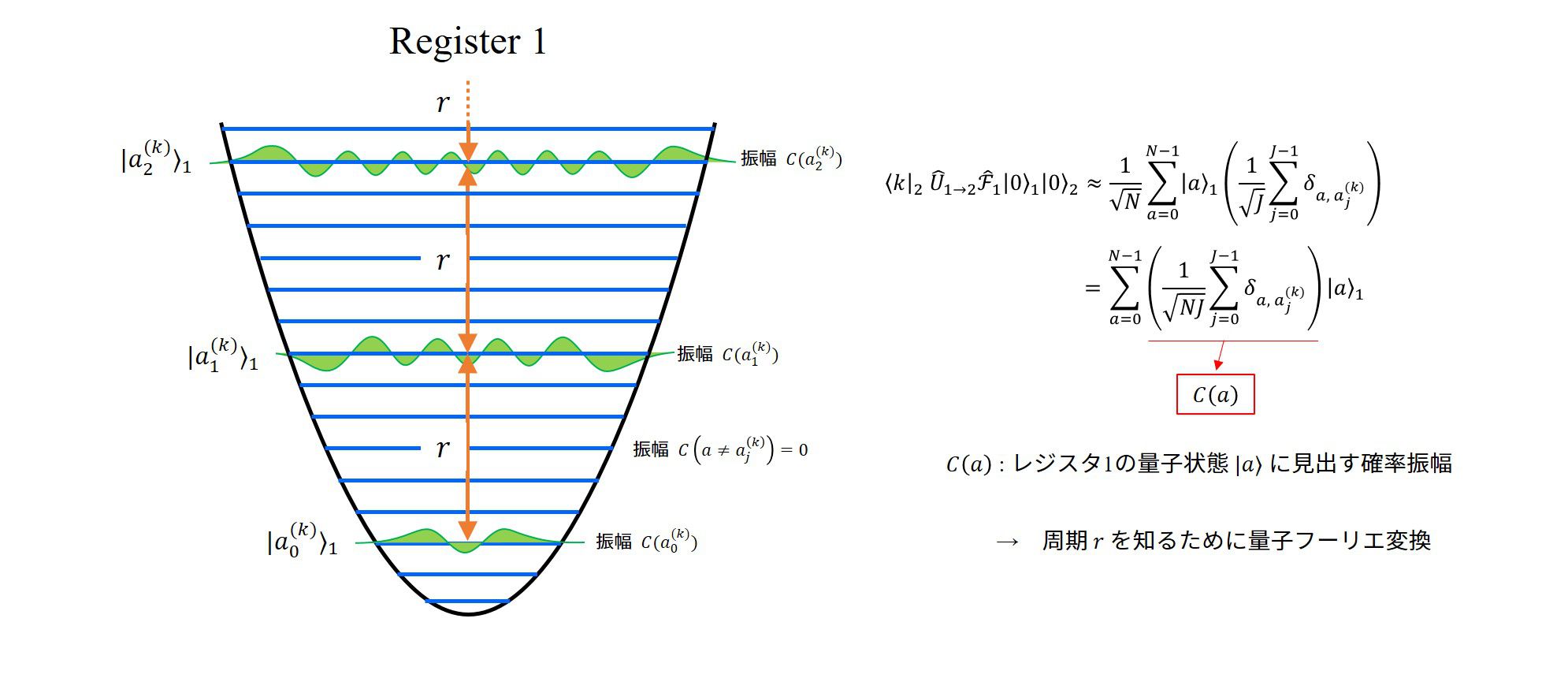
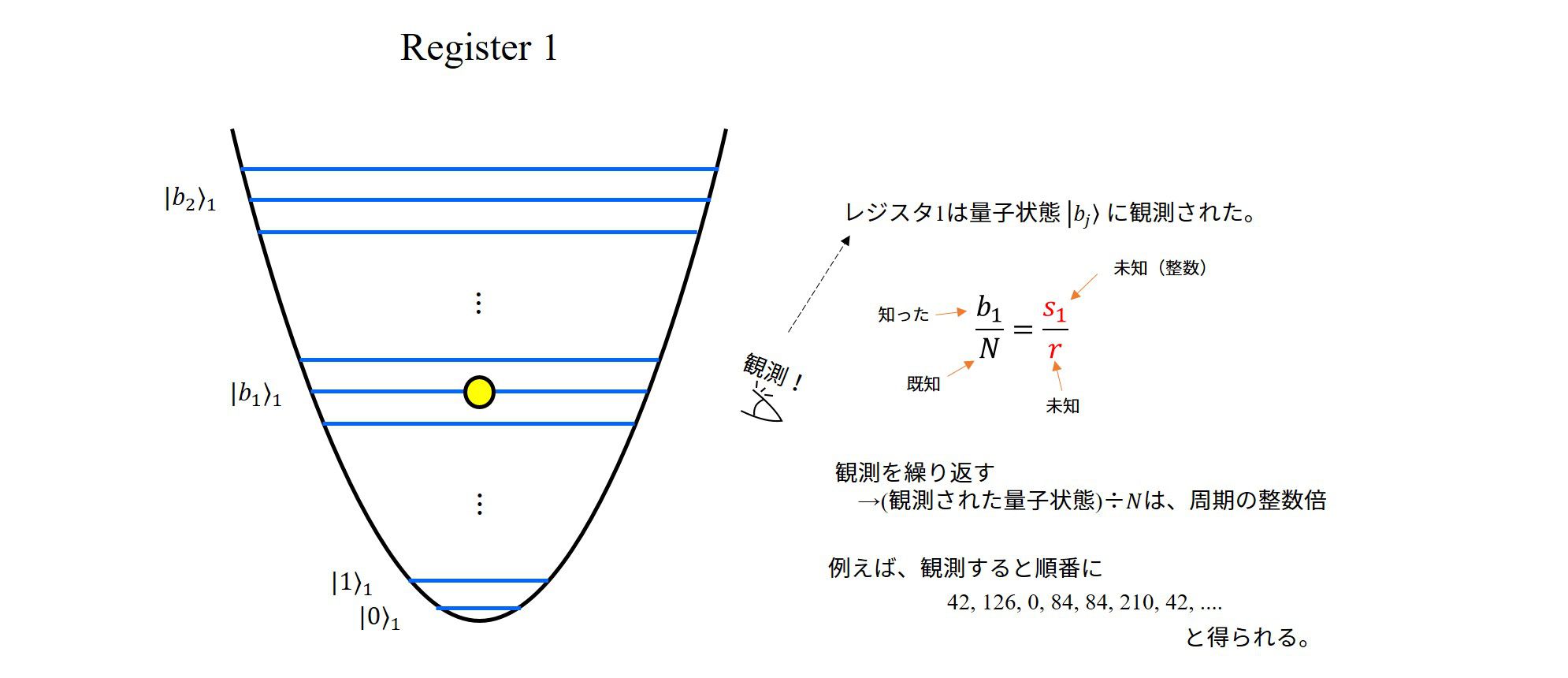
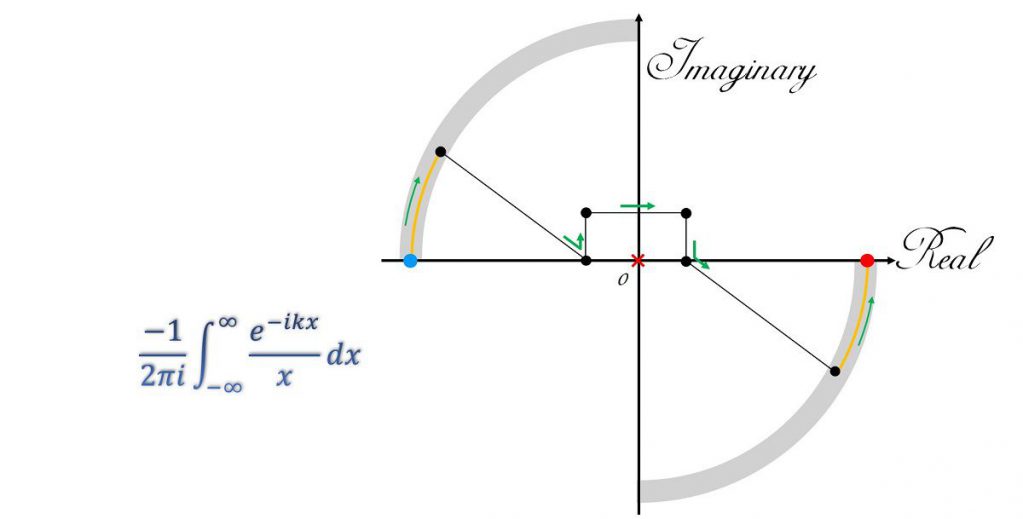
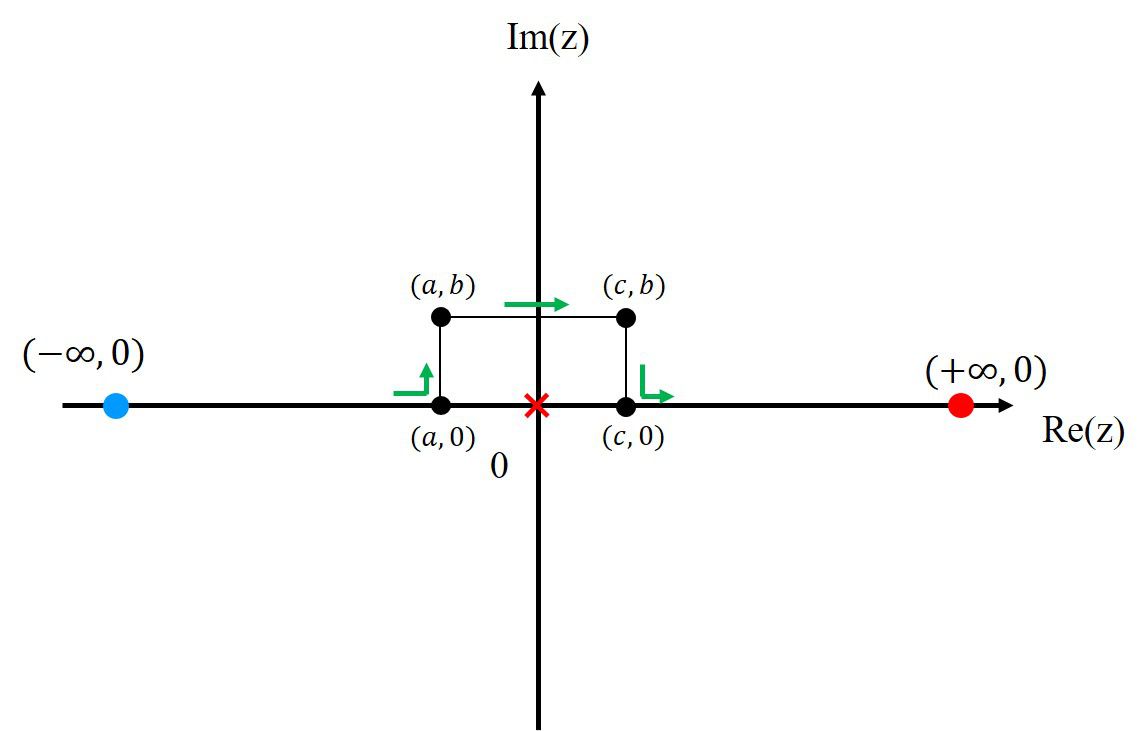
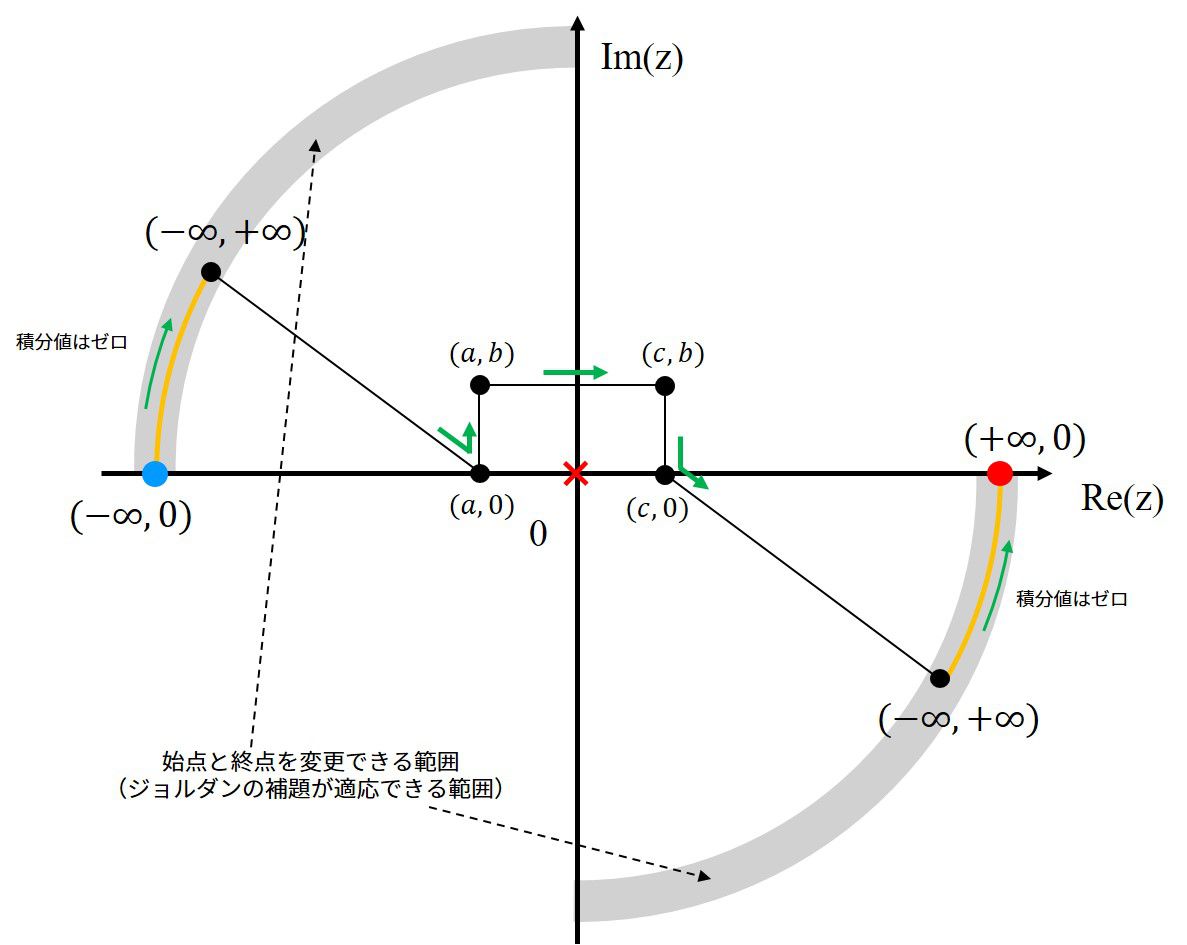
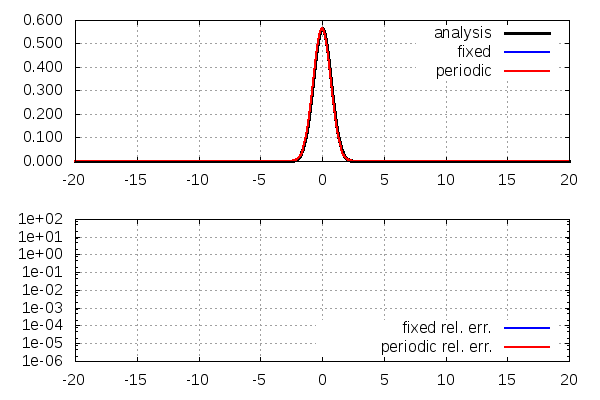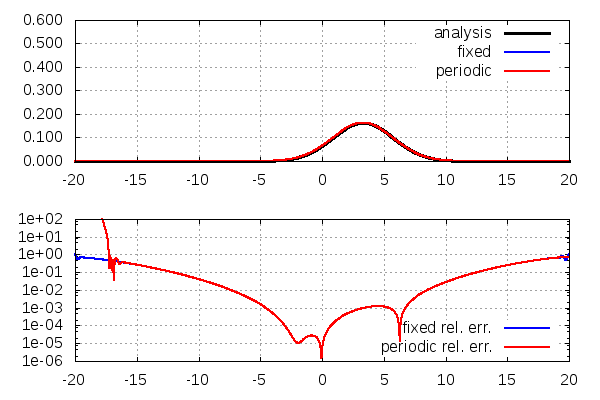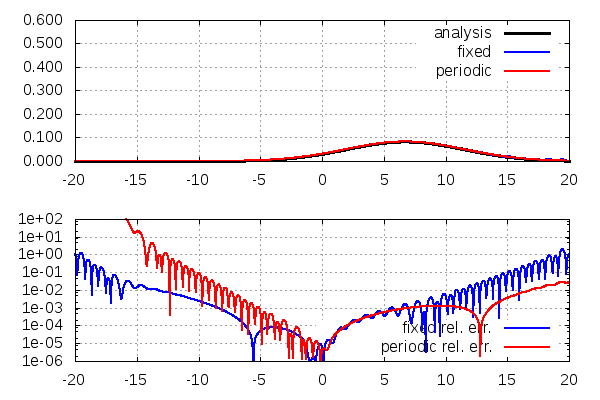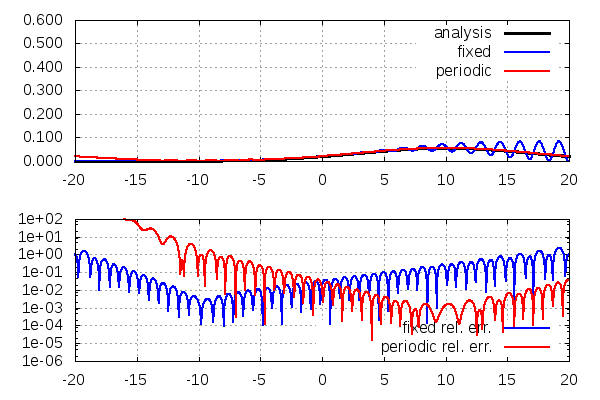
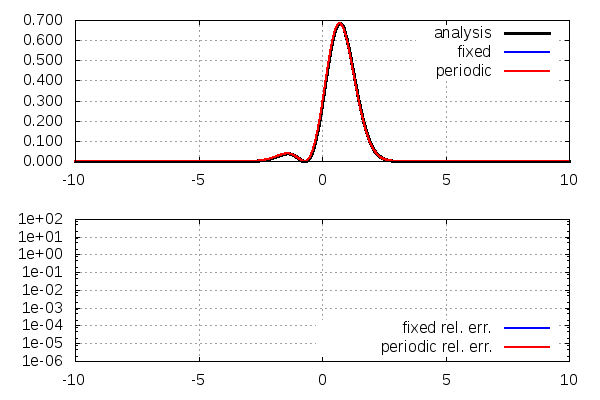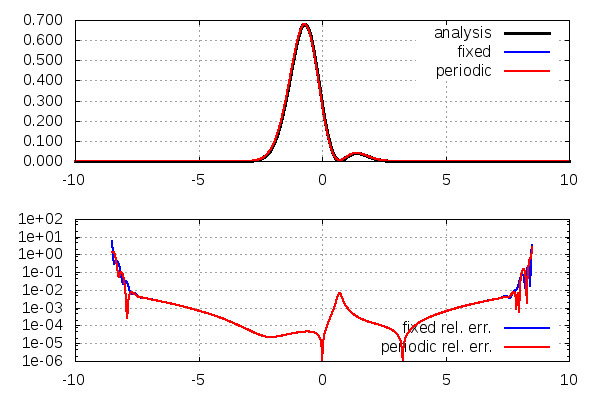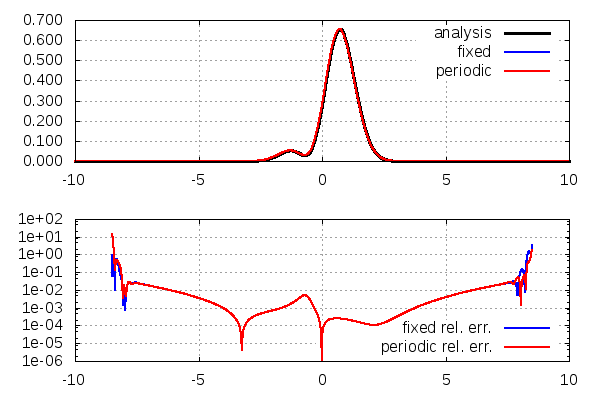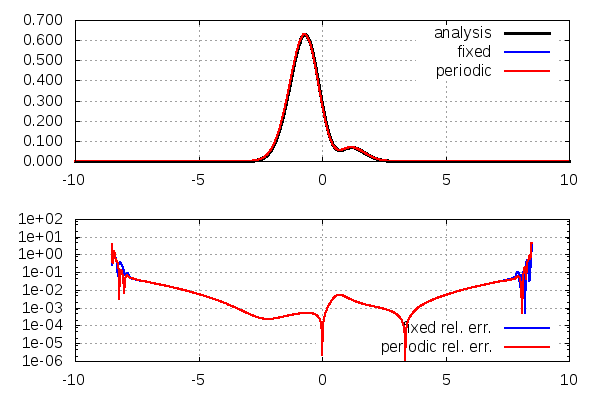
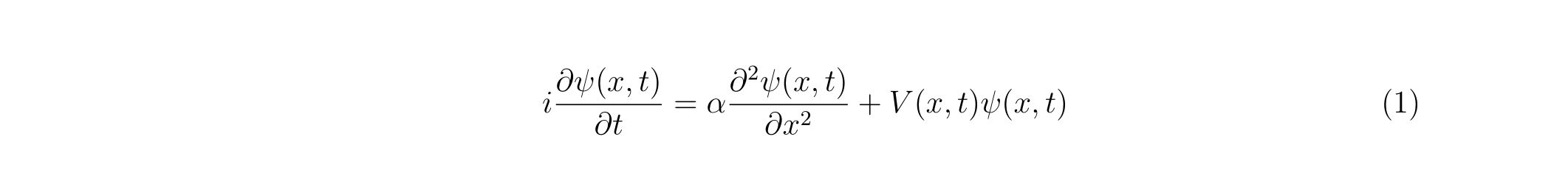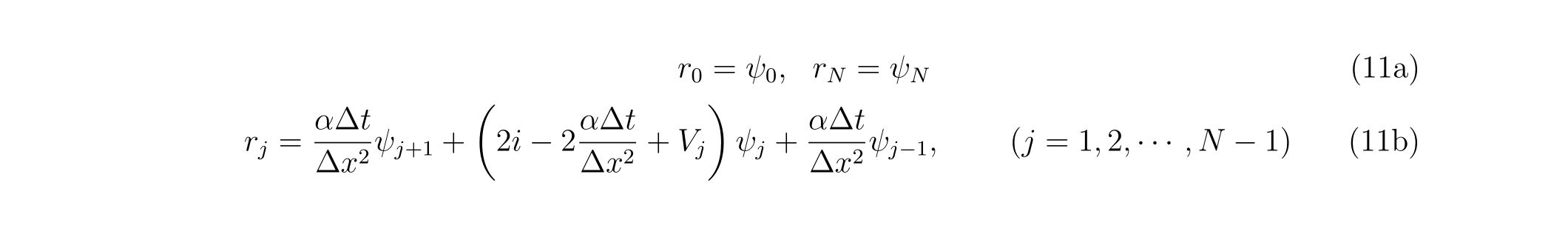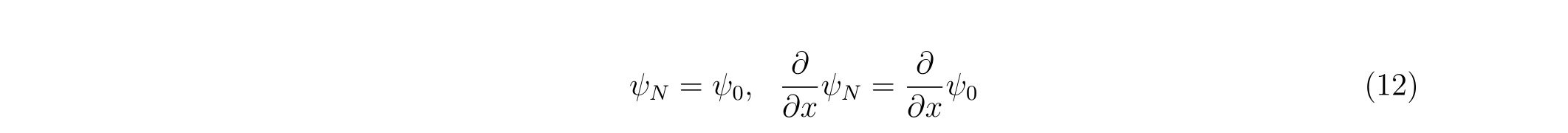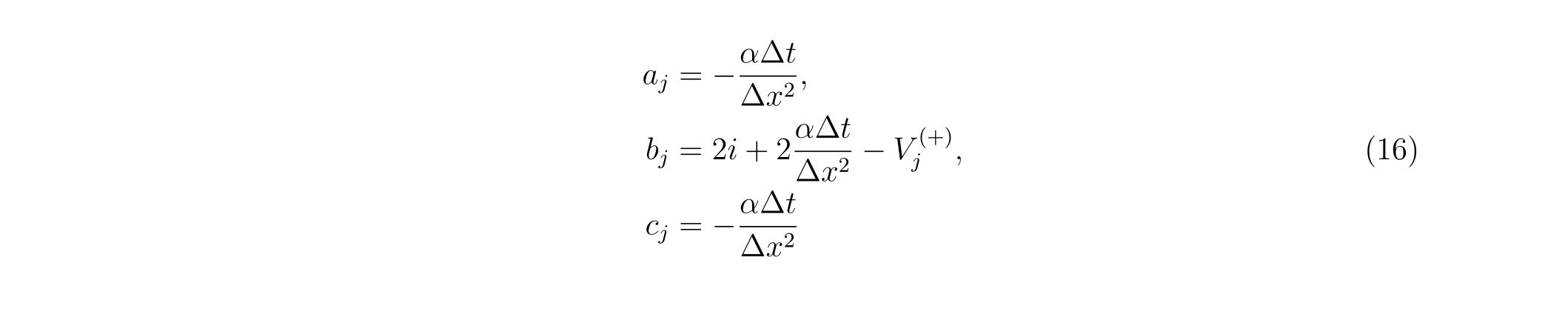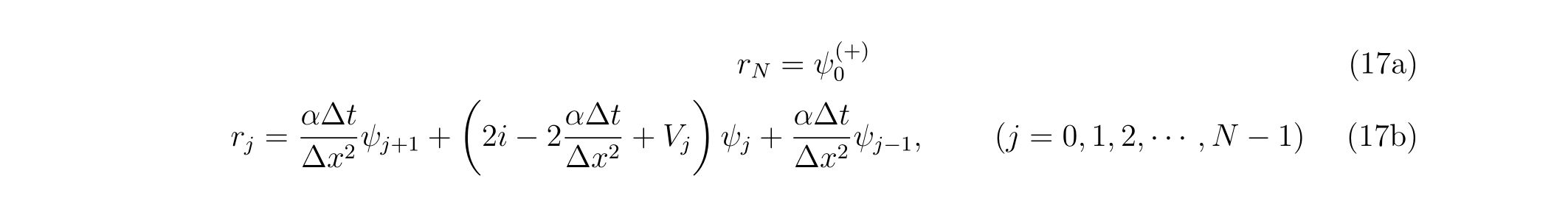program main
implicit none
double precision::xa,xb,ya,yb,za,zb,xeps,yeps,zeps
complex(kind(0d0))::s
complex(kind(0d0)),external::f
xa=1d0
xb=5d0
ya=1d0
yb=3d0
za=0d0
zb=2d0
xeps=1d-10
yeps=1d-10
zeps=1d-10
call dqag43(f,xa,xb,ya,yb,za,zb,xeps,yeps,zeps,s)
write(6,*)s
stop
end program main
function f(x,y,z)
implicit none
double precision::x,y,z
complex(kind(0d0))::f
f=(exp(-dcmplx(0d0,1d0)*sqrt(x)*y)+sin(5d0*y))*exp(dcmplx(0d0,1d0)*z*z)
return
end function f
!===================================
subroutine dqag43(f,a,b,ya,yb,za,zb,eps,yeps,zeps,s)
implicit none
double precision,intent(in)::a,b,eps,ya,yb,yeps,za,zb,zeps
complex(kind(0d0)),intent(out)::s
complex(kind(0d0)),external::f
!
! Quadpack integration package, using key=4
! (Gauss quadrature with 20-41 points)
!
integer::neval,limit,last,ier,lvl,count
integer,allocatable::iwork(:)
double precision,allocatable::alist(:),blist(:),elist(:)
complex(kind(0d0)),allocatable::rlist(:)
double precision::epsabs,abserr
!=============
limit=1000
! limit increase --> converge
!=============
s=dcmplx(0d0,0d0)
allocate(iwork(1:limit))
allocate(alist(1:limit),blist(1:limit),rlist(1:limit),elist(1:limit))
alist=0d0
blist=0d0
elist=0d0
rlist=dcmplx(0d0,0d0)
epsabs=-1d0
ier = 6
neval = 0
last = 0
abserr = 0d0
count = 0
call dqage3(f,a,b,epsabs,eps,limit,s,abserr,neval,&
ier,alist,blist,rlist,elist,iwork,last,count,ya,yb,yeps,za,zb,zeps)
lvl = 0
if(ier.eq.6) lvl = 1
if(ier.ne.0) call xerror("26habnormal return from dqag" ,26,ier,lvl)
! ier = 0 : success, converged.
! ier > 0 : fail
write(6,*)count,ier ! Number of times called integrand function
if(ier.eq.1)then
write(6,*)"Try the parameter 'limit' increase."
endif
deallocate(iwork)
return
end subroutine dqag43
subroutine dqage3(f,a,b,epsabs,epsrel,limit,result,abserr, &
neval,ier,alist,blist,rlist,elist,iord,last,count,ya,yb,yeps,za,zb,zeps)
!***author piessens,robert,appl. math. & progr. div - k.u.leuven
! de doncker,elise,appl. math. & progr. div. - k.u.leuven
! 2019/01/27 edited by sikino, http://slpr.sakura.ne.jp/qp/
double precision a,abserr,alist,a1,a2,b,&
blist,b1,b2,defabs,defab1,defab2,dmax1,elist,epmach,&
epsabs,epsrel,errbnd,errmax,error1,error2,erro12,errsum,&
resabs,uflow,ya,yb,yeps,za,zb,zeps
integer ier,iord,iroff1,iroff2,k,last,limit,maxerr,neval,&
nrmax,igt,igk,count
dimension alist(limit),blist(limit),elist(limit),iord(limit)
complex(kind(0d0))::result,rlist(limit),area,area1,area12,area2
complex(kind(0d0)),external::f
epmach = epsilon(a)
uflow = tiny(a)
ier = 0
neval = 0
last = 0
result = dcmplx(0d0,0d0)
abserr = 0.0d+00
alist(1) = a
blist(1) = b
rlist(1) = dcmplx(0d0,0d0)
elist(1) = 0.0d+00
iord(1) = 0
if(epsabs.le.0.0d+00.and.&
epsrel.lt.dmax1(0.5d+02*epmach,0.5d-28)) ier = 6
if(ier.ne.6)then
neval = 0
call dqk413(f,a,b,result,abserr,defabs,resabs,count,ya,yb,yeps,za,zb,zeps)
last = 1
rlist(1) = result
elist(1) = abserr
iord(1) = 1
errbnd = dmax1(epsabs,epsrel*abs(result))
if(abserr.le.0.5d+02*epmach*defabs.and.abserr.gt.errbnd) ier = 2
if(limit.eq.1) ier = 1
igk=0
if(ier.ne.0.or.(abserr.le.errbnd.and.abserr.ne.resabs)&
.or.abserr.eq.0.0d+00)igk=60
if(igk.ne.60)then
errmax = abserr
maxerr = 1
area = result
errsum = abserr
nrmax = 1
iroff1 = 0
iroff2 = 0
do last = 2,limit
a1 = alist(maxerr)
b1 = 0.5d+00*(alist(maxerr)+blist(maxerr))
a2 = b1
b2 = blist(maxerr)
call dqk413(f,a1,b1,area1,error1,resabs,defab1,count,ya,yb,yeps,za,zb,zeps)
call dqk413(f,a2,b2,area2,error2,resabs,defab2,count,ya,yb,yeps,za,zb,zeps)
neval = neval+1
area12 = area1+area2
erro12 = error1+error2
errsum = errsum+erro12-errmax
area = area+area12-rlist(maxerr)
if(defab1.ne.error1.and.defab2.ne.error2)then
if(abs(rlist(maxerr)-area12).le.0.1d-04*abs(area12)&
.and.erro12.ge.0.99d+00*errmax) iroff1 = iroff1+1
if(last.gt.10.and.erro12.gt.errmax) iroff2 = iroff2+1
endif
rlist(maxerr) = area1
rlist(last) = area2
errbnd = dmax1(epsabs,epsrel*abs(area))
if(errsum.gt.errbnd)then
if(iroff1.ge.6.or.iroff2.ge.20) ier = 2
if(last.eq.limit) ier = 1
if(dmax1(abs(a1),abs(b2)).le.(0.1d+01+0.1d+03* &
epmach)*(abs(a2)+0.1d+04*uflow)) ier = 3
endif
igt=0
if(error2.le.error1)then
alist(last) = a2
blist(maxerr) = b1
blist(last) = b2
elist(maxerr) = error1
elist(last) = error2
igt=20
endif
if(igt.ne.20)then
alist(maxerr) = a2
alist(last) = a1
blist(last) = b1
rlist(maxerr) = area2
rlist(last) = area1
elist(maxerr) = error2
elist(last) = error1
endif
call dqpsrt(limit,last,maxerr,errmax,elist,iord,nrmax)
if(ier.ne.0.or.errsum.le.errbnd)exit
enddo
if(last.eq.limit+1)last=last-1
result = 0.0d+00
do k=1,last
result = result+rlist(k)
enddo
abserr = errsum
endif
end if
return
end subroutine dqage3
subroutine dqk413(f,a,b,result,abserr,resabs,resasc,count,ya,yb,yeps,za,zb,zeps)
!***author piessens,robert,appl. math. & progr. div - k.u.leuven
! de doncker,elise,appl. math. & progr. div. - k.u.leuven
! 2019/01/27 edited by sikino, http://slpr.sakura.ne.jp/qp/
double precision a,absc,abserr,b,centr,abs,dhlgth,dmax1,dmin1,&
epmach,hlgth,resabs,resasc,uflow,wg,wgk,xgk,ya,yb,yeps,za,zb,zeps
integer j,jtw,jtwm1,count
complex(kind(0d0))::result,resg,resk,reskh,fval1,fval2,fv1,fv2,fc,fsum
complex(kind(0d0)),external::f
dimension fv1(20),fv2(20),xgk(21),wgk(21),wg(10)
data wg ( 1) / 0.017614007139152118311861962351853d0 /
data wg ( 2) / 0.040601429800386941331039952274932d0 /
data wg ( 3) / 0.062672048334109063569506535187042d0 /
data wg ( 4) / 0.083276741576704748724758143222046d0 /
data wg ( 5) / 0.101930119817240435036750135480350d0 /
data wg ( 6) / 0.118194531961518417312377377711382d0 /
data wg ( 7) / 0.131688638449176626898494499748163d0 /
data wg ( 8) / 0.142096109318382051329298325067165d0 /
data wg ( 9) / 0.149172986472603746787828737001969d0 /
data wg ( 10) / 0.152753387130725850698084331955098d0 /
!
data xgk ( 1) / 0.998859031588277663838315576545863d0 /
data xgk ( 2) / 0.993128599185094924786122388471320d0 /
data xgk ( 3) / 0.981507877450250259193342994720217d0 /
data xgk ( 4) / 0.963971927277913791267666131197277d0 /
data xgk ( 5) / 0.940822633831754753519982722212443d0 /
data xgk ( 6) / 0.912234428251325905867752441203298d0 /
data xgk ( 7) / 0.878276811252281976077442995113078d0 /
data xgk ( 8) / 0.839116971822218823394529061701521d0 /
data xgk ( 9) / 0.795041428837551198350638833272788d0 /
data xgk ( 10) / 0.746331906460150792614305070355642d0 /
data xgk ( 11) / 0.693237656334751384805490711845932d0 /
data xgk ( 12) / 0.636053680726515025452836696226286d0 /
data xgk ( 13) / 0.575140446819710315342946036586425d0 /
data xgk ( 14) / 0.510867001950827098004364050955251d0 /
data xgk ( 15) / 0.443593175238725103199992213492640d0 /
data xgk ( 16) / 0.373706088715419560672548177024927d0 /
data xgk ( 17) / 0.301627868114913004320555356858592d0 /
data xgk ( 18) / 0.227785851141645078080496195368575d0 /
data xgk ( 19) / 0.152605465240922675505220241022678d0 /
data xgk ( 20) / 0.076526521133497333754640409398838d0 /
data xgk ( 21) / 0.000000000000000000000000000000000d0 /
!
data wgk ( 1) / 0.003073583718520531501218293246031d0 /
data wgk ( 2) / 0.008600269855642942198661787950102d0 /
data wgk ( 3) / 0.014626169256971252983787960308868d0 /
data wgk ( 4) / 0.020388373461266523598010231432755d0 /
data wgk ( 5) / 0.025882133604951158834505067096153d0 /
data wgk ( 6) / 0.031287306777032798958543119323801d0 /
data wgk ( 7) / 0.036600169758200798030557240707211d0 /
data wgk ( 8) / 0.041668873327973686263788305936895d0 /
data wgk ( 9) / 0.046434821867497674720231880926108d0 /
data wgk ( 10) / 0.050944573923728691932707670050345d0 /
data wgk ( 11) / 0.055195105348285994744832372419777d0 /
data wgk ( 12) / 0.059111400880639572374967220648594d0 /
data wgk ( 13) / 0.062653237554781168025870122174255d0 /
data wgk ( 14) / 0.065834597133618422111563556969398d0 /
data wgk ( 15) / 0.068648672928521619345623411885368d0 /
data wgk ( 16) / 0.071054423553444068305790361723210d0 /
data wgk ( 17) / 0.073030690332786667495189417658913d0 /
data wgk ( 18) / 0.074582875400499188986581418362488d0 /
data wgk ( 19) / 0.075704497684556674659542775376617d0 /
data wgk ( 20) / 0.076377867672080736705502835038061d0 /
data wgk ( 21) / 0.076600711917999656445049901530102d0 /
epmach = epsilon(a)
uflow = tiny(a)
centr = 0.5d+00*(a+b)
hlgth = 0.5d+00*(b-a)
dhlgth = abs(hlgth)
resg = 0.0d+00
!fc = f(centr) ! *************
call dqag4yz(f,centr,ya,yb,yeps,za,zb,zeps,fc,count)
resk = wgk(21)*fc
resabs = abs(resk)
do j=1,10
jtw = j*2
absc = hlgth*xgk(jtw)
!fval1 = f(centr-absc) ! *************
!fval2 = f(centr+absc) ! *************
call dqag4yz(f,centr-absc,ya,yb,yeps,za,zb,zeps,fval1,count)
call dqag4yz(f,centr+absc,ya,yb,yeps,za,zb,zeps,fval2,count)
fv1(jtw) = fval1
fv2(jtw) = fval2
fsum = fval1+fval2
resg = resg+wg(j)*fsum
resk = resk+wgk(jtw)*fsum
resabs = resabs+wgk(jtw)*(abs(fval1)+abs(fval2))
enddo
do j = 1,10
jtwm1 = j*2-1
absc = hlgth*xgk(jtwm1)
!fval1 = f(centr-absc) ! *************
!fval2 = f(centr+absc) ! *************
call dqag4yz(f,centr-absc,ya,yb,yeps,za,zb,zeps,fval1,count)
call dqag4yz(f,centr+absc,ya,yb,yeps,za,zb,zeps,fval2,count)
fv1(jtwm1) = fval1
fv2(jtwm1) = fval2
fsum = fval1+fval2
resk = resk+wgk(jtwm1)*fsum
resabs = resabs+wgk(jtwm1)*(abs(fval1)+abs(fval2))
enddo
reskh = resk*0.5d+00
resasc = wgk(21)*abs(fc-reskh)
do j=1,20
resasc = resasc+wgk(j)*(abs(fv1(j)-reskh)+abs(fv2(j)-reskh))
enddo
result = resk*hlgth
resabs = resabs*dhlgth
resasc = resasc*dhlgth
abserr = abs((resk-resg)*hlgth)
if(resasc.ne.0.0d+00.and.abserr.ne.0.d+00)&
abserr = resasc*dmin1(0.1d+01,(0.2d+03*abserr/resasc)**1.5d+00)
if(resabs.gt.uflow/(0.5d+02*epmach)) abserr = dmax1&
((epmach*0.5d+02)*resabs,abserr)
return
end subroutine dqk413
subroutine dqag4yz(f,x,a,b,eps,za,zb,zeps,s,count)
implicit none
integer,intent(inout)::count
double precision,intent(in)::x,a,b,eps,za,zb,zeps
complex(kind(0d0)),intent(out)::s
complex(kind(0d0)),external::f
!
! Quadpack integration package, using key=4
! (Gauss quadrature with 20-41 points)
!
integer::neval,limit,last,ier,lvl
integer,allocatable::iwork(:)
double precision,allocatable::alist(:),blist(:),elist(:)
complex(kind(0d0)),allocatable::rlist(:)
double precision::epsabs,abserr
!=============
limit=1000
! limit increase --> converge
!=============
s=dcmplx(0d0,0d0)
allocate(iwork(1:limit))
allocate(alist(1:limit),blist(1:limit),rlist(1:limit),elist(1:limit))
alist=0d0
blist=0d0
elist=0d0
rlist=dcmplx(0d0,0d0)
epsabs=-1d0
ier = 6
neval = 0
last = 0
abserr = 0d0
!count = 0
call dqageyz(f,x,a,b,epsabs,eps,limit,s,abserr,neval,&
ier,alist,blist,rlist,elist,iwork,last,count,za,zb,zeps)
lvl = 0
if(ier.eq.6) lvl = 1
if(ier.ne.0) call xerror("26habnormal return from dqag" ,26,ier,lvl)
! ier = 0 : success, converged.
! ier > 0 : fail
!write(6,*)count,ier ! Number of times called integrand function
if(ier.eq.1)then
write(6,*)"Try the parameter 'limit' increase."
endif
deallocate(iwork)
return
end subroutine dqag4yz
subroutine dqageyz(f,x,a,b,epsabs,epsrel,limit,result,abserr, &
neval,ier,alist,blist,rlist,elist,iord,last,count,za,zb,zeps)
!***author piessens,robert,appl. math. & progr. div - k.u.leuven
! de doncker,elise,appl. math. & progr. div. - k.u.leuven
! 2019/01/27 edited by sikino, http://slpr.sakura.ne.jp/qp/
double precision a,abserr,alist,a1,a2,b,&
blist,b1,b2,defabs,defab1,defab2,dmax1,elist,epmach,&
epsabs,epsrel,errbnd,errmax,error1,error2,erro12,errsum,&
resabs,uflow,x,za,zb,zeps
integer ier,iord,iroff1,iroff2,k,last,limit,maxerr,neval,&
nrmax,igt,igk,count
dimension alist(limit),blist(limit),elist(limit),iord(limit)
complex(kind(0d0))::result,rlist(limit),area,area1,area12,area2
complex(kind(0d0)),external::f
epmach = epsilon(a)
uflow = tiny(a)
ier = 0
neval = 0
last = 0
result = dcmplx(0d0,0d0)
abserr = 0.0d+00
alist(1) = a
blist(1) = b
rlist(1) = dcmplx(0d0,0d0)
elist(1) = 0.0d+00
iord(1) = 0
if(epsabs.le.0.0d+00.and.&
epsrel.lt.dmax1(0.5d+02*epmach,0.5d-28)) ier = 6
if(ier.ne.6)then
neval = 0
call dqk41yz(f,x,a,b,result,abserr,defabs,resabs,count,za,zb,zeps)
last = 1
rlist(1) = result
elist(1) = abserr
iord(1) = 1
errbnd = dmax1(epsabs,epsrel*abs(result))
if(abserr.le.0.5d+02*epmach*defabs.and.abserr.gt.errbnd) ier = 2
if(limit.eq.1) ier = 1
igk=0
if(ier.ne.0.or.(abserr.le.errbnd.and.abserr.ne.resabs)&
.or.abserr.eq.0.0d+00)igk=60
if(igk.ne.60)then
errmax = abserr
maxerr = 1
area = result
errsum = abserr
nrmax = 1
iroff1 = 0
iroff2 = 0
do last = 2,limit
a1 = alist(maxerr)
b1 = 0.5d+00*(alist(maxerr)+blist(maxerr))
a2 = b1
b2 = blist(maxerr)
call dqk41yz(f,x,a1,b1,area1,error1,resabs,defab1,count,za,zb,zeps)
call dqk41yz(f,x,a2,b2,area2,error2,resabs,defab2,count,za,zb,zeps)
neval = neval+1
area12 = area1+area2
erro12 = error1+error2
errsum = errsum+erro12-errmax
area = area+area12-rlist(maxerr)
if(defab1.ne.error1.and.defab2.ne.error2)then
if(abs(rlist(maxerr)-area12).le.0.1d-04*abs(area12)&
.and.erro12.ge.0.99d+00*errmax) iroff1 = iroff1+1
if(last.gt.10.and.erro12.gt.errmax) iroff2 = iroff2+1
endif
rlist(maxerr) = area1
rlist(last) = area2
errbnd = dmax1(epsabs,epsrel*abs(area))
if(errsum.gt.errbnd)then
if(iroff1.ge.6.or.iroff2.ge.20) ier = 2
if(last.eq.limit) ier = 1
if(dmax1(abs(a1),abs(b2)).le.(0.1d+01+0.1d+03* &
epmach)*(abs(a2)+0.1d+04*uflow)) ier = 3
endif
igt=0
if(error2.le.error1)then
alist(last) = a2
blist(maxerr) = b1
blist(last) = b2
elist(maxerr) = error1
elist(last) = error2
igt=20
endif
if(igt.ne.20)then
alist(maxerr) = a2
alist(last) = a1
blist(last) = b1
rlist(maxerr) = area2
rlist(last) = area1
elist(maxerr) = error2
elist(last) = error1
endif
call dqpsrt(limit,last,maxerr,errmax,elist,iord,nrmax)
if(ier.ne.0.or.errsum.le.errbnd)exit
enddo
if(last.eq.limit+1)last=last-1
result = 0.0d+00
do k=1,last
result = result+rlist(k)
enddo
abserr = errsum
endif
end if
return
end subroutine dqageyz
subroutine dqk41yz(f,x,a,b,result,abserr,resabs,resasc,count,za,zb,zeps)
!***author piessens,robert,appl. math. & progr. div - k.u.leuven
! de doncker,elise,appl. math. & progr. div. - k.u.leuven
! 2019/01/27 edited by sikino, http://slpr.sakura.ne.jp/qp/
double precision a,absc,abserr,b,centr,abs,dhlgth,dmax1,dmin1,&
epmach,hlgth,resabs,resasc,uflow,wg,wgk,xgk,x,za,zb,zeps
integer j,jtw,jtwm1,count
complex(kind(0d0))::result,resg,resk,reskh,fval1,fval2,fv1,fv2,fc,fsum
complex(kind(0d0)),external::f
dimension fv1(20),fv2(20),xgk(21),wgk(21),wg(10)
data wg ( 1) / 0.017614007139152118311861962351853d0 /
data wg ( 2) / 0.040601429800386941331039952274932d0 /
data wg ( 3) / 0.062672048334109063569506535187042d0 /
data wg ( 4) / 0.083276741576704748724758143222046d0 /
data wg ( 5) / 0.101930119817240435036750135480350d0 /
data wg ( 6) / 0.118194531961518417312377377711382d0 /
data wg ( 7) / 0.131688638449176626898494499748163d0 /
data wg ( 8) / 0.142096109318382051329298325067165d0 /
data wg ( 9) / 0.149172986472603746787828737001969d0 /
data wg ( 10) / 0.152753387130725850698084331955098d0 /
!
data xgk ( 1) / 0.998859031588277663838315576545863d0 /
data xgk ( 2) / 0.993128599185094924786122388471320d0 /
data xgk ( 3) / 0.981507877450250259193342994720217d0 /
data xgk ( 4) / 0.963971927277913791267666131197277d0 /
data xgk ( 5) / 0.940822633831754753519982722212443d0 /
data xgk ( 6) / 0.912234428251325905867752441203298d0 /
data xgk ( 7) / 0.878276811252281976077442995113078d0 /
data xgk ( 8) / 0.839116971822218823394529061701521d0 /
data xgk ( 9) / 0.795041428837551198350638833272788d0 /
data xgk ( 10) / 0.746331906460150792614305070355642d0 /
data xgk ( 11) / 0.693237656334751384805490711845932d0 /
data xgk ( 12) / 0.636053680726515025452836696226286d0 /
data xgk ( 13) / 0.575140446819710315342946036586425d0 /
data xgk ( 14) / 0.510867001950827098004364050955251d0 /
data xgk ( 15) / 0.443593175238725103199992213492640d0 /
data xgk ( 16) / 0.373706088715419560672548177024927d0 /
data xgk ( 17) / 0.301627868114913004320555356858592d0 /
data xgk ( 18) / 0.227785851141645078080496195368575d0 /
data xgk ( 19) / 0.152605465240922675505220241022678d0 /
data xgk ( 20) / 0.076526521133497333754640409398838d0 /
data xgk ( 21) / 0.000000000000000000000000000000000d0 /
!
data wgk ( 1) / 0.003073583718520531501218293246031d0 /
data wgk ( 2) / 0.008600269855642942198661787950102d0 /
data wgk ( 3) / 0.014626169256971252983787960308868d0 /
data wgk ( 4) / 0.020388373461266523598010231432755d0 /
data wgk ( 5) / 0.025882133604951158834505067096153d0 /
data wgk ( 6) / 0.031287306777032798958543119323801d0 /
data wgk ( 7) / 0.036600169758200798030557240707211d0 /
data wgk ( 8) / 0.041668873327973686263788305936895d0 /
data wgk ( 9) / 0.046434821867497674720231880926108d0 /
data wgk ( 10) / 0.050944573923728691932707670050345d0 /
data wgk ( 11) / 0.055195105348285994744832372419777d0 /
data wgk ( 12) / 0.059111400880639572374967220648594d0 /
data wgk ( 13) / 0.062653237554781168025870122174255d0 /
data wgk ( 14) / 0.065834597133618422111563556969398d0 /
data wgk ( 15) / 0.068648672928521619345623411885368d0 /
data wgk ( 16) / 0.071054423553444068305790361723210d0 /
data wgk ( 17) / 0.073030690332786667495189417658913d0 /
data wgk ( 18) / 0.074582875400499188986581418362488d0 /
data wgk ( 19) / 0.075704497684556674659542775376617d0 /
data wgk ( 20) / 0.076377867672080736705502835038061d0 /
data wgk ( 21) / 0.076600711917999656445049901530102d0 /
epmach = epsilon(a)
uflow = tiny(a)
centr = 0.5d+00*(a+b)
hlgth = 0.5d+00*(b-a)
dhlgth = abs(hlgth)
resg = 0.0d+00
!fc = f(centr) ! *************
!fc = f(x,centr) ! *************
call dqag4z(f,x,centr,za,zb,zeps,fc,count)
resk = wgk(21)*fc
resabs = abs(resk)
do j=1,10
jtw = j*2
absc = hlgth*xgk(jtw)
!fval1 = f(centr-absc) ! *************
!fval2 = f(centr+absc) ! *************
!fval1 = f(x,centr-absc)
!fval2 = f(x,centr+absc)
call dqag4z(f,x,centr-absc,za,zb,zeps,fval1,count)
call dqag4z(f,x,centr+absc,za,zb,zeps,fval2,count)
fv1(jtw) = fval1
fv2(jtw) = fval2
fsum = fval1+fval2
resg = resg+wg(j)*fsum
resk = resk+wgk(jtw)*fsum
resabs = resabs+wgk(jtw)*(abs(fval1)+abs(fval2))
enddo
do j = 1,10
jtwm1 = j*2-1
absc = hlgth*xgk(jtwm1)
!fval1 = f(centr-absc) ! *************
!fval2 = f(centr+absc) ! *************
!fval1 = f(x,centr-absc)
!fval2 = f(x,centr+absc)
call dqag4z(f,x,centr-absc,za,zb,zeps,fval1,count)
call dqag4z(f,x,centr+absc,za,zb,zeps,fval2,count)
fv1(jtwm1) = fval1
fv2(jtwm1) = fval2
fsum = fval1+fval2
resk = resk+wgk(jtwm1)*fsum
resabs = resabs+wgk(jtwm1)*(abs(fval1)+abs(fval2))
enddo
reskh = resk*0.5d+00
resasc = wgk(21)*abs(fc-reskh)
do j=1,20
resasc = resasc+wgk(j)*(abs(fv1(j)-reskh)+abs(fv2(j)-reskh))
enddo
result = resk*hlgth
resabs = resabs*dhlgth
resasc = resasc*dhlgth
abserr = abs((resk-resg)*hlgth)
if(resasc.ne.0.0d+00.and.abserr.ne.0.d+00)&
abserr = resasc*dmin1(0.1d+01,(0.2d+03*abserr/resasc)**1.5d+00)
if(resabs.gt.uflow/(0.5d+02*epmach)) abserr = dmax1&
((epmach*0.5d+02)*resabs,abserr)
!count=count+41
return
end subroutine dqk41yz
subroutine dqag4z(f,x,y,a,b,eps,s,count)
implicit none
integer,intent(inout)::count
double precision,intent(in)::x,y,a,b,eps
complex(kind(0d0)),intent(out)::s
complex(kind(0d0)),external::f
!
! Quadpack integration package, using key=4
! (Gauss quadrature with 20-41 points)
!
integer::neval,limit,last,ier,lvl
integer,allocatable::iwork(:)
double precision,allocatable::alist(:),blist(:),elist(:)
complex(kind(0d0)),allocatable::rlist(:)
double precision::epsabs,abserr
!=============
limit=1000
! limit increase --> converge
!=============
s=dcmplx(0d0,0d0)
allocate(iwork(1:limit))
allocate(alist(1:limit),blist(1:limit),rlist(1:limit),elist(1:limit))
alist=0d0
blist=0d0
elist=0d0
rlist=dcmplx(0d0,0d0)
epsabs=-1d0
ier = 6
neval = 0
last = 0
abserr = 0d0
!count = 0
call dqagez(f,x,y,a,b,epsabs,eps,limit,s,abserr,neval,&
ier,alist,blist,rlist,elist,iwork,last,count)
lvl = 0
if(ier.eq.6) lvl = 1
if(ier.ne.0) call xerror("26habnormal return from dqag" ,26,ier,lvl)
! ier = 0 : success, converged.
! ier > 0 : fail
!write(6,*)count,ier ! Number of times called integrand function
if(ier.eq.1)then
write(6,*)"Try the parameter 'limit' increase."
endif
deallocate(iwork)
return
end subroutine dqag4z
subroutine dqagez(f,x,y,a,b,epsabs,epsrel,limit,result,abserr, &
neval,ier,alist,blist,rlist,elist,iord,last,count)
!***author piessens,robert,appl. math. & progr. div - k.u.leuven
! de doncker,elise,appl. math. & progr. div. - k.u.leuven
! 2019/01/27 edited by sikino, http://slpr.sakura.ne.jp/qp/
double precision a,abserr,alist,a1,a2,b,&
blist,b1,b2,defabs,defab1,defab2,dmax1,elist,epmach,&
epsabs,epsrel,errbnd,errmax,error1,error2,erro12,errsum,&
resabs,uflow,x,y
integer ier,iord,iroff1,iroff2,k,last,limit,maxerr,neval,&
nrmax,igt,igk,count
dimension alist(limit),blist(limit),elist(limit),iord(limit)
complex(kind(0d0))::result,rlist(limit),area,area1,area12,area2
complex(kind(0d0)),external::f
epmach = epsilon(a)
uflow = tiny(a)
ier = 0
neval = 0
last = 0
result = dcmplx(0d0,0d0)
abserr = 0.0d+00
alist(1) = a
blist(1) = b
rlist(1) = dcmplx(0d0,0d0)
elist(1) = 0.0d+00
iord(1) = 0
if(epsabs.le.0.0d+00.and.&
epsrel.lt.dmax1(0.5d+02*epmach,0.5d-28)) ier = 6
if(ier.ne.6)then
neval = 0
call dqk41z(f,x,y,a,b,result,abserr,defabs,resabs,count)
last = 1
rlist(1) = result
elist(1) = abserr
iord(1) = 1
errbnd = dmax1(epsabs,epsrel*abs(result))
if(abserr.le.0.5d+02*epmach*defabs.and.abserr.gt.errbnd) ier = 2
if(limit.eq.1) ier = 1
igk=0
if(ier.ne.0.or.(abserr.le.errbnd.and.abserr.ne.resabs)&
.or.abserr.eq.0.0d+00)igk=60
if(igk.ne.60)then
errmax = abserr
maxerr = 1
area = result
errsum = abserr
nrmax = 1
iroff1 = 0
iroff2 = 0
do last = 2,limit
a1 = alist(maxerr)
b1 = 0.5d+00*(alist(maxerr)+blist(maxerr))
a2 = b1
b2 = blist(maxerr)
call dqk41z(f,x,y,a1,b1,area1,error1,resabs,defab1,count)
call dqk41z(f,x,y,a2,b2,area2,error2,resabs,defab2,count)
neval = neval+1
area12 = area1+area2
erro12 = error1+error2
errsum = errsum+erro12-errmax
area = area+area12-rlist(maxerr)
if(defab1.ne.error1.and.defab2.ne.error2)then
if(abs(rlist(maxerr)-area12).le.0.1d-04*abs(area12)&
.and.erro12.ge.0.99d+00*errmax) iroff1 = iroff1+1
if(last.gt.10.and.erro12.gt.errmax) iroff2 = iroff2+1
endif
rlist(maxerr) = area1
rlist(last) = area2
errbnd = dmax1(epsabs,epsrel*abs(area))
if(errsum.gt.errbnd)then
if(iroff1.ge.6.or.iroff2.ge.20) ier = 2
if(last.eq.limit) ier = 1
if(dmax1(abs(a1),abs(b2)).le.(0.1d+01+0.1d+03* &
epmach)*(abs(a2)+0.1d+04*uflow)) ier = 3
endif
igt=0
if(error2.le.error1)then
alist(last) = a2
blist(maxerr) = b1
blist(last) = b2
elist(maxerr) = error1
elist(last) = error2
igt=20
endif
if(igt.ne.20)then
alist(maxerr) = a2
alist(last) = a1
blist(last) = b1
rlist(maxerr) = area2
rlist(last) = area1
elist(maxerr) = error2
elist(last) = error1
endif
call dqpsrt(limit,last,maxerr,errmax,elist,iord,nrmax)
if(ier.ne.0.or.errsum.le.errbnd)exit
enddo
if(last.eq.limit+1)last=last-1
result = 0.0d+00
do k=1,last
result = result+rlist(k)
enddo
abserr = errsum
endif
end if
return
end subroutine dqagez
subroutine dqk41z(f,x,y,a,b,result,abserr,resabs,resasc,count)
!***author piessens,robert,appl. math. & progr. div - k.u.leuven
! de doncker,elise,appl. math. & progr. div. - k.u.leuven
! 2019/01/27 edited by sikino, http://slpr.sakura.ne.jp/qp/
double precision a,absc,abserr,b,centr,abs,dhlgth,dmax1,dmin1,&
epmach,hlgth,resabs,resasc,uflow,wg,wgk,xgk,x,y
integer j,jtw,jtwm1,count
complex(kind(0d0))::result,resg,resk,reskh,fval1,fval2,fv1,fv2,fc,fsum
complex(kind(0d0)),external::f
dimension fv1(20),fv2(20),xgk(21),wgk(21),wg(10)
data wg ( 1) / 0.017614007139152118311861962351853d0 /
data wg ( 2) / 0.040601429800386941331039952274932d0 /
data wg ( 3) / 0.062672048334109063569506535187042d0 /
data wg ( 4) / 0.083276741576704748724758143222046d0 /
data wg ( 5) / 0.101930119817240435036750135480350d0 /
data wg ( 6) / 0.118194531961518417312377377711382d0 /
data wg ( 7) / 0.131688638449176626898494499748163d0 /
data wg ( 8) / 0.142096109318382051329298325067165d0 /
data wg ( 9) / 0.149172986472603746787828737001969d0 /
data wg ( 10) / 0.152753387130725850698084331955098d0 /
!
data xgk ( 1) / 0.998859031588277663838315576545863d0 /
data xgk ( 2) / 0.993128599185094924786122388471320d0 /
data xgk ( 3) / 0.981507877450250259193342994720217d0 /
data xgk ( 4) / 0.963971927277913791267666131197277d0 /
data xgk ( 5) / 0.940822633831754753519982722212443d0 /
data xgk ( 6) / 0.912234428251325905867752441203298d0 /
data xgk ( 7) / 0.878276811252281976077442995113078d0 /
data xgk ( 8) / 0.839116971822218823394529061701521d0 /
data xgk ( 9) / 0.795041428837551198350638833272788d0 /
data xgk ( 10) / 0.746331906460150792614305070355642d0 /
data xgk ( 11) / 0.693237656334751384805490711845932d0 /
data xgk ( 12) / 0.636053680726515025452836696226286d0 /
data xgk ( 13) / 0.575140446819710315342946036586425d0 /
data xgk ( 14) / 0.510867001950827098004364050955251d0 /
data xgk ( 15) / 0.443593175238725103199992213492640d0 /
data xgk ( 16) / 0.373706088715419560672548177024927d0 /
data xgk ( 17) / 0.301627868114913004320555356858592d0 /
data xgk ( 18) / 0.227785851141645078080496195368575d0 /
data xgk ( 19) / 0.152605465240922675505220241022678d0 /
data xgk ( 20) / 0.076526521133497333754640409398838d0 /
data xgk ( 21) / 0.000000000000000000000000000000000d0 /
!
data wgk ( 1) / 0.003073583718520531501218293246031d0 /
data wgk ( 2) / 0.008600269855642942198661787950102d0 /
data wgk ( 3) / 0.014626169256971252983787960308868d0 /
data wgk ( 4) / 0.020388373461266523598010231432755d0 /
data wgk ( 5) / 0.025882133604951158834505067096153d0 /
data wgk ( 6) / 0.031287306777032798958543119323801d0 /
data wgk ( 7) / 0.036600169758200798030557240707211d0 /
data wgk ( 8) / 0.041668873327973686263788305936895d0 /
data wgk ( 9) / 0.046434821867497674720231880926108d0 /
data wgk ( 10) / 0.050944573923728691932707670050345d0 /
data wgk ( 11) / 0.055195105348285994744832372419777d0 /
data wgk ( 12) / 0.059111400880639572374967220648594d0 /
data wgk ( 13) / 0.062653237554781168025870122174255d0 /
data wgk ( 14) / 0.065834597133618422111563556969398d0 /
data wgk ( 15) / 0.068648672928521619345623411885368d0 /
data wgk ( 16) / 0.071054423553444068305790361723210d0 /
data wgk ( 17) / 0.073030690332786667495189417658913d0 /
data wgk ( 18) / 0.074582875400499188986581418362488d0 /
data wgk ( 19) / 0.075704497684556674659542775376617d0 /
data wgk ( 20) / 0.076377867672080736705502835038061d0 /
data wgk ( 21) / 0.076600711917999656445049901530102d0 /
epmach = epsilon(a)
uflow = tiny(a)
centr = 0.5d+00*(a+b)
hlgth = 0.5d+00*(b-a)
dhlgth = abs(hlgth)
resg = 0.0d+00
!fc = f(centr) ! *************
fc = f(x,y,centr) ! *************
resk = wgk(21)*fc
resabs = abs(resk)
do j=1,10
jtw = j*2
absc = hlgth*xgk(jtw)
!fval1 = f(centr-absc) ! *************
!fval2 = f(centr+absc) ! *************
fval1 = f(x,y,centr-absc)
fval2 = f(x,y,centr+absc)
fv1(jtw) = fval1
fv2(jtw) = fval2
fsum = fval1+fval2
resg = resg+wg(j)*fsum
resk = resk+wgk(jtw)*fsum
resabs = resabs+wgk(jtw)*(abs(fval1)+abs(fval2))
enddo
do j = 1,10
jtwm1 = j*2-1
absc = hlgth*xgk(jtwm1)
!fval1 = f(centr-absc) ! *************
!fval2 = f(centr+absc) ! *************
fval1 = f(x,y,centr-absc)
fval2 = f(x,y,centr+absc)
fv1(jtwm1) = fval1
fv2(jtwm1) = fval2
fsum = fval1+fval2
resk = resk+wgk(jtwm1)*fsum
resabs = resabs+wgk(jtwm1)*(abs(fval1)+abs(fval2))
enddo
reskh = resk*0.5d+00
resasc = wgk(21)*abs(fc-reskh)
do j=1,20
resasc = resasc+wgk(j)*(abs(fv1(j)-reskh)+abs(fv2(j)-reskh))
enddo
result = resk*hlgth
resabs = resabs*dhlgth
resasc = resasc*dhlgth
abserr = abs((resk-resg)*hlgth)
if(resasc.ne.0.0d+00.and.abserr.ne.0.d+00)&
abserr = resasc*dmin1(0.1d+01,(0.2d+03*abserr/resasc)**1.5d+00)
if(resabs.gt.uflow/(0.5d+02*epmach)) abserr = dmax1&
((epmach*0.5d+02)*resabs,abserr)
count=count+41
return
end subroutine dqk41z
subroutine dqpsrt(limit,last,maxerr,ermax,elist,iord,nrmax)
double precision elist,ermax,errmax,errmin
integer i,ibeg,ido,iord,isucc,j,jbnd,jupbn,k,last,limit,maxerr,&
nrmax,igt,igt1,igt2
dimension elist(last),iord(last)
igt=0
if(last.le.2)then
iord(1) = 1
iord(2) = 2
igt=90
endif
if(igt.ne.90)then
errmax = elist(maxerr)
if(nrmax.ne.1)then
ido = nrmax-1
do i = 1,ido
isucc = iord(nrmax-1)
if(errmax.le.elist(isucc))exit
iord(nrmax) = isucc
nrmax = nrmax-1
enddo
endif
jupbn = last
if(last.gt.(limit/2+2)) jupbn = limit+3-last
errmin = elist(last)
jbnd = jupbn-1
ibeg = nrmax+1
igt1=0
if(ibeg.le.jbnd)then
do i=ibeg,jbnd
isucc = iord(i)
if(errmax.ge.elist(isucc))then
igt1=60
exit
endif
iord(i-1) = isucc
enddo
endif
if(igt1.ne.60)then
iord(jbnd) = maxerr
iord(jupbn) = last
igt=90
endif
igt2=0
if(igt.ne.90)then
iord(i-1) = maxerr
k = jbnd
do j=i,jbnd
isucc = iord(k)
if(errmin.lt.elist(isucc))then
igt2=80
exit
endif
iord(k+1) = isucc
k = k-1
enddo
if(igt2.ne.80)then
iord(i) = last
igt=90
endif
if(igt.ne.90)then
iord(k+1) = last
endif
endif
endif
maxerr = iord(nrmax)
ermax = elist(maxerr)
return
end subroutine dqpsrt
subroutine xerror ( xmess, nmess, nerr, level )
implicit none
integer::level,nerr,nmess
character ( len = * ) xmess
if ( 1 <= LEVEL ) then
WRITE ( *,'(1X,A)') XMESS(1:NMESS)
WRITE ( *,'('' ERROR NUMBER = '',I5,'', MESSAGE LEVEL = '',I5)') &
NERR,LEVEL
end if
return
end subroutine xerror