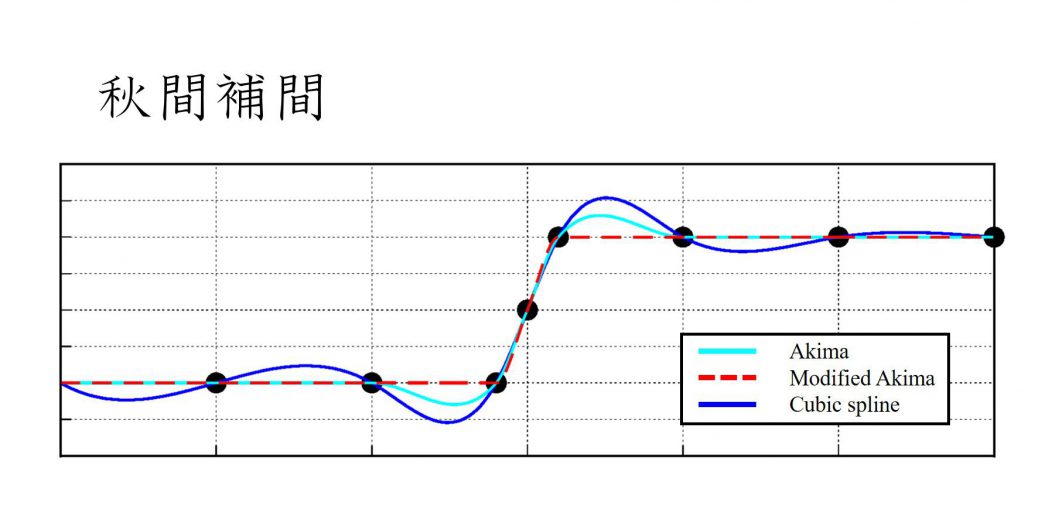
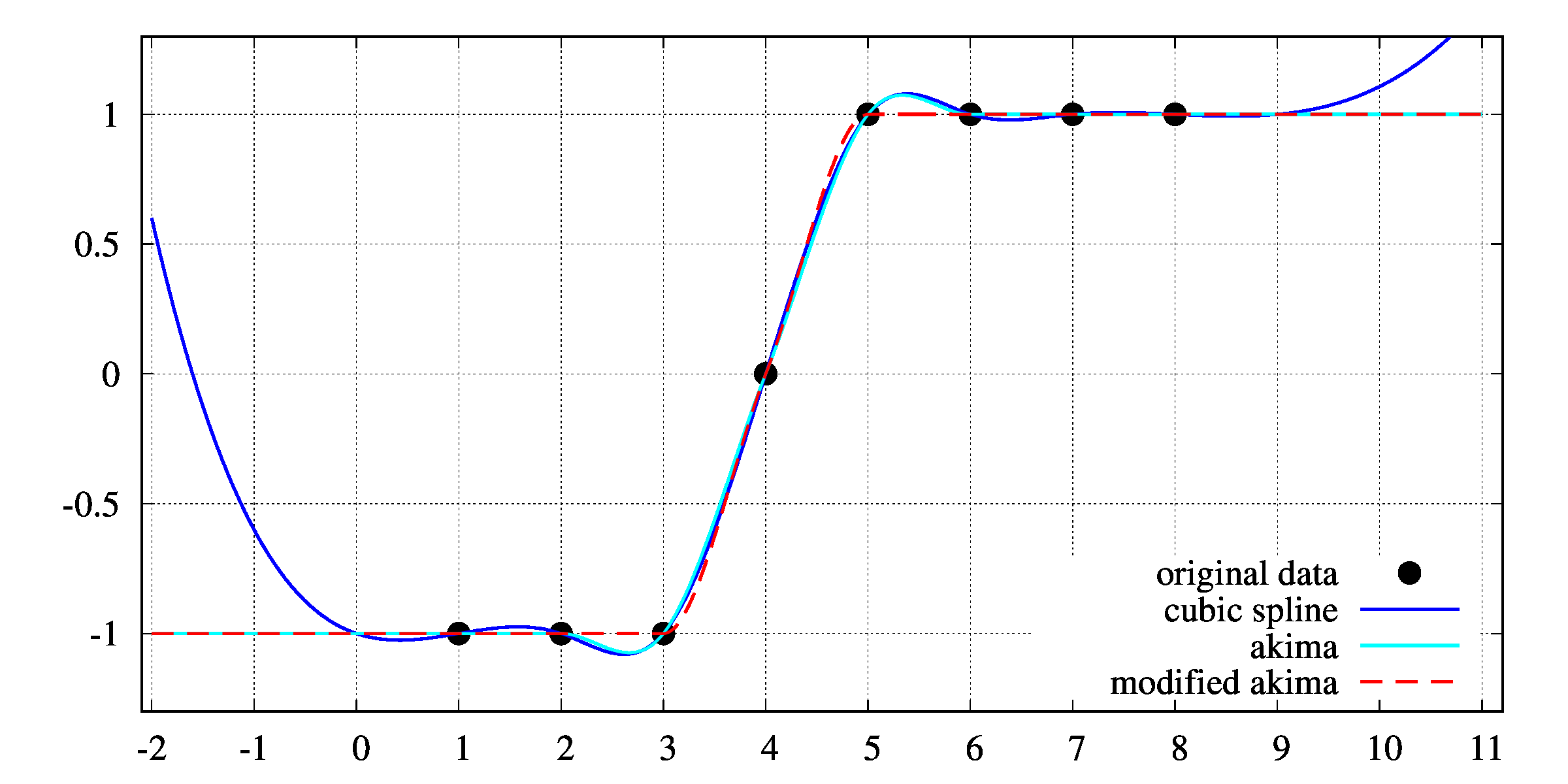
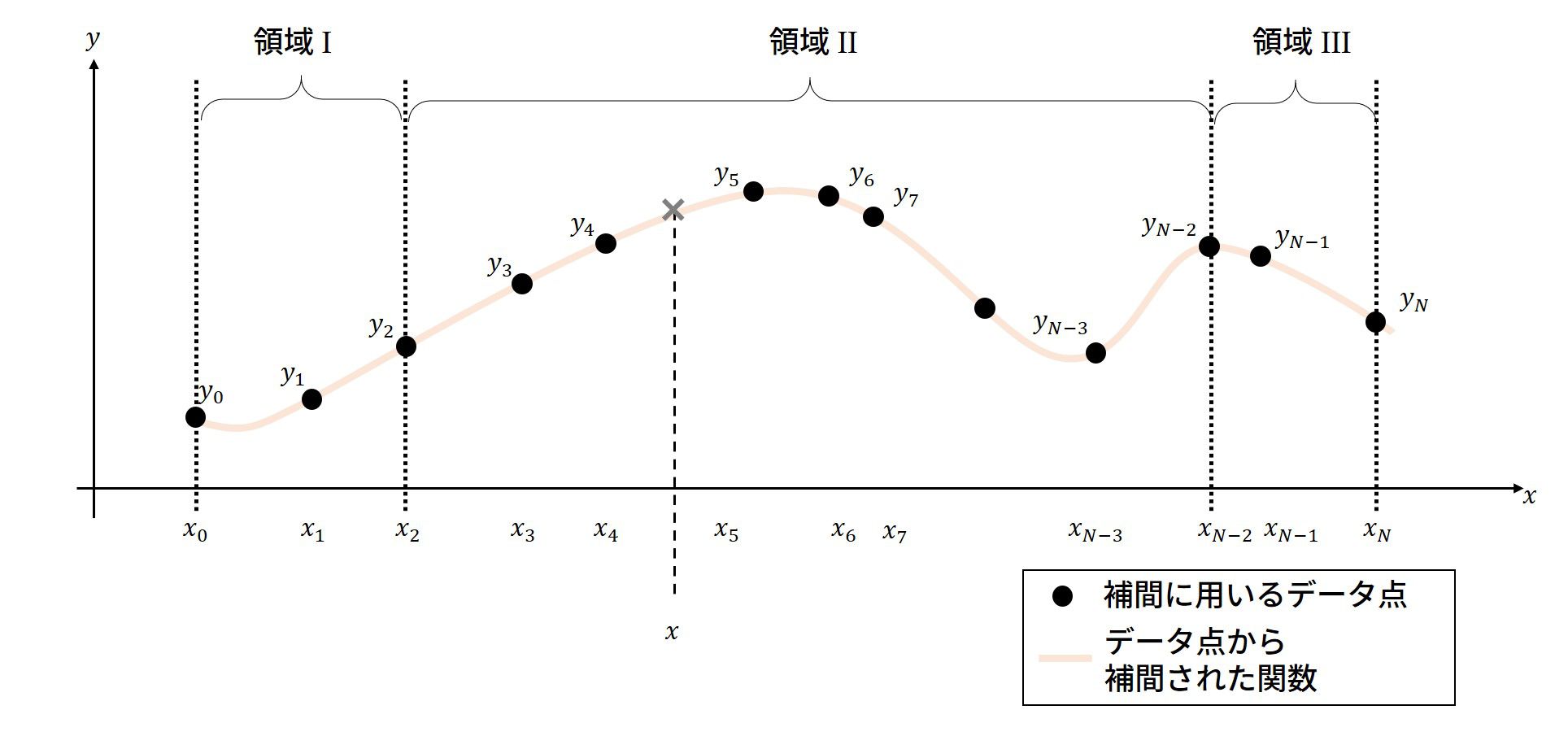
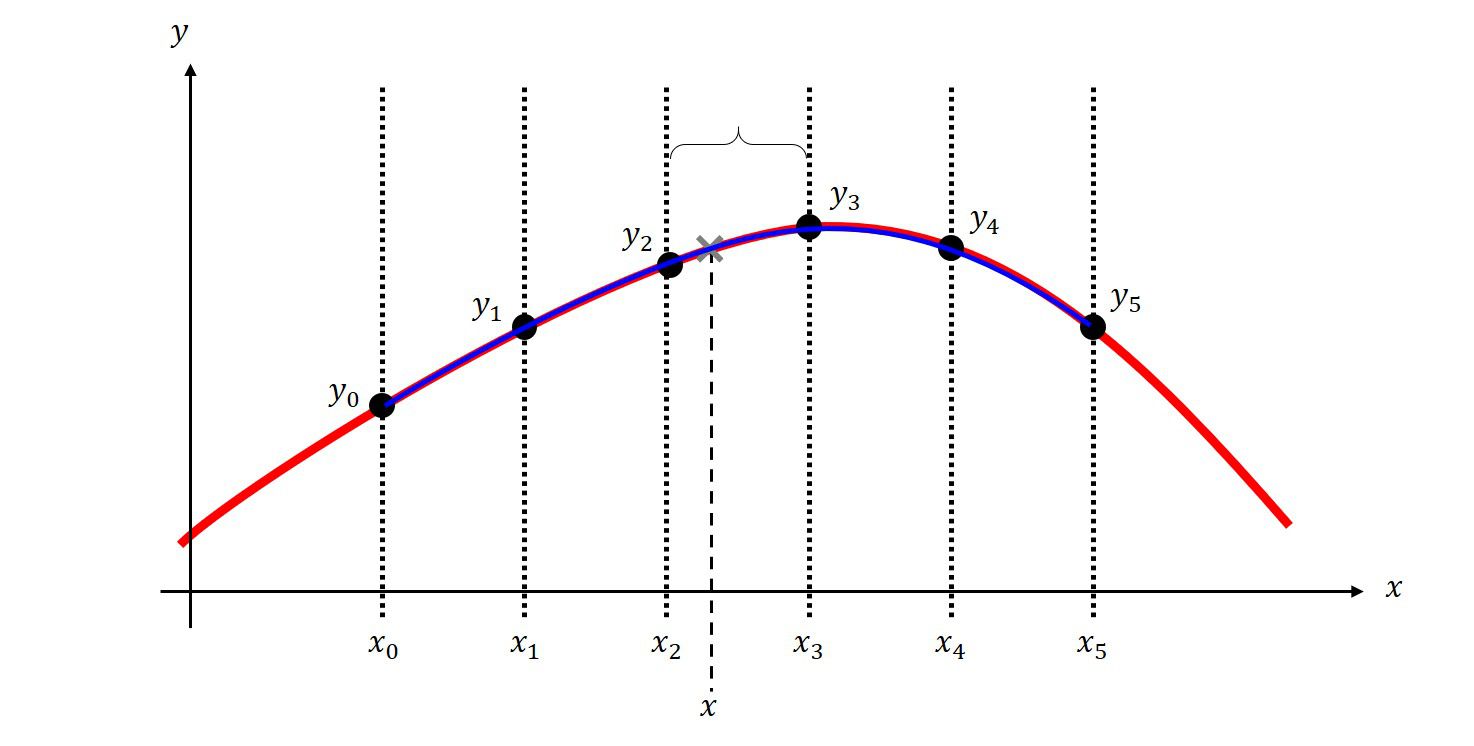
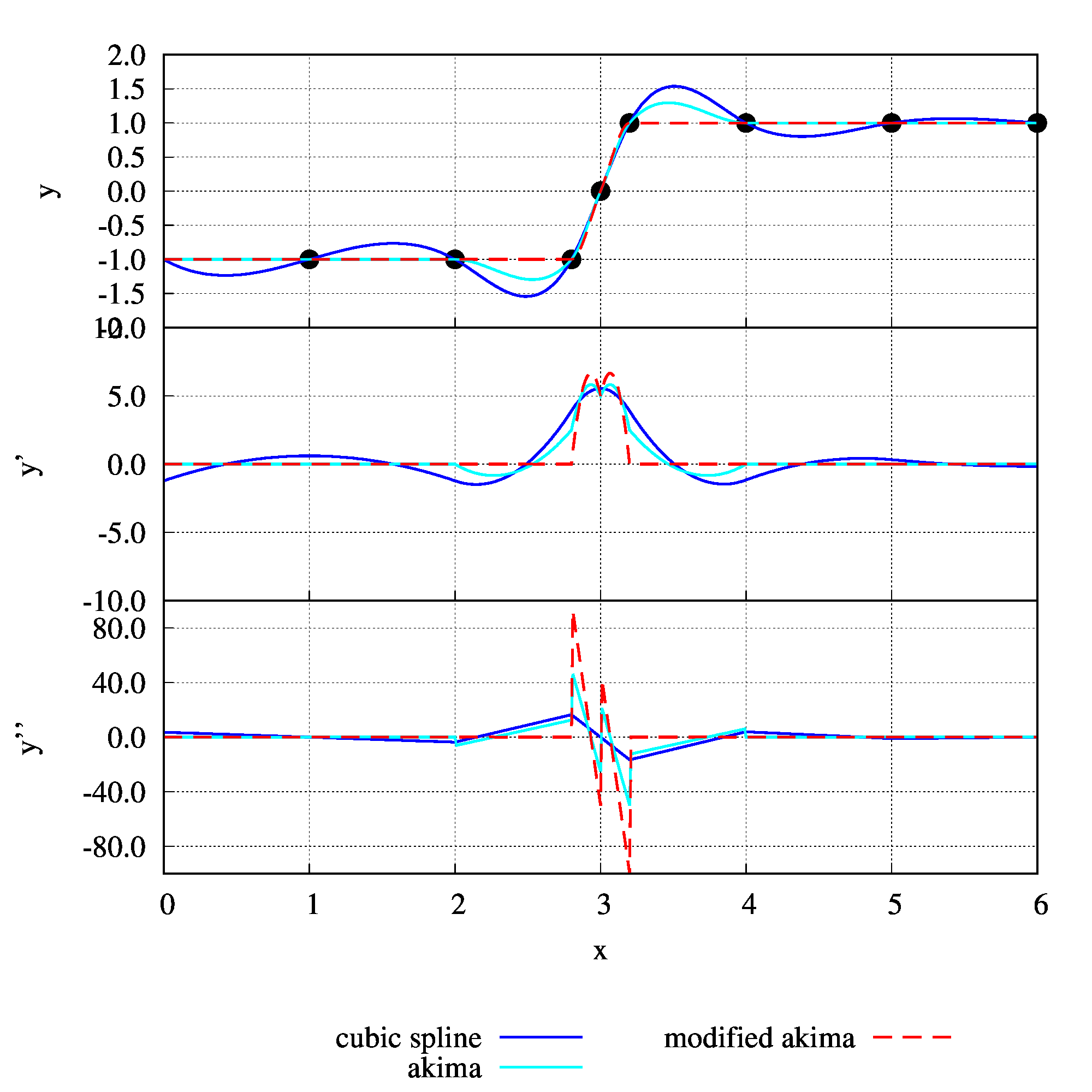
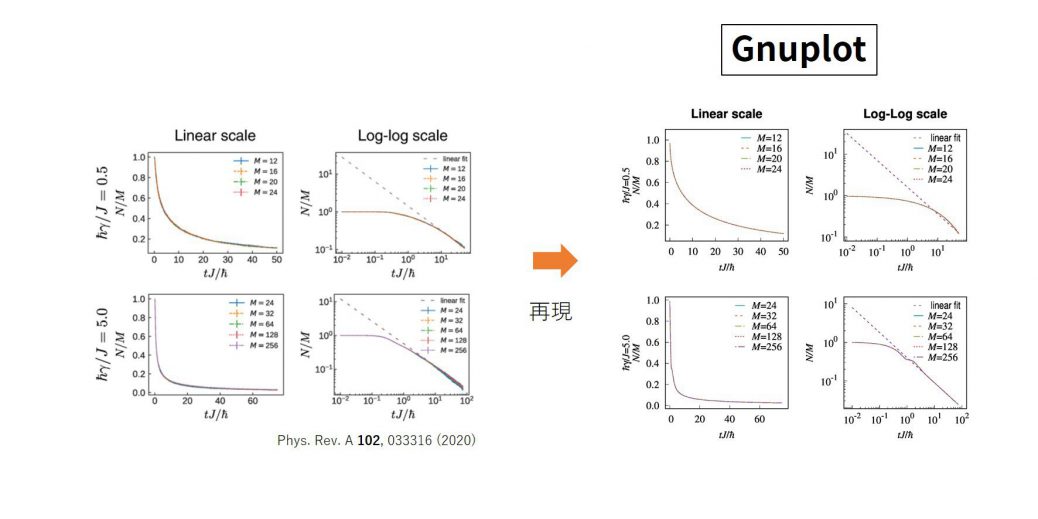
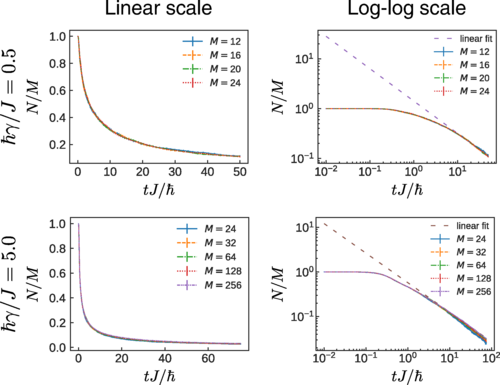
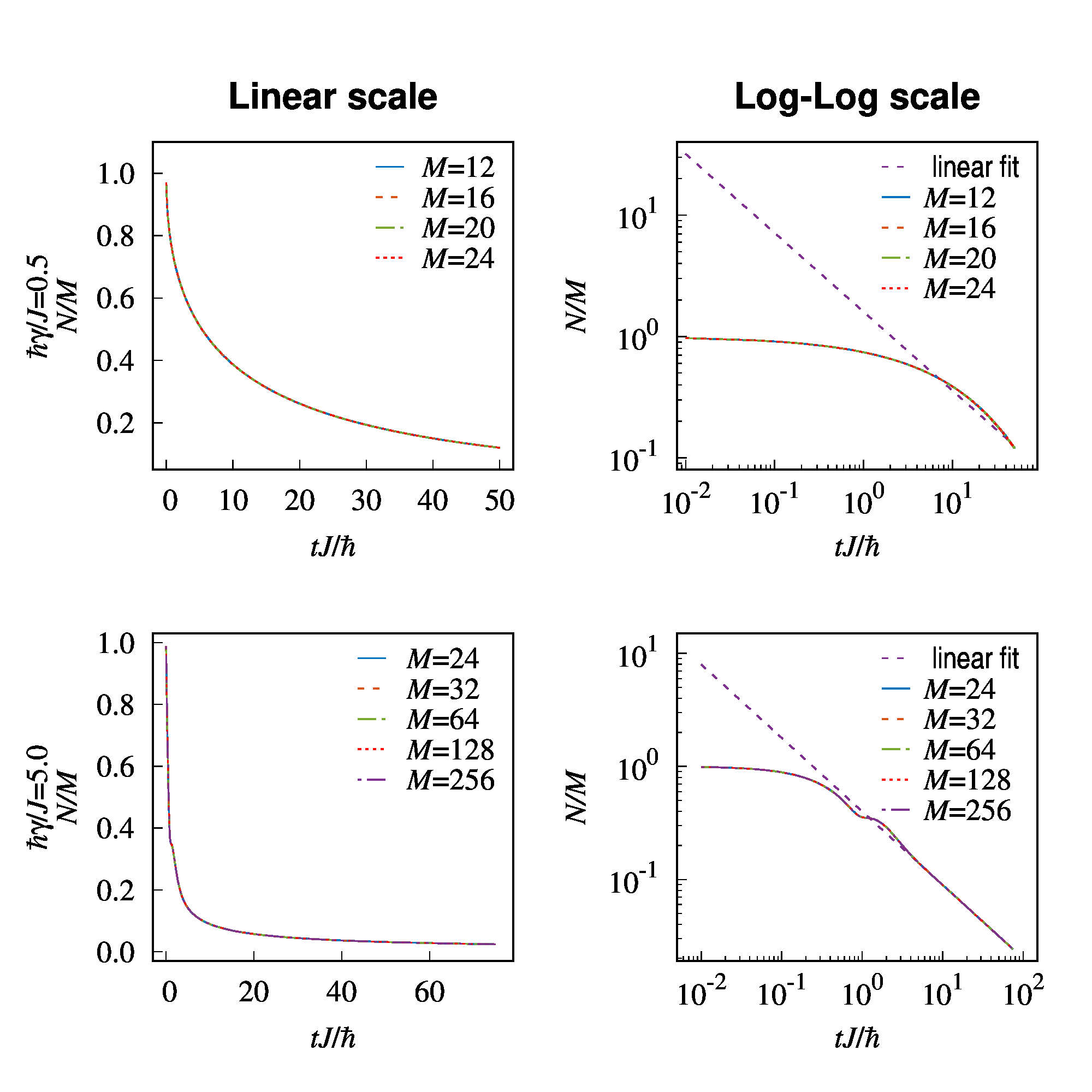
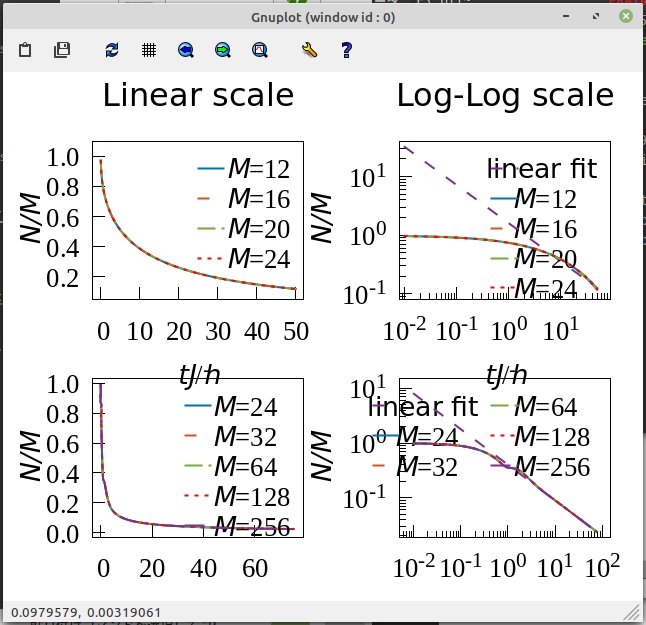
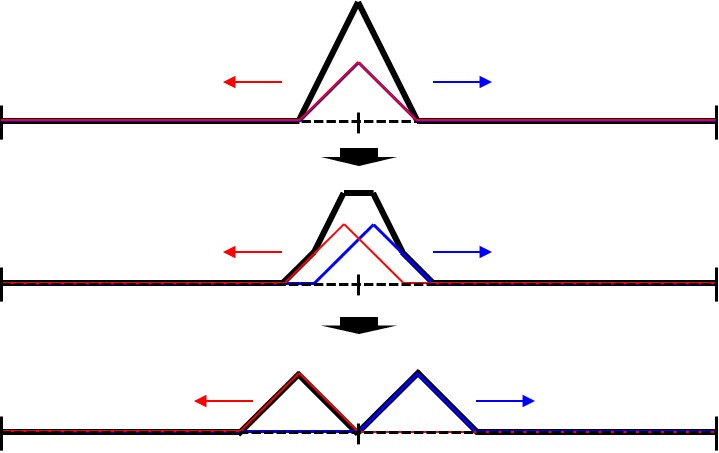
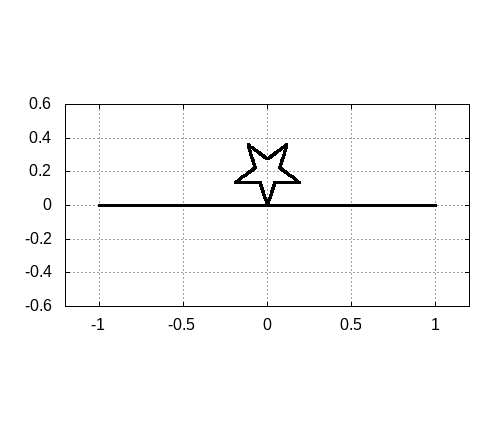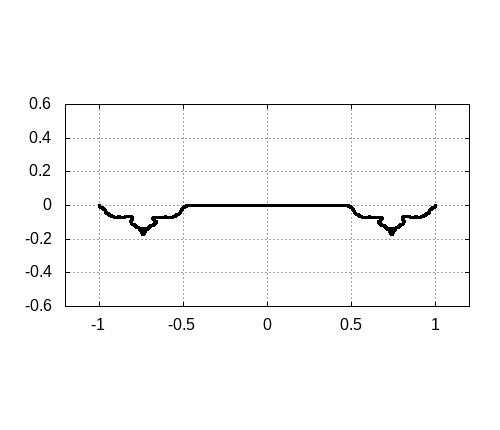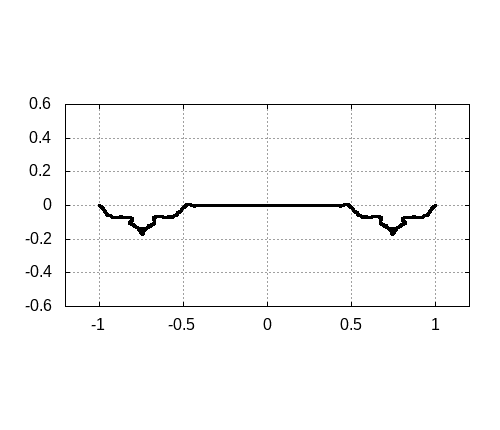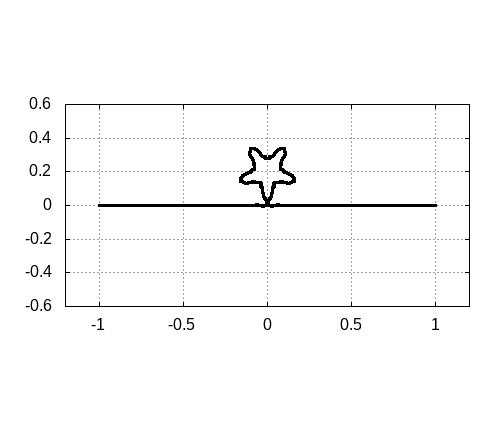
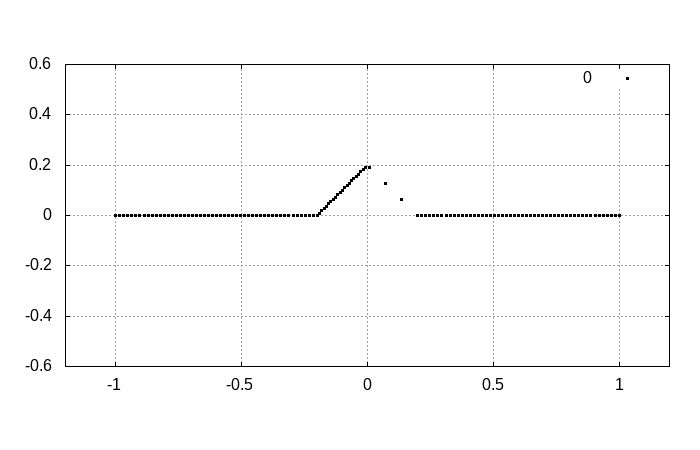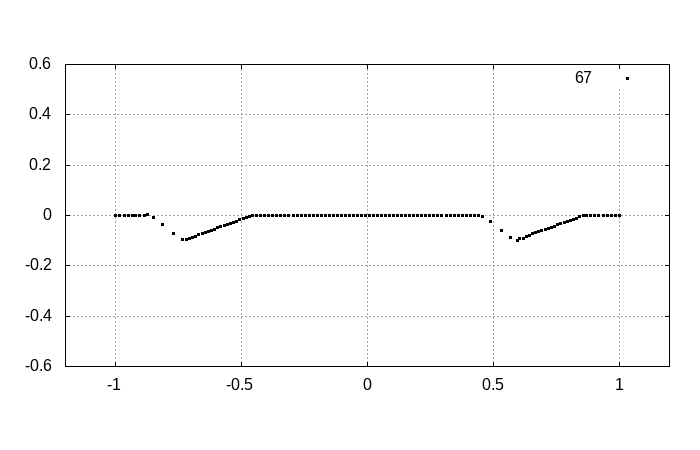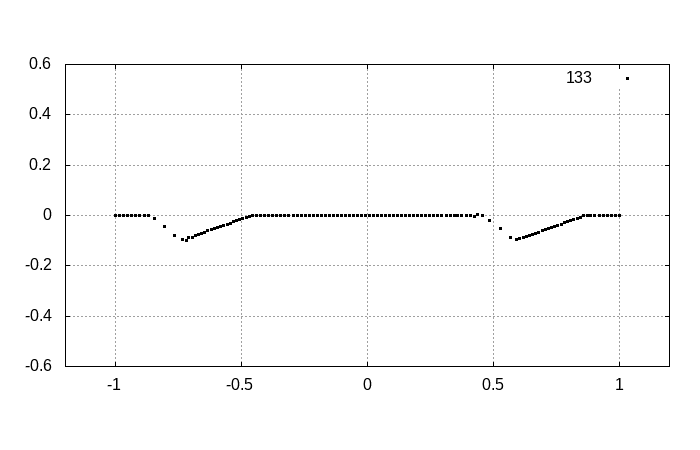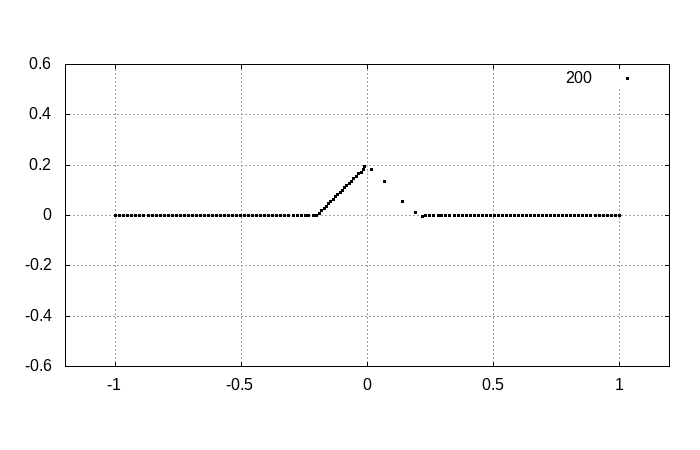
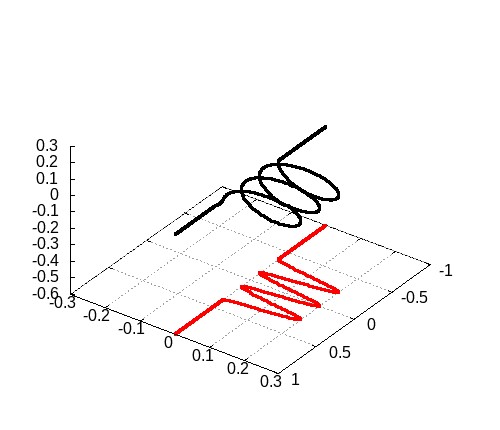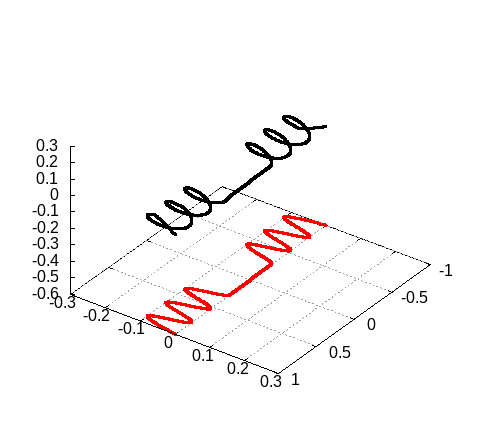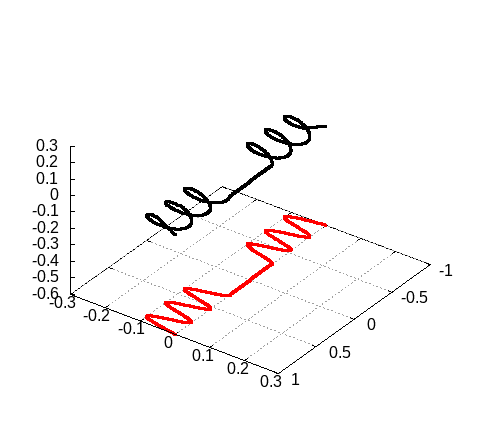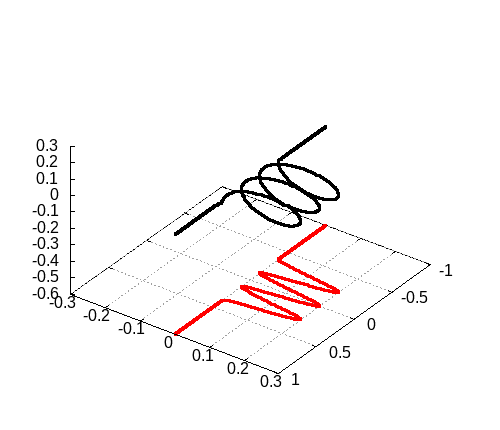
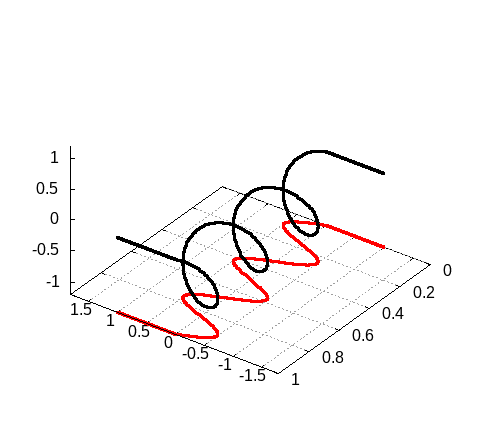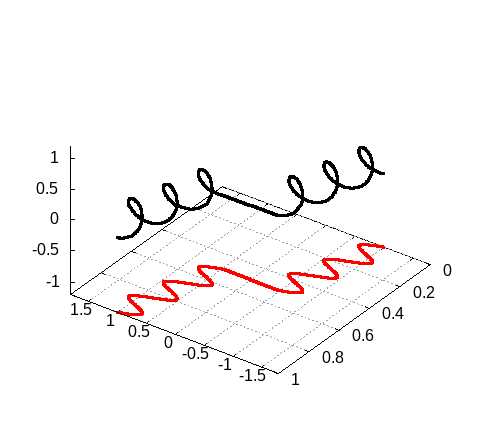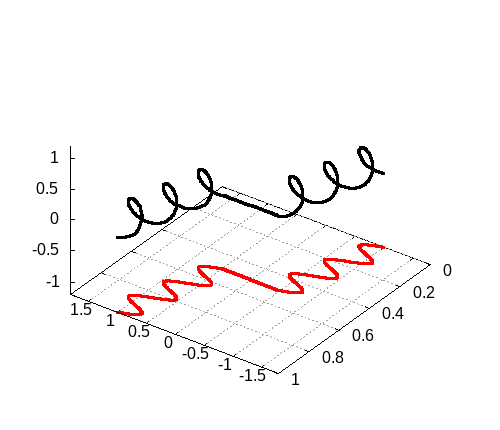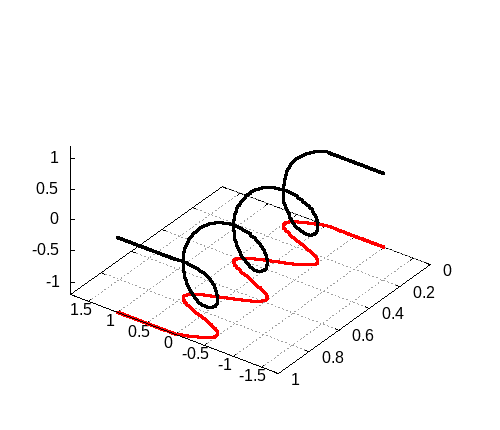
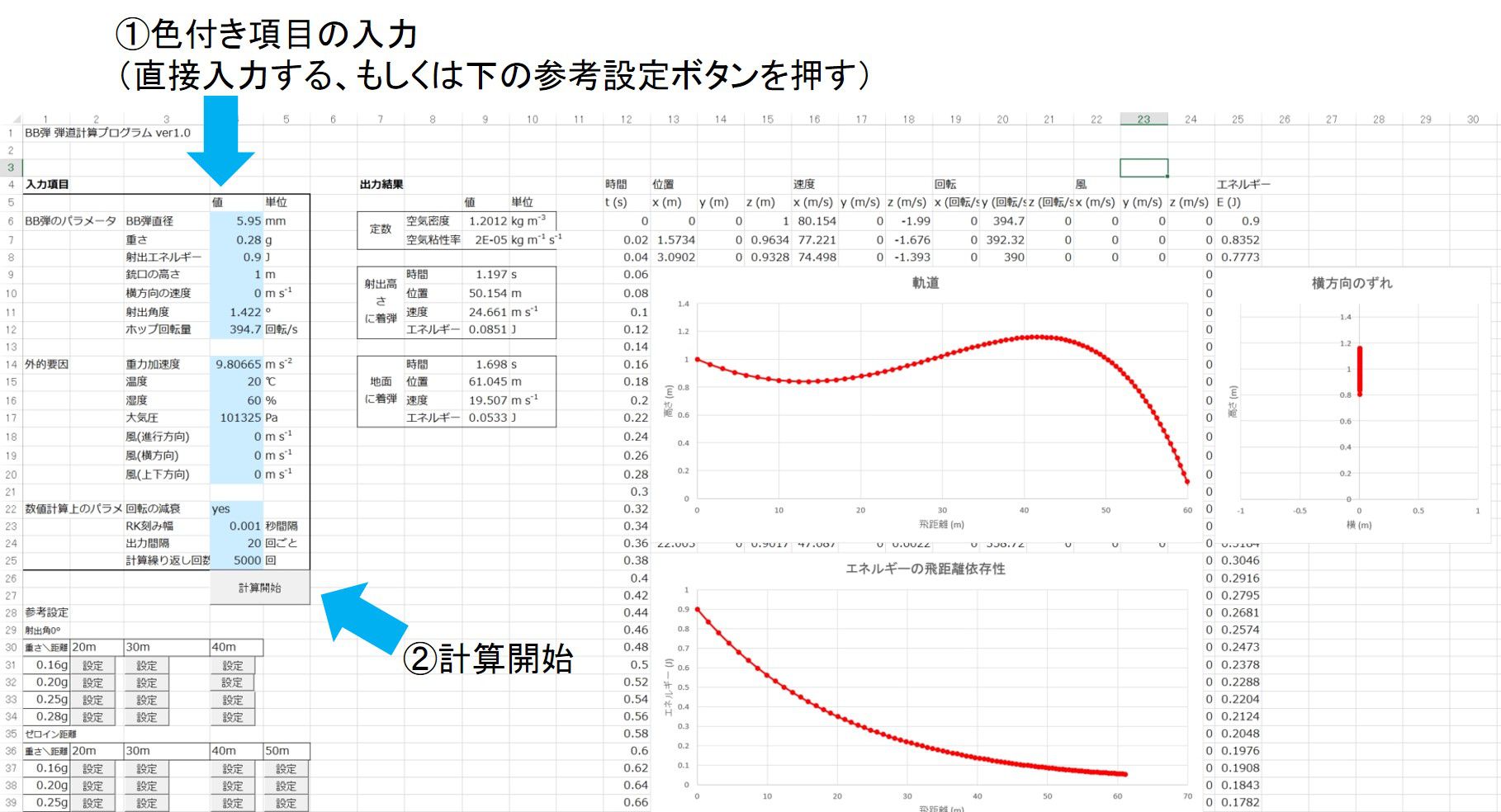
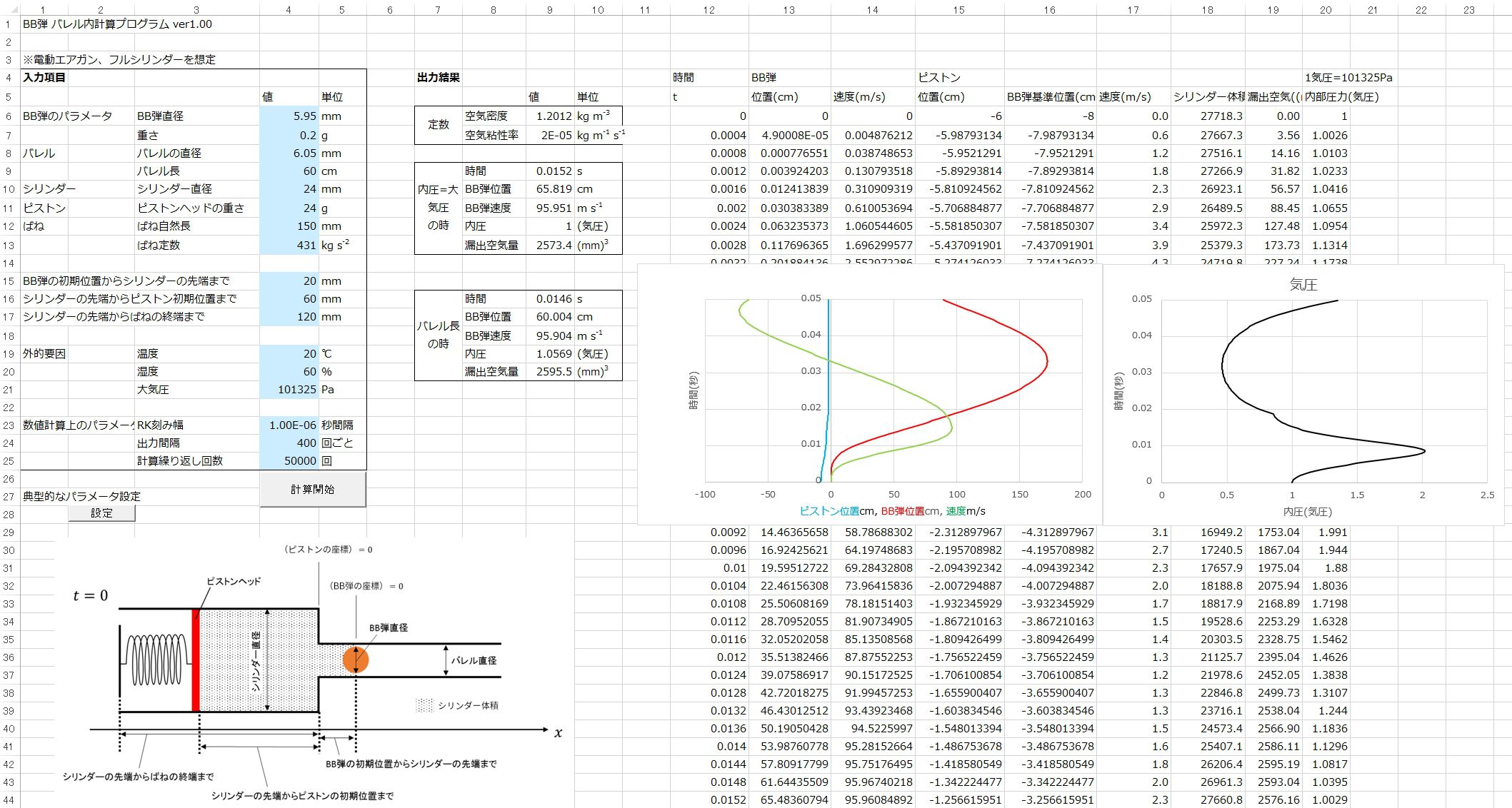
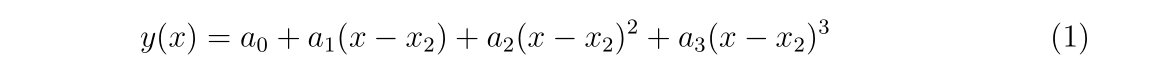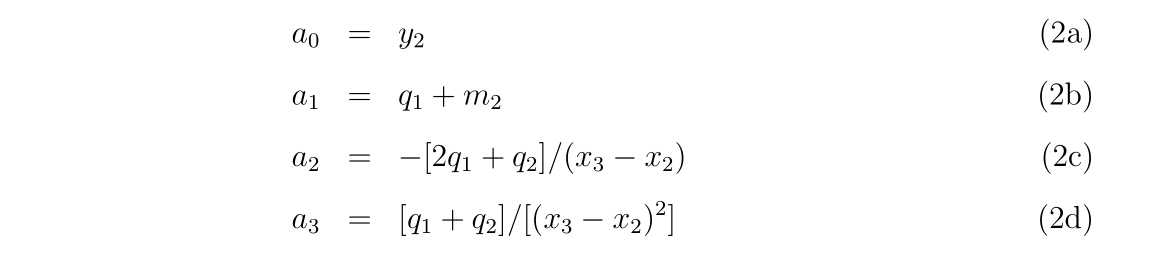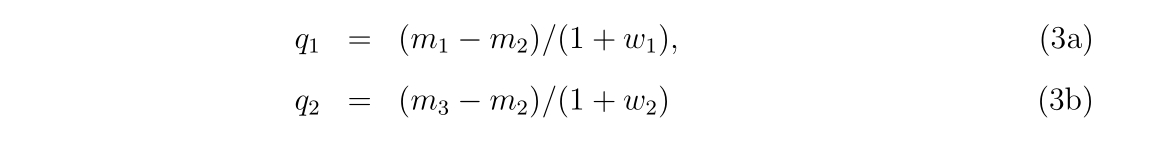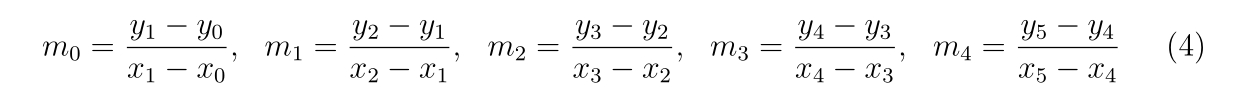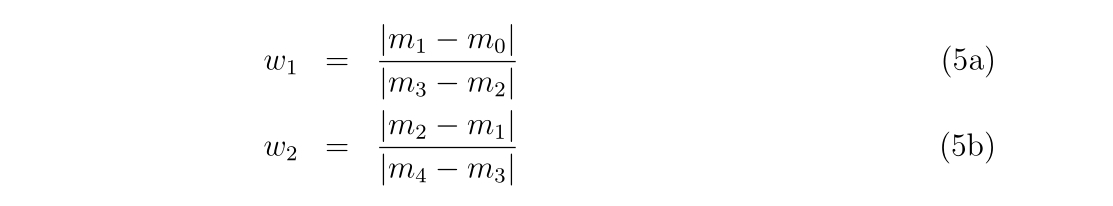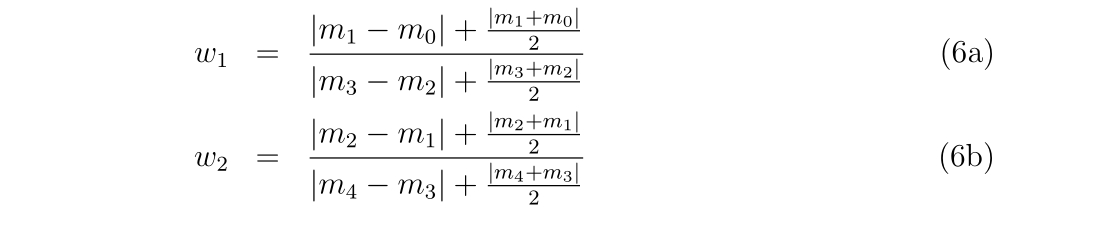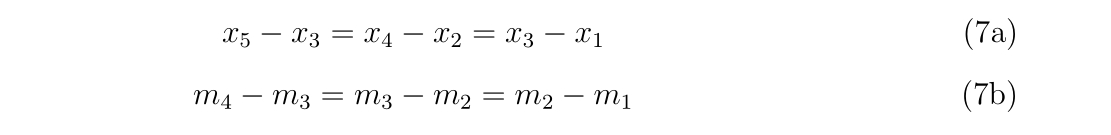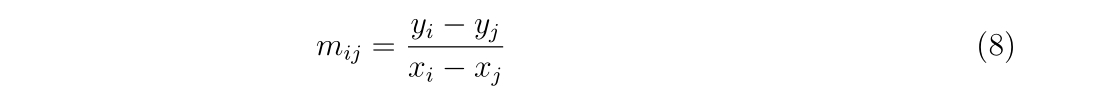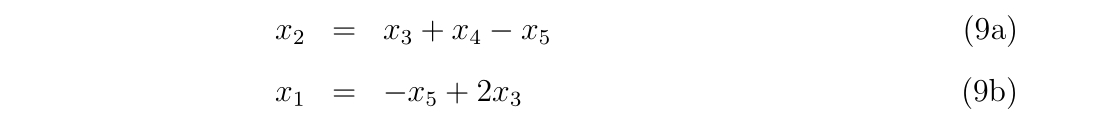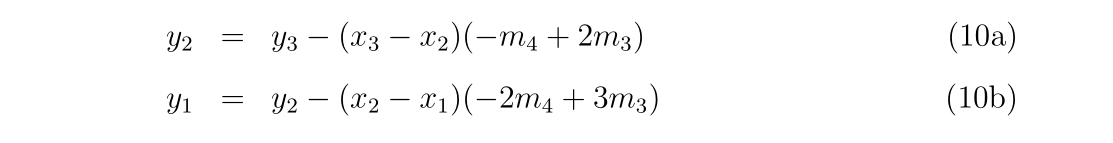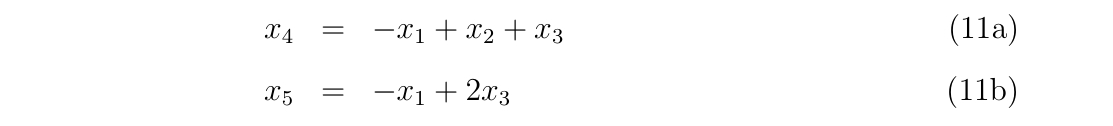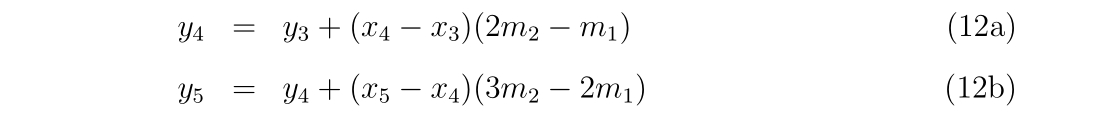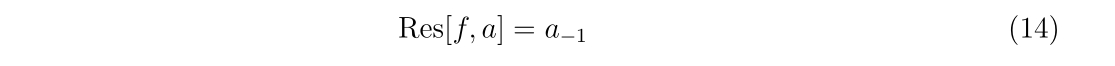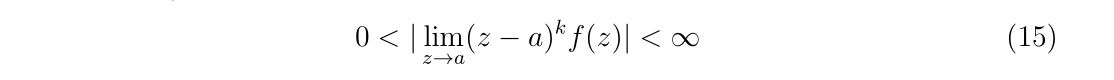program main
implicit none
integer::i,N,M
double precision::x,f,df,ddf
double precision,allocatable::xdata(:),fdata(:)
double precision::a,b
N=7 ! Data points (from 0 to N) for interpolation
M=300 ! Interpolation result index
a=0d0 ! Interpolation result range x=[a,b]
b=7d0 !
!----------
allocate(xdata(0:N),fdata(0:N))
xdata=0d0
fdata=0d0
! x Data for interpolation
xdata(0)=1d0
xdata(1)=2d0
xdata(2)=2.8d0
xdata(3)=3d0
xdata(4)=3.2d0
xdata(5)=4d0
xdata(6)=5d0
xdata(7)=6d0
! y Data for interpolation
fdata(0)=-1d0
fdata(1)=-1d0
fdata(2)=-1d0
fdata(3)=0d0
fdata(4)=1d0
fdata(5)=1d0
fdata(6)=1d0
fdata(7)=1d0
do i=0,N
write(10,*)xdata(i),fdata(i)
enddo
! Interpolation at given points
do i=0,M
x=dble(i)*(b-a)/M + a
! Akima interpolation
call akima1p(f,df,ddf,x,N,fdata,xdata)
write(11,*)x,f,df,ddf
! Modified Akima interpolation
call makima1p(f,df,ddf,x,N,fdata,xdata)
write(12,*)x,f,df,ddf
enddo
stop
end program main
subroutine akima1p(f,df,ddf,x,N,fdata,xdata)
implicit none
integer,intent(in)::N
double precision,intent(in)::x,fdata(0:N),xdata(0:N)
double precision,intent(out)::f,df,ddf
! Akima-Spline interpolation
! Akima H.,
! A New Method of Interpolation and Smooth Curve Fitting Based on Local Procedures.
! Journal of the ACM, 17(4), 589–602 (1970)
integer::i
double precision::t
double precision::a0,a1,a2,a3
double precision::x1,x2,x4,x5
double precision::xx0,xx1,xx2,xx3,xx4,xx5
double precision::yy0,yy1,yy2,yy3,yy4,yy5
double precision::d54,d43,d32,d21
double precision::y1,y2,y4,y5
x1 = -xdata(2) + 2d0*xdata(0)
x2 = xdata(1)- xdata(2) + xdata(0)
d54 = (fdata(2)-fdata(1))/(xdata(2)-xdata(1))
d43 = (fdata(1)-fdata(0))/(xdata(1)-xdata(0))
y2 = fdata(0) - (xdata(0)-x2) * (-d54 + 2d0*d43)
y1 = y2 - (x2-x1) * (-2d0*d54 + 3d0*d43)
x4 = -xdata(N-2) + xdata(N-1) + xdata(N)
x5 = -xdata(N-2) + 2*xdata(N)
d32 = (fdata(N)-fdata(N-1))/(xdata(N)-xdata(N-1))
d21 = (fdata(N-1)-fdata(N-2))/(xdata(N-1)-xdata(N-2))
y4 = fdata(N) + (x4-xdata(N)) * (2d0*d32 - d21)
y5 = y4 + (x5-x4) * (3d0*d32 - 2d0*d21)
t=x
if(x.le.xdata(1))then
t=x-xdata(0)
xx0=x1
xx1=x2
xx2=xdata(0)
xx3=xdata(1)
xx4=xdata(2)
xx5=xdata(3)
yy0=y1
yy1=y2
yy2=fdata(0)
yy3=fdata(1)
yy4=fdata(2)
yy5=fdata(3)
elseif(x.le.xdata(2))then
t=x-xdata(1)
xx0=x2
xx1=xdata(0)
xx2=xdata(1)
xx3=xdata(2)
xx4=xdata(3)
xx5=xdata(4)
yy0=y2
yy1=fdata(0)
yy2=fdata(1)
yy3=fdata(2)
yy4=fdata(3)
yy5=fdata(4)
elseif(x.ge.xdata(N-1))then
t=x-xdata(N-1)
xx0=xdata(N-3)
xx1=xdata(N-2)
xx2=xdata(N-1)
xx3=xdata(N)
xx4=x4
xx5=x5
yy0=fdata(N-3)
yy1=fdata(N-2)
yy2=fdata(N-1)
yy3=fdata(N)
yy4=y4
yy5=y5
elseif(x.ge.xdata(N-2))then
t=x-xdata(N-2)
xx0=xdata(N-4)
xx1=xdata(N-3)
xx2=xdata(N-2)
xx3=xdata(N-1)
xx4=xdata(N)
xx5=x4
yy0=fdata(N-4)
yy1=fdata(N-3)
yy2=fdata(N-2)
yy3=fdata(N-1)
yy4=fdata(N)
yy5=y4
else
do i=2,N-3
if(x.ge.xdata(i).and.x.le.xdata(i+1))then
t=x-xdata(i)
xx0=xdata(i-2)
xx1=xdata(i-1)
xx2=xdata(i)
xx3=xdata(i+1)
xx4=xdata(i+2)
xx5=xdata(i+3)
yy0=fdata(i-2)
yy1=fdata(i-1)
yy2=fdata(i)
yy3=fdata(i+1)
yy4=fdata(i+2)
yy5=fdata(i+3)
exit
endif
enddo
endif
call ms(a0,a1,a2,a3,xx0,xx1,xx2,xx3,xx4,xx5,yy0,yy1,yy2,yy3,yy4,yy5)
f=((a3*t+a2)*t+a1)*t+a0
df=3d0*a3*t**2+2d0*a2*t+a1
ddf=6d0*a3*t+2d0*a2
return
end subroutine akima1p
subroutine ms(a0,a1,a2,a3,x0,x1,x2,x3,x4,x5,y0,y1,y2,y3,y4,y5)
implicit none
double precision,intent(in)::x0,x1,x2,x3,x4,x5
double precision,intent(in)::y0,y1,y2,y3,y4,y5
double precision,intent(out)::a0,a1,a2,a3
double precision::m0,m1,m2,m3,m4
double precision::yp1,q1,q2,w
double precision::numer,denom
m0 = (y1-y0) / (x1-x0)
m1 = (y2-y1) / (x2-x1)
m2 = (y3-y2) / (x3-x2)
m3 = (y4-y3) / (x4-x3)
m4 = (y5-y4) / (x5-x4)
numer = abs(m1-m0)
denom = abs(m3-m2)
if(denom.eq.numer)then
q1 = 0.5d0*(m1-m2)
yp1 = 0.5d0*(m1+m2)
elseif(denom.eq.0.and.numer.ne.0)then
q1 = 0d0
yp1 = m2
else
w = numer/denom
q1 = (m1-m2)/(1d0+w)
yp1 = q1+m2
endif
numer = abs(m4-m3)
denom = abs(m2-m1)
if(denom.eq.numer)then
q2 = 0.5d0*(m3-m2)
elseif(denom.eq.0.and.numer.ne.0)then
q2 = 0d0
else
w = numer/denom
q2 = (m3-m2)/(1d0+w)
endif
a0 = y2
a1 = yp1
a2 = -(2d0*q1+q2)/(x3-x2)
a3 = (q1+q2)/((x3-x2)**2)
return
end subroutine ms
subroutine makima1p(f,df,ddf,x,N,fdata,xdata)
implicit none
integer,intent(in)::N
double precision,intent(in)::x,fdata(0:N),xdata(0:N)
double precision,intent(out)::f,df,ddf
! Modified Akima-Spline interpolation
! Akima H.,
! A New Method of Interpolation and Smooth Curve Fitting Based on Local Procedures.
! Journal of the ACM, 17(4), 589–602 (1970)
integer::i
double precision::t
double precision::a0,a1,a2,a3
double precision::x1,x2,x4,x5
double precision::xx0,xx1,xx2,xx3,xx4,xx5
double precision::yy0,yy1,yy2,yy3,yy4,yy5
double precision::d54,d43,d32,d21
double precision::y1,y2,y4,y5
x1 = -xdata(2) + 2d0*xdata(0)
x2 = xdata(1)- xdata(2) + xdata(0)
d54 = (fdata(2)-fdata(1))/(xdata(2)-xdata(1))
d43 = (fdata(1)-fdata(0))/(xdata(1)-xdata(0))
y2 = fdata(0) - (xdata(0)-x2) * (-d54 + 2d0*d43)
y1 = y2 - (x2-x1) * (-2d0*d54 + 3d0*d43)
x4 = -xdata(N-2) + xdata(N-1) + xdata(N)
x5 = -xdata(N-2) + 2*xdata(N)
d32 = (fdata(N)-fdata(N-1))/(xdata(N)-xdata(N-1))
d21 = (fdata(N-1)-fdata(N-2))/(xdata(N-1)-xdata(N-2))
y4 = fdata(N) + (x4-xdata(N)) * (2d0*d32 - d21)
y5 = y4 + (x5-x4) * (3d0*d32 - 2d0*d21)
t=x
if(x.le.xdata(1))then
t=x-xdata(0)
xx0=x1
xx1=x2
xx2=xdata(0)
xx3=xdata(1)
xx4=xdata(2)
xx5=xdata(3)
yy0=y1
yy1=y2
yy2=fdata(0)
yy3=fdata(1)
yy4=fdata(2)
yy5=fdata(3)
elseif(x.le.xdata(2))then
t=x-xdata(1)
xx0=x2
xx1=xdata(0)
xx2=xdata(1)
xx3=xdata(2)
xx4=xdata(3)
xx5=xdata(4)
yy0=y2
yy1=fdata(0)
yy2=fdata(1)
yy3=fdata(2)
yy4=fdata(3)
yy5=fdata(4)
elseif(x.ge.xdata(N-1))then
t=x-xdata(N-1)
xx0=xdata(N-3)
xx1=xdata(N-2)
xx2=xdata(N-1)
xx3=xdata(N)
xx4=x4
xx5=x5
yy0=fdata(N-3)
yy1=fdata(N-2)
yy2=fdata(N-1)
yy3=fdata(N)
yy4=y4
yy5=y5
elseif(x.ge.xdata(N-2))then
t=x-xdata(N-2)
xx0=xdata(N-4)
xx1=xdata(N-3)
xx2=xdata(N-2)
xx3=xdata(N-1)
xx4=xdata(N)
xx5=x4
yy0=fdata(N-4)
yy1=fdata(N-3)
yy2=fdata(N-2)
yy3=fdata(N-1)
yy4=fdata(N)
yy5=y4
else
do i=2,N-3
if(x.ge.xdata(i).and.x.le.xdata(i+1))then
t=x-xdata(i)
xx0=xdata(i-2)
xx1=xdata(i-1)
xx2=xdata(i)
xx3=xdata(i+1)
xx4=xdata(i+2)
xx5=xdata(i+3)
yy0=fdata(i-2)
yy1=fdata(i-1)
yy2=fdata(i)
yy3=fdata(i+1)
yy4=fdata(i+2)
yy5=fdata(i+3)
exit
endif
enddo
endif
call mms(a0,a1,a2,a3,xx0,xx1,xx2,xx3,xx4,xx5,yy0,yy1,yy2,yy3,yy4,yy5)
f=((a3*t+a2)*t+a1)*t+a0
df=3d0*a3*t**2+2d0*a2*t+a1
ddf=6d0*a3*t+2d0*a2
return
end subroutine makima1p
subroutine mms(a0,a1,a2,a3,x0,x1,x2,x3,x4,x5,y0,y1,y2,y3,y4,y5)
implicit none
double precision,intent(in)::x0,x1,x2,x3,x4,x5
double precision,intent(in)::y0,y1,y2,y3,y4,y5
double precision,intent(out)::a0,a1,a2,a3
double precision::m0,m1,m2,m3,m4
double precision::yp1,q1,q2,w
double precision::numer,denom
m0 = (y1-y0) / (x1-x0)
m1 = (y2-y1) / (x2-x1)
m2 = (y3-y2) / (x3-x2)
m3 = (y4-y3) / (x4-x3)
m4 = (y5-y4) / (x5-x4)
numer = abs(m1-m0)+0.5d0*abs(m1+m0)
denom = abs(m3-m2)+0.5d0*abs(m3+m2)
if(denom.eq.numer)then
q1 = 0.5d0*(m1-m2)
yp1 = 0.5d0*(m1+m2)
elseif(denom.eq.0.and.numer.ne.0)then
q1 = 0d0
yp1 = m2
else
w = numer/denom
q1 = (m1-m2)/(1d0+w)
yp1 = q1+m2
endif
numer = abs(m4-m3)+0.5d0*abs(m4+m3)
denom = abs(m2-m1)+0.5d0*abs(m2+m1)
if(denom.eq.numer)then
q2 = 0.5d0*(m3-m2)
elseif(denom.eq.0.and.numer.ne.0)then
q2 = 0d0
else
w = numer/denom
q2 = (m3-m2)/(1d0+w)
endif
a0 = y2
a1 = yp1
a2 = -(2d0*q1+q2)/(x3-x2)
a3 = (q1+q2)/((x3-x2)**2)
return
end subroutine mms