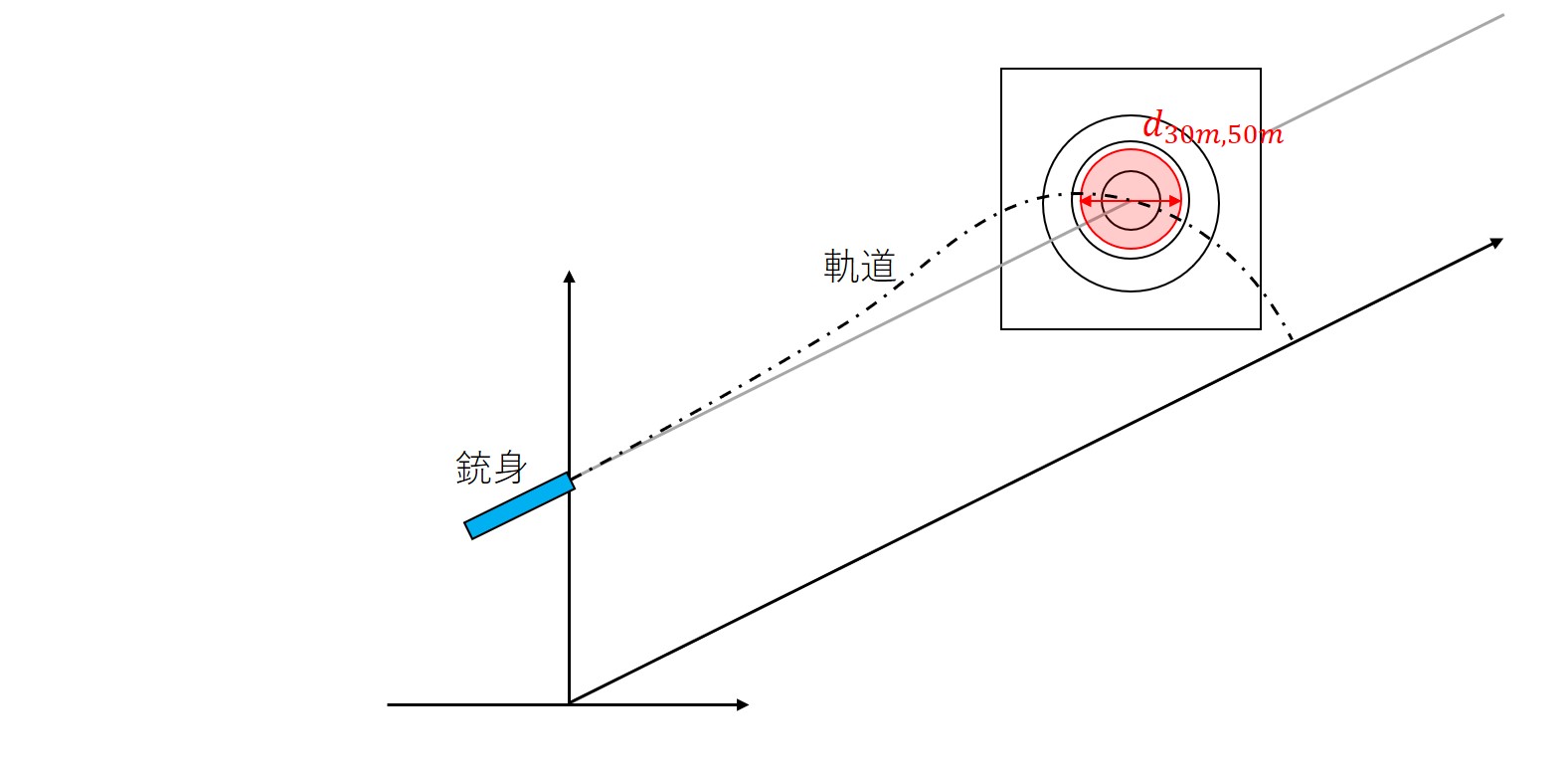
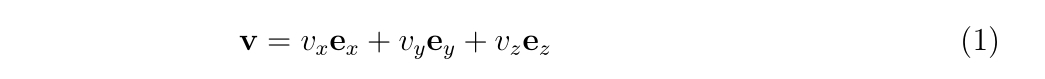理想的なエアガンとBB弾、それに風などが無い理想的な環境があったとします。
バレルとBB弾に直径差があることによって生じるばらつきは、
30m先 | 直径3cm
50m先 | 直径10cm
となります。この直径以下にばらつきを抑えることは構造的に不可能です(60cmのバレルで0.9Jで射出する場合)。
つまり、このばらつきよりも大きくばらつく場合、バレルとBB弾の直径差以外にばらつく原因が存在します。
バレルとBB弾に直径差があることによって生じるこのばらつきを軽減するには、
・バレルの直径を小さくする
・バレルを長くする
・バレル内部の素材とBB弾の反発が起こりにくいものにする
にすることで軽減されますが、他の要因が場合はこの限りではありません。
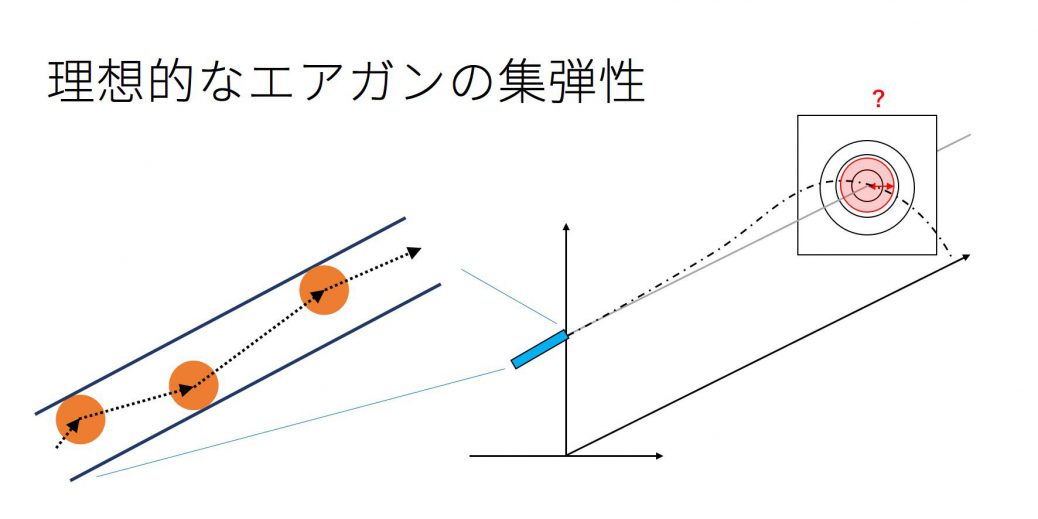
ここでの理想的とは、
・球の直径のばらつきは無い
・いつも同じ初速で撃ち出せる
・無風
とします。この場合でも同じ点に集弾することはありません。
なぜなら、バレルの直径とBB弾の直径が異なる為です。この差によってどの位集弾性が悪くなるのか、見積もりましょう。
これは構造的な問題であり、ばらつきの原因の中で取り除く事ができない1つの原因です。
ばらつく原因として、以下の三つが考えられますが、まず本稿では理想状態のばらつきを考えます。
| ばらつきの種類 | 理想状態のばらつき(本稿) | 製品誤差によるばらつき | セッティングによるばらつき |
|---|---|---|---|
| BB弾重さ | – | あり | なし |
| BB弾の大きさ | なし | あり | なし |
| 回転のばらつき | なし | なし | あり |
| 手振れ | なし | なし | あり |
ばらつきが生じる原因
何故ばらつきが生じるかを考えましょう。
全くの理想であれば、銃口から同じ初速、角度、回転量で射出されたBB弾にばらつきが生じることはありません。
しかし、現実にはバレルの大きさとBB弾の大きさに差があります。これによって銃口から射出する時に進行方向と垂直な平面に速度を持つことになります。
銃口から出てきたBB弾の速度\(\mathbf{v}\)を以下のように表現します。
ここで、\(v_{z}, \mathbf{e}_{z}\)はバレルの方向に沿う速度、単位ベクトルで、
\(v_{x,y}, \mathbf{e}_{x,y}\)はバレルの方向に垂直な面への速度、単位ベクトルです。
すなわち、壁面に垂直な方向に対する速度ベクトルの大きさ\(v_\perp\)は、\(v_\perp=\sqrt{v_x^2+v_y^2}\)と表されます。
ばらつきが無くまっすぐ飛ぶのであれば\(v_{\perp}=0\)であり、そうでなければ\(v_{\perp}\ne 0\)です。
BB弾のばらつきが生じる原因は、射出方向に垂直な方向(横方向)に有限の速度が生じている、と仮定します。
この横方向の速度が生じる原因の一つは、ピストンでBB弾を空気で押す際に圧力が一定ではないとか、回転を掛けるためのゴムで生じる、などいろいろ考えられます。
ここでは、パッキンを通過して、もうこれ以上横揺れを増やすような原因が生じないのだ、と仮定します。壁の反射によって変化はあるものの、速度は減衰する一方であるとします。
それでは、定式化をしていきましょう。
定式化
横方向の速度はそれほど大きくないだろう、と予想するので空気抵抗は考えません。この条件のもと考えていきます。
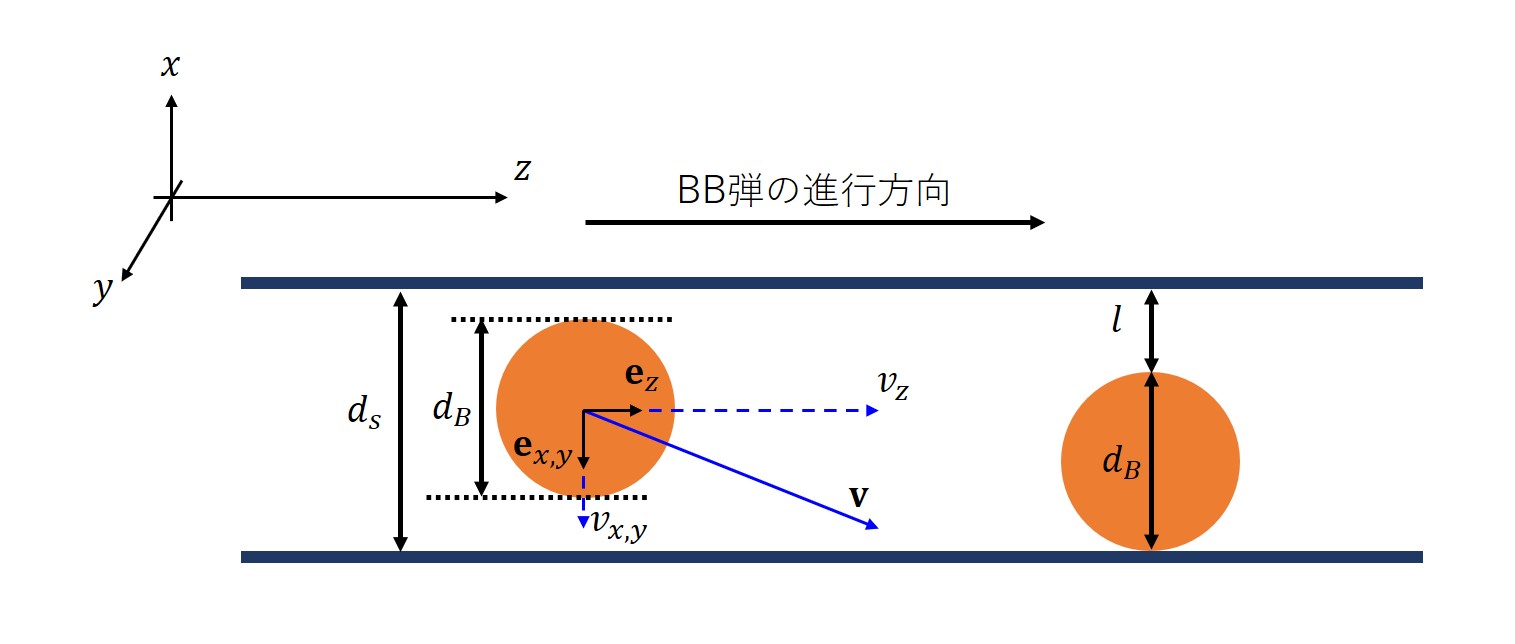
バレルの直径\(d_s\)とBB弾の直径\(d_B\)の差があることによって、バレルに垂直な方向にBB弾が自由に進める距離\(l\)は

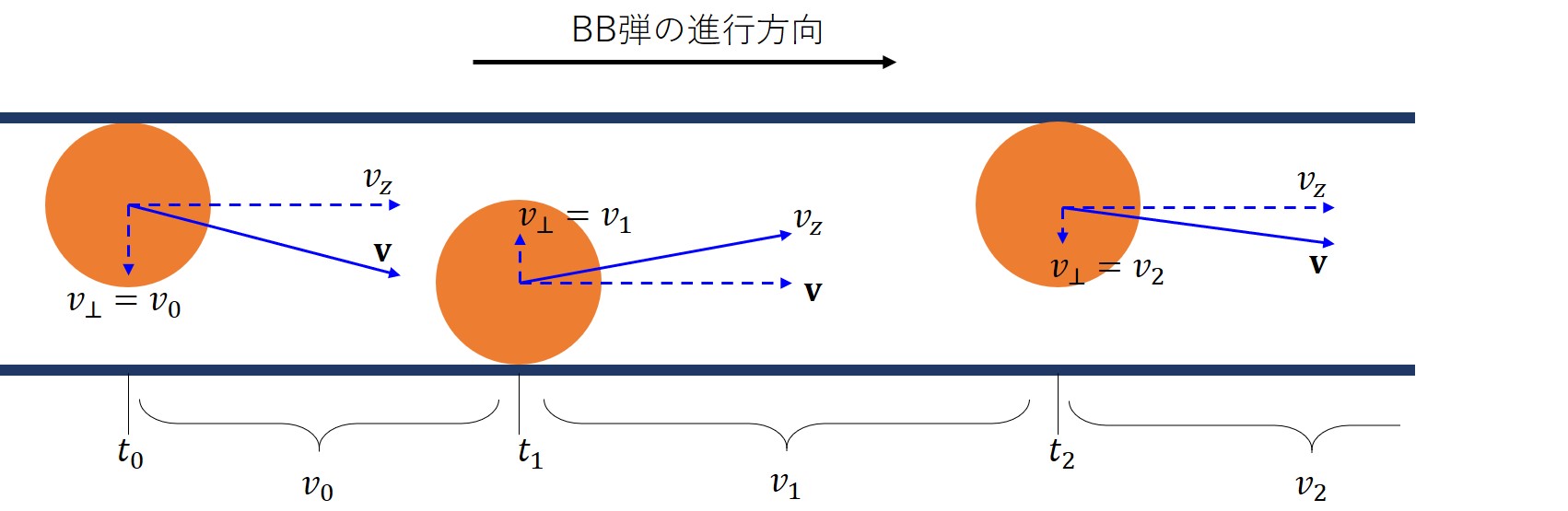
と書けます。\(n\)回目の衝突から\(n+1\)回目の衝突までにかかる時間\(t_n\)は、その間のBB弾の垂直方向の速度\(v_n\)に依存して、

と書けます。よって、\(N\)回衝突するのにかかる時間\(t\)はそれぞれの衝突までに掛かる時間を足し合わせればよいので、
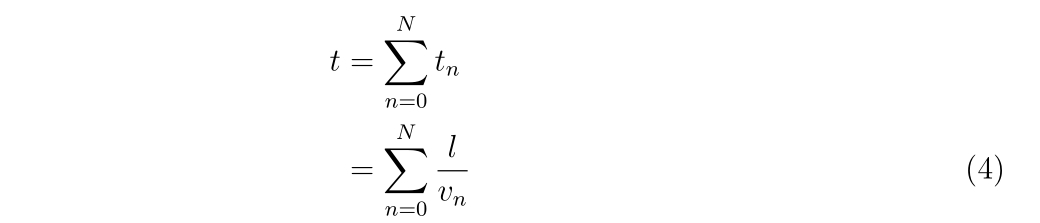
です。バレルの内壁との衝突が起こることによってBB弾の速度の変化するとします。するとBB弾とバレルとの反発係数\(r\)を用いれば、

と表現されます。初速度を\(v_0\)と書いてこれを代入すれば、
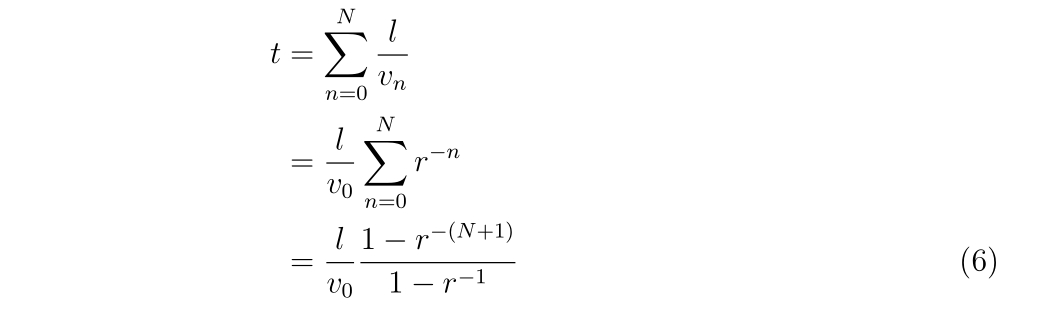
と書くことが出来ます。ただし、\(r\ne 1\)です。\(r=1\)の場合は\(\displaystyle
t=\frac{l}{v_0}(N+1)
\)
です。\(r\ne 1\)の場合に\(N\)について変形すれば、

と書くことが出来ます。
初速\(v_0\)、反発係数\(r\), 銃口に到達するまでに掛かる時間\(t\)が分かれば、銃口から出た時のバレルに垂直な方向の速度\(v_\perp\)は式(5b)より、
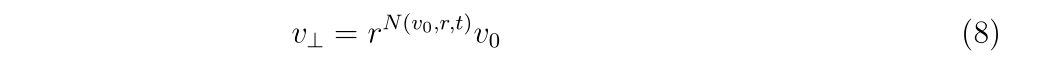
と書けます。具体的に妥当な値を入れて射出時の、進行方向に垂直な方向の速度を計算してみましょう。
具体的な衝突回数の見積もり
60cmのバレル長を持ち、0.20gで0.9J程度の球が射出される場合、セットされた位置から射出までにかかる時間は約\(t=0.015\mathrm{[s]}\)と分かっていますのでこれを利用します(バレル内部の計算より)。
バレルBB弾の直径差は
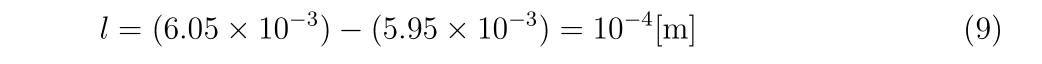
とします。\(r\)はどうにかして求めることにして、\(v_0\)はとりあえず変数としましょう。
反発係数の見積もり
\(r\)を見積もります。
反発係数の見積もりは、実験して大雑把な値を見積もります。
\(r\)を見積もるために、家にある固い材質のものとBB弾とを衝突させて、高さを計測しました。以下の実測結果を得ました。
- BB弾-フローリング 30cmから落として15cm上がる
- BB弾-アクリル板 30cmから落として10cm上がる
- BB弾-アルミ 10cmから落として6cmまで上がる
高さ\(h_0\)から静かに落として、反発した後に極大値をとるときの高さ\(h_1\)が分かっているとき、反発係数\(r\)は

と求められることが分かっているので、反発係数は
- BB弾-フローリング \(r\approx 0.71\)
- BB弾-アクリル板 \(r\approx 0.57\)
- BB弾-アルミ \(r\approx 0.77\)
となります。バレル内部はどちらかといえば金属に近いと思いますので、\(r\approx 0.75\)と仮定して計算を進めていきます。
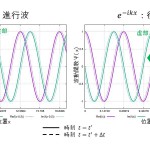
横軸に進行方向に垂直な方向の初速度…つまり、ホップを掛けるためのゴムなどで、進行方向ではない方向の速度のことを意味します…、縦軸に射出時の垂直な方向の速度をプロットしました。横方向の速度が仮に50m/sになっていても、10m/sになっていようともあまり変わらないことが分かります。なので、10m/sと仮定しましょう。
ばらつきの上限を与えるにはよい指標です(※1)。
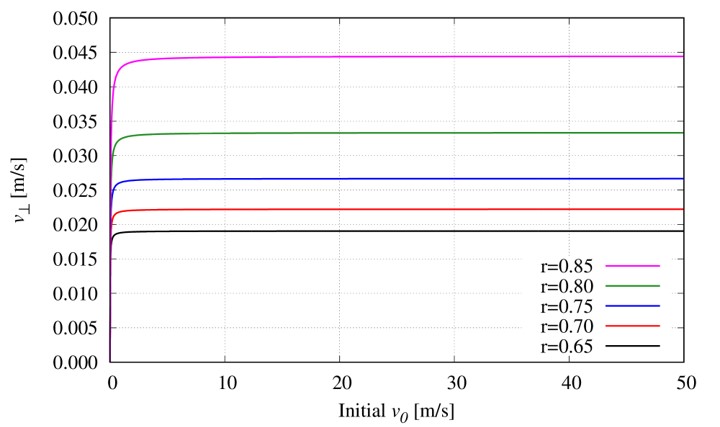
仮に\(r=0.75, v_0=10\mathrm{[m/s]}\)とすると、\(N\approx 20.6\)と計算されます。つまり、20.6回バレルに衝突してから飛び出していくわけです。実際には衝突回数は整数しかありえないので、小数点以下を切り捨てて20回衝突が起こって飛び出していきます。
ただし計算を行う上では衝突回数を切り捨てると不連続性が発生しますので、小数点の衝突回数を認めることにします。
この場合、銃口から飛び出す際の、進行方向に垂直な方向の速度\(v_\perp\)は
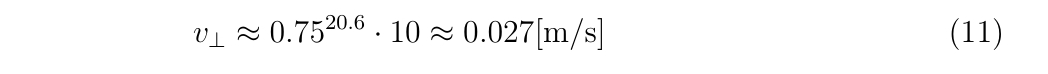
を得ます。この垂直方向の速度は上下左右に振れる可能性がありますが、最も触れる場合は横方向でしょう。
30, 50m先の広がり具合を考えます。
着弾までの時間\(t_{30m}, t_{50m}\)はそれぞれ\(0.5, 2 [s]\)分かっているので(弾道計算(BB弾)の結果)、着弾時の直径\(d_{30m}, d_{50m}\)は
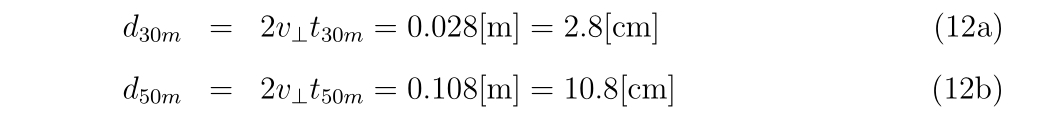
と求められます。ここで垂直方向の速度が非常に遅いので、空気抵抗は無視して考えています。BB弾の重さは関係ありません。軽いものほど空気抵抗を受けて減衰するので、ぶれは小さくなります。
実測定との比較
さて、30mチャレンジというものがあります30mチャレンジ公式ランキング 2016年度。
この記録によると、30m先で直径15cm程度の範囲に収まるようです。
すなわち、バレル-BB弾の直径差による集弾性の悪化よりも大きな影響を及ぼす要因がある、ということです。
恐らくは回転量が一定ではないとか、BB弾の重さにばらつきがあったり、銃身の振動があったりという要因のほうが大きいということでしょう。
逆に言えば、スタンダードな大きさのバレルとBB弾を用いる限り、30m先で3cm以内に収めることは不可能、ということです。
注釈
※1
\(v_0\to \infty\)で射出時の速度\(v_\perp\)は発散しますが対数の発散です。非常にゆっくり発散するため、\(v_0=10\)であろうが\(v_0=50\)であろうがほとんど変化しません。どこかでカットオフ(これ以上はとらない上限)となるような値を取れればよいかもしれません。
豆知識ですが、対数の発散をほとんど無視する目的としてカットオフを設けるやり方は、量子力学の繰り込み論が有名ですね。だからと言って、エアガンの計算で量子力学が現れる!などは言わないでください。全く関係ありません。