プログラミングと数値計算, ルンゲ=クッタ法

ルンゲ=クッタ法の説明と刻み幅制御

5件のコメント

ルンゲ=クッタ法(Runge-Kutta method、RK法)とは?
僕の知る限りの知識で紹介します。

特に良く使われる陽的ルンゲ=クッタ法は、
・実装が簡単
・良いアルゴリズムではない
という手法です。

良いアルゴリズムである陰的ルンゲ=クッタ法は、
陰的ルンゲ=クッタ法
をご覧ください。

もくじ

  1. ルンゲ=クッタ法の系統
  2. 陽的ルンゲ=クッタ法の段数と次数について
  3. 誤差について
  4. Butcher tableによるルンゲ=クッタ法の記述
  5. 埋め込まれた陽的ルンゲ=クッタ法
  6. ルンゲ=クッタ=フェールベルグ法による刻み幅の自動制御(適応刻み幅制御)
  7. ルンゲ=クッタ=フェールベルグ法による刻み幅の自動制御のプログラム(実数/複素数 で １/２ 階微分方程式を解くプログラム)
  8. 不連続な点を含む場合
  9. 刻み幅制御のベンチマーク(振り子)
  10. （追記）ルンゲ=クッタ=ドルマンド=プリンス法
  11. 陽的ルンゲ=クッタ法の導出
  12. 参考文献

理論はいいから4次ルンゲ=クッタ法の数値計算ではどうやるかだけ教えてくれ！という方は4次ルンゲ=クッタ法へどうぞ。

ルンゲ=クッタ法の系統

ルンゲ=クッタ法は微分方程式の数値計算解を得るための手法のことを指します。

通常の参考書で微分方程式を解くために良く紹介されているのは、オイラー法と中点法、４次ルンゲ=クッタ法でしょうか。
オイラー法も中点法も4次ルンゲ=クッタ法も、”陽的ルンゲクッタ法” と呼ばれる枠組みの1つです。

オイラー法は正確には “陽的1段1次ルンゲ=クッタ法” と呼ばれ、
中点法は “陽的2段2次ルンゲ=クッタ法”、
4次ルンゲクッタ法(RK4)は、”陽的4段4次ルンゲ=クッタ法” と呼ばれています。

“段”と”次”とはなんなんでしょう？それは、
計算の大変さ(段)と、計算の正確さ(次)
です。”段“の値が小さければ小さいほど計算時間が少なくて済みますし、”次“の値が高ければ高いほど計算が正確です。

オイラー法は1という計算コストで正確さ1が得られますし、RK4は4という計算コストで正確さ4が得られます。

4次ルンゲ=クッタ法が使われる理由

理由は実装が簡単でそれなりの精度を持つから。です。

陽的ルンゲ=クッタ法において、pという計算コスト(p段)で、pより大きな正確さq(q次)を得ることはできません。
Derivation of Runge–Kutta methodsによれば、
\(q\)次の正確さ(q次のオーダー)を得たい場合、最低限必要な段数\(p_{\mbox{min}}(q)\)は

という関係にあります。

ここで注目するべきは4次の時までは計算コストに比例して計算精度が上がっていきます。
しかし、4次以上では、計算コストの増加と計算の正確さが見合わなくなっていきます。故に
計算効率が良いのは4次だろう、
と予想できます。
また、重要な理由として、4次ルンゲ=クッタ法に現れる係数が5次以降と比べて圧倒的にシンプルであることが挙げられます。4次では\(0,1/2,1/6\)程度の係数だけが使われ、プログラム作成時の入力ミスがほぼ生まれません。しかし、5次では\(28561/56430, -7200/2197\)といった係数が数多く出てきます。
これらの理由から,4次ルンゲ=クッタ法(RK4)が数値計算科学の世界でよく使われるのです。

陽的ルンゲ=クッタ法に限って言えばプログラムの実装が非常に簡単であることが挙げられます。陰的ルンゲ=クッタ法と呼ばれるアルゴリズムもあり、これは陽的ルンゲ=クッタよりも優れていますが、計算量が多くなり、若干複雑なアルゴリズムになります。陰的ルンゲ=クッタ法を詳しく知りたい方は陰的ルンゲ=クッタ法をご覧ください。

Q. オイラー法もものすごく細かい分点を取れば、その計算効率はRK4と同じなんじゃないの？
A. 刻み幅の乗数で効いてくるのでそうではありません。高次を使っても計算が信頼できるのであれば、大きなステップで進めるほうが早いです。例え、目標精度への計算時間が同じだとしても、計算機の有効桁数によって否定されてしまいます。
RK4で典型的にとられる時間ステップの間隔は、おおよそ\(10^{-2}\sim 10^{-4}\)程度であり、RK4のエラーのオーダーは\(O(h^5)\)です。
そして、科学計算で使う際の有効桁数は倍精度型で16桁です。
1ステップ当りの誤差は\(h\)の減少に伴い、解が\(h^4\)の早さで収束していく、と言えます。
だから16桁の計算では\(h=10^{-1}\to h=10^{-4}\)に変化させる時、誤差は\(O(h^5)=c 10^{-5}\to c 10^{-20}\)と変化します。
おおよそ\(c\approx 1\)と見積もれば、(有効桁数16桁を多少超えてしまいますが、)有効桁数いっぱいまで正しい値が出るであろうと期待できます。

これに対し、オイラー法で同じことをするには\(h\)を\(10^{-16}\)にしなくてはいけません。
\(t\)の値が\(10^{-16}\)変わった時に、桁落ちの問題を回避できるほど関数\(x\)の値に変化が生まれるか？
が問題になり、まぁそんな急激な変化は生まれないでしょう、と予想できます。これでは桁落ちの問題を回避するほどの変化は到底望めません。

よって計算の効率と有効桁数の限界から、RK4なのです。

また、あまりに高次の方法を使うとルンゲ現象に代表される不安定性といったことが起こるかもしれません。
高次は高精度という意味とイコールではないことに注意しましょう。この高次≠高精度については等間隔の分点における数値積分の時に書いたので気になる方はどうぞ。。

誤差について

4次ルンゲ=クッタ法の、1ステップ当りの誤差は\(h^5\)に比例,すなわち\(O(h^5)\)です。
しかし、通常は細かいルンゲ=クッタ法を何度も繰り返して計算します。
区間\([a,b]\)を刻み幅\(h\)の4次ルンゲ=クッタ法で\(N\)回のステップを繰り返し計算する場合、誤差は
\(
\displaystyle N\cdot O(h^5)=\frac{b-a}{h}\cdot O(h^5)=O(h^4)\)

となります。よって、\(N\)回繰り返すような計算では、オーダーが１つ落ちる事に注意しましょう。

[adsense1]

陽的ルンゲ=クッタ法の段数と次数について

さて、ここまで“段”は計算コスト、で“次”は計算の正確さ、という曖昧な表現でしたが、その表現をちゃんと知りましょう。
段と次を知るためにはルンゲ=クッタ法の計算方法を知る必要があります。
具体例を載せます。
\(
\displaystyle \frac{dx}{dt}=f(t,x)
\)
の、\(t_{n}\rightarrow t_{n}+h\ \ (=t_{n+1})\)における初期値問題に対する、
陽的1段1次ルンゲ=クッタ法(オイラー法)の計算スキームは、
\(
x_{n+1}=x_{n}+h\cdot f(t_{n},x_{n})
\)
です。

陽的4段4次ルンゲ=クッタ法(RK4)の計算スキームは、
\(
\begin{align}
k_1&=f(t_n, x_n) \\
k_2&=f(t_n+h/2, x_n+h k_1/2) \\
k_3&=f(t_n+h/2, x_n+h k_2/2) \\
k_4&=f(t_n+h, x_n+h k_3) \\
x_{n+1}&=x_{n}+{(k_1+2k_2+2k_3+k_4)}h/6
\end{align}
\)
として与えられます。

一般的に、陽的s段のルンゲ=クッタ法とは
\(
\begin{align}
g_i&=x_n+h\sum_{j=1}a_{i,j}k_j\ \ \ (j\lt i, \ i=1,2,…,s) \\
k_i&=f(t_n+c_ih, g_i) \\
x_{n+1}&=x_n+h\sum_{i=1}^s b_ik_i
\end{align}
\)
として書けます。
ここで行列形式で与えられる係数\(a_{i,j}, b_{i},c_{i}\)によって、そのs段ルンゲ=クッタ法が持つ次数が決められます。段数はここから由来します。

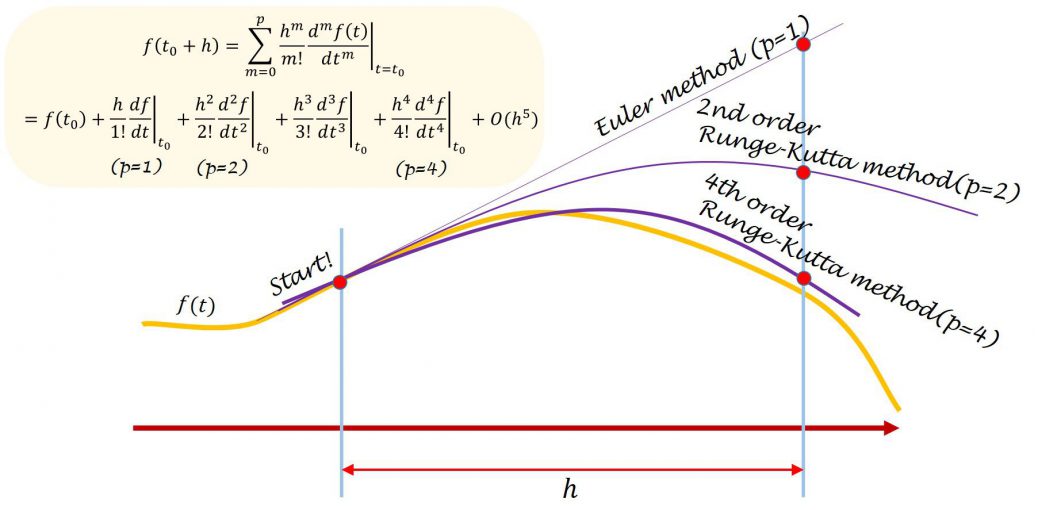
点\((t_n, x(t_n))\)周りで関数をテーラー展開し、その関数が点\((t_n+h\ \ (=t_{n+1}), x(t_{n+1}))\)で作る点を近似解とするのがルンゲ=クッタ法です。
故に、\(x(t_{n+1})\)は、
\(
\begin{align}
x(t_{n+1})=x(t_n)+\left.\frac{h}{1!}\frac{dx}{dt}\right|_{t=t_n}+\left.\frac{h^2}{2!}\frac{d^2x}{dt^2}\right|_{t=t_n}+\left.\frac{h^3}{3!}\frac{d^3x}{dt^3}\right|_{t=t_n}+\left.\frac{h^4}{4!}\frac{d^4x}{dt^4}\right|_{t=t_n}+…
\end{align}
\)
と書けます。
ここで、テイラー展開としてどの程度一致させて\(x(t_n+h)\)を決定するか？を表すのが次数に当たります。

言葉で書くなら、

局所的な精度は，高次項が解のテイラー(Taylor)展開とどの程度マッチしているかによって測定される．オイラー法は一次精度なので，誤差は一次高く\(h^2\)というベキ乗から始まる． ~NDSolveの”ExplicitRungeKutta”メソッドより

ともあります。

Butcher tableによるルンゲ=クッタ法の記述

行列形式で与えられるルンゲ=クッタ法での係数\(a_{i,j}, b_{i},c_{i}\)は何なのか？
具体的に記述してみましょう。
オイラー法(1段1次)はもっとも単純で、係数は
\(
\begin{align}
a_{1,1}&=0　\\
b_{1}&=1 \\
c_{1}&=0
\end{align}
\)
です。これを一般的な表記法の式に当てはめれば、
\(
\begin{align}
g_1&=x_n+h a_{1,1}k_1 \\
k_1&=f(t_n+c_1h, g_1) \\
x_{n+1}&=x_n+h b_1k_1
\end{align}
\)
となります。

中点法は、
\(
\begin{align}
a_{1,1}&=0 \\
a_{1,2}&=0 \\
a_{2,1}&=1/2 \\
a_{2,2}&=0 \\
b_{1}&=0 \\
b_{2}&=1 \\
c_{1}&=0 \\
c_{2}&=1/2
\end{align}
\)
という組で与えられます。

この係数行列の組はまとめてButcher tableと呼ばれる表記をするのが便利です。

これは、\(a_{i,j}, b_{i},c_{i}\)を
Buchertable
としてまとめて書く表記法です。

再び、オイラー法はButcher tableで書くと
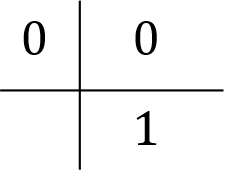
euler_butcher
とまとめて書くことができます。
中点法は
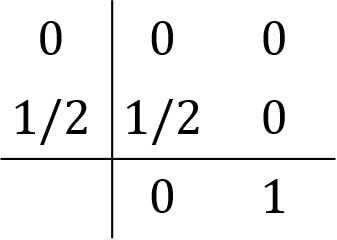
midpoint_butcher
RK4は
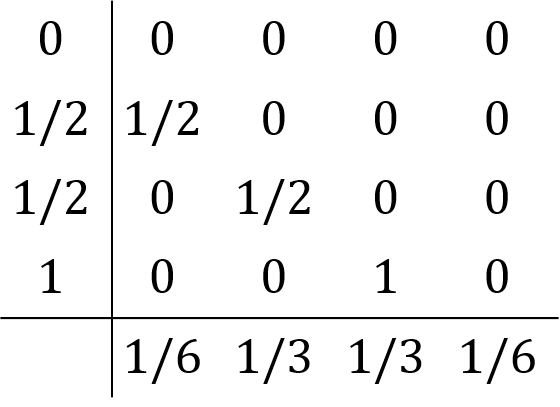
rk4_butcher
です。

高次のルンゲ=クッタ法(10,12,14次)

4次、5次…とずっとあるわけです。
こんなページがありました[3]。
High-Order Explicit Runge-Kutta Methods
この上のページには

  • 17段10次(8次が埋め込まれてる)
  • 25段12次(10次が埋め込まれてる)
  • 35段14次(12次が埋め込まれてる)

といったButcher tableにおける係数の値が書かれています。埋め込まれてる、の意味は次の節で説明します。
ただし、上のページのbutcher tableは
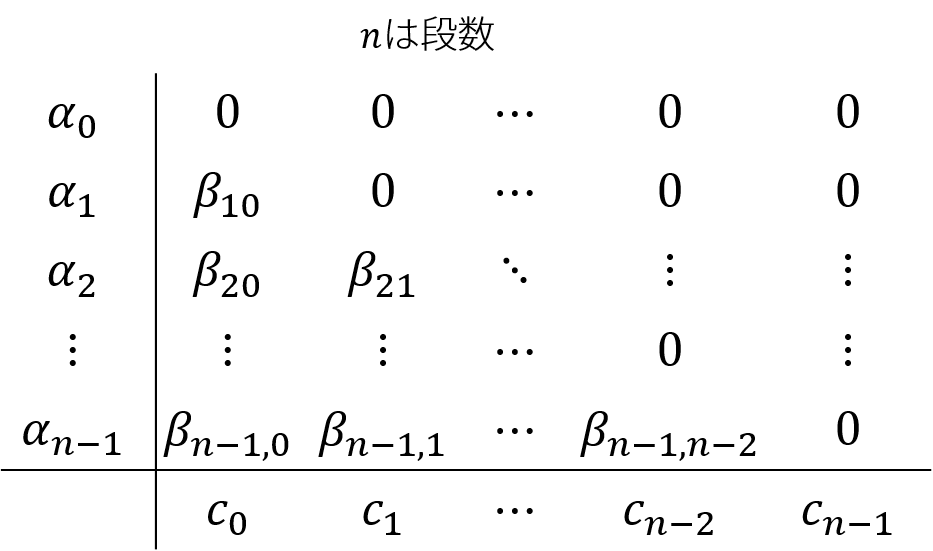
highorderbutcher2
となっているので注意が必要です。

埋め込まれた陽的ルンゲ=クッタ法

“埋め込まれた“という表現が出てきたのでその説明を行いましょう。
日本語では『埋め込まれた陽的ルンゲ=クッタ法』、英語では『embedded explicit runge-kutta method』と呼ばれるものがあります。
これは、p段q次陽的ルンゲ=クッタ法を作ったら、別の次数の陽的ルンゲ=クッタ法も、係数行列\(a_{i,j}, c_{i}\)を使って作れるじゃありませんか!
というものです。

Butcher tableは、この場合extended Butcher tableと呼ばれ、こういう形式で書かれます。
embedded_rk
この埋め込まれたルンゲ=クッタ法のいいところは、

  1. 計算誤差の評価ができる
  2. 刻み幅を自動的に制御できる、適応刻み幅制御。(応用として。)

という点です。ルンゲ=クッタ法によって得られた解が真の解とどのくらい違っているのか？が評価できるんです。

例えば、4次のルンゲ=クッタ法を使って得られた解\(x^{(4)}(t)\)と5次のルンゲ=クッタ法を使って得られた解\(x^{(5)}(t)\)があったとします。
もしも、\(x^{(4)}(t)\)と解\(x^{(5)}(t)\)の解の差を調べ、その差が無かったらその数値計算解は真の解に限りなく近い、と判断することができ、差が大きかったらその解は真の解から離れていて、数値計算の精度が足らない、と判断することができます。どちらも1つだけの解では出来なかったことです。

精度が足らない場合、刻み幅を小さくすれば精度が上がります。また逆に、精度が十分に足りている場合、刻み幅を大きくし、計算時間を減らすことができます。
これが適応刻み幅制御なのです。

違った次数のルンゲ=クッタ法を、まるで別々に計算してもいいのですが、そうすると計算時間が単純に考えておおよそ2倍になります。
解を評価するために2倍の計算時間が必要というのは良くない計算効率です。
そこで考えられたのが埋め込まれたルンゲ=クッタ法なのです。

具体例を挙げましょう。
一番簡単な埋め込まれたルンゲ=クッタ法は、ホイン法と呼ばれています。
butcher_heun
1行目は2次のオーダーを持ち、2行目は1次のオーダーを持ちます。

また、4次と5次を持つ埋め込まれたルンゲ=クッタ法は、ルンゲ=クッタ=フェールベルグ(Runge-Kutta-Fehlberg)法と呼ばれています。
その埋め込まれたルンゲ=クッタ法は、
butcher_rkf45
と書かれます。1行目は5次のオーダー、2行目は4次のオーダーを持ちます。

ルンゲ=クッタ=フェールベルグ法による刻み幅の自動制御(適応刻み幅制御)

さて、次数の違う2つのルンゲ=クッタ法を用いて、適応刻み幅制御を行いたいと考えます。
刻み幅を制御するにあたって、適当に精度良かったから2倍にしてもまだ大丈夫だろ、とか差が大きすぎるから刻み幅半分にしよう、ということをやってはいけません。
適当にやったら計算時間が余計にかかり、精度が良くない変な結果が得られます。

[5~9]によれば、ルンゲ=クッタ=フェールベルグ法において区間\(i\)での最適な刻み幅\(h’\)は区間\(i\)の誤差評価の結果を使って、
\(
\displaystyle h’=\delta h=\left(\frac{\varepsilon h}{2|x^{(5)}_{i}-x^{(4)}_{i}|}\right)^{1/4} h
\)
と予想できます。ここで\(\varepsilon\)はエラーを制御する精度の目安で、おおよそ計算時に要求する相対誤差です。もちろん、この\(h’\)は区間\(i\)の最適な幅ですが、関数に劇的な変化は無いだろうとして、次の区間の計算の一番初めに用いる刻み幅を推定するのです。
なので、\(i+1\)番目の計算区間では、計算するときはこの\(h’\)の値を使えばいいんです。
(ちなみに、m次ルンゲ=クッタ法の場合では
\(
\displaystyle h’=\delta h=\left(\frac{\varepsilon h}{2|x^{(m+1)}_{i}-x^{(m)}_{i}|}\right)^{1/m} h
\)
と推測されます。)

詳しい理由は分かりませんが、5次オーダーではなく、4次です。5次のオーダーは誤差評価のためだけに用いられているようです。
ルンゲ=クッタ=フェールベルグ法の計算スキームは[7]に詳しく書かれています。
日本語訳して、その計算スキームを書けば下のようになります。


ルンゲ=クッタ=フェールベルグ法による刻み幅の自動制御(プログラム)

講義のレポート等の宿題で使うのは僕の意向と異なるので使用はご控えください。
研究目的、趣味、確かめの場合はミスがあるかもしれないことを念頭に置いたうえならば使用と改変をご自由にしてください。
このプログラムを使用して生じた責任は取りません。

fortran90によるプログラムです。ほぼ上の説明をそのままプログラミングしたものです。

  • 実数、1階微分方程式の場合

    • 微分方程式
    \(
    \displaystyle \frac{d}{dx}y=y\cos x,~~y(x=0)=1
    \)
    を倍精度実数、刻み幅制御で\(x=10\)まで解く事を考えます。
    解析解は
    \(
    \displaystyle y(x)=exp(sin(x))
    \)
    です。コードは以下の通りです。

  • 実数、2階微分方程式の場合

    • 微分方程式
    \(
    \displaystyle \frac{d^2}{dx^2}y=-\frac{1}{4}y,~~y(x=0)=1,~ y'(x=0)=0
    \)
    を倍精度実数、刻み幅制御で\(x=20\)まで解く事を考えます。コードは以下の通りです。

    ※ここで使われているサブルーチンdrkf45は実数一階微分のプログラム内にあるルーチンと一字一句同一です。

  • 複素数、1階微分方程式の場合

    • 微分方程式
    \(
    \displaystyle \frac{d}{dx}y=y\cos x,~~ y(x=0)=1+i\frac{1}{2}
    \)
    を倍精度実数、刻み幅制御で\(x=10\)まで解く事を考えます。コードは以下の通りです。

  • 複素数、2階微分方程式

    • 微分方程式
    \(
    \displaystyle \frac{d^2}{dx^2}y=-\frac{1}{4}y,~~ y(x=0)=1+i\frac{1}{2},~y'(x=0)=0+i0
    \)
    を倍精度実数、刻み幅制御で\(x=20\)まで解く事を考えます。コードは以下の通りです。

    ※ここで使われているサブルーチンcrkf45は複素数一階微分のプログラム内にあるルーチンと一字一句同一です。

等間隔の出力の場合は、以下の通りで実行できます。
サブルーチンはdrkf45は変わっていません。

[adsense2]

不連続な点を含む場合

不連続な点を含む場合、境界条件を指定しないと解くことはできません。

さて、ここで微分方程式
\(
\begin{eqnarray}
\frac{dy}{dx}=
\left\{
\begin{aligned}
0\;\;(x\le 0)\\
1\;\;(0\lt x)
\end{aligned}
\right.
\end{eqnarray}
\)
を初期条件\(y(-0.095)=0\)の下で考えます(意図的に境界条件は考えません)。
これを4次ルンゲ=クッタと適応刻み幅ルンゲ=クッタで解いてみましょう。
プログラム上ではそのまま解くことが出来ます。
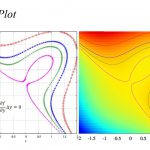
実際に解かせてみますと、
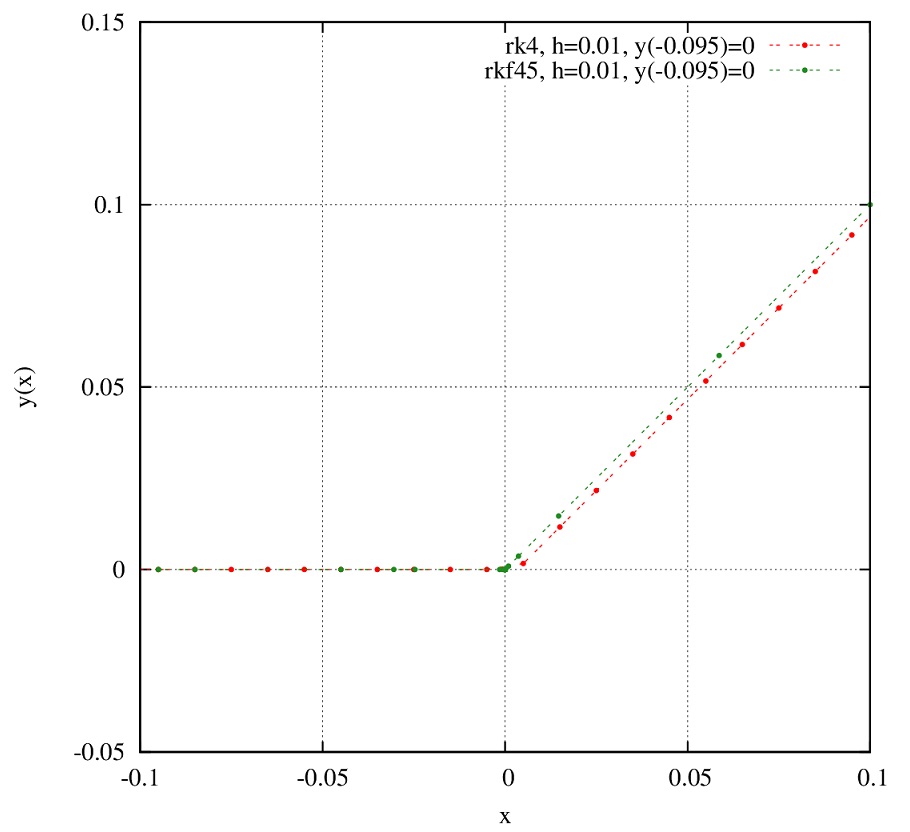
rk4_rkf451_disc
となり、2つの結果(赤：4次ルンゲ=クッタ、緑：刻み幅制御ルンゲ=クッタ)は異なってしまいます。これは1階微分の不連続性のため発生します。
不連続点\(x=0\)で関数\(y(x)\)に境界条件を指定しない限り、どちらも正しい解なのです。

さて、なぜこんなことが発生するのでしょうか？以下のように問題を表すことにします。

不連続な点を含む1階の微分方程式を考えます。
ここで不連続、という意味は関数\(y(x)\)の一階微分が、点\(x’\)で
\(
\displaystyle \left. \frac{dy}{dx}\right|^{x=x’+0}_{x=x’-0}=a,\;\;\;(a\ne 0)
\)
であるような点を指しているとします。

上記の例題を考えてみましょう。
上記の例題では\(a=1\)です。微分方程式を解析的に解いてみますと、
\(
\begin{eqnarray}
y(x)=
\left\{
\begin{aligned}
C_0\;\;(x\le 0)\\
x+C_1\;\;(0\lt x)
\end{aligned}
\right.
\end{eqnarray}
\)
となります。ここで\(C_0, C_1\)は定数です。
\(C_0, C_1\)は\(y(x)\)が解きたい問題の境界条件によって決まります。

例えば、\(y(x)\)は全領域に対して繋がっている、という条件を課しましょう。この場合、不連続点\(x’\)で
\(
\displaystyle \left. y(x)\right|^{x=x’+0}_{x=x’-0}=0
\)
という境界条件を満たさなければなりません。この条件を課すと、\(C_1=C_0\)となり、初めて関数\(y(x)\)を一意に決めることが出来ます。

1階微分方程式を解く場合、適応刻み幅制御では関数\(y(x)\)は計算領域内で繋がっている事が課されています。しかし、4次ルンゲ=クッタではその条件は課されません。\(C_1\)の値は初期条件に依存し、一意に関数が決まりません。
どちらが悪いという話ではありません。

通常は適応刻み幅でも、4次ルンゲ=クッタでも\(y(x)\)にどこか連続ではない変な点がある場合、その点で区間を別々に分けて解きます。その後、境界条件に従って値を調節して全体の関数を構成します。

ベンチマーク用

微分方程式の解法がどれくらい正しそうかのベンチマーク問題として振り子(角度が大きい時)を考えましょう(振り子の詳しい解説はこちら)。
以下の\(\omega=1\)としたときの運動方程式
\(
\displaystyle \frac{d^2\theta}{dt^2}=-\sin\theta
\)
を
\(
t=0,\; \theta=0; \frac{d\theta}{dt}=1.9\cdots (k=0.95)
\)
の初期条件の下解いた場合、
1周期\(T\)は
\(
T=4K(0.95)=10.360044923498004876778\cdots
\)
となります。
この値はwolfram alphaから求めました。
4EllipticK[0.950.95] wolfram alpha

刻み幅制御を行い、45000周期目の値を考えます。45000周期目は時刻
\(
T_{45000}=466202.0215574102\cdots
\)
です。刻み幅制御による精度を\(10^{-12}\)に設定し、数値計算を行わせます。

すると実行結果として”fort.10″に

0.4662020113E+006  -0.2103356901E-001   0.1899883579E+001   0.4224109363E-002
0.4662020155E+006  -0.1300808922E-001   0.1899955473E+001   0.4223843994E-002
0.4662020198E+006  -0.4982881533E-002   0.1899993468E+001   0.4223658015E-002
0.4662020240E+006   0.3042061693E-002   0.1899997567E+001   0.4223520921E-002

というデータが出力されます。
1列目が時刻\(t\)、2列目が\(\theta(t)\),3列目が\(\frac{d\theta(t)}{dt}\),4列目が刻み幅\(h\)です。
1回のステップでの要求精度12桁に対し、最終的な結果は8桁まで正しい値を出しています。
この時、計算回数は77,852,488回\(~10^{8}\)回行われているので、最終的な結果として4桁は少なくとも正しいと考えられます。
4桁合っていればいい状況で8桁もあっているのは、被積分関数が変な振る舞いをしないからでしょう。

また、60000周期で確認してみると(\(T_{60000}=621602.695409880292\cdots\))

0.6216026888E+006  -0.1531918479E-001   0.1899938246E+001   0.4223959920E-002
0.6216026930E+006  -0.7293808996E-002   0.1899986003E+001   0.4223717084E-002
0.6216026973E+006   0.7312355417E-003   0.1899999862E+001   0.4223582630E-002
0.6216027015E+006   0.8756011575E-002   0.1899979827E+001   0.4223462029E-002

です。
1回のステップでの要求精度12桁に対し、最終的な結果は8桁まで正しい値を出しています。
この時、計算回数は103,803,513回\(~10^{8}\)回行われているので、最終的な結果として4桁は少なくとも正しいと考えられます。
･･･まだまだ大丈夫そうですね。

少し特殊な初期条件(\(k=1\))でやってみましょう。
この\(k=1\)は、振り子の質点がちょうど真上に来て静止する非常に不安定な状態です。
何秒間静止していられるか試してみましょう。刻み幅の制御等は上記条件と同じです。
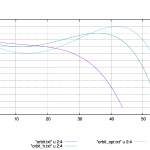
横軸に時間\(t\)、縦軸に\(\theta(t)\)を取った時のグラフです。
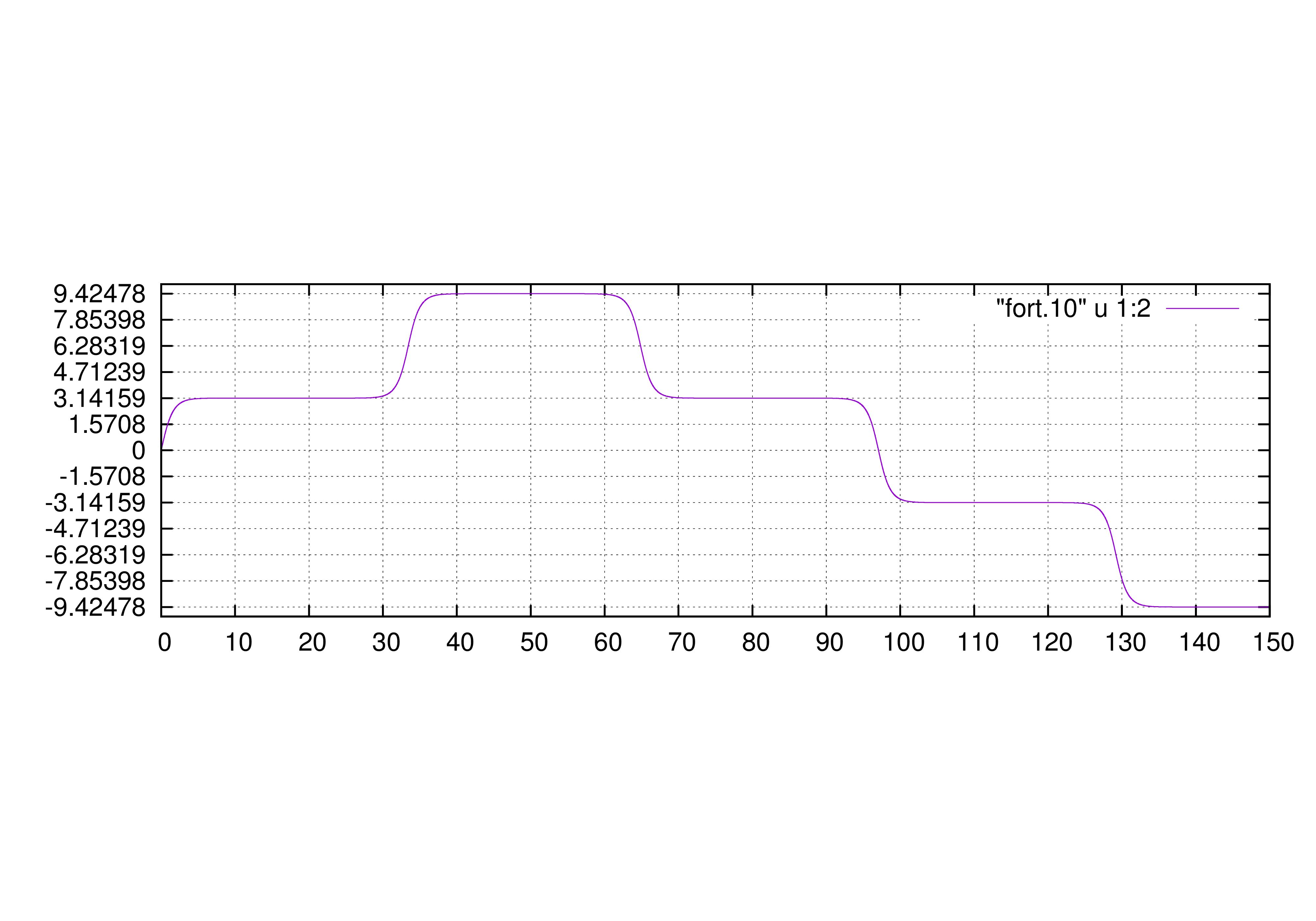
ellk1
すぐに破綻しました。正しい値は\(t=20\)位までですかね。これは、機械的な誤差があることによって不安定な平衡点からほんの少しだけ外れてしまったからです。だからカオスとかを考えるときとかは注意しなければなりません。

ルンゲ=クッタ=ドルマンド=プリンス法

フェールベルグ法は初期の頃に考えられた埋め込まれた方法です。
研究が進み、実用上では別の係数の組み合わせが良いことが分かってきました。
その一つが1980年に発見されたドルマンド=プリンス(Dormand-Prince)法です。

これは、7段4(5)次の方法です。
フェールベルグ法は6段4(5)次の方法ですので、次数は同じです。

良く調べていませんが、この違いは、4次の結果を基準にして求めたブッチャー係数(フェールベルグ法)か、5次の結果を基準に求めたブッチャー係数(ドルマンド=プリンス法)か？の違いのようです。

単純に考えて、同じ次数なのにドルマンド=プリンス法の方が段数が増えていて効率が悪いです。
しかし、本来は7段なのですが、7段目に呼び出した結果を取って置けば、次のステップの1段目に同じ値が使えるように設計されているので、プログラム上は6段と(ほぼ)同じ関数の呼び出し回数になります。

プログラムはこんな感じになるでしょう。

適当な刻み幅で出力

等間隔(サブルーチンは上のものと同じなので省略)

program main
  implicit none
  integer::i,N,info,Nx
  double precision::h,tol
  double precision::xa,xb,tx
  double precision,allocatable::y(:),x(:),work0(:)
  double precision,external::grk

N=1
  allocate(y(1:N),work0(1:N))

Nx=101
  allocate(x(1:Nx))
  xa=0d0
  xb=10d0
  do i=1,Nx
     x(i)=(i-1)*(xb-xa)/dble(Nx-1)+xa
  enddo

!initial conditions
  y(1)=1d0  ! x (0)

tol=1d-8
  write(10,'(2e25.10e3)')x(1),y(1)
  do i=2,Nx
     info=-1
     h=x(i)-x(i-1)
     tx=x(i-1)
     do while(info.le.0)
        call dDP45(grk,tx,h,N,y,x(i),info,tol,work0)
     enddo
     write(10,'(2e25.10e3)')x(i),y(1)
  enddo

stop
end program main

function grk(N,x,y,s)
  implicit none
  integer,intent(in)::N,s
  double precision,intent(in)::x
  double precision,intent(in)::y(1:N)
  double precision::grk

grk=0d0
  if(s.eq.1)then
     grk=y(1)<em>cos(x)
  else
     write(6,</em>)"***Error grk"; stop
  endif

return
end function grk

4倍精度ルーチン

4倍精度のサブルーチンです。
計算速度は倍精度の30~50倍かかるので、必要なとき以外使わないようにしましょう。

陽的ルンゲ=クッタ法の導出

ルンゲ=クッタ法の導出は煩雑です。単に複雑なだけです。
導出過程について詳しく述べられているページは、早川様が記述された以下のpdfを参照すると良いと思います。
Runge-Kutta法についてのノート(早川尚男)
計算過程を含め記述されているので分かりやすいです。

参考文献

[1]Derivation of Runge–Kutta methods
[2]NDSolveの”ExplicitRungeKutta”メソッド
[3]High-Order Explicit Runge-Kutta Methods
[4]List of Runge–Kutta methods
[5]Runge-Kutta-Fehlberg Method (RKF45)
[6]Runge-Kutta-Fehlberg method
[7]Lecture:13Runge-Kutta-Fehlberg Method
[8]GPU acceleration of Runge Kutta-Fehlberg and its comparison with Dormand-Prince method
[9]William H. Pressら著『ニューメリカルレシピ・イン・シー 日本語版―C言語による数値計算のレシピ– 』(1993)

ニューメリカルレシピ・イン・シー 日本語版―C言語による数値計算のレシピ

↑この本が一番有益だと思います。Fortran版もありますが、英語しかありません。ちなみに、英語で,若干古いバージョンでいいのならば
公式のホームページ
Numerical Recipes in C (1992)
Numerical Recipes in Fortran 77 and Fortran 90 (1992, 1996)
で無料で公開されています。

関連記事

このエントリーをはてなブックマークに追加

「ルンゲ=クッタ法の説明と刻み幅制御」への5件のフィードバック

  1. ピンバック: C++でRKF45 Methodを実装した

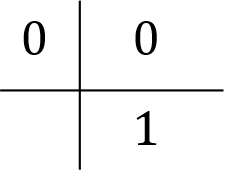
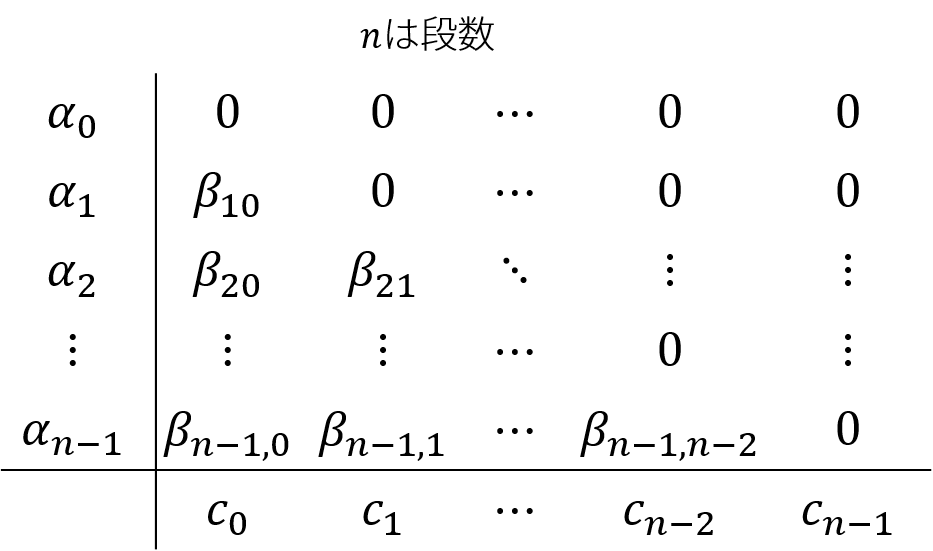
  2. 「ルンゲ=クッタ=フェールベルグ法による刻み幅の自動制御(適応刻み幅制御)」の後の
    「[5~9]によれば、ルンゲ=クッタ=フェールベルグ法において区間iでの最適な刻み幅h′は区間iの誤差評価の結果を使って、」の直後の
    h’を表す式の右辺は間違っています。hは、(1/4)乗にはなりません。
    また、
    「(ちなみに、m次ルンゲ=クッタ法の場合では」の直後の
    h’を表す式の右辺は間違っています。hは、(1/m)乗にはなりません。
    訂正した方が良いです。

    返信

    1. 貴重なご意見ありがとうございます。

      再度調べたところ、間違いとは言い切れないと感じました。
      正確には(1/4)乗もしくは(1/5)乗の両方が散見される、といった方が良いでしょうか。

      例えば検索したところ、以下は(1/4)乗でとっており、
      (https://maths.cnam.fr/IMG/pdf/RungeKuttaFehlbergProof.pdf)
      以下は(1/5)乗でとっております。
      (https://en.wikipedia.org/wiki/Runge%E2%80%93Kutta%E2%80%93Fehlberg_method)

      また主流の方法は刻み幅が減る時は(1/4)乗, 増やすときには(1/5)乗を使うようにする方法のようで、
      NumericalRecipes
      (http://s3.amazonaws.com/nrbook.com/book_C210.html)
      や
      Gurevich, Svetlana (2017). “Appendix A Runge-Kutta Methods”
      (https://www.uni-muenster.de/imperia/md/content/physik_tp/lectures/ss2017/numerische_Methoden_fuer_komplexe_Systeme_II/rkm-1.pdf)
      で散見されました。

      NumericalRecipesの一文にもありますが、”指数0.20と指数0.25は実際あまり違わない”とあります。
      より安全を取るならば上記の方法で実施するべきで、その意味では本稿の説明は間違いです。

      しかしながら、ルンゲクッタ法で局所的に刻み幅を評価するか(1/5乗)、大域的に刻み幅を評価するか(1/4乗)
      どちらでスケールし直すかはどこまで行っても想定でしかないですので、
      (1/4)乗または(1/5)乗かその両方かは好みの問題かと思われます。

      鈴木様の仰る正解は、(1/5)乗か、両方使う方法か、または異なる場所を指摘されているのかは分かりませんが、
      間違いというほどではないかな、というのが私の意見です。
      (1/m)乗も同様です。

      ただし、注釈としては入れておくべき内容と感じましたので、後程更新させていただこうと思います。

      回答になっているでしょうか。
      よろしければ、鈴木様の仰る正解をご教授いただければと思います。
      よろしくお願いいたします。

      返信

  3. sikino様

    上記のご返事をありがとうございました。

    私の書いたことを正しく理解してもらえなかったようですね。
    私は、hの次元が合わないと指摘しました。

    たとえば、
    (https://maths.cnam.fr/IMG/pdf/RungeKuttaFehlbergProof.pdf)
    をご覧ください。
    ＜引用＞
    The optimal step size s h can be determined by multiplying the scalar s times the
    current step size h. The scalar s is
    s = ( tol h /(2|z_k+1 – y_k+1|))^(1/4) ≈ 0.84 ( tol h /(2|z_k+1 – y_k+1|))^(1/4)
    ＜途中を鈴木が省略＞
    where tol is the specified error control tolerance.
    ＜引用はここまで＞
    つまり、最適なステップサイズは、sではなく、sとhの積です。
    ちなみに、上付き文字の直前に「^」を、下付きの文字の直前に「_」を記しています。
    tolの内容を理解していませんが、sが無次元のスカラーなので、
    tolの次元は、z（またはy）の次元をhの次元で割ったもののはずです。
    次元を考察すれば、分かることです。
    したがって、たとえば、
    「[5-9]によれば、」の後のh’の式の右辺に
    「(εh/(2|x_i^(5) – x_i^(4)|)^(1/4)」
    と書かれていますが、それにさらにhを掛ける必要があると思います。
    ただし、εの定義が明記されていませんので、それを記す必要もあると思います。
    εの次元は、xの次元をhの次元で割ったもののはずです。

    また、
    (https://en.wikipedia.org/wiki/Runge%E2%80%93Kutta%E2%80%93Fehlberg_method)
    では、明確に、
    ＜引用＞
    At the completion of the step, a new stepsize is calculated:[3]
    h_new = 0.9・h・(ε/(T E))^(1/5)
    ＜引用はここまで＞
    と記されています。新しいh、つまりh’の値は、hに比例しています。hは(1/5)乗にはなっていません。上記では「ε」と「T E」の次元は同じはずです。

    hの(1/4)乗が良いのか(1/5)乗が良いのかは、私は存じません。

    ちなみに、もう一ヶ所、間違いだと思われる箇所を見つけました。
    「日本語訳して、その計算スキームを書けば下のようになります。」
    の下に画像がありますが、
    その「Step3」のk_6の右辺の最後の項に誤りがあると思われます。
    「-(11/40) k_4」のように記されていますが、その「k_4」は誤りで、おそらく正しくは、
    「k_5」でしょう。ご検討ください。

    返信

    1. なるほど。確かに式が間違えて書かれていますね。
      この式では次元が合わず、確かにおかしいです。
      プログラム上ではh’∝hで実装されており、おかしな動作が無いゆえに気に留めておりませんでした。
      また乗数の値をご指摘されておられたので、刻み幅の予測に関するご指摘だと勘違いしてしまいました。お手数をおかけしました。
      ご指摘ありがとうございます。
      k_5の指摘につきましてもミスですので、後程併せて修正させていただきます。

      返信

コメントを残す

メールアドレスが公開されることはありません。 ※ が付いている欄は必須項目です