module GBL
!sikinote http://slpr.sakura.ne.jp/qp/
!Author : sikino
!Date : 2016/03/18 (yyyy/mm/dd)
! : 2016/03/20
! : 2016/07/23
! : 2016/07/25
! : 2016/08/06
implicit none
!Constant of system
double precision::m,g,a,eta,rho,temperature,pressure,moisture
character(48)::omgdecay
!Example parameter
! 1, tol=1d-10, eps=1d-9
! => very exact, slow computing speed
! 2, tol=1d-6, eps=1d-6
! => enough computation practically.
!Accuracy of rungekutta(tol must be constant)
! 1d-2 < tol : Rouph condition, computing speed is fast.
! 1d-10 < tol < 1d-2 : Intermediate
! 1d-12 < tol < 1d-10 : Exact condition, computing speed is slow.
! tol < 1d-12 : Not reccomended, Maybe cannot computing due to machine epsilon.
double precision,parameter::tol=1d-10
!Conversence epsilon at rootfinding method
! 1d0 < eps : Rouph condition, computing speed is fast.
! 1d-10 < eps < 1d0 : Intermediate
! eps < 1d-10 : Exact condition, computing speed is slow.
! or cannot converge less than 1d-10.
double precision,parameter::eps=1d-7
end module GBL
!================================
function rho_humid(T,P,M)
! T : temperature [degree]
! P : pressure [Pa] ( 1 atm = 101325 Pa )
! M : moisture [no-dimension]
implicit none
double precision,intent(in)::T,P,M
double precision::rho_humid,et,rhoair
et=6.1078d0*10d0**(7.5d0*T/(T+237.3d0)) ! et[hPa]
et=100d0*et
et=M*et
!write(6,*)"et[Pa]",et
rhoair=0.0034856447d0*P/(T+273.15d0-0.670d0)
rho_humid=rhoair*(1d0-0.378d0*et/P)
return
end function rho_humid
function eta_air(T)
! T : temperature [degree]
implicit none
double precision::T,eta_air
eta_air=1.487d-6*((T+273.15d0)**1.5d0)/((T+273.15d0)+117d0)
return
end function eta_air
module RKmod
!sikinote http://slpr.sakura.ne.jp/qp/
!developer => sikino
!date => 2015/07/13
implicit none
!For Butcher table
integer,private::s
double precision,private,allocatable::a(:,:),b1(:),b2(:),c(:),Rc(:)
!-----------------------------
contains
subroutine rk_preparation(method)
!set Butcher table
implicit none
character(*)::method
if(trim(method).eq."rk4")then
s=4
allocate(a(1:s,1:s),b1(1:s),c(1:s))
a=0d0; b1=0d0; c=0d0
c(1:4)=(/0d0, 0.5d0, 0.5d0, 1d0/)
a(1,1:4)=(/0d0,0d0,0d0,0d0/)
a(2,1:4)=(/0.5d0,0d0,0d0,0d0/)
a(3,1:4)=(/0d0,0.5d0,0d0,0d0/)
a(4,1:4)=(/0d0,0d0,1d0,0d0/)
b1(1:4)=(/1d0/6d0, 1d0/3d0, 1d0/3d0, 1d0/6d0/)
elseif(trim(method).eq."rkf45")then
s=6
allocate(a(1:s,1:s),b1(1:s),b2(1:s),c(1:s),Rc(1:s))
a=0d0; b1=0d0; b2=0d0; c=0d0; Rc=0d0
c(1:6)=(/0d0, 0.25d0, 3d0/8d0, 12d0/13d0, 1d0, 0.5d0/)
a(1:6,1:6)=0d0
a(1,1:6)=(/0d0, 0d0, 0d0, 0d0, 0d0, 0d0/)
a(2,1:6)=(/0.25d0, 0d0, 0d0, 0d0, 0d0, 0d0/)
a(3,1:6)=(/0.09375d0, 0.28125d0, 0d0, 0d0, 0d0, 0d0/)
a(4,1:6)=(/1932d0/2197d0, -7200d0/2197d0, 7296d0/2197d0, 0d0, 0d0, 0d0/)
a(5,1:6)=(/439d0/216d0, -8d0, 3680d0/513d0, -845d0/4104d0, 0d0, 0d0/)
a(6,1:6)=(/-8d0/27d0, 2d0, -3544d0/2565d0, 1859d0/4104d0, -11d0/40d0, 0d0/)
b2(1:6)=(/16d0/135d0, 0d0, 6656d0/12825d0, 28561d0/56430d0, -9d0/50d0, 2d0/55d0/)
b1(1:6)=(/25d0/216d0, 0d0, 1408d0/2565d0, 2197d0/4104d0, -0.2d0, 0d0/)
Rc(1:6)=(/1d0/360d0,0d0,-128d0/4275d0,-2197d0/75240d0,1d0/50d0,2d0/55d0/)
else
write(6,*)"program stop at rk_preparation"
stop
end if
return
end subroutine rk_preparation
!------------------------------
subroutine rk_deallocation(method)
implicit none
character(*)::method
if(trim(method).eq."rk4")then
deallocate(a,b1,c)
elseif(trim(method).eq."rkf45")then
deallocate(a,b1,b2,c,Rc)
else
write(6,*)"program stop at rk_deallocation"
stop
end if
return
end subroutine rk_deallocation
!-------------------
subroutine rkf451(func,N,x,h,y,xbound,info,tol,ik)
!------------
!info = -2 (Failed. calclation range has already over.)
! = -1 (Failed.
! h becomes too small. change tol or check condition of func.)
! = 0 (Success. running now)
! = 1 (Success. x reach xbound normally)
!------------
implicit none
interface
function func(iN,ix,iy,is,iik)
implicit none
integer,intent(in)::iN,is,iik
double precision,intent(in)::ix,iy(1:iN)
double precision::func
end function func
end interface
integer,intent(in)::N,ik
double precision,intent(in)::xbound
double precision,intent(in)::tol
double precision,intent(inout)::x,h,y(1:N)
integer,intent(inout)::info
double precision,parameter::hmin=1d-14,hmax=1.d0
integer::i,j,FLAG
double precision::R,delta,tx,tmp(1:N),K(1:s,1:N),Sy,err
if(abs(h).ge.hmax)then
if(h.le.0d0)then
h=-hmax
else
h=hmax
endif
endif
FLAG=1
if(abs(x-xbound).le.1d-15)then
info=1
FLAG=0
else
if(abs(h).le.1d-15)then
write(6,*)"maybe overflow or underflow, please change tol."
write(6,'(A)')"====Err info===="
write(6,'(A,e17.9e3)')"x --> ",x
write(6,'(A,e17.9e3)')"h --> ",h
do i=1,N
write(6,'(A,i0,A,e17.9e3)')"y(",i,") --> ",y(i)
enddo
write(6,'(A)')"================"
info=-1
FLAG=0
stop
endif
if(h.le.0d0.and.xbound-x.ge.0d0)then
info=-2
FLAG=0
elseif(h.gt.0d0.and.xbound-x.le.0d0)then
info=-2
FLAG=0
endif
endif
do while(FLAG.eq.1)
tx=x
do j=1,s
tx=x+c(j)*h
tmp(1:N)=y(1:N)
do i=1,j-1
tmp(1:N)=tmp(1:N)+K(i,1:N)*a(j,i)
enddo
do i=1,N
K(j,i)=h*func(N,tx,tmp,i,ik)
enddo
enddo
!step 4
R=0d0
do i=1,N
R=R+(Rc(1)*K(1,i)+Rc(3)*K(3,i)+Rc(4)*K(4,i)+Rc(5)*K(5,i)+Rc(6)*K(6,i))**2d0
enddo
R=abs(dsqrt(R)/h)
Sy=0d0
do i=1,N
Sy=Sy+(y(i)*y(i))
enddo
Sy=dsqrt(Sy)
if(Sy.ge.1d0)then
err=tol*Sy
else
err=tol
endif
!step 5
if(R.le.err)then
x=x+h
do i=1,s
y(1:N)=y(1:N)+b1(i)*K(i,1:N)
enddo
FLAG=0
endif
!step 6
! Avoid zero deviding.
if(R.ge.1d-20)then
delta=(err/(2d0*R))**0.25d0
else
delta=4d0
endif
!step 7
if(delta.le.0.1d0)then
!function changes dramatically.
h=0.1d0*h
elseif(delta.ge.4d0)then
!function changes loosely.
h=4d0*h
else
!function changes moderately.
h=delta*h
endif
!step 8
if(abs(h).ge.hmax)then
if(h.le.0d0)then
h=-hmax
else
h=hmax
endif
endif
!step 9
if(abs(xbound-x).le.abs(h))then
h=xbound-x
if(abs(h).le.hmin)then
info=1
FLAG=0
endif
end if
enddo
return
end subroutine rkf451
subroutine rkf451_e(func,x,y,xbound,info,tol,ik)
!sikinote
! propagate from y(x) to y(xbound) without interval
!
! info = -1 : h < hmin. Maybe path the singular point.
! = 1 : x reach xbound.
!
implicit none
interface
function func(iN,ix,iy,is,iik)
implicit none
integer,intent(in)::iN,is,iik
double precision,intent(in)::ix,iy(1:iN)
double precision::func
end function func
end interface
integer::N,ik
double precision,intent(in)::xbound,tol
double precision,intent(inout)::x,y(:)
integer,intent(inout)::info
double precision,parameter::hmin=1d-14,hmax=1.d0
integer::i,j,FLAG,key,disc
double precision::R,delta,tx,Sy,err,h,h0
double precision,allocatable::tmp(:),K(:,:)
disc=0
key=0
h0=999d0
N=size(y,1)
allocate(tmp(1:N),K(1:s,1:N))
tmp=0d0; K=0d0
h=xbound-x
if(abs(h).ge.hmax)then
if(h.le.0d0)then
h=-hmax
else
h=hmax
endif
endif
FLAG=1
if(abs(x-xbound).le.hmin*0.1d0)then
info=1
FLAG=0
endif
do while(FLAG.eq.1)
tx=x
do j=1,s
tx=x+c(j)*h
tmp(1:N)=y(1:N)
do i=1,j-1
tmp(1:N)=tmp(1:N)+K(i,1:N)*a(j,i)
enddo
do i=1,N
K(j,i)=h*func(N,tx,tmp,i,ik)
enddo
enddo
!step 4
R=0d0
do i=1,N
R=R+(Rc(1)*K(1,i)+Rc(3)*K(3,i)+Rc(4)*K(4,i)+Rc(5)*K(5,i)+Rc(6)*K(6,i))**2d0
enddo
R=abs(dsqrt(R)/h)
Sy=0d0
do i=1,N
Sy=Sy+(y(i)*y(i))
enddo
Sy=dsqrt(Sy)
if(Sy.ge.1d0)then
err=tol*Sy
else
err=tol
endif
!step 5
if(R.le.err.or.key.eq.1)then
x=x+h
do i=1,s
y(1:N)=y(1:N)+b1(i)*K(i,1:N)
enddo
key=0
endif
!step 6
! Avoid zero deviding.
if(R.ge.1d-20)then
delta=(err/(2d0*R))**0.25d0
else
delta=4d0
endif
!step 7
if(delta.le.0.1d0)then
!function changes dramatically.
h=0.1d0*h
elseif(delta.ge.4d0)then
!function changes loosely.
h=4d0*h
else
!function changes moderately.
h=delta*h
endif
!step 8
if(abs(h).ge.hmax)then
h=sign(1d0,h)*hmax
elseif(abs(h).lt.hmin)then
h=sign(1d0,h)*hmin
key=1
disc=1
endif
!step 9
if(abs(xbound-x).le.abs(h))then
h=xbound-x
if(abs(h).le.hmin)then
info=1
FLAG=0
endif
end if
enddo
if(disc.eq.1)then
info=-1
endif
deallocate(tmp,K)
return
end subroutine rkf451_e
end module RKmod
!--------------------
subroutine seeklm(xa,xb,za,zb,nodes,poles,r0,v0,omg0,u0,ik)
!nodes --> number of nodes
!poles --> number of local maximam/minimam
!
!nodes=0
!
!
! x--------------------------------
! \_______
! \______
! \
! orbit of bullet
!
!nodes=1
! za_____________xa
! __/\_
! ________/ \_
! / \
! x------------------\------------
! \
! \
! \
! \orbit of bullet
!
!nodes=2
!
! zb________________ xb
! /\
! xa / \
! x-----------/--------\------------
! \ / \
! \ / \
! za______\/ \
! \orbit of bullet
!
use RKmod
use GBL
implicit none
integer,intent(in)::ik
double precision,intent(in)::omg0(1:3),r0(1:3),v0(1:3),u0(1:3)
double precision,intent(out)::xa,xb,za,zb
integer,intent(out)::nodes,poles
integer::i,j,info
integer,parameter::N=12
double precision::vz0,vz1,vz2,t0,t1,t2,ta,tb,tbef,rz0,rz1
double precision::x(1:N),tt,th,tx(1:N),bt,bh,bx(1:N)
double precision::t,h,xbound,rkfd
external::rkfd
x(1:3)=r0(1:3)
x(4:6)=v0(1:3)
x(7:9)=omg0(1:3)
x(10:12)=u0(1:3)
xbound=10d0
i=1; t=0d0; h=1d-1; info=0
info=0; nodes=0; poles=0
xa=0d0; xb=0d0; za=0d0; zb=0d0
call rk_preparation("rkf45")
do while(info.eq.0)
tt=t; th=h; tx=x
rz0=x(3); vz0=x(6); t0=t
call rkf451(rkfd,size(x),t,h,x,xbound,info,tol,ik)
rz1=x(3); vz1=x(6); t1=t
if(vz0*vz1.lt.0.d0)then
bt=tt; bh=th; bx=tx
t0=bt; t2=0.5d0*(2d0*bt+th); t1=bt+th
do j=1,60
tt=bt; th=bh; tx=bx
th=t2-bt
call rkf451(rkfd,size(tx),tt,th,tx,xbound,info,tol,ik)
vz2=tx(6)
if(vz2*vz0.ge.0.d0)then
t2=t2+0.5d0*(t1-t2)
else
tbef=t2
t2=t2-0.5d0*(t1-t2)
t1=tbef
endif
if(abs(t1-t2)/t1.lt.1d-10)then
if(poles.eq.0)then
ta=t2; xa=tx(1); za=tx(3)
else
tb=t2; xb=tx(1); zb=tx(3)
endif
exit
endif
enddo
poles=poles+1
endif
if((rz0-r0(3))*(rz1-r0(3)).lt.0d0)then
nodes=nodes+1
endif
if(x(3).lt.0d0)then
info=1
endif
i=i+1
enddo
call rk_deallocation("rkf45")
return
end subroutine seeklm
subroutine seekzeroin(xa,xb,nodes,r0,v0,omg0,u0,ik)
!nodes --> number of nodes
!
!nodes=0
!
!
! x--------------------------------
! \_______
! \______
! \
! orbit of bullet
!
!nodes=1
!
! __/\_
! ________/ \_
! / \ xa
! x------------------\------------
! \
! \
! \
! \orbit of bullet
!
!nodes=2
!
!
! /\
! xa / \ xb
! x-----------/--------\------------
! \ / \
! \ / \
! \/ \
! \orbit of bullet
!
use RKmod
use GBL
implicit none
integer,intent(in)::ik
double precision,intent(in)::omg0(1:3),r0(1:3),v0(1:3),u0(1:3)
double precision,intent(out)::xa,xb
integer,intent(out)::nodes
integer::i,j,info
integer,parameter::N=12
double precision::rz0,rz1,rz2,t0,t1,t2,ta,tb,tbef,rzini
double precision::x(1:N),tt,th,tx(1:N),bt,bh,bx(1:N)
double precision::t,h,xbound,rkfd
external::rkfd
rzini=r0(3)
x(1:3)=r0(1:3)
x(4:6)=v0(1:3)
x(7:9)=omg0(1:3)
x(10:12)=u0(1:3)
xbound=10d0
i=1; t=0d0; h=1d-1; info=0
info=0; nodes=0
xa=0d0; xb=0d0
call rk_preparation("rkf45")
!-----1step-----
call rkf451(rkfd,size(x),t,h,x,xbound,info,tol,ik)
!----------------
do while(info.eq.0)
tt=t; th=h; tx=x
rz0=x(3); t0=t
call rkf451(rkfd,size(x),t,h,x,xbound,info,tol,ik)
rz1=x(3); t1=t
if(rz0-rzini.lt.0.d0.neqv.rz1-rzini.lt.0.d0)then
bt=tt; bh=th; bx=tx
t0=bt; t2=0.5d0*(2d0*bt+th); t1=bt+th
do j=1,60
tt=bt; th=bh; tx=bx
th=t2-bt
call rkf451(rkfd,size(tx),tt,th,tx,xbound,info,tol,ik)
rz2=tx(3)
if(rz2-rzini.lt.0.d0.eqv.rz0-rzini.lt.0.d0)then
t2=t2+0.5d0*(t1-t2)
else
tbef=t2
t2=t2-0.5d0*(t1-t2)
t1=tbef
endif
if(abs(t1-t2)/t1.lt.1d-10)then
if(nodes.eq.0)then
ta=t2; xa=tx(1)
else
tb=t2; xb=tx(1)
endif
nodes=nodes+1
exit
endif
enddo
endif
if(x(3).lt.0d0)then
info=1
endif
i=i+1
enddo
call rk_deallocation("rkf45")
return
end subroutine seekzeroin
subroutine detwy(energy,r,vy,omgx,omgz,u,zeroinx,exwy,exvz,ik)
implicit none
integer,intent(in)::ik
double precision,intent(in)::energy,zeroinx
double precision,intent(in)::r(1:3),omgx,omgz,u(1:3),vy
double precision,intent(out)::exwy,exvz
integer::Nr,count,Nsplit
double precision,parameter::pi=dacos(-1d0)
double precision,allocatable::rd(:)
double precision::ad,bd,wycond
external::wycond
ad=-800d0*2d0*pi; bd=2d0*pi; Nsplit=25; Nr=1
allocate(rd(1:Nr))
rd(1:Nr)=0d0
count=0
call rootfindingw(wycond,energy,r,vy,omgx,omgz,u,zeroinx,ad,bd,Nsplit,Nr,rd,exvz,count,"bisection",1)
exwy=rd(1)
if(ik.eq.0)then
ad=exwy-5d0*2d0*pi; bd=exwy+5d0*2d0*pi; Nsplit=1; Nr=1
rd(1:Nr)=0d0
count=0
call rootfindingw(wycond,energy,r,vy,omgx,omgz,u,zeroinx,ad,bd,Nsplit,Nr,rd,exvz,count,"false_position",0)
exwy=rd(1)
endif
deallocate(rd)
return
end subroutine detwy
!--------------------------
function wycond(energy,r,vy,omgx,omgy,omgz,u,zeroinx,exvz,ik)
use GBL, only:m
implicit none
integer,intent(in)::ik
double precision,intent(in)::energy,r(1:3),u(1:3),vy,omgx,omgy,omgz,zeroinx
double precision,intent(out)::exvz
integer::nodes
double precision::zeroinx1,zeroinx2,wycond,v(1:3),omg(1:3)
omg(1)=omgx; omg(2)=omgy; omg(3)=omgz
call detvz(energy,r,vy,omg,u,exvz,ik)
v(1)=dsqrt((2d0*energy/m)-exvz**2-vy**2)
v(2)=vy
v(3)=exvz
call seekzeroin(zeroinx1,zeroinx2,nodes,r,v,omg,u,ik)
if(zeroinx2.ge.1d-10)then
wycond=zeroinx2-zeroinx
else
wycond=2d0*zeroinx
endif
return
end function wycond
!------------------------------
subroutine detwy2(energy,r,vy,omgx,omgz,u,udh,exwy,exvz,ik)
implicit none
integer,intent(in)::ik
double precision,intent(in)::energy,udh,r(1:3),omgx,omgz,u(1:3),vy
double precision,intent(out)::exwy,exvz
integer::Nr,count,Nsplit
double precision,parameter::pi=dacos(-1d0)
double precision,allocatable::rd(:)
double precision::ad,bd,wycond2
external::wycond2
ad=-1000d0*2d0*pi; bd=2d0*pi; Nsplit=25; Nr=1
allocate(rd(1:Nr))
rd(1:Nr)=0d0
count=0
call rootfindingw(wycond2,energy,r,vy,omgx,omgz,u,udh,ad,bd,Nsplit,Nr,rd,exvz,count,"bisection",1)
exwy=rd(1)
if(ik.eq.0)then
ad=exwy-5d0*2d0*pi; bd=exwy+5d0*2d0*pi; Nsplit=1; Nr=1
count=0; rd(1:Nr)=0d0
call rootfindingw(wycond2,energy,r,vy,omgx,omgz,u,udh,ad,bd,Nsplit,Nr,rd,exvz,count,"false_position",0)
exwy=rd(1)
endif
deallocate(rd)
return
end subroutine detwy2
!--------------------------
function wycond2(energy,r,vy,omgx,omgy,omgz,u,udh,exvz,ik)
use GBL, only:m
implicit none
integer,intent(in)::ik
double precision,intent(in)::energy,r(1:3),u(1:3),vy,omgx,omgy,omgz,udh
double precision,intent(out)::exvz
integer::nodes,poles
double precision::xa,xb,za,zb,z0,wycond2,v(1:3),omg(1:3)
omg(1)=omgx; omg(2)=omgy; omg(3)=omgz
call detvz(energy,r,vy,omg,u,exvz,ik)
v(1)=dsqrt((2d0*energy/m)-exvz**2-vy**2)
v(2)=vy
v(3)=exvz
z0=r(3)
call seeklm(xa,xb,za,zb,nodes,poles,r,v,omg,u,ik)
if(poles.eq.0.or.za.lt.0d0)then
wycond2=10d0
elseif(poles.eq.1)then
wycond2=za-z0
elseif(poles.eq.2)then
wycond2=zb-za
else
write(6,*)"unknown,poles-->",poles
stop
endif
wycond2=wycond2-udh
return
end function wycond2
!-------------------------
subroutine detvz(energy,r,vy,omg,u,exvz,ik)
implicit none
integer,intent(in)::ik
double precision,intent(in)::energy
double precision,intent(in)::r(1:3),omg(1:3),u(1:3),vy
integer::Nr,count,Nsplit
double precision,intent(out)::exvz
double precision,allocatable::rd(:)
double precision::ad,bd,vzcond
external::vzcond
ad=-30d0; bd=1d0; Nsplit=80; Nr=1
allocate(rd(1:Nr))
rd(1:Nr)=0d0
count=0
call vzroot(vzcond,energy,r,vy,omg,u,ad,bd,Nsplit,Nr,rd,count,ik)
exvz=rd(1)
return
end subroutine detvz
!------------------------
function vzcond(energy,r,vy,vz,omg,u,ik)
use GBL, only:m
implicit none
integer,intent(in)::ik
double precision,intent(in)::energy,r(1:3),vy,vz,omg(1:3),u(1:3)
double precision::vzcond,v(1:3)
integer::nodes,poles
double precision::xa,xb,za,zb,z0
v(1)=dsqrt((2d0*energy/m)-vz**2-vy**2)
v(2)=vy
v(3)=vz
z0=r(3)
call seeklm(xa,xb,za,zb,nodes,poles,r,v,omg,u,ik)
if(poles.eq.0)then
vzcond=-z0-1d0
elseif(poles.eq.1)then
vzcond=za-z0
elseif(poles.eq.2)then
vzcond=za+zb-2d0*z0
else
write(6,*)"unknown,poles-->",poles
stop
endif
return
end function vzcond
!--------------------
subroutine vzroot(func,energy,r,vy,omg,u,ad,bd,Nsplit,Nr,rd,count,ik)
!Developer : sikino
use GBL
implicit none
interface
function func(ienergy,ir,ivy,ivz,iomg,iu,iik)
implicit none
integer,intent(in)::iik
double precision,intent(in)::ienergy,ir(1:3),ivy,ivz,iomg(1:3),iu(1:3)
double precision::func
end function func
end interface
integer,intent(in)::Nr,Nsplit,ik
double precision,intent(in)::ad,bd,energy,r(1:3),vy,omg(1:3),u(1:3)
integer,intent(out)::count
double precision,intent(out)::rd(1:Nr)
integer::N,i,j
double precision::h,hd,x0,x1,x2,y0,y1,y2,Dy0,tx1,ty1
!ad < bd
if(ad.ge.bd)then
write(6,'(A,2e15.6e3)')"must be ad < bd, your ad,bd --> ",ad,bd
write(6,'(A)')"program stop at rootfinding"
stop
end if
N=Nsplit
hd=abs(ad-bd)/dble(N)
count=0
x0=ad
y0=func(energy,r,vy,x0,omg,u,ik)
do i=1,N
x1=x0+hd
y1=func(energy,r,vy,x1,omg,u,ik)
if(y0.lt.0.d0.neqv.y1.lt.0.d0)then
tx1=x1
ty1=y1
!bisection rule
do j=1,60
x2=0.5d0*(x0+x1)
y2=func(energy,r,vy,x2,omg,u,ik)
if(y2.lt.0.d0.eqv.y0.lt.0.d0)then
x0=x2
else
x1=x2
endif
if(abs((x1-x0)/x2).lt.eps)then
if(y2.le.1d0)then
count=count+1
rd(count)=x2
exit
endif
endif
enddo
if(j.eq.61)write(6,*)"+--cannot convergence at root-finding method bs--+"
if(count.ge.Nr)exit
x1=tx1
y1=ty1
endif
x0=x1
y0=y1
enddo
return
end subroutine vzroot
subroutine rootfindingw(func,energy,r,vy, &
omgx,omgz,u,zeroinx,ad,bd,Nsplit,Nr,rd,exvz,count,method,ik)
!Date : 2015/07/28
!Developer : sikino
use GBL
implicit none
interface
function func(ienergy,ir,ivy,iomgx,iomgy,iomgz,iu,izin,iexvz,iik)
implicit none
integer,intent(in)::iik
double precision,intent(in)::ienergy,ir(1:3),ivy,iomgx,iomgy,iomgz,izin,iu(1:3)
double precision,intent(out)::iexvz
double precision::func
end function func
end interface
integer,intent(in)::Nr,Nsplit,ik
double precision,intent(in)::ad,bd,energy,r(1:3),vy,u(1:3)
double precision,intent(in)::omgx,omgz,zeroinx
integer,intent(out)::count
double precision,intent(out)::rd(1:Nr),exvz
double precision,parameter::pi=dacos(-1d0)
character(*),intent(in)::method
integer::N,i,j
double precision::h,hd,x0,x1,x2,y0,y1,y2,Dy0,tx1,ty1
!ad < bd
if(ad.ge.bd)then
write(6,'(A,2e15.6e3)')"must be ad < bd, your ad,bd --> ",ad,bd
write(6,'(A)')"program stop at rootfinding"
stop
end if
!Announsment
write(6,'(A,A)')" ---- ",trim(method)
N=Nsplit
hd=abs(ad-bd)/dble(N)
count=0
x0=ad
y0=func(energy,r,vy,omgx,x0,omgz,u,zeroinx,exvz,ik)
do i=1,N
x1=x0+hd
y1=func(energy,r,vy,omgx,x1,omgz,u,zeroinx,exvz,ik)
write(6,'(A,i0,A,i0,A,f14.8,A,f14.8)')" Sequence ",i," of ",N," : omgy/2pi ",x1/2d0/pi, " : zeroin ",y1
if(y0.lt.0.d0.neqv.y1.lt.0.d0)then
write(6,'(A)')" +--- Root find, go to conversion phase --+ "
tx1=x1
ty1=y1
if(trim(method).eq."bisection")then
!bisection rule
do j=1,60
x2=0.5d0*(x0+x1)
y2=func(energy,r,vy,omgx,x2,omgz,u,zeroinx,exvz,ik)
if(y2.lt.0.d0.eqv.y0.lt.0.d0)then
x0=x2
else
x1=x2
endif
write(6,'(A,f16.8,A)')"Conversion => ",eps*abs(x2/(x1-x0))*100d0,"%"
if(abs((x1-x0)/x2).lt.eps)then
!If y2 is large, y2 is singular point.
if(y2.le.1d0)then
count=count+1
rd(count)=x2
endif
exit
endif
enddo
if(j.eq.60)write(6,*)"+--cannot convergence at root-finding method bs--+"
elseif(trim(method).eq."newton_raphson")then
!Newton-Raphson method
do j=1,10
h=1.d-4
y0=func(energy,r,vy,omgx,x0,omgz,u,zeroinx,exvz,ik)
Dy0=(func(energy,r,vy,omgx,x0+h,omgz,u,zeroinx,exvz,ik)-y0)/h
x2=x0-y0/Dy0
if(abs((x0-x2)/x2).lt.eps)then
if(y0.le.1d0)then
count=count+1
rd(count)=x2
endif
exit
endif
x0=x2
enddo
if(j.eq.10)write(6,*)"+--cannot convergence at root-finding method nr--+"
elseif(trim(method).eq."false_position")then
!false position method
if(abs(y1).gt.abs(y0))then
do j=1,30
x2=x0-y0*(x1-x0)/(y1-y0)
write(6,'(A,f16.8,A)')"Conversion => ",eps*abs(x2/(x2-x0))*100d0,"%"
if(abs((x2-x0)/x2).lt.eps)then
if(y0.le.1d0)then
count=count+1
rd(count)=x2
end if
exit
endif
x0=x2
y0=func(energy,r,vy,omgx,x0,omgz,u,zeroinx,exvz,ik)
enddo
else
do j=1,30
x2=x0-y0*(x1-x0)/(y1-y0)
write(6,'(A,f15.8,A)')"Conversion => ",eps*abs(x2/(x1-x2))*100d0,"%"
if(abs((x2-x1)/x2).lt.eps)then
if(y1.le.1d0)then
count=count+1
rd(count)=x2
endif
exit
endif
x1=x2
y1=func(energy,r,vy,omgx,x1,omgz,u,zeroinx,exvz,ik)
enddo
endif
if(j.eq.30)write(6,*)"+--cannot convergence at root-finding method fp--+"
else
write(6,'(A,A)')"unknown type of method, your method--> ",trim(method)
write(6,'(A,A)')"program stop"
stop
end if
if(count.ge.Nr)exit
x1=tx1
y1=ty1
endif
x0=x1
y0=y1
enddo
return
end subroutine rootfindingw
!---------------------------
function rkfd(N,t,x,s,ik)
use GBL
implicit none
integer,intent(in)::N,s,ik
double precision,intent(in)::t,x(1:N)
double precision::r(1:3),v(1:3),relv(1:3),omg(1:3),u(1:3),nw,nv,I
double precision::rkfd,gravity,vis1,vis2,mag,Nz,Nze
double precision,parameter::pi=datan(1d0)*4d0
external::gravity,vis1,vis2,mag,Nz,Nze
r(1:3)=x(1:3)
v(1:3)=x(4:6)
omg(1:3)=x(7:9)
u(1:3)=x(10:12)
relv(1:3)=v(1:3)-u(1:3)
rkfd=0.d0
if(s.le.3)then
! Differential equation of position
! d {x,y,z}/dt = v{x,y,z}
rkfd=v(s)
elseif(s.le.6)then
! Differential equation of velocity
! d v_{x,y,z}/dt = F{x,y,z}
rkfd=gravity(s-3,m,g,r)+vis1(s-3,relv,a,eta) &
+vis2(s-3,relv,a,eta,rho)+mag(s-3,omg,relv,a,rho)
rkfd=rkfd/m
elseif(s.le.9)then
! Differential equation for omega
! d omega{x,y,z}/dt = N_{x,y,z}/I
if(trim(omgdecay).eq."yes")then
I=0.4d0*m*a*a
nv=dsqrt(relv(1)**2+relv(2)**2+relv(3)**2)
nw=dsqrt(omg(1)**2+omg(2)**2+omg(3)**2)
if(nw.le.1d-13)then
rkfd=0d0
else
if(ik.eq.0)then
rkfd=(Nz(nv,a,eta,rho,nw)/I)*x(s)/nw
else
rkfd=(Nze(nv,a,eta,rho,nw)/I)*x(s)/nw
end if
endif
else
rkfd=0d0
endif
else
! Differential equation for wind
! d u{x,y,z}/dt = Fu_{x,y,z}
rkfd=0d0
endif
return
end function rkfd
!-----------------------------
function gravity(dir,m,g,r)
implicit none
integer,intent(in)::dir
double precision::gravity
double precision,intent(in)::m,g,r(1:3)
if(dir.eq.3)then
gravity=-m*g
else
gravity=0.d0
endif
return
end function gravity
!-------------------------------
function c1(a,eta)
implicit none
double precision::c1
double precision,intent(in)::eta,a
double precision,parameter::pi=dacos(-1.d0)
c1=6.d0*pi*eta*a
return
end function c1
!------------------------------
function c2(nv,a,eta,rho)
implicit none
double precision,parameter::pi=dacos(-1.d0)
double precision,intent(in)::nv,eta,a,rho
double precision::Cd,Reynolds,c2
external::Cd,Reynolds
c2=0.5d0*Cd(Reynolds(nv,a,eta,rho))*rho*pi*a*a
return
end function c2
!-----------------------------
function vis1(dir,v,a,eta)
implicit none
integer,intent(in)::dir
double precision,intent(in)::v(1:3),a,eta
double precision::vis1,norm,nv,c1
external::c1
nv=dsqrt(v(1)**2.d0+v(2)**2.d0+v(3)**2.d0)
norm=c1(a,eta)*nv
vis1=-norm*v(dir)/nv
return
end function vis1
!-------------------------
function vis2(dir,v,a,eta,rho)
implicit none
integer,intent(in)::dir
double precision,intent(in)::v(1:3),a,eta,rho
double precision::vis2,norm,nv,c2
external::c2
nv=dsqrt(v(1)*v(1)+v(2)*v(2)+v(3)*v(3))
norm=c2(nv,a,eta,rho)*nv*nv
vis2=-norm*v(dir)/nv
return
end function vis2
!--------------------------
function mag(dir,omg,v,a,rho)
implicit none
integer,intent(in)::dir
double precision,intent(in)::omg(1:3),v(1:3),a,rho
double precision,parameter::pi=dacos(-1.d0)
double precision::mag,L(1:3),nomg,nv,nL,Cl
nomg=dsqrt(omg(1)*omg(1)+omg(2)*omg(2)+omg(3)*omg(3))
if(nomg.le.1.d-14)then
mag=0.d0
return
endif
nv=dsqrt(v(1)*v(1)+v(2)*v(2)+v(3)*v(3))
L(1)=v(2)*omg(3)-v(3)*omg(2)
L(2)=v(3)*omg(1)-v(1)*omg(3)
L(3)=v(1)*omg(2)-v(2)*omg(1)
nL=dsqrt(L(1)*L(1)+L(2)*L(2)+L(3)*L(3))
if(nL.le.1.d-14)then
mag=0.d0
return
endif
! for BB bullet
Cl=0.12d0
mag=-Cl*(4.d0/3.d0)*pi*(a**3d0)*2.d0*rho*nomg*nv*L(dir)/nL
return
end function mag
!--------------------------
function Reynolds(nv,a,eta,rho)
!Reynolds number
! nv : norm of velocity of object
! a : radius of object
!eta : viscosity (not Kinetic viscosity)
!rho : density of fluid
implicit none
double precision,intent(in)::nv,a,eta,rho
double precision::keta,Reynolds
!keta means Kinetic viscosity
keta=eta/rho
Reynolds=nv*2.d0*a/keta
return
end function Reynolds
!---------------------------
function Cd(Re)
!From
!http://www.chem.mtu.edu/~fmorriso/DataCorrelationForSphereDrag2013.pdf
!Drag coefficient Cd,
!Cd depend on Reynolds number,Re.
!Fource of Drug,D is written by
! 1
! D= ---Cd*rho*pi*a**2*|V|**2
! 2
! ^ This Cd!
implicit none
double precision,intent(in)::Re
double precision::Cd,c1,c2,c3,c4
c1=24.d0/Re
c2=Re/5.d0
c2=2.6d0*c2/(1.d0+c2**(1.52d0))
c3=Re/263000d0
c3=0.411d0*c3**(-7.94d0)/(1.d0+c3**(-8d0))
c4=Re**0.8d0/461000d0
Cd=c1+c2+c3+c4
return
end function Cd
!----------------------------
function Nz(nv,a,eta,rho,omg)
!Moment of omg direction
implicit none
double precision,intent(in)::nv,a,eta,rho,omg
double precision::Nz,Cf,Fintegral
external::Cf,Fintegral
Nz=0.5d0*rho*Cf(nv,a,eta,rho)*a**3
Nz=Nz*Fintegral(nv,a,omg)
return
end function Nz
function Nze(nv,a,eta,rho,omg)
implicit none
double precision,intent(in)::nv,a,eta,rho,omg
double precision::Nze,Cf,Fintegral
double precision,parameter::pi=atan(1d0)*4d0
external::Cf,Fintegral
double precision::pc,tc,vu,vd,t
pc=pi/5.32065d0 ! magic phi
tc=pi/3.60475d0 ! magic theta
vu= nv*sin(pc)-a*omg*sin(tc)
vd=-nv*sin(pc)-a*omg*sin(tc)
Nze=-0.5d0*rho*Cf(nv,a,eta,rho)
Nze=Nze*(4d0*pi*a**2)*a*0.5d0
Nze=-Nze*(abs(vu)*vu+abs(vd)*vd)
return
end function Nze
!-------------------
function Cf(nv,a,eta,rho)
implicit none
! nv : norm of velocity of object
! a : radius of object
!eta : viscosity (not Kinetic viscosity)
!rho : density of fluid
double precision,intent(in)::nv,a,eta,rho
double precision::Reynolds,Cf
external::Reynolds
! Laminar flow
Cf=1.328d0/dsqrt(Reynolds(nv,a,eta,rho))
! Turbulent flow Re > 10^7
!Cf=0.455d0/(log10(Reynolds(nv,a,eta,rho))**(2.58d0))
return
end function Cf
!----------------------------------
function Fintegral(u,R,omega)
! 2016/07/23
! 2pi pi
! / /
! | dphi | |u*sin(phi)-R*omega*sin(theta)|*{u*sin(phi)-R*omega*sin(theta)}*sin^2(theta) d theta
! / /
! 0 0
implicit none
double precision,intent(in)::u,R,omega
double precision,parameter::pi=datan(1.d0)*4d0
double precision::Fintegral,s,Fphi,x(1:15),w(1:15)
external::Fphi
integer::i
s=0d0
call GaussKronrod15ab(0d0,pi,x,w)
do i=1,15
s=s+w(i)*Fphi(u,R,omega,x(i))
enddo
call GaussKronrod15ab(pi,2d0*pi,x,w)
do i=1,15
s=s+w(i)*Fphi(u,R,omega,x(i))
enddo
Fintegral=s
return
end function Fintegral
!------------------------------
subroutine GaussKronrod15ab(a,b,x,w)
!Gauss-Kronrod Quadrature Nodes and Weights
!http://www.advanpix.com/2011/11/07/gauss-kronrod-quadrature-nodes-weights/
implicit none
double precision,intent(in)::a,b
double precision,intent(out)::x(1:15),w(1:15)
integer::i
integer,parameter::N=15
x=0d0; w=0d0
x( 8) = 0d0
x( 9) = 2.077849550078984676006894037732449d-1
x(10) = 4.058451513773971669066064120769615d-1
x(11) = 5.860872354676911302941448382587296d-1
x(12) = 7.415311855993944398638647732807884d-1
x(13) = 8.648644233597690727897127886409262d-1
x(14) = 9.491079123427585245261896840478513d-1
x(15) = 9.914553711208126392068546975263285d-1
do i=1,7
x(i)=-x(N-i+1)
enddo
w( 8) = 2.094821410847278280129991748917143d-1
w( 9) = 2.044329400752988924141619992346491d-1
w(10) = 1.903505780647854099132564024210137d-1
w(11) = 1.690047266392679028265834265985503d-1
w(12) = 1.406532597155259187451895905102379d-1
w(13) = 1.047900103222501838398763225415180d-1
w(14) = 6.309209262997855329070066318920429d-2
w(15) = 2.293532201052922496373200805896959d-2
do i=1,7
w(i)=w(N-i+1)
enddo
x=0.5d0*((b-a)*x+(a+b))
w=0.5d0*(b-a)*w
return
end subroutine GaussKronrod15ab
!----------------------------------------
function Fphi(u,R,omega,phi)
! using analysis solution.
!
! pi
! /
! | |u*sin(phi)-R*omega*sin(theta)|*{u*sin(phi)-R*omega*sin(theta)}*sin^2(theta) d theta
! /
! 0
!
implicit none
double precision,intent(in)::u,R,omega,phi
double precision,parameter::pi=dacos(-1d0)
double precision::a,b,c,tp,Fphi,Rw
a=(u/(R*omega))*sin(phi)
if(a.le.0d0)then
Fphi=-(0.5d0*a*a*pi-8d0*a/3d0+3d0*pi/8d0)
elseif(a.ge.1d0)then
Fphi=0.5d0*a*a*pi-8d0*a/3d0+3d0*pi/8d0
elseif(a.gt.0d0.and.a.lt.1d0)then
tp=asin(a)
b=-a*a*pi*0.5d0-8d0*a/3d0-3d0*pi/8d0+(2d0*a*a+3d0/2d0)*tp
c=-(a*a+1d0)*dsin(2d0*tp)+dsin(4d0*tp)/8d0+6d0*a*dcos(tp)-2d0*a*dcos(3d0*tp)/3d0
Fphi=b+c
else
write(6,*)"undefined at Fphi, program stop",a
stop
endif
Rw=R*omega
Fphi=Fphi*Rw*abs(Rw)
return
end function Fphi
!---------------------------------
subroutine bullet_orbit(N,x0,Nt,time,filename,ik)
!sikinote http://slpr.sakura.ne.jp/qp/
!Author : sikino
!Date : 2016/03/18 (yyyy/mm/dd)
! : 2016/03/20
use GBL
use RKmod
implicit none
integer,intent(in)::ik,N,Nt
double precision,intent(in)::x0(1:N),time(0:Nt)
character(*),intent(in)::filename
double precision,parameter::pi=datan(1d0)*4d0
integer::info,i,j
double precision::x(1:N),Ene,h,t,tbound,rkfd
external::rkfd
x=x0
info=0
t=time(0)
open(22,file=trim(filename),status='replace')
write(22,'(A,e12.5e1,A)')"# m: ",m,"[kg]"
write(22,'(A,f12.5,A)')"# g: ",g,"[m s^{-2}]"
write(22,'(A,e12.5e1,A)')"# a: ",a,"[m]"
write(22,'(A,f12.5,A)')"# temperature: ",temperature,"[degree Celsius]"
write(22,'(A,f12.5,A)')"# moisture: ",moisture,"[no-dimension]"
write(22,'(A,f12.5,A)')"# pressure: ",pressure,"[Pa]"
write(22,'(A,e12.5e1,A)')"# eta:",eta,"[kg m^{-1} s^{-1}]"
write(22,'(A,f12.5,A)')"# rho:",rho,"[kg m^{-3}]"
write(22,'(A,e12.5e1)')"# tol:",tol
write(22,'(A,e12.5e1)')"# eps:",eps
write(22,'(A,14A13)')"#","t[s]","x[m]","y[m]","z[m]","vx[m/s]","vy[m/s]","vz[m/s]" &
,"wx[rot/s]","wy[rot/s]","wz[rot/s]","windx[m/s]","windy[m/s]","windz[m/s]","Energy[J]"
Ene=0.5d0*m*(x(4)**2+x(5)**2+x(6)**2)
write(22,'(14f13.6)')t,(x(i),i=1,6),(x(i)/(2d0*pi),i=7,9),(x(i),i=10,12),Ene
call rk_preparation("rkf45")
do j=0,Nt-1
t=time(j); tbound=time(j+1); h=tbound-t
call rkf451_e(rkfd,t,x,tbound,info,tol,ik)
Ene=0.5d0*m*(x(4)**2+x(5)**2+x(6)**2)
write(22,'(14f13.6)')t,(x(i),i=1,6),(x(i)/(2d0*pi),i=7,9),(x(i),i=10,12),Ene
!Stop calculation when bullet reach ground.
if(x(3).lt.0d0)exit
enddo
call rk_deallocation("rkf45")
close(22)
write(6,'(A,e10.3)')"Reach ground at ",t
return
end subroutine bullet_orbit
program main
use GBL
implicit none
integer::i,N,Nt,ik
double precision,allocatable::x(:),time(:),r(:),u(:)
double precision,parameter::pi=datan(1d0)*4d0
double precision::rx,ry,rz,vx,vy,vz,ux,uy,uz,omgx,omgy,omgz
double precision::energy,zeroinx,updownz,stept,exvz,exwy,theta
character(48)::outputfile,filename,search_zeroin,search_updown
double precision::tbound
double precision::rho_humid,eta_air
double precision::r0(1:3),v0(1:3),omg0(1:3),u0(1:3)
external::rho_humid,eta_air
double precision::xa,xb,za,zb
integer::nodes,poles
real::t1,t0
namelist /input/m,a,energy,g,temperature,pressure,moisture &
,omgdecay,search_zeroin,zeroinx,search_updown,updownz &
,theta,rx,ry,rz,vy,ux,uy,uz,omgx,omgy,omgz &
,stept,outputfile,ik
open(10,file="./input")
read(10,nml=input)
close(10)
write(*,nml=input)
N=12
eta=eta_air(temperature)
rho=rho_humid(temperature,pressure,moisture)
vx=dsqrt((2d0*energy/m)-vy**2)*dcos(pi*theta/180d0)
vz=dsqrt((2d0*energy/m)-vy**2)*dsin(pi*theta/180d0)
omgx=omgx*2*pi
omgy=omgy*2*pi
omgz=omgz*2*pi
allocate(x(1:N))
x(1)=rx; x(4)=vx; x(7)=omgx; x(10)=ux
x(2)=ry; x(5)=vy; x(8)=omgy; x(11)=uy
x(3)=rz; x(6)=vz; x(9)=omgz; x(12)=uz
tbound=100d0
Nt=nint(tbound/stept)
allocate(time(0:Nt)); time=0d0
do i=0,Nt
time(i)=dble(i)*stept
enddo
filename=trim(outputfile)//".txt"
call bullet_orbit(N,x,Nt,time,filename,ik)
call cpu_time(t0)
if(trim(search_zeroin).eq."yes")then
write(6,'(A)')"==============================="
write(6,'(A,f10.5)')" search vz and wy by zeroin --> ", zeroinx
allocate(r(1:3),u(1:3)); r(1:3)=x(1:3); u(1:3)=x(10:12)
call detwy(energy,r,x(5),x(7),x(9),u,zeroinx,exwy,exvz,ik)
write(6,*)exwy/(2d0*pi),exvz
x(4)=dsqrt((2d0*energy/m)-exvz**2-vy**2)
x(5)=vy
x(6)=exvz
x(8)=exwy
filename=trim(outputfile)//"_opt.txt"
call bullet_orbit(N,x,Nt,time,filename,ik)
deallocate(r,u)
endif
if(trim(search_updown).eq."yes")then
write(6,'(A)')"==============================="
write(6,'(A,f10.5)')" search vz and wy by up-down height --> ", updownz
allocate(r(1:3),u(1:3)); r(1:3)=x(1:3); u(1:3)=x(10:12)
call detwy2(energy,r,x(5),x(7),x(9),u,updownz,exwy,exvz,ik)
write(6,*)exwy/(2d0*pi),exvz
x(4)=dsqrt((2d0*energy/m)-exvz**2-vy**2)
x(5)=vy
x(6)=exvz
x(8)=exwy
filename=trim(outputfile)//"_h.txt"
call bullet_orbit(N,x,Nt,time,filename,ik)
deallocate(r,u)
endif
call cpu_time(t1)
write(6,'(f10.3,A)')(t1-t0),"[CPU sec]"
stop
end program main





初めまして
とても興味深い研究をされていますね、難しくて理解が中々追いつきませんが・・・
私もパラメータを変えて色々調べてみたくなり
本日gfortranとgnuplotで上記コードと実行結果のinputファイルを合わせたのですが
どうにも計算結果が合わないのです・・・
inputファイル読み込み後のReach ground at 0.490E+00あたりからずれてきます
無知ですみません、どこか問題あるのでしょうか・・・
初めまして。ご連絡ありがとうございます。
恐らく、その原因は私が1週間ほど前にプログラムを変更したからだと思います。
その際にプログラムだけを変更し、画像やその他データは変更以前のままにしてしまいました。
その変更に伴って現在のコードでは、最適な軌道を探すことはできなくなっているようです。
今週末か来週末くらいには訂正いたしますので、それまでお待ちください。
私の間違いです。お手数おかけしてすみません。
sikinoさん:
ご返答ありがとうございます
そういう事だったんですね、調査頂き少し安心致しました
研究の妨げにならない程度に進めていただければ結構ですので
気長にお待ちしております
よろしくお願いいたします
purinさん
プログラムの変更を行いました。
問題なく動くと思うので試してみてください。
もしも不具合がありましたらご連絡いただけると幸いです。
こんにちは
試したところ、うまく動作致しました
ありがとうございます!
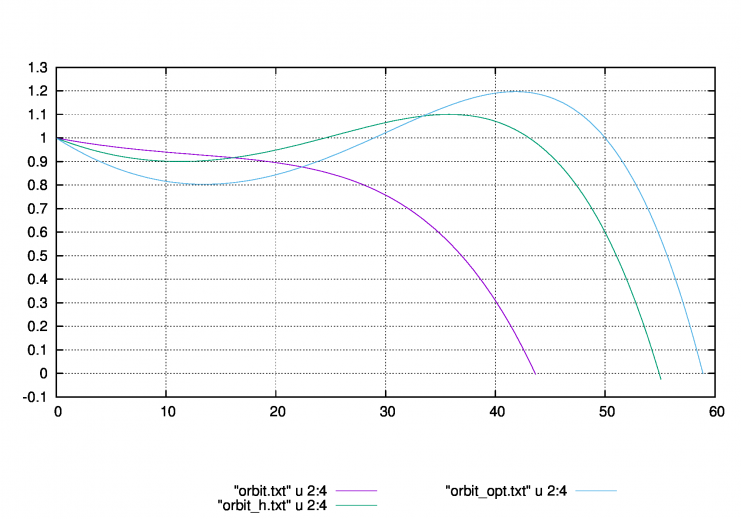
私の銃は0.28gでは弾道を見る限り全然ホップが足りていないようです・・・調整の目指す方向が数値から見えるのはやっぱり素晴らしいです。
また弾道データにスコープの照準ラインを追加して、ゼロイン時のホップ調整の参考に致します。
purinさん
動作してよかったです。
スコープのラインを入れれば確かに見やすそうですね。
恐らく線に色を付けたほうがスコープで覗くことを考えた際良いと思います。
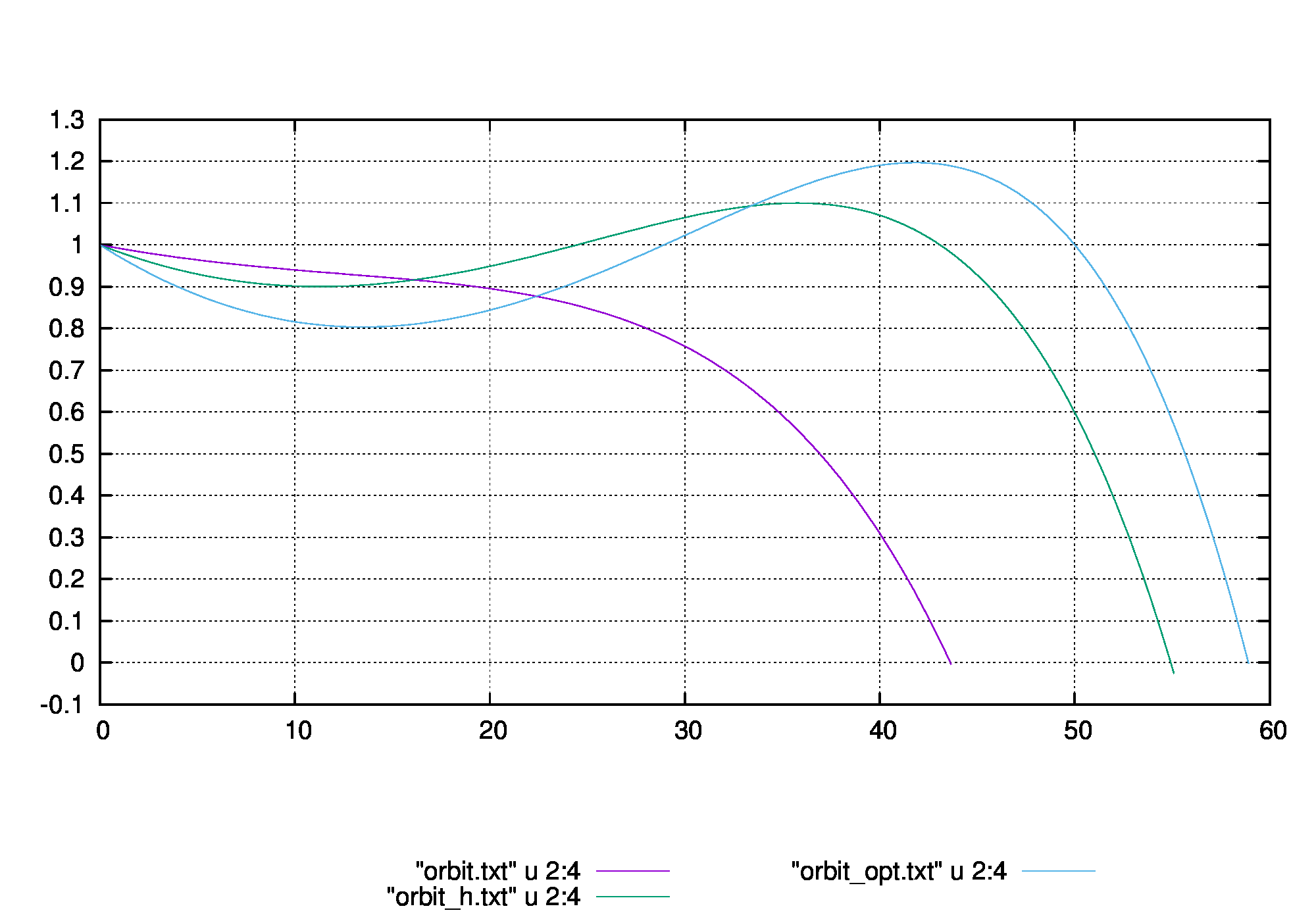
例えばgnuplot上では
とすることで
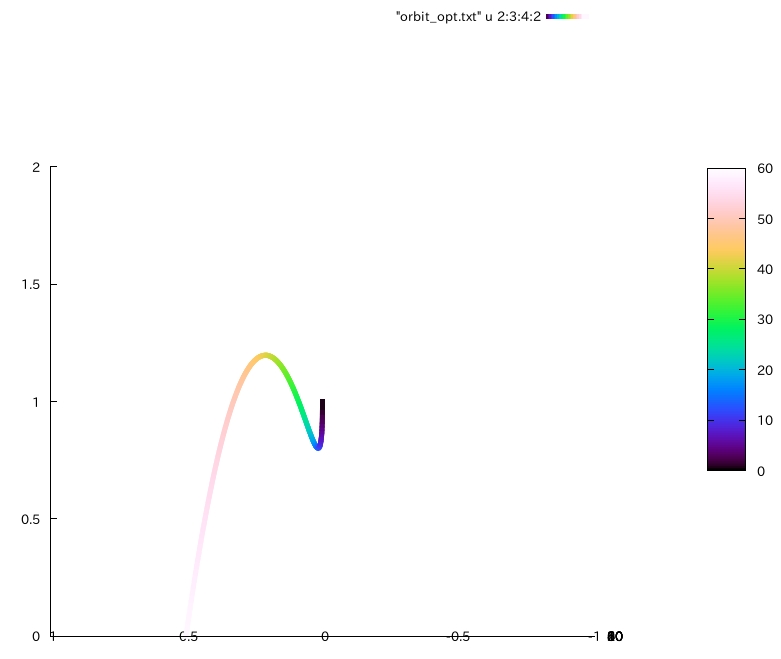
というような画像が得られます。ご参考ください。
初めまして、飛翔する物体について調べたいと思い、何か良いサイトはないかと思い検索をかけていたところこのサイトに辿り着きました。
球体に対する力に関する方程式や、RK法の解説など詳しく解説がされており、この分野についての教養を深めることができたと思います。
弾道計算のプログラムについても公開をされていたので、試しに私も計算をシミュレーションしてみようと考えたのですが、gfortranにおいてコンパイルを行った後に、./a.outにてプログラムを実行しようとした際に
At line 1457 of file main.f90 (unit=10,file=’./input’)
Fortran rutime error: End of file
と表示がされ、エラーにてストップしてしまいました。
最初は作成をしたinputファイルに実行の許可がないために起きているのかと思い、chmodにて実行許可を出してみたりもしたのですが、実行することができませんでした。
このエラーについて何かご存知であれば教えて頂ければと思い、コメントさせて頂きました。
お手数ですが、お返事頂ければと思います。
初めまして。
方程式、数値計算法を含めご覧いただき嬉しい限りです。
gfortranでコンパイルした際、確かに
At line 1457 of file main.f90 (unit=10,file=’./input’)
Fortran rutime error: End of file
というエラーがでました。現在のところ詳しい理由は分かりません。
inputの中の変数 “ik” に原因があるようです。とりあえずの処置としては、inputファイルの中のikを消し、プログラム本文にて直接ik=0と書いてください。こうすればエラーが出ません。
幾日かの間に原因を見つけたいと思います。
ifortでは問題なく動作したため、gfortranの問題だと考えています。
>>sikinoさん
お返事いただきありがとうございます。
ご教授頂いたように、inputファイル中の変数ikを消し、一先ず本文プログラム中のprogram main内における1461行目に「ik=0」と追加をし、gfortranにてコンパイルを行い再実行を行ったのですが、先程投稿した内容と同様のエラーが出てきてしまいました。
此方あまりfortranには詳しくないのですが、この場合のinputファイルはlinuxにおいて拡張子なしのファイルで「input」と命名する形でよろしいのでしょうか。
ifortにおいては問題なく実行できるとのことですので、入手ができましたらそちらの方でも試してみたいと思います。
adeluguさん
inputファイルはおっしゃる通りの意味です。
あるディレクトリ”dir”の中に
dir
├── input
└── main.f90
というファイルが作られることを想定しています。
「inputファイル」は拡張なしのファイル名”input”というファイルのことです。
“dir”, “main.f90″の名前は何でも構いませんが、”input”はinputという名前でなければなりません。
試していただきたいのが以下の2つの手順です。
・内容は変わっていませんが、新たなディレクトリを用意し、新たに上記プログラムと”input”をコピペしてください。
・inputファイルの最後、&end の後に改行を入れてください。
—————————
&input
….
&end
—————————
ではなく、
—————————
&input
….
&end
—————————
としてみてください。恐らくgfortranの仕様です。
>>sikinoさん
ご教授頂いた内容の通り、&end後に1行改行を入れた結果コードを無事に動かすことができました。
私の知識不足により貴重なお時間を割いて返信をいただけたこと、お礼申し上げます。
gfortranに限らず、様々なプログラム、コンパイラを使用する上での仕様を理解しておくことの重要さを今回のことで理解できた気がします・・・。
adeluguさん
動作したようで安心しました。
計算をどうぞお楽しみください。
こんにちは。
ナポレオン時代の砲弾の弾道計算をしたいと思い、色々と調べて
このホームページを見つけました。プログラムを使わせて頂き
試算した所、精度の良い結果を得る事ができました。
大変ありがとうございます。
なお、私の環境(OS : Windows10 64bit)では、gfortranの古いVer5.1を
使うとinputのデータを読込む際に(write文で)Segmentation faultエラーが
発生しました。新しいVer6.2では発生しませんので、コンパイラーの問題
のようです。Ver5.1以前のものは使わないように注記されては如何でしょうか。
Bernadotte66さん
こんにちは。
ご報告ありがとうございます。
砲弾に対しても良い結果が得られたとのことで、嬉しく思います。
若干詳細に入るのですが、砲弾…おそらく球形だと思いますが、これは物理的に本当に下回転がかかる仕組みになっているのか、と疑問に思いました。
そうでなければ、別の要因を考える必要が出てきます。
gfortranコンパイラに問題があることは感じていました。
それも指摘して頂いた通り、inputファイルに関連する問題です。
私はlinux mint, gfortranのver4.8.4を使用しており、
”inputファイルの最後に空行を入れる事”
で何とか回避ができる、ということが分かっています。
ただし、これはreadの部分であって、writeの部分ではありません。
もしかしたら、上記問題とは別の問題がwindows版のgfortranコンパイラでは起こっているのかもしれません。
windows版についてgfortranのバージョンに関して注記いたしました。ご連絡ありがとうございました。
>>sikinoさん
弾道計算した砲弾は鉄の球体です。また、ナポレオン時代の大砲の砲身は、
内部に砲弾の回転を掛ける仕組みはありません。ライフルのような溝を
切っている訳ではなく、単純な筒状のものです。
従って、揚力が効いている根拠となる物理的なデータは、ありません・・・。
しかし、次の理由で揚力か、それに相当するものが効いていると思います。
1)砲弾が地面に跳ね返って進む跳弾の計算をした場合に、地面に初めて
着弾する距離はパラメータの調整で合わせる事はできる。
2)しかし、同じ計算式を使って2回目と3回目の着弾距離が実測値(本に
記載されたもの)と同様な値になるのは、計算式が正しいからである。
計算例)1つの砲弾が2回地面に跳ね返って3回着弾する距離の計算結果
⇒大砲の射出口を基準0mとして水平方向に測った距離。
1回目 2回目 3回目
実測値 365m 548m 640m
計算値 367m 563m 641m
Bernadotte66さん
ご返信ありがとうございます。
現在のところ、1),2)に関しましては以下のように考えています。
1)に関してはまさにその通りで、パラメータは調整するべきだと思います。
2)に関しては状況を反映していないので賛成はできません。
状況を把握するためにBernadotte66さんのページを拝見させていただきました。
余計なおせっかいかもしれませんが、私なりの意見を述べさせていただきたいと思います。
私の結論としては「初速が異なっている」です。
初速が異なる、を考えた理由としまして
着弾距離:Artillery Equipments of the Napoleonic Wars p28
初速:Manuel d’Artillerie p212の8ポンド砲
と別の文献から得られていることから、両者で使用している大砲が同一のものであるか不明であった点です。
前者の本を閲覧できる状況にないので、私が直接確認することが出来ませんでした。
なので、もし異なる大砲であり、着弾距離を基準にする場合初速や仰角、砲台の高さも若干変わるかもしれません。
また、砲弾の描像としましては、以下の事が起きていると考えます。
[発射~1回目の着弾]
私は発射直後、1回目の着弾までは回転はほとんど起きていない、と考えます。
もしも発射時の高さが決まっていれば、初速は1回目の着弾位置を回転無しで逆算するのが良いと思います。
これが余りにも的外れな初速でしたら別の要因を考えなければいけません。
[1回目の着弾~2回目の着弾]
1回目の着弾後は地面と接触し、前方向への回転が発生するはずです。
この場合、1回目と2回目の着弾までの間はトップスピンになるわけですから、早くに着弾すると思います。
また無視できるかもしれませんが、砲弾の運動エネルギーは回転のエネルギーへいくらか変換されるはずです。
もちろん、Bernadotte66さんの考察通り反発係数も考える必要が出てきます。
[2回目の着弾~3回目の着弾]
その後の着弾では回転は弱まり、3回目の着弾を迎える、というのが正しい描像だと考えています。
(もしかして
1364 Pied/second = 416 m/s
ではないでしょうか。
1364 Pied/secondはManuel d’Artillerie p212を参考にしましたので、間違いはないと思います。)
こんにちは。
私のブログまで見て頂き、ご意見ありがとうございます。
いつかの点について、補足致します。
1) 着弾距離と初速を記述している大砲が同一かどうか
個体としては同一ではないと思います。
但し、フランス軍の8ポンド砲は、グリボーバル・システムと呼ばれる大砲の
標準化を基に大量に製造されたものです。個体差のバラつきはありますが、
平均的な性能を検討するので同じで良いと考えました。
2) Piedの換算
国際フィートでは0.3048mですので、1364 Pied/second = 416 m/sになります。
しかし、Manuel d’Artillerieは1836年に出版されたもので、国際フィートが
制定された1958年よりも前です。下記のホームページに記載されたフランスで
1799年まで使われていた0.324839mの方が適切と思って採用しました。
https://fr.wikipedia.org/wiki/Pied_(unit%C3%A9)#Le_pied_entre_1668_et_1799
3) ご指摘の回転なしで逆算した初速
850m/sとなり、Manuel d’Artillerieの2倍近くです。
フランス軍8ポンド砲は、砲弾と火薬が一体化された弾薬を使うので、
初速がこれほど違うのは考えにくいです。
4) 個体差のバラつきなどを考慮
10%以上の差はないと思いますが、以下のようにデータを10%変更した場合の
第1回着弾距離は275mです。本に記載されている365mと余りにも違うので、
個体差のバラつきではないと思います。
半径 0.0515m ⇒ 0.0464m
初速 443m/s ⇒ 487m/s
砲身の高さ 1.11m ⇒ 1.22m
仰角 0° ⇒ 0.1°
温度 20℃ ⇒ 0℃ (バラつきでなく、条件を良くする為)
湿度 40% ⇒ 20% (バラつきでなく、条件を良くする為)