「数学」カテゴリーアーカイブ

exp(-ikx)/x の無限区間に渡る積分を数値的に計算したい。

2018年5月3日 sikino コメントする

問題：以下の積分を数値的に計算せよ。
$ \displaystyle
-\frac{1}{2\pi i}\int_{-\infty}^{\infty} \frac{e^{-ikx}}{x}dx,~~(kは任意の実数)
$

1/xのフーリエ変換である
$ \displaystyle
\int_{-\infty}^{\infty} \frac{e^{-ikx}}{x}dx,~~(kは任意の実数)
$
を数値的に計算します。

この積分値は一意には決まりません。
複素関数論によると、この積分値は$x=0$周りに存在する特異点を上周りに迂回して積分するか、下周りに迂回して積分するか、で答えが異なります。

特異点を上周りに回る場合、答えは
$
\begin{eqnarray}
\lim_{\varepsilon\to +0} \int_{-\infty}^{\infty}\frac{e^{-ikx}}{x+i\varepsilon}dx =
\left\{
\begin{aligned}
-2\pi i~~~(k\gt 0)\\
0~~~(k\lt 0)
\end{aligned}
\right.
\end{eqnarray}
$
であり、特異点を下周りに回る場合、
$
\begin{eqnarray}
\lim_{\varepsilon\to +0} \int_{-\infty}^{\infty}\frac{e^{-ikx}}{x-i\varepsilon}dx =
\left\{
\begin{aligned}
0~~~(k\gt 0)\\
2\pi i~~~(k \lt 0)
\end{aligned}
\right.
\end{eqnarray}
$
となります。
私が疑問に思うのは、積分すると本当にステップ状の関数が現れるのか？ということです。にわかには信じられません。

ここでは、上を回った時の計算にのみ注目します。
答えに出てくる係数を減らしたいため、被積分関数
$ \displaystyle
-\frac{1}{2\pi i}\int_{-\infty}^{\infty} \frac{e^{-ikx}}{x}dx
$
を考えます。

数値計算方法

さて、問題を整理しましょう。今取り組む問題は、

問題：以下の積分を数値的に計算せよ。
$ \displaystyle
-\frac{1}{2\pi i}\int_{-\infty}^{\infty} \frac{e^{-ikx}}{x}dx,~~(kは任意の実数)
$
です。読み取れる情報は

・始点は、実軸上のマイナス無限大
・終点は、実軸上のプラス無限大
・$x=0$に特異点が存在する

という情報です。これらは理由なく勝手に変えてはいけません。
被積分関数が収束するならば、xがどんなに大きくても無限遠まで振動していきますが、フレネル積分のように積分結果は収束することを期待しましょう。

さて、$x=0$に特異点があるために、実軸上のマイナス無限からプラス無限まで積分していこうとすると$x=0$を通過しようとする時に無限大になるため、オーバーフローします。
ということで、積分経路を特異点周りで迂回します。

始点と終点は決められていますが、積分経路の指定はありませんので何も問題ありません。
積分経路は以下の図のように取ります。

このようにとると、積分経路上に特異点はないですので計算することが出来ます。
始点と終点は十分大きい値、ここでは(±2000,0)という値にします。

横軸をkとして、積分を計算すると以下のようになります。

複素関数論から、特異点を複素平面上方を迂回した場合に得られる解は
$
\begin{eqnarray}
\lim_{\varepsilon\to +0} -\frac{1}{2\pi i}\int_{-\infty}^{\infty}\frac{e^{-ikx}}{x+i\varepsilon}dx =
\left\{
\begin{aligned}
1~~~(k\gt 0)\\
0~~~(k\lt 0)
\end{aligned}
\right.
\end{eqnarray}
$
です。数値計算によって得られた解は、$k\lt 0$で値0, $k\gt 0$で値1であるので、数値的にも正しそうです。
しかし、厳密にそれぞれの値になっているわけではないことに気が付きます。なぜならば、$k=0$周りでは値は収束していないように見えます。
この原因は始点と終点としてとった、大きい値(±2000,0)が十分ではない事を意味しています。kが小さいと、被積分関数の$\exp(-ikx)$による振動はゆっくりになるため、収束が遅くなっている、と考えられます。

ジョルダンの補題の利用

この振動を無くすためには被積分関数が漸近領域で収束するように積分経路を変えればいいのです。

始点と終点は変わりません。図は$k$が負の時の経路です。

経路の取り方は無数にあり、上の経路は一つ前の計算で選んだ経路を出来る限り変更しないように経路をとっているだけにすぎません。

ジョルダンの補題を利用すれば、被積分関数が収束する領域であれば積分の寄与はゼロなので、数値的に積分する場合の視点、終点を複素平面上へ移すことが出来ます。
この考えの下実際に計算すると積分結果はこうなります。

綺麗なエッジが作られました。これならば解析解と数値解が一致した、と言えるでしょう。複素平面上の数値計算は一筋縄ではいかないことが実感できました。

数値計算プログラム

プログラムは以下のものを用いています。

数値積分はquadpackのガウス=ルジャンドル求積法の自動積分コードを複素関数用に変更して用いています。
実際に使用しているquadpackコードは以下のもので、
https://slpr.sakura.ne.jp/qp/supplement_data/quadpack_cqag.f90
これと、下のはmainプログラムです。

program main
implicit none
integer::ier,Nt,i,j,sn
double precision::eps
complex(kind(0d0))::a,b,s,s0
complex(kind(0d0))::xa(1:5),xb(1:5)
complex(kind(0d0)),external::g

eps=1d-10
ier=1

Nt=1000
do i=1,Nt
t=i*(1d0-(-1d0))/dble(Nt)-1d0
s=dcmplx(0d0,0d0)

sn=1
if(t.gt.0d0)sn=-1
if(t.eq.0)sn=0

xa(1)=dcmplx(-2000d0,sn*2000d0)
xb(1)=dcmplx(-1d0,0d0)

xa(2)=dcmplx(-1d0,0d0)
xb(2)=dcmplx(-1d0,1d0)

xa(3)=dcmplx(-1d0,1d0)
xb(3)=dcmplx( 1d0,1d0)

xa(4)=dcmplx( 1d0,1d0)
xb(4)=dcmplx( 1d0,0d0)

xa(5)=dcmplx( 1d0,0d0)
xb(5)=dcmplx( 2000d0,sn*2000d0)

do j=1,5
s0=dcmplx(0d0,0d0)
call cqag_sk(g,xa(j),xb(j),eps,s0,3,ier)
s=s+s0
enddo
write(10,*)t,dble(s),dimag(s)
enddo

stop
end program main

function g(z)
implicit none
complex(kind(0d0))::g
complex(kind(0d0)),intent(in)::z

double precision::pi=dacos(-1d0)

g=exp(-dcmplx(0d0,1d0)*z*t)/(z)
g=g*(-1d0/(2d0*pi*dcmplx(0d0,1d0)))

return
end function g

オリジナルのquadpackコードは
http://www.netlib.org/quadpack/（パブリックドメイン）です。

数学

1/(x^n)のフーリエ変換

2017年11月18日 sikino コメントする

その他フーリエ変換
ヘヴィサイド関数のフーリエ変換
 1のフーリエ変換
 $x$のフーリエ変換
 $1/x$のフーリエ変換
 $1/(x^n)$のフーリエ変換 ← 今ここ

$\frac{1}{x}$のフーリエ変換から$\frac{1}{x^n}$のフーリエ変換を導けます。
$
\begin{align}
\int_{-\infty}^{\infty}\frac{1}{x}e^{-ikx}dx =-\pi i ~\text{sgn}(k)
\end{align}
$
（導出は$\frac{1}{x}$のフーリエ変換へ）

部分積分を用いると$\frac{1}{x^2}$のフーリエ変換
$
\begin{align}
&\int_{-\infty}^{\infty}\frac{1}{x}\left(\frac{1}{-ik}e^{-ikx}\right)’dx \\
&=\left[\frac{1}{x}\cdot\frac{1}{-ik}e^{-ikx}\right]_{-\infty}^{\infty} -\frac{1}{ik}\int_{-\infty}^{\infty}\frac{1}{x^2}e^{-ikx} dx
\end{align}
$
第一項はゼロになります。第二項と残りの項と$1/x$のフーリエ変換の右辺が等しいので、
$
\begin{align}
\int_{-\infty}^{\infty}\frac{1}{x^2}e^{-ikx} dx =-\pi k ~\text{sgn}(k)
\end{align}
$
が得られます。
これを繰り返すことで$\frac{1}{x^n}$のフーリエ変換
$
\begin{align}
\int_{-\infty}^{\infty}\frac{1}{x^n}e^{-ikx}dx &=-\pi i \frac{(-ik)^{n-1}}{(n-1)!}~\text{sgn}(k)
\end{align}
$
が導かれます。

数学

1/xのフーリエ変換

2017年11月18日 sikino コメントする

\begin{align}
\int_{-\infty}^{\infty}\frac{1}{x}e^{-ikx}dx =-\pi i ~\text{sgn}(k)
\end{align}
※ただし、$x=0$での値は定義しない。また、$\text{sgn}(x)$は符号関数

数値計算による上式の確かめはexp(-ikx)/x の無限区間に渡る積分を数値的に計算したい。をご覧ください。

その他フーリエ変換
ヘヴィサイド関数のフーリエ変換
 1のフーリエ変換
 $x$のフーリエ変換
 $1/x$のフーリエ変換 ← 今ここ
$1/(x^n)$のフーリエ変換

実軸上の積分は複素平面の上から近づいた値と下から近づいた値の平均をとって定めるとします。すなわち、
$
\begin{align}
&\int_{-\infty}^{\infty}\frac{1}{x}e^{-ikx}dx \nonumber \\
&=\lim_{\varepsilon\to +0} \frac{1}{2}\left[\int_{-\infty}^{\infty}\frac{1}{x+i\varepsilon}e^{-ikx}dx +\int_{-\infty}^{\infty}\frac{1}{x-i\varepsilon}e^{-ikx}dx \right]
\end{align}
$
で表されると仮定します。
そして、第1項、第2項をそれぞれ計算していきます。

$
\displaystyle \lim_{\varepsilon\to +0}\int_{-\infty}^{\infty}\frac{1}{x\pm i\varepsilon}e^{-ikx}dx
$
を計算するにあたり、複素x平面上の漸近で収束する半径が$k$の符号によって異なるので場合分けをしてます。

$k\gt 0$の時

まず、$\varepsilon$の符号が正である場合を考えます。
この実軸上の積分は実軸への近づき方を指定して
$
\begin{align}
\lim_{\varepsilon\to +0} \int_{-\infty}^{\infty}\frac{1}{x+i\varepsilon}e^{-ikx}dx =
\left[\int_{-\infty}^{-\varepsilon’}+\int_{\Gamma_+}+\int_{\varepsilon’}^{\infty}\right]\frac{e^{ikx}}{x}dx
\end{align}
$
です。ここで、$\int_{\Gamma_+}$は特異点周りを複素平面上半面を通る経路です。
この積分を計算するために閉路積分を考えます。すなわち、以下の図の左側のように回った積分を考えます。

すると、この閉経路に対して、
$
\begin{align}
\oint \frac{e^{-ikx}}{x}dx&=
\lim_{R\to\infty}\left[\int_{-R}^{-\varepsilon’}+\int_{\Gamma_+}+\int_{\varepsilon’}^{R}+\int_{\Gamma’}\right]
\frac{e^{ikx}}{x}dx\\
&=\lim_{\varepsilon\to +0} \int_{-\infty}^{\infty}\frac{1}{x+i\varepsilon}e^{-ikx}dx+\lim_{R\to\infty}\int_{\Gamma’}\frac{e^{-ikx}}{x}dx
\end{align}
$
が成立します。今、閉経路内に特異点が一つ存在し、負の方向に回っているので、左辺$\oint \frac{e^{-ikx}}{x}dx=-2\pi i$です。また、大きく外側を回る経路$\Gamma’$の積分はゼロです。よって、
$
\begin{align}
\lim_{\varepsilon\to +0}\int_{-\infty}^{\infty}\frac{1}{x+i\varepsilon}e^{-ikx}dx =-2\pi i.
\end{align}
$
が示されます。

また、特異点を下に回る積分（図の左の経路）では、閉経路内に特異点は存在しないので、$\oint \frac{e^{-ikx}}{x}dx=0$です。なので、
$
\begin{align}
\lim_{\varepsilon\to +0}\int_{-\infty}^{\infty}\frac{1}{x-i\varepsilon}e^{-ikx}dx =0.
\end{align}
$
と導けます。

$k\lt 0$の時

まず、$\varepsilon$の符号が正である場合を考えます。

kが正の時と異なる点は、漸近で収束する領域が複素x平面の上半面であるという点です。

図の左のような閉経路を考えます。

同様に計算を行うと
$
\begin{align}
\oint \frac{e^{-ikx}}{x}dx&=
\lim_{R\to\infty}\left[\int_{-R}^{-\varepsilon’}+\int_{\Gamma_+}+\int_{\varepsilon’}^{R}+\int_{\Gamma’}\right]
\frac{e^{ikx}}{x}dx\\
&=\lim_{\varepsilon\to +0} \int_{-\infty}^{\infty}\frac{1}{x+i\varepsilon}e^{-ikx}dx+\lim_{R\to \infty}\int_{\Gamma’}\frac{e^{-ikx}}{x}dx
\end{align}
$
今、閉経路内に特異点を含まないので、左辺$\oint \frac{e^{-ikx}}{x}dx=0$、また遠方ではゼロに近づくので、$\int_{\Gamma’}\frac{e^{ikx}}{x}dx=0$です。よって、
$
\begin{align}
\lim_{\varepsilon\to +0}\int_{-\infty}^{\infty}\frac{1}{x+i\varepsilon}e^{-ikx}dx =0.
\end{align}
$
また、特異点周りを正方向に回る場合、閉経路内に特異点を含むので、
$
\begin{align}
\lim_{\varepsilon\to +0}\int_{-\infty}^{\infty}\frac{1}{x-i\varepsilon}e^{-ikx}dx =2\pi i.
\end{align}
$
となります。

$k= 0$の時

$k=0$では被積分関数は漸近で収束しません。なので漸近で大きく回った時の値がゼロになりません。

ここからは誤解を恐れずに計算します。
今求めたい積分は
$
\int_{-\infty}^{\infty}\frac{1}{x}e^{-i0x}dx =\int_{-\infty}^{\infty}\frac{1}{x}dx
$
です。実軸上の積分がこのページで書いた
$
\begin{align}
&\int_{-\infty}^{\infty}\frac{1}{x}e^{-ikx}dx \nonumber \\
&=\lim_{\varepsilon\to +0} \frac{1}{2}\left[\int_{-\infty}^{\infty}\frac{1}{x+i\varepsilon}e^{-ikx}dx +\int_{-\infty}^{\infty}\frac{1}{x-i\varepsilon}e^{-ikx}dx \right]
\end{align}
$
で定義されているのだとすれば、
$
\begin{align}
\int_{-\infty}^{\infty}\frac{1}{x}dx =\lim_{\varepsilon\to +0} \frac{1}{2}\left[\int_{-\infty}^{\infty}\frac{1}{x+i\varepsilon}dx +\int_{-\infty}^{\infty}\frac{1}{x-i\varepsilon}dx \right]
\end{align}
$
です。簡単のため、特異点を含まない閉経路を取れば第1項は
$
\begin{align}
\lim_{R\to \infty}
\left[\int_{-R}^{-\varepsilon’}+\int_{\Gamma_+}
+\int_{\varepsilon’}^{R}+\int_{\Gamma’} \right]\frac{1}{x}dx =\oint \frac{1}{x}dx=0
\end{align}
$
なので、
$
\begin{align}
\lim_{\varepsilon\to +0} \int_{-\infty}^{\infty}\frac{1}{x+i\varepsilon}dx +\int_{\Gamma’} \frac{1}{x}dx =0
\end{align}
$
となります。外側を回る経路$\Gamma’$を通った積分は
$
\begin{align}
\int_{\Gamma’} \frac{1}{x}dx &=\int_0^\pi \frac{1}{re^{i\theta}}ire^{i\theta} d\theta \\
&=\pi i
\end{align}
$
と計算できてしまうので、代入すれば
$
\begin{align}
\lim_{\varepsilon\to +0} \int_{-\infty}^{\infty} \frac{1}{x+i\varepsilon} dx=-\pi i
\end{align}
$
となります。また、同様にして
$
\begin{align}
\lim_{\varepsilon\to +0} \int_{-\infty}^{\infty} \frac{1}{x-i\varepsilon} dx=\pi i
\end{align}
$
を得ます。
よって、実軸上の積分の式に代入すれば
$
\begin{align}
\int_{-\infty}^{\infty}\frac{1}{x}dx =\lim_{\varepsilon\to +0} \frac{1}{2}\left[(-\pi i) +\pi i \right] =0
\end{align}
$
を得ます。すなわち、フーリエ変換後の$k=0$の値はゼロということです。

計算結果のまとめ

以上をまとめると、3つの関係式
$
\begin{eqnarray}
\lim_{\varepsilon\to +0} \int_{-\infty}^{\infty}\frac{e^{-ikx}}{x+i\varepsilon}dx =
\left\{
\begin{aligned}
-2\pi i~~~(k\gt 0)\\
0~~~(k\lt 0)
\end{aligned}
\right.
\end{eqnarray}
$

$
\begin{eqnarray}
\lim_{\varepsilon\to +0} \int_{-\infty}^{\infty}\frac{e^{-ikx}}{x-i\varepsilon}dx =
\left\{
\begin{aligned}
0~~~(k\gt 0)\\
2\pi i~~~(k \lt 0)
\end{aligned}
\right.
\end{eqnarray}
$

$
\begin{align}
\int_{-\infty}^{\infty}\frac{1}{x}e^{-i0x}dx=0
\end{align}
$

を得ることが出来ました。
これを実軸上の積分の式に代入すると、
$
\begin{align}
\int_{-\infty}^{\infty}\frac{1}{x}e^{-ikx}dx =-\pi i ~\text{sgn}(k)
\end{align}
$
となります。ここで、$\text{sgn}(x)$は符号関数で、
$
\begin{eqnarray}
\text{sgn}(x) =
\left\{
\begin{aligned}
-1~~~(x\lt 0)\\
0~~~(x=0) \\
1~~~(x\gt 0)
\end{aligned}
\right.
\end{eqnarray}
$
で定義される関数です。

数学

xのフーリエ変換

2017年11月18日 sikino コメントする

その他フーリエ変換
ヘヴィサイド関数のフーリエ変換
 1のフーリエ変換
 $x$のフーリエ変換 ← 今ここ
$1/x$のフーリエ変換
 $1/(x^n)$のフーリエ変換

1のフーリエ変換結果
$
\begin{align}
\int_{-\infty}^{\infty}e^{-ikx}dx =2\pi\delta(k)
\end{align}
$
を利用します（1のフーリエ変換）。

両辺を$k$で微分すると$x$のフーリエ変換
$
\begin{align}
\int_{-\infty}^{\infty}(-i)xe^{-ikx}dx &=2\pi\delta'(k) \\
\int_{-\infty}^{\infty}xe^{-ikx}dx &=i2\pi\delta'(k)
\end{align}
$
が導けます。

これを繰り返せば、$x^n$のフーリエ変換
$
\begin{align}
\int_{-\infty}^{\infty}x^ne^{-ikx}dx &=i^n 2\pi\delta^{(n)}(k)
\end{align}
$
も導くことが出来ます。

数学

1のフーリエ変換

2017年11月18日 sikino コメントする

\begin{align}
\int_{-\infty}^{\infty}e^{-ikx}dx &=-\frac{1}{i}\lim_{\varepsilon\to +0}\left[\frac{1}{k+i\varepsilon }-\frac{1}{k-i\varepsilon }\right] \\
&=-\frac{1}{i}\left[\frac{1}{k+i0}-\frac{1}{k-i0}\right] \\
&=2\pi\delta(k)
\end{align}

その他フーリエ変換
ヘヴィサイド関数のフーリエ変換
 1のフーリエ変換 ← 今ここ
$x$のフーリエ変換
 $1/x$のフーリエ変換
 $1/(x^n)$のフーリエ変換

1のフーリエ変換

1のフーリエ変換を求めるためには、ヘヴィサイド関数の無限積分が
$
\begin{align}
\int_{-\infty}^{\infty} \theta(x)e^{\pm ikx}dx &=\int_{0}^{\infty} e^{\pm ikx}dx\\
&=\lim_{\varepsilon\to +0}\mp\frac{1}{i}\frac{1}{k- i\varepsilon} \\
&=\mp\frac{1}{i}\frac{1}{k\pm i0}
\end{align}
$
であることを用います（ヘヴィサイド関数のフーリエ変換）。

1のフーリエ変換
$
\displaystyle \int_{-\infty}^{\infty} \theta(x)e^{-ikx}dx
$
は、ヘヴィサイド関数の無限積分を用いて
$
\begin{align}
&\int_{-\infty}^{\infty}e^{-ikx}dx \\
&=\int_{-\infty}^{0}e^{-ikx}dx+\int_{0}^{\infty}e^{-ikx}dx \nonumber \\
&=\int_{0}^{\infty}e^{ikx}dx+\int_{0}^{\infty}e^{-ikx}dx \nonumber \\
&=-\frac{1}{i}\frac{1}{k+i0} +\frac{1}{i}\frac{1}{k-i0} \nonumber \\
&=-\frac{1}{i}\left[\frac{1}{k+i0}-\frac{1}{k-i0}\right]
\end{align}
$
と求められます。2行目から3行目の式変形は、第1項目に関して変数変換$x\to -x$を行っています。

ここで、計算結果
$
\begin{align}
\int_{-\infty}^{\infty}e^{-ikx}dx=-\frac{1}{i}\left[\frac{1}{k+i0}-\frac{1}{k-i0}\right]
\end{align}
$
の右辺が示す意味を考えます。
適当な関数に右辺を作用させたときを考えると、この右辺がデルタ関数の定数倍に等しいことが分かります。

$
\begin{align}
g(x)=-\frac{1}{i}\left[\frac{1}{x+i0}-\frac{1}{x-i0}\right]
\end{align}
$
とおいて、ある関数$f(x)$に掛けて$x$で積分すると

$
\begin{align}
&\int_{-\infty}^{\infty}f(x)g(x)dx \nonumber\\
&=\int_{-\infty}^{\infty}f(x)\left[ -\frac{1}{i }\left(\frac{1}{x+i0}-\frac{1}{x-i0}\right)\right]dx \nonumber\\
&=\lim_{\varepsilon\to +0} \int_{-\infty}^{\infty}f(x)\left[ -\frac{1}{i }\left(\frac{1}{x+i\varepsilon}-\frac{1}{x-i\varepsilon}\right)\right]dx\nonumber \\
&=-\frac{1}{i}\left[\lim_{\varepsilon\to +0} \int_{-\infty}^{\infty}f(x) \frac{1}{x+i\varepsilon}dx-\lim_{\varepsilon\to +0}\int_{-\infty}^{\infty}f(x)\frac{1}{x-i\varepsilon}dx\right] \nonumber\\
&=-\frac{1}{i}\left[
\left\{ \mathcal{P}\int_{-\infty}^{\infty}\frac{f(x)}{x}dx-\pi i f(0)\right\}
-\left\{\mathcal{P}\int_{-\infty}^{\infty}\frac{f(x)}{x}dx+\pi i f(0)\right\}
\right]\nonumber \\
&=2\pi f(0) \nonumber\\
&=\int_{-\infty}^{\infty}f(x)\cdot 2\pi \delta(x)dx
\end{align}
$

計算前と比較すると
$
\begin{align}
g(x)&=2\pi \delta(x) \\
&\to \delta(x)=-\frac{1}{2\pi i}\left[\frac{1}{x+i0}-\frac{1}{x-i0}\right]
\end{align}
$
としてデルタ関数が表現されていることが分かります。

数学

ヘヴィサイド関数のフーリエ変換

2017年11月17日 sikino コメントする

\begin{align}
\int_{-\infty}^{\infty} \theta(x)e^{-ikx}dx
=\lim_{\varepsilon\to +0}\frac{1}{i}\frac{1}{k- i\varepsilon}
=\frac{1}{i}\frac{1}{k- i0}
\end{align}
を導出します。
ここでは、アーベル総和の考えを用いません。使うのはフーリエ変換のユニタリー性です。

※いろいろ数学的に自信が持てない点があります。これは僕が納得した解釈であるので、完全に正しい導出方法ではないかもしれません。

また、ここではフーリエ変換を
$
\begin{align}
& g(k)=\int_{-\infty}^{\infty}f(x)e^{-ikx} dx \\
& f(x)=\int_{-\infty}^{\infty}g(k)e^{ikx} \frac{dk}{2\pi}
\end{align}
$
で定義しています。

その他フーリエ変換
ヘヴィサイド関数のフーリエ変換 ← 今ここ
1のフーリエ変換
 $x$のフーリエ変換
 $1/x$のフーリエ変換
 $1/(x^n)$のフーリエ変換

ヘヴィサイド関数のフーリエ変換

ヘヴィサイド関数$\theta(x)$は
$
\begin{eqnarray}
\theta(x) =
\left\{
\begin{aligned}
0~~~(x\gt 0)\\
1~~~(x\lt 0)
\end{aligned}
\right.
\end{eqnarray}
$
と定義されます。この関数のフーリエ変換、すなわち積分
$
\displaystyle \int_{-\infty}^{\infty}\theta(x)e^{- ikx} dx
$
を考えます。上の積分は$x\lt 0$ではヘヴィサイド関数はゼロなので、
$
\begin{align}
\int_{-\infty}^{\infty}\theta(x)e^{- ikx} dx=\int_{0}^{\infty}e^{-ikx}dx
\end{align}
$
となります。後はこの積分が計算出来れば良いです。

$k\ne0$の場合

もしも$k\ne 0$であれば、この積分は計算可能です。
被積分関数を複素x平面に解析接続して、以下の図のような閉経路を考えます。

今、閉経路内に特異点は無いので、一周回った時の周回積分の値はゼロです。また、大きく外側を回る経路$\Gamma’$は、被積分関数が漸近で収束する領域なので、無限遠方での線積分の値はゼロです。このことから、
$
\begin{align}
\oint f(x) dx &= \lim_{R\to\infty} \left[\int_0^R f(x)dx + \int_{\Gamma’}f(x)dx+\int_{R}^0 f(re^{i\theta})re^{i\theta}dr\right]\nonumber \\
0&= \lim_{R\to\infty}\left[ \int_0^R f(x)dx +\int_{R}^0 f(re^{i\theta})re^{i\theta}dr\right] \nonumber\\
\lim_{R\to\infty} \int_0^R f(x)dx &=\lim_{R\to\infty}\int_{0}^R f(re^{i\theta})re^{i\theta}dr \nonumber
\end{align}
$
が成立します。

$e^{-ikx}$で$k\ne 0$の場合、
$\pi \lt \theta\lt 0 (k\gt 0),~~0 \lt \theta\lt \pi (k\lt 0) $では
$
\begin{align}
\int_0^{\infty}e^{-ikx}dx &= \lim_{R\to\infty}\int_0^{R e^{i\theta}}e^{-ikz}dz \nonumber \\
&= \lim_{R\to\infty}\left[\frac{e^{-ikz}}{-ik}\right]^{R e^{i\theta}}_{0} \nonumber \\
&=\frac{1}{i}\frac{1}{k}
\end{align}
$
となります。
しかし、$k=0$は漸近で収束しないので同様の方法で計算することができません。

$k=0$の場合

$k=0$で、被積分関数は無限大に発散します。
なぜなら、
$
\begin{align}
\int_{0}^{\infty}e^{-i0x}dx= \int_{0}^{\infty}dx =\infty
\end{align}
$
だからです。ここで問題なのは、無限大への発散の仕方です。

これが示すことは、フーリエ変換後の空間で$k=0$は特異点ということです。

以上から
$
\begin{eqnarray}
\int_{-\infty}^{\infty}\theta(x)e^{- ikx} dx =
\left\{
\begin{aligned}
\frac{1}{i}\frac{1}{k}~~~(k\ne 0)\\
\infty~~~(k= 0)
\end{aligned}
\right.
\end{eqnarray}
$
というフーリエ変換結果を得ました。

特異点の周り方の指定

さて、前回の計算結果から、$k=0$に特異点がある事が分かりました。
この特異点の性質を知るために、逆フーリエ変換を考えます。

なぜなら、フーリエ変換はユニタリー変換であることを考えれば、フーリエ変換した関数を逆フーリエ変換した時には元に戻っていて欲しい、という条件が課されているからです。

そして、逆フーリエ変換時にはこれを避けて回らねばならりません。
特異点を回る方法として考えられるのは以下の3つです。

複素k平面上で特異点周りを上方向を回る
複素k平面上で特異点周りを下方向を回る
複素k平面上で特異点周りを上方向と下方向を回った結果の平均をとる

結果的に正しいのは下方向を回った時の2です。そしてこの特異点を回る方法をフーリエ変換後の結果に含めると、
$
\displaystyle \int_{-\infty}^{\infty}\theta(x)e^{- ikx} dx = \lim_{\varepsilon \to +0 }\frac{1}{i}\frac{1}{k-i\varepsilon}
$
という結論を得ることが出来ます。
ここで、$-i\varepsilon$が意味するのは、複素k平面を積分する時には下方向を回りなさい、ということを数学的に表しています。

実際にそれぞれ計算して確かめてみましょう。
被積分関数が漸近で収束する領域は$e^{ikx}$なので
$x\gt 0$の時、複素k平面の上半面、
$x\lt 0$の時、複素k平面の下半面になります。
一位の特異点を閉経路内に含み、正の方向に回る場合、コーシーの積分定理より値は$2\pi i$です。

1. 複素k平面上で特異点周りを上方向を回る場合

フーリエ変換後の関数$f(x)$は
$
\begin{eqnarray}
f(x)=\lim_{\varepsilon\to +0} \int_{-\infty}^{\infty}\frac{-i}{k+i\varepsilon}e^{ikx}\frac{dk}{2\pi} =
\left\{
\begin{aligned}
1~~~(x\lt 0) \\
0~~~(0\lt x)
\end{aligned}
\right.
\end{eqnarray}
$
なので、これは元のヘヴィサイド関数ではないので特異点を回る方法として欲しいものではありません。

2. 複素k平面上で特異点周りを下方向を回る

フーリエ変換後の関数$f(x)$は
$
\begin{eqnarray}
f(x)=\lim_{\varepsilon\to +0} \int_{-\infty}^{\infty}\frac{-i}{k-i\varepsilon}e^{ikx}\frac{dk}{2\pi} =
\left\{
\begin{aligned}
0~~~(x\lt 0) \\
1~~~(0\lt x)
\end{aligned}
\right.
\end{eqnarray}
$
なので、これはフーリエ変換前のヘヴィサイド関数に一致します。よってこれが適切です。

3. 複素k平面上で特異点周りを上方向と下方向を回った結果の平均をとる

フーリエ変換後の関数$f(x)$は1. 2. の結果から、
$
\begin{eqnarray}
f(x)=\left\{
\begin{aligned}
1/2~~~(x\lt 0) \\
1/2~~~(0\lt x)
\end{aligned}
\right.
\end{eqnarray}
$
なので、これは元のヘヴィサイド関数ではないので特異点を回る方法として欲しいものではありません。

以上から、複素k平面上の$k=0$にある特異点の回り方を指定して、ヘヴィサイド関数
$
\displaystyle \int_{-\infty}^{\infty}\theta(x)e^{- ikx} dx = \lim_{\varepsilon \to +0 }\frac{1}{i}\frac{1}{k-i\varepsilon}
$
と導くことが出来ます。良く、$\varepsilon\to 0$の表記を省略して
$
\displaystyle \int_{-\infty}^{\infty}\theta(x)e^{- ikx} dx = \frac{1}{i}\frac{1}{k-i0}
$
と記述されます。

演算子としての表現

ヘヴィサイド関数のフーリエ変換後の結果
$
\displaystyle \int_{-\infty}^{\infty}\theta(x)e^{- ikx} dx = \frac{1}{i}\frac{1}{k-i0}
$
の右辺に現れる特徴的な量
$
\displaystyle \frac{1}{k-i0}
$
を演算子として捉えた場合を考えます。この時、$k$を$x$に入れ替えて、ある関数$f(x)$に作用させると
$
\begin{align}
\int_{-\infty}^{\infty} \left(\frac{1}{x-i0}\right) f(x)dx&=
\lim_{\varepsilon\to +0} \int_{-\infty}^{\infty} \frac{f(x)}{x-i\varepsilon} dx\nonumber \\
&=\lim_{R\to \infty}
\left[\int_{-R}^{-\varepsilon’} \frac{f(x)}{x} dx+\int_{\Gamma_-} \frac{f(x)}{x}dx+\int_{\varepsilon’}^{R} \frac{f(x)}{x}dx\right]
\end{align}
$
となります。

ここで、$\Gamma_-$は特異点を下に回る経路です。
注記しますが、コーシーの積分定理があるため、この段階で$\varepsilon’$をゼロに近づける必要は全くありません。

特に$\lim_{\varepsilon’\to +0}$を考えますと、コーシーの主値を用いて
$
\begin{align}
&=\mathcal{P}\int_{-\infty}^{\infty}\frac{f(x)}{x} dx +\pi i f(0)\nonumber \\
&=\mathcal{P}\int_{-\infty}^{\infty}\frac{f(x)}{x} dx +\pi i \int_{-\infty}^{\infty}f(x)\delta(x)dx \nonumber \\
&=\int_{-\infty}^{\infty}\left(\mathcal{P} \frac{1}{x}+\pi i \delta(x)\right) f(x)dx \nonumber
\end{align}
$
と書き表せます。以上から、右辺に現れる特徴的な量は
$
\begin{align}
\frac{1}{x-i0}=\mathcal{P} \frac{1}{x}+\pi i \delta(x)
\end{align}
$
と書き換えて解釈しても良い、となります。

数学

実軸上の積分とコーシーの主値積分

2017年11月1日 sikino コメントする

結論

実軸上の積分とは、複素平面からの近づき方を指定して、
$
\begin{align}
\int_{-\infty}^{\infty}f(x)dx=
\frac{1}{2}\left[\lim_{\varepsilon\to +0}\int_{-\infty+i\varepsilon}^{\infty+i\varepsilon}f(x)dx+
\lim_{\varepsilon\to +0}\int_{-\infty-i\varepsilon}^{\infty-i\varepsilon}f(x)dx\right]
\end{align}
$
と求められるようです。
このように表現されていると考えなければ、$\int_{-\infty}^{\infty} e^{ikx}/x dx$の解が得られません。
図にするとこういう極限を取る、という意味です。

特に、実軸上$x=0$に１位の特異点が１つ存在する場合、
$
\begin{align}
\int_{-\infty}^{\infty}\frac{f(x)}{x}dx=
\int_{-\infty}^{-\varepsilon}\frac{f(x)}{x}dx+
\frac{1}{2}\left[
\int_{\Gamma_+}\frac{f(x)}{x}dx+\int_{\Gamma_-}\frac{f(x)}{x}dx
\right]+
\int_{\varepsilon}^{\infty}\frac{f(x)}{x}dx
\end{align}
$
と書かれます。ここで、$\varepsilon\to +0$である必要はありません。

$\Gamma_+$は実軸上の点$x=-\varepsilon$から複素平面で、特異点の上を通って実軸上$x=\varepsilon$に戻る経路、
$\Gamma_-$は実軸上の点$x=-\varepsilon$から複素平面で、特異点の下を通って実軸上$x=\varepsilon$に戻る経路
です。

図では

という経路です。
右図の点線の経路でも積分結果が変わりません。なぜなら、点線と実線で囲まれた領域内に特異点が無い状況を考えているです。

コーシーの主値とは、複素平面の迂回部分を消した値であり、さらに$\varepsilon\to +0$を課した実軸上のみの積分結果です。$x=0$に１位の特異点がある場合、
$
\begin{align}
\mathcal{P}\int_{-\infty}^{\infty}\frac{f(x)}{x}dx=
\lim_{\varepsilon \to +0}\left[
\int_{-\infty}^{-\varepsilon}\frac{f(x)}{x}dx+
\int_{\varepsilon}^{\infty}\frac{f(x)}{x}dx
\right]
\end{align}
$と表現されるはずです。

コーシーの主値を用いて、本来の実軸上の積分を評価しようとすれば、
$
\begin{align}
\int_{-\infty}^{\infty}\frac{f(x)}{x}dx=
\mathcal{P}\int_{-\infty}^{\infty}\frac{f(x)}{x}dx+
\frac{1}{2}\lim_{\varepsilon\to +0}\left[
\int_{\Gamma_+}\frac{f(x)}{x}dx+\int_{\Gamma_-}\frac{f(x)}{x}dx
\right]
\end{align}
$
と書けるはずです。ここで、複素平面を回る経路は特異点を回る半径を無限小にした時の値でなければなりません。

実軸上に特異点が無い場合、積分の$\Gamma_{+/-}$からの寄与はゼロになります。なので、コーシーの主値積分と本来の実軸上の積分は一致します。すなわち、
$
\displaystyle \int_{-\infty}^{\infty}f(x)dx=\mathcal{P}\int_{-\infty}^{\infty}f(x)dx
$
が成立します。

特異点をずらす操作について

特異点が実軸上にある時、

特異点を迂回する経路を通って積分
特異点をずらして積分

の二通りが頻出します。結局は同じことをしています。重要なのは、特異点の上を通るか下を通るかという点のみです。
１位の特異点が実軸上に存在する時、特異点をずらす場合、ずらし方として
$
\frac{f(x)}{x+i\varepsilon}, \frac{f(x)}{x-i\varepsilon}
$
となります。
ここで、$\lim \varepsilon\to 0$を取らなければなりませんが、この操作の本質は、特異点の無い積分領域の端では実軸上にいなければならない、という要請から来るものです。

特異点周りを半径無限小で回らなければならない理由はありません。

なので、特異点をずらしてから実軸上に近づける操作は、上、もしくは下を迂回して積分することと同じです。

具体的な関数をずらした時はこんな感じ。$\varepsilon=0.2$にとって描画しています。

注意

これは私の解釈です。

以下の4つの計算が正しい場合、上記の解釈でなければ正しい結果が出ません。
ヘヴィサイド関数のフーリエ変換
 1のフーリエ変換
 $x$のフーリエ変換
 $1/x$のフーリエ変換
 $1/(x^n)$のフーリエ変換

しかし、上記の説明を行っている教科書、解説ページを見受けることはできませんでした。
なので、あくまで私が正しいと思い、この考えでないと導出が出来ず、また反例が今のところ見つかっていないだけです。

コーシーの主値に意味を見出すことができません。
実際に現れる値は（実軸上の経路）＋（特異点周りをまわる経路）であるからです。

コーシーの主値でなければならない理由がありましたら、是非ともお知らせいただけると幸いです。
特異点の周りを半径+0で回らなくていいことは、具体的に複素平面上の数値積分を行って確かめています。

プログラミングと数値計算, 数学

離散フーリエ変換と畳み込みの計算

2017年7月22日 sikino コメントする

こちらのページは後程消去いたします。

以下のページに統合しますので、ご参照ください。
https://slpr.sakura.ne.jp/qp/dft-for-numerical-calculation/

本ページにはミスもあり、上の方が正しいですのでご参照ください。

まとめ

離散フーリエ変換(Discrete Fourier Transform,DFT)を
$
\begin{eqnarray}
\left\{
\begin{aligned}
f(\tilde{k}_n)&=\mathcal{F}[f(x)](\tilde{k}_n)=\sum_{m=0}^{N-1}f(x_m)e^{-i2\pi\tilde{k}_nx_m}\Delta x \\
f(x_m)&=\mathcal{F}^{-1}[f(\tilde{k})](x_m)=\sum_{n=0}^{N-1}f(\tilde{k}_n)e^{i2\pi\tilde{k}_nx_m}\Delta \tilde{k}
\end{aligned}
\right.
\end{eqnarray}
$
と定義し、畳み込み(Convolution)を
$
\displaystyle (f\ast g)(x_l)= \sum_{m} f(x_m) g(x_l-x_m) \Delta x
$
と定義します。この時、畳み込みは上で定義した離散フーリエ変換を用いて以下の通り書けます。
$
\displaystyle (f\ast g)(x_l)=\mathcal{F}^{-1}\left[\mathcal{F}[f(x)](\tilde{k})\cdot \mathcal{F}[g(x)](\tilde{k})\right](x_l)
$

intel®マス・カーネル・ライブラリ(MKL)に実装されているフーリエ変換は
$
\begin{eqnarray}
\left\{
\begin{aligned}
(-1)^n f(\tilde{k}_n)&=\sum_{m=0}^{N-1}f(x_m)e^{-i2\pi nm/N} \\
f(x_m)&=\sum_{n=0}^{N-1}(-1)^n f(\tilde{k}_n)e^{i2\pi nm/N}
\end{aligned}
\right.
\end{eqnarray}
$
の形で定義されています。ここで、$f(\tilde{k}_n)$は、正しいフーリエ変換後の関数。計算したもの。この時、上で定義されている場合、畳み込みは、
$
\displaystyle (f\ast g)(x_m)=\frac{\Delta x}{N}\mathcal{F}_{MKL}^{-1}\left[\mathcal{F}_{MKL}[f(x)]\cdot\mathcal{F}_{MKL}[g(x)] (-1)^n\right](x_m)
$
で計算できます。ここで、$N$は離散フーリエ変換に用いた分点数、$n$は順方向フーリエ変換後の空間を離散化した時のインデックスです。

intel®MKLの離散フーリエ変換ルーチンを用いた畳み込みは、プログラムでは$h(x)=(f\ast g)(x)$とした時、

$
\begin{align}
& Status = DftiComputeForward(hand,f) \\
& Status = DftiComputeForward(hand,g) \\
& h(\tilde{k}_n)=z(\tilde{k}_n)\times g(\tilde{k}_n)\times (-1)^n ~~~~~(\mbox{for all } k_n) \\
& Status = DftiComputebackward(hand,h) \\
& h(x_m)=h(x_m)\times \frac{\Delta x}{N} ~~~~~(\mbox{for all } x_m)\\
\end{align}
$

とする必要があります。
※離散フーリエ変換はフーリエ変換の積分を短冊近似したものです。

▼ここクリックで畳み込みを計算するfortranコードを展開

[adsense1]

フーリエ変換の定義
離散フーリエ変換の定義
- フーリエ変換が元に戻ることの証明
- 離散フーリエ変換が元に戻ることの証明
たたみ込みの定義
離散たたみ込みと離散フーリエ変換
- フーリエ変換が元に戻ることの証明
- 離散フーリエ変換が元に戻ることの証明
数値計算で使われている離散フーリエ変換アルゴリズム (例: intel®MKL)
- 離散フーリエ変換時の注意点とコード
- フーリエ変換を介する畳み込み時の注意点とコード

フーリエ変換の定義

フーリエ変換の定義方法には複数の慣例があり、
数値計算分野、化学、音の解析等においては
$
\begin{align}
f(\tilde{k})&=\int_{-\infty}^{\infty} f(x)e^{-i2\pi\tilde{k}x}dx \\
f(x)&=\int_{-\infty}^{\infty} f(\tilde{k})e^{i2\pi\tilde{k}x}d\tilde{k}
\end{align}
$
の形で良く定義されます。
ここで、例えば$x$は位置[m]であれば$\tilde{k}$は波数[1/m]です。
また、$x$が時間[s]であれば$\tilde{k}$は周波数[1/s]です。

このページでは扱いませんが、物理科学の世界では
$
\begin{align}
f(k)&=\int_{-\infty}^{\infty} f(x)e^{-ikx}dx \\
f(x)&=\int_{-\infty}^{\infty} f(k)e^{ikx}\frac{dk}{2\pi}
\end{align}
$
の形で良く定義されます。
ここで、例えば$x$は位置[m]であれば$k$は角波数[1/m]です。
また、$x$が時間[s]であれば$k$は角周波数[1/s]です。

この２つの違いは周波数か、角周波数のどちらが本質であるか？という事だと思います。
物理では、周波数よりも角周波数の方が式が簡便になります。
ですが、人間の理解がしやすいのは1秒当たり何回振動するか？という周波数だろう、と思うため工学よりの分野では周波数が使われるのでしょう。もしかしたら、単に慣例だけかもしれません。

どちらも定数倍の変数変換の違いだけなので、本質は変わりません。
数値計算依りの話をしていきたいので、ここからは前者の位置⇔波数で考えていきます。

また、

順方向フーリエ変換：$e^{-i2\pi\tilde{k}x}$の因子が掛かっている式、空間→波数
逆方向フーリエ変換：$e^{+i2\pi\tilde{k}x}$の因子が掛かっている式、波数→空間

と呼び、
”関数$f(x)$の順方向フーリエ変換して波数$\tilde{k}$の空間に移る”
という操作を華文字$\mathcal{F}$を用いて
$
\mathcal{F}[f(x)](\tilde{k})
$
と表します。また、
”関数$f(k)$の逆方向フーリエ変換して位置$x$の空間に移る”
という操作を
$
\mathcal{F}^{-1}[f(\tilde{k})](x)
$
と表します。

離散フーリエ変換の定義

このページでは離散フーリエ変換を
$
\begin{align}
f(\tilde{k}_n)&=\sum_{m=0}^{N-1}f(x_m)e^{-i2\pi\tilde{k}_nx_m}\Delta x \\
f(x_m)&=\sum_{n=0}^{N-1}f(\tilde{k}_n)e^{i2\pi\tilde{k}_nx_m}\Delta \tilde{k}
\end{align}
$
と定義します。
$\Delta x$, $\Delta \tilde{k}$は、それぞれ位置、波数空間の刻み幅を表します。

この上の定義は簡便さのために良く使われる
$
\begin{align}
f(\tilde{k}_n)&=\frac{1}{N}\sum_{m=0}^{N-1}f(x_m)e^{-i2\pi\tilde{k}_nx_m} \\
f(x_m)&=\hspace{1.5em}\sum_{n=0}^{N-1}f(\tilde{k}_n)e^{i2\pi\tilde{k}_nx_m}
\end{align}
$
という定義と同一です。
ただし、これは積分をそのまま離散化したものではないため、積分の意味は薄れてしまいます。
その結果、畳み込みなど、フーリエ変換後同士の物を掛け算する時は違った結果になってしまいます。
このページではこの簡便さの為の離散フーリエ変換は使いません。

上の２つの定義が同じ理由は、順方向→逆方向を行い、元に戻った時に係数が$\Delta x\Delta \tilde{k}=\frac{1}{N}$になるためです。

	$x_m$	$\tilde{k}_n$
添え字	$m=0,1,2,\cdots,N-1$	$n=0,1,2,\cdots,N-1$
区間	$\displaystyle [a,b]$	$\displaystyle \left[-\frac{1}{2\Delta x},\frac{1}{2\Delta x}\right]$
刻み幅	$\displaystyle \Delta x=\frac{b-a}{N}$	$\displaystyle \Delta \tilde{k}=\frac{1}{b-a}$
分点の位置	$\displaystyle x_m=m\Delta x +a$	$\displaystyle \tilde{k}_n=n\Delta \tilde{k} -\frac{1}{2\Delta x}$

ただし、$x_m, \tilde{k}_n$は以下の関係式を見たします。
$
\begin{align}
& x_m+N\Delta x=x_m\\
& \tilde{k}_n+N\Delta \tilde{k}=\tilde{k}_n
\end{align}
$

ナイキスト(Nyquist)周波数について

ナイキスト周波数とはサンプリングする間隔でどの周波数を持つ関数までを表現できるか？という下限と上限を与えます。
今回の場合、上の表の通り$\tilde{k}$空間で表現できる上限と下限は$\pm\frac{1}{2\Delta x}$です。この絶対値、すなわち$\frac{1}{2\Delta x}$をナイキスト周波数と呼びます。

ナイキスト周波数が意味しているのは、高周波の成分を取り出したければサンプリングする間隔を小さくしなければならない。ということです。”サンプリングの間隔”は周波数と同じ意味ですので、サンプルする周波数を高くしなければならない。と言い換えることもできます。

具体例を上げましょう。

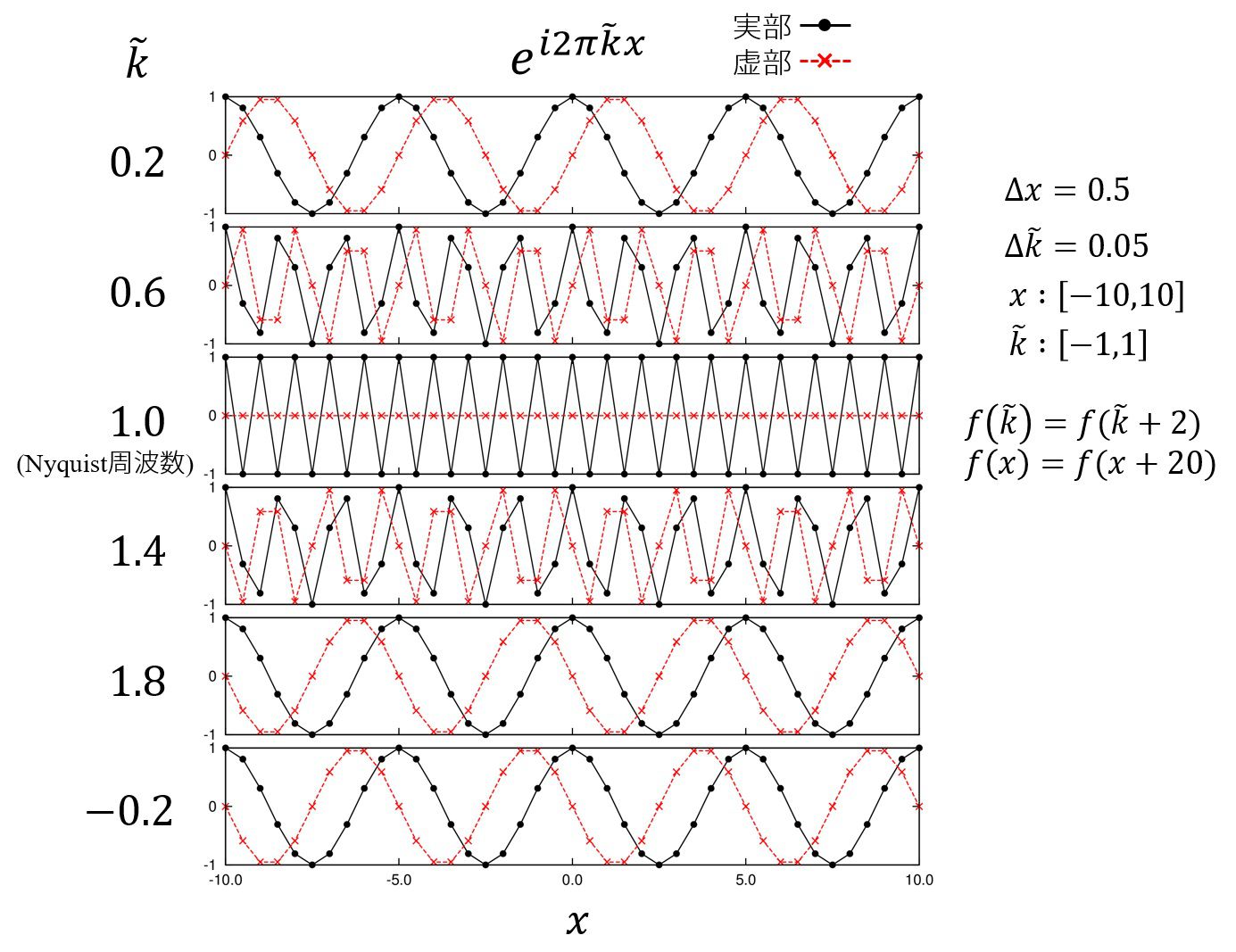
上の図は関数$\displaystyle f(x)=e^{i2\pi \tilde{k}x}$をサンプル間隔$\Delta x = 0.5$で離散的な関数で表現したものです。
この場合、ナイキスト周波数は$\frac{1}{2\times 0.5}$より、$1$です。
すなわち、このサンプル間隔では$\tilde{k}$が$[-1,1]$の範囲を持つものしか表現することが出来ません。
では、実際にサンプル出来ない関数$\displaystyle f(x)=e^{i2\pi 1.8 x},~~(\tilde{k}=1.8)$を考えた時に何が起こるのでしょうか。
それを示したのが下から2番目の関数です。
本来は早く振動する関数であるのに、あたかも非常にゆっくりとした関数だ、と捉えられてしまいます。しかも位相が反転しています。

これは、元々は$e^{i\theta}$の周期性によるものです。簡単な計算の通り、
$
\begin{align}
e^{i(\theta+2\pi)}=e^{i\theta}e^{i2\pi}=e^{i\theta}
\end{align}
$
となります。この周期性のために、$\tilde{k}:[-1,1]$の範囲でしか表現できない空間で、
その範囲外の$\tilde{k}$を表現しようとした時には、$\tilde{k}$空間の大きさ（…この場合は$2$）を足したり引いたりして$\tilde{k}:[-1,1]$の範囲に強制的に押し込まれます。
$\tilde{k}=1.8$の場合は、$\tilde{k}=1.8-2=-0.2$となります。
言葉で言えば、
$\tilde{k}=1.8$を持つ波形は$\tilde{k}=-0.2$を持つ波形としてとして表現される
ということです。

本来の関数を薄く描いて重ねたものが以下のものになります。

フーリエ変換が元に戻ることの証明

上記のフーリエ変換、離散フーリエ変換はある制限を課しています。
それは、
ある関数に順方向フーリエ変換を行い、続いて逆方向フーリエ変換を施した場合、元と同じ関数に戻っていて欲しい。
という要望です。
それは、以下のように証明できます。

フーリエ変換

$
\begin{align}
f(x)&=\int_{-\infty}^{\infty}d\tilde{k} f(\tilde{k})e^{i2\pi\tilde{k}x} \\
&=\int_{-\infty}^{\infty}d\tilde{k} \left[\int_{-\infty}^{\infty}dx’ f(x’)e^{-i2\pi\tilde{k}x’}\right]e^{i2\pi\tilde{k}x} \\
&=\int_{-\infty}^{\infty}dx’ f(x’)\int_{-\infty}^{\infty}d\tilde{k}
e^{i2\pi\tilde{k}(x-x’)} \\
&=\int_{-\infty}^{\infty}dx’ f(x’)\delta(x-x’) \\
&=f(x)
\end{align}
$

離散フーリエ変換

$
\begin{align}
f(x_m)&=\sum_{n=0}^{N-1}f(\tilde{k}_n)e^{i2\pi\tilde{k}_nx_m}\Delta \tilde{k}\\
&=\sum_{n=0}^{N-1}\left[\sum_{m’=0}^{N-1}f(x_{m’})e^{-i2\pi\tilde{k}_nx_{m’}}\Delta x\right]e^{i2\pi\tilde{k}_nx_m}\Delta \tilde{k} \\
&=\Delta \tilde{k}\Delta x\sum_{m’=0}^{N-1}f(x_{m’})\sum_{n=0}^{N-1}e^{i2\pi\tilde{k}_n(x_m’-x_m)} \\
&=\frac{1}{N}\sum_{m’=0}^{N-1}f(x_{m’})\sum_{n=0}^{N-1}e^{i2\pi n (m’-m)/N +i2\pi(\theta_{m}-\theta_{m’})} \\
&=\frac{1}{N}\sum_{m’=0}^{N-1}f(x_{m’})e^{i2\pi(\theta_{m}-\theta_{m’})}N\delta_{m,m’} \\
&=f(x_m)
\end{align}
$
ここで、
$
\begin{align}
\tilde{k}_n x_{m}=\frac{nm}{N}+\frac{an}{N\Delta x}+\theta_{m} \\
\theta_{m}=-\frac{a}{2\Delta x}-\frac{m}{2}
\end{align}
$
そして、等比級数の考えから、
$
\begin{eqnarray}
\sum_{n=0}^{N-1}e^{i2\pi n a}=
\left\{
\begin{aligned}
&\frac{e^{i2\pi aN}-1}{e^{i2\pi a}-1}, \hspace{1em} ( a\ne 0) \\
& N, \hspace{4em} (a=0) \\
\end{aligned}
\right.
\end{eqnarray}
$
という関係式を用いました。

畳み込み(convolution)の定義

このページでは、畳み込みを
$
\displaystyle (f\ast g)(x)=\int f(\tau) g(x-\tau) d\tau
$
という積分であると定義し、離散的な畳み込みを
$
\displaystyle (f\ast g)(x_l)= \sum_{m} f(x_m) g(x_l-x_m) \Delta x
$
と定義します。

畳み込みの定義には$\Delta x$が掛けられていないものが存在しますが、積分の意味が薄れてしまうため、離散フーリエ変換時と同様、このページでは$\Delta x$を掛けたものを畳み込み、と定義します。

区間$[a,b]$で定義された離散的な畳み込みの場合、関数$f(x),g(x)$は区間が$[a,b]$で決められている場合がほとんどです。
この場合、引数$x_m-x_l$が定義域内に収まらない場合が現れます。

定義域からはみ出てしまった場合は推定するしかありません。
推定の仕方によって
循環畳み込みと呼ばれる方法と直線畳み込みと呼ばれる方法が良くつかわれています。

循環畳み込みは領域に対して周期境界条件を課したもの、すなわち、上限bと下限aが繋がっていると考えます。
直線畳み込みは領域に対して固定端条件を課したもの、すなわち、[a,b]の範囲外の関数値はゼロと考えます。

問題に大きく依るので、どちらがいいかはありません。

離散畳み込みと離散フーリエ変換

離散畳み込みは定義通り
$
\displaystyle (f\ast g)(x_l)= \sum_{m} f(x_m) g(x_l-x_m) \Delta x
$
で計算することが出来ます。計算量は$O(n^2)$です。

しかし、実用上は離散フーリエ変換を利用すると計算量を$O(n\log n)$に抑えられます。
計算方法はたたみ込み定理を利用して、
$
\displaystyle \mathcal{F}[(f\ast g)(x)](k)=\mathcal{F}[f(x)](k)\cdot \mathcal{F}[g(x)](k)
$
より、$(f\ast g)(x)$は
$
\displaystyle (f\ast g)(x)=\mathcal{F}^{-1}\left[\mathcal{F}[f(x)](k)\cdot \mathcal{F}[g(x)](k)\right]
$
と書けるため、フーリエ変換を介することで計算量を減らせます。
離散フーリエ変換を介して畳み込みを計算する場合、必ず循環畳み込みで計算することになります。

畳み込み定理の証明

連続畳み込み

$
\displaystyle \mathcal{F}[(f\ast g)(x)](k)=\mathcal{F}[f(x)](k)\cdot \mathcal{F}[g(x)](k)
$

左辺）
$
\begin{align}
\mathcal{F}[(f\ast g)(x)](\tilde{k})
&=\int \left[\int f(\tau)g(x-\tau) d\tau\right] e^{-i2\pi \tilde{k} x} dx \\
& x-\tau=y\mbox{の変数変換を行って} \nonumber \\
&=\int dy\int d\tau f(\tau)g(y) e^{-i2\pi \tilde{k} (\tau+y)} \\
&=\int dx\int dx’ f(x)g(x’) e^{-i2\pi \tilde{k} (x+x’)}
\end{align}
$

右辺）
$
\begin{align}
\mathcal{F}[f(x)](\tilde{k})\cdot \mathcal{F}[g(x)](\tilde{k})
&=\int f(x) e^{-i2\pi \tilde{k} x} dx \cdot \int g(x’) e^{-i2\pi \tilde{k} x’} dx’ \\
&=\int dx\int dx’ f(x)g(x’) e^{-i2\pi \tilde{k} (x+x’)}
\end{align}
$
より、証明終了。また、逆変換により戻ることを示します。
$
\begin{align}
&\mathcal{F}^{-1}\left[\mathcal{F}[f(x)](\tilde{k})\cdot \mathcal{F}[g(x)](\tilde{k})\right] \\
&=\int \left[\int dx\int dx’ f(x)g(x’) e^{-i2\pi \tilde{k} (x+x’)}\right] e^{i2\pi \tilde{k} y} dk\\
&=\int dx\int dx’ f(x)g(x’) \int e^{-i2\pi \tilde{k} (x+x’-y)} dk\\
&=\int dx\int dx’ f(x)g(x’) \delta(x’-(y-x)) \\
&=\int dx f(x)g(y-x) \\
&=\int d\tau f(\tau)g(x-\tau) \\
\end{align}
$
となり、フーリエ変換を介してたたみ込みが計算できることが示せました。

離散畳み込み

$
\displaystyle \mathcal{F}[(f\ast g)](\tilde{k})=\mathcal{F}[f(x)](\tilde{k})\cdot \mathcal{F}[g(x)](\tilde{k})
$

左辺）
$
\begin{align}
\mathcal{F}[(f\ast g)(x)](\tilde{k}_n)
&=\mathcal{F}\left[\sum_{m=0}^{N-1}f(x_m)g(x-x_m)\Delta x\right] \\
&=\sum_{l=0}^{N-1}\left[\sum_{m=0}^{N-1}f(x_m)g(x_l-x_m)\Delta x\right]e^{i2\pi \tilde{k}_n x_l}\Delta x \\
&=(\Delta x)^2\sum_{l=0}^{N-1}\sum_{m=0}^{N-1}f(x_m)g(x_l-x_m) e^{i2\pi \tilde{k}_n x_l} \\
&\mbox{ここで、循環たたみ込みを想定し、}x_l-x_m=x_{m’}\mbox{となるように}x_{m’}\mbox{を決めると}\nonumber \\
&=(\Delta x)^2\sum_{m=0}^{N-1}\sum_{m’=0}^{N-1}f(x_m)g(x_{m’}) e^{i2\pi \tilde{k}_n (x_m+x_{m’})} \\
\end{align}
$

右辺）
$
\begin{align}
\mathcal{F}[(f(x)](k_n)\cdot \mathcal{F}[(g(x)](k_n)
&=\sum_{m=0}^{N-1}f(x_m) e^{i2\pi \tilde{k}_n (x_m)}\Delta x\cdot \sum_{m’=0}^{N-1}f(x_{m’}) e^{i2\pi \tilde{k}_n (x_{m’})}\Delta x \\
&=(\Delta x)^2\sum_{m=0}^{N-1}\sum_{m’=0}^{N-1}f(x_m)g(x_{m’}) e^{i2\pi \tilde{k}_n (x_m+x_{m’})}
\end{align}
$
よって右辺と左辺が正しくなります。

逆変換によって離散畳み込みになることを示します。

$
\begin{align}
\mathcal{F}^{-1}[\mathcal{F}[(f\ast g)(x)](k)](x_l)
&=\mathcal{F}^{-1}\left[(\Delta x)^2\sum_{m=0}^{N-1}\sum_{m’=0}^{N-1}f(x_m)g(x_{m’}) e^{i2\pi \tilde{k}_n (x_m+x_{m’})}\right]\\
&=\sum_{n=0}^{N-1}\left[(\Delta x)^2\sum_{m=0}^{N-1}\sum_{m’=0}^{N-1}f(x_m)g(x_{m’}) e^{i2\pi \tilde{k}_n (x_m+x_{m’})}\right]e^{-i2\pi \tilde{k}_n x_l}\Delta \tilde{k}\\
&=(\Delta x)^2 \Delta \tilde{k} \sum_{m=0}^{N-1}\sum_{m’=0}^{N-1} f(x_m)g(x_{m’})\sum_{n=0}^{N-1}e^{i2\pi \tilde{k}_n (x_m+x_{m’}-x_l)} \\
&=\frac{\Delta x}{N} \sum_{m=0}^{N-1}\sum_{m’=0}^{N-1} f(x_m)g(x_{m’})N\delta_{x_{m’},x_l-x_m} \\
&=\sum_{m=0}^{N-1}f(x_m)g(x_l-x_m)\Delta x \\
&=(f\ast g)(x_l)
\end{align}
$

よって畳み込みの定理通りに戻るため、離散フーリエ変換を介して畳み込みの計算ができます。

※注意
$\Delta x, \Delta \tilde{k}$が掛けられていない方の離散フーリエ変換と畳み込みでは元に戻りません。畳み込みの計算時に係数倍違って出てきます。

数値計算で使われている離散フーリエ変換アルゴリズム (例: intel®MKL)

数値計算では、上記の離散フーリエ変換の形、指数の肩に$\tilde{k},x$を含む物はあまり使われません。
そして、数値計算上での離散フーリエ変換の定義方法は複数存在します。
マニュアルを見てください。

ここでは、intel®マス・カーネル・ライブラリ(MKL)に使われている離散フーリエ変換アルゴリズムについて言及します。

MKLの変換はどうやら
$
\begin{align}
(-1)^n f(\tilde{k}_n)&=\sum_{m=0}^{N-1}f(x_m)e^{-i2\pi nm/N} \\
f(x_m)&=\sum_{m=0}^{N-1}(-1)^n f(\tilde{k}_n)e^{i2\pi nm/N}
\end{align}
$
という定義に従い変換しているようです。規格化因子$\frac{1}{N}$はユーザー任せです。
ここで、
$f(\tilde{k}_n)$は本来のフーリエ変換後の関数、
$f(x)$は$x$空間での関数
を表します。

”しているようです”と書いたのは、マニュアルと異なっているからです。マニュアルでは$(-1)^n$など存在しませんが、実際試してみると、こういう変換をしているからです。

MKLではどういう$\tilde{k}$を想定しているかを考えたところ、以下の状況のようです。

	$x_m$	$\tilde{k}_n$
添え字	$m=0,1,2,\cdots,N-1$	$n=0,1,2,\cdots,N-1$
区間	$\displaystyle [-a,a]$	$\displaystyle \left[0,N\Delta \tilde{k}\right]$
刻み幅	$\displaystyle \Delta x=\frac{2a}{N}$	$\displaystyle \Delta \tilde{k}=\frac{1}{2a}$
分点の位置	$ \begin{eqnarray} x_m=\left\{ \begin{aligned} & m\Delta x ~~~~(m=0,\cdots,\frac{N}{2}-1) \\ & m\Delta x-\frac{1}{\Delta \tilde{k}} (m=\frac{N}{2},\cdots,N-1) \end{aligned} \right. \end{eqnarray} $	$\displaystyle \tilde{k}_n=n\Delta \tilde{k} ~~~~(n=0,\cdots,N-1)$

ただし、$x_m, \tilde{k}_n$は以下の周期境界条件を見たします。
$
\begin{align}
& x_m+N\Delta x=x_m\\
& \tilde{k}_n+N\Delta \tilde{k}=\tilde{k}_n
\end{align}
$

区間[-a,a]で定義された$x_m$の順番がおかしく感じますが、これは周期境界条件を用いて、
区間[0,2a]で定義された$x_m=m\Delta x ~~~~(m=0,\cdots,N-1)$
と見ても良いです。
なので、実用上どうやって関数$f(x)$を入れればよいか？に困ることは無いでしょう。
この上記離散フーリエ変換を考えると、上で提示したMKLの離散フーリエ変換が導くことが出来、プログラム上でも一致します。

MKLの離散フーリエ変換の導出）

▼ここクリックでこの場に展開

離散フーリエ変換時の注意点

上に記した、余分な係数$(-1)^n$のためにMKLを利用して求められた離散フーリエ変換の値は、本来のフーリエ変換後の関数と異なります。
具体的に例を示しましょう。

$e^{-\alpha x^2}$のフーリエ変換は
$
\displaystyle \int_{-\infty}^{\infty} e^{-\alpha x^2}e^{-i2\pi\tilde{k} x}dx=\sqrt{\frac{\pi}{\alpha}}e^{-\pi^2\tilde{k}^2/\alpha}
$
です。離散フーリエ変換を定義通り計算したものと、MKLを用いて離散フーリエ変換すると以下のようになります。
左から$f(x), \mathcal{F}[f(x)](\tilde{k}),\mathcal{F}^{-1}[\mathcal{F}[f(x)]](x)$になっています。

ここで、因子$(-1)^n$のために交互に符号が変わっていることが分かるでしょう。
後でやりますが、このせいで畳み込みの計算をする際には気を付けなければなりません。

計算コードはこちら。

▼ここクリックでこの場に展開

program main
implicit none
integer::n,m,Nf
double precision,allocatable::x(:),k(:)
complex(kind(0d0)),allocatable::z(:)
double precision::a,b,dx,dk

Nf=64
allocate(x(0:Nf-1),k(0:Nf-1),z(0:Nf-1))
x=0d0; k=0d0; z=dcmplx(0d0,0d0)

a=-10d0
b=10d0
dx=(b-a)/dble(Nf)
dk=1d0/(b-a)

do m=0,Nf-1
x(m)=m*dx+a
enddo

do n=0,Nf-1
k(n)=n*dk
if(n.ge.Nf/2)k(n)=n*dk-Nf*dk
enddo

do m=0,Nf-1
z(m)=exp(-x(m)**2)
enddo

!=== DFT mkl ===

do m=0,Nf-1
write(10,*)x(m),dble(z(m)),dimag(z(m))
enddo
call fft(Nf,z,1)
z=z*dx
do n=0,Nf-1
write(11,*)k(n),dble(z(n)),dimag(z(n))
enddo
call fft(Nf,z,-1)
z=z*dk
do n=0,Nf-1
write(12,*)x(n),dble(z(n)),dimag(z(n))
enddo

!=== DFT define ===

do m=0,Nf-1
z(m)=exp(-x(m)**2)
enddo

do m=0,Nf-1
write(20,*)x(m),dble(z(m)),dimag(z(m))
enddo
call dftdefine(Nf,z,x,k,1)
z=z*dx
do n=0,Nf-1
write(21,*)k(n),dble(z(n)),dimag(z(n))
enddo
call dftdefine(Nf,z,x,k,-1)
z=z*dk
do m=0,Nf-1
write(22,*)x(m),dble(z(m)),dimag(z(m))
enddo

stop
end program main

include "/home/sikino/mkl/include/mkl_dfti.f90"
subroutine fft(N,z,ifb)
use MKL_DFTI
implicit none
integer,intent(in)::N,ifb
complex(kind(0d0)),intent(inout)::z(0:N-1)

integer::Status
TYPE(DFTI_DESCRIPTOR),POINTER::hand

Status = DftiCreateDescriptor(hand,DFTI_DOUBLE,DFTI_COMPLEX,1,N)
Status = DftiCommitDescriptor(hand)

if(ifb.eq.1)Status = DftiComputeForward(hand,z)
if(ifb.eq.-1)Status = DftiComputeBackward(hand,z)

Status = DftiFreeDescriptor(hand)

return
end subroutine fft

subroutine dftdefine(Nf,z,x,k,ifb)
implicit none
integer,intent(in)::Nf,ifb
double precision,intent(in)::x(0:Nf-1),k(0:Nf-1)
complex(kind(0d0)),intent(inout)::z(0:Nf-1)

integer::n,m
complex(kind(0d0))::w(0:Nf-1)
double precision,parameter::pi=dacos(-1d0)

w=dcmplx(0d0,0d0)
if(ifb.eq.1)then
do n=0,Nf-1
do m=0,Nf-1
w(n)=w(n)+z(m)*exp(-dcmplx(0d0,1d0)*2d0*pi*k(n)*x(m))
enddo
enddo
elseif(ifb.eq.-1)then
do m=0,Nf-1
do n=0,Nf-1
w(m)=w(m)+z(n)*exp(dcmplx(0d0,1d0)*2d0*pi*k(n)*x(m))
enddo
enddo
endif
z=w

return
end subroutine dftdefine

MKLのルーチンは優秀です。誤差が余りたまらないようです。
定義通り、愚直に作ったプログラムでは計算速度が遅いだけでなく、計算精度も悪くなります。
下の画像は、離散フーリエ変換→逆変換を複数回繰り返した時、元の関数とどれだけずれるかを表しています。

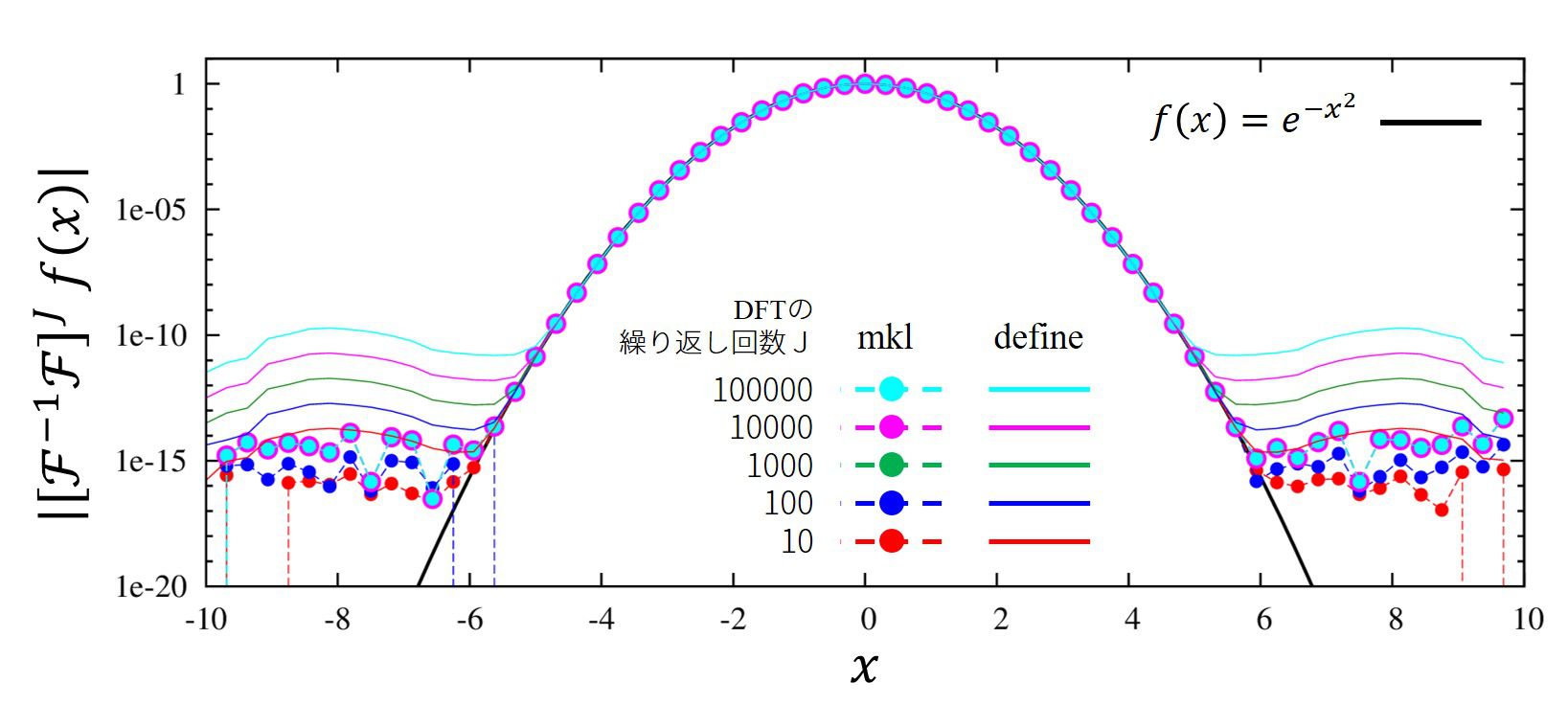
定義通りの離散フーリエ変換を$10^n$回繰り返すと$n$に対し線形にあがっていきます。この誤差は丸め誤差に起因しているのだと思います。しかし、MKLのルーチンには起こっていません。どういうアルゴリズムか知りませんが、優秀なのでしょう。

[adsense2]

フーリエ変換を介する畳み込み時の注意点

MKLの離散フーリエ変換ルーチンを使って畳み込みを計算します。
例として、以下の関数を考えましょう。
$
\begin{align}
h(x)&=\int \tau^5 e^{-\tau^2}\cdot e^{-4(x-\tau)^2}d\tau \\
&=\frac{1}{3125}\sqrt{\frac{\pi}{5}}x(1024x^4+1600x^2+375)e^{-\frac{4}{5}x^2}
\end{align}
$
ここで、
$
\begin{align}
f(\tau)=\tau^5 e^{-\tau^2}
g(\tau)=e^{-4\tau^2}
\end{align}
$
です。

このページで紹介した定義の畳み込みでは証明した通り、
$
h(x_m)=\mathcal{F}^{-1}\left[\mathcal{F}[f(x)](\tilde{k})\cdot\mathcal{F}[g(x)](\tilde{k})\right](x_m)
$
で計算できます。
しかし、MKLの離散フーリエ変換($\mbox{DFT}_{MKL}$)の場合は簡単にはできません。計算は、
$
\displaystyle (f\ast g)(x_m)=\frac{\Delta x}{N}\mathcal{F}_{MKL}^{-1}[\mathcal{F}_{MKL}[f(x)]\cdot\mathcal{F}_{MKL}[g(x)] (-1)^n](x_m)
$
としなければなりません。$(-1)^n$は順方向フーリエ変換が2回あり、MKLの逆方向離散フーリエ変換に必要なこの係数が落ちてしまうため入れなければなりません。また、MKLのルーチンでは係数$\Delta x, \Delta\tilde{k}$を含んでいないので計算しておく必要があります。

intel®MKLを用いる際、
順方向離散フーリエ変換にはDftiComputeForward、
逆方向離散フーリエ変換にはDftiComputeBackward
を使うと、擬コードはこのように書けるかと思います。

$\displaystyle \Delta x \Delta\tilde{k}=\frac{1}{N}$の関係を用いて最後にまとめて定数倍しています。

上の計算方法に従うと正しく畳み込みが計算出来ます。
実際にやってみますと、

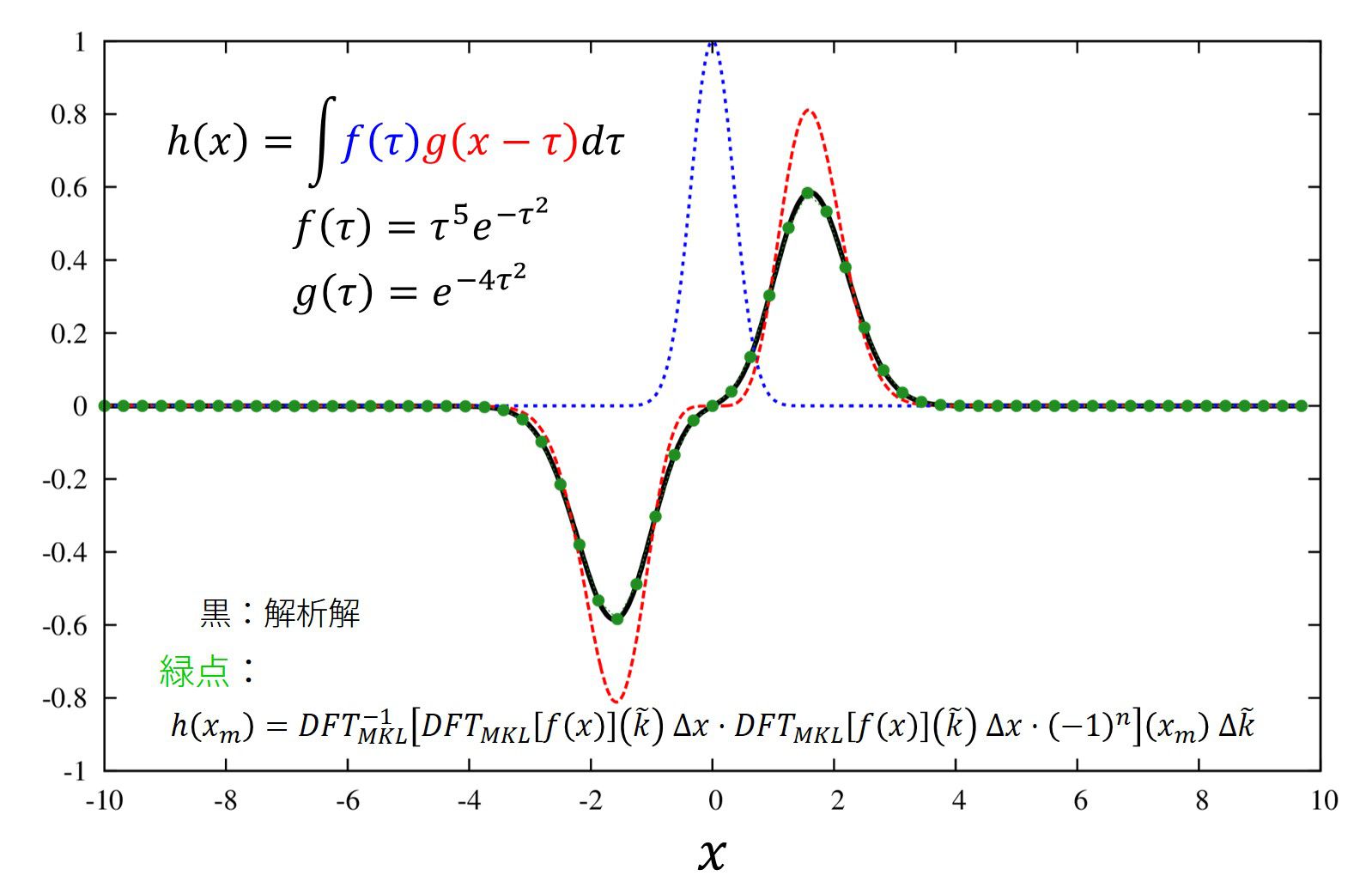
という結果を得ます。

畳み込みを計算するコードはこちら

▼ここクリックでこの場に展開

program main
! compute convolution using mkl dft routine
implicit none
integer::n,m,Nf
double precision,allocatable::x(:),k(:)
complex(kind(0d0)),allocatable::f(:),g(:),h(:)
double precision::a,b,dx,dk

Nf=64
allocate(x(0:Nf-1),k(0:Nf-1),f(0:Nf-1),g(0:Nf-1),h(0:Nf-1))
x=0d0; k=0d0; f=dcmplx(0d0,0d0); g=dcmplx(0d0,0d0); h=dcmplx(0d0,0d0)

a=-10d0
b=10d0
dx=(b-a)/dble(Nf)
dk=1d0/(b-a)

do m=0,Nf-1
x(m)=m*dx+a
enddo

do n=0,Nf-1
k(n)=n*dk
if(n.ge.Nf/2)k(n)=n*dk-Nf*dk
enddo

do m=0,Nf-1
f(m)=x(m)**5*exp(-x(m)**2)
g(m)=exp(-4d0*x(m)**2)
enddo

!=== DFT mkl ===
h=dcmplx(0d0,0d0)
do m=0,Nf-1
write(10,'(5e20.7e3)')x(m),dble(f(m)),dimag(f(m)),dble(g(m)),dimag(g(m))
enddo

call fft(Nf,f,1)
f=f*dx
call fft(Nf,g,1)
g=g*dx
do n=0,N-1
h(n)=f(n)*g(n)*(-1)**n
enddo
call fft(Nf,h,-1)
h=h*dk

do m=0,Nf-1
write(12,'(3e20.7e3)')x(m),dble(h(m)),dimag(h(m))
enddo

!=== DFT define ===
h=dcmplx(0d0,0d0)
do m=0,Nf-1
f(m)=x(m)**5*exp(-x(m)**2)
g(m)=exp(-4d0*x(m)**2)
enddo
do m=0,Nf-1
write(20,'(5e20.7e3)')x(m),dble(f(m)),dimag(f(m)),dble(g(m)),dimag(g(m))
enddo

call dftdefine(Nf,f,x,k,1)
f=f*dx
call dftdefine(Nf,g,x,k,1)
g=g*dx

h=f*g
call dftdefine(Nf,h,x,k,-1)
h=h*dk

do m=0,Nf-1
write(22,'(3e20.7e3)')x(m),dble(h(m)),dimag(h(m))
enddo

stop
end program main

include "/home/sikino/mkl/include/mkl_dfti.f90"
subroutine fft(N,z,ifb)
use MKL_DFTI
implicit none
integer,intent(in)::N,ifb
complex(kind(0d0)),intent(inout)::z(0:N-1)

integer::Status
TYPE(DFTI_DESCRIPTOR),POINTER::hand

Status = DftiCreateDescriptor(hand,DFTI_DOUBLE,DFTI_COMPLEX,1,N)
Status = DftiCommitDescriptor(hand)

if(ifb.eq.1)Status = DftiComputeForward(hand,z)
if(ifb.eq.-1)Status = DftiComputeBackward(hand,z)

Status = DftiFreeDescriptor(hand)

return
end subroutine fft

subroutine dftdefine(Nf,z,x,k,ifb)
implicit none
integer,intent(in)::Nf,ifb
double precision,intent(in)::x(0:Nf-1),k(0:Nf-1)
complex(kind(0d0)),intent(inout)::z(0:Nf-1)

integer::n,m
complex(kind(0d0))::w(0:Nf-1)
double precision,parameter::pi=dacos(-1d0)

w=dcmplx(0d0,0d0)
if(ifb.eq.1)then
do n=0,Nf-1
do m=0,Nf-1
w(n)=w(n)+z(m)*exp(-dcmplx(0d0,1d0)*2d0*pi*k(n)*x(m))
enddo
enddo
elseif(ifb.eq.-1)then
do m=0,Nf-1
do n=0,Nf-1
w(m)=w(m)+z(n)*exp(dcmplx(0d0,1d0)*2d0*pi*k(n)*x(m))
enddo
enddo
endif
z=w

return
end subroutine dftdefine

数学

ニュートン写像に現れる綺麗な画像

2016年12月31日 sikino コメントする

ニュートン写像はニュートン=ラフソン法によって、ある初期値から適当な値へ収束するまでの回数でその関数を特徴づけるものです。
フラクタルと似ている考えであることを明記しておきます。

ニュートン写像

$
\displaystyle N_f(z)=z-\frac{f(z)}{f'(z)}
$
の繰り返しによって適当な初期値からスタートし、収束させていきます。このページでは画像が主です。説明の方はリーマンのゼータ関数の複素力学系をご覧ください。

基本はこれだけです。簡単な複素関数でも相当複雑になります。
早速適当な関数を用意して、ニュートン写像を見ていきましょう。

[adsense1]

まずは基本的な多項式を見ます。
$
f(z)=z^2-1
$

$
f(z)=z^3-1
$

$
f(z)=z^4-1
$

$
\displaystyle f(z)=z^5-1, z^6-1, z^7-1, z^10-1
$

少し複雑な関数の場合
$
\displaystyle f(z)=\ln z, e^z-1
$

$
\displaystyle f(z)=e^{1/z}-0.01
$

$
\displaystyle f(z)=ze^{z}\ln z-0.01
$

$
\displaystyle f(z)=z^5e^z-0.1
$

$
\displaystyle f(z)=z^4e^z\ln z-0.1
$

$
\displaystyle f(z)=sin(z)/z
$

$
\displaystyle f(z)=z^2 e^{-z^2}-1
$

$
\displaystyle f(z)=ln(z) e^{-z^2}-1
$

最後にリーマンのゼータ関数

複素関数$f(z)$が多くの根を持つとき、非常に複雑で綺麗な画像が得られるようです。
恐らく遠く離れたところからたまたま根のあたりに到達することが多くなるからでしょう。

[adsense2]

fortran90によるプログラム

fortran90によるプログラムを置いておきます。入力するべき場所は!=====の間と、関数fと導関数dfです。

program main
implicit none
integer,parameter::kmax=49
double precision,parameter::eps=1d-8
integer::i,j,k,Nx,Ny
double precision::xa,xb,ya,yb,x,y,hx,hy
complex(kind(0d0))::f,df,z,z1
external::f,df

!==================
xa=-5d0; xb=5d0
Nx=201

ya=-5d0; yb=5d0
Ny=201
!==================

hx=(xb-xa)/dble(Nx-1)
hy=(yb-ya)/dble(Ny-1)
do i=0,Nx-1
x=xa+i*hx
do j=0,Ny-1
y=ya+j*hy
z=dcmplx(x,y)
do k=0,kmax
z1=z-f(z)/df(z)
if(abs((z-z1)/z).le.eps)exit
z=z1
enddo
write(10,'(2e18.8e3,i5)')x,y,k
enddo
write(10,*)
if(mod(i,100).eq.0)write(6,'(A,i6,A,i6)')" ",i," / ",Nx
enddo

stop
end program main

function f(z)
implicit none
complex(kind(0d0))::f,z

f=z**5*exp(z)-0.1d0

return
end function f

function df(z)
implicit none
complex(kind(0d0))::df,z

df=5*z**4*exp(z)+z**5*exp(z)

return
end function df

プログラミングと数値計算, 数学

リーマンのゼータ関数の複素力学系

2016年12月31日 sikino コメントする

本稿の目的はリーマンのゼータ関数を、ニュートン法による写像を用いて別の視点から見ることです。
綺麗な絵が得られる[1]ので自分のコンピュータ上で見てみたいと思いました。

複素力学系とは？

複素力学系とは、簡単に言えば写像のことです。
実関数による写像の繰り返しで得られる系を力学系と呼び、
複素関数による写像の繰り返しで得られる系を複素力学系と呼びます。
”力学”の言葉の由来はニュートン力学から来ています。

”ニュートン力学”は目に見えるくらいの物体を扱う学問ですが、その正体は時間に関する2階の微分方程式です。
なので、時刻$t$の物体の振る舞い$x(t)$からちょっとの時間$\Delta t$秒後の物体の振る舞い$x(t+\Delta t)$は、適当な時間発展をさせる演算子$f$によって
$
x(t)\overset{f}{\longrightarrow} x(t+\Delta t)
$
と移り変わります。これを何度も繰り返し作用させて任意の時刻$t’$まで時間発展させる事が出来ます。

$
x(t)\overset{f}{\longrightarrow} x(t+\Delta t)\overset{f}{\longrightarrow} x(t+2\Delta t)\overset{f}{\longrightarrow}x(t+3\Delta t)\overset{f}{\longrightarrow} \cdots\overset{f}{\longrightarrow} x(t’)
$
となると、ニュートン力学を性質を知ろうとするときに重要な情報は、演算子$f$と初期値に集約されます。

演算子$f$の空間へどんどん写像していくわけですので、ある写像の繰り返しも力学のようだ、だから”力学系”という名前が付けられたわけです。
もう少し詳しく知りたければ、まずは[3]を読むと良いでしょう。

本稿では複素力学系の一つであるニュートン＝ラフソン法によって得られる写像(ここでは便宜的にニュートン写像と呼ぶことにします)を考えます。

複素関数$f(z)$の具体的なニュートン写像の数式は以下で与えられます。
$
\displaystyle N_f(z)=z-\frac{f(z)}{f'(z)}
$
ある複素平面の初期値からスタートして、この写像を何回繰り返したら収束したか？をその系を特徴づける値とします。
要は、ニュートン＝ラフソン法の初期値を複素平面上の全ての点を取り、収束するまでの回数をカウントするのです。

[adsense1]

ニュートン写像の具体例

本稿の目的はゼータ関数に対して行うことですが、まずは簡単な複素関数のニュートン写像を見てみましょう。
まず、複素関数
$
\displaystyle f(z)=z^2-1
$
を考えます。根の周り（$z=\pm 1$）では収束回数は少なくなることが予想できます。実際にやってみますとこんな感じに。

非常に単調です。実部の値が正か負かでのみ特徴づけられるようです。

続いて、複素関数
$
\displaystyle f(z)=z^3-1
$
を考えます。根は$z=1, e^{\pm i2\pi/3}$。

3つは確かに分けられていますが、その境界辺りでは非常に奇怪な模様になります。

さらに、複素関数
$
\displaystyle f(z)=z^4-1
$
を考えます。根は$z=\pm 1, \pm i$。

ゼータ関数のニュートン写像

では、ゼータ関数に適応してみましょう。
ゼータ関数の導関数は導出方法とプログラムは[2],[9]/リーマンのゼータ関数の数値計算コード(複素平面)に追記したのでそちらをご覧ください。
するとこんなニュートン写像になります。

ゼロ点付近では収束が早くなっています。ゼロ点のある場所がマークしたところです。

カラーを対数にしますとこんな図に。

(2017/01/13 追記)
もっとほかの範囲のニュートン写像を見ていきます。

全体像

拡大その1(全体像の左側の四角)

拡大その2(全体像の右側の四角)

拡大その２, 高解像度版 highres_zetanewton.png (15MB)

元の画像はこちらからダウンロードできます。

[adsense2]

ゼータ関数のニュートン写像を得るfortran90のプログラムはこちらです。

ifort -O3 -qopenmp main.f90

計算範囲はxa,xb,ya,ybで指定されています。

▼ここクリックで計算コードをこの場に展開

program main
implicit none
integer::i,j,Nx,Ny,prog,omp_get_thread_num
double precision::x,xa,xb,y,ya,yb,hx,hy
integer,allocatable::ns(:,:)

complex(kind(0d0))::czeta,cdzeta
external::czeta,cdzeta

xa=-20d0; xb=20d0
Nx=201
ya=-20d0; yb=20d0
Ny=201

hx=(xb-xa)/dble(Nx-1)
hy=(yb-ya)/dble(Ny-1)

allocate(ns(0:Nx,0:Ny)); ns=0
call omp_set_num_threads(1)
prog=0
!$omp parallel do shared(prog) schedule(dynamic,1)
do i=0,Nx
call tomp(i,Nx,xa,hx,Ny,ya,hy,ns)
prog=prog+1
if(mod(prog,1).eq.0)write(6,'(A,2i6,A,i6)')&
" ",omp_get_thread_num(),prog," / ",Nx
enddo
!$omp end parallel do

do i=0,Nx
x=xa+i*hx
do j=0,Ny
y=ya+j*hy
write(10,*)x,y,ns(i,j)
enddo
write(10,*)
enddo

stop
end program main

subroutine tomp(i,Nx,x0,hx,Ny,y0,hy,ns)
implicit none
integer::i,Nx,Ny
double precision::x0,hx,y0,hy
integer::ns(0:Nx,0:Ny)

integer::j,k,kmax
double precision::x,y,eps
complex(kind(0d0))::z0,z1,czeta,cdzeta,zt,dzt
external::czeta,cdzeta

eps=1d-8
kmax=59

x=x0+i*hx
do j=0,Ny
y=y0+j*hy
z0=dcmplx(x,y)
do k=0,kmax
zt=czeta(z0)
dzt=cdzeta(z0)
z1=z0-zt/dzt
if(abs((z0-z1)/z0).le.eps)exit
z0=z1
enddo
ns(i,j)=k
enddo

return
end subroutine tomp

function czeta(s)
!Checked : ifort (success : version 16.0.2 20160204)
! : gfortran(success : version 4.8.4)
! : gfortran(success : version 4.4.7)
!
!http://slpr.sakura.ne.jp/qp/
! Author : sikino
! date: 2016/06/02, (yyyy/mm/dd)
! : 2016/06/03
! : 2016/06/04
! : 2016/06/05
! : 2016/12/25
! : 2017/01/12
implicit none
complex(kind(0d0)),intent(in)::s
integer,parameter::nmax=100
complex(kind(0d0))::czeta

integer::n,k
double precision::nq,nq1,ln1,ln2
double precision,parameter::eps=1d-15
double precision,parameter::pi=3.14159265358979324d0
complex(kind(0d0))::ds,is,d,s0,tc,tt,qzeta
complex(kind(0d0))::a(0:Nmax),b(0:nmax),cgamma
external::cgamma

ds=dble(s); is=imag(s)
if(ds.eq.1d0.and.is.eq.0d0)then
czeta=1d+300
elseif(ds.eq.0d0.and.is.eq.0d0)then
czeta=-0.5d0
else
if(real(s).lt.1d0)then
s0=1d0-s
else
s0=s
endif

tt=1d0/(1d0-2d0**(1d0-s0))
qzeta=0.5d0*tt

a=cmplx(0d0,0d0,kind=8); b=cmplx(0d0,0d0,kind=8)
b(0)=0.25d0*tt
do n=1,nmax
nq=n
nq1=nq+1d0

a(0)=b(0)
do k=1,n-1
a(k)=b(k)*nq/(n-k)
enddo
!----
ln2=log(nq/nq1)
if(n.eq.1)then
ln1=log(0.5d0)
d=s0*ln1
a(1)=-a(0)*exp(d)/nq
else
d=(ln2/ln1)*d
a(n)=-a(n-1)*exp(d)/nq
ln1=ln2
endif
!----

tc=cmplx(0d0,0d0,kind=8)
do k=0,n
tc=tc+a(k)
enddo

qzeta=qzeta+tc

if(abs(qzeta).ge.1d0)then
if(abs(tc/qzeta).le.eps)exit
else
if(abs(tc).le.eps)exit
endif

b=0.5d0*a
enddo

if(real(s).lt.1d0)then
czeta=(2d0**s)*pi**(-s0)*sin(0.5d0*pi*s)*qzeta*cgamma(s0)
else
czeta=qzeta
endif
end if

return
end function czeta

function cdzeta(s)
!Checked : ifort (success : version 16.0.2 20160204)
! : gfortran(success : version 4.8.4)
!
!http://slpr.sakura.ne.jp/qp/
! Author : sikino
! date: 2016/12/30
! : 2017/01/13
implicit none
complex(kind(0d0)),intent(in)::s
integer,parameter::nmax=100
complex(kind(0d0))::cdzeta

integer::n,k
double precision::nq,nq1,x,y,g1,g2,ds,is
complex(kind(0d0))::d
double precision,parameter::eps=1q-14
double precision,parameter::pi=3.14159265358979324d0
double precision,parameter::ln4=1.386294361119890619d0 ! ln(4)
complex(kind(0d0))::s0,tc,tt,ys,gs,zs,s1,s2,h1,h2
complex(kind(0d0))::a(0:Nmax),b(0:nmax)
complex(kind(0d0))::cgamma
complex(kind(0d0))::czeta,digamma
external::cgamma,czeta,digamma

ds=dble(s); is=imag(s)
if(ds.eq.1d0.and.is.eq.0d0)then
cdzeta=1d+300
elseif(ds.eq.0d0.and.is.eq.0d0)then
cdzeta=-0.5d0*log(2d0*pi)
else
if(real(s).lt.1d0)then
s0=1d0-s
else
s0=s
endif

s1=2d0**s0
s2=s1-2d0
tt=-s1*ln4/(s2*s2)
cdzeta=0.5d0*tt

a=cmplx(0d0,0d0,kind=8); b=cmplx(0d0,0d0,kind=8)
b(0)=cmplx(0.25d0,0d0,kind=8)*tt
do n=1,nmax
nq=n
nq1=nq+1d0

a(0)=b(0)
do k=1,n-1
a(k)=b(k)*nq/(n-k)
enddo
!----
g2=log(nq/nq1)
if(n.eq.1)then
h1=ln4
d=s0*log(0.5d0)
else
d=d*g2/g1
endif
h2=s2*log(nq1)+ln4
a(n)=-a(n-1)*exp(d)*h2/(h1*nq)
g1=g2
h1=h2
!----

tc=cmplx(0d0,0d0,kind=8)
do k=0,n
tc=tc+a(k)
enddo
cdzeta=cdzeta+tc

if(abs(cdzeta).ge.1d0)then
if(abs(tc/cdzeta).le.eps)exit
else
if(abs(tc).le.eps)exit
endif

b=0.5d0*a
enddo

if(real(s).lt.1d0)then
x=-log(2d0*pi)
y=-pi*0.5d0
ys=-y*s0
zs=czeta(1d0-s)
gs=cgamma(s0)
cdzeta=-2d0*(2d0*pi)**(-s0)*(&
(x*cos(ys)+y*sin(ys))*gs*zs+cos(ys)*(digamma(1d0-s)*gs*zs+gs*cdzeta))
else
cdzeta=cdzeta
endif
end if

return
end function cdzeta

function cgamma(z)
! sikinote (http://slpr.sakura.ne.jp/qp)
! author : sikino
! date : 2017/01/09
! 2017/01/10

implicit none
complex(kind(0d0)),intent(in)::z
complex(kind(0d0))::cgamma

integer::i,n,M
double precision,parameter::pi=3.14159265358979324d0
double precision,parameter::e1=0.3678794411714423216d0
double precision,parameter::ln2pi2=0.91893853320467274d0
double precision,parameter::sq2pi=2.5066282746310005d0
double precision::a(1:30),AB(1:14),dz,iz
complex(kind(0d0))::q,s,w,r,q1,q2

dz=dble(z)
iz=imag(z)

if(dz.eq.nint(dz).and.iz.eq.0d0)then
if(dz.gt.0d0)then
s=dcmplx(1d0,0d0)
n=nint(dz)
do i=2,n
s=s*i
enddo
else
s=1d+300
endif
cgamma=s
else
q=z
if(dz.lt.0d0)q=1d0-z

if(abs(iz).lt.1.45d0)then
! For x=arb, |y|\lt 1.45
n=int(dble(q))
s=1d0
do i=1,n
s=s*(q-i)
enddo
w=q-dble(n)

a(1) = 1d0
a(2) = 0.57721566490153286d0
a(3) =-0.65587807152025388d0
a(4) =-0.42002635034095236d-1
a(5) = 0.16653861138229149d0
a(6) =-0.42197734555544337d-1
a(7) =-0.96219715278769736d-2
a(8) = 0.72189432466630995d-2
a(9) =-0.11651675918590651d-2
a(10)=-0.21524167411495097d-3
a(11)= 0.12805028238811619d-3
a(12)=-0.20134854780788239d-4
a(13)=-0.12504934821426707d-5
a(14)= 0.11330272319816959d-5
a(15)=-0.20563384169776071d-6
a(16)= 0.61160951044814158d-8
a(17)= 0.50020076444692229d-8
a(18)=-0.11812745704870201d-8
a(19)= 0.10434267116911005d-9
a(20)= 0.77822634399050713d-11
a(21)=-0.36968056186422057d-11
a(22)= 0.51003702874544760d-12
a(23)=-0.20583260535665068d-13
a(24)=-0.53481225394230180d-14
a(25)= 0.12267786282382608d-14
a(26)=-0.11812593016974588d-15
a(27)= 0.11866922547516003d-17
a(28)= 0.14123806553180318d-17
a(29)=-0.22987456844353702d-18
a(30)= 0.17144063219273374d-19

M=int(11.3*abs(w)+13)
if(M.gt.30)M=30
r=a(M)
do i=M-1,1,-1
r=r*w+a(i)
enddo

cgamma=s/(r*w)
else
! For x=arb, |y|\gt 1.45
s=1d0
if(abs(q).lt.9d0)then
do i=0,7
s=s*(q+i)
enddo
s=1d0/s
q=q+8d0
endif

AB(1) = 0.83333333333333333d-1
AB(2) =-0.27777777777777778d-2
AB(3) = 0.79365079365079365d-3
AB(4) =-0.59523809523809524d-3
AB(5) = 0.84175084175084175d-3
AB(6) =-0.19175269175269175d-2
AB(7) = 0.64102564102564103d-2
AB(8) =-0.29550653594771242d-1

q1=1d0/q
q2=q1*q1

r=AB(8)
do i=7,1,-1
r=r*q2+AB(i)
enddo
cgamma=s*exp((q-0.5d0)*log(q)-q+ln2pi2+r*q1)
endif
if(dz.lt.0d0)cgamma=pi/(cgamma*sin(pi*z))
endif

return
end function cgamma

function digamma(z)
! digamma function for complex plane
! sikinote, http://slpr.sakura.ne.jp/qp/
! author : sikino
! date : 2016/07/04 (yyyy/mm/dd)
! date : 2016/07/07 (yyyy/mm/dd)
implicit none
complex(kind(0d0)),intent(in)::z
complex(kind(0d0))::digamma

integer::i,n,m,as,key
integer,parameter::nmax=50
double precision::eps=1d-13
double precision::pi=4d0*atan(1d0)
complex(kind(0d0))::w,ds,s
double precision::B
external::B

as=10

if(dble(z).ge.dble(as))then
w=z
key=0
elseif(dble(z).ge.1d0)then
w=z+dble(as)
key=1
elseif(dble(z).ge.-dble(as-1))then
w=1d0-z+dble(as)
key=2
else
w=1d0-z
key=3
endif

! Asymptotic expansion
s=log(w)-0.5d0/w
do n=1,nmax
m=2*n
ds=B(m)/(m*w**m)
s=s-ds
if(abs(ds)/abs(s).le.eps)exit
enddo
if(n.eq.nmax+1)then
write(6,*)"Worning! did not converge at digamma"
endif

if(key.eq.1.or.key.eq.2)then
!Recurrence relation
do i=1,as
s=s+1d0/(1d0-w)
w=w-1d0
enddo
endif
if(key.eq.2.or.key.eq.3)then
! Reflection Formula
s=s-pi/tan(pi*z)
endif

digamma=s

return
end function digamma
!--------------------------
function B(n)
! 1st bernoulli number B(n), 0 <= n <= 100
! from wolfram alpha
! " Table[bernoulli b(i), {i,0,100}] with 17 digits "
implicit none
integer,intent(in)::n
double precision::B
double precision::A(0:100)

if(n.lt.0.or.n.gt.100)then
write(6,*)"Not expected n at bernoulli number function. "
write(6,*)"program stop"
stop
endif

A(0:100)=(/1d0 &
, -0.50000000000000000d0, 0.16666666666666667d0, 0d0, -0.033333333333333333d0, 0d0 &
, 0.023809523809523810d0, 0d0, -0.033333333333333333d0, 0d0, 0.075757575757575758d0, 0d0 &
, -0.25311355311355311d0, 0d0, 1.1666666666666667d0, 0d0, -7.0921568627450980d0, 0d0 &
, 54.971177944862155d0, 0d0, -529.12424242424242d0, 0d0, 6192.1231884057971d0, 0d0 &
, -86580.253113553114d0, 0d0, 1.4255171666666667d+6, 0d0, -2.7298231067816092d+7, 0d0 &
, 6.0158087390064237d+8, 0d0, -1.5116315767092157d+10, 0d0, 4.2961464306116667d+11, 0d0 &
, -1.3711655205088333d+13, 0d0, 4.8833231897359317d+14, 0d0, -1.9296579341940068d+16, 0d0 &
, 8.4169304757368262d+17, 0d0, -4.0338071854059455d+19, 0d0, 2.1150748638081992d+21, 0d0 &
, -1.2086626522296526d+23, 0d0, 7.5008667460769644d+24, 0d0, -5.0387781014810689d+26, 0d0 &
, 3.6528776484818123d+28, 0d0, -2.8498769302450882d+30, 0d0, 2.3865427499683628d+32, 0d0 &
, -2.1399949257225334d+34, 0d0, 2.0500975723478098d+36, 0d0, -2.0938005911346378d+38, 0d0 &
, 2.2752696488463516d+40, 0d0, -2.6257710286239576d+42, 0d0, 3.2125082102718033d+44, 0d0 &
, -4.1598278166794711d+46, 0d0, 5.6920695482035280d+48, 0d0, -8.2183629419784576d+50, 0d0 &
, 1.2502904327166993d+53, 0d0, -2.0015583233248370d+55, 0d0, 3.3674982915364374d+57, 0d0 &
, -5.9470970503135448d+59, 0d0, 1.1011910323627978d+62, 0d0, -2.1355259545253501d+64, 0d0 &
, 4.3328896986641192d+66, 0d0, -9.1885528241669328d+68, 0d0, 2.0346896776329074d+71, 0d0 &
, -4.7003833958035731d+73, 0d0, 1.1318043445484249d+76, 0d0, -2.8382249570693707d+78/)

B=A(n)

return
end function B

参考文献

[1]Tomoki Kawahira “Riemann’s zeta function and Newton’s method: Numerical experiments from a complex-dynamical viewpoint”

[2]Tom M. Apóstol “Formulas for Higher Derivatives of the Riemann Zeta Function”, Math. of. Comp vol 44, 169, 1985, pp. 223-232.

[3]Chapter 14 力学系（補講１）

[4]ジュリア集合の色付けを工夫して芸術的なフラクタル図形を描く

[5]複素力学系, ニュートン法, ジュリア集合

[6]西沢清子, 藤村雅代 “多項式のニュートン写像における鉢の幅について(カオスをめぐる力学系の諸問題)”

[7]Riemann Zeta Function -wolfram mathworld

[8]ディガンマ関数の数値計算 -シキノート
[9]リーマンのゼータ関数の数値計算コード(複素平面) -シキノート

本ページの更新はもうしません。https://slpr.sakura.ne.jp/sikinote に移行します。

更新履歴

2023年10月1日更新
ようこそ
Mod by:sikino
2023年7月7日更新
更新停止のお知らせ
Mod by:sikino
2023年3月5日更新
マイナス×マイナス=プラスはなぜ？
Mod by:sikino
2023年2月26日更新
一般固有値問題の対角化のプログラム（実対称行列、Fortran90）
Mod by:sikino
2023年2月15日更新
latexで数式全体を小さくする
Mod by:sikino
2023年1月21日更新
gnuplotのカラーマップ
Mod by:sikino
2023年1月5日更新
時間依存シュレーディンガー方程式の数値解法クランク＝ニコルソン法
Mod by:sikino
2022年12月5日更新
信号と窓関数
Mod by:sikino

	\(x_m\)	\(\tilde{k}_n\)
添え字	\(m=0,1,2,\cdots,N-1\)	\(n=0,1,2,\cdots,N-1\)
区間	\(\displaystyle [a,b]\)	\(\displaystyle \left[-\frac{1}{2\Delta x},\frac{1}{2\Delta x}\right]\)
刻み幅	\(\displaystyle \Delta x=\frac{b-a}{N}\)	\(\displaystyle \Delta \tilde{k}=\frac{1}{b-a}\)
分点の位置	\(\displaystyle x_m=m\Delta x +a\)	\(\displaystyle \tilde{k}_n=n\Delta \tilde{k} -\frac{1}{2\Delta x}\)

	\(x_m\)	\(\tilde{k}_n\)
添え字	\(m=0,1,2,\cdots,N-1\)	\(n=0,1,2,\cdots,N-1\)
区間	\(\displaystyle [-a,a]\)	\(\displaystyle \left[0,N\Delta \tilde{k}\right]\)
刻み幅	\(\displaystyle \Delta x=\frac{2a}{N}\)	\(\displaystyle \Delta \tilde{k}=\frac{1}{2a}\)
分点の位置	\( \begin{eqnarray} x_m=\left\{ \begin{aligned} & m\Delta x ~~~~(m=0,\cdots,\frac{N}{2}-1) \\ & m\Delta x-\frac{1}{\Delta \tilde{k}} (m=\frac{N}{2},\cdots,N-1) \end{aligned} \right. \end{eqnarray} \)	\(\displaystyle \tilde{k}_n=n\Delta \tilde{k} ~~~~(n=0,\cdots,N-1)\)

数値計算方法

ジョルダンの補題の利用

数値計算プログラム

\(k\gt 0\)の時

\(k\lt 0\)の時

\(k= 0\)の時

計算結果のまとめ

1のフーリエ変換

ヘヴィサイド関数のフーリエ変換

\(k\ne0\)の場合

\(k=0\)の場合

特異点の周り方の指定

1. 複素k平面上で特異点周りを上方向を回る場合

2. 複素k平面上で特異点周りを下方向を回る

3. 複素k平面上で特異点周りを上方向と下方向を回った結果の平均をとる

演算子としての表現

結論

特異点をずらす操作について

注意

まとめ

目次

フーリエ変換の定義

離散フーリエ変換の定義

ナイキスト(Nyquist)周波数について

フーリエ変換が元に戻ることの証明

フーリエ変換

離散フーリエ変換

畳み込み(convolution)の定義

離散畳み込みと離散フーリエ変換

畳み込み定理の証明

連続畳み込み

離散畳み込み

数値計算で使われている離散フーリエ変換アルゴリズム (例: intel®MKL)

MKLの離散フーリエ変換の導出）

離散フーリエ変換時の注意点

フーリエ変換を介する畳み込み時の注意点

ニュートン写像

fortran90によるプログラム

複素力学系とは？

ニュートン写像の具体例

ゼータ関数のニュートン写像

全体像

拡大その1(全体像の左側の四角)

拡大その2(全体像の右側の四角)

参考文献

本ページの更新はもうしません。https://slpr.sakura.ne.jp/sikinote に移行します。