球体の抗力係数

説明

本稿では、完全な球体に働く抗力係数について述べます。
ここでは概要だけを説明します。詳細は以下のPDFをご覧ください。

https://slpr.sakura.ne.jp/qp/supplement_data/drag_coefficient_air/drag_coefficient.pdf

概要

速度\(v(=|\mathbf{v}|)\)で動く半径\(R\)の完全な球体に働く空気抵抗力の大きさ\(F_d(=|\mathbf{F}_d|)\)は,
\begin{align}
F_d =\frac{1}{2} C_d(R_e) \rho \pi R^2 v^2
\end{align}
と書けます. 空気抵抗力\(\mathbf{F}_d\)は, 球体の速度方向と反対に働くので, 方向を含めれば
\begin{align}
\mathbf{F}_d =-\frac{1}{2} C_d(R_e) \rho \pi R^2 v^2\frac{\mathbf{v}}{v}
\end{align}
と書けます.

つまり、重力加速度\(g\)の重力下における質量\(m\)の完全な球体に対する運動方程式は
\begin{align}
m\frac{d^2}{dt^2}\mathbf{r} =-mg\mathbf{k}-\frac{1}{2} C_d(R_e) \rho \pi R^2 v^2\frac{\mathbf{v}}{v}
\end{align}
となります。ここで、\(\mathbf{k}\)は重力の方向の単位ベクトル（多くの場合では鉛直上向きを\(z\)軸の正の方向、単位ベクトル\(\mathbf{k}\)とするので、負号が付いています）です。
速度が非常に遅い極限\((R_e\to 0)\)においては、\( C_d(R_e)|_{R_e\to 0}\to \frac{24}{R_e}\)となります。

完全な球体の抗力係数\(C_d\)における近似式は、レイノルズ数を\(R_e\)として以下の通り与えられます。

\(R_e\lt 2\times 10^5\)層流領域のみ
\begin{align}
C_d(R_e)&=\left[\frac{24}{R_e}(1+0.15 R_e^{0.687})\right]+\frac{0.42}{1+(\frac{42500}{R_e^{1.16}})},~~~\mbox{式(1)}
\end{align}
ただし、\(R_e \lt 2\times 10^5~~\mbox{and}~~K_n \lt 0.01 ~~\mbox{and}~~ M_a\to 0 \)
\(R_e\lt 2\times 10^5\)の層流領域のみ、マッハ数\(M_a\)依存性込み
\begin{align}
C_d(R_e)
=\frac{24}{R_e}(1+0.15 R_e^{0.687})H_M
+\frac{0.42 C_M}{1+(\frac{42500}{R_e^{1.16C_M}})+\frac{G_M}{R_e^{0.5}}} ,~~~\mbox{式(2)}
\end{align}
ここで、\(C_M, G_M, H_M\)は以下の通り与えられます。
\(\displaystyle
\begin{eqnarray}
C_M=\left\{~~
\begin{aligned}
&1.65+0.65\tanh(4M_a-3.4)~~~~~\mbox{for} ~~~M_a\lt 1.5\\
&2.18-0.13\tanh(0.9M_a-2.7)~~~\mbox{for} ~~~M_a\gt 1.5
\end{aligned}
\right.
\end{eqnarray}
\)
\(\displaystyle
\begin{eqnarray}
G_M=\left\{~~
\begin{aligned}
&166M_a^3+3.29M_a^2-10.9M_a+20~~~\mbox{for} ~~~M_a\lt 0.8\\
&5+40M_a^{-3}~~~\hspace{9.4em}\mbox{for} ~~~ M_a\gt 0.8
\end{aligned}
\right.
\end{eqnarray}
\)

\(\displaystyle
\begin{eqnarray}
H_M=\left\{~~
\begin{aligned}
&0.0239M_a^3+0.212M_a^2-0.074M_a+1~~~\mbox{for} ~~~ M_a\lt 1\\
&0.93+\frac{1}{3.5+M_a^5}~~~\hspace{8.8em}\mbox{for} ~~~ M_a\gt 1
\end{aligned}
\right.
\end{eqnarray}
\)
定性的、広範囲
\begin{align}
C_d
=\frac{24}{R_e}
+\frac{2.6\left(\frac{R_e}{5.0}\right)}{1+\left(\frac{R_e}{5.0}\right)^{1.52}}
+ \frac{0.411\left(\frac{R_e}{263000}\right)^{-7.94}}{1+\left(\frac{R_e}{263000}\right)^{-8.00}}
+ \left(\frac{0.25\frac{R_e}{10^6}}{1+\frac{R_e}{10^6}}\right),~~~\mbox{式(3)}
\end{align}

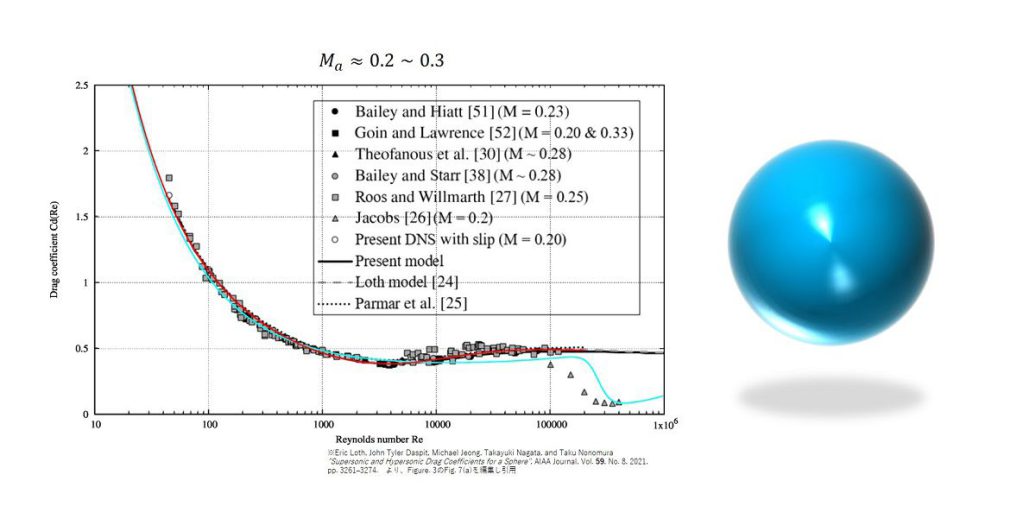
対象物が流体中を高速で動かなければ、層流領域で実験値を良く合う式(1)（図中の赤線）, 式(2)で十分でしょう。
温度なども含めたいならば、PDFで説明しているレイノルズ数、マッハ数を置き換えて利用することを勧めます。
また精度はあまりいらない状況で、定性的な理解だけを対象とするならば、乱流領域の振る舞いを含む式(3)（図中の水色線）を用いると良いです。

以降、詳細は
https://slpr.sakura.ne.jp/qp/supplement_data/drag_coefficient_air/drag_coefficient.pdf
をご覧ください。