オンラインで使える数学用の検索エンジン
Wolfram alpha
を使うといろいろな事が出来ます。それらを紹介します。
積分
基本中の基本、積分です。複雑な積分でも定積分でも不定積分でも無限大でも受け付けてくれます。
ただし、計算してくれるかは分かりません。
例えば\(\rm{sinc}\)関数\(\left(\rm{sinc}(x)=\frac{sin(x)}{x}\right)\)のゼロから無限大までの積分は、
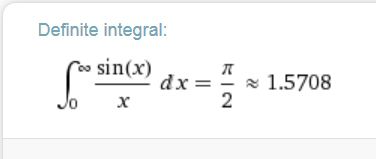
のように出力してくれます。\(\pi\)で出力されるのは凄いです。
\(\rm{sinc}\)関数のように有名な関数であれば、
としたほうがたくさんの情報が得られます。
微分方程式の解
と入力すると微分方程式を解いてくれます。また、
な風にすると、初期条件を与えたうえで解いてくれます。
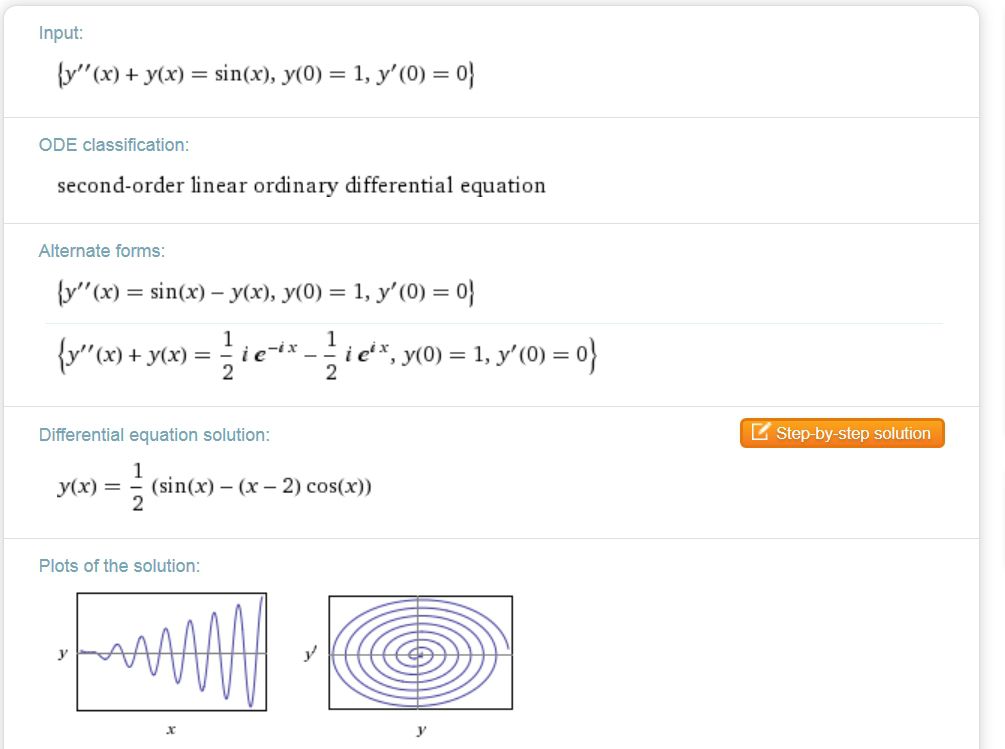
自分の与えた数式通りに認識しているか、確かめましょう。
行列の対角化
行列の対角化を行ってくれます。上を入力すると行列
\(
\begin{eqnarray}
\left(
\begin{array}{ccc}
-2 & 2 & 4 \\
-2 & 4 & 2 \\
-2 & 1 & 4
\end{array}
\right)
\end{eqnarray}
\)を対角化し、その固有値と固有ベクトルを出力してくれます。
級数展開
関数の級数展開を出力してくれます。
例えば、
と入力するとベッセル関数\(J_1(x)\)を\(x\)について、\(x=0\)回りで、\(x^5\)まで展開して出力してくれます。
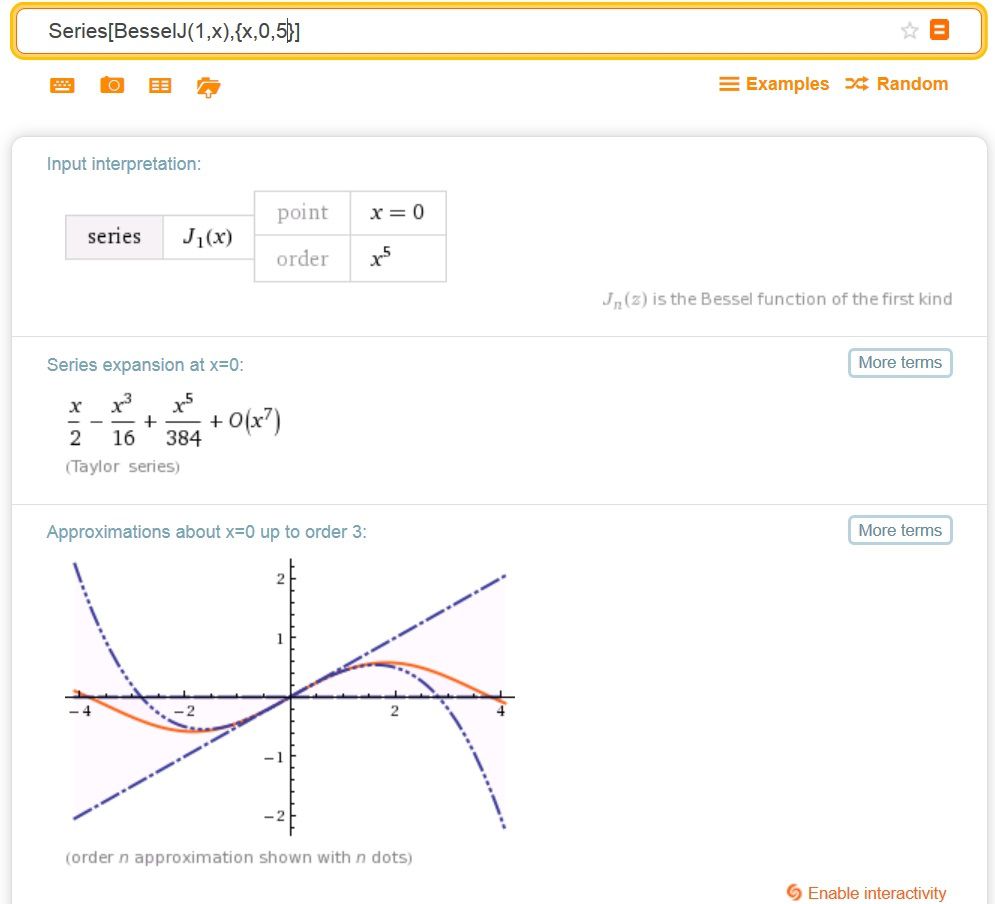
また、
とすると、\(\cos(x)\)を\(x\)について、\(x=1\)回りで、\(x^{10}\)まで展開して出力してくれます。
また、
としても展開してくれます。この場合はローラン(Laurent)展開であり、特異点周りの展開となっています。
上の場合、出力として、
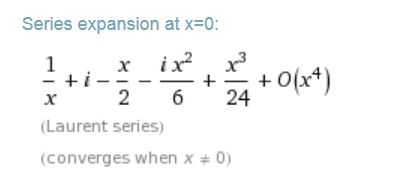
という結果が得られます。
もう一つ、ガンマ関数\(\Gamma(x)\)の\(x=0\)まわりでのローラン展開です。
と入力するとガンマ関数\(\Gamma(x)\)を\(x\)について、\(x=0\)回りで、\(x^3\)まで展開して出力してくれます。
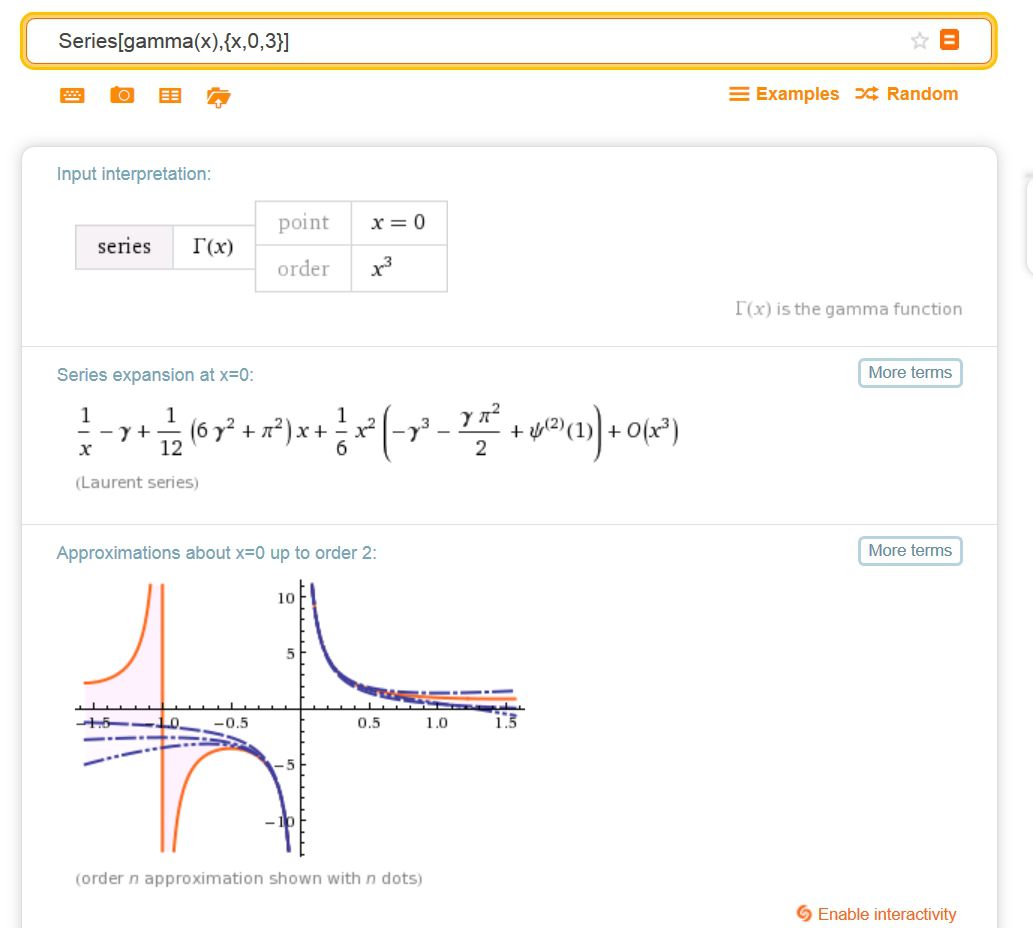
すごい・・・
キャラクターの曲線
様々なキャラクターの曲線のグラフを出力してくれます。
その曲線はWolfram alpha named parametric curvesにまとめられていましたので紹介します。
もしくは、↓をクリックすることで展開されます。
上の他には、wolframで
や
や
と入力して,moreを押していってください。
例を挙げます。
“tachikoma”は、攻殻機動隊に出てくる戦車です。こんな感じです。

——————–
“charmander”は、ヒトカゲの事のようです。
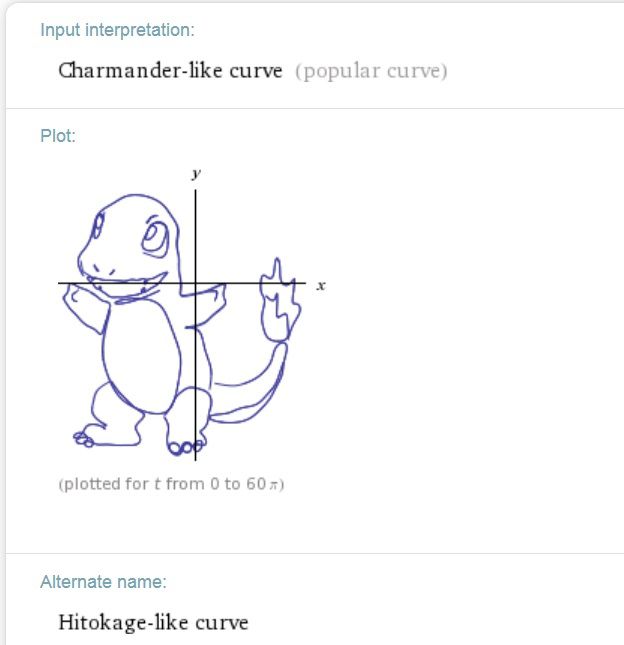
———————
もしも、上のグラフの数式をコピペしたい場合は、各グラフの下に
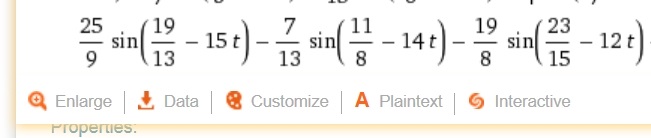
という欄の、”plain text”というところをクリックすれば数式を取得できます。