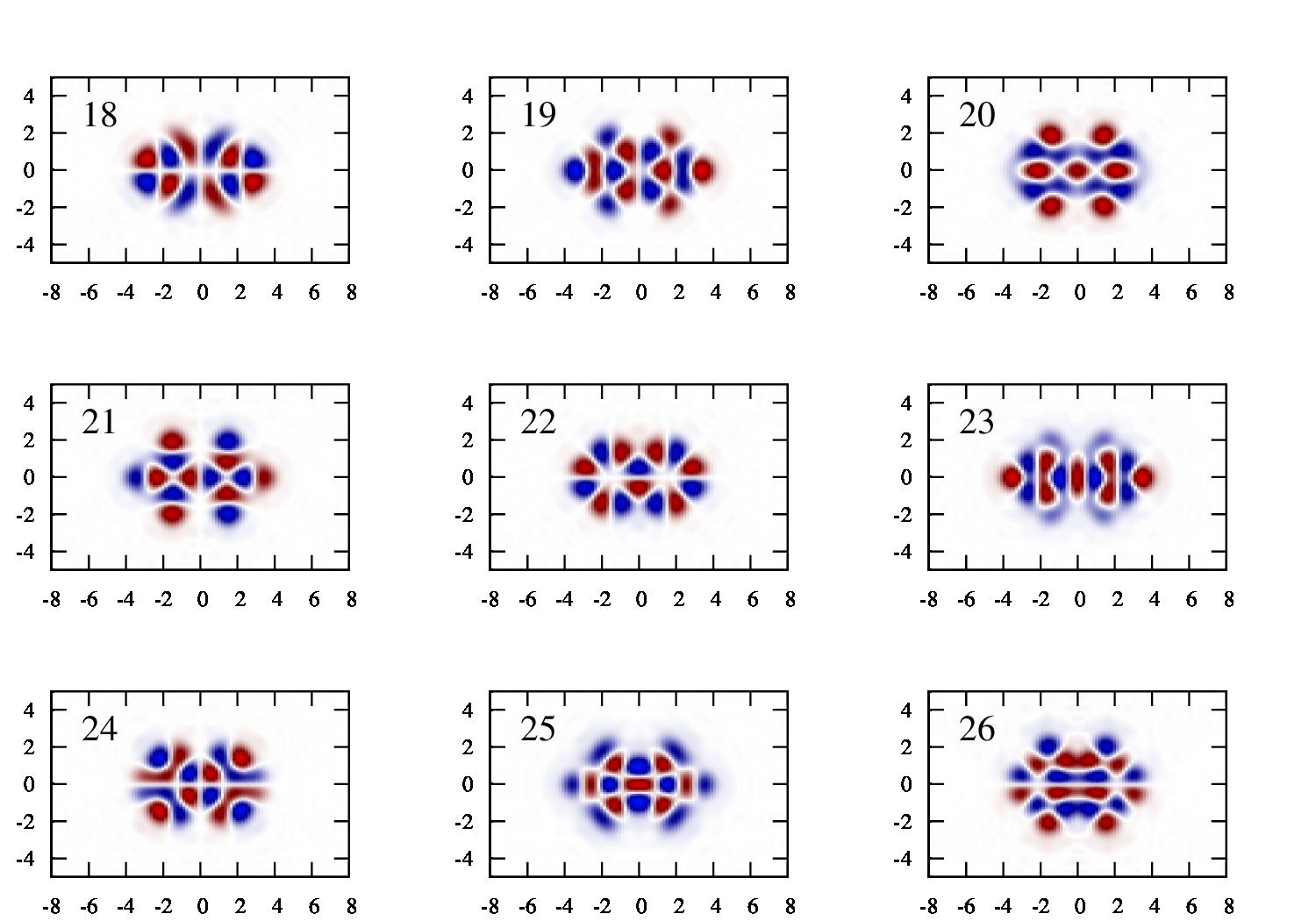
2次元の時間依存しないシュレーディンガー方程式を変分原理に基づいて解きます。

対象とする問題は以下の時間依存しないシュレーディンガー方程式です。

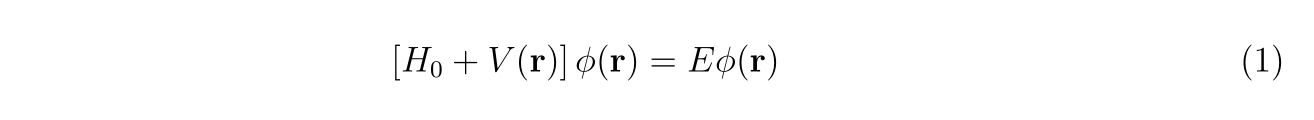
ここで、\(H_0\)は数値計算で用いる基底関数のハミルトニアン、\(V(\mathbf{r})\)はその他のポテンシャルです。

この系の固有関数\(\phi(\mathbf{r})\)を

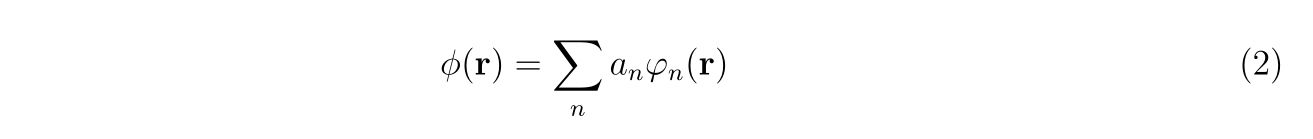
として\(H_0\)の固有関数で展開します。ここで、\(\varphi_{\mathbf{r}}\)は

の固有値問題の解である、固有値\(E’_n\)に属する固有関数です。また、\(\varphi_{\mathbf{r}}\)は

として規格直交化されています。

式(2)を式(1)に代入した後、左から\(\varphi^*_{\mathbf{r}}\)を掛けて全空間で積分すれば

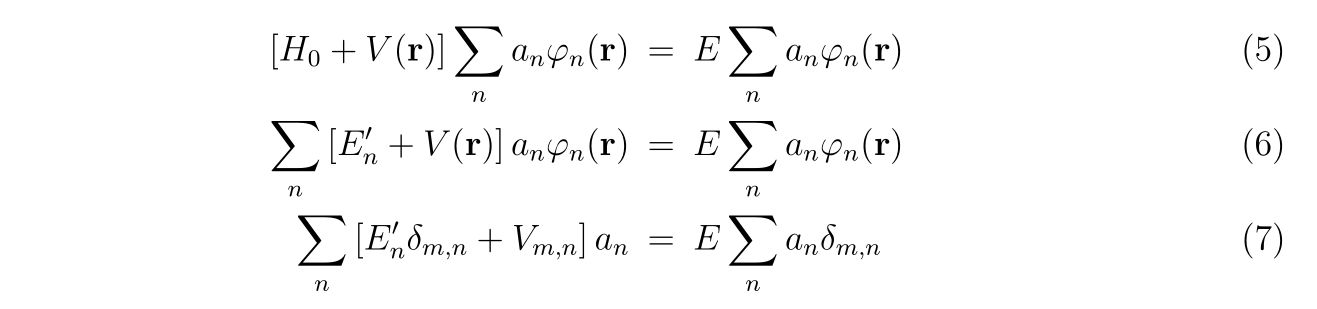
が得られます。ここで、\(V_{m,n}\)を

と置きました。式(7)を別の表現をすれば

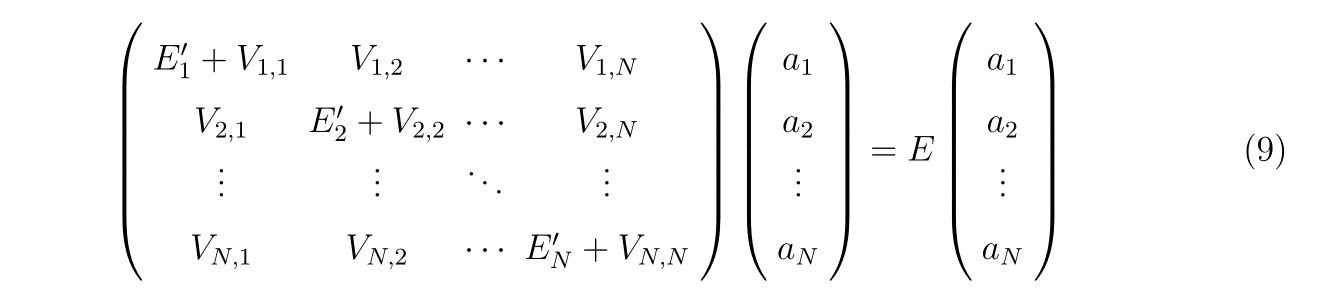
と書くことが出来ます。なので、左辺のハミルトニアンの行列形式を対角化すれば、求めたい系の固有値、固有ベクトルが得られるわけです。固有ベクトルが得られたら式(2)に従って波動関数を構成すれば良いのです。

これが一般的な変分原理による解法です。
以降は2次元の問題に限り考えていきます。

2次元の場合

2次元の場合かつ\(H_0\)はxだけ含む部分とyだけ含む部分とで分離することが出来る場合を考えます。

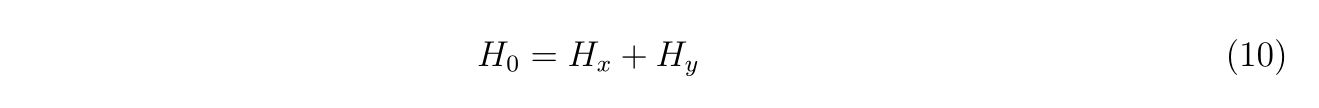
この場合、固有関数は変数分離することが出来るので、2次元の基底関数を1次元系の基底関数の直積をとして考える方法を取ることが出来ます。すなわち、x,y方向の量子数\(n_x,n_y\)を用いて量子数\(n\)と以下のように関係して構成される、と考えるのです。

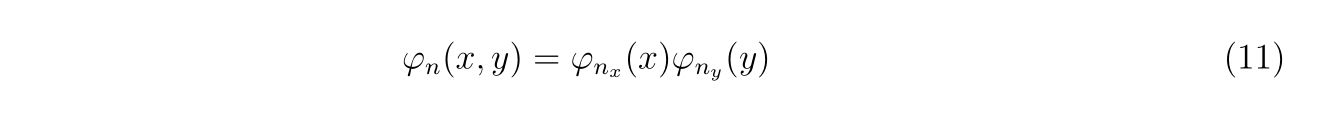
ここで、\(n\)と\(n_x,n_y\)には1対1の関係があれば順番は関係ないことに注意してください。それぞれの基底関数は

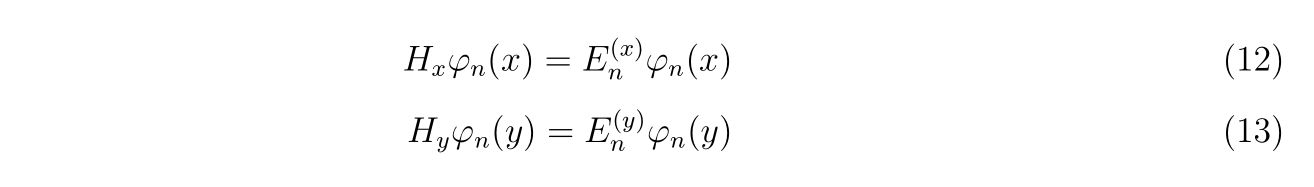
を満たします。もちろん、1次元系の基底関数がそれぞれ正規直交化されていれば二次元の場合でもその関係は保たれ、

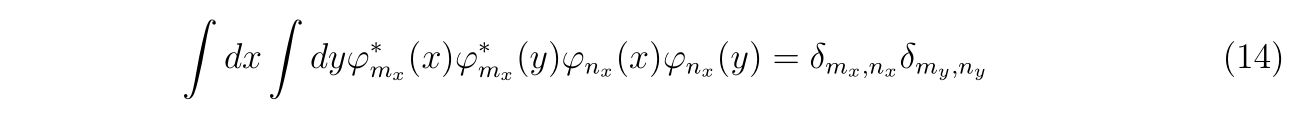
が成立します。この基底関数で式(7)を書き換えてやれば

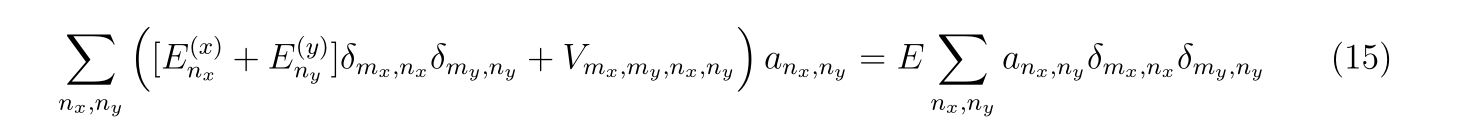
となります。

基底関数の対応

この問題はある長径、短径で指定される楕円内に存在する格子点の個数を数える問題と同じです。

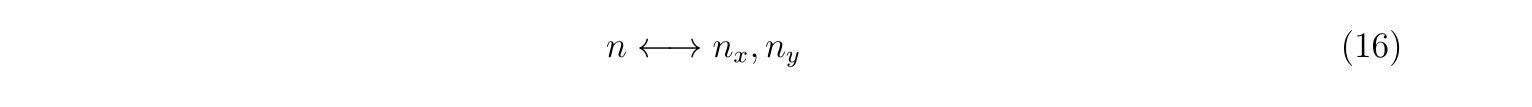
nの順番を記録しておきさえすればどんな順番でも構いません。適当に求めればよいです。
ただし、ここではシュレーディンガー方程式を解いた結果、エネルギーの低い状態から順に欲しいので、\((n_x, n_y)\)の組み合わせでエネルギーが低い順に決定していきます。

今、エネルギーは\(x,y\)方向ともに単調に増加します。
\((n_x,n_y)\)の考えられる組み合わせで、
一番小さいエネルギーは\((1,1)\)なので、まず\(n=1\)は\((1,1)\)に対応させます。
次に小さいエネルギーで考えられるのは\((1,2),(2,1)\)のどちらかです。
ここで重要なのは現在より前に出てきた\((n_x,n_y)\)の組に1を足した組み合わせしか候補にあがりません。
なので、探索するのはこの条件を満たすものだけで充分です。

これをプログラムしたものは、下のtar.gz内に”qnumber”という名前でサブルーチンに入っています。

プログラム

こちらです。
https://slpr.sakura.ne.jp/qp/supplement_data/highprecision_tise2d.tar.gz

解凍すると、中にintegrate.f90 main.f90というファイルがはいっています。
Lapackを使うのでそれにリンクしてコンパイルしてください。intel®fortranならば、

で良いと思います。
実行すると、

という結果が得られるでしょう。ここで、** / 100という数字はハミルトニアン行列要素の計算の経過を表しています。100は行列が\(100\times 100\)の行列であるという意味です。
1 1.0000086267300243
は、対角化後の固有エネルギーの一番低い状態から順に出力しています。
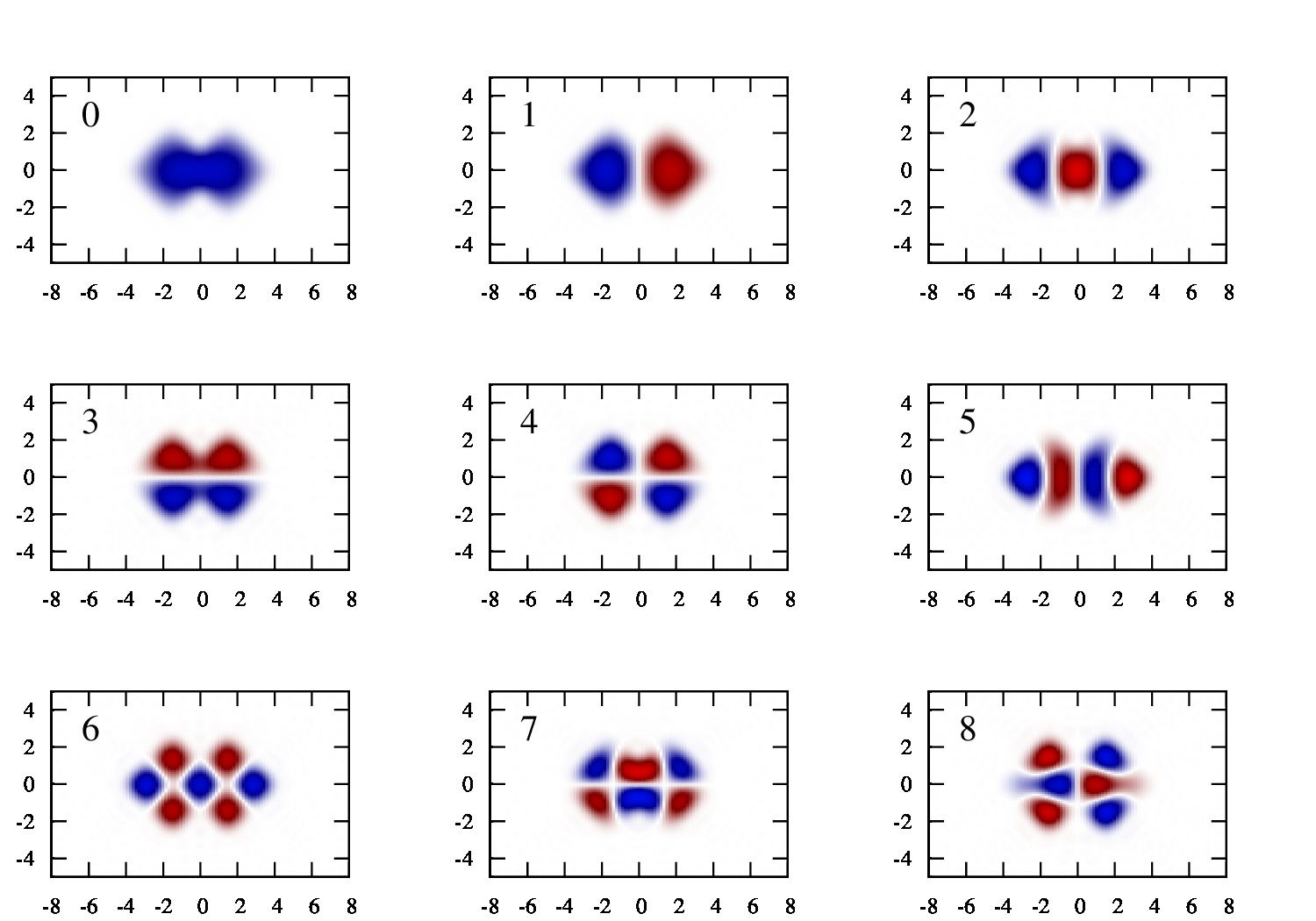
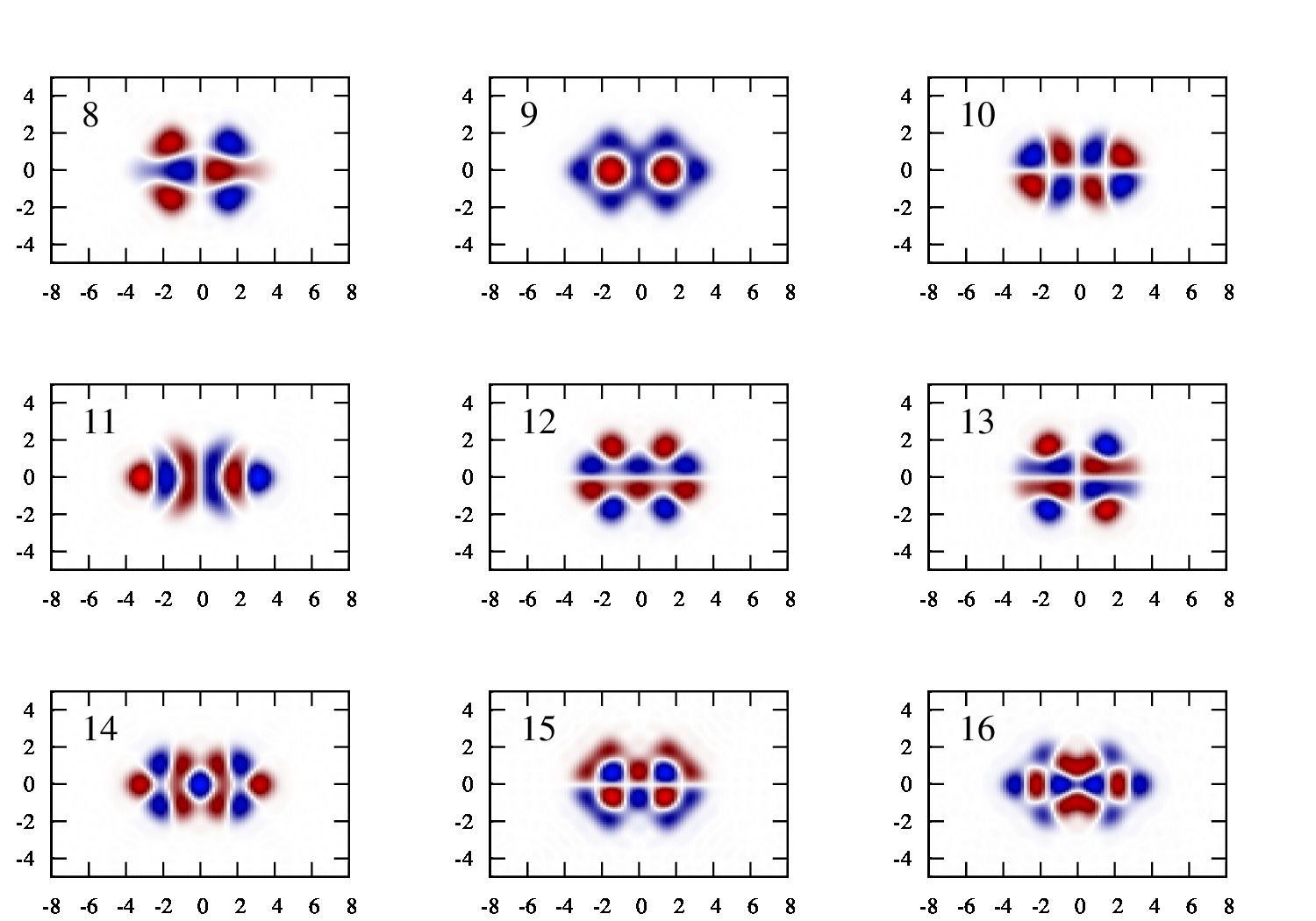
デフォルトでは二次元の調和振動子ですので、
\(
E_n=(n_x+1/2)+(n_y+1/2)
\)
の順になります。一番低いエネルギーから順に\(1,2,2,3,3,3,4,4…\)が解析解となります。

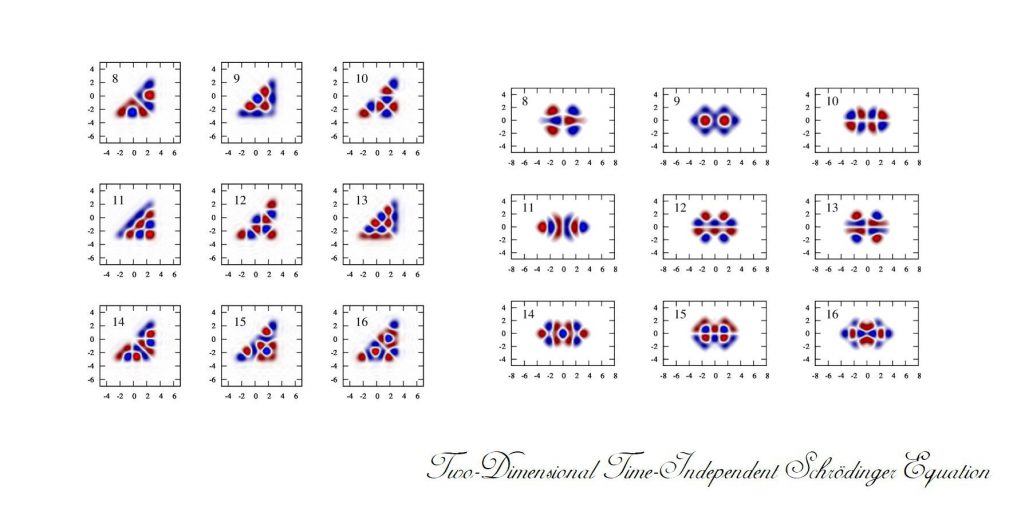
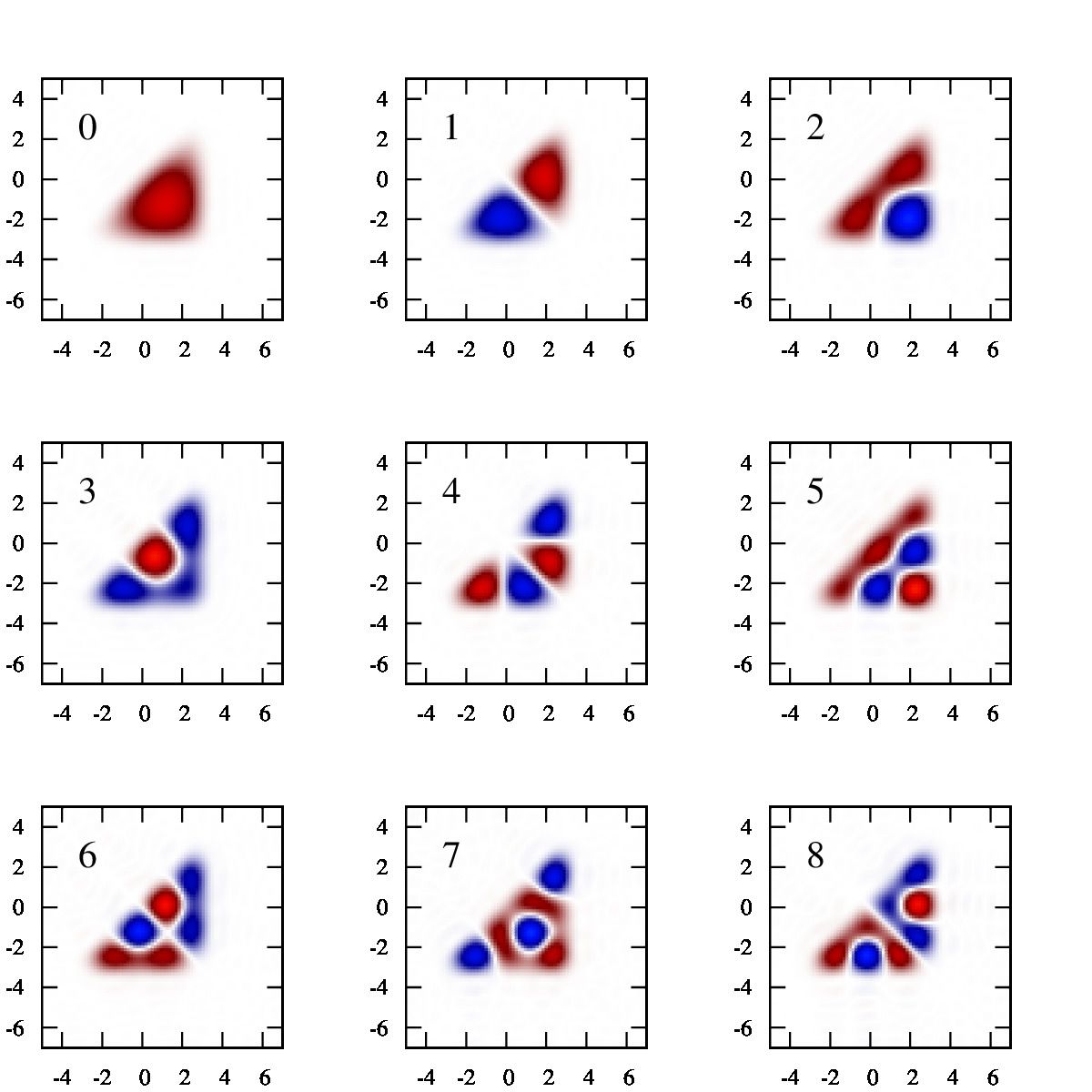
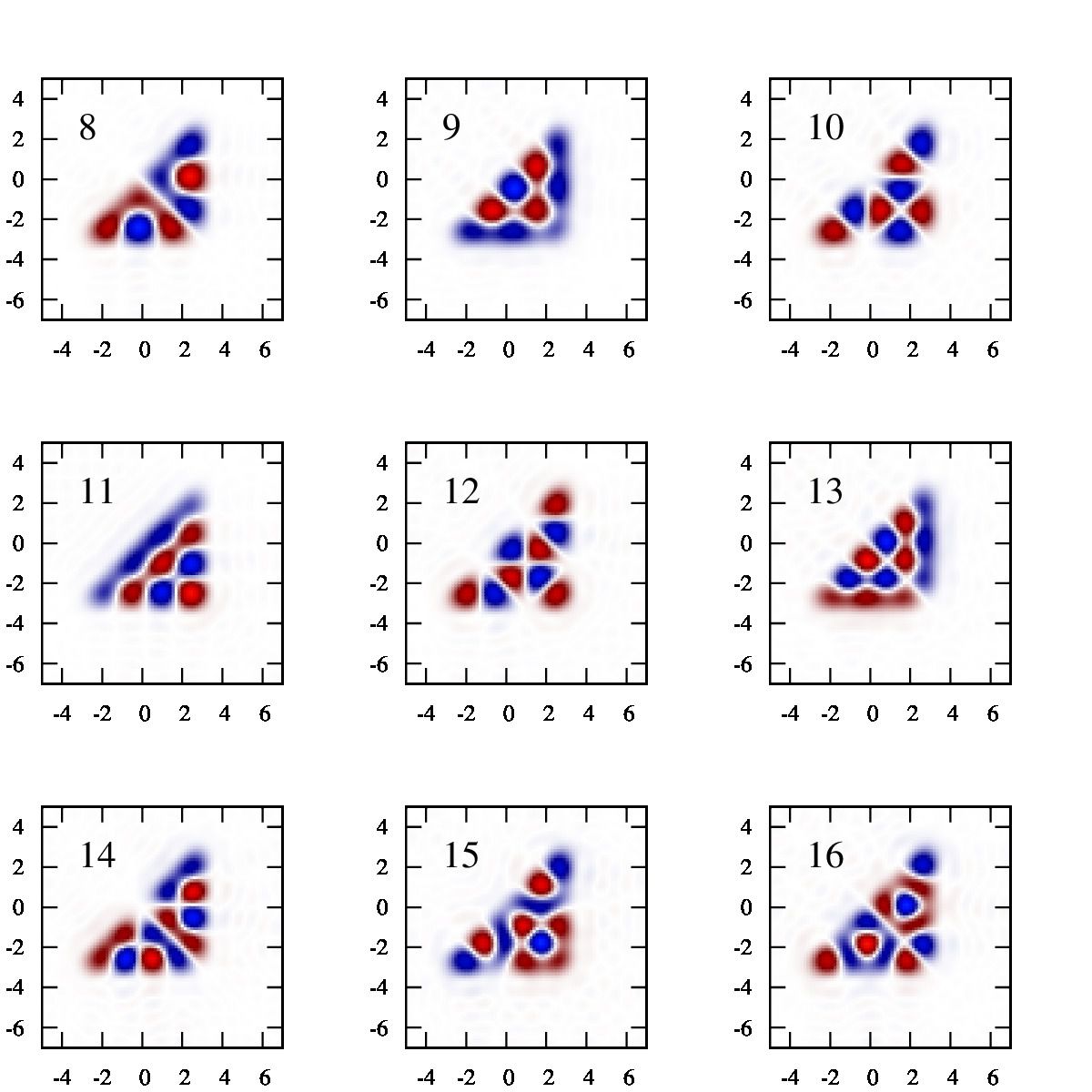
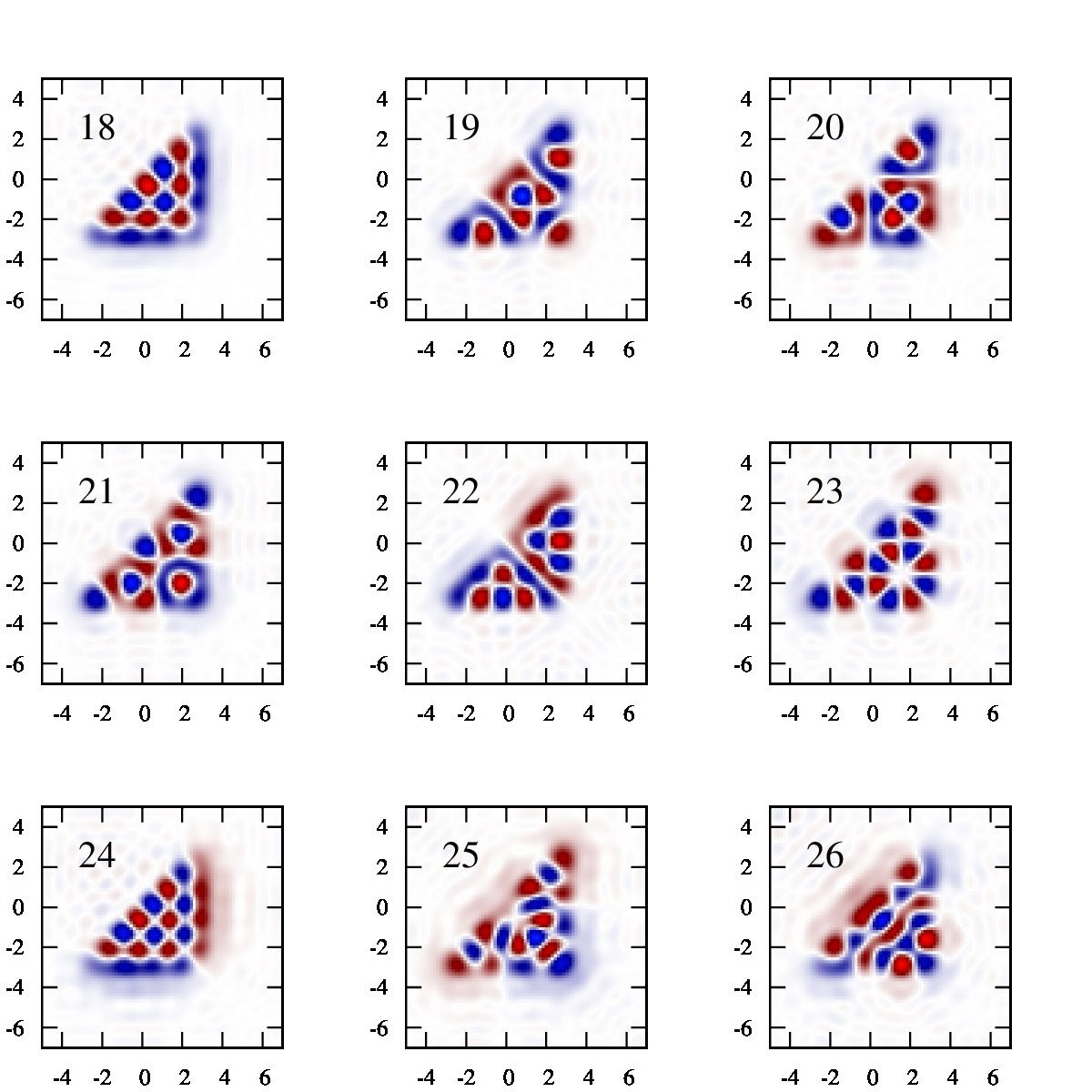
具体的な計算例

三角形型のポテンシャル

\(
\begin{equation}
V(x,y)=\left\{
\begin{array}{c}
0,~~~(y\lt x \cap x\lt a \cap y\gt -a) \\
10,~~~(otherwise)
\end{array}
\right.
\end{equation}
\)
ここで、\(a=3\).

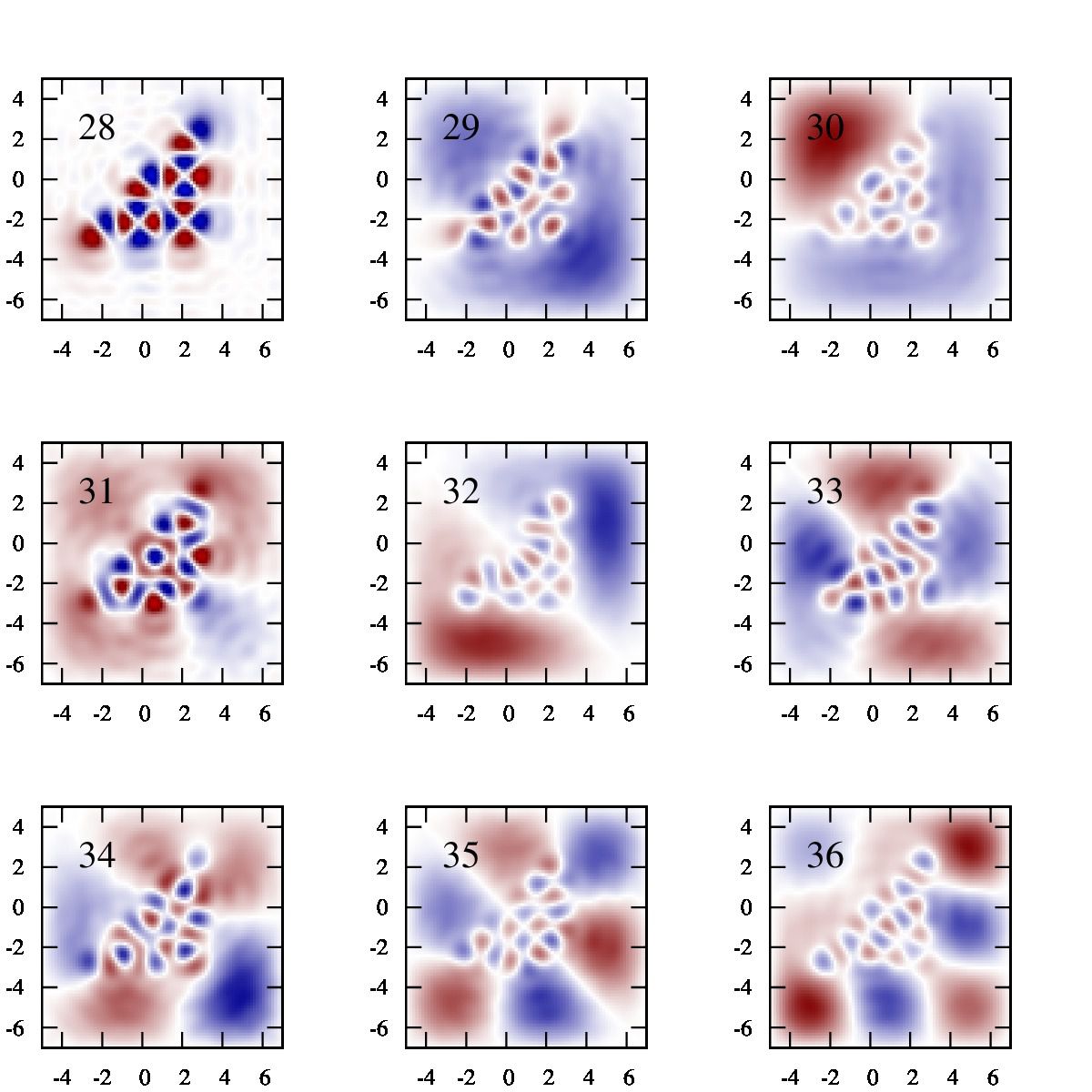
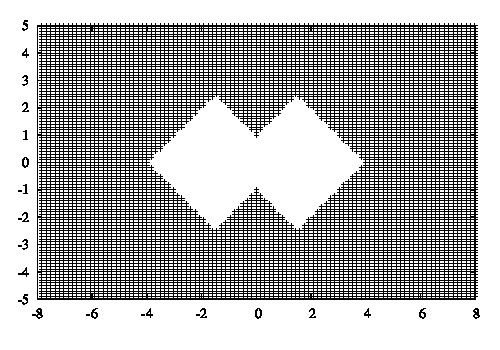
2つの四角形のポテンシャル

\(
\begin{equation}
V(x,y)=\left\{
\begin{array}{c}
0,~~~(y\lt (x+b) \cap y \gt -(x+b) \cap y\lt -(x+b)+a \cap y \gt (x+b)-a) \\
0,~~~(y\gt (x-b) \cap y \lt -(x-b) \cap y\gt -(x-b)+a \cap y \lt (x-b)+a) \\
10,~~~(otherwise)
\end{array}
\right.
\end{equation}
\)
ここで、\(a=3\)

Tweet