動かない壁に対する束縛運動と反射を考えます。
例えば、初め跳ねてた運動が、壁に沿って動く運動に変化する、という状況です。
あんまり見たことが無いので、面白そうだと思いました。

束縛されている時と反発するときは、式(1),(2)によってあらわされます。それらは
壁に束縛されている場合

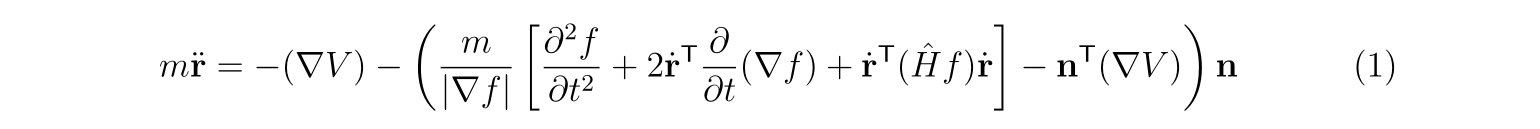
壁と反発する場合

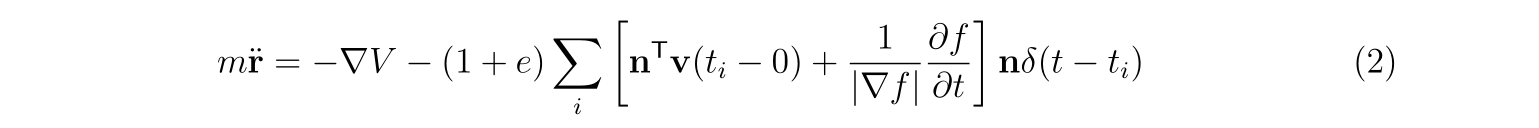
です。壁と反発する場合、反発後の速度は式(3)に沿って動きます。

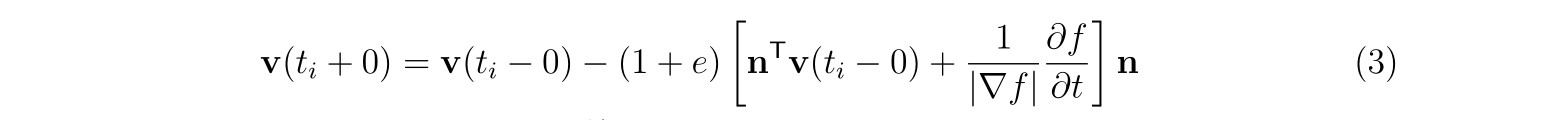
※式(1), (2)では壁が時間依存しても良いように定式化しています。この定式化は恐らく正しいです。また、本稿に載せているプログラムも壁が時間依存しても良いように作成していますが、動く壁の場合、プログラムではうまく計算が出来ません。

ここで、\(e\)は反発係数、\(\mathbf{n}\)は壁の法線ベクトルであり、

\(\nabla\)はナブラ演算子であり

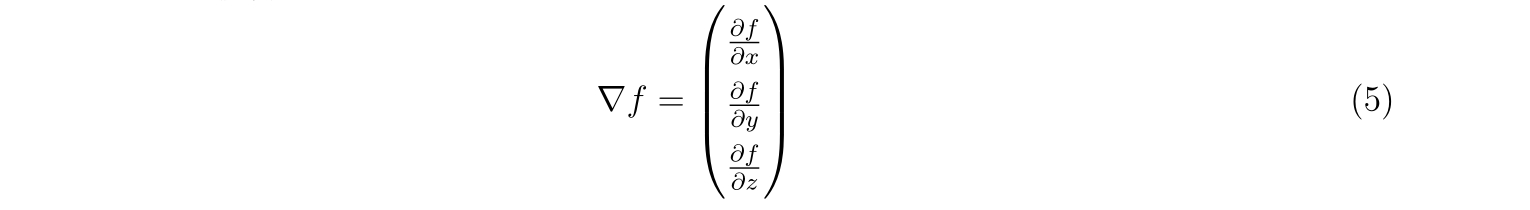
と与えられます。また、\(\hat{H}f\)は関数\(f\)のヘッセ行列であり,

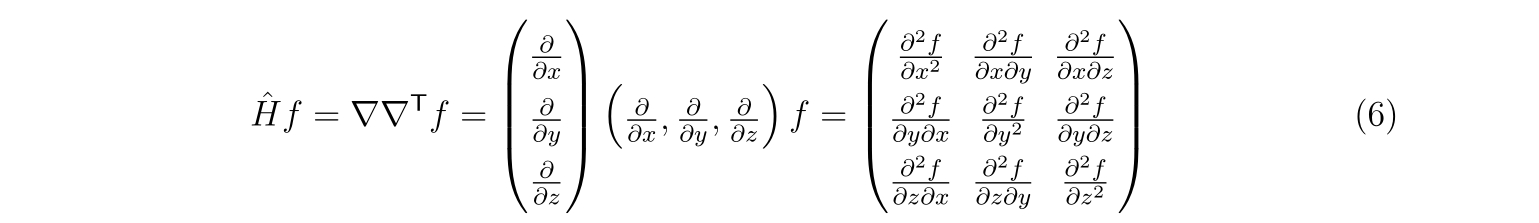
と与えられます。

定式化や数値計算手法の詳細は以下のページを参照してください。

壁との反発と束縛運動の定式化

質点と壁との反発を表す運動方程式
束縛条件下の運動 – 自由度がうまく落とせない運動

数値計算手法

ルンゲ=クッタ法の説明と刻み幅制御
Hyper-dual numbersによる二階偏微分の計算
ゼロ点を探す（二分法、挟み撃ち法、Anderson-Björk法、Brent法、Newton法、Steffensen法）

解放・束縛判定

ここでいう”解放”とは、束縛されていなく、反射を繰り返している状態を表します。また、”束縛”は壁に沿って運動している状態です。

前提として、壁を通り抜けることは無いと考えます。

すなわち、時刻\(t=t_0\)で位置\(\mathbf{r}=\mathbf{r}_0\)の時、任意の時刻\(t\)について

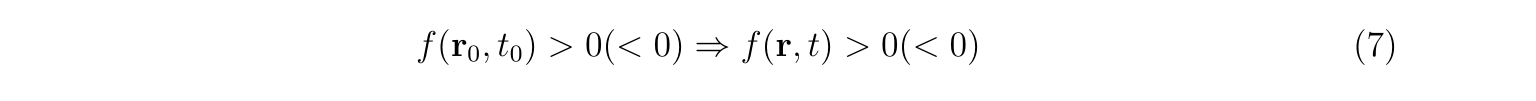
が満たされるとします。
もし、\(f(\mathbf{r}_0,t_0) =0\)ならば判断がつかないため、プラスかマイナスはこちらから与えます。

解放→解放判定、解法→束縛判定

解放状態から壁によって単に反発する場合

関数\(f(\mathbf{r},t)\)の符号が変化した時、壁との反発を考えます。
壁の法線方向の速度が十分に大きい場合、壁と反発し、そうでない場合、壁に束縛されると考えます。
その前提の元、

を満たす\(t=t_i, \mathbf{r}=\mathbf{r}_i\)を見つけます。
その後、式(6)に従い、速度を変化させます。

数値計算的には、衝突直前の時刻を採用します。すなわち、
ゼロ点を探す際にある範囲\(t_a \leq t_i \leq t_b\)で挟み込んでいくのですが、\(t_b\)は壁を越えてしまうので採用しません。

解放状態から壁沿いに束縛される場合

もし、壁の法線方向の速度が十分に小さい場合（ある閾値を下回った場合）、壁に束縛されると考えます。
この時、壁の法線方向の速度はゼロに変更します。
すなわち、速度は時刻\(t=t_i\)で

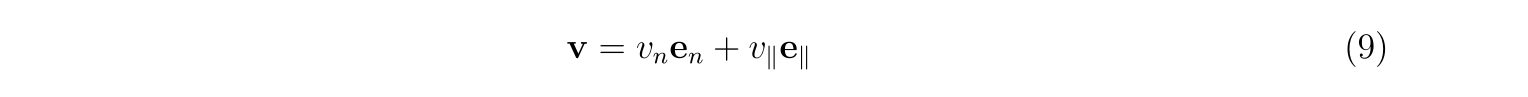
を持ちますが、\(v_{\parallel}=0\)にしてから、束縛運動に移行するということです。
これは、\(\mathbf{v}\)と壁の法線方向のベクトル\(\mathbf{e}_n\)の内積を取ることで得られます。
また、束縛された瞬間(\(t=t_i\))の束縛力\(C(t_i)\)を計算し、その符号を記録しておきます。
束縛力\(C(t)\)は、

です。
この符号が変化した瞬間が壁からの束縛が無くなる時なので、そのために記録します。

束縛→解放判定

束縛力\(C(t)\)の符号と\(C(t_i)\)の符号が変わるまで、式(1)に従い、時間発展させます。
すなわち、

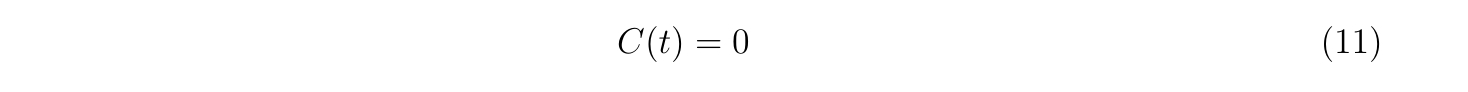
を満たす\(t=t’, \mathbf{r}=\mathbf{r}’\)を見つけます。
その後、式(2)に従い運動します。
式(2)の運動では束縛力は働かないので、符号は自然と初期条件の符号と同一になる（※）。

※この条件はあまり良くありません。この判別方法のせいで、壁が時間依存している場合、束縛力が働いていない一瞬で質点が壁を超えてしまいます。プログラム自体は壁は時間依存しても良いことになっていますが、この条件分岐は上手く動きません。以下に示す計算プログラムは、質点が束縛されている場合に壁が時間依存しなければ正しいです。

プログラム

プログラムは以下のリンク先においておきます。

https://slpr.sakura.ne.jp/qp/supplement_data/lag_ver1.0.tar.gz

適当なディレクトリで展開し、lag_ver1.0というディレクトリに移動してから以下のコマンドで実行できます。

動かすと以下のような動画が描画されます。

デフォルトでは
ポテンシャル\(V=mgy\)（サブルーチンfp2d）
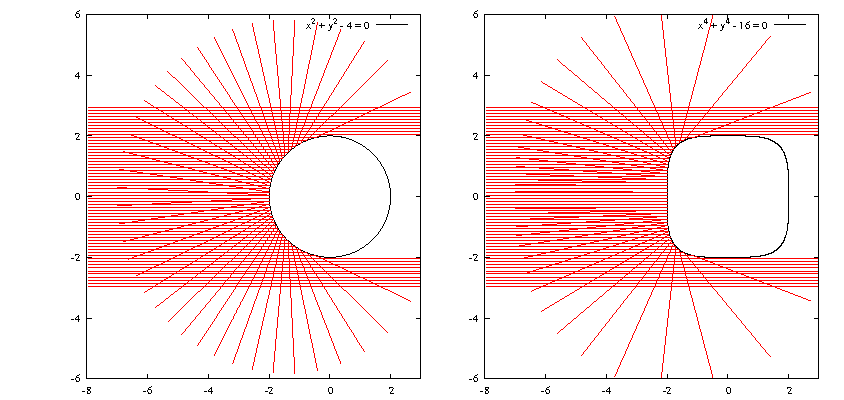
壁\(f(x,y)=x^2+y^2-4\)（サブルーチンfw2d）
に書かれています。
摩擦、空気抵抗は入っていません。唯一、反発係数(els)だけがinputファイルの中に書かれています。

初期条件の

だけを上の通り変更すると以下のような振る舞いをします。

確かめ

確かめを行います。
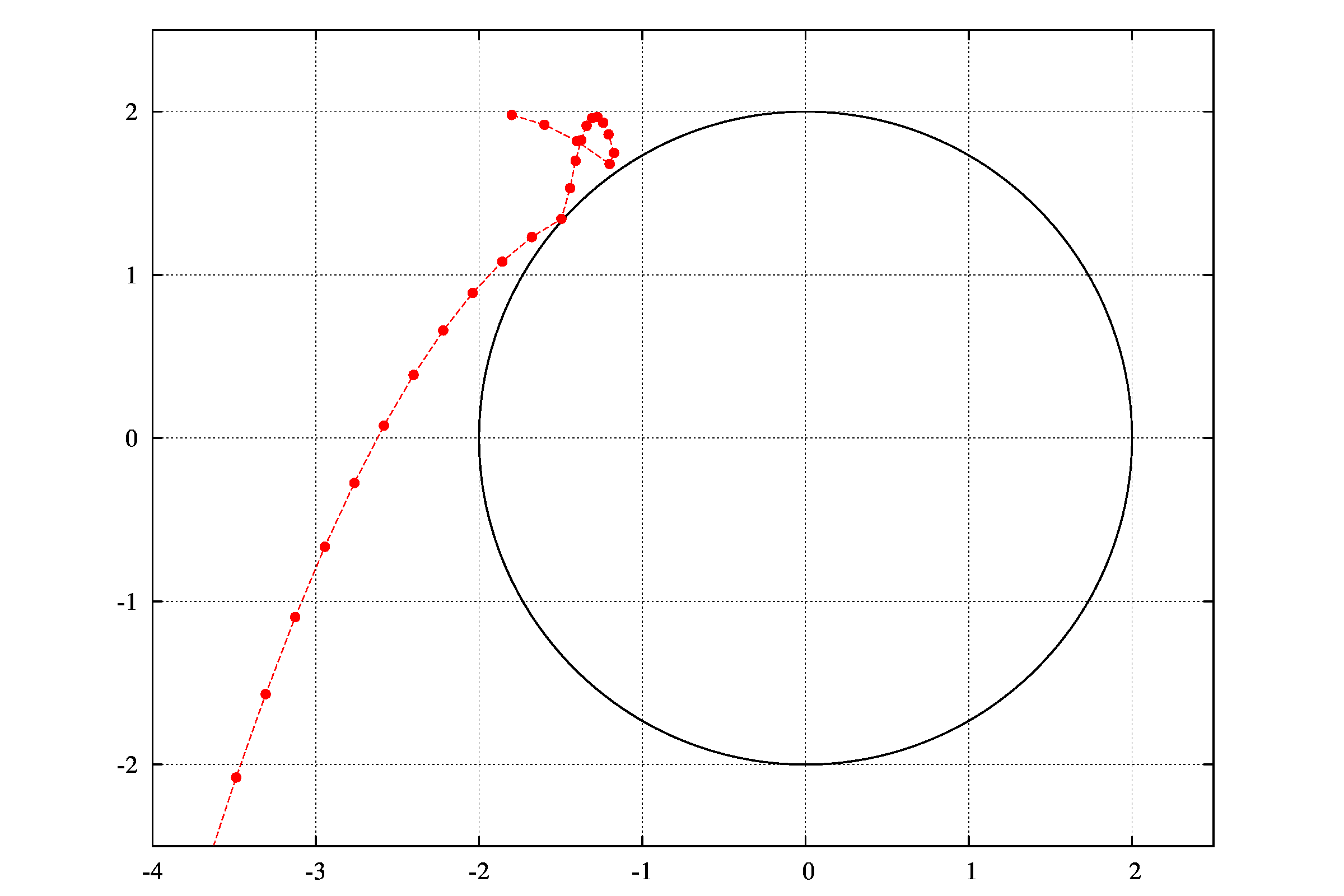
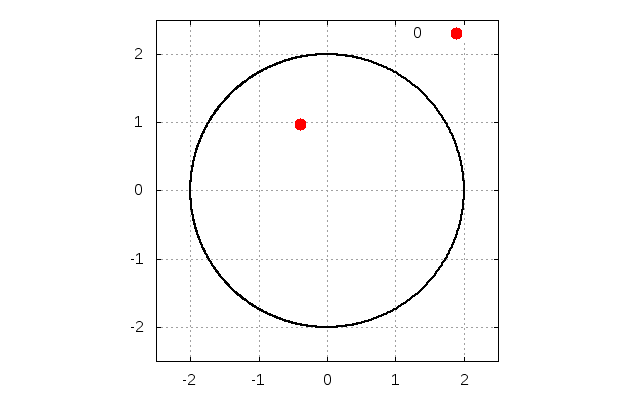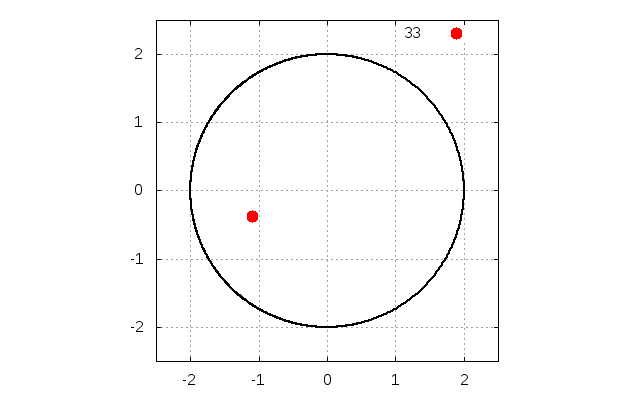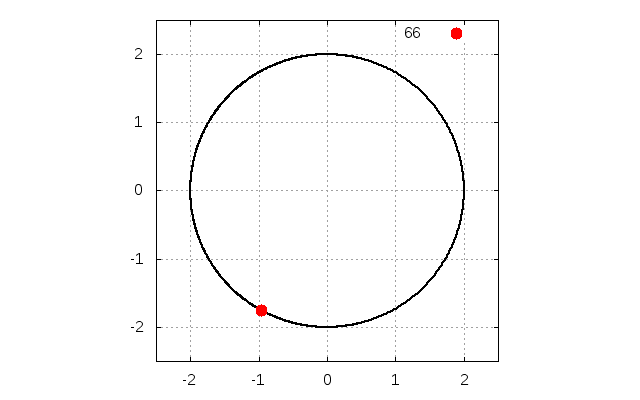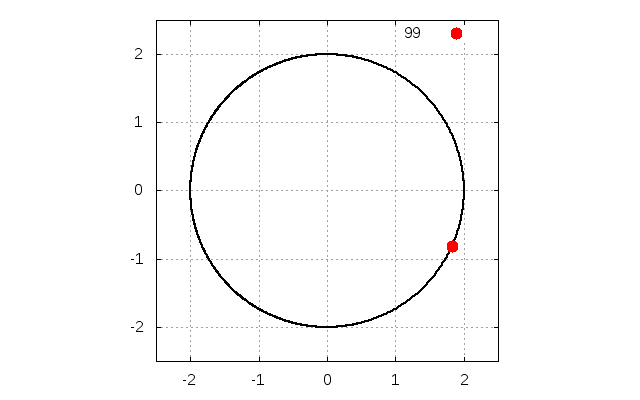
重力\(g\)の下で、質量\(m\)の物体が、半径\(r\)の円形の壁の内側に沿ってボールが進み、壁からの抗力が無くなり、壁から離れる状況を考えます(下の図を参照)。

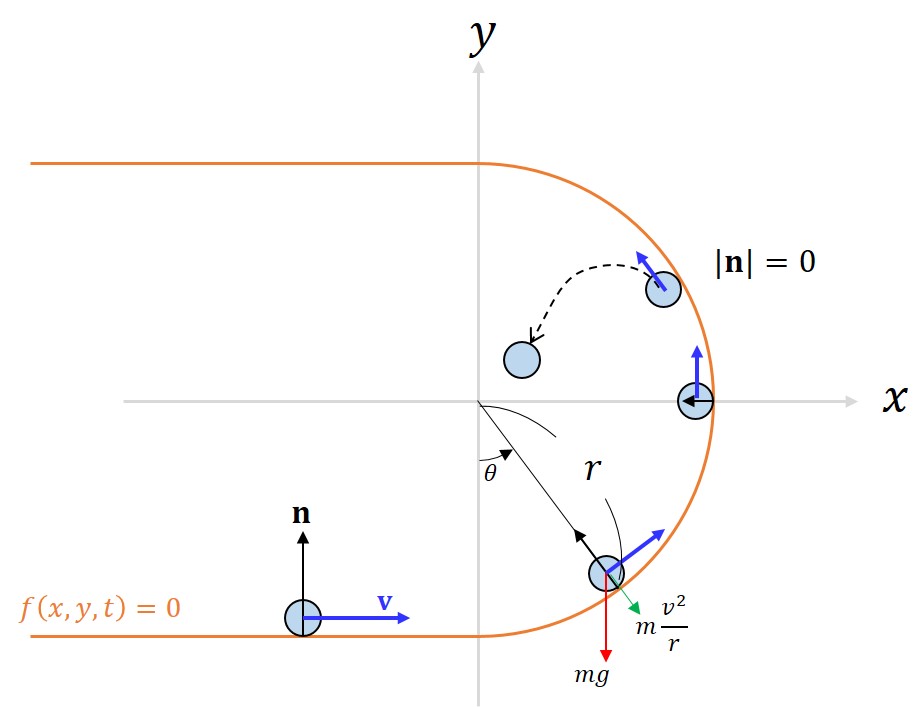
円形の壁に沿っている時、垂直抗力\(N\)は

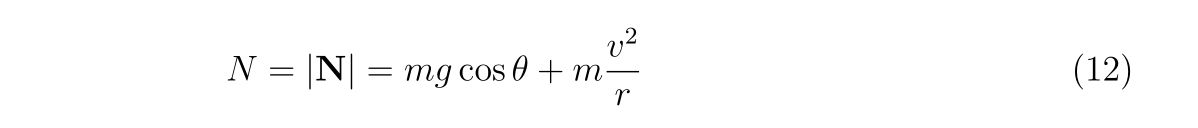
と書けます。エネルギー保存則より、

が成り立っています。ここで、\(v_0\equiv v(t=0)\)と置きました。
垂直抗力\(N\)がゼロになる点が壁から離れる条件ですので、\(v_0\)を用いて

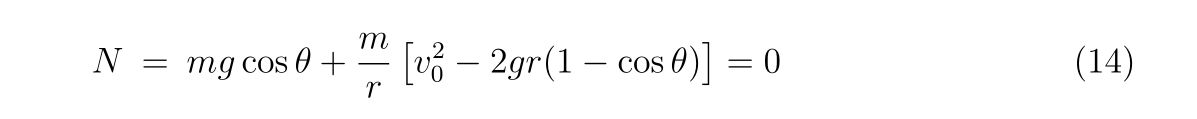
と書けます。初速度が分かっている時、壁から離れる角度は

です。もしくは、壁から離れる角度が分かっている場合、初速度は

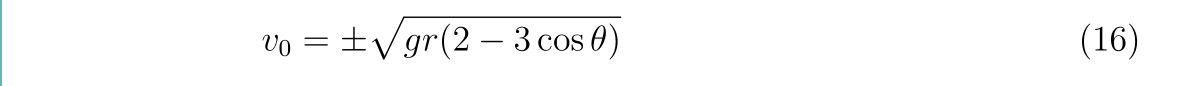
と与えられます。重力加速度, 半径を\(g=1, r=2\)とし、\(y=1\)と壁との交点、すなわち\(\theta=2\pi/3\)の場合、初速度は

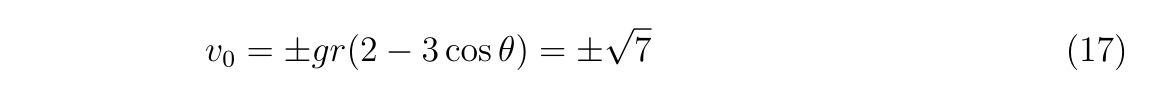
です。実際に本稿のプログラムを動かしますと、\(y=1\)でちょうど離れていることが確認できます。

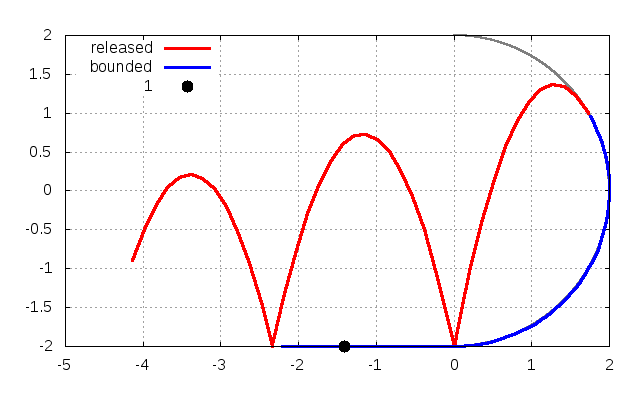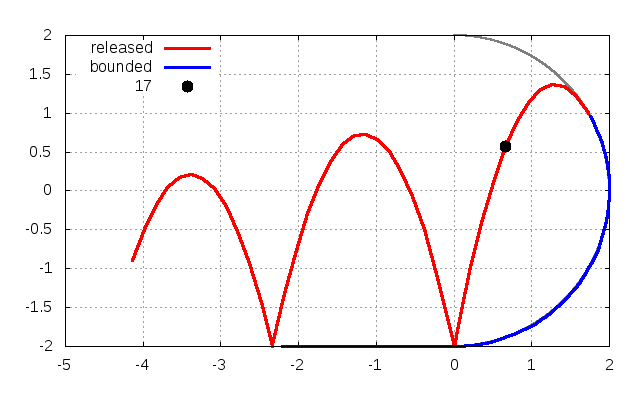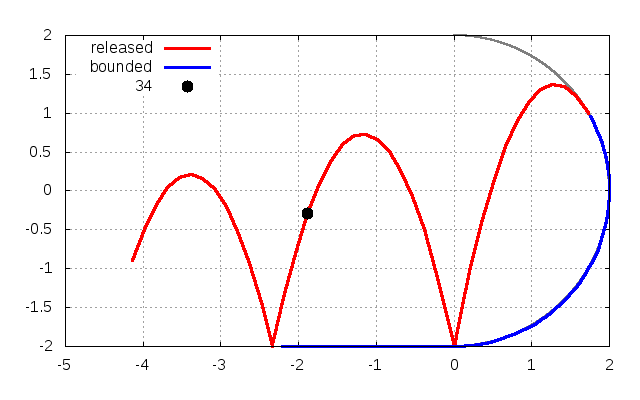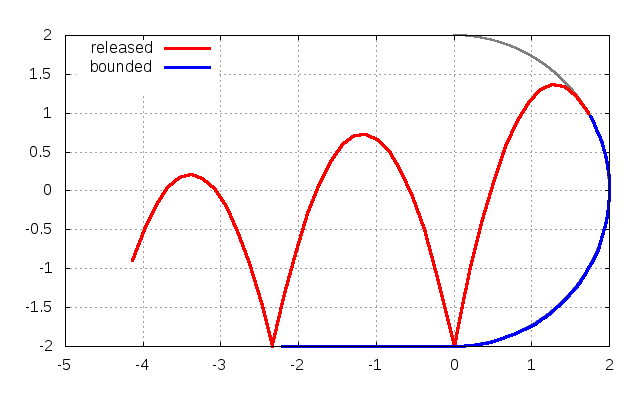
ここで、青線は壁に沿って動いて運動している状態であり、赤線は壁から離れている運動している状態です。

剛体に対する散乱

ポテンシャルを無くし(g=0)、弾性散乱(els=1)を考えると
古典的な散乱問題的なものもできます。

Tweet