fortran90においての乱数の発生方法です。

乱数を１から作るのは、乱数を研究するとかでない限り止めましょう。
ここではfortran90で乱数を発生させるためにどうすればいいか？を記述します。

私は乱数について詳しくありませんが、調べた限りメルセンヌツイスタという乱数発生法が良い乱数を発生するようです。
メルセンヌツイスタの詳細はMersenne Twister Home Page にあるのでご参照ください。
fortran90コードはhttps://gist.github.com/ykonishi/5569005にあります。

上記のリンクから、メルセンヌツイスタのfortran90コード（mt19937.f90）をダウンロードします。
そして、メインプログラム

をmt19937.f90と一緒に

というオプションを付けてコンパイル（※1）します。実行すると、

という結果を得ることが出来ます。

（※1）
このオプションが、型が扱える範囲を超えていても無視するためのオプションです。
何故かgfortranコンパイラ(ver4.8.4で確認)で出ます。
そして、これはコンパイラの問題だと私は結論付けました。
fortranの整数は
-2147483648から2147483647までで定義されているのにもかかわらず、
gfortran(ver4.8.4)は
-2147483647から2147483647の範囲でなければエラーを出すようです。
しかし、実際に整数に-2147483648を代入し、このエラーを無視する上のオプションを付けて実行すると、ちゃんと値が入ります。なので、コンパイラに問題があると判断しました。

[adsense1]

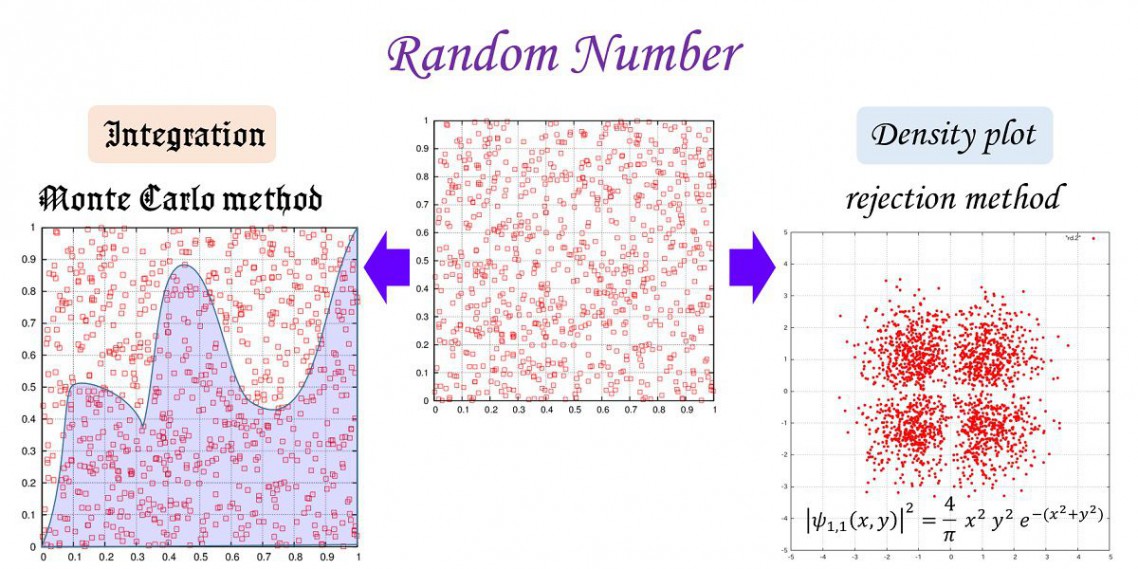
任意の関数に従う乱数(von Neumannの棄却法)

このページのサムネイル画像の右は等方的２次元調和振動子励起状態の密度
\(
\begin{align}
f(x,y)=\frac{4}{\pi}x^2y^2e^{-(x^2+y^2)}
\end{align}
\)
を点の濃さで表現するためのプログラムです。

これは、上の関数に従う乱数分布を書くことにほかなりません。
一様乱数を任意の関数に従う乱数に変換する方法として、
von Neumannの棄却法と呼ばれる方法があります。

以下のようにすると一様乱数を関数\(f(x)\)に従う乱数に変えることが出来ます。

\(x\)の範囲\([x_a,x_b]\)で定義された関数\(f(x)\)に従う乱数を発生させたい。
区間\([x_a,x_b]\)で関数は\([f_a,f_b]\)の値を持つとすると、
　1.　範囲\([x_a,x_b]\)の一様乱数\(x_r\)を生成する。
　2.　範囲\([f_a,f_b]\)の一様乱数\(f_r\)を生成する。
　3.　もしも\(f_r\le f(x_r)\)ならば、その\(x_r\)は\(f(x)\)に従う乱数である。そうでなければ、発生させた乱数は捨てる。
　4.　1-3を繰り返す。
という方法です。アルゴリズムを見て分かる通り、この方法は無駄が多いです。
発生させた乱数を捨てる操作は出来ればしたくありません。
ですが、この方法は非常に簡単に実装できるのでとりあえず実装したいという場合には良い方法です。

以下は、上の考えの二次元版です。

カラーマップと３次元での表現はこうなります。

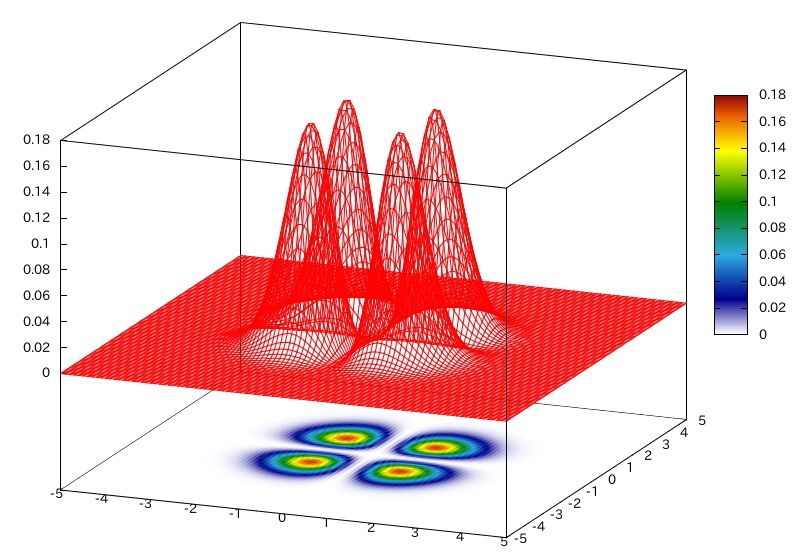
乱数を用いた密度表示(下のプログラム)ではこう表現されます。

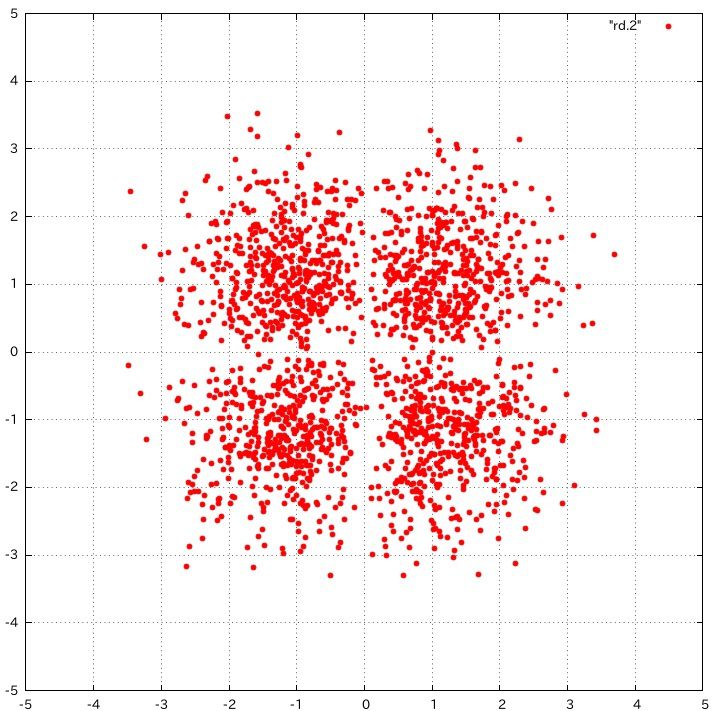
[adsense2]

参考

任意分布の乱数生成　https://www.slideshare.net/shogoosawa581/ss-65259938

以降はfortranの標準組み込み関数を用いる場合のものです。
消すのは忍びないため、一応おいておきます。

Tweet