ニュートン写像はニュートン=ラフソン法によって、ある初期値から適当な値へ収束するまでの回数でその関数を特徴づけるものです。
フラクタルと似ている考えであることを明記しておきます。

ニュートン写像

\(
\displaystyle N_f(z)=z-\frac{f(z)}{f'(z)}
\)
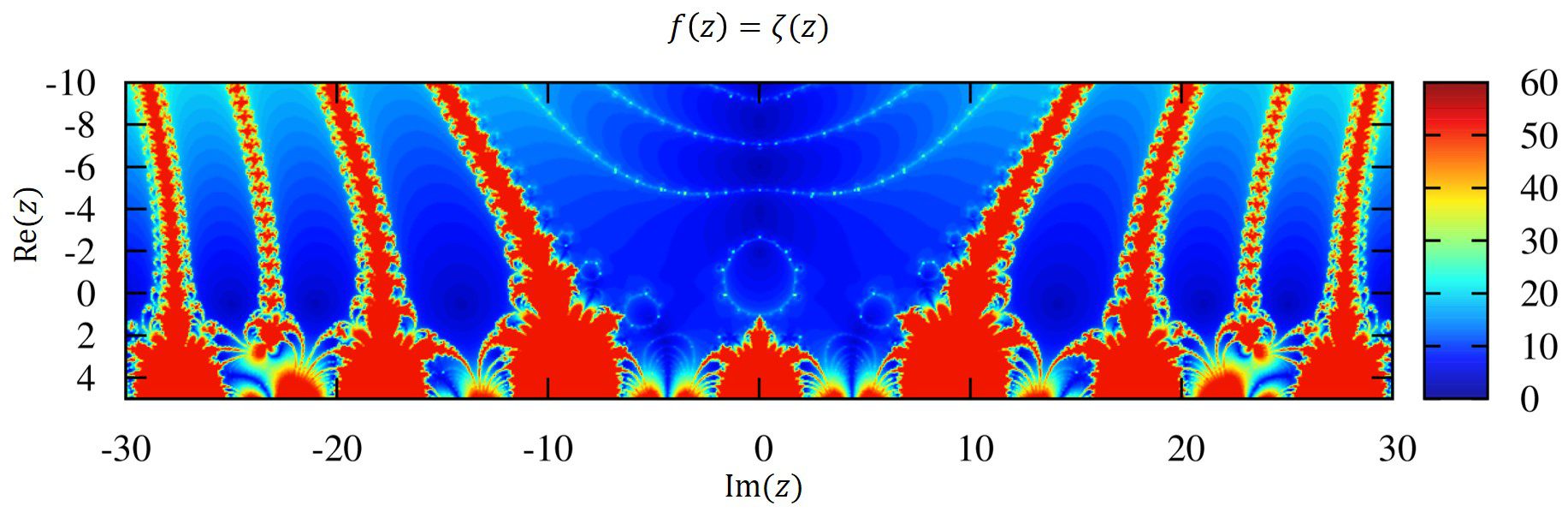
の繰り返しによって適当な初期値からスタートし、収束させていきます。このページでは画像が主です。説明の方はリーマンのゼータ関数の複素力学系をご覧ください。

基本はこれだけです。簡単な複素関数でも相当複雑になります。
早速適当な関数を用意して、ニュートン写像を見ていきましょう。

[adsense1]

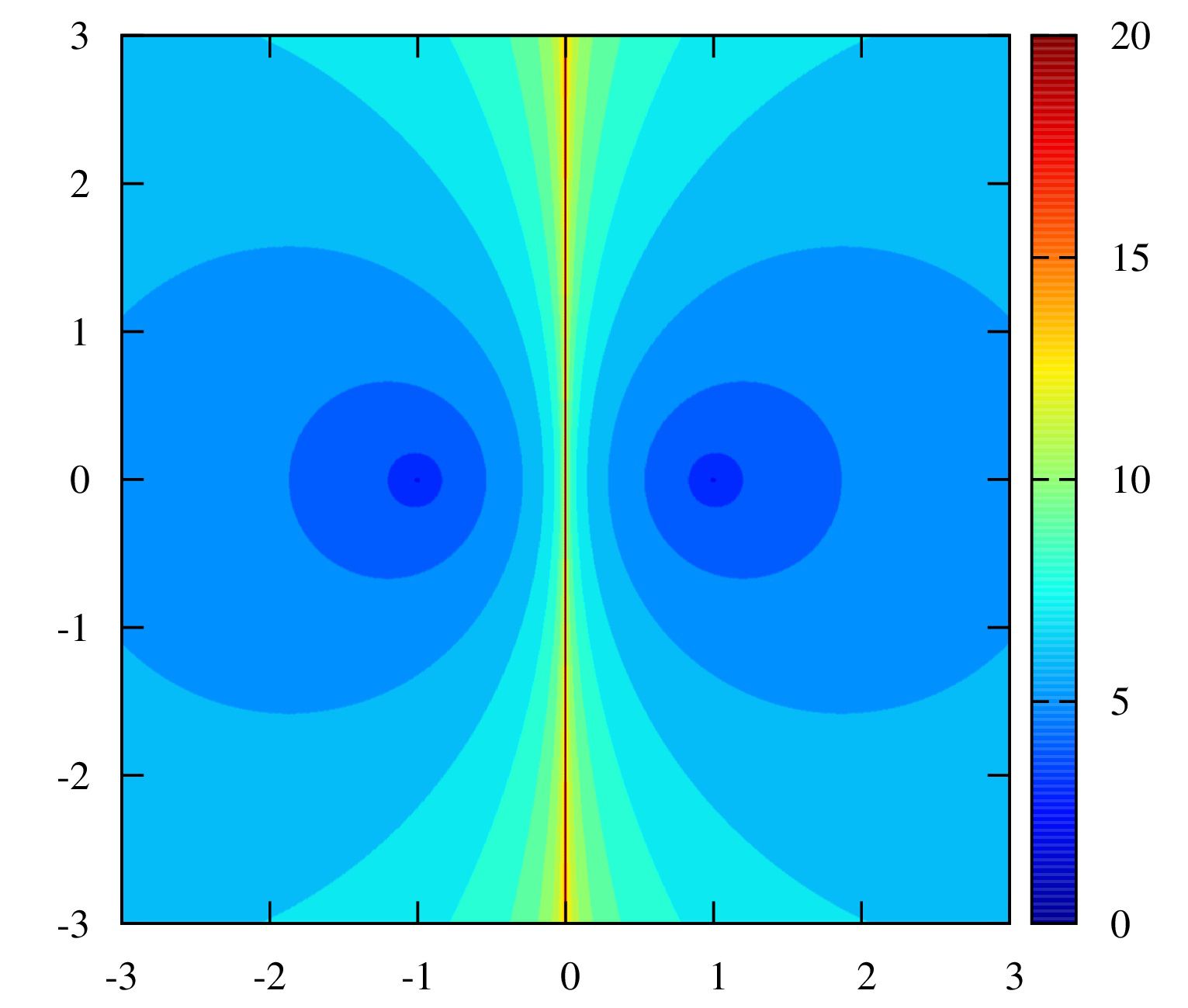
まずは基本的な多項式を見ます。
\(
f(z)=z^2-1
\)

\(
f(z)=z^3-1
\)

\(
f(z)=z^4-1
\)

\(
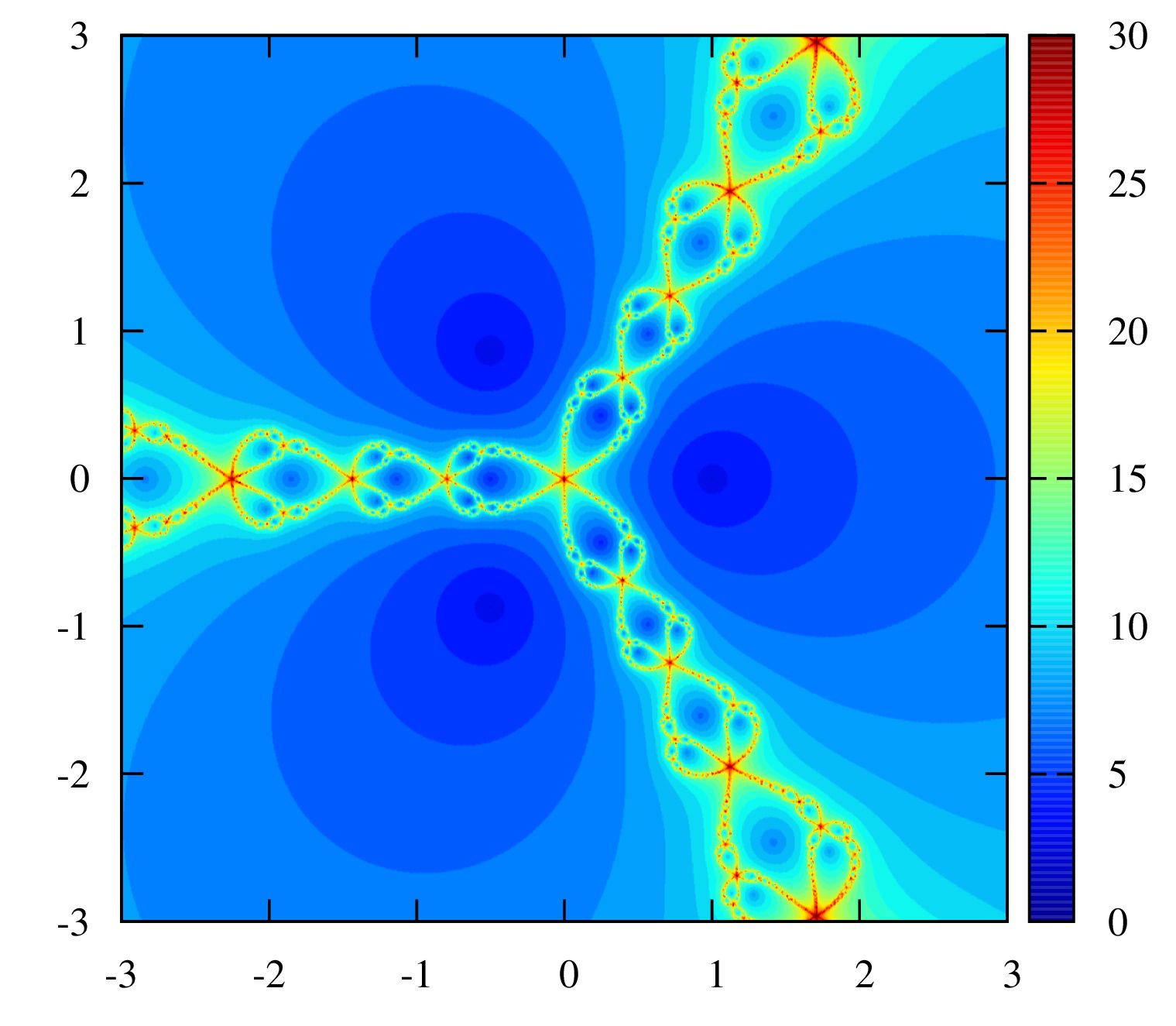
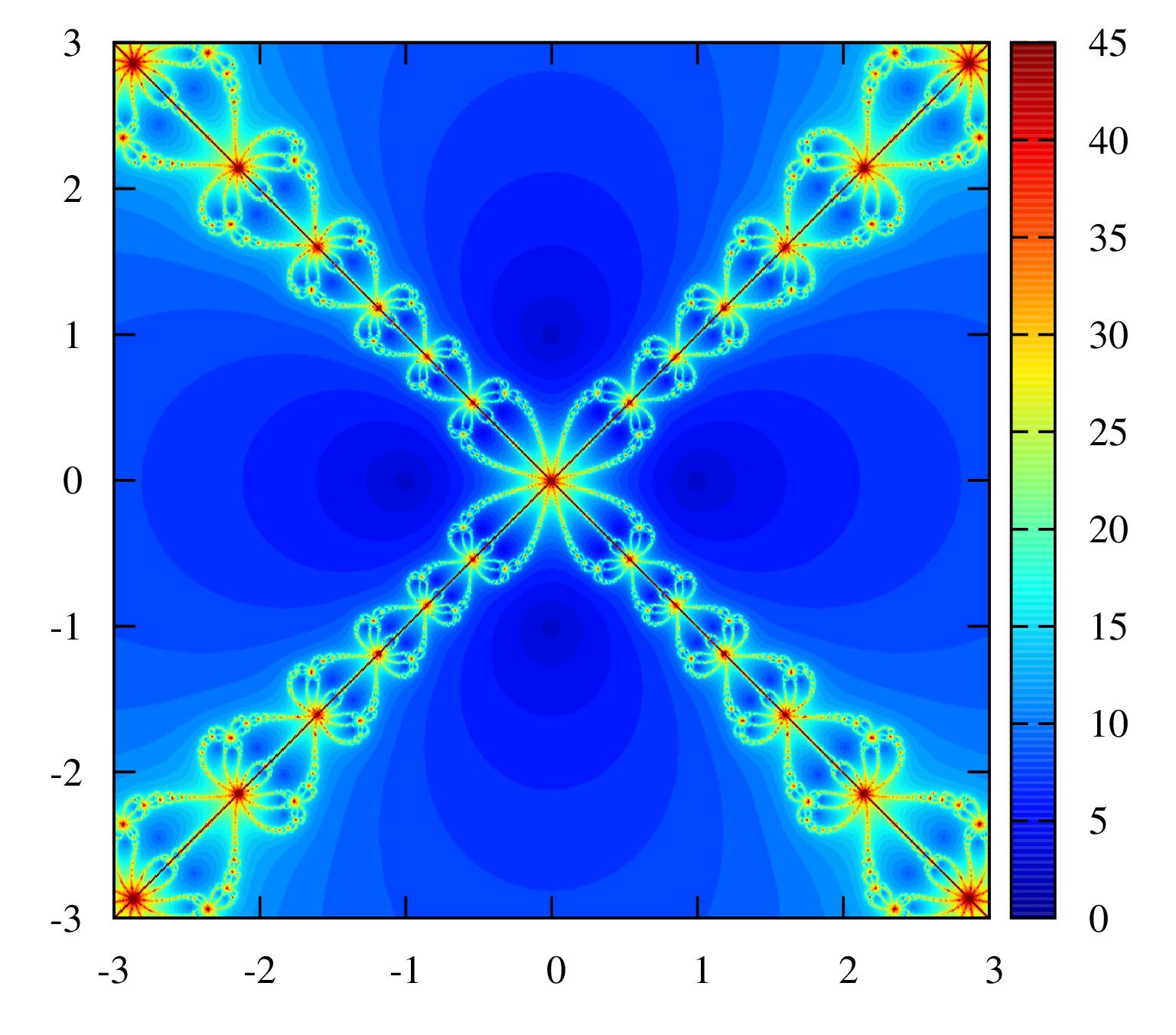
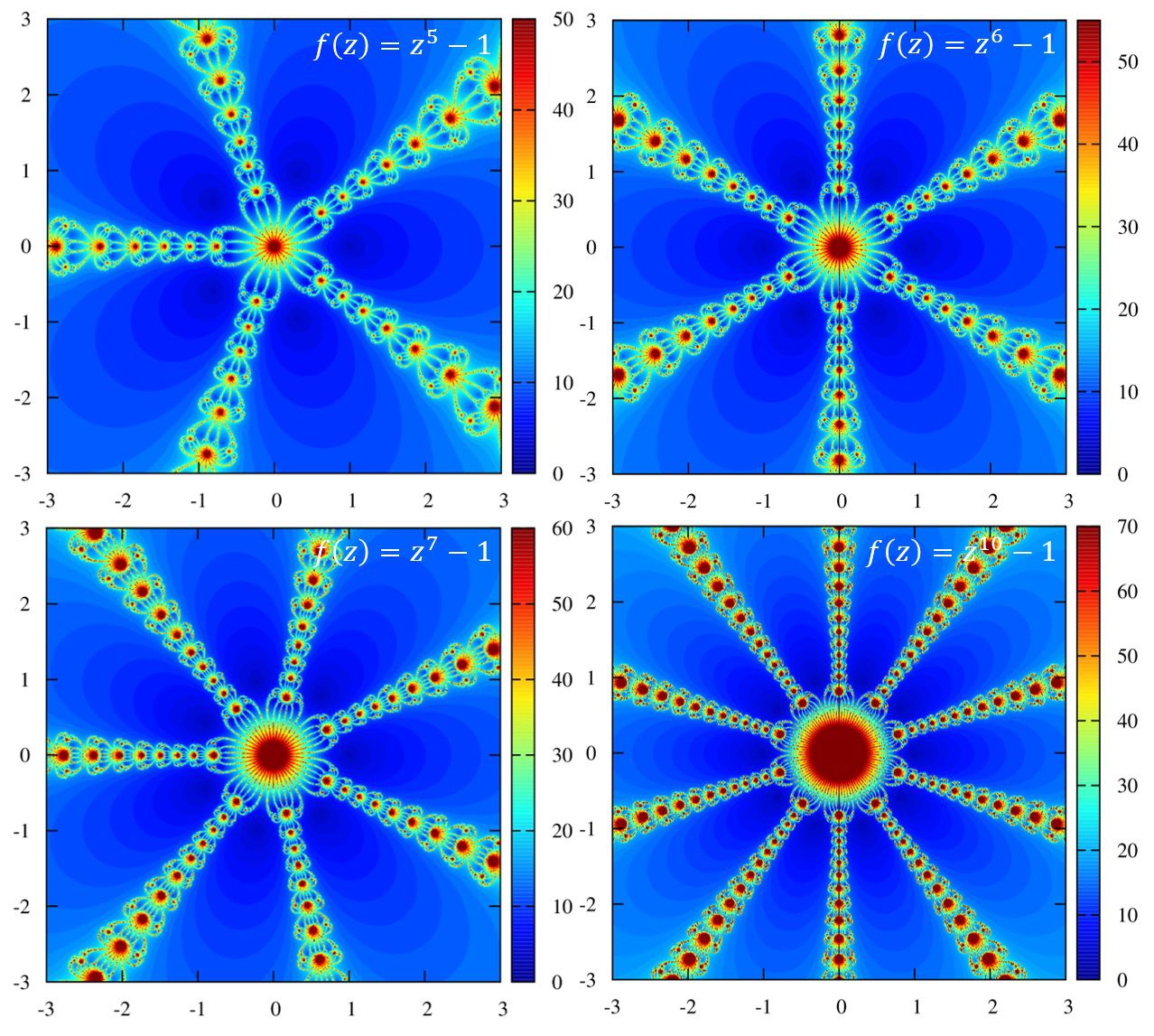
\displaystyle f(z)=z^5-1, z^6-1, z^7-1, z^10-1
\)

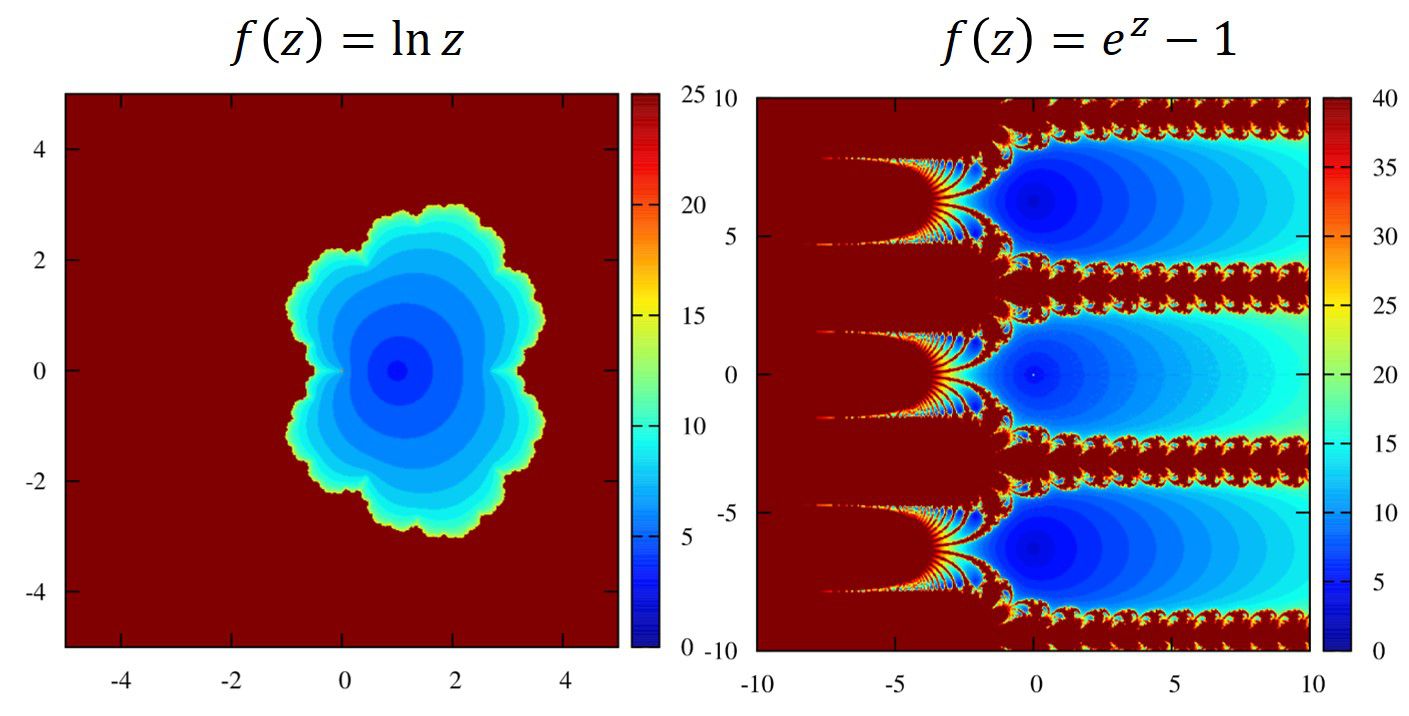
少し複雑な関数の場合
\(
\displaystyle f(z)=\ln z, e^z-1
\)

\(
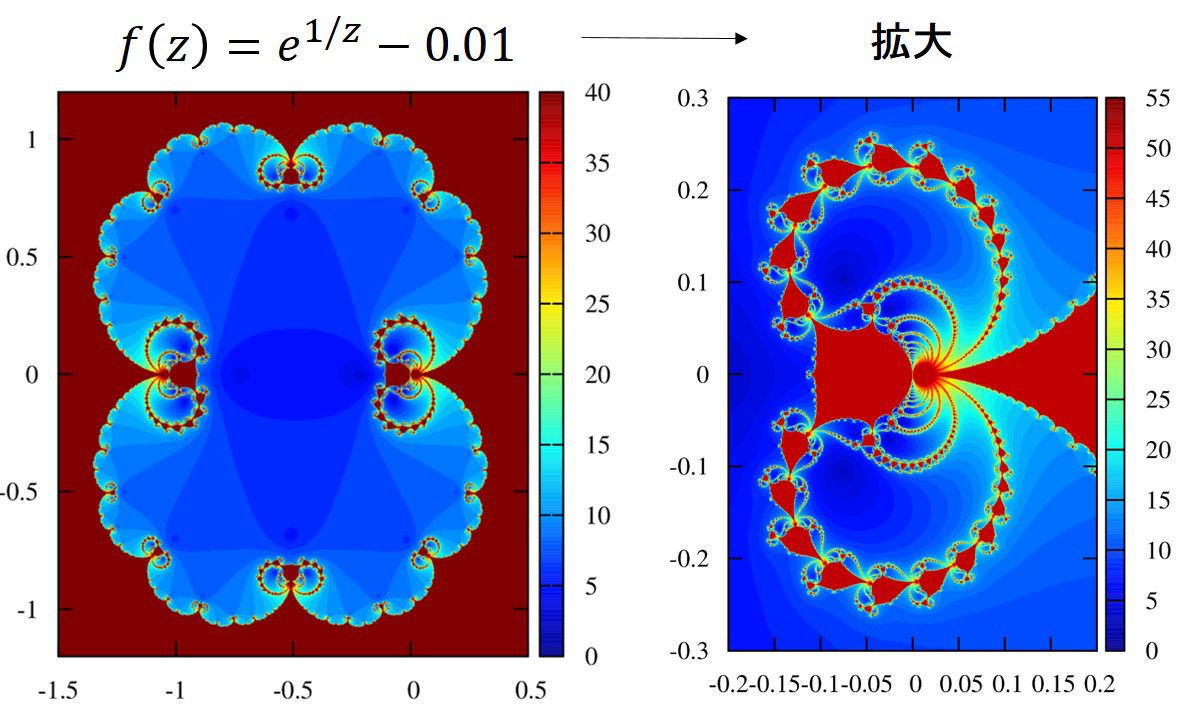
\displaystyle f(z)=e^{1/z}-0.01
\)

\(
\displaystyle f(z)=ze^{z}\ln z-0.01
\)

\(
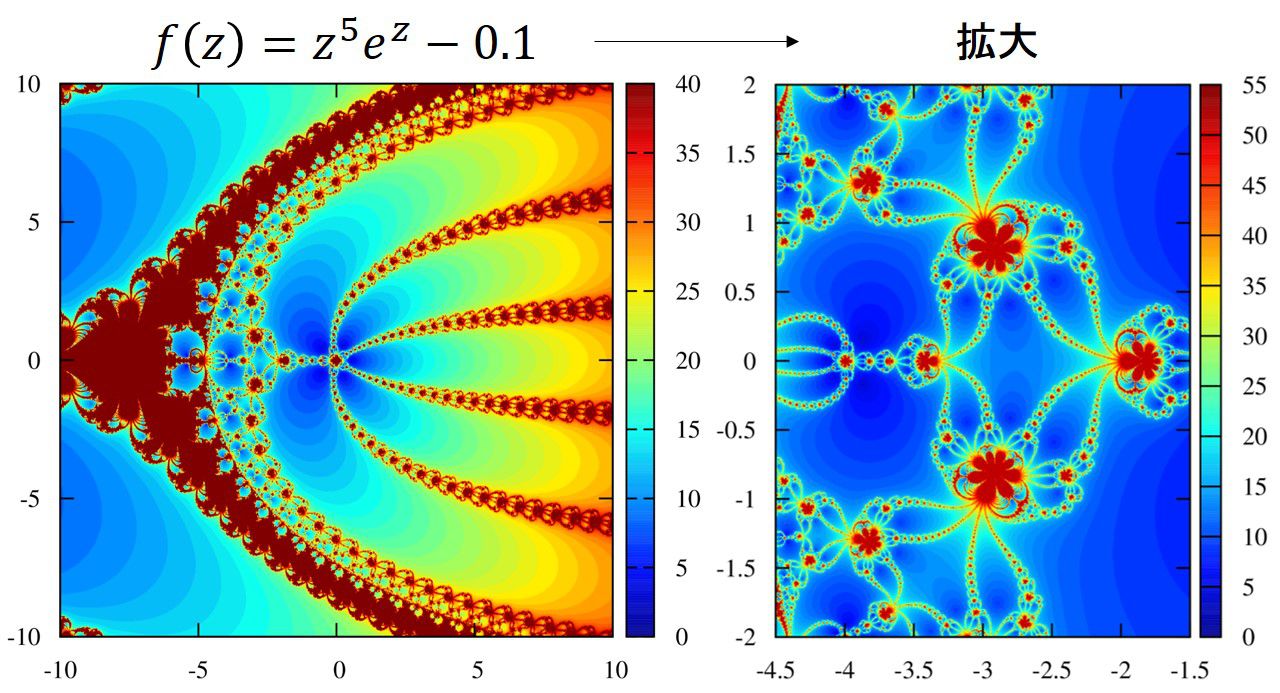
\displaystyle f(z)=z^5e^z-0.1
\)

\(
\displaystyle f(z)=z^4e^z\ln z-0.1
\)

\(
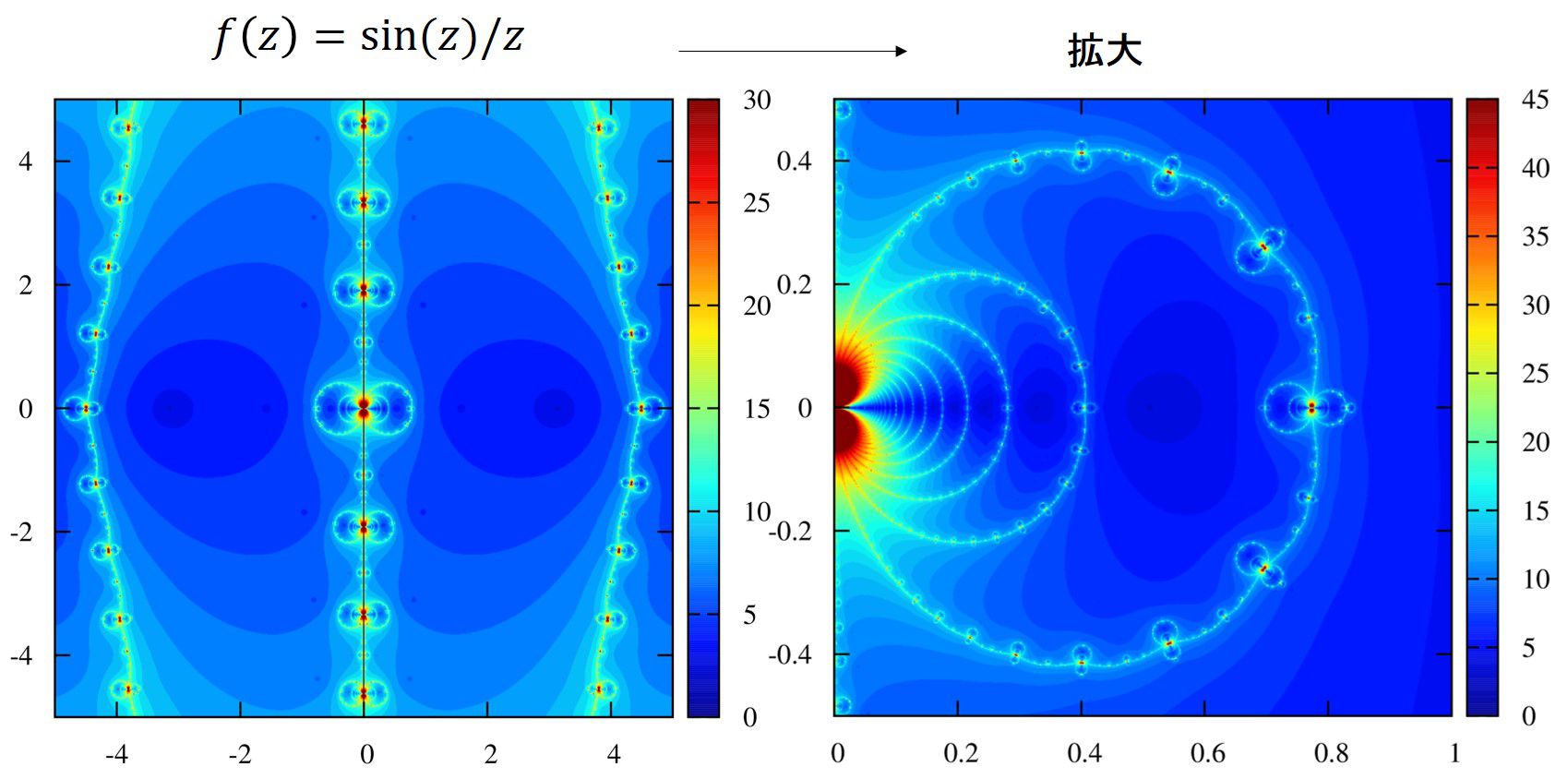
\displaystyle f(z)=sin(z)/z
\)

\(
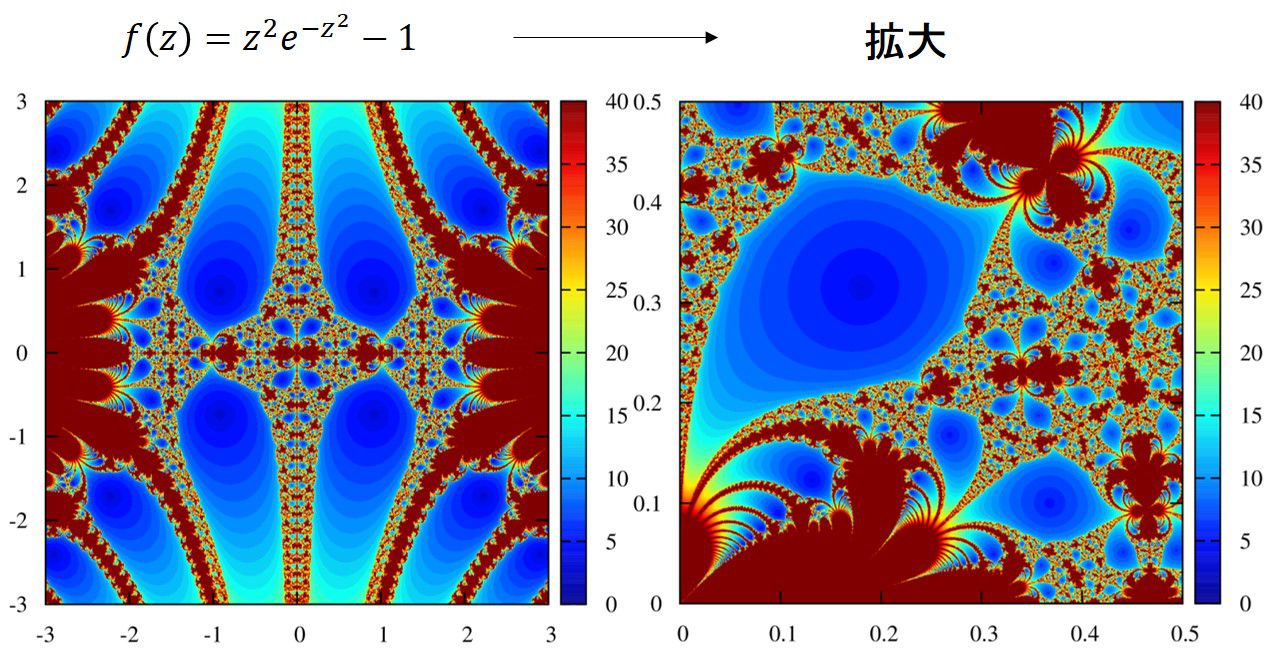
\displaystyle f(z)=z^2 e^{-z^2}-1
\)

\(
\displaystyle f(z)=ln(z) e^{-z^2}-1
\)

最後にリーマンのゼータ関数

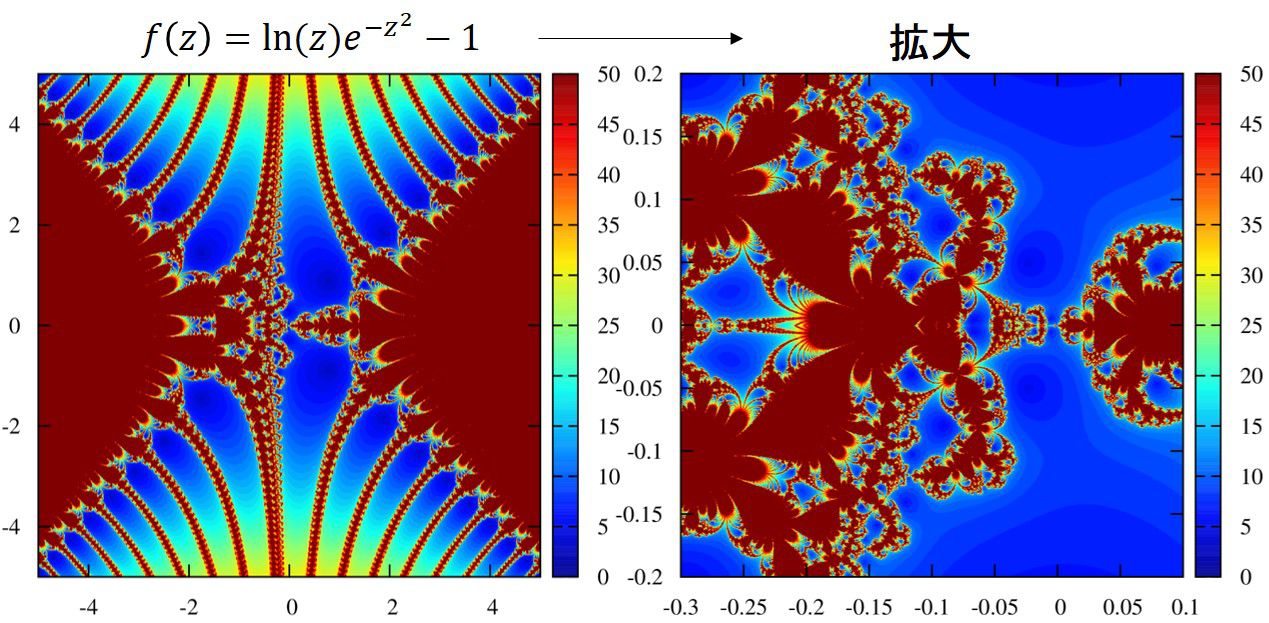
複素関数\(f(z)\)が多くの根を持つとき、非常に複雑で綺麗な画像が得られるようです。
恐らく遠く離れたところからたまたま根のあたりに到達することが多くなるからでしょう。

[adsense2]

fortran90によるプログラム

fortran90によるプログラムを置いておきます。入力するべき場所は!=====の間と、関数fと導関数dfです。

Tweet