プログラミングと数値計算

-1のn乗の計算速度

コメントする

fortran90で、
\(a=(-1)^n, ~(n=0,1,\cdots, M)\)を計算する早いアルゴリズムは

a=1
if(mod(n,2).eq.1)a=-1

です。

物理、数学をやっていると至る所で\((-1)^n\)を見受けます。
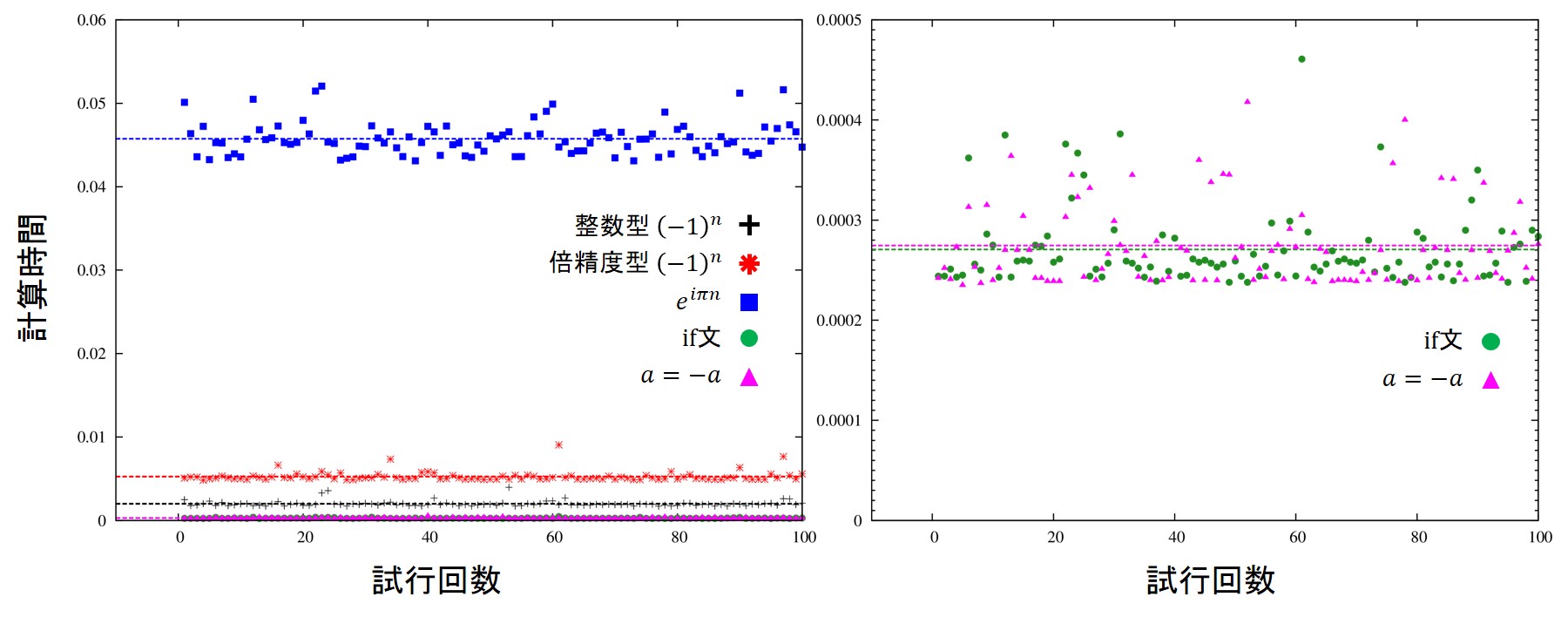
これを数値計算する際に早い計算方法は何でしょうか？

試してみるのは以下のものです。

①
\(
(-1)^n
\)

②
\(
(-1)^n
\)
※①を倍精度型で計算

③
\(
e^{i\pi n}
\)
※\(i\)は虚数単位、\(\pi\)は円周率

④
\(
\begin{eqnarray}
\left\{
\begin{aligned}
& 1 ,~~(n=0,\mbox{偶数})\\
& -1 ,~~(n=\mbox{奇数})\\
\end{aligned}
\right.
\end{eqnarray}
\)

⑤
\(
a=-a
\)で逐次計算

使ったプログラムは以下のものです。

関連記事

このエントリーをはてなブックマークに追加

コメントを残す

メールアドレスが公開されることはありません。 ※ が付いている欄は必須項目です