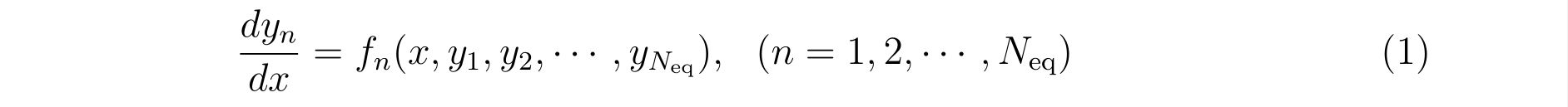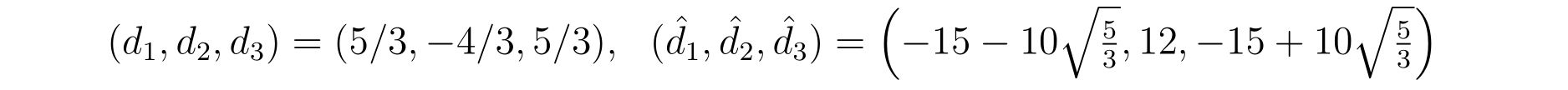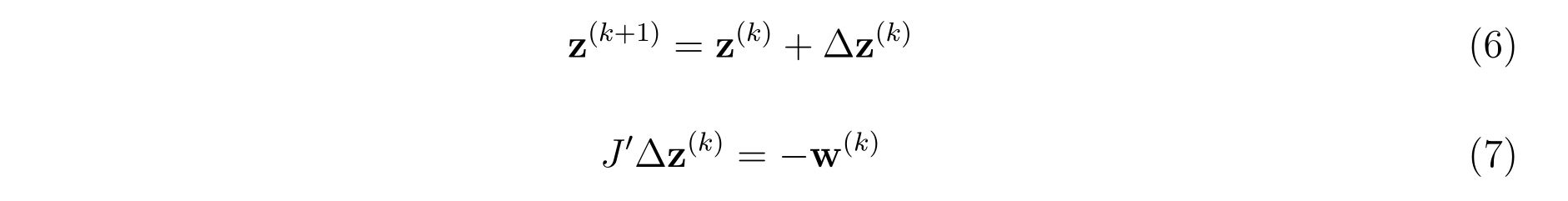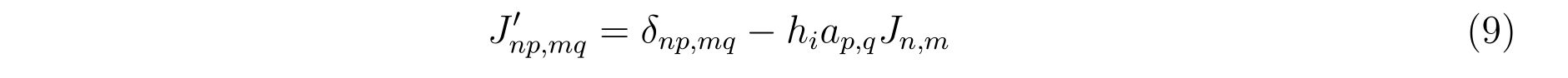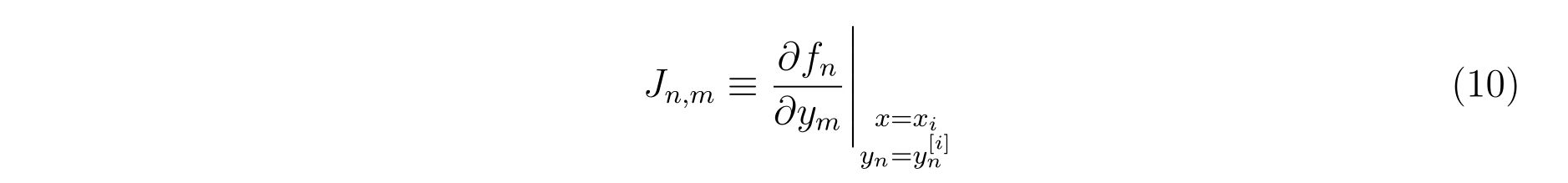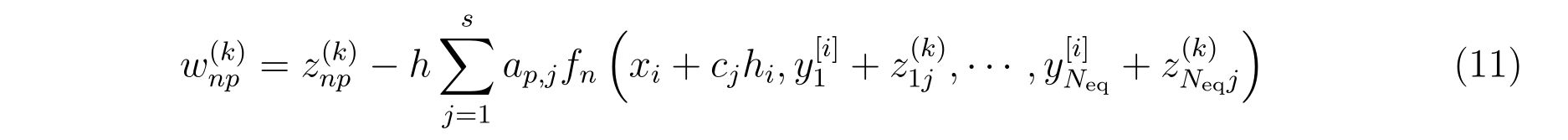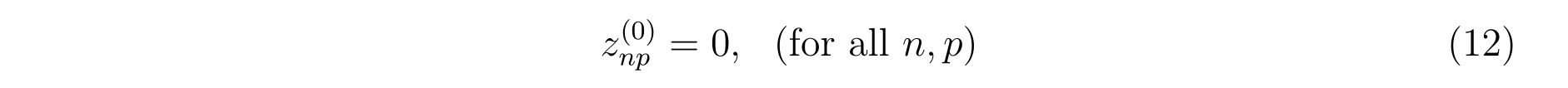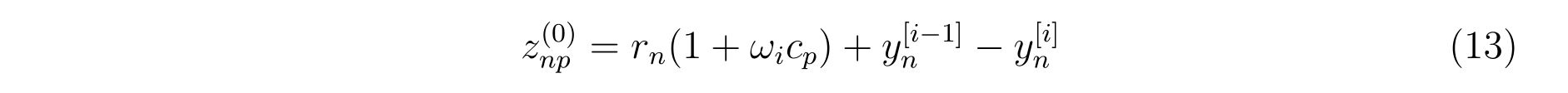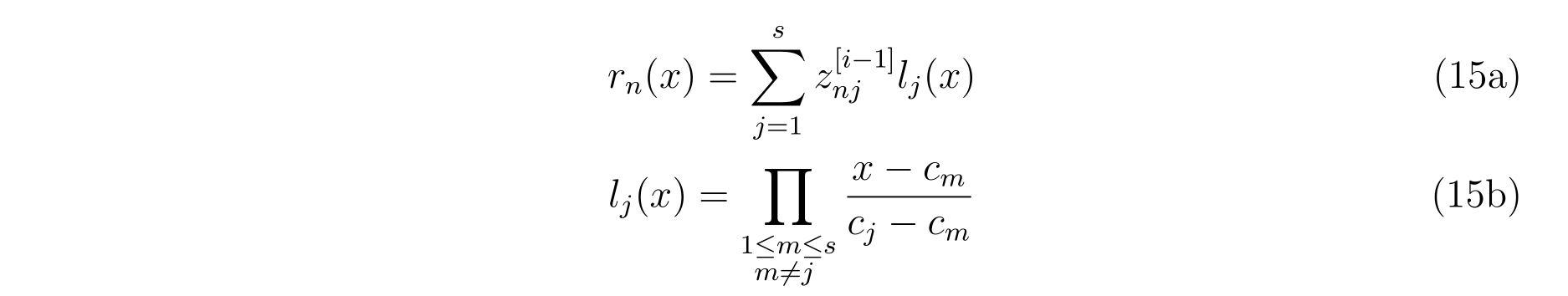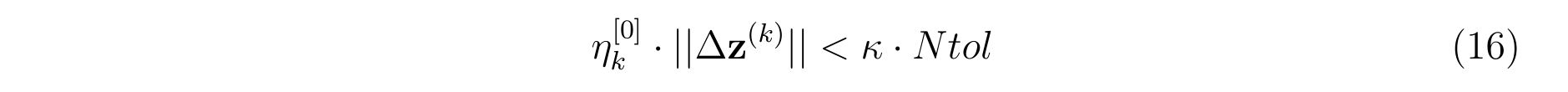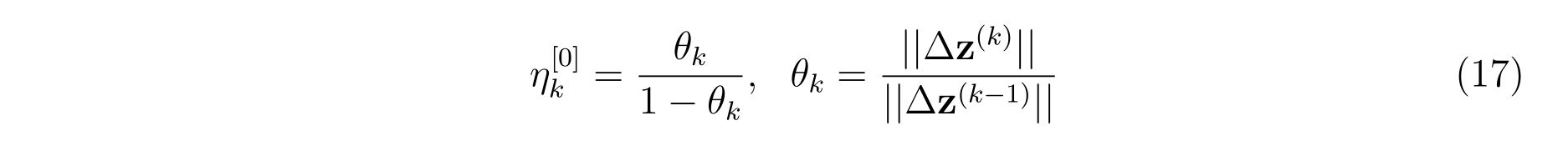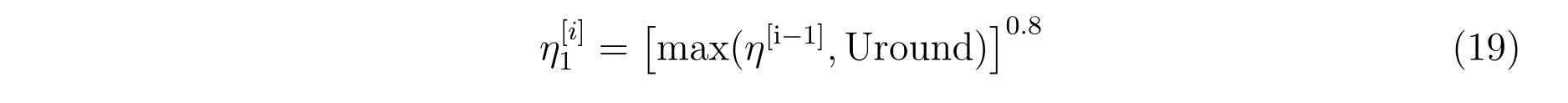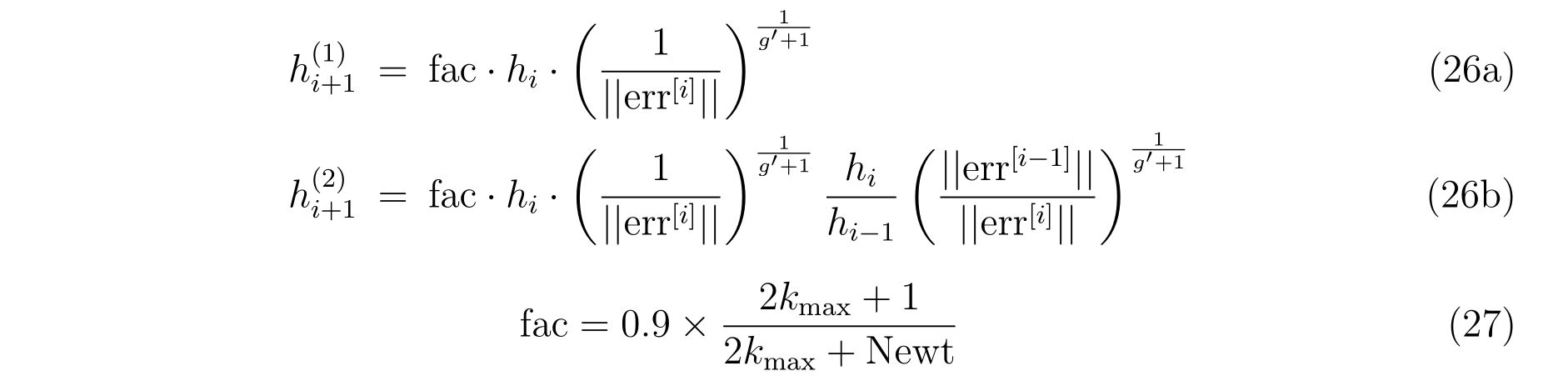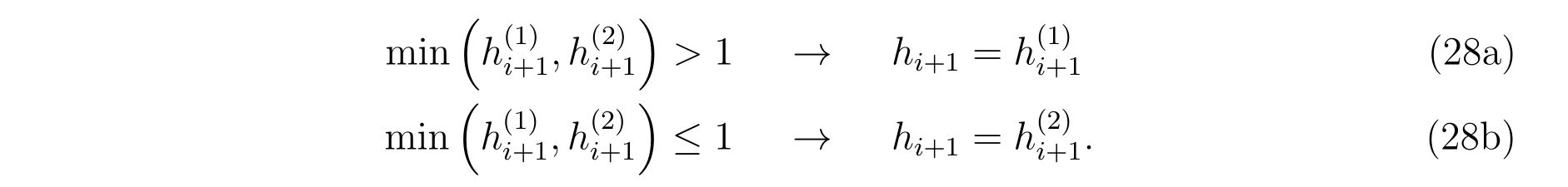module GBL
implicit none
integer::count
end module GBL
program main
use GBL
implicit none
integer::N,Ns,istep,ih0,Jup,info,ih,iJac
double precision::x,xend,h,h0,err0,eta0,tol
integer,allocatable::ipiv(:),epiv(:)
double precision,allocatable::y(:),Rtol(:),Atol(:)
double precision,allocatable::Jmat(:,:),errJ(:,:),z0(:),Jac(:,:)
external::grk
N=2 ! Number of 1st order ODEs
allocate(y(1:N),Rtol(1:N),Atol(1:N))
y=0d0; Rtol=0d0; Atol=0d0
x=0d0 ! Initial values of x
xend=2d0 ! End point of x
y(1)=2d0 ! Initial values at x of y_1
y(2)=-0.66d0 ! Initial values at x of y_2
tol=1d-4 ! Tolerance
h=1d-6 ! Initial step size
Rtol(1:N)=tol ! Relative tolerance
Atol(1:N)=tol ! Absolute tolerance
!------------ Initial set up ------------
Ns=N*3 ! Ns=N*s, s means s-stage IRK.
allocate(ipiv(1:Ns),epiv(1:N))
allocate(Jmat(1:Ns,1:Ns),errJ(1:N,1:N),z0(1:Ns),Jac(1:N,1:N))
ipiv=0; epiv=0; Jmat=0d0; errJ=0d0; Jup=0; ih=0
ih0=0; z0=0d0; eta0=0d0; h0=0d0; err0=0d0; iJac=0; Jac=0d0
!----------------------------------------
count=0
istep=0
info=0
do while(info.le.0)
call irkgl(istep,grk,N,x,h,xend,y,info,Atol,Rtol &
,ih,z0,ih0,h0,eta0,err0,Jup,ipiv,Jmat,epiv,errJ,iJac,Jac)
write(10,'(4e25.15e3,1i5)')x,y(1),y(2),h
enddo
write(6,*)count
stop
end program main
subroutine grk(N,x,y,f)
use GBL
implicit none
integer,intent(in)::N
double precision,intent(in)::x,y(1:N)
double precision,intent(out)::f(1:N)
! Write right-hand-side of 1st order ODEs
f(1)=y(2)
f(2)=1d6*((1d0-y(1)**2)*y(2)-y(1))
count=count+1
return
end subroutine grk
!=====================================
subroutine irkgl(istep,grk,Neq,x,h,xend,y,info,Atol,Rtol &
,ih,z0,ih0,h0,eta0,err0,Jup,ipiv,Jmat,epiv,errJ,iJac,Jac)
implicit none
integer,parameter::s=3
integer,intent(in)::Neq
integer,intent(inout)::istep,info,Jup,ipiv(1:Neq*s),epiv(1:Neq)
double precision,intent(in)::xend,Atol(1:Neq),Rtol(1:Neq)
double precision,intent(inout)::x,h,y(1:Neq)
integer,intent(inout)::ih0,ih,iJac
double precision,intent(inout)::z0(1:Neq*s),h0,eta0,err0
double precision,intent(inout)::Jmat(1:Neq*s,1:Neq*s),errJ(1:Neq,1:Neq)
double precision,intent(inout)::Jac(1:Neq,1:Neq)
external::grk
!
! Implicit Runge-Kutta method based on
! the Gauss-Legendre 3-stage 6-order
!
! Properties of this routine:
! 1. A-stable
! 2. Symplectic
! 3. Symmetric
! 4. Step size control
! Note, Gauss-Legendre IRK method is Symplectic
! even if we change the step size.
!
! Meaning of parameters
! istep : Number of IRK step
! grk : Right hand Side of ODEs
! Neq : Number of 1st-order ODEs
! x : Integral parameter (automatically updated)
! h : Step size (automatically updated)
! xend : End point of the x range
! y : Values of ODEs
! info : Information of the IRK process
! Atol : Absolute tolerance
! Rtol : Relative tolerance
!
! Other parameters are work parameters,
! referenced for istep >= 1
! ***0 : Previous parameters
! Jmat : LU decomposited J' (= I-hAJ) matrix
! ipiv : Pivot information for Jmat
! errJ : LU decomposited (I-h\gamma J) matrix
! epiv : Pivot information for errJ
! Jup : Decide the update of Jmat and errJ,
! Jup = 0 --> No update
! Jup = 1 --> Update
! Jac : Jacobian matrix of the grk function
! iJac : Decide the update of Jac,
! iJac = 0 --> No update when Jup=1
! iJac = 1 --> Update when Jup=1
!
! How to use?
! 1. Call this routine with istep = 0 and info = 0.
! 2. Call and Loop this routine while info <= 0.
!
! ==== Example =====
! istep=0
! info=0
! do while(info.le.0)
! call irk(istep,grk,Neq,x,h,xend,y,info,Atol,Rtol &
! ,ih,z0,ih0,h0,eta0,err0,Jup,ipiv,Jmat,epiv,errJ,iJac,Jac)
! enddo
! ==================
!
! After starting computation with istep=0,
! you must not touch WORK parameters.
!
!
! istep = 0 : when you start computation,
! set WORK parameters like ;
! ih = 0
! z0(1:Ns) = 0d0
! ih0 = 0
! h0 = 0d0
! eta0 = 0d0
! err0 = 0d0
! Jup = 0
! ipiv(1:Ns) = 0
! Jmat(1:Ns,1:Ns) = 0d0
! epiv(1:Neq) = 0
! errJ(1:Neq,1:Neq) = 0d0
! iJac = 0
! Jac(1:Neq,1:Neq) = 0d0
!
! Author : sikino
! URL : http://slpr.sakura.ne.jp/qp/
! Date : 2019/01/14 (yyyy/mm/dd)
! 2019/01/21 keep Jacobian matrix
! 2019/01/22 did Something
! 2019/01/23 initial value estimation
!
double precision::tx,th
double precision,allocatable::ty(:),tz0(:)
integer,parameter::kmax=7 ! Newton iteration limit
double precision,parameter::hmin=1d-13,hmax=1d0
integer::kexit,Ns,key,FLAG,Newt
double precision::theta,err,fac,del,del1,del2,teta0,th0
if(istep.le.-1)then
write(6,*)"**** Error, unexpected istep"
stop
endif
Ns=Neq*s
if(abs(h).ge.hmax)then
h=sign(1d0,h)*hmax
endif
if(h.ge.abs(xend-x))h=xend-x
FLAG=1
if(abs(x-xend).le.hmin)then
info=1
FLAG=0
endif
if(istep.eq.0)then
ipiv=0; epiv=0; Jmat=0d0; errJ=0d0; Jup=0; ih=0
ih0=0; z0=0d0; eta0=0d0; h0=0d0; err0=0d0; iJac=0; Jac=0d0
call discrete_h(h,ih,th,hmin,hmax)
h=th
ih0 = ih+1
Jup = 1
iJac = 1
else
endif
key=0
allocate(ty(1:Neq),tz0(1:Ns))
ty=0d0; tz0=0d0
do while(FLAG.eq.1)
if(ih.ne.ih0)then
Jup=1
endif
tx=x
ty(1:Neq)=y(1:Neq)
tz0(1:Ns)=z0(1:Ns)
teta0 = eta0
th0=h0
call dirk6(istep,grk,Neq,tx,h,ty,Jup &
,tz0,th0,teta0,ipiv,Jmat,epiv,errJ,Atol,Rtol &
,err,kmax,kexit,Newt,theta,iJac,Jac)
! Even if the step is fail, ipiv,Jmat,epiv,errJ are updated if Jup=1.
if(Jup.eq.1)then
Jup=0
endif
if(kexit.eq.1)then
! Change step size
!fac = 0.9d0*(2d0*kmax+1d0)/(2d0*kmax+dble(Newt-1))
fac = 0.95d0*(2d0*kmax+1d0)/(2d0*kmax+dble(Newt))
if(err.ge.1d-30)then
if(istep.eq.0)then
del = fac*((1d0/err)**(0.33d0)) !(27)
else
del1 = fac*((1d0/err)**(0.33d0)) !(27)
del2 = del1*(h/h0)*((err0/err)**(0.33d0)) !(27)
del = del1
if(del2.lt.del)del=del2
if(del.gt.1d0)then
del=del1
else
del=del2
endif
endif
else
del=100d0
endif
elseif(kexit.eq.2)then
del=0d0
else
write(6,*)" **** detect unexpected kexit"
stop
endif
! Accept or Reject
if(err.le.1d0.or.key.eq.1)then
FLAG=0 ! This step with h is accepted
x=x+h
y(1:Neq)=ty(1:Neq)
z0(1:Ns)=tz0(1:Ns)
h0=h
ih0=ih
eta0=teta0
err0=err
iJac = 1
Jup=1
! Don't update Jacobian for next step
if(Newt.le.2.or.theta.lt.1d-3)Jup=0
!if(Newt.le.1.or.theta.lt.1d-3)Jup=0
endif
if(del.le.0.1d0)then
!function changes dramatically.
h=0.1d0*h
elseif(del.ge.4d0)then
!function changes loosely.
h=4d0*h
else
!function changes moderately.
h=del*h
endif
if(abs(h).ge.hmax)then
h=sign(1d0,h)*hmax
elseif(abs(h).lt.hmin)then
h=sign(1d0,h)*hmin
key=1
endif
! Step size alignment
if(abs(xend-x).le.abs(h))then
h=xend-x
Jup=1
if(abs(h).le.hmin)then
info=1
FLAG=0
endif
else
call discrete_h(h,ih,th,hmin,hmax)
h=th
endif
if(h.le.0d0.and.xend-x.ge.0d0)then
info=1
FLAG=0
elseif(h.ge.0d0.and.xend-x.le.0d0)then
info=1
FLAG=0
endif
if(key.eq.1)then
write(6,'(A,f10.5,A,f10.5)')"Strange point between ",x-h," and ",x
info=-9
endif
enddo
istep=istep+1
return
end subroutine irkgl
subroutine dirk6(istep,grk,Neq,x,h,y,Jup &
,z0,h0,eta0,ipiv,Jmat,epiv,errJ,Atol,Rtol &
,err,kmax,kexit,Newt,theta,iJac,Jac)
implicit none
integer,parameter::s=3
integer,intent(in)::istep,Neq,Jup,kmax
integer,intent(out)::kexit,Newt
double precision,intent(in)::h,Atol(1:Neq),Rtol(1:Neq)
double precision,intent(inout)::x,y(1:Neq),z0(1:Neq*s),h0,eta0
double precision,intent(out)::err,theta
integer,intent(inout)::ipiv(1:Neq*s),epiv(1:Neq),iJac
double precision,intent(inout)::Jmat(1:Neq*s,1:Neq*s),errJ(1:Neq,1:Neq)
double precision,intent(inout)::Jac(1:Neq,1:Neq)
external::grk
!
! istep >= 0
!
! Input
! Jup = 0 : Don't update Jacobian
! = 1 : Update Jacobian
! Output
! kexit = 1 : Newton iteration converge.
! = 2 : Newton iteration didn't converge.
!
! Below parameters have meaning when kexit = 1.
! Newt : Number of Newton iteration till converge.
! theta : Convergion rate, \theta < 1.
! err : Estimated err, if err < 1, satisfied required tol.
!
integer::i,j,k,n,m,p,q,Ns,info
double precision,parameter::kappa=5d-2
double precision,parameter::Uround=5d-16
double precision,parameter::sq15=sqrt(15d0)
! Real eigenvalue of A matrix in butcher table for Gauss-Legendre
double precision,parameter::gamma=0.215314423116112178244733530380696d0
double precision::a(1:s,1:s),c(1:s),d(1:s),d2(1:s),dc(1:s)
double precision::c12,c23,c31,xc1,xc2,xc3,xx,omega
double precision::x0,tx
double precision,allocatable::z(:),y0(:),dy(:),f(:),tf(:),ty(:),tf0(:)
double precision,allocatable::w(:,:),w0(:,:),e(:)
double precision::Ntol,sc,sdz,sdz0,tmp,eta
Ns=Neq*s
allocate(z(1:Ns))
z=0d0
! 3-stage Gauss-Legendre
c(1:3)=(/0.5d0-0.1d0*sq15, 0.5d0, 0.5d0+0.1d0*sq15/)
a(1,1:3)=(/5d0/36d0, 2d0/9d0-sq15/15d0, 5d0/36d0-sq15/30d0/)
a(2,1:3)=(/5d0/36d0+sq15/24d0, 2d0/9d0, 5d0/36d0-sq15/24d0/)
a(3,1:3)=(/5d0/36d0+sq15/30d0, 2d0/9d0+sq15/15d0, 5d0/36d0/)
d(1:3)=(/5d0/3d0,-4d0/3d0,5d0/3d0/)
d2(1:3)=(/-15d0-10d0*sqrt(5d0/3d0),12d0,-15d0+10d0*sqrt(5d0/3d0)/)
dc(1:3)=(/(5d0+sq15)*10d0/3d0, -40d0/3d0 ,(5d0-sq15)*10d0/3d0/)
if(istep.eq.0)then
z(1:Ns)=0d0
else
allocate(dy(1:Neq))
dy=0d0
do n=1,Neq
do j=1,s
dy(n)=dy(n)+d(j)*z0((n-1)*s+j)
enddo
enddo
! Lagrange interpolation
omega=h/h0
c12=1d0/(c(1)-c(2))
c23=1d0/(c(2)-c(3))
c31=1d0/(c(3)-c(1))
do n=1,Neq
do p=1,s
xx=1d0+omega*c(p)
xc1=xx-c(1)
xc2=xx-c(2)
xc3=xx-c(3)
z((n-1)*s+p)=&
-z0((n-1)*s+1)*xc2*xc3*(c12*c31)*xx/c(1) &
-z0((n-1)*s+2)*xc3*xc1*(c12*c23)*xx/c(2) &
-z0((n-1)*s+3)*xc1*xc2*(c31*c23)*xx/c(3) &
-dy(n)
enddo
enddo
deallocate(dy)
endif
if(Jup.eq.1)then
! LU decomposition of J' matrix
if(iJac.eq.1)then
call Jacobian(Neq,x,y,grk,Jac)
iJac=0
endif
do m=1,Neq
do n=1,Neq
do q=1,s
do p=1,s
Jmat(s*(n-1)+p,s*(m-1)+q) = - h*Jac(n,m)*a(p,q)
enddo
enddo
enddo
enddo
do n=1,Neq
do m=1,Neq
errJ(n,m) = - h*gamma*Jac(n,m)
enddo
enddo
do i=1,Ns
Jmat(i,i) = 1d0 + Jmat(i,i)
enddo
do i=1,Neq
errJ(i,i) = 1d0 + errJ(i,i)
enddo
! LU factorization for main part of IRK
call dgetrf(Ns,Ns,Jmat,Ns,ipiv,info)
! LU factorization for estimate error
call dgetrf(Neq,Neq,errJ,Neq,epiv,info)
endif
allocate(f(1:Ns),tf(1:Neq),ty(1:Neq),w(1:Ns,1:1))
f=0d0; tf=0d0; ty=0d0; w=0d0
!===============================
Ntol=sqrt(Rtol(1))
!if(0.03d0.le.Ntol)Ntol=0.03d0
!if(1d-12.le.Ntol)Ntol=1d-12
if(1d-12.le.Ntol)Ntol=1d-12
!if(1d-6.le.Ntol)Ntol=1d-6
!===============================
sdz0=0d0 ! Initialize
! Simple Newton iteration
kexit=0
do k=1,kmax
do j=1,s
tx = x + c(j)*h
do n=1,Neq
ty(n) = y(n) + z((n-1)*s+j)
enddo
call grk(Neq,tx,ty,tf)
do n=1,Neq
f((n-1)*s+j) = tf(n)
enddo
enddo
w(1:Ns,1:1)=0d0
do n=1,Neq
do p=1,s
do j=1,s
w((n-1)*s+p,1) = w((n-1)*s+p,1) + a(p,j)*f((n-1)*s+j)
enddo
w((n-1)*s+p,1) = z((n-1)*s+p) - h*w((n-1)*s+p,1)
enddo
enddo
! Solve J' \delta z = - w
do i=1,Ns
w(i,1) = - w(i,1)
enddo
call dgetrs('N',Ns,1,Jmat,Ns,ipiv,w,Ns,info)
! --> Now, w is \Delta z
! z^{(k+1)} = z^{(k)} + Delta z
do i=1,Ns
z(i) = z(i) + w(i,1)
enddo
sdz=0d0
do i=1,Ns
sdz = sdz + w(i,1)**2
enddo
sdz=sqrt(sdz)
! Stop iteration criteria
if(istep.eq.0.and.k.eq.1)then
! Do nothing
kexit=0
elseif(istep.eq.0.and.k.ge.2)then
if(sdz0-sdz.lt.0d0)then
! Convergion rate > 1, must change small step size.
kexit=2
elseif(sdz0*sdz**(kmax-k+1).gt.kappa*Ntol*(sdz0-sdz)*sdz0**(kmax-k))then
! Rough convergion estimation fail, must change small step size.
kexit=2
elseif(sdz*sdz.lt.kappa*Ntol*(sdz0-sdz))then
! Good behavior. Iteration finish.
kexit=1
endif
elseif(istep.ge.1.and.k.eq.1)then
tmp = Uround
if(eta0.gt.tmp)tmp=eta0
tmp=tmp**0.8d0
if(tmp*sdz.lt.kappa*Ntol)then
kexit=1
endif
elseif(istep.ge.1.and.k.ge.2)then
if(sdz0-sdz.lt.0d0)then
! Convergion rate > 1, must change small step size.
kexit=2
elseif(sdz0*sdz**(kmax-k+1).gt.kappa*Ntol*(sdz0-sdz)*sdz0**(kmax-k))then
! Rough convergion estimation fail, must change small step size.
kexit=2
elseif(sdz*sdz.lt.kappa*Ntol*(sdz0-sdz))then
! Good behavior. Iteration finish.
kexit=1
endif
else
write(6,*)" *****Unexpected parameters"
stop
endif
if(kexit.ne.0)exit
sdz0 = sdz
enddo
!
! 0 < \eta < \infty --> Good.
! if \eta ~ 0, good behavior
! -\infty < \eta < -1, --> Bad.
! Error increase as iteration increase.
!
if(k.eq.kmax+1.or.kexit.eq.2.or.kexit.eq.0)then
! Did not converge k_max iteration.
kexit=2
eta=100d0
Newt=kmax
err=100d0
theta=1000d0 ! Convergion ratio, \theta ~ 0 is Good.
! h0, z0, x, y are don't updated
return
else
! (sdz0-sdz) > 0
if(k.eq.1)then
! No sdz0 case.
eta = Uround
if(eta0.gt.eta)eta=eta0
eta = eta**0.8d0
theta = 100d0 ! Here, \theta cannot evaluate because k=1.
else
if(sdz0.eq.sdz)then
! z does not change --> converge enough.
eta = Uround
theta = 0d0 ! \theta=0.
else
! General case.
eta = sdz/(sdz0-sdz)
theta = sdz/sdz0
endif
endif
Newt = k
endif
deallocate(w)
x0=x
allocate(y0(1:Neq))
y0(1:Neq)=y(1:Neq)
! Update x and y(1:Neq)
x=x+h
do n=1,Neq
do j=1,s
y(n) = y(n) + d(j)*z((n-1)*s+j)
enddo
enddo
! Error estimation
allocate(w(1:Neq,1:1),w0(1:Neq,1:1),tf0(1:Neq),e(1:Neq))
w=0d0; w0=0d0; tf0=0d0; e=0d0
do n=1,Neq
do j=1,s
w(n,1) = w(n,1) + dc(j)*z((n-1)*s+j)
enddo
enddo
w0(1:Neq,1:1)=w(1:Neq,1:1)
call dgetrs('N',Neq,1,errJ,Neq,epiv,w,Neq,info)
do n=1,Neq
e(n)=w(n,1)
enddo
err=0d0
do n=1,Neq
sc=abs(y0(n))
if(abs(y(n)).gt.y0(n))sc=abs(y(n))
sc=Atol(n)+sc*Rtol(n)
err=err+(e(n)/sc)**2
enddo
err=sqrt(err/dble(Neq))
if(err.ge.1d0)then
call grk(Neq,x0,y0,tf0)
do n=1,Neq
ty(n) = y0(n) + e(n)
enddo
call grk(Neq,x0,ty,tf)
do n=1,Neq
w(n,1) = w0(n,1) + gamma*h*(tf(n)-tf0(n))
enddo
call dgetrs('N',Neq,1,errJ,Neq,epiv,w,Neq,info)
do n=1,Neq
e(n)=w(n,1)
enddo
err=0d0
do n=1,Neq
sc=abs(y0(n))
if(abs(y(n)).gt.y0(n))sc=abs(y(n))
sc=Atol(n)+sc*Rtol(n)
err=err+(e(n)/sc)**2
enddo
err=sqrt(err/dble(Neq))
endif
z0(1:Ns)=z(1:Ns)
h0=h
eta0=eta
return
end subroutine dirk6
subroutine discrete_h(h,ih,th,hmin,hmax)
implicit none
double precision,intent(in)::h,hmin,hmax
integer,intent(out)::ih
double precision,intent(out)::th
double precision::dx,hmin1,hmax1
integer,parameter::imax=200
hmin1=0.10d0*hmin
hmax1=1d0*hmax
dx=(log10(hmax1)-log10(hmin1))/dble(imax)
do ih=0,imax
th=10d0**(-ih*dx+log10(hmax1))
if(th.le.abs(h))exit
enddo
if(h.lt.0d0)th=-th
return
end subroutine discrete_h
subroutine Jacobian(Neq,x,y,fxy,Jac)
implicit none
integer,intent(in)::Neq
double precision,intent(in)::x,y(1:Neq)
double precision,intent(out)::Jac(1:Neq,1:Neq)
external::fxy
integer::n,m
double precision::dy
double precision,parameter::delta=2d-8
double precision,allocatable::f0(:),f1(:),ty(:)
allocate(f0(1:Neq),f1(1:Neq),ty(1:Neq))
f0=0d0; f1=0d0; ty=0d0
call fxy(Neq,x,y,f0)
do m=1,Neq
ty(1:Neq) = y(1:Neq)
dy=sqrt(abs(y(m)))
if(dy.lt.1d0)dy=1d0
dy=delta*dy
ty(m) = ty(m)+dy
call fxy(Neq,x,ty,f1)
do n=1,Neq
Jac(n,m) = (f1(n)-f0(n)) / dy
enddo
enddo
return
end subroutine Jacobian