このページは
束縛条件下の運動 – ホロノミックな束縛 1
の続きです。
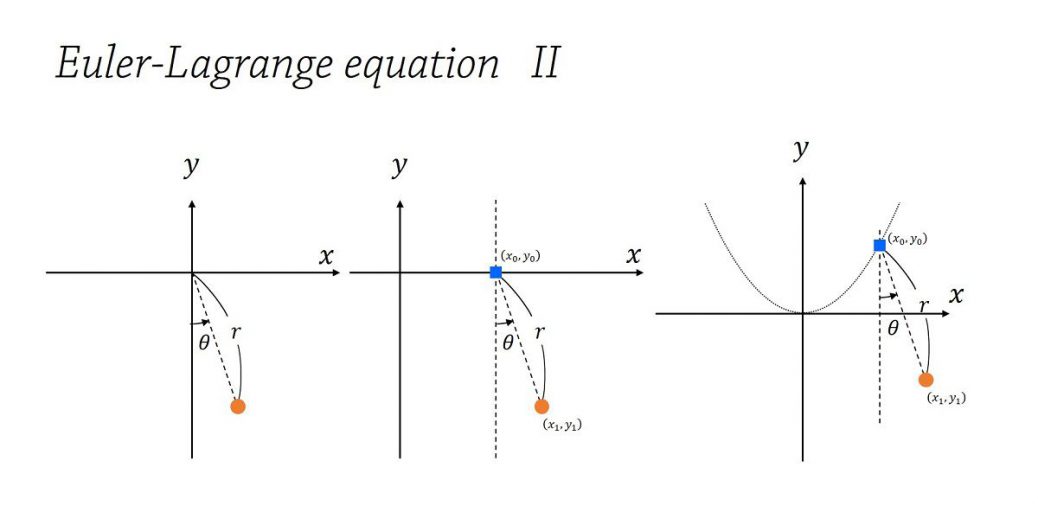
単振り子
ポテンシャルが存在し、ホロノミックな束縛が課されている代表的な問題である、単振り子を考えましょう。
単振り子は、束縛条件下の運動 – ホロノミックな束縛 1で考えた円に束縛されている問題に対してポテンシャルが加わった問題です。
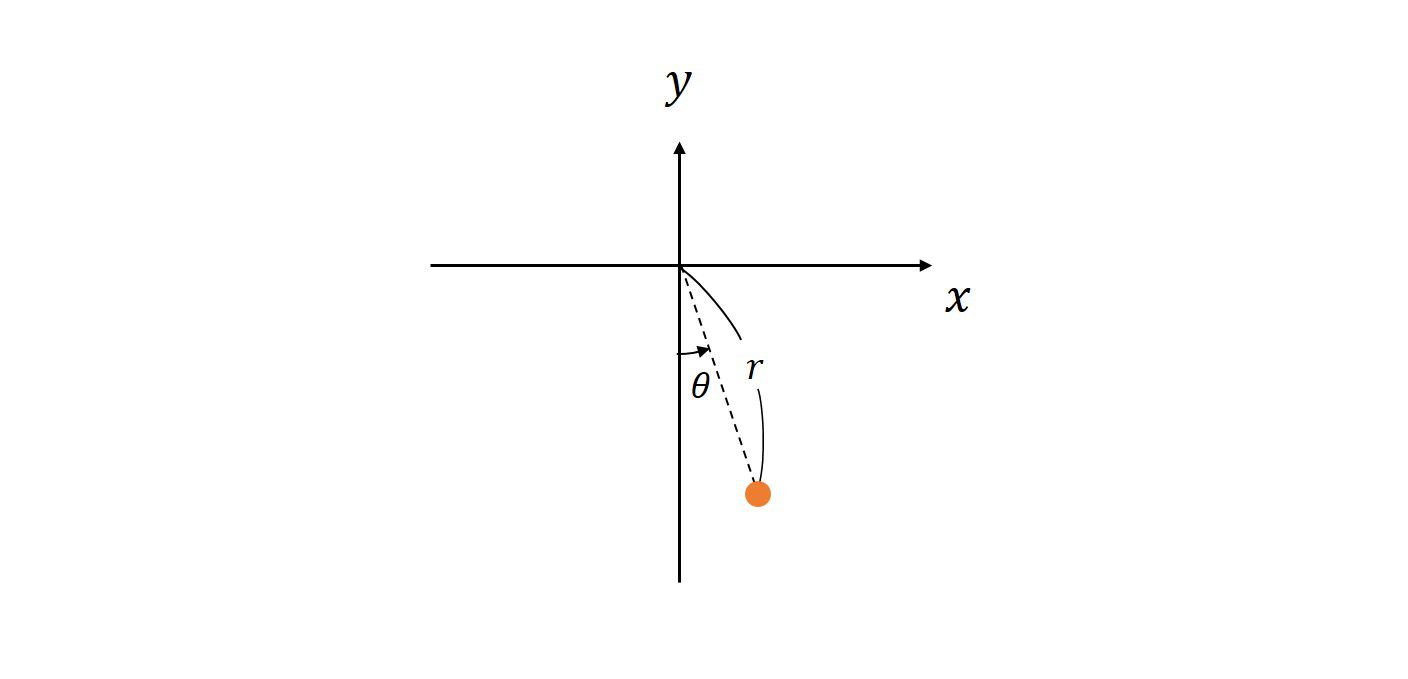
座標系は以下のような極座標系を選びます。
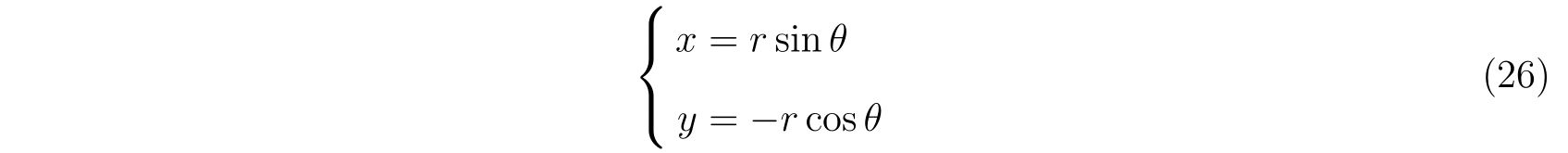
通常の極座標系とは異なります。\(\theta=0\)で鉛直下方向にとる座標系にしたかったので、通常の極座標系とは変えています。
ホロノミックな束縛条件\(f(x,y,t)=0\)を含めたラグランジアンは、デカルト座標系から極座標系に変えて
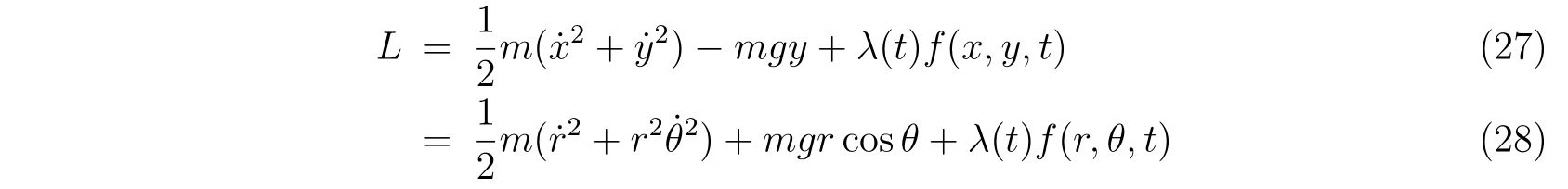
と書くことが出来ます。注記しますが、ラグランジュの未定乗数は時間に依存していて構いません。
ラグランジアンの偏微分をそれぞれ計算すれば、
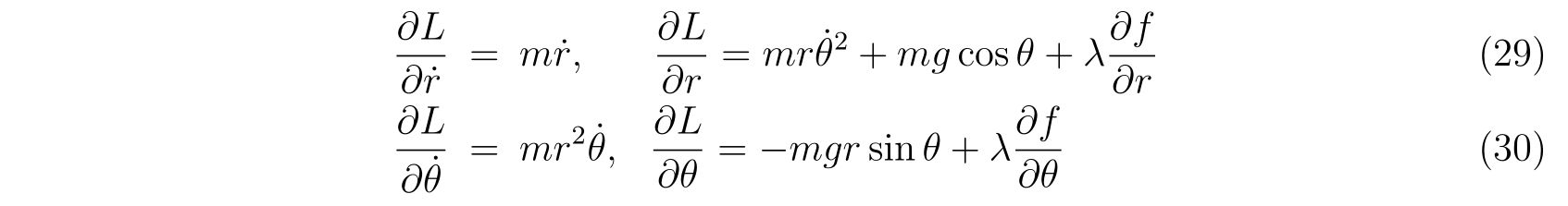
ですので、運動方程式と束縛条件
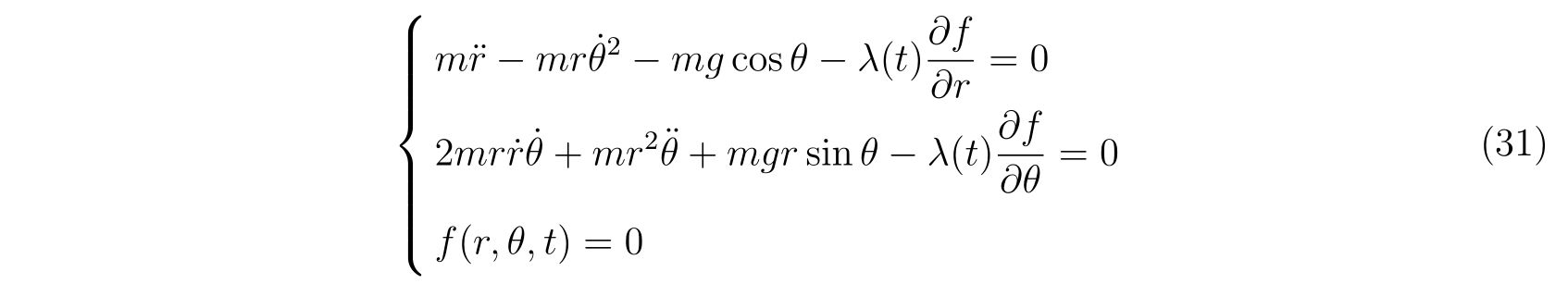
が得られます。連立微分方程式(31)の3本の方程式に対して未知の関数は\(r(t),\theta(t),\lambda(t)\)の3つなので、方程式を立てて\(r(t),\theta(t)\)を求めることが出来ます。
では、伸び縮みしない振り子を考えましょう。束縛条件は

をして表現することが出来ます。束縛条件の一般化座標による偏微分は

ですので、運動方程式

を得ます。式(34)の第2式を変形すると
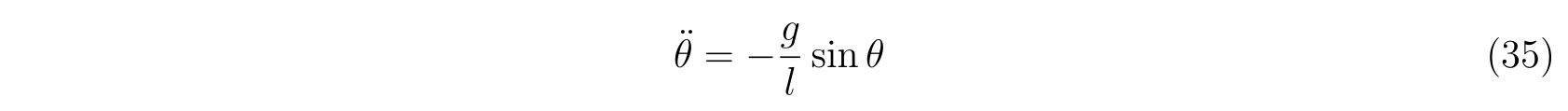
ですので、これはまさに振り子を表す運動方程式です。
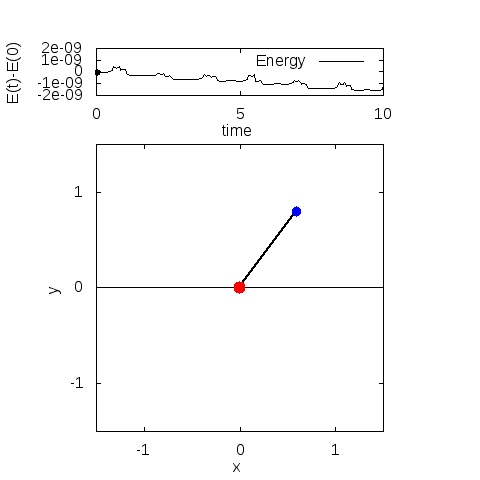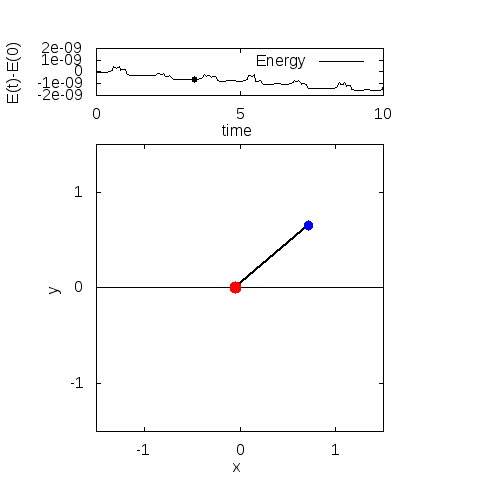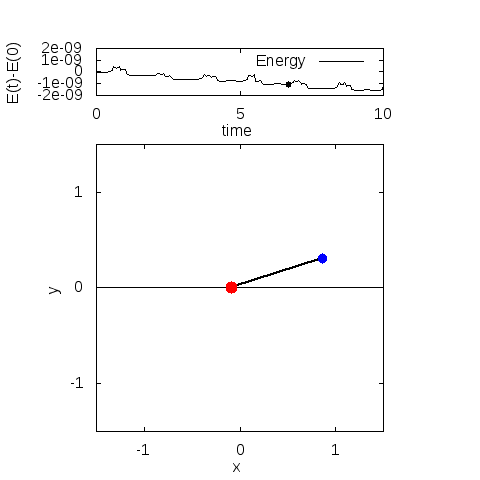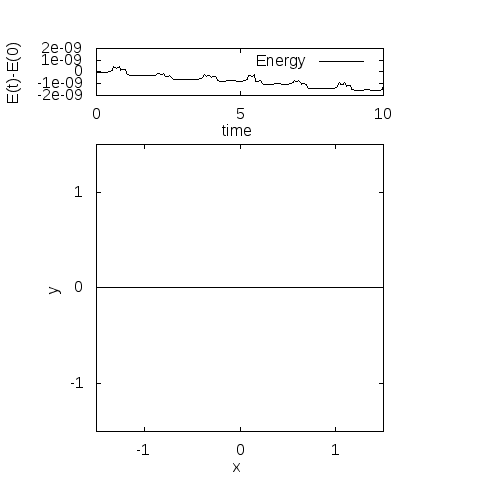
実際に解いてみると、こんなグラフが得られます。
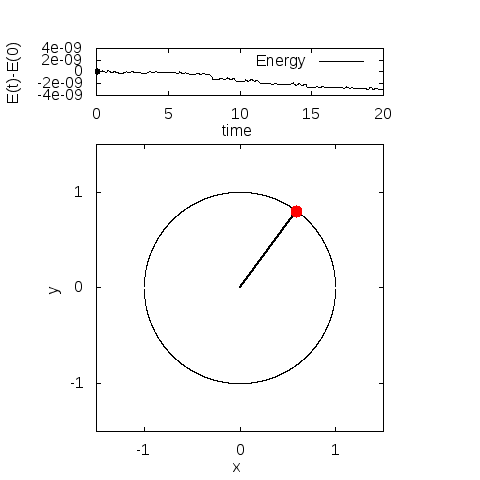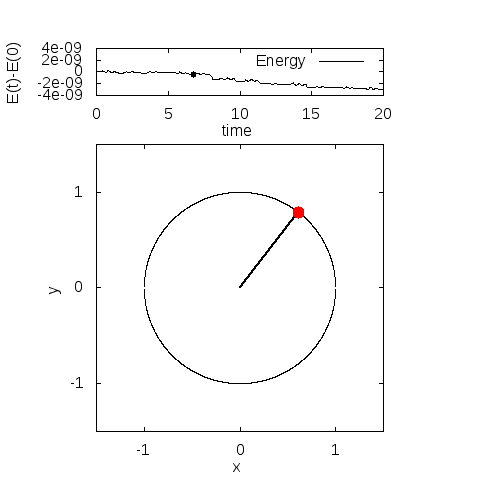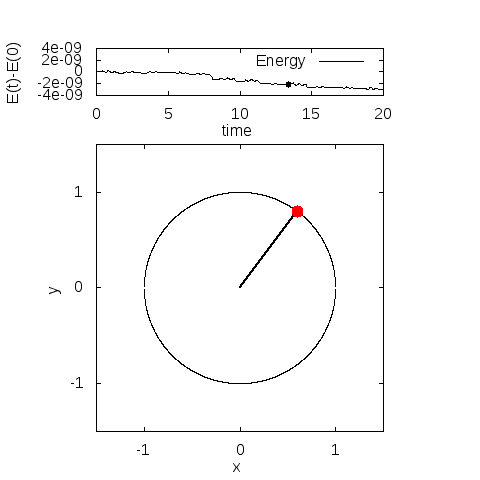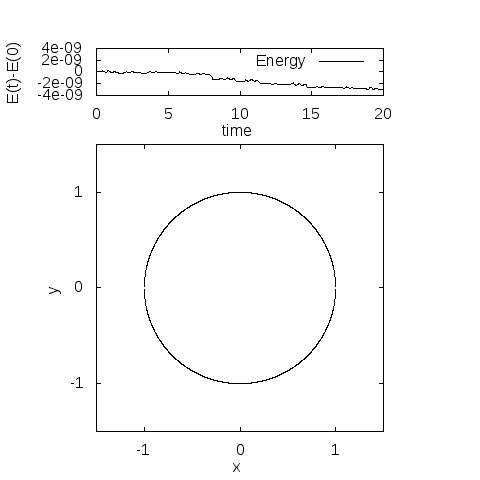
・パラメータ
\(m=3, l=1, g=9.8\)
\(\theta(0)=\frac{4\pi}{5}, \theta'(0)=0\)
・計算手法
陰的ルンゲクッタ法
支点が動く振り子
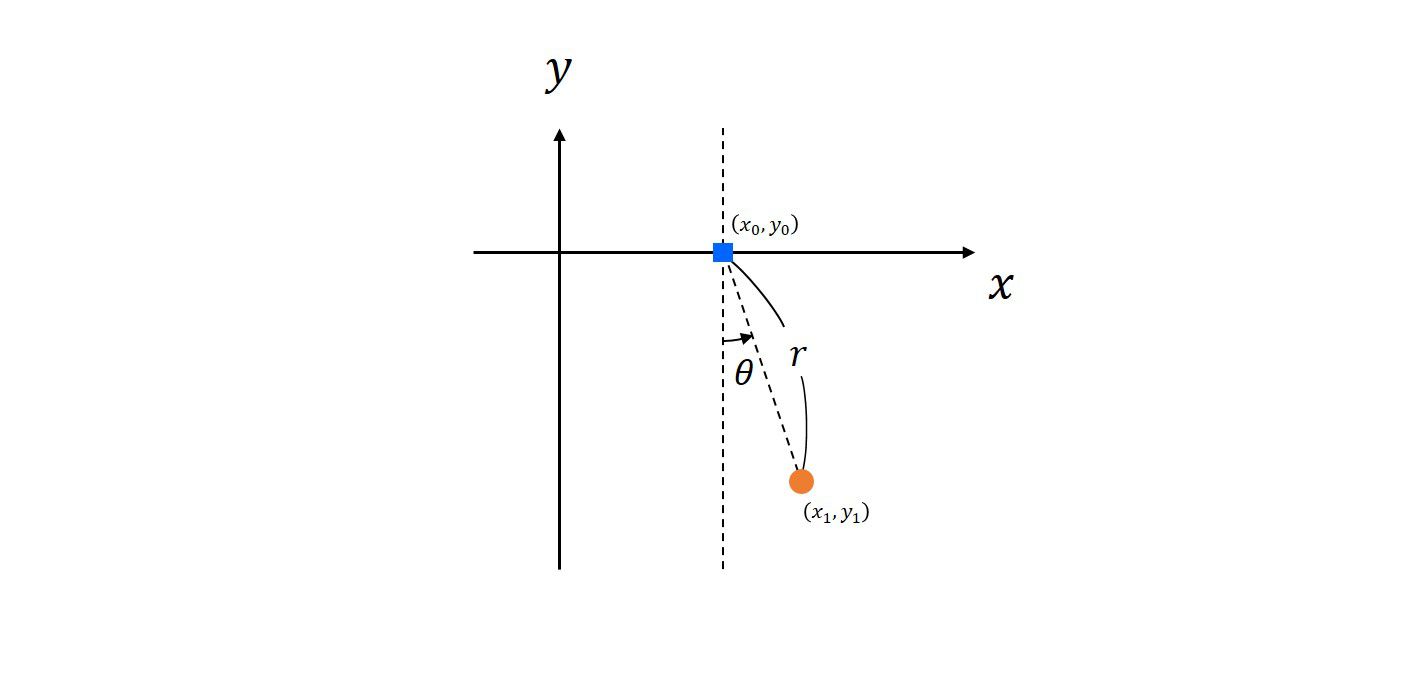
次に、束縛条件が2つある場合を考えましょう。その例題として、
振り子の支点が摩擦の無いレールの上に載っていることを考えます。
ラグランジアンは
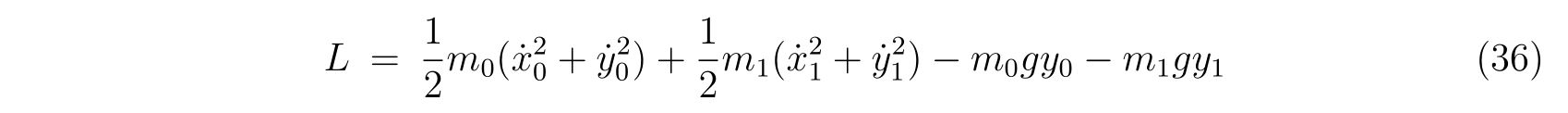
です。2つのホロノミックな束縛条件
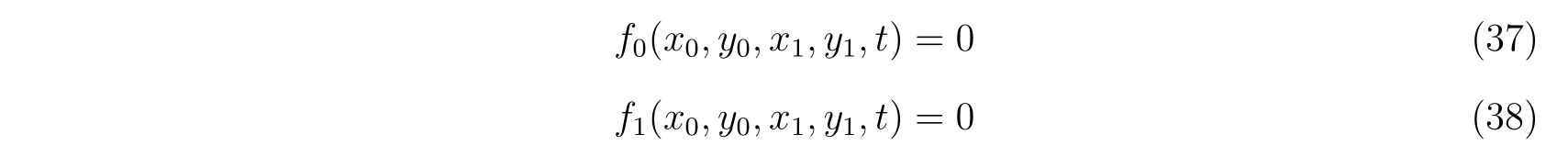
を考えます。すると、ホロノミックな束縛条件を含めたラグランジアンは、

と書くことが出来ます。
これから伸び縮みしない振り子を考えることを見越して、座標系
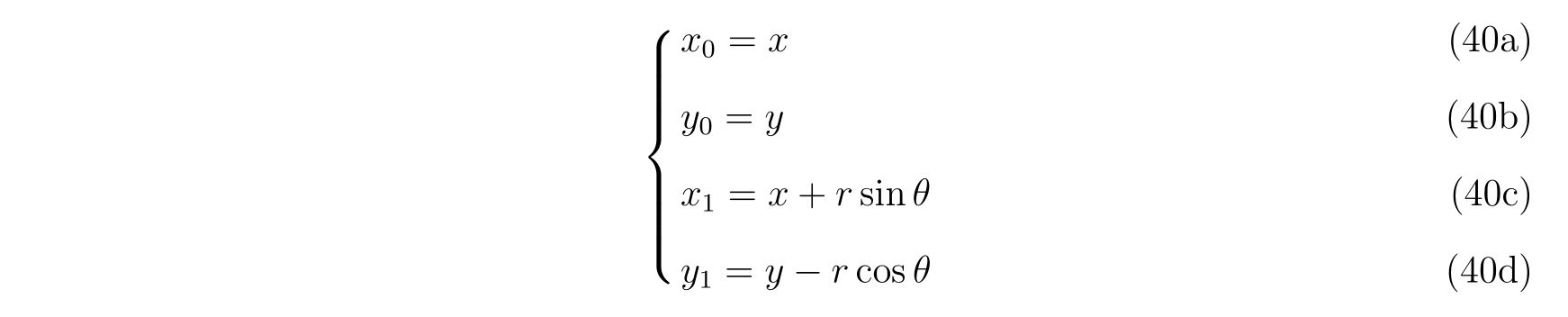
を考えます。この新たな座標系でのラグランジアンは、
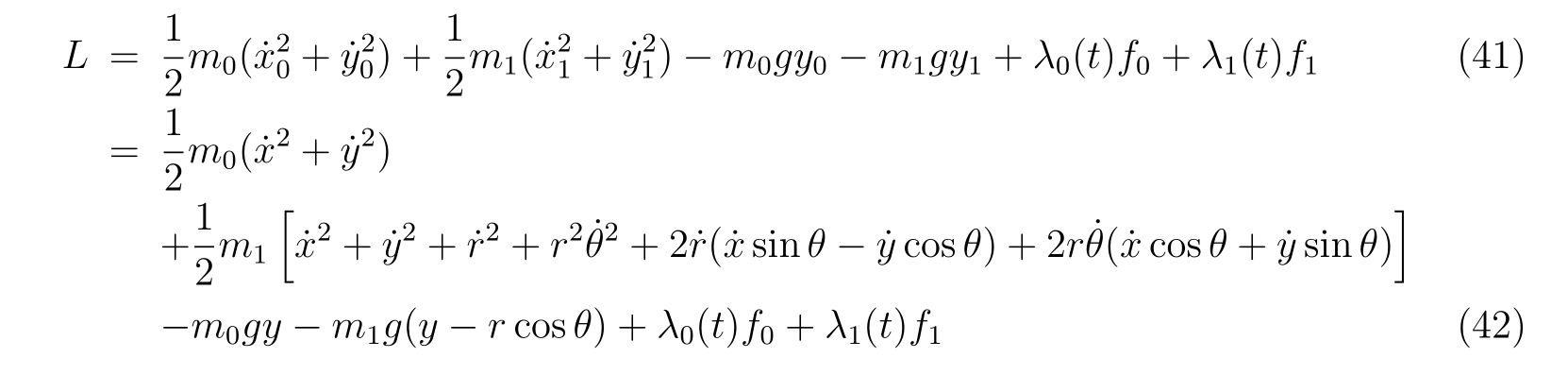
と書けます。それぞれの偏微分である
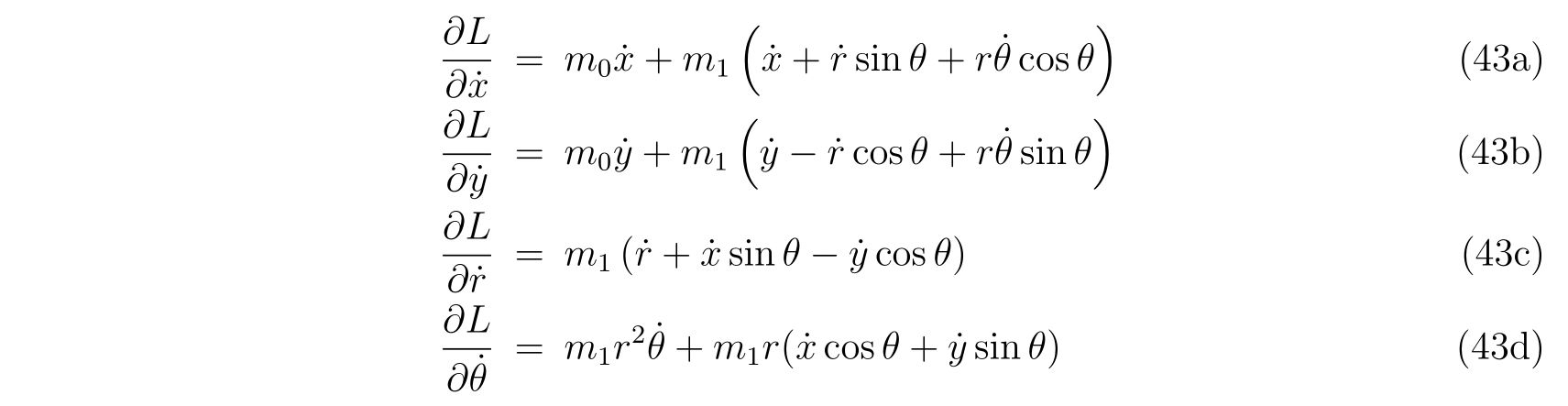
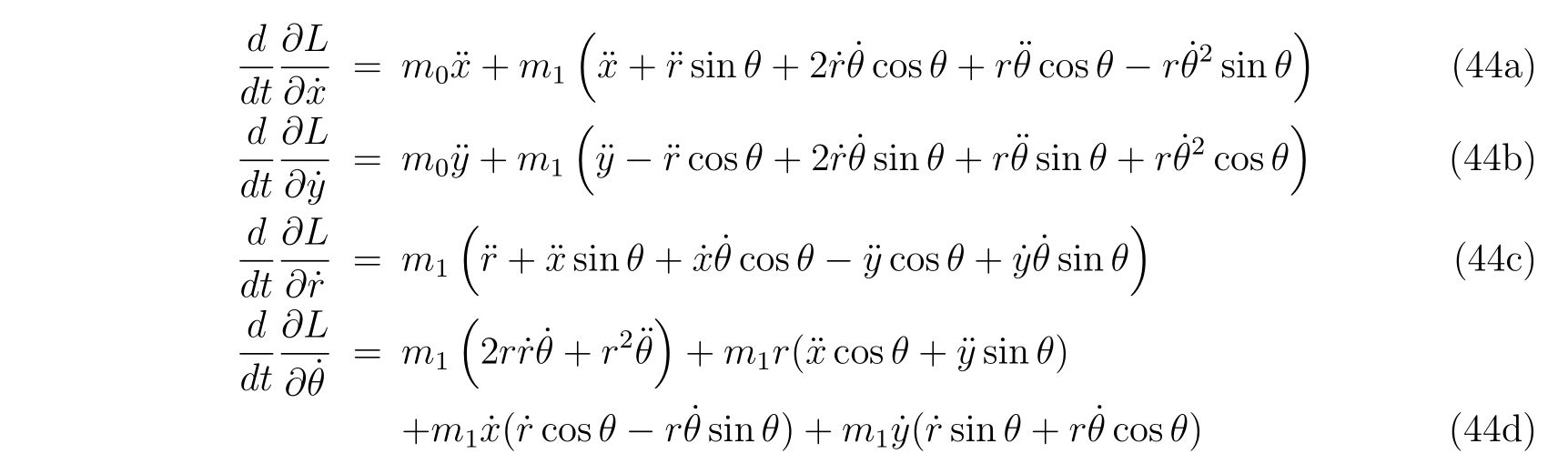
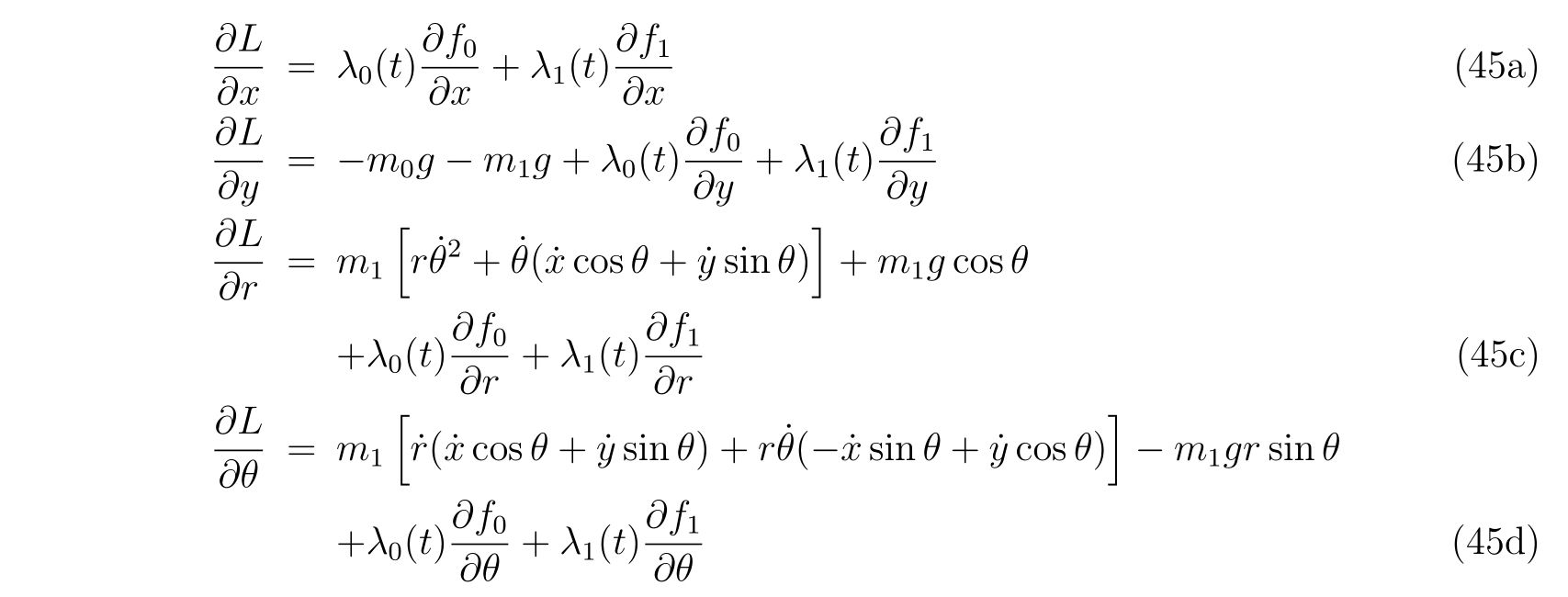
を用いると、運動方程式
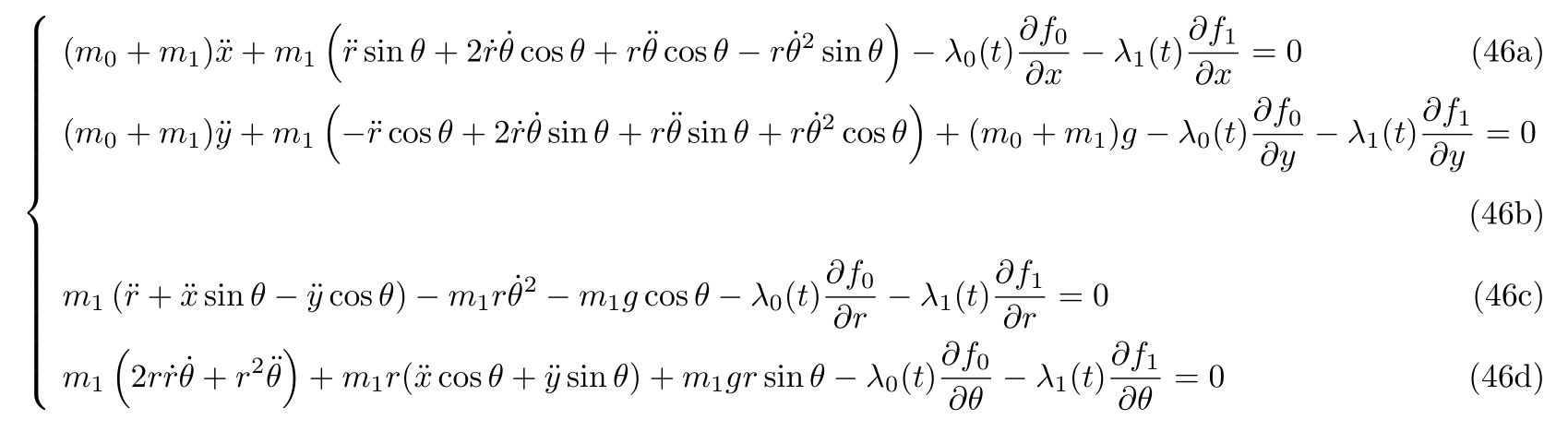
を得ます。
連立微分方程式(46)の4本の方程式と2本の束縛条件に対して、未知の関数は\(x(t), y(t), r(t), \theta(t), \lambda_0(t), \lambda_1(t)\)の6つなので、方程式を立ててそれぞれの関数を求めることが出来ます。
では、支点が直線状のレールの上に置かれている状況を考えましょう。
支点に関する束縛条件\(f_0\)と, 振り子の紐の長さが変わらないという束縛条件\(f_1\)を考えると
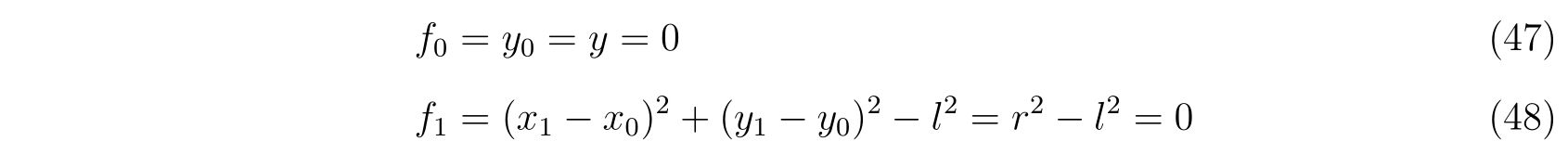
と書くことが出来ます。なので、
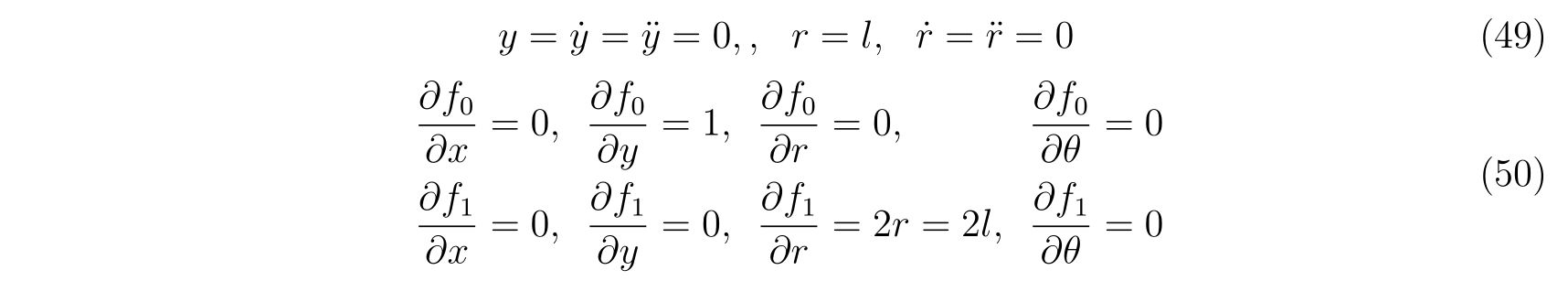
とそれぞれ計算できるので、運動方程式
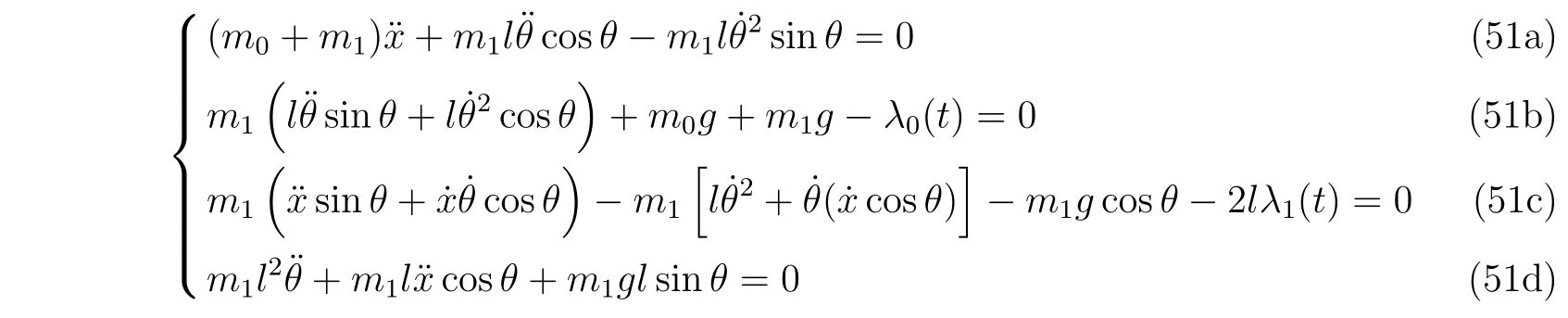
を得ます。求めたい未知の関数は\(x(t), \theta(t)\)です。
式(51a)と(51b)から、\(x(t), \theta(t)\)に関する運動方程式
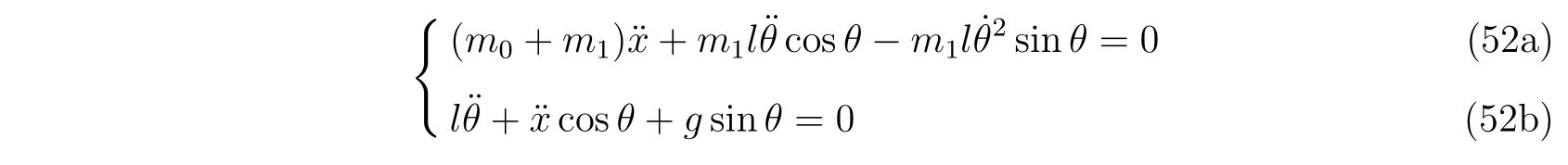
を得ます。変形すると
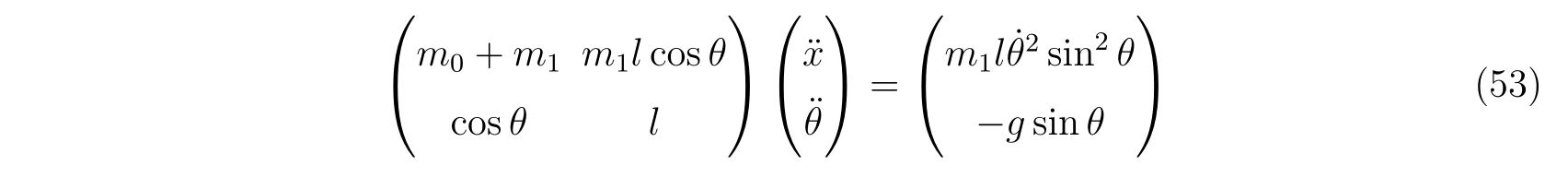
ですので、あらわに求めれば、
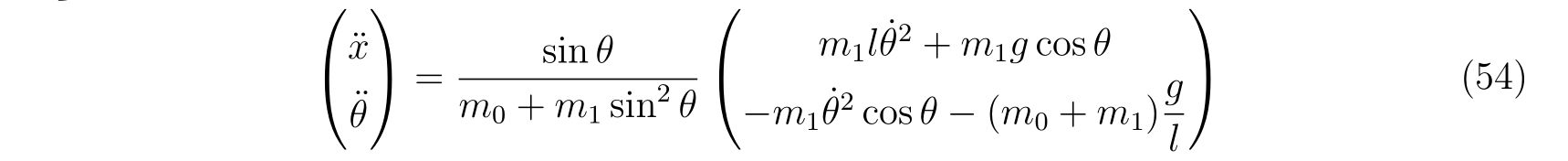
を得ます。
特に支点の質量が振り子の質量に比べて非常に重い場合、すなわち\(m_0 \gg m_1\)の場合、
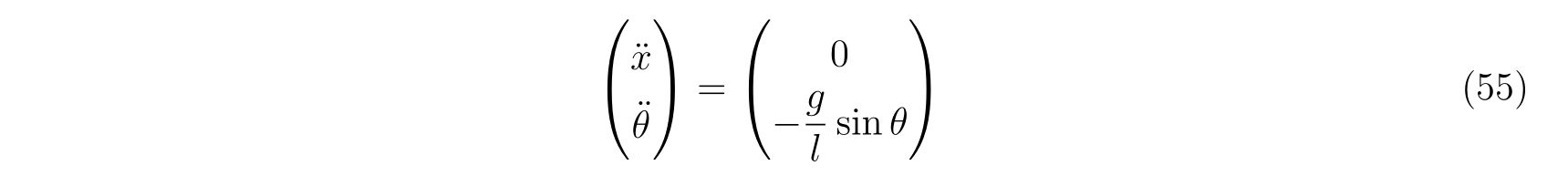
になります。第2式はまさに単振り子の方程式となっています。
・パラメータ
\(m_0=3, m_1=1, l=1, g=9.8\)
\(x(0)=0, x'(0)=0, \theta(0)=\frac{4\pi}{5}, \theta'(0)=0\)
・計算手法
陰的ルンゲクッタ法
支点が放物線上に束縛されている振り子

座標系は1つ前の問題と同じく、
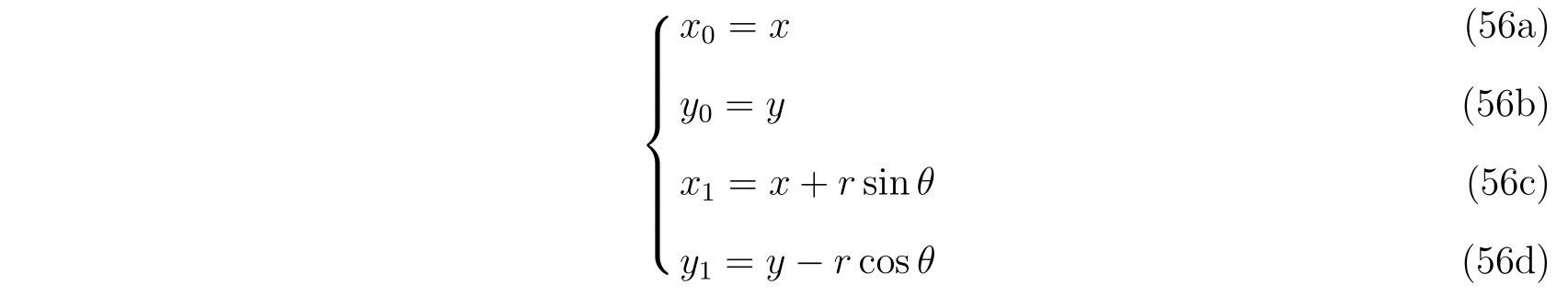
にとることにします。すると運動方程式は式(46)で表されるので、運動方程式の導出過程を省略することが出来ます。
問題設定から、束縛条件は

と書くことが出来ます。なので、それぞれの偏微分は
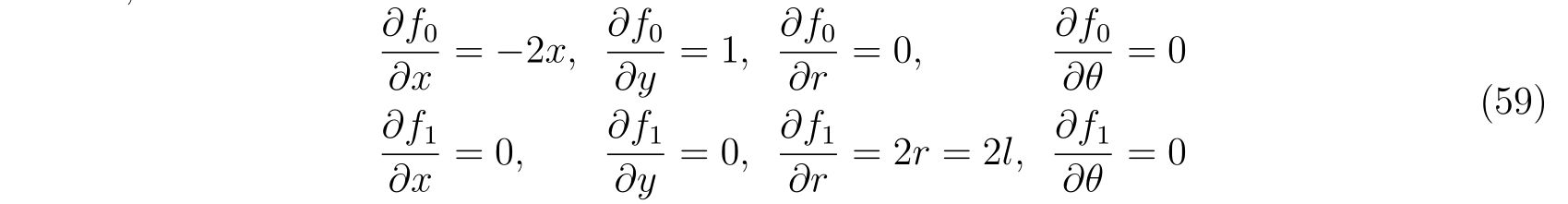
と書けますので、運動方程式は
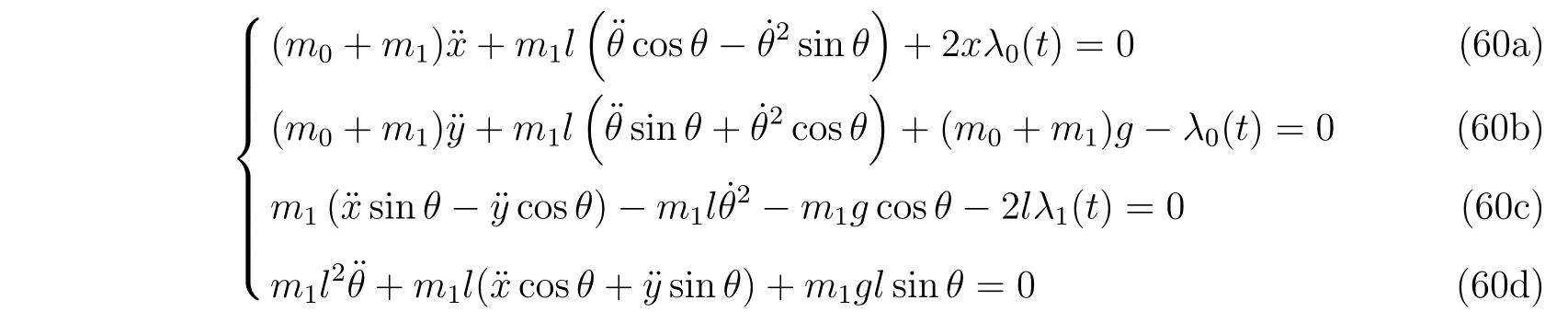
です。式(60a)と(60b)から\(\lambda_0(t)\)を消去すると、
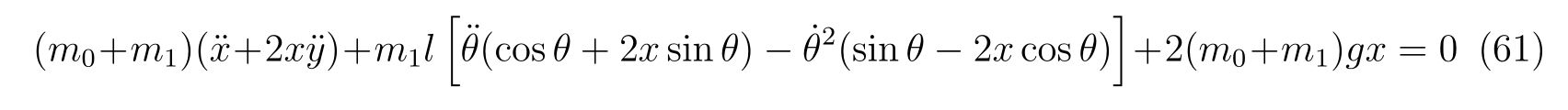
を得ます。更に、束縛条件から座標\(y(t)\)の時間変化は\(x(t)\)を用いて

と書くことが出来ます。式(61)と式(60d)から、\(x(t), \theta(t)\)の運動方程式
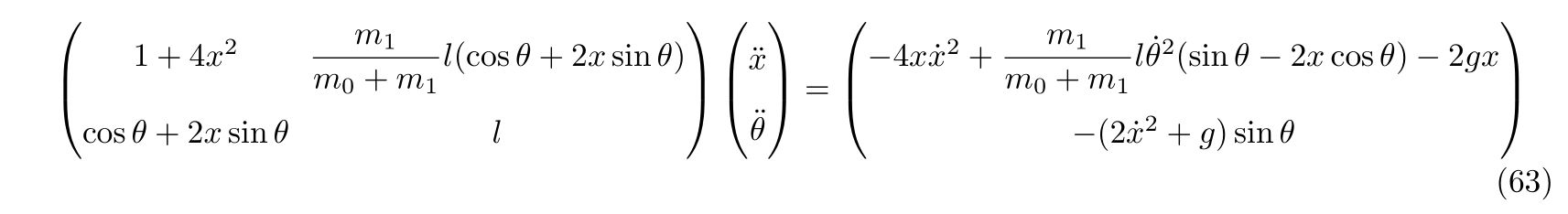
を得ます。あらわに解くと式が長くなってしまうので、ここで止めておきます。
・パラメータ
\(m_0=3, m_1=1, l=1, g=9.8\)
\(x(0)=0, x'(0)=5, \theta(0)=0, \theta'(0)=0\)
・計算手法
陰的ルンゲクッタ法
単振り子と空気抵抗
束縛条件と、非保存力である空気抵抗が存在する場合を考えます
座標系は
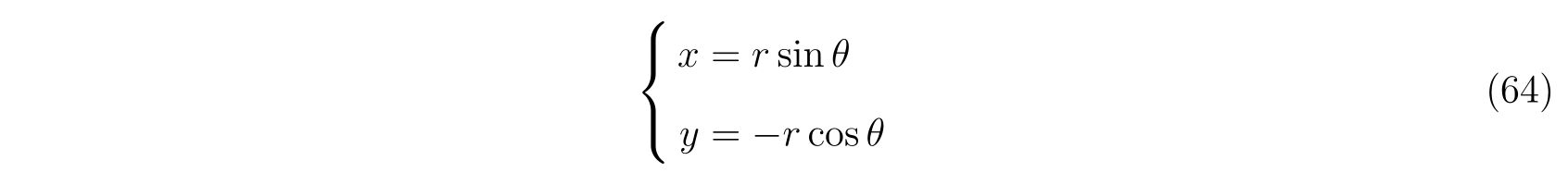
です。ホロノミックな束縛条件を含めたラグランジアンは、
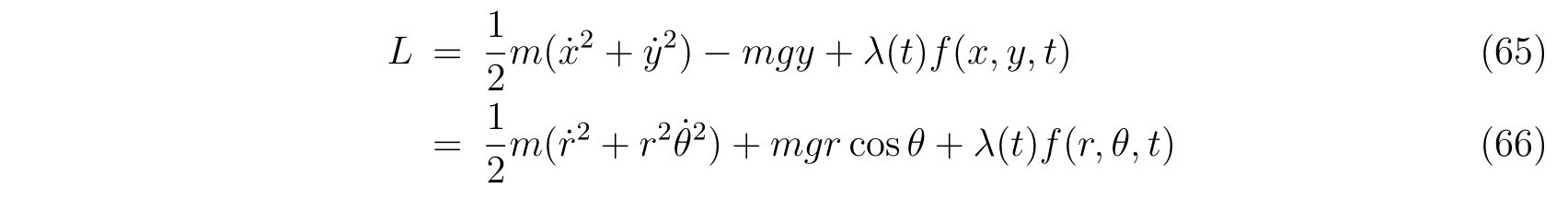
と書けます。
さて、非保存力である空気抵抗が存在することを考えましょう。
非保存力なのでラグランジアンで書くことは出来ませんので、個別に求める必要があります。
空気抵抗の力\(F_x, F_y\)はデカルト座標系において
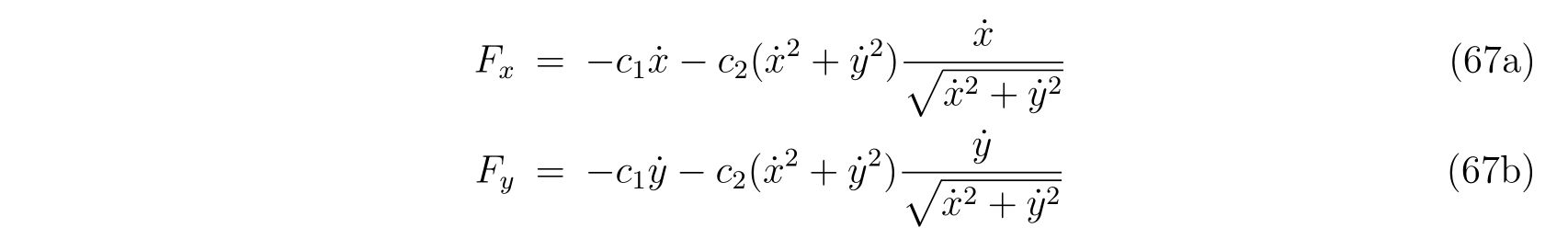
で掛ける事を既知とします。今知りたいことは、式(64)で表される一般化座標\(r, \theta\)で式(67)がどのように表されるのか?ということです。
\(r, \theta\)において、一般化座標における空気抵抗\(Q_x, Q_y\)は、
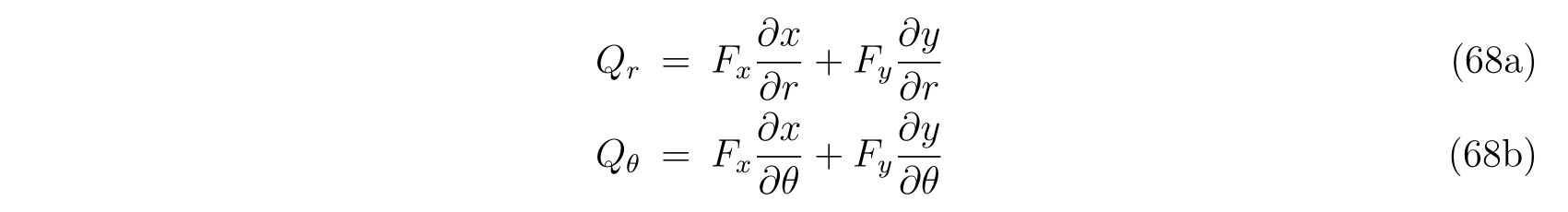 。
。
で変換することが出来ます。具体的にそれぞれの力を示せば、
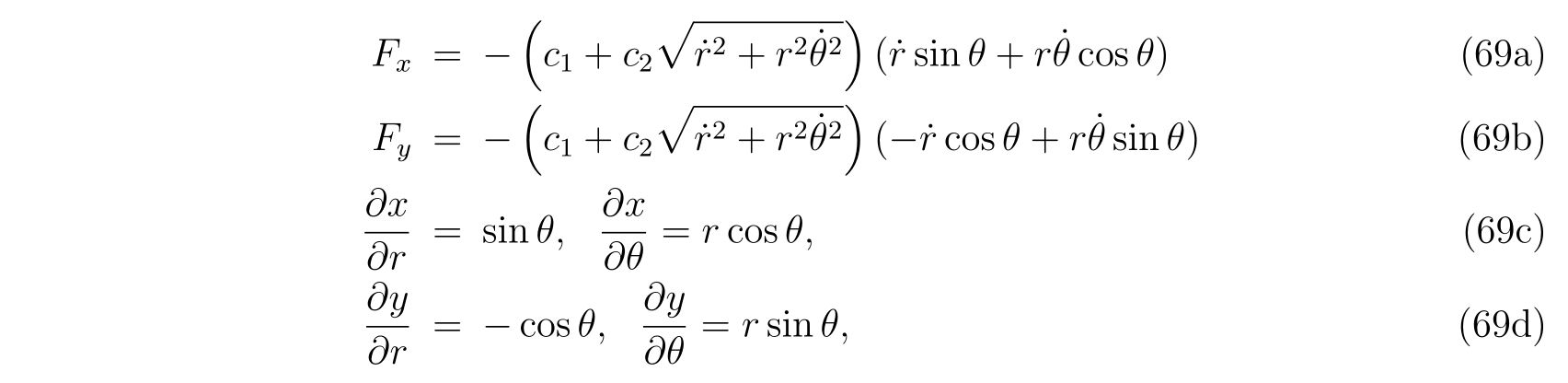
ですので\(Q_x, Q_y\)は、
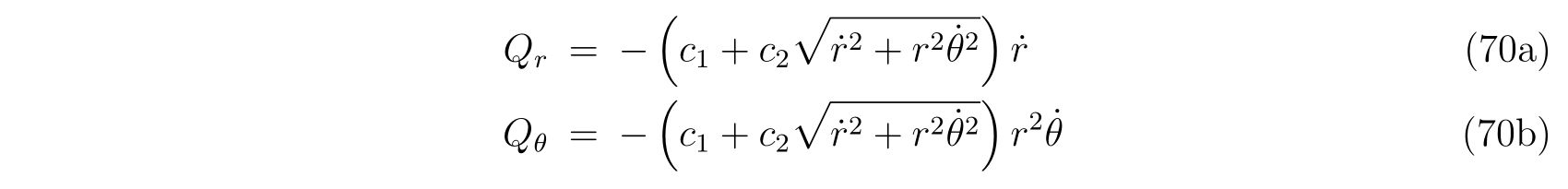
と表せられます。非保存力がある場合、ラグランジュの方程式の右辺にそれを入れれば良いので、
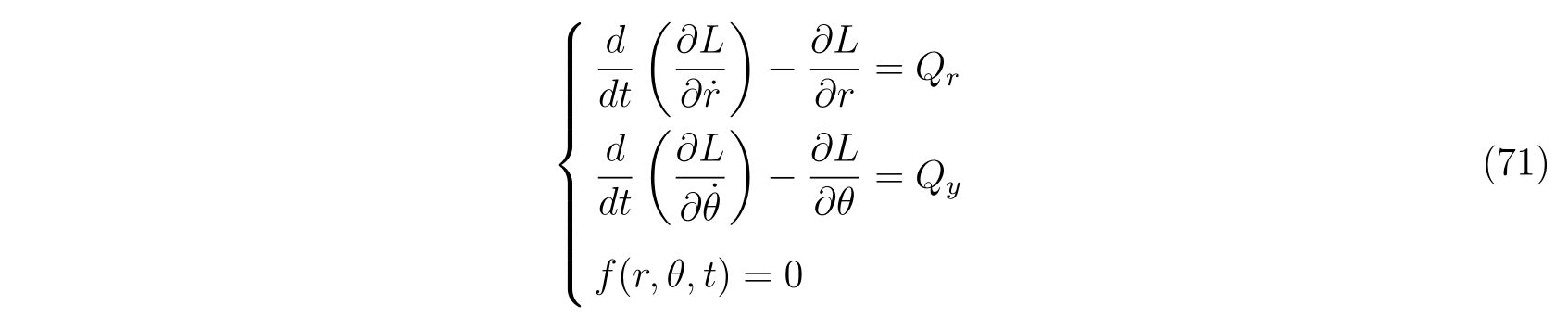
と表されます。よって運動方程式
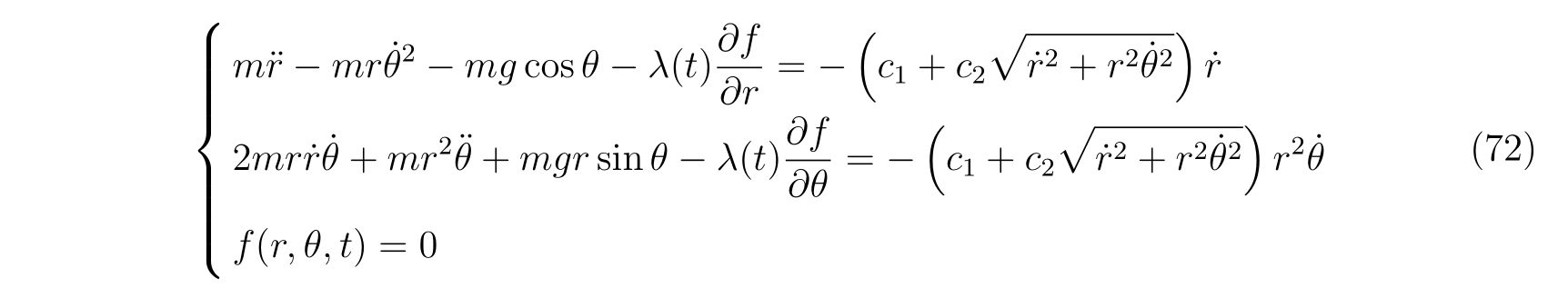
を得ます。
長さ\(l\)の伸び縮みしない紐に繋がれた振り子をを考えれば、束縛条件は
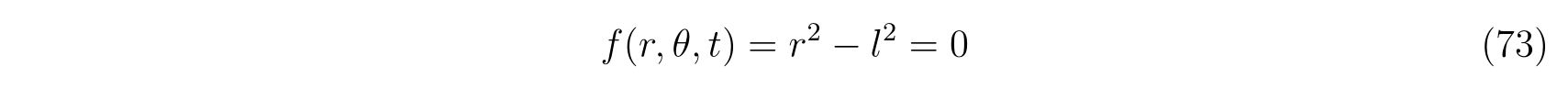
ですので、運動方程式
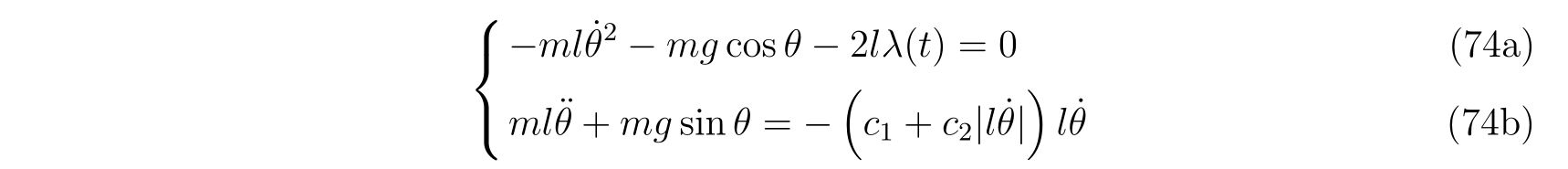
を得ます。
実際に解きますと
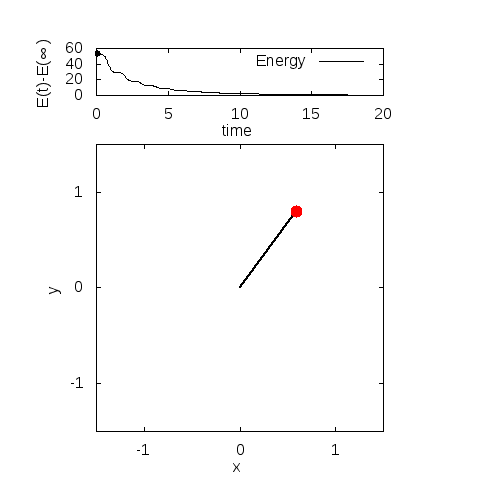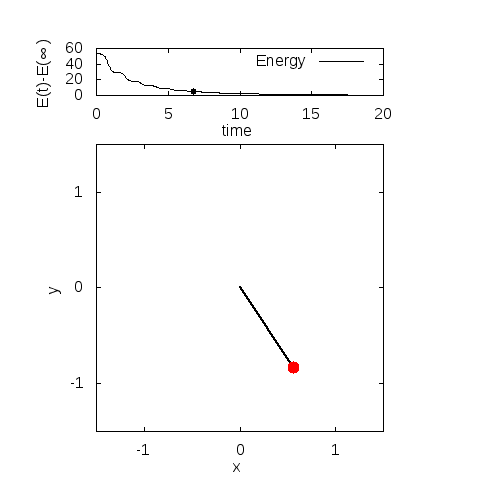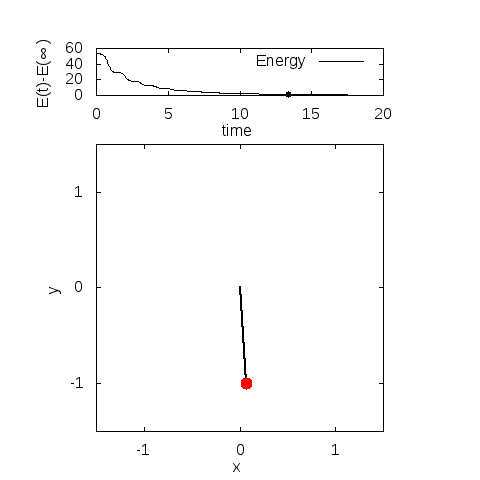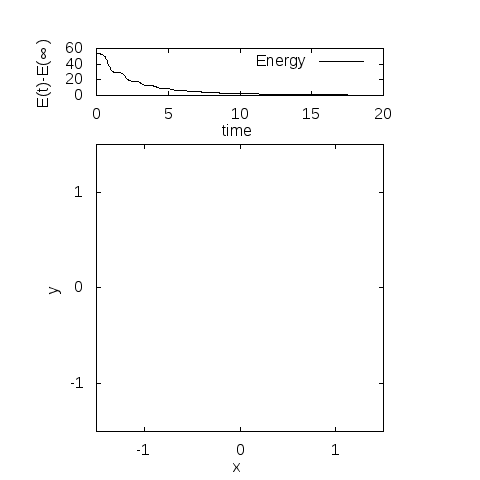
・パラメータ
\(m=3, l=1, g=9.8, c_1=0.3, c_2=0.3\)
\(\theta(0)=0.8\pi, \theta'(0)=0\)
・計算手法
陰的ルンゲクッタ法
このページはここで終わりです。
続いて、自由度がうまく落とせない、うまい座標系が見付からない場合を考えます。
次のリンク
束縛条件下の運動 – 自由度がうまく落とせない運動
参考文献
田辺行人、品田正樹著『理・工基礎 解析力学』 裳華房