本稿の主要な結果は、様々なパラメータでの、BB弾の軌道の詳細なデータです。
この結果に付随して、
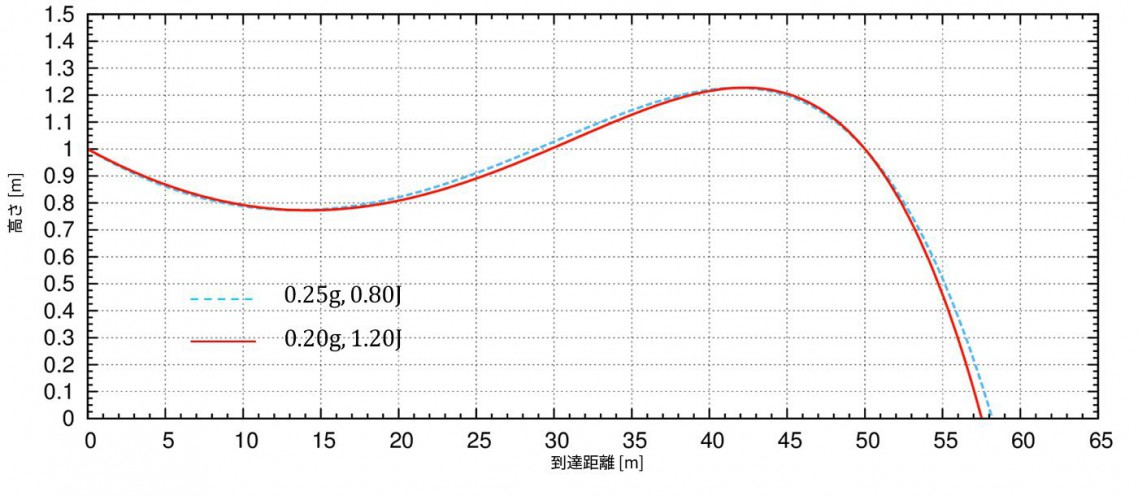
0.25gで0.8Jの軌道は
0.20gで1.2Jの軌道と同じであることが分かりました。
上下振れ幅が最小になる軌道における、重さとエネルギー、ゼロイン位置を様々にとった時のそれぞれのデータです。
弾道計算を数値計算によって行い、結果を考察することが本稿の目的となります。
※本稿では規定のエネルギーを超える場合のデータがありますが、このデータは全て数値シミュレーションであるため、こういったエアガンを持っている訳ではありません。
弾道計算に関するその他ページ
弾道計算(BB弾)の理論
BB弾の回転量について(実験との比較)
弾道計算(BB弾)の結果
弾道計算の結果2, 比較と詳細データ←今ここ
弾道計算(BB弾)のコード(fortran90)
バレル内部でのBB弾の方程式
水中下でのBB弾の弾道計算
様々なパラメータの最適な軌道
ここで載せるデータは、以下の組み合わせです。
BB弾の重さ: 0.20g , 0.25g
エネルギー:0.60J 0.65J 0.70J 0.75J 0.80J 0.85J 0.90J
ゼロイン位置:25m 30m 35m 40m 45m 50m 55m 60m(0.25gのみ)
各々でどのような軌道を描くかの計算結果を載せます。
破線はホップ無しの軌道に対応しています。
↓これは低画質です。高画質版はこのリンク(4.3MB)を踏んでください。
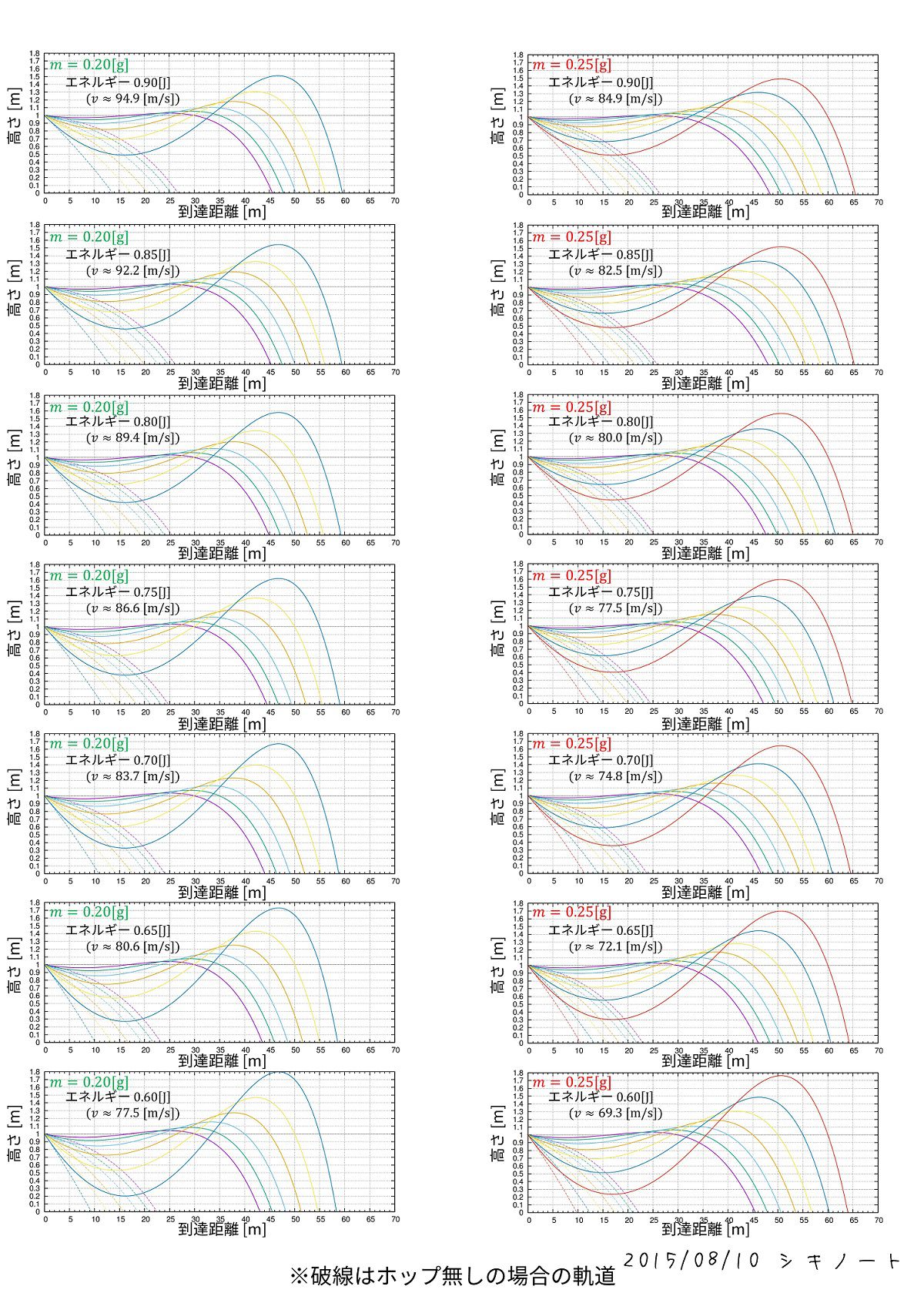
最適な軌道に合わせるためには下向きに初速を与えます。
その時、下向きに何度傾けて撃てばいいか、のデータはこちらです。
前提
まず、規定速度うんぬんは別にしまして、事実を述べます。
- BB弾は重いほど弾はまっすぐ飛ぶ
- 射出速度が早いほど弾はまっすぐ飛ぶ
- ホップを掛けるほど弾は上下に揺れる
これらは紛れもない事実です。
よって、BB弾を飛ばす最高の条件とは、
「射出速度を早くし、ホップは余りかけないで重いBB弾を使うこと」
となります。
だからこそ、射出速度を速めようとして規定速度の話になります。
最適な軌道とは?
BB弾を飛ばすうえで最適な軌道とはどんな軌道でしょう?
それはホップによる上下方向の揺れを最小限に抑える軌道です。
この最適な軌道とは、BB弾の重さとエネルギーとゼロイン位置を決めた時の理想的な軌道、ということです。
ゼロイン位置と上下の振れ幅とは何かは、下の画像をご覧ください。

重さとエネルギーを決めても、どの角度で射出すればいいか、回転数はいくつか、など他のパラメータが残ります。
それを決めるため、ホップによる上下方向の揺れを最小限に抑える軌道を定めます。
この軌道を ”最適な軌道” と呼ぶことにします。
重さの違いによる軌道の具体的な影響
今度は、ゼロイン位置を固定します。
そして、BB弾の重さとエネルギーを変化させたとき、どのような軌道をたどるか見てみましょう。
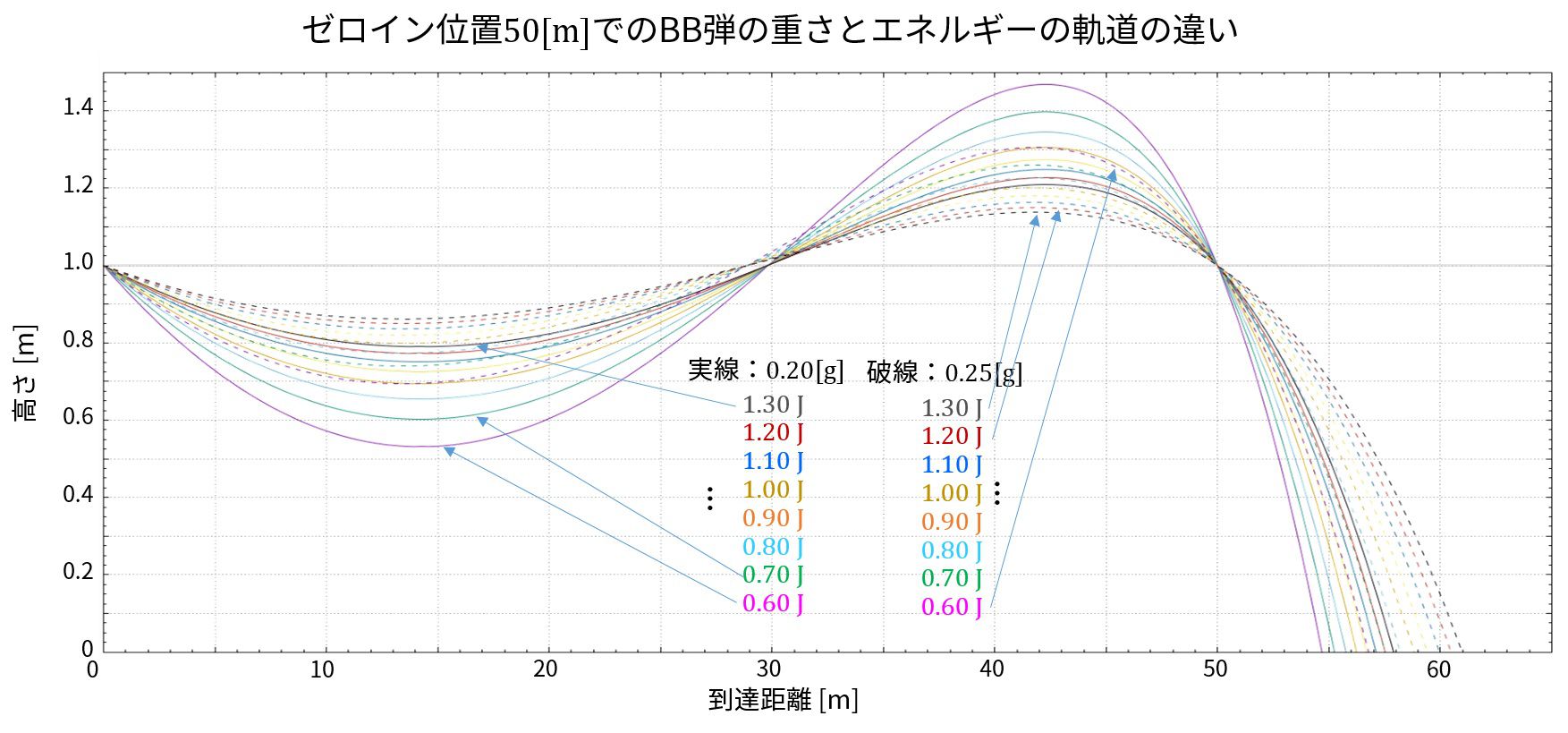
この結果から分かることは2点あります。
1つ目は、エネルギーを上げていくと軌道の変化が小さくなる
2つ目は、重いBB弾の軌道ほどまっすぐ飛ぶ
ということです。
エネルギーを上げると軌道の変化が小さくなる
0.20gの場合でゼロインを50mに合わせ、エネルギーを0.1Jずつ増やしていったとき、上下振れ幅がどのくらい減少していくのか見てみましょう。
0.60J→0.70J … 14.2cm
0.70J→0.80J … 10.4cm
0.80J→0.90J … 8.0cm
0.90J→1.00J … 6.2cm
1.00J→1.10J … 5.0cm
1.10J→1.20J … 4.2cm
1.20J→1.30J … 3.6cm
1.30J→1.40J … 3.0cm
となります。エネルギーを変えるよりも重さを変えるべきです。
それだけで軌道は大きく変わります。
例えば、0.80Jで射出できるエアガンで、使うBB弾を0.25gで射出すると、この時、軌道は0.20gの1.2Jの軌道にほぼ一致します。
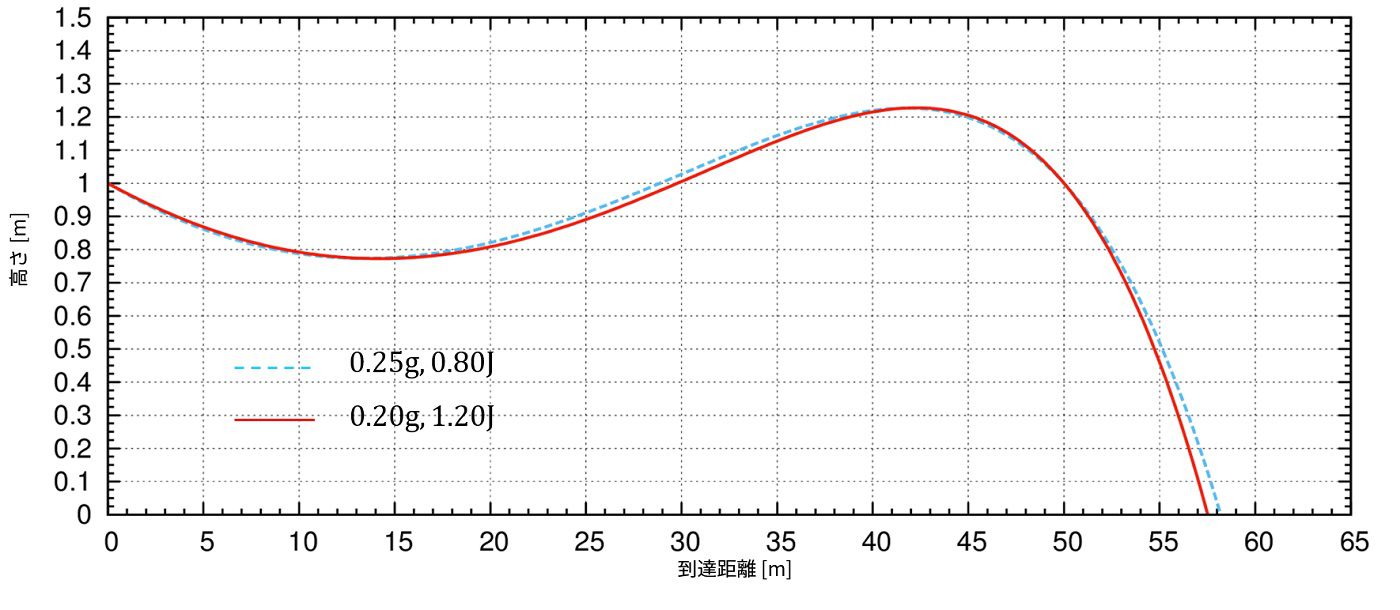
まぁ、軌道自体は一致するのですが、残念ながら到達時間は一致しません。
約0.1秒(まばたき程度)、0.20g1.2Jのほうが早くなります。
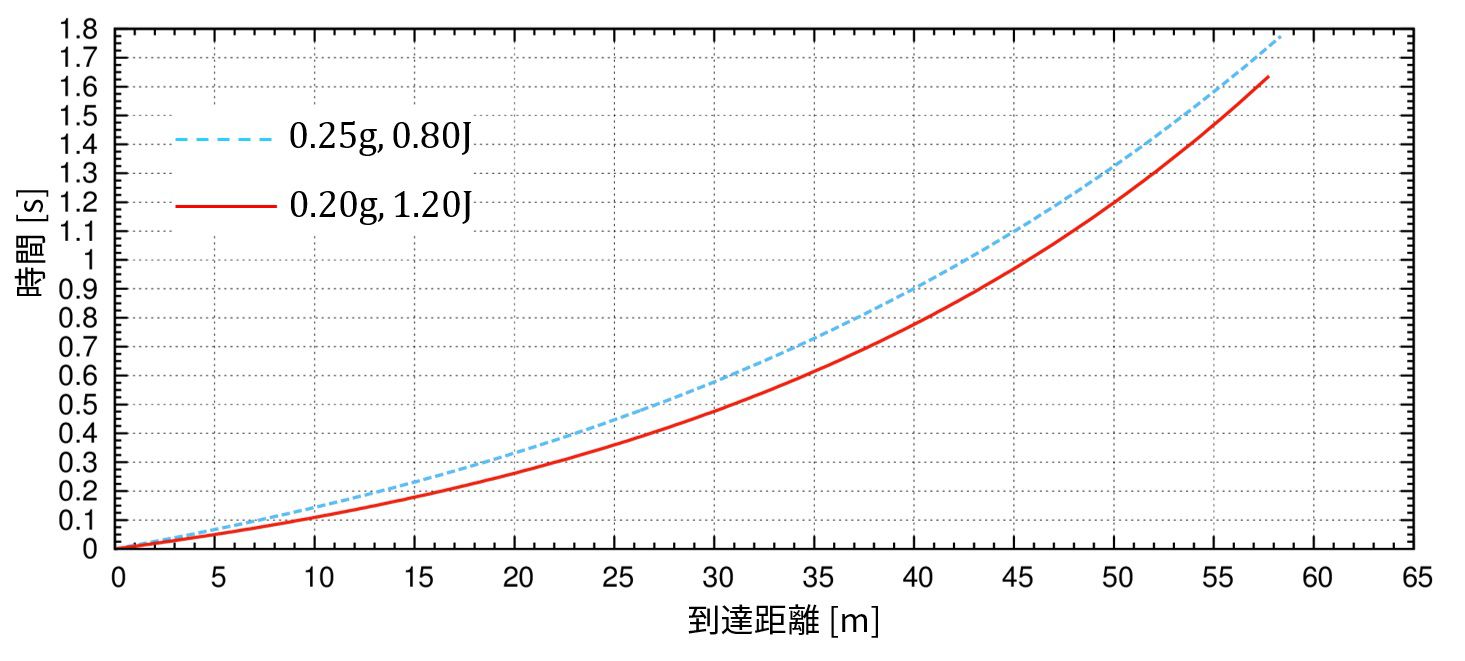
追記)
0.25gで0.90Jは、0.20gの1.35Jの軌道におおよそ相当します。
0.30gで0.80Jは、0.20gの1.60J, 0.25gの1.05Jの軌道におおよそ相当します。
0.30gで0.90Jは、0.20gの1.80J, 0.25gの1.20Jの軌道におおよそ相当します。
0.25gで0.8Jでうまく合わせられたら50m飛ばしても上下の振れ幅40cmです。
上に20cm、下に20cmしかずれません。
また、エネルギーを上げても空気抵抗の強さは速度の2乗に比例して強くなるため、それに見合うようなの飛距離の伸びは得られません。
補足
「流速チューン」というものがあるそうですね。
流速チューンの問題点と改善案について -週休5日
や
流速チューン比較テスト その1「初速変化」 -Gunsmithバトン
にあるように。
本稿ではこれらのことについては全く触れていません。
というのも、銃口から射出された直後の初速と回転数の2つだけが軌道に影響するためであり、発射するまでの過程に何があったか?などどうでもいいのです。
数値計算の観点から言いますと、通常の軌道よりも「まっすぐ遠くまで飛ぶ」場合、初速が上がっていること以外には考えられません。
BB弾を飛んでいる最中で加速させる要因など無いのです。
※1
なぜBB弾を使う限り初速を稼ぐことが無駄なのか?
これは空気抵抗が関係します。
空気抵抗の大きさは弾道計算(BB弾)の理論で書いたように、BB弾の半径\(R\)と速度\(v\)にのみ依存します。
空気抵抗力を半径\(R\)と速度\(v\)の関数として\(F_d(R,v)\)、質量\(m\)とすると、その運動方程式は
\(
m\frac{d^2\vec{r}}{dt^2}=F_d(R,v)
\)
であり、両辺をmで割れば
\(
\frac{d^2\vec{r}}{dt^2}=F_d(R,v)/m
\)
となります。BB弾の半径や、温度、空気は変えられないので、可変なパラメータは質量と速度のみです。
そして右辺だけに注目すれば、質量が大きいほど空気抵抗力があたかも小さくなるのです。
すなわち、空気抵抗力を減らそうとするにはBB弾の重さを変えるほかない。
また、初速を変えても空気抵抗は速度の2乗で効いてくるため、皮肉なことに速度が早いほど空気抵抗力が強くなっていくのです。
よって、高いエネルギーでは初速を上げてもそれに見合っただけの結果は得ることはできないのです。



初めまして。
詳しい解析に感嘆しております。
さて、かつての石岡さんの実験結果では、30m以降での軌跡にフゴイド運動と思わきし上下動が現れますが、この点について、ご意見をいただけますと幸いです。
HalQさん、初めまして。
お恥ずかしながら、フゴイド運動なるものを初めて聞きました。
wikipediaや他のサイトで簡単に調べたところ、
”準安定時に、進行方向に対して垂直方向に振動する運動”
と理解しました。
仰る通り、見返した所、30m以降に上下振動らしきものが観測できます。
私の意見は、この上下の振動はフゴイド運動ではない、です。
これは、銃口の向き、ターゲットの位置、微弱な風の流れによってたまたまそう見えているだけ、だと考えています。
フゴイド運動には準安定状態と復元力が必要です。フゴイド運動がはっきり表れる航空機では準安定状態に至るために必要な、揚力、推力、そして復元力として姿勢制御の機構が存在します。
この状態において、フゴイド運動が可視化できるほどの長い時間の準安定状態が持続するのだと思います。
一方、BB弾には回転による揚力は存在するものの、推力と復元力が存在しません。
もし無理矢理にフゴイド運動が起こっている、とみなすにしても長周期振動の1/4周期程度で、落ちていく球があがるような挙動は決して起こらないと考えます。
復元力として回転の角運動量が考えられるのでは?と思いますが、ホップアップの場合には保存する角運動量の方向が違うので関係ないでしょう。
以上が上下方向の振動がフゴイド運動ではない、とみる私の意見です。
もしも別の意味でのフゴイド運動でしたら、ご指摘くだされば幸いです。
シキノ
シキノさん、
返信ありがとうございます。
フゴイドは位置エネルギーと運動エネルギーの交換作用だと思います。
その前提で極めて単純に考えます。
ホップ弾道の頂点から落ち始めたとき、位置エネルギーと「前向き揚力」によって少し増速するのではないか。
ということです。
そして回復した弾速によってふたたび微小な揚力の回復をみる。
ということの反復がグラフの波として表れているように感じています。
こういう話を振っておいて申し訳ないのですが、自分自身では解析をしていないので、ただのヤマ勘です。
もし、位置エネルギーを考慮しての式をご検討済みでしたら、平謝りの次第です。
HalQさん
仰っていた現象が理解できました。
確かにBB弾が下がっていく時、揚力の方向を考えると上向きの力が働きます。
結論を言うと ”現実的な状況では起こらない” です。
実際に計算してみたのでこれを元に理解していきます。
ちなみに、全ての計算では揚力の向きはBB弾の速度によって変化していっていますので、HalQさんのおっしゃっている位置エネルギーと…の現象は再現されています。
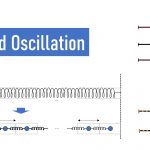
上図は、ある高さから回転を与え、速度0で放した時のBB弾の軌道です。
上:現実の状況、
中:回転が減衰しない
下:空気抵抗が無く、回転も減衰しない
の計算結果を表しています。
上)現実の状況では空気抵抗と回転の減衰によって急激に揚力が減少します。
そのため、BB弾を上、もしくは「前向き」に押し上げるほどの揚力を持つ間というのは撃ち出した直後のみです。それ以降は軌道を振動させるほどの力は無いのでしょう。
もし解析するならば数百m~数kmの長さで見ることが必要だと思います(中、下の結果を参照)。
中)回転が減衰しない状況では上)よりも揚力は減衰しにくいです。
その結果、一度頂点を迎えた後でもほんの多少軌道を振動させています。恐らく、HalQさんの仰っているのはこの現象でしょう。ただし、この後はものすごく長い距離が必要だと思います。
下)空気抵抗が無く、回転も減衰しない場合、BB弾は落ちません。
が、この状況は真空中でない限り起こりえないという点と、振動の周期が400m前後です。なので、100m程度のエアガンの距離では起こることはありません。
以上が私の答えです。貴重な意見ありがとうございます。こうやって調べないと何故フゴイド運動が起こらないのか?が答えられなかったですね。
シキノさん、
調べていただいてありがとうございます。
大変参考になります。
回転の減衰については、50m先とかでの回転数が判るといろいろ面白いですが、技術的に難しいですね…
私の認識が不明で理解できなかった一点だけ、教えていただけないでしょうか。
「上図は、ある高さから回転を与え、速度0で放した時のBB弾の軌道です。」
とありますが、初速0m/sでの軌道のプロット、ということでしょうか?
HalQさん
>初速0m/sでの軌道のプロット、ということでしょうか?
その通りです。回転の効果のみを見たかったのでそうしました。
知りたかったのは、ホップで上がり切った後の軌道だからです。
こんにちは。こんなに詳しく定量的な考察をしているWebサイトはなかなか見ないので、目から鱗でした。最近はAmazonなどで0.5g程度までの弾が買えますが、ここまで重くしても飛距離は伸びていくのでしょうか。予想ですと、重さに見合う回転数に設定すれば飛距離伸は伸びると思いますが、現実的に達成できなさそうな回転数が出てきそうな気がします。0.5gの0.9Jは0.2gの何Jの軌道にほぼ一致するか興味があります。一度是非記事にしていただけないでしょうか。
masahiroさん
こんにちは。コメントありがとうございます。
以前計算した時、約0.70gまでは理論上飛距離は伸びていきます。
詳細は本にまとめてあるので、更に詳しく知りたい場合はそちらにあります。
回転数に関しましては、おっしゃる通り、その回転数は実現できるのか?
が重要です。どこまで回転をかけれるかはエアガンに依ってしまうので、
私の方からコメントは出来ません。
また、0.50gの0.9Jの軌道は、0.20gのおおよそ3Jの軌道になりました。
早速のお返事ありがとうございます。面白そうなので本の方拝読させて頂きます。