こちらのページは後程消去いたします。

以下のページに統合しますので、ご参照ください。
https://slpr.sakura.ne.jp/qp/dft-for-numerical-calculation/

本ページにはミスもあり、上の方が正しいですのでご参照ください。

---

まとめ

---

離散フーリエ変換(Discrete Fourier Transform,DFT)を
\(
\begin{eqnarray}
\left\{
\begin{aligned}
f(\tilde{k}_n)&=\mathcal{F}[f(x)](\tilde{k}_n)=\sum_{m=0}^{N-1}f(x_m)e^{-i2\pi\tilde{k}_nx_m}\Delta x \\
f(x_m)&=\mathcal{F}^{-1}[f(\tilde{k})](x_m)=\sum_{n=0}^{N-1}f(\tilde{k}_n)e^{i2\pi\tilde{k}_nx_m}\Delta \tilde{k}
\end{aligned}
\right.
\end{eqnarray}
\)
と定義し、畳み込み(Convolution)を
\(
\displaystyle (f\ast g)(x_l)= \sum_{m} f(x_m) g(x_l-x_m) \Delta x
\)
と定義します。この時、畳み込みは上で定義した離散フーリエ変換を用いて以下の通り書けます。
\(
\displaystyle (f\ast g)(x_l)=\mathcal{F}^{-1}\left[\mathcal{F}[f(x)](\tilde{k})\cdot \mathcal{F}[g(x)](\tilde{k})\right](x_l)
\)

intel®マス・カーネル・ライブラリ(MKL)に実装されているフーリエ変換は
\(
\begin{eqnarray}
\left\{
\begin{aligned}
(-1)^n f(\tilde{k}_n)&=\sum_{m=0}^{N-1}f(x_m)e^{-i2\pi nm/N} \\
f(x_m)&=\sum_{n=0}^{N-1}(-1)^n f(\tilde{k}_n)e^{i2\pi nm/N}
\end{aligned}
\right.
\end{eqnarray}
\)
の形で定義されています。ここで、\(f(\tilde{k}_n)\)は、正しいフーリエ変換後の関数。計算したもの。この時、上で定義されている場合、畳み込みは、
\(
\displaystyle (f\ast g)(x_m)=\frac{\Delta x}{N}\mathcal{F}_{MKL}^{-1}\left[\mathcal{F}_{MKL}[f(x)]\cdot\mathcal{F}_{MKL}[g(x)] (-1)^n\right](x_m)
\)
で計算できます。ここで、\(N\)は離散フーリエ変換に用いた分点数、\(n\)は順方向フーリエ変換後の空間を離散化した時のインデックスです。

intel®MKLの離散フーリエ変換ルーチンを用いた畳み込みは、プログラムでは\(h(x)=(f\ast g)(x)\)とした時、

\(
\begin{align}
& Status = DftiComputeForward(hand,f) \\
& Status = DftiComputeForward(hand,g) \\
& h(\tilde{k}_n)=z(\tilde{k}_n)\times g(\tilde{k}_n)\times (-1)^n ~~~~~(\mbox{for all } k_n) \\
& Status = DftiComputebackward(hand,h) \\
& h(x_m)=h(x_m)\times \frac{\Delta x}{N} ~~~~~(\mbox{for all } x_m)\\
\end{align}
\)

とする必要があります。
※離散フーリエ変換はフーリエ変換の積分を短冊近似したものです。

[adsense1]

目次

---

1. フーリエ変換の定義
2. 離散フーリエ変換の定義
   • フーリエ変換が元に戻ることの証明
   • 離散フーリエ変換が元に戻ることの証明
3. たたみ込みの定義
4. 離散たたみ込みと離散フーリエ変換
   • フーリエ変換が元に戻ることの証明
   • 離散フーリエ変換が元に戻ることの証明
5. 数値計算で使われている離散フーリエ変換アルゴリズム (例: intel®MKL)
   • 離散フーリエ変換時の注意点とコード
   • フーリエ変換を介する畳み込み時の注意点とコード

フーリエ変換の定義

---

フーリエ変換の定義方法には複数の慣例があり、
数値計算分野、化学、音の解析等においては
\(
\begin{align}
f(\tilde{k})&=\int_{-\infty}^{\infty} f(x)e^{-i2\pi\tilde{k}x}dx \\
f(x)&=\int_{-\infty}^{\infty} f(\tilde{k})e^{i2\pi\tilde{k}x}d\tilde{k}
\end{align}
\)
の形で良く定義されます。
ここで、例えば\(x\)は位置[m]であれば\(\tilde{k}\)は波数[1/m]です。
また、\(x\)が時間[s]であれば\(\tilde{k}\)は周波数[1/s]です。

このページでは扱いませんが、物理科学の世界では
\(
\begin{align}
f(k)&=\int_{-\infty}^{\infty} f(x)e^{-ikx}dx \\
f(x)&=\int_{-\infty}^{\infty} f(k)e^{ikx}\frac{dk}{2\pi}
\end{align}
\)
の形で良く定義されます。
ここで、例えば\(x\)は位置[m]であれば\(k\)は角波数[1/m]です。
また、\(x\)が時間[s]であれば\(k\)は角周波数[1/s]です。

この２つの違いは周波数か、角周波数のどちらが本質であるか？という事だと思います。
物理では、周波数よりも角周波数の方が式が簡便になります。
ですが、人間の理解がしやすいのは1秒当たり何回振動するか？という周波数だろう、と思うため工学よりの分野では周波数が使われるのでしょう。もしかしたら、単に慣例だけかもしれません。

どちらも定数倍の変数変換の違いだけなので、本質は変わりません。
数値計算依りの話をしていきたいので、ここからは前者の位置⇔波数で考えていきます。

また、

順方向フーリエ変換：\(e^{-i2\pi\tilde{k}x}\)の因子が掛かっている式、空間→波数
逆方向フーリエ変換：\(e^{+i2\pi\tilde{k}x}\)の因子が掛かっている式、波数→空間

と呼び、
”関数\(f(x)\)の順方向フーリエ変換して波数\(\tilde{k}\)の空間に移る”
という操作を華文字\(\mathcal{F}\)を用いて
\(
\mathcal{F}[f(x)](\tilde{k})
\)
と表します。また、
”関数\(f(k)\)の逆方向フーリエ変換して位置\(x\)の空間に移る”
という操作を
\(
\mathcal{F}^{-1}[f(\tilde{k})](x)
\)
と表します。

離散フーリエ変換の定義

---

このページでは離散フーリエ変換を
\(
\begin{align}
f(\tilde{k}_n)&=\sum_{m=0}^{N-1}f(x_m)e^{-i2\pi\tilde{k}_nx_m}\Delta x \\
f(x_m)&=\sum_{n=0}^{N-1}f(\tilde{k}_n)e^{i2\pi\tilde{k}_nx_m}\Delta \tilde{k}
\end{align}
\)
と定義します。
\(\Delta x\), \(\Delta \tilde{k}\)は、それぞれ位置、波数空間の刻み幅を表します。

この上の定義は簡便さのために良く使われる
\(
\begin{align}
f(\tilde{k}_n)&=\frac{1}{N}\sum_{m=0}^{N-1}f(x_m)e^{-i2\pi\tilde{k}_nx_m} \\
f(x_m)&=\hspace{1.5em}\sum_{n=0}^{N-1}f(\tilde{k}_n)e^{i2\pi\tilde{k}_nx_m}
\end{align}
\)
という定義と同一です。
ただし、これは積分をそのまま離散化したものではないため、積分の意味は薄れてしまいます。
その結果、畳み込みなど、フーリエ変換後同士の物を掛け算する時は違った結果になってしまいます。
このページではこの簡便さの為の離散フーリエ変換は使いません。

上の２つの定義が同じ理由は、順方向→逆方向を行い、元に戻った時に係数が\(\Delta x\Delta \tilde{k}=\frac{1}{N}\)になるためです。

	\(x_m\)	\(\tilde{k}_n\)
添え字	\(m=0,1,2,\cdots,N-1\)	\(n=0,1,2,\cdots,N-1\)
区間	\(\displaystyle [a,b]\)	\(\displaystyle \left[-\frac{1}{2\Delta x},\frac{1}{2\Delta x}\right]\)
刻み幅	\(\displaystyle \Delta x=\frac{b-a}{N}\)	\(\displaystyle \Delta \tilde{k}=\frac{1}{b-a}\)
分点の位置	\(\displaystyle x_m=m\Delta x +a\)	\(\displaystyle \tilde{k}_n=n\Delta \tilde{k} -\frac{1}{2\Delta x}\)

ただし、\(x_m, \tilde{k}_n\)は以下の関係式を見たします。
\(
\begin{align}
& x_m+N\Delta x=x_m\\
& \tilde{k}_n+N\Delta \tilde{k}=\tilde{k}_n
\end{align}
\)

ナイキスト(Nyquist)周波数について

---

ナイキスト周波数とはサンプリングする間隔でどの周波数を持つ関数までを表現できるか？という下限と上限を与えます。
今回の場合、上の表の通り\(\tilde{k}\)空間で表現できる上限と下限は\(\pm\frac{1}{2\Delta x}\)です。この絶対値、すなわち\(\frac{1}{2\Delta x}\)をナイキスト周波数と呼びます。

ナイキスト周波数が意味しているのは、高周波の成分を取り出したければサンプリングする間隔を小さくしなければならない。ということです。”サンプリングの間隔”は周波数と同じ意味ですので、サンプルする周波数を高くしなければならない。と言い換えることもできます。

具体例を上げましょう。

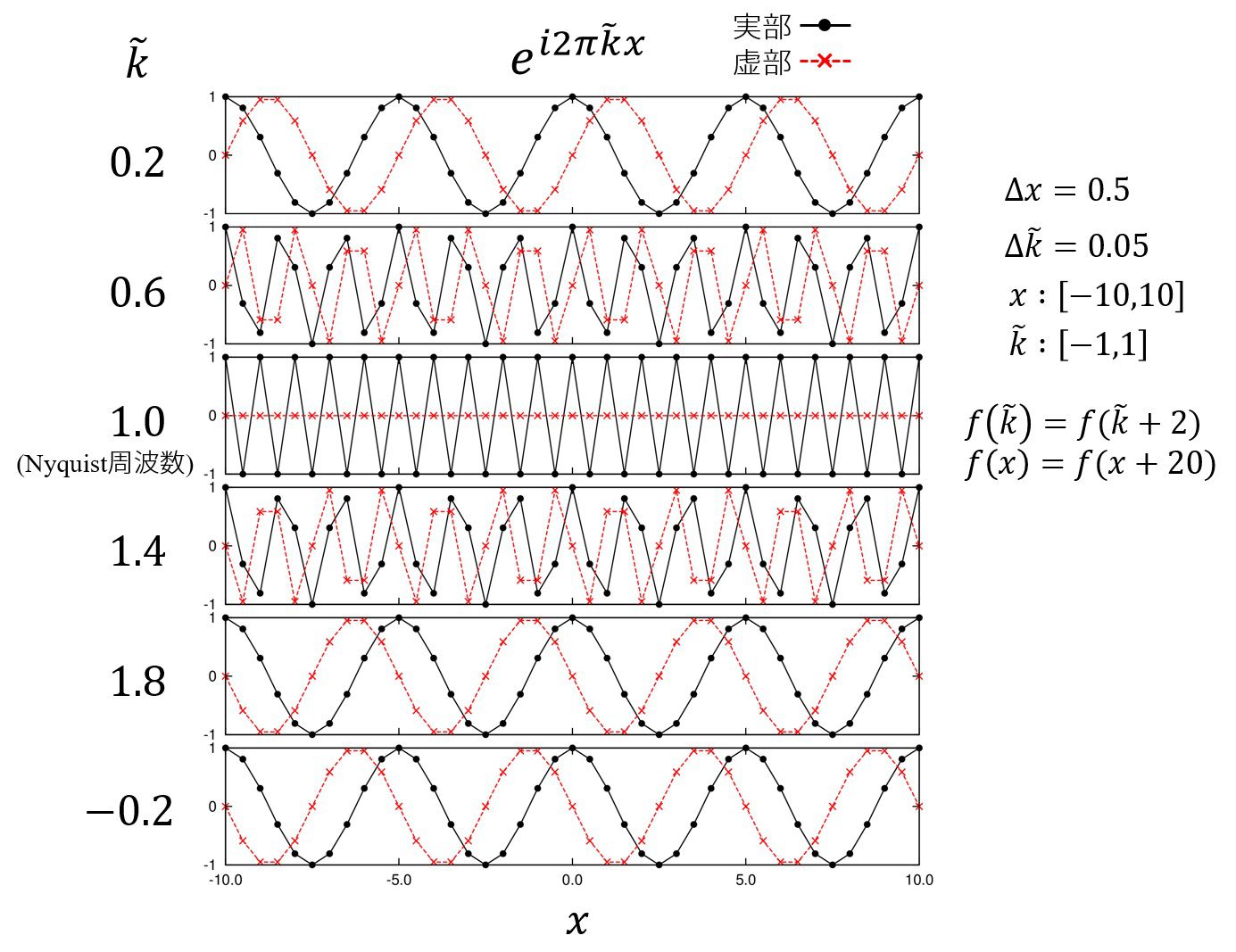
上の図は関数\(\displaystyle f(x)=e^{i2\pi \tilde{k}x}\)をサンプル間隔\(\Delta x = 0.5\)で離散的な関数で表現したものです。
この場合、ナイキスト周波数は\(\frac{1}{2\times 0.5}\)より、\(1\)です。
すなわち、このサンプル間隔では\(\tilde{k}\)が\([-1,1]\)の範囲を持つものしか表現することが出来ません。
では、実際にサンプル出来ない関数\(\displaystyle f(x)=e^{i2\pi 1.8 x},~~(\tilde{k}=1.8)\)を考えた時に何が起こるのでしょうか。
それを示したのが下から2番目の関数です。
本来は早く振動する関数であるのに、あたかも非常にゆっくりとした関数だ、と捉えられてしまいます。しかも位相が反転しています。

これは、元々は\(e^{i\theta}\)の周期性によるものです。簡単な計算の通り、
\(
\begin{align}
e^{i(\theta+2\pi)}=e^{i\theta}e^{i2\pi}=e^{i\theta}
\end{align}
\)
となります。この周期性のために、\(\tilde{k}:[-1,1]\)の範囲でしか表現できない空間で、
その範囲外の\(\tilde{k}\)を表現しようとした時には、\(\tilde{k}\)空間の大きさ（…この場合は\(2\)）を足したり引いたりして\(\tilde{k}:[-1,1]\)の範囲に強制的に押し込まれます。
\(\tilde{k}=1.8\)の場合は、\(\tilde{k}=1.8-2=-0.2\)となります。
言葉で言えば、
\(\tilde{k}=1.8\)を持つ波形は\(\tilde{k}=-0.2\)を持つ波形としてとして表現される
ということです。

本来の関数を薄く描いて重ねたものが以下のものになります。

フーリエ変換が元に戻ることの証明

---

上記のフーリエ変換、離散フーリエ変換はある制限を課しています。
それは、
ある関数に順方向フーリエ変換を行い、続いて逆方向フーリエ変換を施した場合、元と同じ関数に戻っていて欲しい。
という要望です。
それは、以下のように証明できます。

フーリエ変換

\(
\begin{align}
f(x)&=\int_{-\infty}^{\infty}d\tilde{k} f(\tilde{k})e^{i2\pi\tilde{k}x} \\
&=\int_{-\infty}^{\infty}d\tilde{k} \left[\int_{-\infty}^{\infty}dx’ f(x’)e^{-i2\pi\tilde{k}x’}\right]e^{i2\pi\tilde{k}x} \\
&=\int_{-\infty}^{\infty}dx’ f(x’)\int_{-\infty}^{\infty}d\tilde{k}
e^{i2\pi\tilde{k}(x-x’)} \\
&=\int_{-\infty}^{\infty}dx’ f(x’)\delta(x-x’) \\
&=f(x)
\end{align}
\)

離散フーリエ変換

\(
\begin{align}
f(x_m)&=\sum_{n=0}^{N-1}f(\tilde{k}_n)e^{i2\pi\tilde{k}_nx_m}\Delta \tilde{k}\\
&=\sum_{n=0}^{N-1}\left[\sum_{m’=0}^{N-1}f(x_{m’})e^{-i2\pi\tilde{k}_nx_{m’}}\Delta x\right]e^{i2\pi\tilde{k}_nx_m}\Delta \tilde{k} \\
&=\Delta \tilde{k}\Delta x\sum_{m’=0}^{N-1}f(x_{m’})\sum_{n=0}^{N-1}e^{i2\pi\tilde{k}_n(x_m’-x_m)} \\
&=\frac{1}{N}\sum_{m’=0}^{N-1}f(x_{m’})\sum_{n=0}^{N-1}e^{i2\pi n (m’-m)/N +i2\pi(\theta_{m}-\theta_{m’})} \\
&=\frac{1}{N}\sum_{m’=0}^{N-1}f(x_{m’})e^{i2\pi(\theta_{m}-\theta_{m’})}N\delta_{m,m’} \\
&=f(x_m)
\end{align}
\)
ここで、
\(
\begin{align}
\tilde{k}_n x_{m}=\frac{nm}{N}+\frac{an}{N\Delta x}+\theta_{m} \\
\theta_{m}=-\frac{a}{2\Delta x}-\frac{m}{2}
\end{align}
\)
そして、等比級数の考えから、
\(
\begin{eqnarray}
\sum_{n=0}^{N-1}e^{i2\pi n a}=
\left\{
\begin{aligned}
&\frac{e^{i2\pi aN}-1}{e^{i2\pi a}-1}, \hspace{1em} ( a\ne 0) \\
& N, \hspace{4em} (a=0) \\
\end{aligned}
\right.
\end{eqnarray}
\)
という関係式を用いました。

畳み込み(convolution)の定義

---

このページでは、畳み込みを
\(
\displaystyle (f\ast g)(x)=\int f(\tau) g(x-\tau) d\tau
\)
という積分であると定義し、離散的な畳み込みを
\(
\displaystyle (f\ast g)(x_l)= \sum_{m} f(x_m) g(x_l-x_m) \Delta x
\)
と定義します。

畳み込みの定義には\(\Delta x\)が掛けられていないものが存在しますが、積分の意味が薄れてしまうため、離散フーリエ変換時と同様、このページでは\(\Delta x\)を掛けたものを畳み込み、と定義します。

区間\([a,b]\)で定義された離散的な畳み込みの場合、関数\(f(x),g(x)\)は区間が\([a,b]\)で決められている場合がほとんどです。
この場合、引数\(x_m-x_l\)が定義域内に収まらない場合が現れます。

定義域からはみ出てしまった場合は推定するしかありません。
推定の仕方によって
循環畳み込みと呼ばれる方法と直線畳み込みと呼ばれる方法が良くつかわれています。

循環畳み込みは領域に対して周期境界条件を課したもの、すなわち、上限bと下限aが繋がっていると考えます。
直線畳み込みは領域に対して固定端条件を課したもの、すなわち、[a,b]の範囲外の関数値はゼロと考えます。

問題に大きく依るので、どちらがいいかはありません。

離散畳み込みと離散フーリエ変換

---

離散畳み込みは定義通り
\(
\displaystyle (f\ast g)(x_l)= \sum_{m} f(x_m) g(x_l-x_m) \Delta x
\)
で計算することが出来ます。計算量は\(O(n^2)\)です。

しかし、実用上は離散フーリエ変換を利用すると計算量を\(O(n\log n)\)に抑えられます。
計算方法はたたみ込み定理を利用して、
\(
\displaystyle \mathcal{F}[(f\ast g)(x)](k)=\mathcal{F}[f(x)](k)\cdot \mathcal{F}[g(x)](k)
\)
より、\((f\ast g)(x)\)は
\(
\displaystyle (f\ast g)(x)=\mathcal{F}^{-1}\left[\mathcal{F}[f(x)](k)\cdot \mathcal{F}[g(x)](k)\right]
\)
と書けるため、フーリエ変換を介することで計算量を減らせます。
離散フーリエ変換を介して畳み込みを計算する場合、必ず循環畳み込みで計算することになります。

畳み込み定理の証明

連続畳み込み

\(
\displaystyle \mathcal{F}[(f\ast g)(x)](k)=\mathcal{F}[f(x)](k)\cdot \mathcal{F}[g(x)](k)
\)

左辺）
\(
\begin{align}
\mathcal{F}[(f\ast g)(x)](\tilde{k})
&=\int \left[\int f(\tau)g(x-\tau) d\tau\right] e^{-i2\pi \tilde{k} x} dx \\
& x-\tau=y\mbox{の変数変換を行って} \nonumber \\
&=\int dy\int d\tau f(\tau)g(y) e^{-i2\pi \tilde{k} (\tau+y)} \\
&=\int dx\int dx’ f(x)g(x’) e^{-i2\pi \tilde{k} (x+x’)}
\end{align}
\)

右辺）
\(
\begin{align}
\mathcal{F}[f(x)](\tilde{k})\cdot \mathcal{F}[g(x)](\tilde{k})
&=\int f(x) e^{-i2\pi \tilde{k} x} dx \cdot \int g(x’) e^{-i2\pi \tilde{k} x’} dx’ \\
&=\int dx\int dx’ f(x)g(x’) e^{-i2\pi \tilde{k} (x+x’)}
\end{align}
\)
より、証明終了。また、逆変換により戻ることを示します。
\(
\begin{align}
&\mathcal{F}^{-1}\left[\mathcal{F}[f(x)](\tilde{k})\cdot \mathcal{F}[g(x)](\tilde{k})\right] \\
&=\int \left[\int dx\int dx’ f(x)g(x’) e^{-i2\pi \tilde{k} (x+x’)}\right] e^{i2\pi \tilde{k} y} dk\\
&=\int dx\int dx’ f(x)g(x’) \int e^{-i2\pi \tilde{k} (x+x’-y)} dk\\
&=\int dx\int dx’ f(x)g(x’) \delta(x’-(y-x)) \\
&=\int dx f(x)g(y-x) \\
&=\int d\tau f(\tau)g(x-\tau) \\
\end{align}
\)
となり、フーリエ変換を介してたたみ込みが計算できることが示せました。

離散畳み込み

\(
\displaystyle \mathcal{F}[(f\ast g)](\tilde{k})=\mathcal{F}[f(x)](\tilde{k})\cdot \mathcal{F}[g(x)](\tilde{k})
\)

左辺）
\(
\begin{align}
\mathcal{F}[(f\ast g)(x)](\tilde{k}_n)
&=\mathcal{F}\left[\sum_{m=0}^{N-1}f(x_m)g(x-x_m)\Delta x\right] \\
&=\sum_{l=0}^{N-1}\left[\sum_{m=0}^{N-1}f(x_m)g(x_l-x_m)\Delta x\right]e^{i2\pi \tilde{k}_n x_l}\Delta x \\
&=(\Delta x)^2\sum_{l=0}^{N-1}\sum_{m=0}^{N-1}f(x_m)g(x_l-x_m) e^{i2\pi \tilde{k}_n x_l} \\
&\mbox{ここで、循環たたみ込みを想定し、}x_l-x_m=x_{m’}\mbox{となるように}x_{m’}\mbox{を決めると}\nonumber \\
&=(\Delta x)^2\sum_{m=0}^{N-1}\sum_{m’=0}^{N-1}f(x_m)g(x_{m’}) e^{i2\pi \tilde{k}_n (x_m+x_{m’})} \\
\end{align}
\)

右辺）
\(
\begin{align}
\mathcal{F}[(f(x)](k_n)\cdot \mathcal{F}[(g(x)](k_n)
&=\sum_{m=0}^{N-1}f(x_m) e^{i2\pi \tilde{k}_n (x_m)}\Delta x\cdot \sum_{m’=0}^{N-1}f(x_{m’}) e^{i2\pi \tilde{k}_n (x_{m’})}\Delta x \\
&=(\Delta x)^2\sum_{m=0}^{N-1}\sum_{m’=0}^{N-1}f(x_m)g(x_{m’}) e^{i2\pi \tilde{k}_n (x_m+x_{m’})}
\end{align}
\)
よって右辺と左辺が正しくなります。

逆変換によって離散畳み込みになることを示します。

\(
\begin{align}
\mathcal{F}^{-1}[\mathcal{F}[(f\ast g)(x)](k)](x_l)
&=\mathcal{F}^{-1}\left[(\Delta x)^2\sum_{m=0}^{N-1}\sum_{m’=0}^{N-1}f(x_m)g(x_{m’}) e^{i2\pi \tilde{k}_n (x_m+x_{m’})}\right]\\
&=\sum_{n=0}^{N-1}\left[(\Delta x)^2\sum_{m=0}^{N-1}\sum_{m’=0}^{N-1}f(x_m)g(x_{m’}) e^{i2\pi \tilde{k}_n (x_m+x_{m’})}\right]e^{-i2\pi \tilde{k}_n x_l}\Delta \tilde{k}\\
&=(\Delta x)^2 \Delta \tilde{k} \sum_{m=0}^{N-1}\sum_{m’=0}^{N-1} f(x_m)g(x_{m’})\sum_{n=0}^{N-1}e^{i2\pi \tilde{k}_n (x_m+x_{m’}-x_l)} \\
&=\frac{\Delta x}{N} \sum_{m=0}^{N-1}\sum_{m’=0}^{N-1} f(x_m)g(x_{m’})N\delta_{x_{m’},x_l-x_m} \\
&=\sum_{m=0}^{N-1}f(x_m)g(x_l-x_m)\Delta x \\
&=(f\ast g)(x_l)
\end{align}
\)

よって畳み込みの定理通りに戻るため、離散フーリエ変換を介して畳み込みの計算ができます。

※注意
\(\Delta x, \Delta \tilde{k}\)が掛けられていない方の離散フーリエ変換と畳み込みでは元に戻りません。畳み込みの計算時に係数倍違って出てきます。

数値計算で使われている離散フーリエ変換アルゴリズム (例: intel®MKL)

---

数値計算では、上記の離散フーリエ変換の形、指数の肩に\(\tilde{k},x\)を含む物はあまり使われません。
そして、数値計算上での離散フーリエ変換の定義方法は複数存在します。
マニュアルを見てください。

ここでは、intel®マス・カーネル・ライブラリ(MKL)に使われている離散フーリエ変換アルゴリズムについて言及します。

MKLの変換はどうやら
\(
\begin{align}
(-1)^n f(\tilde{k}_n)&=\sum_{m=0}^{N-1}f(x_m)e^{-i2\pi nm/N} \\
f(x_m)&=\sum_{m=0}^{N-1}(-1)^n f(\tilde{k}_n)e^{i2\pi nm/N}
\end{align}
\)
という定義に従い変換しているようです。規格化因子\(\frac{1}{N}\)はユーザー任せです。
ここで、
\(f(\tilde{k}_n)\)は本来のフーリエ変換後の関数、
\(f(x)\)は\(x\)空間での関数
を表します。

”しているようです”と書いたのは、マニュアルと異なっているからです。マニュアルでは\((-1)^n\)など存在しませんが、実際試してみると、こういう変換をしているからです。

MKLではどういう\(\tilde{k}\)を想定しているかを考えたところ、以下の状況のようです。

	\(x_m\)	\(\tilde{k}_n\)
添え字	\(m=0,1,2,\cdots,N-1\)	\(n=0,1,2,\cdots,N-1\)
区間	\(\displaystyle [-a,a]\)	\(\displaystyle \left[0,N\Delta \tilde{k}\right]\)
刻み幅	\(\displaystyle \Delta x=\frac{2a}{N}\)	\(\displaystyle \Delta \tilde{k}=\frac{1}{2a}\)
分点の位置	\( \begin{eqnarray} x_m=\left\{ \begin{aligned} & m\Delta x ~~~~(m=0,\cdots,\frac{N}{2}-1) \\ & m\Delta x-\frac{1}{\Delta \tilde{k}} (m=\frac{N}{2},\cdots,N-1) \end{aligned} \right. \end{eqnarray} \)	\(\displaystyle \tilde{k}_n=n\Delta \tilde{k} ~~~~(n=0,\cdots,N-1)\)

ただし、\(x_m, \tilde{k}_n\)は以下の周期境界条件を見たします。
\(
\begin{align}
& x_m+N\Delta x=x_m\\
& \tilde{k}_n+N\Delta \tilde{k}=\tilde{k}_n
\end{align}
\)

区間[-a,a]で定義された\(x_m\)の順番がおかしく感じますが、これは周期境界条件を用いて、
区間[0,2a]で定義された\(x_m=m\Delta x ~~~~(m=0,\cdots,N-1)\)
と見ても良いです。
なので、実用上どうやって関数\(f(x)\)を入れればよいか？に困ることは無いでしょう。
この上記離散フーリエ変換を考えると、上で提示したMKLの離散フーリエ変換が導くことが出来、プログラム上でも一致します。

MKLの離散フーリエ変換の導出）

離散フーリエ変換時の注意点

上に記した、余分な係数\((-1)^n\)のためにMKLを利用して求められた離散フーリエ変換の値は、本来のフーリエ変換後の関数と異なります。
具体的に例を示しましょう。

\(e^{-\alpha x^2}\)のフーリエ変換は
\(
\displaystyle \int_{-\infty}^{\infty} e^{-\alpha x^2}e^{-i2\pi\tilde{k} x}dx=\sqrt{\frac{\pi}{\alpha}}e^{-\pi^2\tilde{k}^2/\alpha}
\)
です。離散フーリエ変換を定義通り計算したものと、MKLを用いて離散フーリエ変換すると以下のようになります。
左から\(f(x), \mathcal{F}[f(x)](\tilde{k}),\mathcal{F}^{-1}[\mathcal{F}[f(x)]](x)\)になっています。

ここで、因子\((-1)^n\)のために交互に符号が変わっていることが分かるでしょう。
後でやりますが、このせいで畳み込みの計算をする際には気を付けなければなりません。

計算コードはこちら。

MKLのルーチンは優秀です。誤差が余りたまらないようです。
定義通り、愚直に作ったプログラムでは計算速度が遅いだけでなく、計算精度も悪くなります。
下の画像は、離散フーリエ変換→逆変換を複数回繰り返した時、元の関数とどれだけずれるかを表しています。

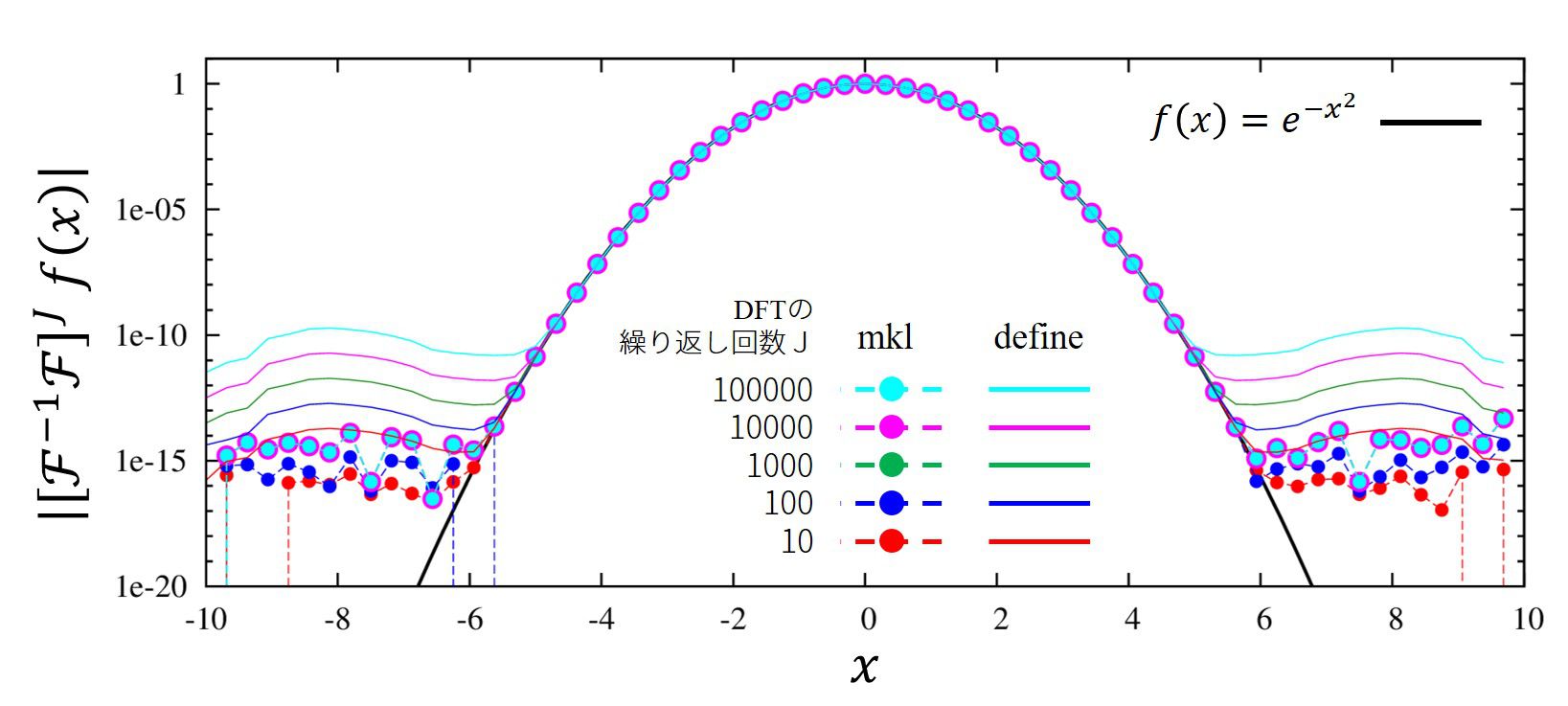
定義通りの離散フーリエ変換を\(10^n\)回繰り返すと\(n\)に対し線形にあがっていきます。この誤差は丸め誤差に起因しているのだと思います。しかし、MKLのルーチンには起こっていません。どういうアルゴリズムか知りませんが、優秀なのでしょう。

[adsense2]

フーリエ変換を介する畳み込み時の注意点

MKLの離散フーリエ変換ルーチンを使って畳み込みを計算します。
例として、以下の関数を考えましょう。
\(
\begin{align}
h(x)&=\int \tau^5 e^{-\tau^2}\cdot e^{-4(x-\tau)^2}d\tau \\
&=\frac{1}{3125}\sqrt{\frac{\pi}{5}}x(1024x^4+1600x^2+375)e^{-\frac{4}{5}x^2}
\end{align}
\)
ここで、
\(
\begin{align}
f(\tau)=\tau^5 e^{-\tau^2}
g(\tau)=e^{-4\tau^2}
\end{align}
\)
です。

このページで紹介した定義の畳み込みでは証明した通り、
\(
h(x_m)=\mathcal{F}^{-1}\left[\mathcal{F}[f(x)](\tilde{k})\cdot\mathcal{F}[g(x)](\tilde{k})\right](x_m)
\)
で計算できます。
しかし、MKLの離散フーリエ変換(\(\mbox{DFT}_{MKL}\))の場合は簡単にはできません。計算は、
\(
\displaystyle (f\ast g)(x_m)=\frac{\Delta x}{N}\mathcal{F}_{MKL}^{-1}[\mathcal{F}_{MKL}[f(x)]\cdot\mathcal{F}_{MKL}[g(x)] (-1)^n](x_m)
\)
としなければなりません。\((-1)^n\)は順方向フーリエ変換が2回あり、MKLの逆方向離散フーリエ変換に必要なこの係数が落ちてしまうため入れなければなりません。また、MKLのルーチンでは係数\(\Delta x, \Delta\tilde{k}\)を含んでいないので計算しておく必要があります。

intel®MKLを用いる際、
順方向離散フーリエ変換にはDftiComputeForward、
逆方向離散フーリエ変換にはDftiComputeBackward
を使うと、擬コードはこのように書けるかと思います。

\(
\begin{align}
& Status = DftiComputeForward(hand,f) \\
& Status = DftiComputeForward(hand,g) \\
& h(\tilde{k}_n)=z(\tilde{k}_n)\times g(\tilde{k}_n)\times (-1)^n ~~~~~(\mbox{for all } k_n) \\
& Status = DftiComputebackward(hand,h) \\
& h(x_m)=h(x_m)\times \frac{\Delta x}{N} ~~~~~(\mbox{for all } x_m)\\
\end{align}
\)

\(\displaystyle \Delta x \Delta\tilde{k}=\frac{1}{N}\)の関係を用いて最後にまとめて定数倍しています。

上の計算方法に従うと正しく畳み込みが計算出来ます。
実際にやってみますと、

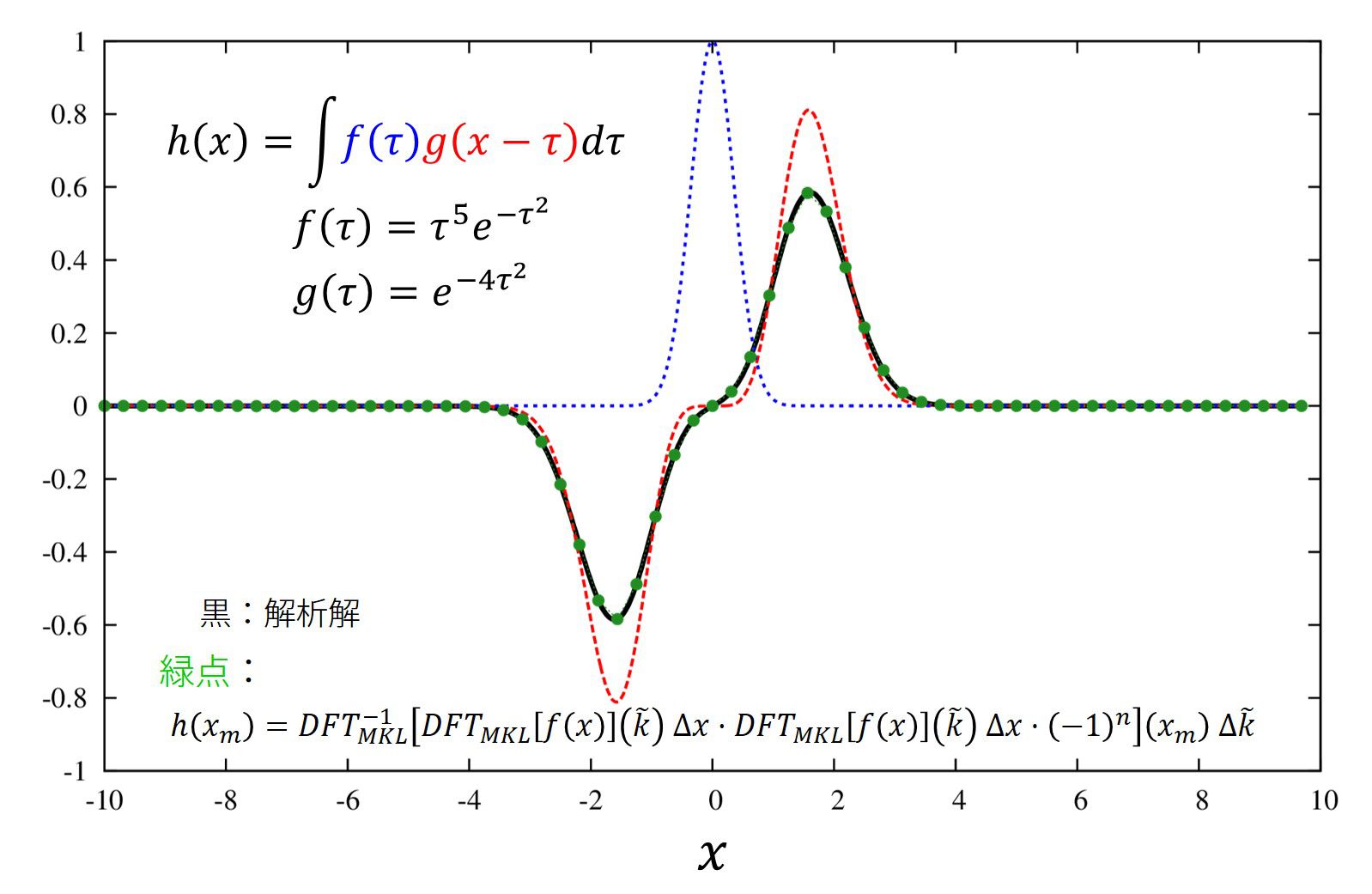
という結果を得ます。

畳み込みを計算するコードはこちら